Как посчитать объём в емкостях различных форм?
Содержание
- Объем шара
- Объем куба
- Объем пирамиды
- Объем параллелепипеда
- Объем правильного тетраэдра
- Объем конуса
- Объем призмы
- Как высчитать объем бочки в литрах?
- Как найти объем бочки по диаметру?
- Как узнать объём прямоугольной тары
- Как определить объём сферического изделия
- Как вычислить объём цистерны выполненной в виде цилиндра
- Как рассчитать объем цилиндра с помощью калькулятора
- Внутренний объем погонного метра трубы в литрах — таблица
- Расчет объема воды, находящейся во всей системе
- Способы перевода кубометров в другие кубические единицы
1 Объем шара
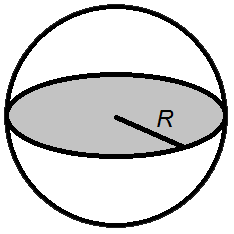
Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V — объем шара,
R — радиус шара,
π = 3.141592
к меню ↑
2 Объем куба
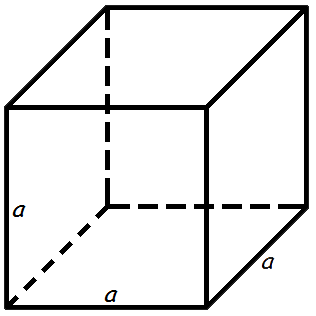
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3где V — объем куба,
a — длина грани куба
к меню ↑
3 Объем пирамиды
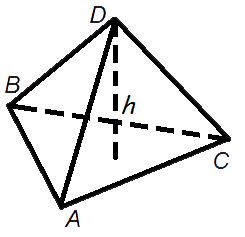
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V — объем пирамиды,
So — площадь основания пирамиды,
h — длина высоты пирамиды
к меню ↑
4 Объем параллелепипеда

Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · hгде V – объем параллелепипеда,
So – площадь основания,
h – длина высоты
к меню ↑
5 Объем правильного тетраэдра
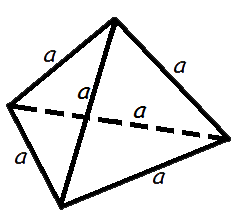
Формула объема правильного тетраэдра:
где V – объем правильного тетраэдра,
a – длина ребра правильного тетраэдра
к меню ↑
6 Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса:
где V – объем конуса,
So – площадь основания конуса,
R – радиус основания конуса,
h – высота конуса,
π = 3.141592.
к меню ↑
7 Объем призмы

Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So hгде V – объем призмы,
So – площадь основания призмы,
h – высота призмы
к меню ↑
8 Как высчитать объем бочки в литрах?
Теперь, когда мы знаем объем бочки в м.куб, можно перевести это значение в литры, а для этого использую соотношение: 1 куб. метр = 1000 литров.
Тогда, объем бочки в литрах будет равен:
0.31 м3 * 1000 литров = 310 литров
к меню ↑
9 Как найти объем бочки по диаметру?
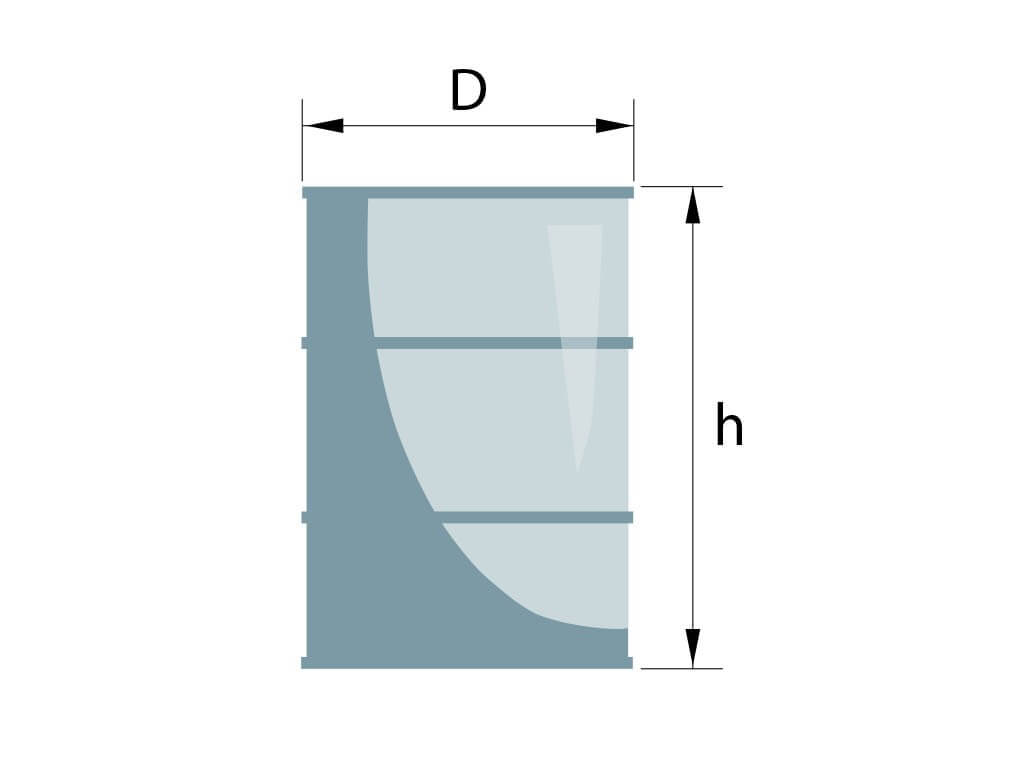
Для того, чтобы найти объем бочки по диаметру необходимо преобразовать стандартную формулу, по которой обычно находят объем цилиндра через радиус и высоту:
V = Пи * r² * h
Зная, что диаметр равен двум радиусам, получаем следующую формулу, которую можно применить для нахождения объема бочки в м3, по диаметру и высоте:
V = Пи * d²/4 * h
Все расчеты необходимо проводить в единой мере измерения длины, в нашем случае — это метры.
Для примера, необходимо найти объем цилиндрической бочки зная диаметр и высоту:
- D = 84 см — диаметр бочки;
- h = 56 см — высота бочки.
Подставляем данные в формулу, предварительно переведя см в метры:
V бочки в м3 = 3,14159 * (0,84 м)² / 4 * 0,56 м = 0,3103 м3
Если округлить, то получается, что объем цилиндрической бочки с размерами D = 84 см, h = 56 см = 0,31 м3
к меню ↑
10 Как узнать объём прямоугольной тары
В сфере строительства все показатели объёма приведены к конкретным величинам. Расчёты могут проводиться в литрах или дм 3 , но чаще всего для определения количества того или иного материала используются кубические метры. Как рассчитать кубатуру самых простых прямоугольных ёмкостей опишем дальше на конкретном примере.

Для работы нам понадобится тара, строительная рулетка и блокнот с ручкой или карандашом для проведения вычислений. Из курса геометрии известно, что объём подобных тел вычисляется умножением длины, ширины и высоты изделия. Формула расчётов сводится к следующему
V=a*b*c, где a, b и с – стороны тары.
Например, длина нашего изделия равняется 150 сантиметрам, ширина 80 сантиметрам, высота 50 сантиметров. Для правильного подсчёта кубатуры указанные величины переводим в метры и проводим необходимые расчёты V=1,5*0,8*0,5=0,6м3.
к меню ↑
11 Как определить объём сферического изделия
Сферические изделия встречаются в нашей жизни почти каждый день. Это может быть элемент подшипника, футбольный мяч или пишущая часть шариковой ручки. В некоторых случаях нам необходимо узнать, как рассчитать кубатуру сферы для определения количества жидкости в ней.
Как утверждают эксперты, для вычисления объёма этой фигуры используется формула V=4/3ԉr3, где:
- V – подсчитываемый объём детали;
- R- радиус сферы;
- ԉ – постоянная величина, которая равняется 3,14.
Для проведения необходимых вычислений нам нужно взять рулетку, зафиксировать начало измерительной шкалы и провести замер, причём лента рулетки должна проходить по экваторe шара. После этого узнают диаметр детали, поделив размер на число ԉ.
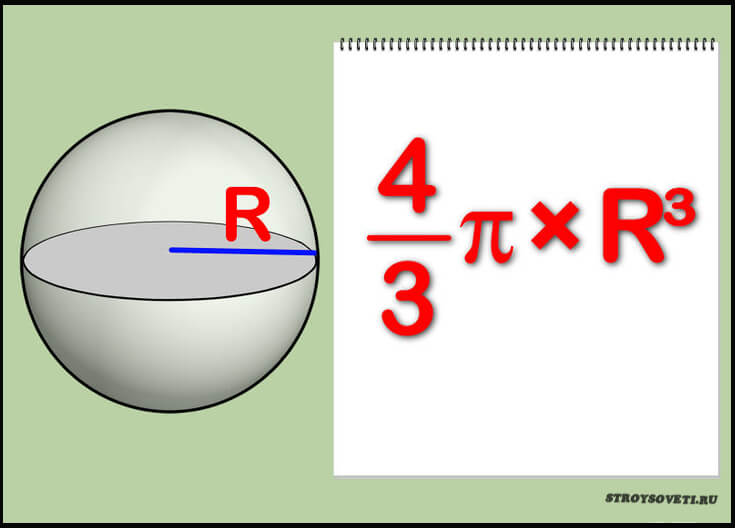
А теперь ознакомимся с конкретным примером вычисления для сферы, если её длина по окружности равняется 2,5 метрам. Сначала определим диаметр 2,5/3,14=0,8 метра. Теперь подставляем это значение в формулу:
к меню ↑
12 Как вычислить объём цистерны выполненной в виде цилиндра
Подобные геометрические фигуры используются для хранения пищевых продуктов, транспортирования топлива и других целей. Многие не знают, как рассчитать объем воды, но основные нюансы такого процесса опишем дальше в нашей статье.
Высоту жидкости в цилиндрической ёмкости определяют по специальному устройству метрштоку. В данном случае емкость цистерны вычисляется по специальным таблицам. Изделия со специальными таблицами измерения объёма в жизни встречаются редко, поэтому подойдём к решению проблемы другим путём и опишем, как рассчитать объём цилиндра по специальной формуле – V=S*L, где
- V- объём геометрического тела;
- S – площадь сечения изделия в конкретных единицах измерения (м³);
- L – длина цистерны.
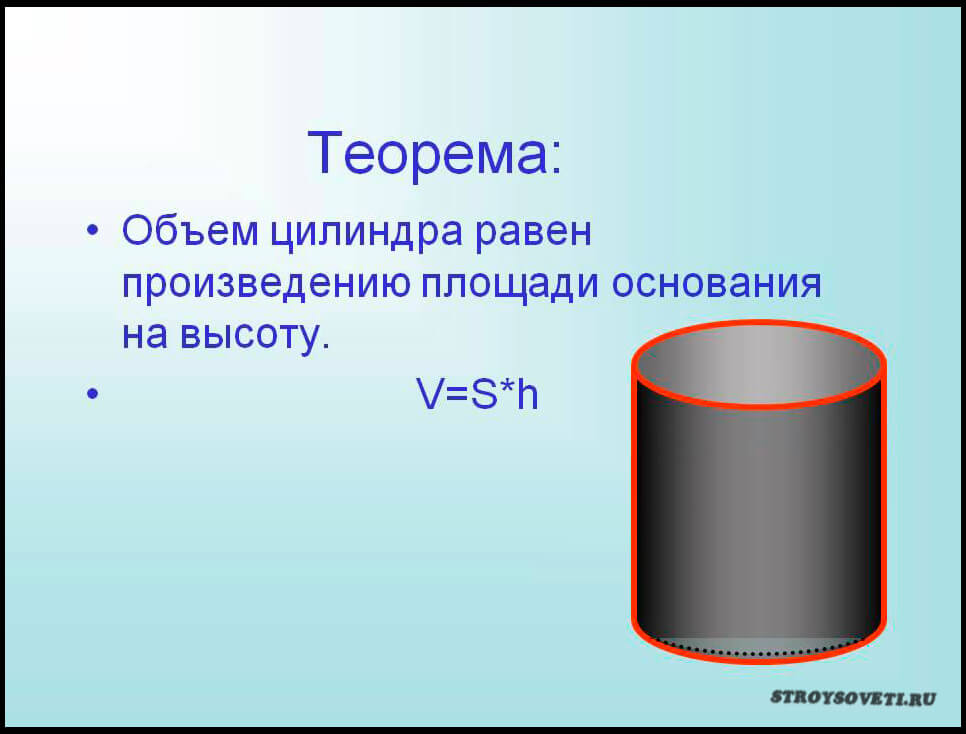
Показатель L можно измерить при помощи всё той же рулетки, но площадь сечения цилиндра придётся считать. Показатель S вычисляют по формуле S=3,14*d*d/4, где d – диаметр окружности цилиндра.
А теперь ознакомимся с конкретным примером. Допустим, длина нашей цистерны имеет значение 5 метров, её диаметр 2,8 метра. Сначала вычислим площадь сечения геометрической фигуры S= 3,14*2,8*2,8/4=6,15м. А теперь можно приступать к вычислению объёма цистерны 6,15*5= 30,75 м³.
к меню ↑
12.1 Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
к меню ↑
13 Внутренний объем погонного метра трубы в литрах — таблица
Таблица показывает внутренний объем погонного метра трубы в литрах. То есть сколько потребуется воды, антифриза или другой жидкости (теплоносителя), чтобы заполнить трубопровод. Взят внутренний диаметр труб от 4 до 1000 мм.
Внутренний диаметр,ммВнутренний объем 1 м погонного трубы, литровВнутренний объем 10 м погонных трубы, литров
| 4 | 0.0126 | 0.1257 |
| 5 | 0.0196 | 0.1963 |
| 6 | 0.0283 | 0.2827 |
| 7 | 0.0385 | 0.3848 |
| 8 | 0.0503 | 0.5027 |
| 9 | 0.0636 | 0.6362 |
| 10 | 0.0785 | 0.7854 |
| 11 | 0.095 | 0.9503 |
| 12 | 0.1131 | 1.131 |
| 13 | 0.1327 | 1.3273 |
| 14 | 0.1539 | 1.5394 |
| 15 | 0.1767 | 1.7671 |
| 16 | 0.2011 | 2.0106 |
| 17 | 0.227 | 2.2698 |
| 18 | 0.2545 | 2.5447 |
| 19 | 0.2835 | 2.8353 |
| 20 | 0.3142 | 3.1416 |
| 21 | 0.3464 | 3.4636 |
| 22 | 0.3801 | 3.8013 |
| 23 | 0.4155 | 4.1548 |
| 24 | 0.4524 | 4.5239 |
| 26 | 0.5309 | 5.3093 |
| 28 | 0.6158 | 6.1575 |
| 30 | 0.7069 | 7.0686 |
| 32 | 0.8042 | 8.0425 |
| 34 | 0.9079 | 9.0792 |
| 36 | 1.0179 | 10.1788 |
| 38 | 1.1341 | 11.3411 |
| 40 | 1.2566 | 12.5664 |
| 42 | 1.3854 | 13.8544 |
| 44 | 1.5205 | 15.2053 |
| 46 | 1.6619 | 16.619 |
| 48 | 1.8096 | 18.0956 |
| 50 | 1.9635 | 19.635 |
| 52 | 2.1237 | 21.2372 |
| 54 | 2.2902 | 22.9022 |
| 56 | 2.463 | 24.6301 |
| 58 | 2.6421 | 26.4208 |
| 60 | 2.8274 | 28.2743 |
| 62 | 3.0191 | 30.1907 |
| 64 | 3.217 | 32.1699 |
| 66 | 3.4212 | 34.2119 |
| 68 | 3.6317 | 36.3168 |
| 70 | 3.8485 | 38.4845 |
| 72 | 4.0715 | 40.715 |
| 74 | 4.3008 | 43.0084 |
| 76 | 4.5365 | 45.3646 |
| 78 | 4.7784 | 47.7836 |
| 80 | 5.0265 | 50.2655 |
| 82 | 5.281 | 52.8102 |
| 84 | 5.5418 | 55.4177 |
| 86 | 5.8088 | 58.088 |
| 88 | 6.0821 | 60.8212 |
| 90 | 6.3617 | 63.6173 |
| 92 | 6.6476 | 66.4761 |
| 94 | 6.9398 | 69.3978 |
| 96 | 7.2382 | 72.3823 |
| 98 | 7.543 | 75.4296 |
| 100 | 7.854 | 78.5398 |
| 105 | 8.659 | 86.5901 |
| 110 | 9.5033 | 95.0332 |
| 115 | 10.3869 | 103.8689 |
| 120 | 11.3097 | 113.0973 |
| 125 | 12.2718 | 122.7185 |
| 130 | 13.2732 | 132.7323 |
| 135 | 14.3139 | 143.1388 |
| 140 | 15.3938 | 153.938 |
| 145 | 16.513 | 165.13 |
| 150 | 17.6715 | 176.7146 |
| 160 | 20.1062 | 201.0619 |
| 170 | 22.698 | 226.9801 |
| 180 | 25.4469 | 254.469 |
| 190 | 28.3529 | 283.5287 |
| 200 | 31.4159 | 314.1593 |
| 210 | 34.6361 | 346.3606 |
| 220 | 38.0133 | 380.1327 |
| 230 | 41.5476 | 415.4756 |
| 240 | 45.2389 | 452.3893 |
| 250 | 49.0874 | 490.8739 |
| 260 | 53.0929 | 530.9292 |
| 270 | 57.2555 | 572.5553 |
| 280 | 61.5752 | 615.7522 |
| 290 | 66.052 | 660.5199 |
| 300 | 70.6858 | 706.8583 |
| 320 | 80.4248 | 804.2477 |
| 340 | 90.792 | 907.9203 |
| 360 | 101.7876 | 1017.876 |
| 380 | 113.4115 | 1134.1149 |
| 400 | 125.6637 | 1256.6371 |
| 420 | 138.5442 | 1385.4424 |
| 440 | 152.0531 | 1520.5308 |
| 460 | 166.1903 | 1661.9025 |
| 480 | 180.9557 | 1809.5574 |
| 500 | 196.3495 | 1963.4954 |
| 520 | 212.3717 | 2123.7166 |
| 540 | 229.0221 | 2290.221 |
| 560 | 246.3009 | 2463.0086 |
| 580 | 264.2079 | 2642.0794 |
| 600 | 282.7433 | 2827.4334 |
| 620 | 301.9071 | 3019.0705 |
| 640 | 321.6991 | 3216.9909 |
| 660 | 342.1194 | 3421.1944 |
| 680 | 363.1681 | 3631.6811 |
| 700 | 384.8451 | 3848.451 |
| 720 | 407.1504 | 4071.5041 |
| 740 | 430.084 | 4300.8403 |
| 760 | 453.646 | 4536.4598 |
| 780 | 477.8362 | 4778.3624 |
| 800 | 502.6548 | 5026.5482 |
| 820 | 528.1017 | 5281.0173 |
| 840 | 554.1769 | 5541.7694 |
| 860 | 580.8805 | 5808.8048 |
| 880 | 608.2123 | 6082.1234 |
| 900 | 636.1725 | 6361.7251 |
| 920 | 664.761 | 6647.6101 |
| 940 | 693.9778 | 6939.7782 |
| 960 | 723.8229 | 7238.2295 |
| 980 | 754.2964 | 7542.964 |
| 1000 | 785.3982 | 7853.9816 |
Если у вас специфическая конструкция или труба, то в формуле выше показано как вычислить точные данные для правильного расхода воды или иного теплоносителя.
к меню ↑
13.1 Расчет объема воды, находящейся во всей системе
Для определения такого параметра, необходимо в формулу подставить значение внутреннего радиуса. Однако сразу появляется проблема. А как рассчитать полный объем воды в трубе всей отопительной системы, в которую входят:
- Радиаторы;
- Расширительный бачок;
- Котел отопления.
Сначала рассчитывается объём радиатора. Для этого открывается его технический паспорт и выписывается значения объема одной секции. Этот параметр умножается на число секций в конкретной батарее. Например, одна секция чугунного радиатора равен 1,5 литрам.
Когда установлен биметаллический радиатор, это значение намного меньше. Количество воды в котле можно узнать из паспорта устройства.
Для определения объема расширительного бака, его заполняют измеренным заранее, количеством жидкости.
Очень просто определяется объём труб. Имеющиеся данные для одного метра, определенного диаметра, нужно просто умножить на длину всего трубопровода.
Заметим что в глобальной сети и справочной литературе, можно увидеть специальные таблицы. Они показывают ориентировочные данные изделия. Погрешность приведенных данных достаточно мала, поэтому приведенные в таблице значения, можно смело использовать для вычисления объема воды.
Надо сказать, что при расчете значений, нужно учитывать некоторые характерные отличия. Металлические трубы, имеющие большой диаметр, пропускают количество воды, значительно меньше, чем такие же полипропиленовые трубы.
Причина кроется в гладкости поверхности труб. У стальных изделий она выполнена с большой шероховатостью. ППР трубы не имеют шероховатости на внутренних стенках. Однако при этом стальные изделия имеют больший объем воды, чем в других трубах, одинакового сечения. Поэтому чтобы убедиться, что расчет объема воды в трубах произведен верно, нужно несколько раз перепроверить все данные и подкрепить результат онлайн-калькулятором.
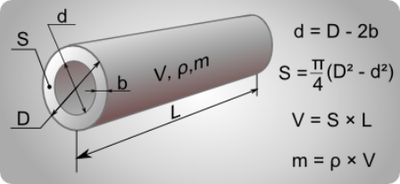
Формула определения площади сечения неполностью заполненных труб:
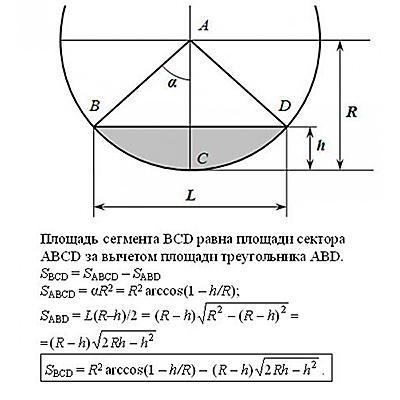
к меню ↑
14 Способы перевода кубометров в другие кубические единицы
Рассчитывая объемности, необходимо придерживаться одинаковых единиц замеров. Если данные представлены другими единицами, а конечный результат должен быть получен в кубах, то достаточно будет правильно сделать преобразование.
Если V измерен в мм3, см3, дм3, л, то в м3 переводим соответственно:
- 1 м3 = 1 мм3 х х 0, 000000001 = 1 мм3 х 10-9;
- 1 м3 = 1 см3 х 0, 000001 = 1 см3 х 10-6;
- 1 м3 = 1 дм3 х 0,001 = 1 дм3 х 10-3. Такой же перевод применяют и для литров, поскольку в 1 л содержится 1 дм3.
Чтобы найти кубы вещества, зная его массу, нужно по таблице отыскать его плотность или определить вручную. Разделив заданную массу М (кг) на показатель плотности Р (кг/ м3), получим V материала (м3).
Подсчитать кубические метры не составляет трудностей для человека, не имеющего математических наклонностей, несмотря на то что в каждом случае требуется разный подход.
Знания для определения объемов необходимы и специалистам, и обычным людям в повседневной жизни.
Источники
- https://ru.onlinemschool.com/math/formula/volume/
- https://exceltut.ru/formuly-obema-geometricheskih-figur-najti-vse-obemy/
- https://zametkiddach.ru/obem-bochki-kalkulyator
- https://iobogrev.ru/rasschitat-obem-baka-v-litrah-po-razmeram
- https://StroySoveti.ru/kanalizaciya/kak-rasschitat-obem-emkosti-razlichnoy-formyi.html
- https://VseProTruby.ru/vodoprovodnye/raschet-obema-vody-v-trube.html
- http://LediZnaet.ru/deti/mir-znanij/kak-poschitat-obyom.html
[свернуть]
‘;
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим
Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример – объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a – длина, b – ширина, c – высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще – достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³.
Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед – фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула.
Galina7v7 7 лет назад Если ваш вопрос трактовать так: “как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах.
Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона – 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3
Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно – длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических.
moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать.
vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы – это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3.
EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |
Начиная с 5 класса, ученики начинают знакомство с объемными фигурами, которые окружают нас во внешней среде. Ученики изучают их свойства и учатся рассчитывать их объем. Чтобы было легче находить объемы различных фигур, предлагаем вам необходимые формулы и простые правила-подсказки.
Содержание статьи
- Формула расчета объема цилиндра
- Как вычислить объем параллелепипеда формула
- Чему равен объем пирамиды формула
- Формула объема правильной четырехугольной пирамиды
- Формула объема шестиугольной пирамиды
- Объем правильной треугольной пирамиды формула
- Объем шара формула через радиус
- Объем шара формула через диаметр
- Какие формулы объема куба
- Формула вычисления объема конуса
- Объем усеченного конуса формула
Чтобы вычисление объема было несложной и увлекательной задачей, важно хорошо разбираться с базовыми определениями. Объем — характеристика пространства в количественном виде, которое занимает любое геометрическое тело. Иными словами, объем можно назвать определенным местом, которое занимает тело в представленном пространстве.
Объем измеряется в установленных единицах, например, в м³, а также в см³ или мм³. Полученная величина объема показывает нам то количество измерительных единиц, которые есть в данном теле.
Также важно помнить свойства объема тел:
- Если тела одинаковые, их объемы равны.
- Объемные предметы обязательно имеют свой объем. Например, всегда можно вычислить объем вазы, мяча, кровати.
- Если объемная фигура вмещает два и более тел, ее объем образуется из всех составляющих.
Формула расчета объема цилиндра
Рассчитать объем представленного цилиндра можно двумя способами, исходя из имеющихся данных:
объём через площадь основания и высоту

Первый вариант ― расчет объема через площадь и известную высоту фигуры. В данном случае объем цилиндра (обозначаем V) — произведение высоты и вместе с ней площади цилиндрического основания. Вид формулы: V=S*h.
Пример:

объём через высоту и радиус основания
Второй вариант ― расчет объема через высоту цилиндра и радиус его основы. Как известно, основания данной фигуры представлены кругом. Его площадь поможет рассчитать формула: S = ∏*R²
Исходя из этой формулы, легко находим объем: V = ∏*R²*h
Пример:

Как вычислить объем параллелепипеда формула
Любой многогранник, представленный шестью гранями в виде параллелограммов, правильно именовать параллелепипедом. Когда его грани — прямоугольники, фигура становится прямоугольным параллелепипедом. В зависимости от вида параллелепипеда используется удобная в конкретном случае формула.
Для того чтобы узнать объем параллелепипеда, прибегают к такой формуле:
объём параллелепипеда по площади основания и высоте

Пример:

Если требуется объем параллелепипеда прямоугольной формы, применяется формула такого вида:
объём параллелепипеда прямоугольной формы по длине, ширене, высоте

Пример:

Чему равен объем пирамиды формула
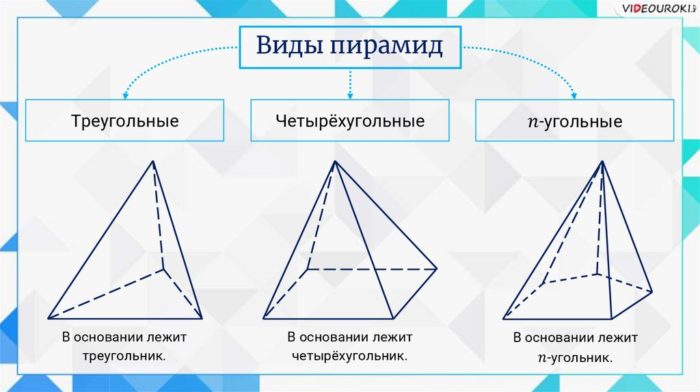
Любой многогранник, в основе которого многоугольник, а его грани — треугольники, именуется пирамидой. Рассчитать ее объем можно несколькими способами в зависимости от типа самой пирамиды.
Объем обычной пирамиды можно рассчитать по площади и высоте данного тела. Объемом в данном случае будет умножение трети площади на имеющуюся высоту: V=1/3*S*h.
формула объём пирамиды по площади основания и высоте

Пример:

Формула объема правильной четырехугольной пирамиды
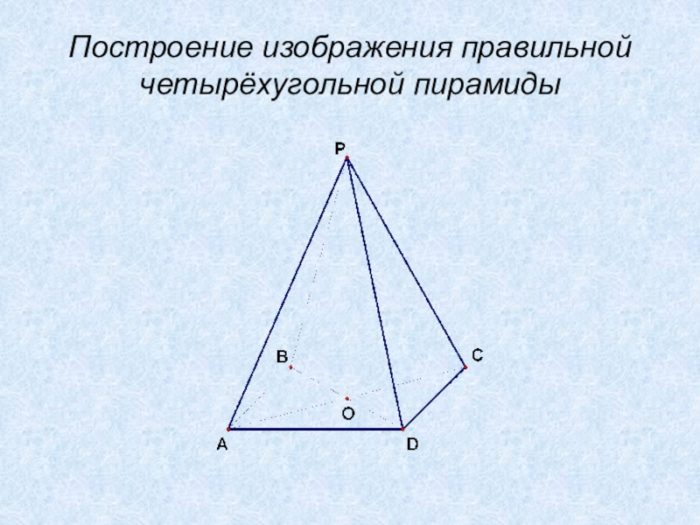
Объема четырехугольной пирамиды (ее особенность — основание-квадрат) определяется с учетом таких величин, как высота тела и сторона его основы:

Пример:

Формула объема шестиугольной пирамиды
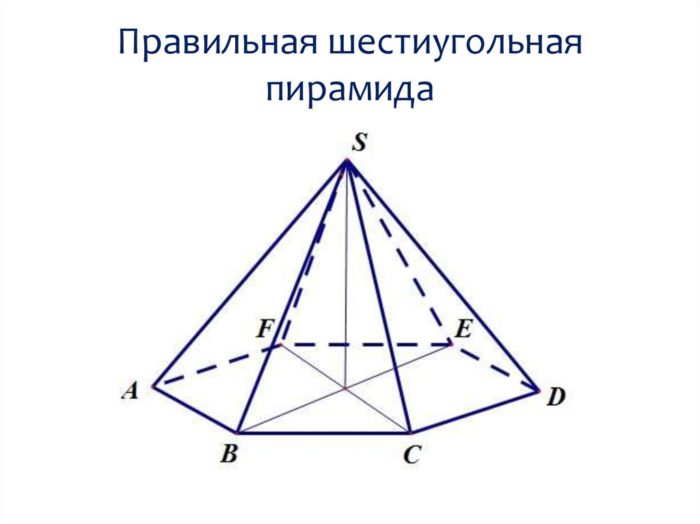
Многогранник, основой которого является правильный шестиугольник, а его грани формируют правильные треугольники, принято называть шестиугольной пирамидой. Она обладает особенными свойствами:
- Длина всех сторон ее основы всегда одинаковая.
- Углы, которые лежат в основе равные.
- Боковые грани обязательно имеют одинаковую площадь.
Чтобы рассчитать объем такой пирамиды, достаточно знать площадь основы и высоту фигуры:
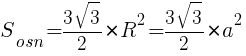
Теперь вернемся к формуле объема нашей пирамиды. Выглядит она так:
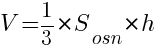
Пример:

Объем правильной треугольной пирамиды формула
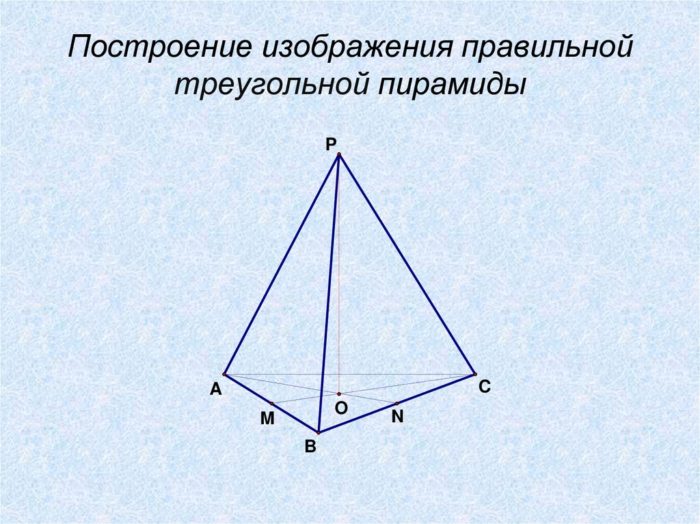
Если перед нами стоит задача посчитать объем треугольной пирамиды применяется следующая формула:

Пример:

Объем шара формула через радиус
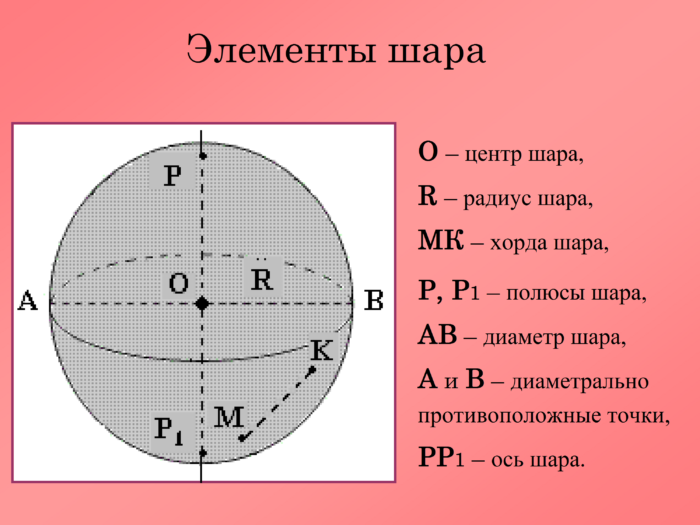
Объемная фигура, точки которой находятся от центра на расстоянии, которое не больше радиуса, принято называть шаром. При этом шар, точно так же, как и круг имеет диаметр, который вдове больше радиус шара. Для вычисления объема данной фигуры необходимо знать лишь радиус и число π.
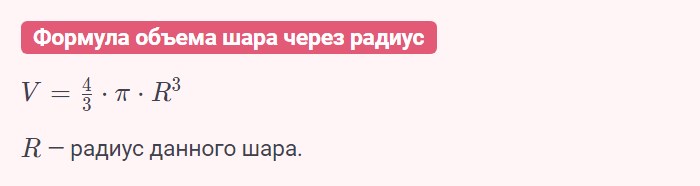
Пример:

Объем шара формула через диаметр
Рассчитать объем шара можно через его диаметр. Для этого вспоминаем, что R=D/2. С помощью этой формулы находим радиус, а затем возвращаемся к базовой формуле и выводим несложную формулу в данном случае:
![]()
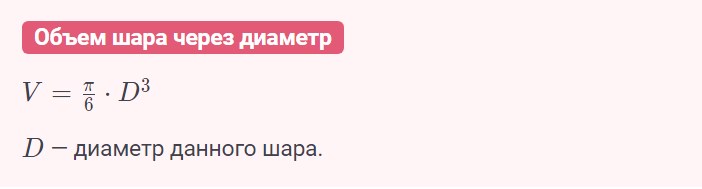
Пример:

Какие формулы объема куба
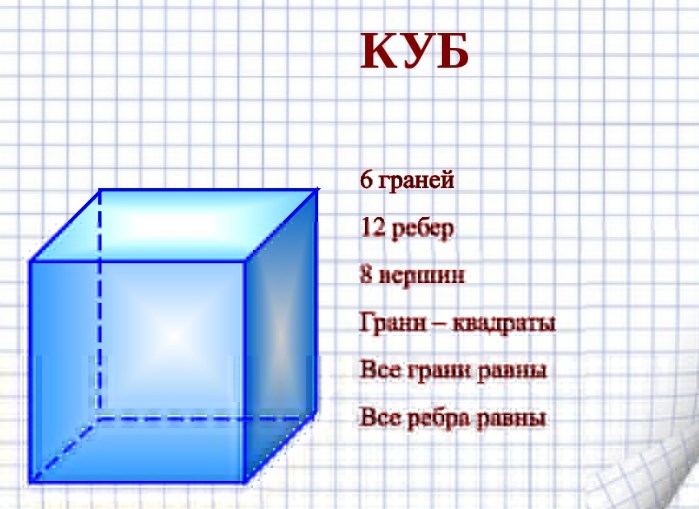
Куб ― фигура в виде правильного многогранника, многоугольники которого являются квадратами. Часто эту фигуру называют гексаэдром. Особенностью данной фигуры можно назвать наличие 12 ребер, 6 граней, а также 8 вершин.
Объем куба через его ребро. Нахождение объема куба не составляет труда. Необходимо всего лишь умножить его измерения, под которыми имеются ввиду: ширина, длина, и, конечно же, высота. Помня о том, что куб состоит из нескольких квадратов, делаем выводы, что его измерения равны и соответствуют длине ребра.
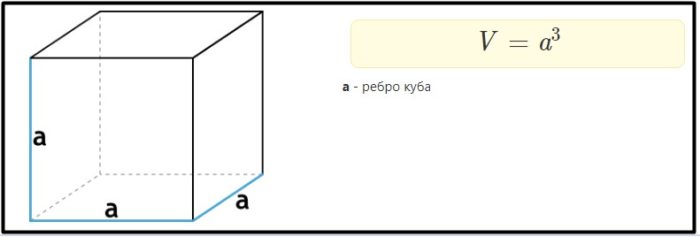
Пример:

Объем куба через диагональ его грани. Факт, что грани куба равны и образуют квадрат, является доказанным. Поэтому вычислить сторону a через диагональ можно, используя формулу: a=d/√2. Исходя из этого, рассчитать объем поможет формула:
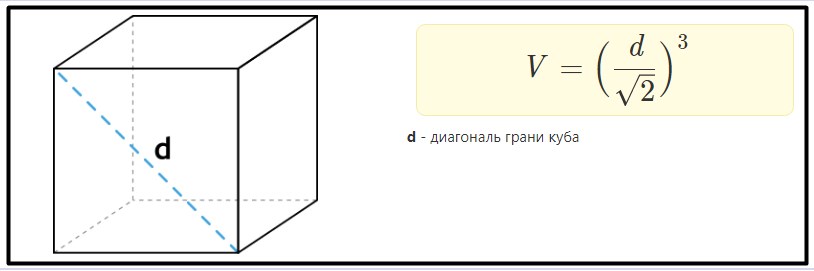
Пример:

Объем через периметр грани. Зная, что все стороны грани одинаковые, легко найти сторону а, разделив известный периметр на 4. Потом остается лишь возвести результат в третью степень.
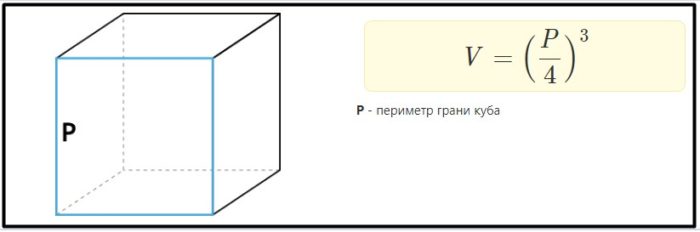
Пример:

Также есть две вспомогательные формулы расчета объема:
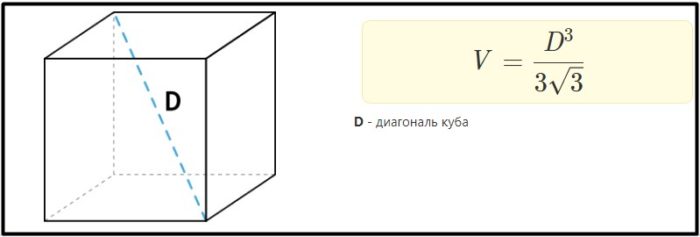
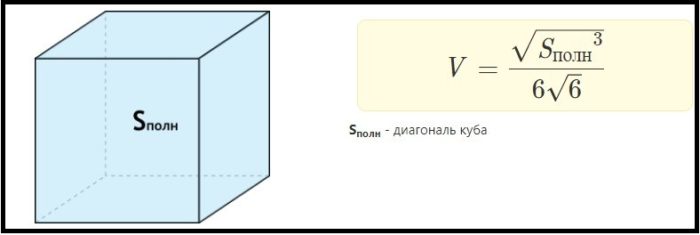
Пример:

Формула вычисления объема конуса
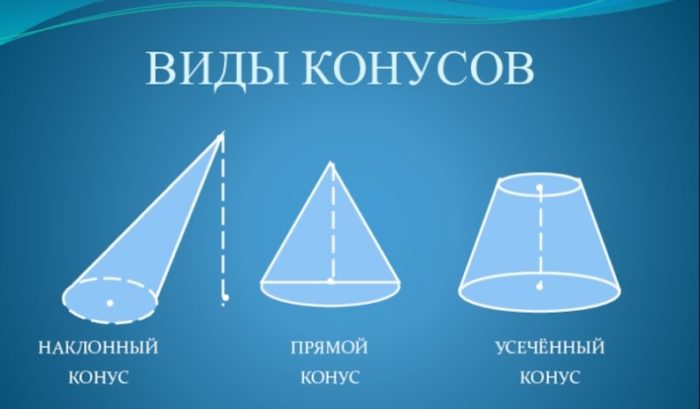
В результате вращения правильного треугольника вокруг катета, в пространстве возникает еще одно тело ― конус. Он является результатом совокупности лучей, которые исходят из вершины конуса и пересекают плоскость.
Объем прямого конуса рассчитывается по формуле:

Пример:

Объем усеченного конуса формула
Когда обычный конус пересекает плоскость, идущая параллельно его основанию, получается усеченный конус. Фигура оказывается между парой плоскостей, поэтому имеет два основания в виде двух кругов разного диаметра. Также у усеченного конуса есть высота, соединяющая основания и идущая перпендикулярно к ним.
Объем такого конуса рассчитывается через радиусы двух его оснований и высоты:

Решение:

Данные онлайн калькуляторы объема горшка в литрах для растений и рассады помогут рассчитать емкость в зависимости от формы (4 вида). Будет полезен для тех, кто хочет выяснить вместимость тары в литрах для:
- горшки под комнатные растения и цветы;
- некоторые виды кашпо с похожей формой внутренней емкости;
- определения объема стаканчиков и кассет для рассады;
- а также можно использовать для расчета объема тары с похожей формой, например, кастрюля или прямая бочка.
Каждый калькулятор объема горшка в литрах для растений и рассады соответствует своему виду и/или форме.
В полях укажите внутренние диаметры емкости или ширину, длину и высоту в сантиметрах.
Онлайн калькуляторы объема горшка в литрах
В зависимости от состава почвосмеси, объем земли может отличаться.
Калькулятор объема горшка и кашпо — по диаметру
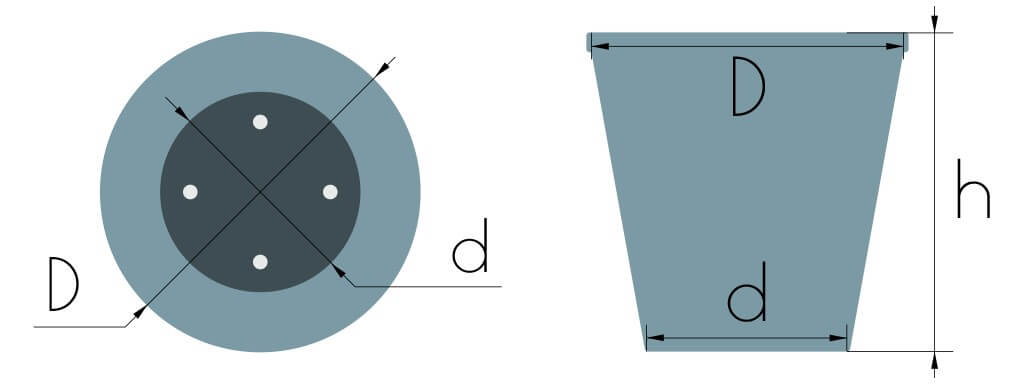
Верхний диаметр, в см
Внутри емкости. Например, 10.5
Диаметр основания, в см
Внутри емкости. Например, 9
Высота горшка (емкости), в см
Под прямым углом к основанию. Например, 16.5
Результаты
Объем горшка (емкости), в литрах
Результаты округлены, являются примерными
Калькулятор объема круглого кашпо в виде шара
Чтобы рассчитать объем круглого кашпо (подвесное, напольное, настольное), который выполнен в виде шара, необходимо измерить внутренние диаметры и его высоту под прямым углом к основанию, а затем подставить полученные значения в калькулятор.

Пожалуйста, обратите внимание на следующий моменты:
- данный калькулятор подходит именно для усеченной формы кашпо в виде шара. Его основание должно быть плоским, а форма напоминать шар;
- внутри емкости, на дне, может располагаться специальная вставка, которая ограничивает помещаемый объем грунта в круглое кашпо (под ней, обычно располагается дренаж). Если такая вставка имеется, то замеряем ее диаметр (в калькуляторе — диаметр основания);
- в зависимости от состава грунта, формы — реальный объем круглого кашпо в виде шара может отличаться.
Верхний диаметр, в см
Внутри емкости. Например, 25.5
Диаметр основания, в см
Внутри емкости. Например, 11
Высота горшка (емкости), в см
Под прямым углом к основанию. Например, 17.5
Результаты
Объем горшка (емкости), в литрах
Результаты округлены, являются примерными
Калькулятор объема четырехгранных емкостей и кашпо
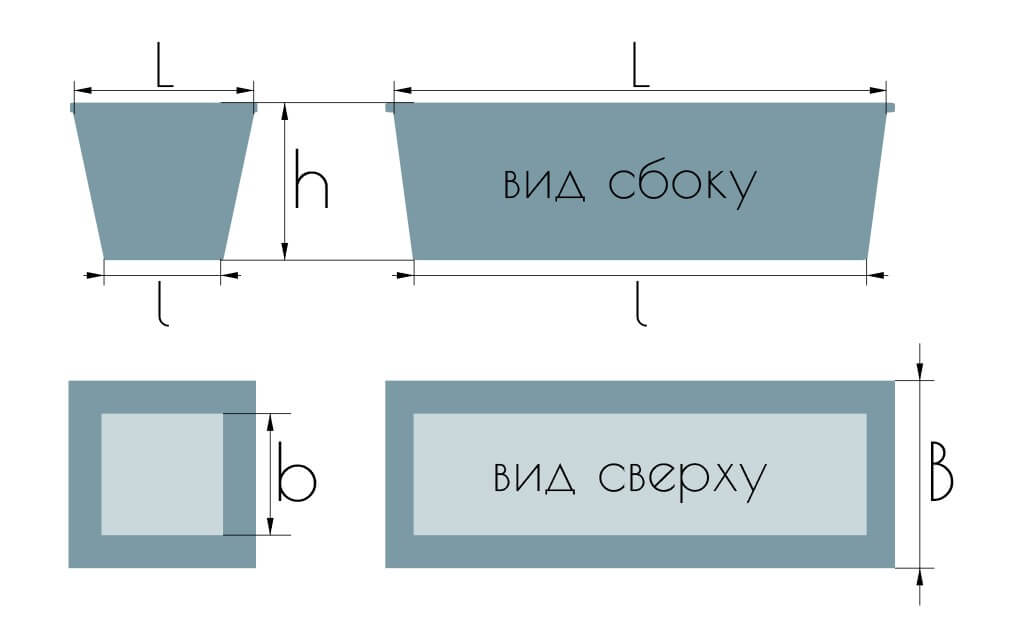
Подходит для емкостей с разными размерами оснований, например, четырехгранные горшки, вазоны, кассеты для рассады и т.д.
Если расчет делается для определения объема кассеты для рассады, то в соответствующих полях указывайте размеры стаканчика кассеты и их количество.
Длина верхнего основания, в см
На схеме – L. Например, 49
Ширина верхнего основания, в см
На схеме – B. Например, 14.5
Длина нижнего основания, в см
На схеме – I. Например, 44.5
Ширина нижнего основания, в см
На схеме – b. Например, 11
Высота емкости, в см
На схеме – H. Например, 13.5
Стаканчиков в кассете
Если нет, введите 1
Результаты
Объем горшка, кашпо (емкости), в литрах
Результаты округлены, являются примерными
Калькулятор объема емкости цилиндрической формы
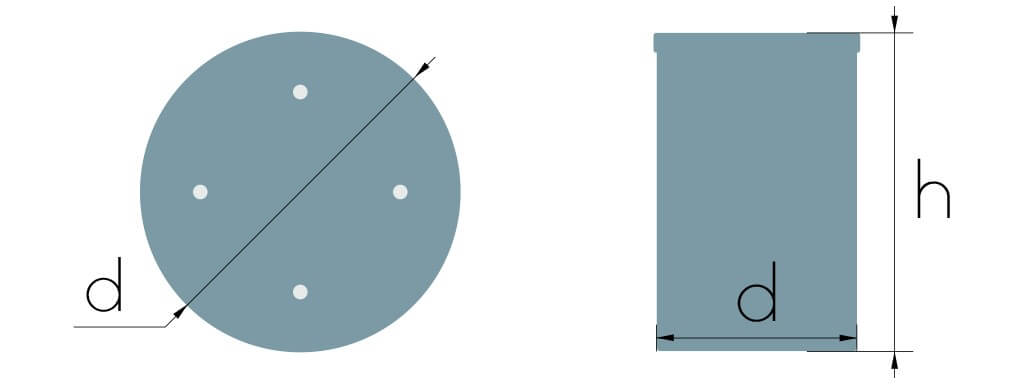
Для определения объема в литрах сложной формы цветочных горшков, можно воспользоваться мерным стаканчиком и водой, предварительно закрыв отверстия.
Диаметр основания, в см
Внутри емкости. Например, 10.5
Высота горшка, в см
Под прямым углом к основанию. Например, 16.5
Результаты
Объем горшка, кашпо (емкости), в литрах
Результаты округлены, являются примерными
Перевести литр земли в кг, килограммы земли в литры
Что во что переводить
Введите литры или кг земли
Например, 17.7
Результаты
Результаты округлены, являются примерными
Виды горшков для комнатных растений, отличия
Для того, чтобы комнатное растение не только радовало глаз, но и органично вписывалось в интерьер, следует подобрать правильную емкость. Даже самый экзотический и красивый цветок в неказистом и старом горшке потеряет свою прелесть. На данный момент никакого дефицита с выбором нет. Однако стоит разобраться в том, какие виды горшков для комнатных растений существуют и чем они отличаются, и стоит ли переплачивать.
Пластиковые горшки
Самые распространенные и дешёвые это пластиковые горшки. Сейчас производители выпускают большое многообразие расцветок и форм. Пластиковые горшки можно увидеть в любом магазине или на рынке.
Плюсами таких горшков можно считать их низкую стоимость, небольшой вес и прочность. Такие горшки разумно размещать на полках, стенках и других поверхностях, которые опасно перегружать. При падении с высоты горшок останется невредимым.
Стоит отметить, что такие горшки смотрятся дёшево, их очень сложно вписать в интерьер.
Горшки из глины

Глиняные горшки всегда ценились высоко. Это натуральный материал, который хорошо воспринимается растениями. Даже покрытый обычным лаком глиняный горшок очень приятно смотрится глазу. А если выбирать с росписью различными глазурями, то такой горшок может стать гордостью любой гостиной.
К минусам относится их высокая стоимость и небольшой ассортимент.
Керамика
Это наиболее популярный материал для производства горшков в настоящее время. Он смотрится намного богаче, чем пластиковый и имеет больше разнообразия, чем глиняные горшки. В настоящее время можно найти керамические горшки любых размеров, формы, цвета и узора. Растение чувствует себя хорошо в подобных ёмкостях.
Такой горшок имеет достаточно большой вес, что затрудняет его размещение. Современные керамические вазоны достаточно прочные и некоторые могут пережить даже удар о землю.
Стекло
Вазоны из полупрозрачного стекла смотрятся утонченно и изысканно. Особенно отличаются горшки в стиле потресканного стекла. Главным их преимуществом является полупрозрачность, благодаря которой можно видеть корни растение. Чаще всего они применяются для орхидей.
Самым большим минусом таких горшков является их высокая стоимость и хрупкость.
Натуральные материалы

Широко распространены также горшки из лозы, дерева, бамбука и даже текстильные. Они подойдут не в любую гостиную. Также их можно назвать непрактичными. Обычно их используют в виде кашпо или прячут внутрь прозрачную пластиковую ёмкость.
Главным критерием выбора одного из вышеописанного вида горшков для комнатных растений должно быть высокое качество. Дешевый пластик со временем трескается, а некачественная краска на керамике вздувается и облазит.
Однако, если выбирается временный горшок, то лучше выбрать пластиковый вариант и не переплачивать.
На долгосрочную перспективу лучше потратиться и приобрести хороший керамический или стеклянный горшок, который будет радовать, и подчёркивать уникальный стиль интерьера.
Калькуляторы объема от КАЛК.ПРО предоставляют возможность выполнить точный расчет кубатуры геометрических фигур и реальных предметов по базовым формулам тригонометрии, стереометрии, начертательной и Евклидовой геометрии. Инструменты будут полезны как в научной деятельности при определении объема цилиндра, пирамиды, конуса… так и в практической деятельности при необходимости рассчитать грузы, емкости, сооружения. Все расчеты сопровождаются подробным описанием алгоритма, формулами и примерами. Результаты предоставляются в условных единицах или в единицах СИ.
Единицы измерения объема (СИ)
- 1 мм3 (куб. миллиметр) = 0.000000001 м3;
- 1 см3 (куб. сантиметр) = 0.000001 м3;
- 1 дм3 (куб. дециметр / литр) = 0.001 м3;
- 1 км3 (куб. километр) = 1.000.000.000 м3.
Единицы измерения объема (внесистемные и имперские)
- 1 мл (миллилитр) = 0.001 л = 0.000001 м3;
- 1 л (литр) = 0.001 м3;
- 1 унция (англ.) = 28.413 мл = 0.028413 л = 0.000028413 м3;
-
1 унция (амер.) = 29.573 мл = 0.029573 л = 0.000029573 м3;
-
1 галлон (англ.) = 4.55 литра = 0.00455 м3;
-
1 галлон (амер.) = 3.785 литра = 0.00378541 м3;
-
1 дюйм3 = 0,0000163871 м3;
- 1 фут3 = 0.0283168 м3;
- 1 ярд3 = 0,76455 м3.
Для того чтобы начать расчет объема, выберите необходимый калькулятор:
