Посчитать объём коробки
- Главная
- /
- Логистика
- /
- Посчитать объём коробки
Чтобы посчитать объем коробки или нескольких коробок воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
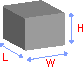
Расчет объема коробки
Длина коробки
Ширина коробки
Высота коробки
Объем коробки:
0
Просто введите длину, ширину и высоту коробки и узнаете её объём.
Расчет объема нескольких коробок
Количество коробок
шт
Длина коробки
Ширина коробки
Высота коробки
Объем одной коробки:
0
Общий объем всех коробок:
0
Теория
Коробка это прямоугольный параллелепипед, который имеет длину A, ширину B и высоту (глубину) C. Её объём считается по следующей формуле:
Формула
V = A⋅B⋅C
Пример
К примеру, возьмём коробку, у которой ширина равна 56 см, высота – 40 см, глубина – 32 см и посчитаем её объём:
V = 56⋅40⋅32 = 71680 см³
Если нам необходимо знать объём в кубометрах, нужно полученную цифру разделить на 1 000 000:
V = 71680/1000000 = 0.07168 ≈ 0.07 м³
См. также
У этого термина существуют и другие значения, см. Объём (значения).
| Объём | |
|---|---|
 |
|
| Размерность | L3 |
| Единицы измерения | |
| СИ | м3 |
| СГС | см3 |
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей[1].
Единица объёма в СИ — кубический метр; от неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма[править | править код]
На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.
Математически[править | править код]
Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром 

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.
Сводка формул[править | править код]
| Форма тела | Формула для вычисления объёма | Обозначения |
|---|---|---|
| Куб | 
|

|
| Прямоугольный параллелепипед | 
|

|
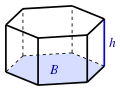
| Призма
(B: площадь основания) |

|
|
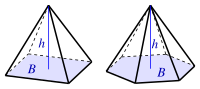
| Пирамида
(B: площадь основания) |

|
|
| Параллелепипед | 
|

|
| Тетраэдр | 
|

|
| Шар | 
|

|
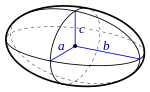
| Эллипсоид | 
|
|
| Прямой круговой цилиндр | 
|

|
| Конус | 
|

|
| Тело вращения | 
|

|
Через плотность[править | править код]
Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: 
Единицы объёма жидкости[править | править код]
- 1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона
Русские[2][править | править код]
- Ведро = 12,3 литра
- Бочка = 40 вёдер = 492 литра
Английские[править | править код]
- 1 пинта = 0,568 литра
- 1 кварта (жидкостная) = 2 пинтам = 1,136 литра
- 1 галлон = 8 пинтам = 4,55 литра
- 1 галлон (амер.) = 3,785 литра
Античные[править | править код]
- Котила = 0,275 литра
Немецкие[править | править код]
- Шоппен
Древнееврейские[3][править | править код]
- Эйфа = 24,883 литра
- Гин = 1/6 эйфы = 4,147 литра
- Омер = 1/10 эйфы = 2,4883 литра
- Кав = 1/3 гина = 1,382 литра
Единицы объёма сыпучих веществ[править | править код]
Русские[править | править код]
- Четверик = 26,24 литра (1 пуд зерна)
- Гарнец = 3,28 литра
- Четверть = 1/4 ведра = 3,075 литра
- Штоф = 1/8 ведра = 1,54 литра
- Кружка = 1/10 ведра = 1,23 литра
- Бутылка (винная) = 1/16 ведра = 0,77 литра
- Бутылка (пивная) = 1/20 ведра = 0,61 литра
- Чарка = 1/10 кружки = 0,123 литра
- Шкалик (косушка) = 1/2 чарки = 0,0615 литра
Английские[править | править код]
- 1 бушель = 8 галлонов = 36,36872 литра
- 1 баррель = 163,65 литра
Прочие единицы[править | править код]
- 1 унция (англ.) = 2,841⋅10−5 м³
- 1 унция (амер.) = 2,957⋅10−5 м³
- 1 кубический дюйм = 1,63871⋅10−5 м³
- 1 кубический фут = 2,83168⋅10−2 м³
- 1 кубический ярд = 0,76455 м³
- 1 кубическая астрономическая единица =3,348⋅1024 км³
- 1 кубический световой год = 8,466⋅1038 км³
- 1 кубический парсек = 2,938⋅1040 км³
- 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅1049 км³
Примечания[править | править код]
- ↑ Математическая энциклопедия, 1982, с. 1149.
- ↑ Меры объёма в Древней Руси. Дата обращения: 17 ноября 2013. Архивировано 14 июля 2014 года.
- ↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4
Литература[править | править код]
- Объём // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- Объём // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки[править | править код]
- Формулы объёма и программы для расчета объёма. Дата обращения: 26 ноября 2020. Архивировано 24 ноября 2020 года.
Объем геометрических фигур
Рассчитывает объем геометрических фигур (куб, призма, пирамида, усеченная пирамида, конус, цилиндр, сфера, эллипсоид, тороид).
Данная статья содержит калькуляторы для расчета объема различных геометрических фигур. Основной источник формул: Spiegel, Murray R. Mathematical Handbook of Formulas and Tables. Schaum’s Outline series in Mathematics. McGraw-Hill Book Co., 1968.
Объем куба
Формула:
Объем куба
Точность вычисления
Знаков после запятой: 5
Объем прямоугольной призмы
Формула:
Объем прямоугольной призмы
Точность вычисления
Знаков после запятой: 5
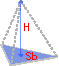
Объем пирамиды
Формула:
Объем пирамиды
Точность вычисления
Знаков после запятой: 5
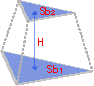
Объем усеченной пирамиды
Формула:
Объем усеченной пирамиды
Площадь первого основания (Sb1)
Площадь второго основания (Sb2)
Точность вычисления
Знаков после запятой: 5
Объем конуса
Формула:
Объем конуса
Точность вычисления
Знаков после запятой: 5
Объем цилиндра
Formula:
Объем цилиндра
Точность вычисления
Знаков после запятой: 5
Объем сферы
Формула:
Объем сферы
Точность вычисления
Знаков после запятой: 5
Объем эллипсоида
Формула:
Объем эллипсоида
Точность вычисления
Знаков после запятой: 5
Объем тороида
Формула:
Объем тора
Точность вычисления
Знаков после запятой: 5
Ссылка скопирована в буфер обмена
PLANETCALC, Объем геометрических фигур
Загрузить PDF
Загрузить PDF
Объем фигуры представляет собой занимаемое этой фигурой трехмерное пространство.[1]
Представьте себе объем как количество жидкости (или воздуха, или песка), которым можно заполнить данную фигуру. Объем измеряется в кубических единицах (мм3, см3, м3).[2]
Эта статья расскажет вам, как вычислять объем шести трехмерных фигур. Вы можете заметить, что многие формулы для вычисления объема схожи, что упрощает их запоминание.
-
1
Куб – это трехмерная фигура, которая имеет шесть одинаковых квадратных граней, то есть все ее стороны (ребра) равны.[3]
- Например, игральная кость – это куб.
-
2
Формула нахождения объема куба: V = s3, где V – объем, а s – длина ребра.
- Возведение в куб аналогично следующему умножению: s3 = s * s * s
-
3
Найдите длину стороны (ребра) куба. Она будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой). Так как ребра куба равны, измеряйте любое ребро.
- Если вы не уверены, что ваша фигура является кубом, измерьте каждую сторону, чтобы убедиться, что они равны. Если они не равны, перейдите к следующему разделу.
-
4
Подставьте длину ребра куба в формулу V = s3. Например, если ребро куба равно 5 см, напишите формулу следующим образом: V = 53 = 5 * 5 * 5 = 125 см3 – это объем куба.
-
5
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребро куба измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах. Если, например, сторона куба равна 3 см, то V = 33 = 27см3.
Реклама
-
1
Прямоугольный параллелепипед или прямоугольная призма – это трехмерная фигура с шестью гранями, каждая из которых является прямоугольником (вспомните коробку из под обуви). [4]
- Куб – это частный случай прямоугольного параллелепипеда, у которого все ребра равны.
-
2
Формула нахождения объема прямоугольного параллелепипеда или прямоугольной призмы: V = l*w*h, где V = объем, l = длина, w = ширина, h = высота.[5]
-
3
Длина прямоугольного параллелепипеда – это самое длинное ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Длина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: длина прямоугольного параллелепипеда равна 4 см, то есть l = 4 см.
- Не беспокойтесь о том, какие ребра выбрать в качестве длины, ширины и высоты. В любом случае в итоге вы получите правильный ответ (только измерьте три ребра, перпендикулярные друг другу).
-
4
Ширина прямоугольного параллелепипеда – это самое короткое ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Ширина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: ширина прямоугольного параллелепипеда равна 3 см, то есть w = 3 см.
- Если вы измеряете ребра параллелепипеда линейкой или рулеткой, не забудьте измерить их в одинаковых единицах измерения. Не измеряйте одно ребро в миллиметрах, а другое в сантиметрах.
-
5
Высота прямоугольного параллелепипеда – это расстояние между его нижней и верхней гранями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: высота прямоугольного параллелепипеда равна 6 см, то есть h = 6 см.
-
6
Подставьте найденные значения в формулу V = l*w*h.
- В нашем примере l = 4, w = 3 и h = 6. Поэтому V = 4*3*6 = 72.
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребра измерялись в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 72 см3.
- Если в прямоугольной призме l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см3
Реклама
-
1
Цилиндр – это трехмерная фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.[6]
- Например, банка или батарейка АА имеют форму цилиндра.
-
2
Формула нахождения объема цилиндра: V = πr2h, где V – объем, h – высота, r – радиус основания и πr2 – площадь основания цилиндра.
- В некоторых задачах ответ требуется представить с пи, а в некоторых вместо пи подставить 3,14.
- Формула для нахождения объема цилиндра на самом деле очень похожа на формулу вычисления объема прямоугольной призмы, то есть вы перемножаете высоту и площадь основания. В прямоугольной призме площадь основания равна l*w, а в цилиндре она равна πr2.
-
3
Найдите радиус основания. Он, скорее всего, дан в задаче. Если дан диаметр, разделите его на 2, чтобы найти радиус (d = 2r).
-
4
Если радиус не дан, измерьте его. Для этого измерьте основание цилиндра при помощи линейки или рулетки. Измеряйте основание в его самой широкой части (то есть измерьте диаметр основания), а затем разделите полученное значение на 2, чтобы найти радиус.
- Другой вариант – измерьте длину окружности цилиндра (то есть измерьте обхват цилиндра) при помощи рулетки, а затем найдите радиус по формуле r = с/2π, где с – обхват (длина окружности) цилиндра (2π = 6,28).
- Например, если обхват цилиндра равен 8 см, то радиус будет равен 1,27 см.
- Если вам нужно точное измерение, вы можете использовать оба метода, чтобы убедиться, что значения радиуса совпадают (нахождение радиуса через длину окружности является более точным методом).
-
5
Вычислите площадь круглого основания. Для этого подставьте радиус в формулу πr2.
- Если радиус основания равен 4 см, то площадь основания равна π42.
- 42 = 4 * 4 = 16. 16*π = 16*3,14 = 50,24 см2
- Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус.
-
6
Найдите высоту цилиндра. Это расстояние между двумя круглыми основаниями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
-
7
Умножьте площадь основания на высоту цилиндра, чтобы найти его объем. Или же просто подставьте значения соответствующих величин в формулу V = πr2h. В нашем примере, когда радиус основания равен 4 см, а высота равна 10 см:
- V = π4210
- π42 = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 502,4 см3.
Реклама
-
1
Пирамида – это трехмерная фигура, в основании которой лежит многоугольник, а грани являются треугольниками, имеющими общую вершину. [7]
Правильная пирамида – это трехмерная фигура, в основании которой лежит правильный многоугольник (с равными сторонами), а вершина проецируется в центр основания.[8]
- Обычно мы представляем пирамиду, имеющую квадратное основание, но в основании пирамиды может лежать многоугольник с 5, 6 или даже со 100 сторонами!
- Пирамида с круглым основанием называется конусом, который будет обсуждаться в следующем разделе.
-
2
Формула нахождения объема правильной пирамиды: V = 1/3bh, где b – площадь основания пирамиды, h – высота пирамиды (перпендикуляр, соединяющий основание и вершину пирамиды).
- Эта формула для вычисления объема пирамиды одинаково годна как для правильных пирамид (в которых вершина проецируется в центр основания), так и для наклонных (в которых вершина не проецируется в центр основания).
-
3
Вычислите площадь основания. Формула будет зависеть от фигуры, лежащей в основании пирамиды. В нашем примере в основании пирамиды лежит квадрат со стороной 6 см. Площадь квадрата равна s2, где s – сторона квадрата. Таким образом, в нашем примере площадь основания пирамиды равна 62 = 36 см2
- Площадь треугольника равна 1/2bh, где h – высота треугольника, b – сторона, к которой проведена высота.
- Площадь любого правильного многоугольника можно вычислить по формуле: А = 1/2ра, где А – площадь, р – периметр фигуры, а – апофема (отрезок, соединяющий центр фигуры с серединой любой стороны фигуры). Для получения дополнительной информации о нахождении площади многоугольников прочитайте эту статью.[9]
-
4
Найдите высоту пирамиды. Высота будет дана в задаче. В нашем примере высота пирамиды равна 10 см.
-
5
Умножьте площадь основания пирамиды на ее высоту, а затем разделите полученный результат на 3, чтобы найти объем пирамиды. Формула для вычисления объема пирамиды: V = 1/3bh. В нашем примере площадь основания равна 36, а высота равна 10, поэтому объем: 36*10*1/3 = 120.
- Если, например, дана пирамида с пятиугольным основанием площадью 26, а высота пирамиды равна 8, то объем пирамиды: 1/3*26*8 = 69,33.
-
6
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 120 см3.
Реклама
-
1
Конус – это трехмерная фигура, которая имеет круглое основание и одну вершину. Или конус – это особый случай пирамиды с круглым основанием.[10]
- Если вершина конуса находится непосредственно над центром круглого основания, то конус называется прямым; в противном случае конус называется наклонным. Но формула для вычисления объема конуса одинаковая для обоих типов конуса.
-
2
Формула для вычисления объема конуса: V = 1/3πr2h, где r – радиус круглого основания, h – высота конуса.
- b = πr2 – это площадь круглого основания конуса. Таким образом, формулу для вычисления объема конуса можно записать так: V = 1/3bh, что совпадает с формулой нахождения объема пирамиды!
-
3
Вычислите площадь круглого основания. Радиус должен быть дан в задаче. Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Для вычисления площади круглого основания подставьте радиус в формулу πr2.
- Например, радиус круглого основания конуса равен 3 см. Тогда площадь этого основания равна π32.
- π32 = π(3*3) = 9π.
- = 28,27 см2
-
4
Найдите высоту конуса. Это перпендикуляр, опущенный из вершины к основанию пирамиды. В нашем примере высота конуса равна 5 см.
-
5
Перемножьте высоту конуса и площадь основания. В нашем примере площадь основания равна 28,27 см2, а высота равна 5 см, поэтому bh = 28,27 * 5 = 141,35.
-
6
Теперь умножьте полученный результат на 1/3 (или просто разделите его на 3), чтобы найти объем конуса. В описанном выше шаге вы нашли объем цилиндра, а объем конуса всегда в 3 раза меньше объема цилиндра.
- В нашем примере: 141,35 * 1/3 = 47,12 – это объем конуса.
- Или: 1/3π325 = 47,12
-
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 47,12 см3.
Реклама
-
1
Шар – это идеально круглая трехмерная фигура, каждая точка поверхности которой равноудалена от одной точки (центра шара). [11]
-
2
Формула для вычисления объема шара: V = 4/3πr3, где r – радиус шара.[12]
-
3
Найдите радиус шара. Радиус должен быть дан в задаче. Если дан диаметр шара, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Например, радиус шара равен 3 см.
-
4
Если радиус не дан, вычислите его. Для этого измерьте длину окружности шара (например, теннисного мяча) в его самой широкой части при помощи веревки, нити или другого подобного предмета. Затем измерьте длину веревки, чтобы найти длину окружности. Разделите полученное значение на 2π (или на 6,28), чтобы вычислить радиус шара.
- Например, если вы измерили мяч и нашли, что длина его окружности равна 18 см, разделите это число на 6,28 и получите, что радиус мяча равен 2,87 см.
- Проделайте 3 измерения окружности шара, а затем усредните полученные значения (для этого сложите их и сумму разделите на 3), чтобы убедиться, что вы получили значение, близкое к истинному.
- Например, в результате трех измерений длины окружности вы получили следующие результаты: 18 см, 17,75 см, 18,2 см. Сложите эти значения: 18 + 17,5 + 18,2 = 53,95, а затем разделите их на 3: 53,95/3 = 17,98. Используйте это среднее значение в расчетах объема шара.
-
5
Возведите радиус в куб (r3). То есть r3 = r*r*r. В нашем примере r = 3, поэтому r3 = 3 * 3 * 3 = 27.
-
6
Теперь умножьте полученный результат на 4/3. Вы можете использовать калькулятор или выполнить умножение вручную, а затем упростить дробь. В нашем примере: 27*4/3 = 108/3 = 36.
-
7
Умножьте полученный результат на π (3,14), чтобы найти объем шара.
- В нашем примере: 36*3,14 = 113,09.
-
8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 113,09 см3.
Реклама
Об этой статье
Эту страницу просматривали 74 320 раз.
Была ли эта статья полезной?
|
Один метр кубический является единицей объема. Чтобы найти объем какого-то предмета, имеющего КУБИЧЕСКУЮ форму (например, параллелепипед), нужно его длину (в метрах) умножить на ширину (тоже в метрах) и умножить на высоту (опять в метрах). Логично, не правда ли, что метр, умноженный сам на себя три раза превращается в метр кубический! Если требуется посчитать объем предмета НЕ КУБИЧЕСКОЙ формы (например, шар, призма, конус), то для вычисления их объема есть специальные формулы. Если они вам нужны, то советую посмотреть учебник по геометрии. автор вопроса выбрал этот ответ лучшим Ксарфакс 5 лет назад Думаю, всем понятно, что формула расчёта объёма в кубических метрах для каждой геометрической фигуры будет разной. Поэтому нужно произвести все необходимые измерения, а затем воспользоваться соответствующей формулой. Если фигура имеет неправильную формулу, то разбиваем её на несколько стандартных фигур, а затем складываем их объёмы между собой. Нужно помнить, что все измерения проводятся именно в метрах. Например, если высота объекта 70 см, то её нужно перевести в метры: 70 см = 0,7 м. Самый простейший пример – объём помещения Для того, чтобы посчитать объём, нужно воспользоваться формулой нахождения объёма прямоугольного параллелепипеда. V = abc. a – длина, b – ширина, c – высота. Таким образом, измеряем длину / ширину / высоту комнаты, а затем перемножаем эти значения между собой. Если вы знаете площадь, то посчитать объём ещё проще – достаточно измерить высоту и умножить это значение на данное значение. Например, длина комнаты = 6 м, ширина = 5 м, высота = 2,5 м. V = 6 * 5 * 2,5 = 75 м³. Nelli4ka 5 лет назад Для примера возьмем прямоугольник и параллелепипед. Прямоугольник лежит на плоскости, и мы можем найти либо его периметр (т.е. длину всех сторон данной фигуры), либо его площадь, которая будет выражаться, скажем, в сантиметрах или метрах квадратных. Параллелепипед – фигура трехмерного пространства, у нее есть помимо ширины и длины еще и высота. Когда значения высоты, длины и ширины умножаются друг на друга, находится объем трехмерной фигуры, которая уже будет выражаться не в квадратных, а в кубических сантиметрах, метрах и т.д., но для каждого некубического случая существует своя индивидуальная формула. Galina7v7 7 лет назад Если ваш вопрос трактовать так: “как посчитать объём 1 метра кубического , то V = 1м * 1 м = 1м = 1 м ^3 (1 метр кубический ) , и это единица измерения объёма в системе СИ. Если вас интересует тело в форме параллелепипеда ,где все соседние ребра перпендикулярны друг другу , то объём такого тела определяется путём произведения : длина *ширина * высота. ОБЪЁМ ТЕЛА = ДЛИНА (м) х ШИРИНА (м) х ВЫСОТА (м)Для того,чтобы получить объём в м^3 нужно все 3 параметра тоже выразить в метрах. Zolotynka 5 лет назад В метрах кубических можно высчитать объем предмета, который представляет собой форму куба. Для этого следует воспользоваться формулой: длина*ширина*высота. ** Данная формула имеет важное практическое значение. Рассмотрим на примере: Предположим, нам нужно рассчитать, расход бетона для того, чтобы сделать пол в сарае, размер которого: ширина 2.0 м, длина 2.0 м, а желаемая толщина бетона – 100 мм. Формула для расчета объема бетона в м3 будет выглядеть следующими образом: 2,0 × 2,0 × 0,1 = 0.4m3 Математика обязательный предмет в школьной программе, но знания уходят, забываются формулы, как проводить вычисления уже не каждый вспомнит, остается в голове то, что используется нами ежедневно, и на работе требуется все время, поэтому формула расчета кубического метра может придти в голову не сразу, и придется искать эту информацию, для тех, кому нужно – длину умножить на ширину и умножить на высоту. Kerbal Space Program 6 лет назад Крайне просто. Для этого достаточно брать длины и расстояния в метрах: будь то длина, высота и ширина или же радиус, при вычислении объема круга или цилиндра. Например, имеем: Параллелепипед длиной 1245 см, шириной 3 см и высотой 25 см. Эти длины переведем в метры и получим:
Считаем теперь объем: V=1,245*0,03*0,25=0,00933 метра кубических. moreljuba 5 лет назад Посчитать объём в метрах кубических вы вполне спокойно можете. Для это вам необходимо иметь представление о значениях для таких величин как высота, ширина (толщина) и длина. Переводите в метры и перемножаете эти три составляющие и получаете в результате объём в метрах кубических. FantomeRU 5 лет назад Чтобы вычислить объем необходимо умножить длину на ширину и на высоту. При этом, чтобы искомый результат был в кубических метрах, сначала нужно все стороны данного предмета выразить в метрах и только потом перемножать. vksvovko 6 лет назад Один из распространенных способов найти объем предмета неправильной формы – это налить воду в измерительный сосут и опустить туда предмет. далее смотрим сколько он вытеснил воды и легко подсчитываем объем в м3. EvgeniyAlekseevich 7 лет назад Высоту, выраженную в м3, умножить на длину и умножить на ширину. Знаете ответ? |