Решение задач на количество вещества,
массу и объем
Ключевые слова: решение задач на количество вещества, решение задач по химии на массу и объем, какое количества вещества содержится, какое число молекул содержится, определите объем (н.у.), определите массу, какова масса порции, определите молярную массу, назовите вещество, найдите молярную массу, определите абсолютную массу молекулы, сколько атомов содержится, определите относительную плотность.
ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ
Количество вещества характеризует число структурных единиц (атомов, молекул, ионов), которое содержится в определенном образце данного вещества. Единицей измерения количества вещества является моль. Количество вещества (ν) связано с числом структурных единиц (N) в образце вещества, его массой (m) и объемом (V) — для газообразных веществ при н. у. — следующими уравнениями:
 в которых
в которых
Vm = 22,4 л/моль (мл/ммоль, м3/кмоль) при н.у.,
Na = 6,02 • 1023 (постоянная Авогадро),
а молярная масса (М) численно равна относительной молекулярной массе вещества:

Наличие подобной взаимосвязи позволяет, зная одну из величин (количество вещества, массу, объем, число структурных величин) определить все другие величины.
РЕШЕНИЯ ПРОСТЫХ ЗАДАЧ
Задача № 1.
Какое количество вещества содержится в 33 г оксида углерода (IV)?

Ответ: ν(СО2) = 0,75 моль.
Задача № 2.
Какое число молекул содержится в 2,5 моль кислорода?

Ответ: N(O2) = 1,505 • 1024.
Задача № 3.
Определите объем (н. у.), который займут 0,25 моль водорода.

Задача № 4.
Какую массу будет иметь порция оксида серы (IV), объем которой 13,44 л (н. у.)?

Задача № 5.
Имеется 3 моль кислорода О2 при н.у. Определите массу кислорода, его объем, а также число имеющихся молекул кислорода.
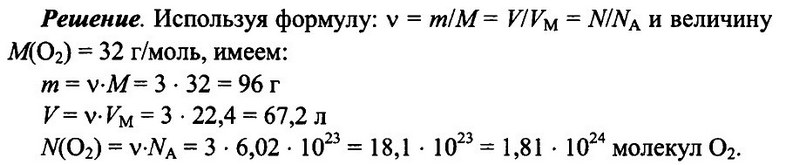
Ответ: m = 96 г; V = 67.2 л; N(O2) = 1,81 • 1024.
Задача № 6.
Имеется 10 г водорода Н2. Определите количество водорода, его объем при н.у., а также число имеющихся молекул водорода.
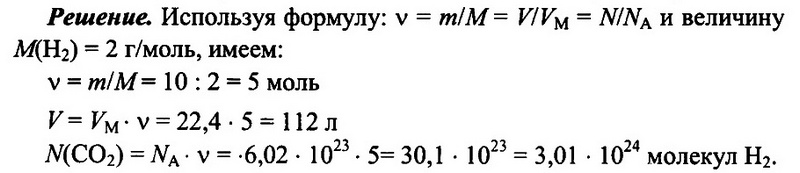
Ответ: 5 моль; 112 л; 3,01 • 1024.
Задача № 7.
Имеется 56 л хлора Сl2 при н.у. Определите количество вещества хлора, его массу и число имеющихся молекул хлора.

Ответ: 2,5 моль; 177,5 г; 1,5 • 1024.
Задача № 8.
Имеется 2,4 • 1023 молекул оксида углерода (IV) СO2. Определите количество вещества углекислого газа, его массу, а также объем (н.у.) углекислого газа.
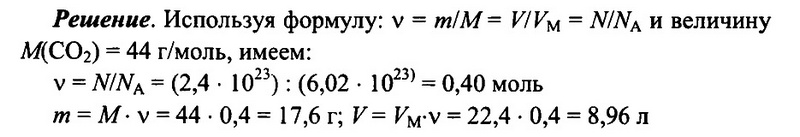
Ответ: 0,4 моль; 17,6 г; 8,96 л.
Задача № 9.
Какова масса порции оксида азота (IV), содержащей 4,816 • 1023 молекул? Каков ее объем (н. у.)?

Задача № 10.
Масса порции простого вещества, содержащей 1,806 • 1024 молекул, равна 6 г. Определите молярную массу данного вещества и назовите его.

Внимание! В данном конспекте рассматриваются задачи обычной сложности. Чтобы перейти к конспекту решения сложных задач на количественные характеристики и задачи с кратким ответом нажмите на кнопку ниже…
Сложные задачи на количество …
Решение задач на количество вещества, массу и объем. Выберите дальнейшие действия:
- Перейти дальше: Решение задач с долей вещества в смеси, в соединении
- Вернуться к списку конспектов по Химии.
- Проверить знания по Химии.
У этого термина существуют и другие значения, см. Объём (значения).
| Объём | |
|---|---|
 |
|
| Размерность | L3 |
| Единицы измерения | |
| СИ | м3 |
| СГС | см3 |
Объём — количественная характеристика пространства, занимаемого телом или веществом. Объём тела определяется его формой и линейными размерами. Основное свойство объёма — аддитивность , то есть объём любого тела равен сумме объёмов его (непересекающихся) частей[1].
Единица объёма в СИ — кубический метр; от неё образуются производные единицы — кубический сантиметр, кубический дециметр (литр) и т. д. В разных странах для жидких и сыпучих веществ используются также различные внесистемные единицы объёма — галлон, баррель и др.
В формулах для обозначения объёма традиционно используется заглавная латинская буква V, являющаяся сокращением от лат. volume — «объём», «наполнение».
Слово «объём» также используют в переносном значении для обозначения общего количества или текущей величины. Например, «объём спроса», «объём памяти», «объём работ». В изобразительном искусстве объёмом называется иллюзорная передача пространственных характеристик изображаемого предмета художественными методами.
Вычисление объёма[править | править код]
На практике приблизительный объём тела, в том числе сложной формы, можно вычислить по закону Архимеда, погрузив это тело в жидкость: объём вытесненной жидкости будет равен объёму измеряемого тела.
Математически[править | править код]
Для объёмов тел простой формы имеются специальные формулы. Например, объём куба с ребром 

Объём тела сложной формы вычисляется разбиением этого тела на отдельные части простой формы и суммированием объёмов этих частей. В интегральном исчислении объёмы частей, из которых складывается объём всего тела, рассматриваются как бесконечно малые величины.
Сводка формул[править | править код]
| Форма тела | Формула для вычисления объёма | Обозначения |
|---|---|---|
| Куб | 
|

|
| Прямоугольный параллелепипед | 
|

|
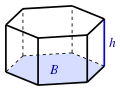
| Призма
(B: площадь основания) |

|
|
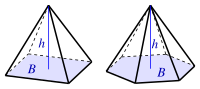
| Пирамида
(B: площадь основания) |

|
|
| Параллелепипед | 
|

|
| Тетраэдр | 
|

|
| Шар | 
|

|
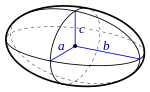
| Эллипсоид | 
|
|
| Прямой круговой цилиндр | 
|

|
| Конус | 
|

|
| Тело вращения | 
|

|
Через плотность[править | править код]
Зная массу (m) и среднюю плотность (ρ) тела, его объём рассчитывают по формуле: 
Единицы объёма жидкости[править | править код]
- 1 литр = 1 кубический дециметр = 1,76 пинты = 0,23 галлона
Русские[2][править | править код]
- Ведро = 12,3 литра
- Бочка = 40 вёдер = 492 литра
Английские[править | править код]
- 1 пинта = 0,568 литра
- 1 кварта (жидкостная) = 2 пинтам = 1,136 литра
- 1 галлон = 8 пинтам = 4,55 литра
- 1 галлон (амер.) = 3,785 литра
Античные[править | править код]
- Котила = 0,275 литра
Немецкие[править | править код]
- Шоппен
Древнееврейские[3][править | править код]
- Эйфа = 24,883 литра
- Гин = 1/6 эйфы = 4,147 литра
- Омер = 1/10 эйфы = 2,4883 литра
- Кав = 1/3 гина = 1,382 литра
Единицы объёма сыпучих веществ[править | править код]
Русские[править | править код]
- Четверик = 26,24 литра (1 пуд зерна)
- Гарнец = 3,28 литра
- Четверть = 1/4 ведра = 3,075 литра
- Штоф = 1/8 ведра = 1,54 литра
- Кружка = 1/10 ведра = 1,23 литра
- Бутылка (винная) = 1/16 ведра = 0,77 литра
- Бутылка (пивная) = 1/20 ведра = 0,61 литра
- Чарка = 1/10 кружки = 0,123 литра
- Шкалик (косушка) = 1/2 чарки = 0,0615 литра
Английские[править | править код]
- 1 бушель = 8 галлонов = 36,36872 литра
- 1 баррель = 163,65 литра
Прочие единицы[править | править код]
- 1 унция (англ.) = 2,841⋅10−5 м³
- 1 унция (амер.) = 2,957⋅10−5 м³
- 1 кубический дюйм = 1,63871⋅10−5 м³
- 1 кубический фут = 2,83168⋅10−2 м³
- 1 кубический ярд = 0,76455 м³
- 1 кубическая астрономическая единица =3,348⋅1024 км³
- 1 кубический световой год = 8,466⋅1038 км³
- 1 кубический парсек = 2,938⋅1040 км³
- 1 кубический килопарсек = 1 000 000 000 пк³ = 2,938⋅1049 км³
Примечания[править | править код]
- ↑ Математическая энциклопедия, 1982, с. 1149.
- ↑ Меры объёма в Древней Руси. Дата обращения: 17 ноября 2013. Архивировано 14 июля 2014 года.
- ↑ «ТЕГИЛАТ ГАШЕМ» — ISBN 965-310-008-4
Литература[править | править код]
- Объём // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
- Объём // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Ссылки[править | править код]
- Формулы объёма и программы для расчета объёма. Дата обращения: 26 ноября 2020. Архивировано 24 ноября 2020 года.
План урока:
Понятие объема
Свойства объема
Объем куба и прямоугольного параллелепипеда
Объем прямой призмы
Объем цилиндра
Понятие объема
Понятие объема появилось у человечества задолго до того, как геометрия оформилась как строгая наука. Многие вещества и товары, такие как зерно, рис и вода, необходимо хранить и транспортировать в различных упаковках (сосуды, бочки, ящики, контейнеры). При этом разные емкости могут вместить разное количество товаров. Например, пусть есть бочка, имеющая форму цилиндра, и контейнер, выглядящий как прямоугольный параллелепипед:

Предположим, что в бочку можно поместить 5 кг пшеницы, а в контейнер помещается уже 15 кг пшеницы, то есть в контейнер можно положить в 3 раза больше пшеницы, чем в бочку. Можно сказать, что вместимость контейнера втрое больше вместимости бочки. Однако измерять вместимость емкости с помощью массы пшеницы, помещаемой в него, неудобно, ведь в них можно класть и другие вещества. Мы можем положить в емкости что-нибудь более тяжелое, например сухой песок. Тогда в бочку может влезть уже 10 кг песка, а в контейнер – 30 кг. И снова получается, что вместимость контейнера втрое больше, хотя масса вещества увеличилась.
Именно для измерения вместимости и было введено понятие объема. Если в одну упаковку помещается вдвое больше товаров, чем во вторую упаковку, то и объем у нее будет вдвое больше. С древнейших времен замечено, что отношение объемов двух сосудов не зависит от того вещества, которое в них хранят. Например, если в один сосуд помещается в 5 раз больше риса, чем в другой сосуд, то в него также будет помещаться в 5 раз больше воды, в 5 раз больше песка, в 5 раз больше нефти и т. д. Таким образом, в практическом смысле объем – это количественная характеристика вместимости тех или иных упаковок.
В рамках стереометрии изучаются не реальные сосуды, а абстрактные тела. Каждое из них занимает определенную часть пространства, большую или меньшую. Объем используется для измерения этих частей пространства. Для обозначения объема используется латинская буква V.

Для измерения объема необходима единица измерения. Условно принимается, что куб, чьим ребром является единичный отрезок, имеет объем, равный единице. Такой куб именуется единичным. Заметим, что грани единичного куба – это единичные квадраты.

В случае, когда длина ребра куба является безразмерной величиной, то объем также будет безразмерной величиной. Если же указана единица измерения длины, то объем куба будет измеряться этой же единицей, к которой приписано слово «кубический». Например, если ребро куба равно 1 м, то объем куба будет равен 1 кубическому метру, или 1 м3. Объем куба с ребром 1 мм будет составлять 1 мм3 и т. д.
 ,
,
Свойства объема
Свойства объема во многом совпадают со свойствами площади. Ясно, что у равных тел будут одинаковы и объемы.

Второе свойство объема связано с тем, что он является аддитивной величиной. Это значит, что если тело можно разбить на несколько тел, то его объем будет равен сумме объемов этих тел.

Это свойство аддитивности объема уже позволяет решать некоторые стереометрические задачи.
Задание. Тело состоит из цилиндра объемом 12 см3 и конуса объемом 4 см3. Каков объем этого тела?

Решение. Здесь надо просто сложить объемы цилиндра и конуса, чтобы найти общий объем всей фигуры:

Ответ: 16 см3.
Задание. Найдите объем фигуры, показанной на рисунке:

Решение. Данную фигуру несложно разбить на три единичных куба:

Тогда объем тела будет равен сумме объемов трех единичных кубов, то есть трем:

Ответ: 3.
Задание. Вычислите объем фигуры, получающейся при рассечении куба плоскостью, проходящей через два его ребра.
Решение. Ясно, что такая секущая плоскость будет делить куб на две равные фигуры (иначе просто не удастся провести плоскость через два ребра):

Также понятно, что два получившихся многогранника равны друг другу. Обозначим объем каждого из них как V. Тогда в сумме их объем должен быть равен 1, ведь вместе эти фигуры образуют единичный куб. Это позволяет составить уравнение, из которого можно вычислить величину V:

Объем куба и прямоугольного параллелепипеда
Докажем важную вспомогательную теорему:

Действительно, пусть у двух параллелепипедов одинаковы основания. Тогда их можно совместить. Пусть общим основанием будет АВСD, а высотами параллелепипедов будут отрезки АР и АК, причем АР <АК. Объем меньшего параллелепипеда с высотой АР обозначим как VР, а большего – как VK:

Нам надо доказать, что объемы фигур пропорциональны их высотам:

Для начала рассмотрим случай, когда отношение высот является рациональным числом. Это означает, что существует некоторая дробь m/n, такая, что

где m и n – натуральные числа. Тогда разобьем отрезок АК как раз на n равных отрезков. В этом случае отрезок АР будет состоять в точности из m таких отрезков. Далее через концы отрезков проведем плоскости, параллельные основанию:

В результате мы получили n равных параллелепипедов («пластин»), которые все вместе образуют большой параллелепипед объемом VK. Поэтому объем одной такой пластины равен величине VK/n:

Итак, мы доказали теорему для случая, когда отношение высот является рациональным числом. Теперь перейдем к более сложному случаю, когда это отношение представляет собой иррациональное число. Здесь можно рассуждать от противного. Предположим, что теорема ошибочна, тогда для каких-нибудь двух параллелепипедов отношение их объемов будет равно не отношению их высот, а какому-то другому числу k:

Это значит, что k либо меньше, либо больше, чем отношение АР/АК. Рассмотрим случай, когда k< АР/АК (случай, когда k> АР/АК, рассматривается аналогичным образом). Тогда возьмем какое-нибудь рациональное число R, находящееся между числами k и АР/АК:

(Примечание. Здесь мы неявно используем утверждение, которое можно доказать в рамках алгебры – между любыми двумя различными действительными числами располагается хотя бы одно рациональное число).
Умножим это неравенство на длину АК:

Построим параллелепипеды с общим основанием АВСD и высотами АК и АР, а также с высотой АЕ = R•АК. Так как R•АК < АР, то точка Е будет лежать между А и Р:

Объем параллелепипеда с высотой АЕ обозначим как VЕ. Ясно, что

ведь число k не может быть одновременно и больше, и меньше R. Полученное противоречие означает, что исходное предположение об ошибочности теоремы неверно, и на самом деле она справедлива, ч. т. д.
Теперь с помощью доказанной теоремы можно вывести известную ещё из младших классов формулу для расчета объема прямоугольного параллелепипеда.Пусть измерения прямоугольного параллелепипеда являются числами а, b и c. Построим:
- единичный куб;
- параллелепипед с габаритами а, 1, 1 с объемом V1;
- параллелепипед с габаритами а, b, 1 с объемом V2;
- параллелепипед с габаритами а, b, c с объемом V.
Тогда можно последовательно вычислить их объемы. Объем первого параллелепипеда будет в а раз больше объема единичного куба, то есть он будет равен а. Объем второго параллелепипеда будет больше ещё в bраз, а третьего – ещё в с раз:

Соответственно, для расчета объема параллелепипеда используется формула

Иногда эту формулу формулируют несколько иначе: объем параллелепипеда – это произведение площади его основания на длину высоты, перпендикулярной этому основанию.
Задание. Три смежных ребра прямоугольного параллелепипеда имеют длины 9, 4 и 7 см. Каков объем параллелепипеда?
Решение. Здесь надо просто перемножить габариты параллелепипеда:

Ответ: 252 см3.
Куб можно рассматривать как прямоугольный параллелепипед с одинаковыми измерениями. Поэтому для вычисления его объема надо умножить ребро куба само на себя дважды, то есть возвести его в куб.

Задание. Вычислите объем куба с ребром 8 метров.
Решение. Просто возводим сторону ребро куба в третью степень:

Задание. Если ребро куба увеличить на 2 дм, то его объем вырастет на 98 дм3. Какова длина ребра этого куба?
Решение. Обозначим длину ребра буквой х. Тогда объем куба будет составлять х3 дм. Если ребро увеличить на 2 дм, то оно будет иметь длину х + 2 дм, и тогда объем куба будет равен уже (х + 2)3 дм. Условие задачи можно записать в виде уравнения:

Это квадратное уравнение имеет два корня, 3 и (– 5), что можно проверить с помощью теоремы Виета. Корень х = – 5 не имеет геометрического смысла, поэтому остается ответ х = 3.
Ответ: 3 дм.
Далее рассмотрим перевод единиц измерения объема. Например, как перевести 1 м3 в кубические сантиметры? Рассмотрим куб с ребром 1 м. Ясно, что его объем будет равен 1 м3. С другой стороны, можно сказать, что длина ребра этого куба составляет 100 см:

Тогда объем этого куба можно посчитать так:

Аналогично можно переводить и другие единицы измерения.
Объем прямой призмы
Рассмотрим сначала прямую призму, в чьем основании располагается прямоугольный треугольник. Ее можно достроить до прямоугольного параллелепипеда:

Ясно, что объем параллелепипеда будет вдвое больше объема исходной призмы, ведь он состоит из двух таких призм. Аналогично и площадь основания у параллелепипеда будет вдвое больше. Обозначим площадь основания призмы буквой S, а ее высоту как h, тогда площадь основания параллелепипеда будет 2S, а его объем составит 2S•h. Тогда объем призмы будет вдвое меньше, то есть он окажется равным S•h.

Далее рассмотрим прямую призму, в основании которой лежит уже произвольный треугольник. Проведем в этом треугольнике высоту, которая упадет на противоположную сторону (такую высоту всегда можно провести). Далее через эту высоту проведем плоскость, перпендикулярную основанию. В результате мы разделим призму на две прямых призмы, в основании каждой из которых будет лежать прямоугольный треугольник:

Пусть площади получившихся прямоугольных треугольников обозначены как S1и S2, а общая площадь основания исходной призмы – это S. Мы можем вычислить объемы этих призм:

Теперь, наконец, рассмотрим прямую призму, чье основание – произвольный многоугольник. Этот многоугольник можно разбить на несколько треугольников с площадями S1, S2, S3…, а призма соответственно будет разбита на несколько треугольных призм с объемами V1, V2, V3 и. т. д.

Объем каждой треугольный призмы мы можем рассчитать:

Задание. Все ребра правильной шестиугольной призмы одинаковы, их длина обозначена буквой а. Найдите объем такой призмы.
Решение. Сначала необходимо найти площадь основания призмы, то есть площадь правильного шестиугольника. Напомним формулы для правильных многоугольников, изученные ещё в девятом классе:

Для вычисления объема надо лишь умножить полученную площадь на высоту призмы, а она также равна а:

Задание. В кубе АВСDА1В1С1D1 через середины ребер СD и BC проведено сечение, параллельное ребру СС1. Это сечение отсекает от куба треугольную призму, чей объем равен 19. Найдите объем куба.

Решение. Ясно, что и куб, и треугольная призма будут прямыми призмами, причем у них одинаковая высота СС1. Тогда можно утверждать, что отношение их объемов равно отношению площадей их оснований:

Пусть сторона АВ имеет длину а. Тогда площадь квадрата АВСD будет составлять а2. Отрезки ЕС и FC будут вдвое короче АВ, то есть их длина составляет a/2. ∆EFC – прямоугольный, и его площадь может быть рассчитана как половина произведения его катетов:

Объем цилиндра
Цилиндр не получится разбить на несколько призм, поэтому для вычисления его объема используется другой метод. Впишем цилиндр в правильную n-угольную призму. Одновременно построим и другую правильную n-угольную призму, которая сама будет вписана в цилиндр. Объем вписанной призмы обозначим как Vв, а объем описанной призмы как Vо. Объем самого цилиндра – это Vц. При этом высоты всех трех фигур одинаковы:

Ясно, что объем вписанной призмы меньше объема цилиндра, а тот в свою очередь меньше объема описанной призмы:

Теперь будем неограниченно увеличивать число n. При этом площади Sв и Sо будут стремиться к площади основания цилиндра, равной величине πr2, где r– радиус основания цилиндра. Это возможно лишь в том случае, если справедливо равенство

Задание. Найдите объем цилиндра с высотой 5 см и радиусом 6 см.
Решение. Сначала находим площадь основания:

Задание. Известно, что высота цилиндра вдвое больше его радиуса, а объем цилиндра равен 54π. Найдите радиус цилиндра.
Решение. Обозначим радиус цилиндра буквой х. Тогда по условию высота будет вдвое больше, то есть она составит 2х. Вычислим объем цилиндра:

Ответ: 3.
Задание. Труба изготовлена из металла с плотностью 11,4 г/см3. Внутренний диаметр трубы равен 13 мм, а ее стенка имеет толщину 4 мм. Длина трубы – 25 метров. Какова ее масса?

Решение. Для расчета массы необходимо сперва вычислить объем трубы. Ясно, что если к объему трубы прибавить объем внутреннего отверстия, то в итоге получится объем большого цилиндра, чей диаметр равен наружному диаметру трубы:

Легко найти объем отверстия, ведь оно имеет форму цилиндра. Его радиус вдвое меньше диаметра, то есть он равен 13/2 = 6,5 мм. При расчете важно не забыть перевести высоту в миллиметры:

Сегодня мы узнали о такой характеристике тел, как объем. Если объем куба и прямоугольного параллелепипеда мы умели находить ещё в средней школе, то определять объем цилиндра и прямой призмы мы научились только сейчас. Однако все эти случаи по сути одинаковы – надо перемножить высоту фигуры и площадь ее основания. В будущем мы научимся вычислять объемы более сложных фигур – пирамиды, конуса, шара.
Загрузить PDF
Загрузить PDF
Объем фигуры представляет собой занимаемое этой фигурой трехмерное пространство.[1]
Представьте себе объем как количество жидкости (или воздуха, или песка), которым можно заполнить данную фигуру. Объем измеряется в кубических единицах (мм3, см3, м3).[2]
Эта статья расскажет вам, как вычислять объем шести трехмерных фигур. Вы можете заметить, что многие формулы для вычисления объема схожи, что упрощает их запоминание.
-

1
Куб – это трехмерная фигура, которая имеет шесть одинаковых квадратных граней, то есть все ее стороны (ребра) равны.[3]
- Например, игральная кость – это куб.
-

2
Формула нахождения объема куба: V = s3, где V – объем, а s – длина ребра.
- Возведение в куб аналогично следующему умножению: s3 = s * s * s
-

3
Найдите длину стороны (ребра) куба. Она будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой). Так как ребра куба равны, измеряйте любое ребро.
- Если вы не уверены, что ваша фигура является кубом, измерьте каждую сторону, чтобы убедиться, что они равны. Если они не равны, перейдите к следующему разделу.
-

4
Подставьте длину ребра куба в формулу V = s3. Например, если ребро куба равно 5 см, напишите формулу следующим образом: V = 53 = 5 * 5 * 5 = 125 см3 – это объем куба.
-

5
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребро куба измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах. Если, например, сторона куба равна 3 см, то V = 33 = 27см3.
Реклама
-

1
Прямоугольный параллелепипед или прямоугольная призма – это трехмерная фигура с шестью гранями, каждая из которых является прямоугольником (вспомните коробку из под обуви). [4]
- Куб – это частный случай прямоугольного параллелепипеда, у которого все ребра равны.
-

2
Формула нахождения объема прямоугольного параллелепипеда или прямоугольной призмы: V = l*w*h, где V = объем, l = длина, w = ширина, h = высота.[5]
-

3
Длина прямоугольного параллелепипеда – это самое длинное ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Длина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: длина прямоугольного параллелепипеда равна 4 см, то есть l = 4 см.
- Не беспокойтесь о том, какие ребра выбрать в качестве длины, ширины и высоты. В любом случае в итоге вы получите правильный ответ (только измерьте три ребра, перпендикулярные друг другу).
-

4
Ширина прямоугольного параллелепипеда – это самое короткое ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Ширина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: ширина прямоугольного параллелепипеда равна 3 см, то есть w = 3 см.
- Если вы измеряете ребра параллелепипеда линейкой или рулеткой, не забудьте измерить их в одинаковых единицах измерения. Не измеряйте одно ребро в миллиметрах, а другое в сантиметрах.
-

5
Высота прямоугольного параллелепипеда – это расстояние между его нижней и верхней гранями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: высота прямоугольного параллелепипеда равна 6 см, то есть h = 6 см.
-

6
Подставьте найденные значения в формулу V = l*w*h.
- В нашем примере l = 4, w = 3 и h = 6. Поэтому V = 4*3*6 = 72.
-

7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребра измерялись в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 72 см3.
- Если в прямоугольной призме l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см3
Реклама
-

1
Цилиндр – это трехмерная фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.[6]
- Например, банка или батарейка АА имеют форму цилиндра.
-

2
Формула нахождения объема цилиндра: V = πr2h, где V – объем, h – высота, r – радиус основания и πr2 – площадь основания цилиндра.
- В некоторых задачах ответ требуется представить с пи, а в некоторых вместо пи подставить 3,14.
- Формула для нахождения объема цилиндра на самом деле очень похожа на формулу вычисления объема прямоугольной призмы, то есть вы перемножаете высоту и площадь основания. В прямоугольной призме площадь основания равна l*w, а в цилиндре она равна πr2.
-

3
Найдите радиус основания. Он, скорее всего, дан в задаче. Если дан диаметр, разделите его на 2, чтобы найти радиус (d = 2r).
-

4
Если радиус не дан, измерьте его. Для этого измерьте основание цилиндра при помощи линейки или рулетки. Измеряйте основание в его самой широкой части (то есть измерьте диаметр основания), а затем разделите полученное значение на 2, чтобы найти радиус.
- Другой вариант – измерьте длину окружности цилиндра (то есть измерьте обхват цилиндра) при помощи рулетки, а затем найдите радиус по формуле r = с/2π, где с – обхват (длина окружности) цилиндра (2π = 6,28).
- Например, если обхват цилиндра равен 8 см, то радиус будет равен 1,27 см.
- Если вам нужно точное измерение, вы можете использовать оба метода, чтобы убедиться, что значения радиуса совпадают (нахождение радиуса через длину окружности является более точным методом).
-

5
Вычислите площадь круглого основания. Для этого подставьте радиус в формулу πr2.
- Если радиус основания равен 4 см, то площадь основания равна π42.
- 42 = 4 * 4 = 16. 16*π = 16*3,14 = 50,24 см2
- Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус.
-

6
Найдите высоту цилиндра. Это расстояние между двумя круглыми основаниями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
-

7
Умножьте площадь основания на высоту цилиндра, чтобы найти его объем. Или же просто подставьте значения соответствующих величин в формулу V = πr2h. В нашем примере, когда радиус основания равен 4 см, а высота равна 10 см:
- V = π4210
- π42 = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
-

8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 502,4 см3.
Реклама
-

1
Пирамида – это трехмерная фигура, в основании которой лежит многоугольник, а грани являются треугольниками, имеющими общую вершину. [7]
Правильная пирамида – это трехмерная фигура, в основании которой лежит правильный многоугольник (с равными сторонами), а вершина проецируется в центр основания.[8]
- Обычно мы представляем пирамиду, имеющую квадратное основание, но в основании пирамиды может лежать многоугольник с 5, 6 или даже со 100 сторонами!
- Пирамида с круглым основанием называется конусом, который будет обсуждаться в следующем разделе.
-

2
Формула нахождения объема правильной пирамиды: V = 1/3bh, где b – площадь основания пирамиды, h – высота пирамиды (перпендикуляр, соединяющий основание и вершину пирамиды).
- Эта формула для вычисления объема пирамиды одинаково годна как для правильных пирамид (в которых вершина проецируется в центр основания), так и для наклонных (в которых вершина не проецируется в центр основания).
-

3
Вычислите площадь основания. Формула будет зависеть от фигуры, лежащей в основании пирамиды. В нашем примере в основании пирамиды лежит квадрат со стороной 6 см. Площадь квадрата равна s2, где s – сторона квадрата. Таким образом, в нашем примере площадь основания пирамиды равна 62 = 36 см2
- Площадь треугольника равна 1/2bh, где h – высота треугольника, b – сторона, к которой проведена высота.
- Площадь любого правильного многоугольника можно вычислить по формуле: А = 1/2ра, где А – площадь, р – периметр фигуры, а – апофема (отрезок, соединяющий центр фигуры с серединой любой стороны фигуры). Для получения дополнительной информации о нахождении площади многоугольников прочитайте эту статью.[9]
-

4
Найдите высоту пирамиды. Высота будет дана в задаче. В нашем примере высота пирамиды равна 10 см.
-

5
Умножьте площадь основания пирамиды на ее высоту, а затем разделите полученный результат на 3, чтобы найти объем пирамиды. Формула для вычисления объема пирамиды: V = 1/3bh. В нашем примере площадь основания равна 36, а высота равна 10, поэтому объем: 36*10*1/3 = 120.
- Если, например, дана пирамида с пятиугольным основанием площадью 26, а высота пирамиды равна 8, то объем пирамиды: 1/3*26*8 = 69,33.
-

6
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 120 см3.
Реклама
-

1
Конус – это трехмерная фигура, которая имеет круглое основание и одну вершину. Или конус – это особый случай пирамиды с круглым основанием.[10]
- Если вершина конуса находится непосредственно над центром круглого основания, то конус называется прямым; в противном случае конус называется наклонным. Но формула для вычисления объема конуса одинаковая для обоих типов конуса.
-

2
Формула для вычисления объема конуса: V = 1/3πr2h, где r – радиус круглого основания, h – высота конуса.
- b = πr2 – это площадь круглого основания конуса. Таким образом, формулу для вычисления объема конуса можно записать так: V = 1/3bh, что совпадает с формулой нахождения объема пирамиды!
-

3
Вычислите площадь круглого основания. Радиус должен быть дан в задаче. Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Для вычисления площади круглого основания подставьте радиус в формулу πr2.
- Например, радиус круглого основания конуса равен 3 см. Тогда площадь этого основания равна π32.
- π32 = π(3*3) = 9π.
- = 28,27 см2
-

4
Найдите высоту конуса. Это перпендикуляр, опущенный из вершины к основанию пирамиды. В нашем примере высота конуса равна 5 см.
-

5
Перемножьте высоту конуса и площадь основания. В нашем примере площадь основания равна 28,27 см2, а высота равна 5 см, поэтому bh = 28,27 * 5 = 141,35.
-

6
Теперь умножьте полученный результат на 1/3 (или просто разделите его на 3), чтобы найти объем конуса. В описанном выше шаге вы нашли объем цилиндра, а объем конуса всегда в 3 раза меньше объема цилиндра.
- В нашем примере: 141,35 * 1/3 = 47,12 – это объем конуса.
- Или: 1/3π325 = 47,12
-

7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 47,12 см3.
Реклама
-

1
Шар – это идеально круглая трехмерная фигура, каждая точка поверхности которой равноудалена от одной точки (центра шара). [11]
-

2
Формула для вычисления объема шара: V = 4/3πr3, где r – радиус шара.[12]
-

3
Найдите радиус шара. Радиус должен быть дан в задаче. Если дан диаметр шара, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Например, радиус шара равен 3 см.
-

4
Если радиус не дан, вычислите его. Для этого измерьте длину окружности шара (например, теннисного мяча) в его самой широкой части при помощи веревки, нити или другого подобного предмета. Затем измерьте длину веревки, чтобы найти длину окружности. Разделите полученное значение на 2π (или на 6,28), чтобы вычислить радиус шара.
- Например, если вы измерили мяч и нашли, что длина его окружности равна 18 см, разделите это число на 6,28 и получите, что радиус мяча равен 2,87 см.
- Проделайте 3 измерения окружности шара, а затем усредните полученные значения (для этого сложите их и сумму разделите на 3), чтобы убедиться, что вы получили значение, близкое к истинному.
- Например, в результате трех измерений длины окружности вы получили следующие результаты: 18 см, 17,75 см, 18,2 см. Сложите эти значения: 18 + 17,5 + 18,2 = 53,95, а затем разделите их на 3: 53,95/3 = 17,98. Используйте это среднее значение в расчетах объема шара.
-

5
Возведите радиус в куб (r3). То есть r3 = r*r*r. В нашем примере r = 3, поэтому r3 = 3 * 3 * 3 = 27.
-

6
Теперь умножьте полученный результат на 4/3. Вы можете использовать калькулятор или выполнить умножение вручную, а затем упростить дробь. В нашем примере: 27*4/3 = 108/3 = 36.
-

7
Умножьте полученный результат на π (3,14), чтобы найти объем шара.
- В нашем примере: 36*3,14 = 113,09.
-

8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 113,09 см3.
Реклама
Об этой статье
Эту страницу просматривали 74 580 раз.
Была ли эта статья полезной?
11. Сюжетные текстовые задачи
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на растворы, смеси и сплавы
(blacktriangleright) Концентрация вещества в растворе (сплаве) – это процент содержания этого вещества в растворе (сплаве): [text{концентрация вещества}=dfrac{text{масса вещества}}{text{масса раствора}}cdot 100%]
(blacktriangleright) Заметим, что в задачах из данной подтемы зачастую удобно составлять уравнения относительно кислоты или активного вещества.
Задание
1
#846
Уровень задания: Равен ЕГЭ
Сергей смешал раствор, содержащий (20%) кислоты и раствор, содержащий (40%) той же кислоты. В итоге у него получился раствор, содержащий (32,5%) кислоты, причём объём полученного раствора (4) литра. Сколько литров раствора, содержащего (20%) кислоты, использовал Сергей при смешивании?
Пусть (x) литров раствора, содержащего (20%) кислоты использовал Сергей при смешивании, тогда
(4 – x) литров раствора, содержащего (40%) кислоты использовал Сергей при смешивании,
(dfrac{20}{100}x) – объём кислоты в растворе, содержащем (20%) кислоты, (dfrac{40}{100}(4 – x)) – объём кислоты в растворе, содержащем (40%) кислоты.
Так как в итоге кислоты оказалось (dfrac{32,5}{100} cdot 4 = 1,3) литра, то:
[dfrac{20}{100}x + dfrac{40}{100}(4 – x) = 1,3,] откуда находим (x = 1,5).
Ответ: 1,5
Задание
2
#844
Уровень задания: Равен ЕГЭ
Один газ в сосуде А содержал (21%) кислорода, второй газ в сосуде В содержал (5%) кислорода. Масса первого газа в сосуде А была больше массы второго газа в сосуде В на 300 г. Перегородку между сосудами убрали так, что газы перемешались и получившийся третий газ теперь содержит (14,6%) кислорода. Найдите массу третьего газа. Ответ дайте в граммах.
Пусть (x) грамм – масса второго газа, тогда
(x + 300) грамм – масса первого газа,
(dfrac{21}{100}(x + 300)) грамм – масса кислорода в первом газе,
(dfrac{5}{100}x) грамм – масса кислорода во втором газе,
тогда масса кислорода в третьем газе составляет (dfrac{14,6}{100}(2x + 300)) грамм.
Так как третий газ возник в результате смешивания первого и второго, то:
[dfrac{21}{100}(x + 300) + dfrac{5}{100}x = dfrac{14,6}{100}(2x + 300),] откуда находим (x = 600). Таким образом, масса третьего газа равна (600 + 600 + 300 = 1500) грамм.
Ответ: 1500
Задание
3
#843
Уровень задания: Равен ЕГЭ
Иван случайно смешал молоко жирностью (2,5%) и молоко жирностью (6%). В итоге у него получилось 5 литров молока жирностью (4,6%). Сколько литров молока жирностью (2,5%) было у Ивана до смешивания?
Пусть (x) литров молока жирностью (2,5%) было у Ивана, тогда
(5 – x) литров молока жирностью (6%) было у Ивана,
(dfrac{2,5}{100}x) – объём жира в молоке жирностью (2,5%), (dfrac{6}{100}(5 – x)) – объём жира в молоке жирностью (6%).
Так как в итоге жира оказалось (dfrac{4,6}{100} cdot 5 = 0,23) литра, то:
(dfrac{2,5}{100}x + dfrac{6}{100}(5 – x) = 0,23), откуда находим (x = 2).
Ответ: 2
Задание
4
#841
Уровень задания: Равен ЕГЭ
В сосуде А содержится 3 литра 17-процентного водного раствора вещества Х. Из сосуда В в сосуд А перелили 7 литров 19-процентного водного раствора вещества Х. Сколько процентов составляет концентрация полученного в сосуде А раствора?
Концентрация в процентах – это отношение объёма вещества к объёму смеси, умноженное на 100(%). До переливания в сосуде А было (3 cdot 0,17 = 0,51) литра вещества Х, в сосуде В было (7 cdot 0,19 = 1,33) литра вещества Х.
После переливания объём вещества Х в сосуде А стал (0,51 + 1,33 = 1,84) литра, а объём всего раствора (3 + 7 = 10) литров. Тогда концентрация в процентах составила [dfrac{1,84}{10} cdot 100% = 18,4%.]
Ответ: 18,4
Задание
5
#2133
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (5)-процентного раствора кислоты, чем объём (10)-процентного раствора той же кислоты, чтобы при смешивании получить (7)-процентный раствор?
Пусть объём (5)-процентного раствора кислоты равен (x) литров, а объём (10)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,05x + 0,1y = 0,07(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = dfrac{3}{2} = 1,5,,] таким образом, ответ: (1,5).
Ответ: 1,5
Задание
6
#2134
Уровень задания: Равен ЕГЭ
Во сколько раз больше должен быть объём (20)-процентного раствора кислоты, чем объём (14)-процентного раствора той же кислоты, чтобы при смешивании получить (18)-процентный раствор?
Пусть объём (20)-процентного раствора кислоты равен (x) литров, а объём (14)-процентного раствора равен (y) литров, тогда требуется найти значение величины (dfrac{x}{y}) при условии [0,2x + 0,14y = 0,18(x + y)
qquadLeftrightarrowqquad
dfrac{x}{y} = 2,,] таким образом, ответ: (2).
Ответ: 2
Задание
7
#2629
Уровень задания: Равен ЕГЭ
Смешав (25)-процентный и (95)-процентный растворы кислоты и добавив (20) кг чистой воды, получили (40)-процентный раствор кислоты. Если бы вместо (20) кг воды добавили (20) кг (30)-процентного раствора той же кислоты, то получили бы (50)-процентный раствор кислоты. Сколько килограммов (25)-процентного раствора использовали для получения смеси?
Заметим, что вода – это раствор, не содержащий кислоту, то есть содержащий (0%) кислоты.
Пусть (x) кг – масса раствора с (25)-процентным содержанием кислоты, (y) кг – масса раствора с (95)-процентным содержанием кислоты. Составим схему, описывающую получение (40)-процентного раствора:
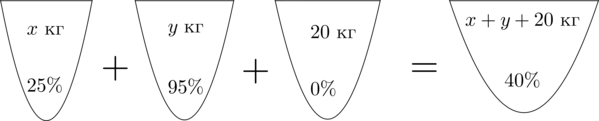
Заметим, что количество кислоты во всех трех растворах равно количеству кислоты в получившемся растворе. Найдем количество кислоты в первом растворе.
Если раствор весит (x) кг, а в нем (25%) кислоты, то в килограммах в нем (dfrac{25}{100}cdot x) кислоты.
Таким же образом можно посчитать количество кислоты в остальных растворах. Получим первое уравнение:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{0}{100}cdot 20=dfrac{40}{100}cdot (x+y+20)]
Аналогично составим схему, описывающую получение (50)-процентного раствора:
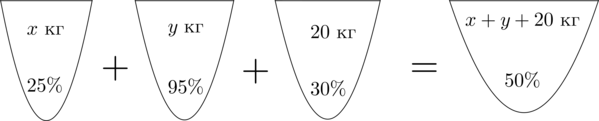
Значит, уравнение, описывающее эту ситуацию, будет выглядеть так:
[dfrac{25}{100}cdot x+dfrac{95}{100}cdot y+
dfrac{30}{100}cdot 20=dfrac{50}{100}cdot (x+y+20)]
Таким образом, решив систему из полученных двух уравнений, найдем (x). Для этого можно умножить оба уравнения на (100), чтобы сделать их проще на вид:
[begin{cases}
25x+95y+0=40(x+y+20)\
25x+95y+30cdot 20=50(x+y+20)
end{cases}]
Вычтем из второго уравнения первое и получим новую систему:
[begin{aligned} &begin{cases}
25x+95y=40(x+y+20)\
30cdot 20=10(x+y+20)
end{cases} quad Rightarrow quad begin{cases}
5x+19y=8(x+y+20)\
y=40-x end{cases} quad Rightarrow \[2ex] Rightarrow quad
&begin{cases}
3x-11(40-x)+160=0\
y=40-x end{cases} quad Rightarrow quad begin{cases}
x=20\y=20end{cases} end{aligned}]
Таким образом, раствора с (25%) кислоты было (20) кг.
Ответ: 20

УСТАЛ? Просто отдохни

