In geometry, an octagon is a polygon with eight sides. A regular octagon has eight equal sides and equal angles. The regular octagon is commonly recognized from stop signs. An octahedron is an eight-sided polyhedron. A regular octahedron has eight triangles with edges of equal length. It is effectively two square pyramids meeting at their bases.
Octagon Area Formula
The formula for the area of a regular octagon with sides of length “a” is 2(1+sqrt(2))a^2, where “sqrt” indicates the square root.
Derivation
An octagon can be viewed as 4 rectangles, one square in the center and four isosceles triangles in the corners.
The square is of area a^2.
The triangles have sides a, a/sqrt(2) and a/sqrt(2), by the Pythagorean theorem. Therefore, each has an area of a^2/4.
The rectangles are of area a * a/sqrt(2).
The sum of these 9 areas is 2a^2 (1 + sqrt(2)).
Octahedron Volume Formula
The formula for the volume of a regular octahedron of sides “a” is a^3 * sqrt(2)/3.
Derivation
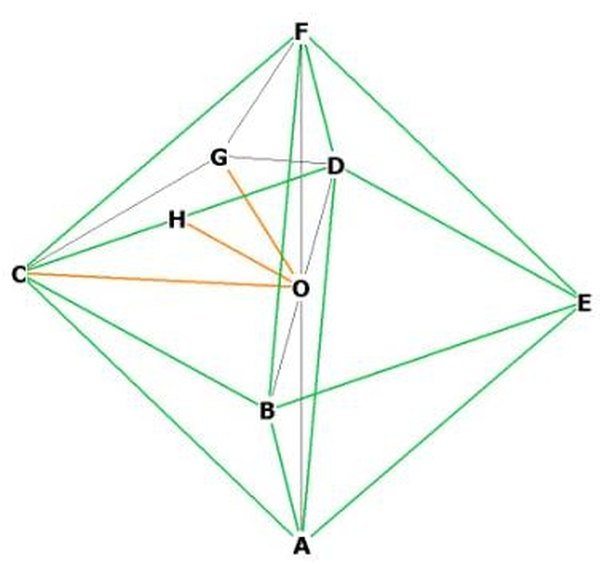
The area of a four-sided pyramid is area of base * height / 3. The area of a regular octagon is therefore 2 * base * height / 3.
Base = a^2 trivially.
Pick two adjacent vertices, say “F” and “C.” “O” is at the center. FOC is an isosceles right triangle with base “a,” so OC and OF have length a/sqrt(2) by the Pythagorean theorem. So height = a/sqrt(2).
So the volume of a regular octahedron is 2 * (a^2) * a/sqrt(2) / 3 = a^3 * sqrt(2) / 3.
Surface Area
The regular octahedron’s surface is the area of an equilateral triangle of side “a” times 8 faces.
To use the Pythagorean theorem, drop a line from the apex to the base. This creates two right triangles, with the hypotenuse of length “a” and one side length “a/2.” Therefore, the third side must be sqrt[a^2 – a^2/4] = sqrt(3)a/2. So the area of an equilateral triangle is height * base/2 = sqrt(3)a/2 * a/2 = sqrt(3)a^2/4.
With 8 sides, the surface area of a regular octahedron is 2 * sqrt(3) * a^2.
Чтобы рассчитать объем октаэдра, можно воспользоваться on-line калькулятором. Он поможет сделать правильные вычисления. Октаэдра – это восьмигранник, который часто встречается в математических науках. Онлайн калькулятор для вычисления объема – удобная программа, которая не требует особых знаний.
Здесь нужно только указать длину ребра октаэдра. Далее программа сделает все сама. Пару секунд и на экране появится число, которое и является показателем объема. Выполняя расчеты объема октаэдра, вы с данным калькулятором сделаете все значительно быстрее. Мгновенное вычисление – это преимущество данной программы.
Инструкция
– Введите данные.
– Нажмите “Вычислить объем октаэдра”.
Объем октаэдра определяется по формуле:
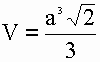
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Объем октаэдра
Объем тел
Октаэдром (восьмигранником) является многогранник, у которого имеется 8 граней. Все грани октаэдра являются равносторонними треугольниками. У октаэдра насчитывается 6 вершин и 12 ребер. Зная длину ребра октаэдра, можно определить его объем по формуле:
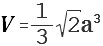
a — длина ребра.
Т.е. найдя произведение длины ребра в кубе на корень квадратный из 2 и разделив все это на 3, мы получим величину объема октаэдра.
Чтобы вычислить объем октаэдра с помощью онлайн калькулятора, вам не понадобится особых знаний и не потребуется много времени. Нужно лишь ввести в формулу исходные данные.
Расчет объема октаэдра онлайн
Вычисление правильного восьмиугольника (многоугольник с восемью вершинами). Эта форма хорошо нам знакома, так как используется на некоторых дорожных знаках.
.
Поделиться расчетом:
Калькулятор восьмиугольника, введите одно известное значение
Длина стороны(a)
Меньшая диагональ(d1)
Средняя диагональ(e)
Большая диагональ(d3)
Периметр(p)
Площадь(S)
Радиус описанной окружности(R)
Радиус вписанной окружности(r)
Вычислить
Очистить
Формулы:
 d = a * √4 + 2 * √2
d = a * √4 + 2 * √2
e = a * ( 1 + √2 )
f = a * √2 + √2
Высота = e = 2 * r
Р = 8 * а
S = 2 * a2 * ( 1 + √2 )
R = a / 2 * √4 + 2 * √2
r = a / 2 * ( 1 + √2 )
Угол: 135°, 20 диагоналей.
Зная объем октаэдра, можно вычислить его ребро, путем извлечения кубического корня из трех объемов, деленных на квадратный корень из двух.
a=∛(3V/√2)
Высота октаэдра проходит через его внутреннюю область, соединяя две вершины четырехугольных пирамид. Таким образом, из любой пирамиды можно найти половину высоты октаэдра, и получить ее значение, умножив полученную цифру на два. Высота октаэдра через объем выглядит как кубический корень из трех объемов, деленных на четыре.
h=∛(3V/4)
Чтобы найти периметр октаэдра, необходимо умножить значение ребра на их количество. Если выразить периметр через объем октаэдра, то получится шесть кубических корней из объема, умноженного на 12 корней из двух.
P=6∛(12√2) V
Чтобы вычислить площадь полной поверхности октаэдра через объем, можно совместить коэффициенты для ребра октаэдра в формуле с коэффициентами, приведенными для объема, тогда получится, что площадь октаэдра равна кубическому корню из 36 корней из шести объемов.
S=∛(36√6 V)
В октаэдр также можно вписать сферу, радиус которой будет равен одной шестой кубического корня из 18 корней из трех, умноженных на объем. Радиус сферы, описанной около октаэдра, равен половине кубического корня из шести объемов.
r=∛(18√3 V)/6
R=∛6V/2
