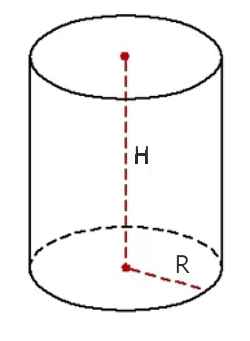
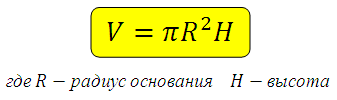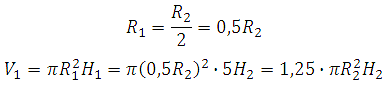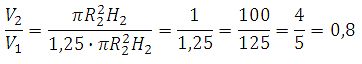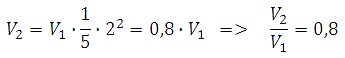Как найти обьем второго цилиндра высота в - Сайт, где вы сможете решить свои вопросы

Определение цилиндра

Цилиндр — геометрическое тело, получаемое при вращении прямоугольника вокруг какой-либо его стороны.

Онлайн-калькулятор объема цилиндра

Это определение самого простого, так называемого, прямого кругового цилиндра. Более полное и общее определение цилиндра следующее:

Цилиндром называют геометрическое тело, которое получается путем пересечения двух плоскостей, которые параллельны друг другу, с прямыми, которые так же параллельны друг другу.

Эти прямые получили название образующих цилиндра. Плоскости – это основания цилиндра.
Прямая, которая перпендикулярна плоскостям, содержащим основания цилиндра, называется высотой данного цилиндра.

Типы цилиндров

Они зависят от того, под каким углом пересекаются основания и образующие цилиндра. Если угол равен 90 градусам, тогда цилиндр называется прямым. Линия, которая соединяет центр одного основания с другим, называется осью симметрии. Если угол не прямой, то цилиндр называется наклонным (косым).

Если форма основания цилиндра — гипербола, то цилиндр гиперболический, если парабола, круг или эллипс, то, соответственно параболический, круговой и эллиптический.

Формула объема кругового цилиндра

Для того, чтобы вычислить объем прямого кругового цилиндра нужно просто умножить площадь его основания (то есть, площадь круга, лежащего в основании цилиндра) на высоту этого цилиндра.

Формула объема кругового цилиндра

V=Sосн⋅hV=S_{text{осн}}cdot h

SоснS_{text{осн}} — площадь основания цилиндра;
hh — высота этого цилиндра.

Для кругового цилиндра, площадь основания SоснS_{text{осн}} это площадь круга:

Sосн=π⋅R2S_{text{осн}}=picdot R^2

RR — радиус круга.

Рассмотрим несколько примеров.

Задача 1

Найдите объем цилиндра, если площадь его основания равна 196π см2196pitext{ см}^2, а его высота hh в 2 раза больше радиуса основания RR.

Решение

Sосн=196πS_{text{осн}}=196pi
h=2⋅Rh=2cdot R

Сначала вычисляем радиус основания:

Sосн=π⋅R2S_{text{осн}}=picdot R^2

Выразим отсюда радиус RR:

R2=SоснπR^2=frac{S_{text{осн}}}{pi}

R=SоснπR=sqrt{frac{S_{text{осн}}}{pi}}

R=196ππR=sqrt{frac{196pi}{pi}}

R=196R=sqrt{196}

R=14R=14

По условию задачи, высота цилиндра в два раза больше RR:

h=2⋅R=2⋅14=28h=2cdot R=2cdot 14=28

Тогда объем цилиндра по формуле:

V=Sосн⋅h=196⋅π⋅28≈17232 см3V=S_{text{осн}}cdot h=196cdotpicdot28approx17232text{ см}^3

Ответ

17232 см3.17232text{ см}^3.

Задача 2

Определить, чему равен объем цилиндра, если радиус его основания RR равен 7 см7text{ см}, а высота – 14 см14text{ см}.

Решение

R=7R=7
h=14h=14

По формуле для объема цилиндра получаем:

V=Sосн⋅h=π⋅R2⋅h=π⋅72⋅14≈2154 см3V=S_{text{осн}}cdot h=picdot R^2cdot h=picdot7^2cdot14approx2154text{ см}^3

Ответ

2154 см3.2154text{ см}^3.

Задача 3

В квадрат со стороной aa равной 4 см4text{ см} вписана окружность, являющаяся основанием цилиндра, высота которого равна 20 см20text{ см}. Вычислите его объем.

Решение

a=4a=4
h=20h=20

Исходя из того, что сторона квадрата, в который вписана окружность, равна диаметру DD этой окружности, можно найти площадь основания цилиндра:

Sосн=π⋅R2=π⋅D24=π⋅a24=π⋅424≈12.56S_{text{осн}}=picdot R^2=frac{picdot D^2}{4}=frac{picdot a^2}{4}=frac{picdot 4^2}{4}approx12.56

Объем цилиндра:

V=Sосн⋅h≈12.56⋅20=251.2 см3V=S_{text{осн}}cdot happrox12.56cdot20=251.2text{ см}^3

Ответ

251.2 см3.251.2text{ см}^3.

На нашем сайте вы можете оформить решение задач по геометрии на заказ у профильных экспертов!

Тест по теме «Объем цилиндра»

Источник

Как найти объем второго цилиндра?

Alvares Antonio

Ученик

(99),
закрыт

11 лет назад

Объем первого цилиндра равен 12 кубометрам. У второго цилиндра высота в три раза больше, а радиус основания – в два раза меньше, чем у первого.
По каким формулам найти объем второго цилиндра?

AL

Мастер

(1017)

11 лет назад

Vцилиндра=пи*радиус в квадрате*высоту
объём 2-ого цил. =пи*радиус в квадрате: 2*3 *высоту
так как объём 1-ого цилиндра равен 12, то 3*12:4=9
ответ: 9

Источник

Объём цилиндра. Здравствуйте, дорогие друзья! В этой статье мы с вами рассмотрим две задачи, в условии которых речь идёт об изменении параметров цилиндра, а именно радиуса основания и высоты. Поставленный вопрос касается изменения объёма. Необходимо знать формулу объёма цилиндра:

Также нужно понимать как «связать» объёмы двух данных тел учитывая условие задачи. Основная рекомендация будет такой:

1. Выражаем объёмы цилиндров, различно обозначив их радиусы и высоты (R₁и Н₁ также R₂и Н₂).

2. Затем связываем формально эти величины используя данные в условии.

3. Далее выражаем объёмы цилиндров через один и тот же радиус основания и высоту.

4. Затем определив взаимосвязь без труда можно ответить на поставленный вопрос, не важно требуется ли найти отношение объёмов, или конкретный объём одного из цилиндров.

На примерах ниже всё подробно посмотрим.

27053. Объем первого цилиндра равен 12 м³. У второго цилиндра высота в три раза больше, а радиус основания — в два раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах.

Нужно найти как соотносятся объёмы цилиндров. Обозначим радиус основания 2-го цилиндра как R₂, а высоту как Н₂. Тогда её объем будет равен:

Объём первого цилиндра соответственно будет равен:

Сказано, что у второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, то есть можем записать:

Подставим значения высоты и радиуса в формулу (1) и получим объём второго цилиндра выраженный через высоту и радиус первого:

Получили, что объём второго цилиндра равен 0,75 объёма первого. Таким образом:

Ответ: 9

*Примечание! Есть ещё путь рассуждения для решения данной задачи. Посмотрите, высота второго цилиндра в три раза больше — это значит, что если мы так увеличим высоту, то объём второго цилиндра станет 36 м³. Затем при уменьшении радиуса основания этого цилиндра в два раза мы получим (0,5R)²=0,25R².

То есть произойдёт уменьшение в 4 раза и объём получится 36:4=9 м³. И решение задачи укладывается в одну строчку V₂=12∙3∙0,25=9.

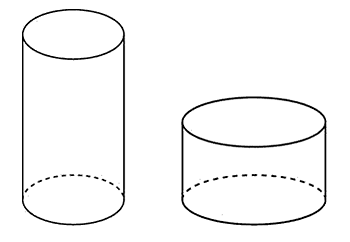
Первая цилиндрическая кружка в пять раз выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.

Нам необходимо найти отношение объёмов. Обозначим радиус основания 2-й кружки как R₂, а высоту как Н₂. Тогда её объем будет равен:

Объём первой кружки соответственно:

Сказано, что первая кружка в пять раз выше второй, а вторая в два раза шире, то есть можем записать:

Выразим R₁ и запишем формулу объёма для первой кружки:

Таким образом, отношение объема второй кружки к объему первой будет равно:

Ответ: 0,8

*Примечание! Решение можно записать кратко в таком виде:

Пояснение: взяли первый цилиндр, уменьшили его высоту в пять раз, а радиус увеличили в два раза (учитываем квадрат радиуса) и получили зависимость объёмов. Далее просто выразили отношение.

27118. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

Посмотреть решение

С уважением, Александр.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Как посчитать объем цилиндра

Главная
/
Математика
/
Геометрия
/
Как посчитать объем цилиндра

Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

радиус r и высоту h цилиндра
диаметр d и высоту h цилиндра
площадь основания S_o и высоту h цилиндра
площадь боковой поверхности S_b и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра если его радиус

r = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

V = π⋅r²⋅h

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 2² ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см³

Зная диаметр d и высоту h

Чему равен объем цилиндра если его диаметр

d = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

V = π⋅(^d/₂)²⋅h

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ (¹/₂)² ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см³

Зная площадь основания S_o и высоту h

Чему равен объем цилиндра если площадь его основания

S_o = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его площадь основания S_o и высота h?

Формула

V = S_o⋅h

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания S_o = 5 см², то:

V = 10 ⋅ 5 = 50 см³

Зная площадь боковой поверхности S_b и высоту h

Чему равен объем цилиндра если площадь его боковой поверхности

S_b = ,

а высота

h = ?

Ответ: V =

Чему равен объем цилиндра V если известны его площадь боковой поверхности S_b и высота h?

Формула

V = ^S_b²/_4πh

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности S_b = 30 см², то:

V =^30²/_{4 ⋅ 3.14⋅ 5} = ⁹⁰⁰/_62.8 = 14.33 см³

См. также

Источник

10
Сен 2013

Категория: 02 Стереометрия

02. Цилиндр.

2013-09-10
2022-09-11

Задача 1. Радиус основания цилиндра равен высота равна Найдите площадь боковой поверхности цилиндра, деленную на .

Решение: + показать

Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен Найдите высоту цилиндра.

Решение: + показать

Задача 3. Длина окружности основания цилиндра равна высота равна Найдите площадь боковой поверхности цилиндра.

Решение: + показать

Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на .

Решение: + показать

Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м).

Решение: + показать

Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

Решение: + показать

Задача 7. В цилиндрический сосуд налили см воды. Уровень воды при этом достигает высоты см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на см. Чему равен объем детали? Ответ выразите в см

Решение: + показать

Задача 8. В цилиндрический сосуд налили см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в раза. Найдите объем детали.

Ответ выразите в см

Решение: + показать

Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в сантиметрах.