Как найти объем второго шара - Сайт, где вы сможете решить свои вопросы

Тема 2.

Геометрия в пространстве (стереометрия)

Отношение площадей поверхностей и отношение объемов тел

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами – ЛЕГКО!

Подтемы раздела

геометрия в пространстве (стереометрия)

Решаем задачи

Во сколько раз уменьшится объем конуса, если радиус его основания останется прежним, а высота уменьшится в 3
раза?

Показать ответ и решение

Пусть площадь основания конуса равна а его высота равна Тогда объём конуса равен

1
V1 = 3Sh

Если высота уменьшится в 3 раза, то объем конуса станет равен

( )
V2 = 1S⋅ h- = 1Sh = V1
3 3 9 3

Тогда объем конуса уменьшится в 3 раза.

Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в 2 раза?

Показать ответ и решение

Пусть — изначальный радиус шара. Площадь поверхности шара вычисляется по формуле

2
S = 4πR

После увеличения радиуса шара в 2 раза площадь поверхности равна

2 2
S1 = 4π(2R ) =16πR

Это в 4 раза больше, чем изначальная площадь поверхности.

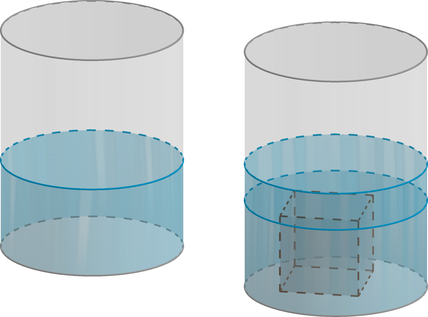
В сосуд цилиндрической формы, объем которого 2400 см, налили жидкость, заполнив сосуд
на треть, а затем в жидкость полностью погрузили некоторый предмет, вследствие чего
уровень жидкости в сосуде поднялся на четверть. Найдите объем предмета в кубических
сантиметрах.

Показать ответ и решение

Объем цилиндра вычисляется по формуле , где – радиус основания, – высота. Таким
образом, во сколько раз увеличивается/уменьшается высота цилиндра, во столько же раз
увеличивается/уменьшается объем цилиндра.
Следовательно, если жидкость заполнила сосуд лишь на треть, то есть высота жидкости в 3 раза
меньше высоты сосуда, то и объем жидкости в 3 раза меньше объема сосуда, следовательно, объем
жидкости равен см.

Так как после погружения в жидкость предмета уровень повысился на четверть, то и занимаемый в
сосуде объем повысился на четверть.
Закон Архимеда гласит, что объем вытесненной жидкости равен объему погруженного в нее предмета.
Следовательно, объем предмета равен четверти объема жидкости, то есть см.

В цилиндрическом сосуде уровень жидкости достигает см. На какой
высоте будет находиться уровень жидкости, если её перелить во второй
цилиндрический сосуд, диаметр которого в 2,5 раза больше диаметра первого?
Ответ дайте в сантиметрах.

В цилиндрическом сосуде уровень воды достигает 384 см. На какой высоте будет находиться уровень воды, если её перелить во
второй цилиндрический сосуд, диаметр которого в 8 раз больше диаметра первого? Ответ дайте в сантиметрах.

Показать ответ и решение

Пусть уровень воды в первом цилиндрическом сосуде равен см, а во втором — см.

Пусть диаметр первого сосуда равен см. Тогда площадь дна этого сосуда равна

π⋅D2
S1 = --4--см2

Значит, объем воды в сосуде равен

2
V = S1h1 = π-⋅D ⋅384 см3
4

По условию диаметр второго сосуда равен см. Тогда площадь его дна равна

π⋅(8D-)2 2
S2 = 4 см

Так как количество воды не изменилось, то

π⋅(8D)2
V = S2h2 = ---4---⋅h2 см3

Тогда искомый уровень воды равен

π-⋅D2- π⋅D2-
h = V- = --4--⋅384-= --4--⋅384= 384-= 6 см
2 S2 π⋅(8D)2 π-⋅D2 ⋅64 64
4 4

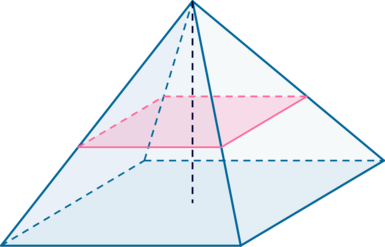
В правильной четырехугольной пирамиде с высотой через точку на боковом ребре, лежащую на расстоянии 1h
3 от плоскости
основания, проведена плоскость, параллельная плоскости основания, которая отсекает от пирамиды меньшую пирамиду. Найдите
объем полученной меньшей пирамиды, если объем исходной пирамиды равен 54.

Показать ответ и решение

Также отсюда следует, что 2
SQ = 3SO .

, следовательно,

′ ′ ′
2-= SA-- = A-B-- ⇒ A ′B ′ = 2AB
3 SA AB 3

Таким образом, объемы маленькой и большой пирамид относятся как

( ) ( )
Vм 1⋅ SQ ⋅ A ′B ′2 SQ A ′B′ 2 2 2 2 8
---= 31----------2--= ----⋅ ----- = --⋅ -- = ---
Vб 3 ⋅ SO ⋅ AB SO AB 3 3 27

Следовательно, объем маленькой пирамиды равен

Vм = 8--⋅ 54 = 16.
27

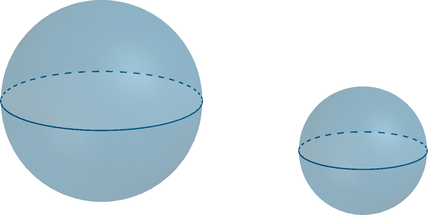
Радиус первого шара в 5 раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади
поверхности первого шара?

Показать ответ и решение

Площадь поверхности шара радиуса ищется по формуле Следовательно, площадь поверхности первого шара
относится к площади поверхности второго шара как

2 2
S1 = 4πR12= R12-
S2 4πR2 R2

Так как радиус первого шара больше радиуса второго шара в 5 раз, то Следовательно,

S (5R )2
S1= -R22--= 25
2 2

Тогда площадь поверхности второго шара в 25 раз меньше площади поверхности первого.

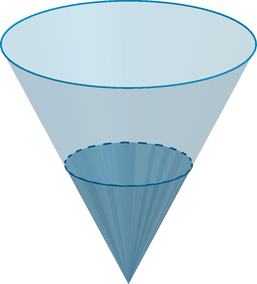
Сосуд имеет форму конуса и вмещает в себя 2700 мл жидкости. Определите, сколько мл жидкости
налито в сосуд, если высота жидкости в 3 раза меньше высоты сосуда.

Показать ответ и решение

QB--= QS--= 1-
OA OS 3

Тогда объем налитой жидкости к объему всего сосуда относится как

Следовательно объем жидкости равен

Vж = 1-V = 100
27

В сосуд, имеющий форму конуса, налили 75 грамм жидкости до половины высоты сосуда. Сколько
грамм этой же жидкости нужно долить в сосуд, чтобы заполнить его доверху?

Показать ответ и решение

OA-- OS-- 2-
QB = QS = 1

так
как по условию высота жидкости в два раза меньше высоты сосуда. Тогда для жидкости
имеем:

Следовательно, весь сосуд вмещает этой же жидкости

( )
1- 2 1- 2 1- 2
m = V ρ = 3 ⋅π⋅OS ⋅OA ⋅ρ = 3 ⋅π ⋅2QS ⋅(2QB ) ⋅ρ = 8 ⋅ 3 ⋅ π ⋅ QS ⋅ QB ⋅ ρ = 8⋅75 = 600 грам м

Значит, долить нужно

Заметим, что в данной задаче использование плотности – чистая формальность.

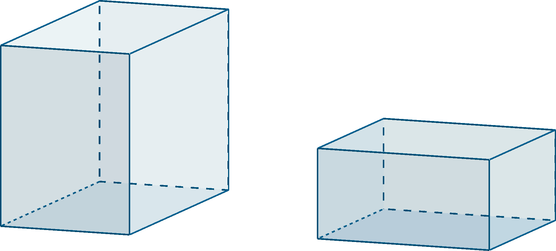
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного
параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго,
ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины
второго.

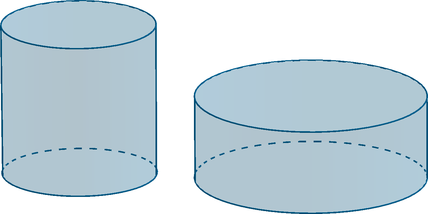
Объем первого цилиндра равен 16, причем известно, что его радиус в 7 раз меньше радиуса второго цилиндра, а высота второго
цилиндра в 8 раз меньше высоты первого. Найдите объем второго цилиндра.

Показать ответ и решение

Объем цилиндра с высотой и радиусом основания ищется по формуле Тогда объем первого относится к объему
второго цилиндра как

2 ( )2
16 = πR-12H1-= R1- ⋅ H1
V2 πR 2H2 R2 H2

Из условия следует, что R1 = 1R2,
7 H2 = 1H1,
8 следовательно,

(1 )2
16 = 7R2- ⋅1H1-= -1 ⋅8 ⇒ V2 = 98
V2 R2 8H1 49

Площадь боковой поверхности первого цилиндра равна . Найдите площадь боковой поверхности
второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты
первого цилиндра.

Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса
как 3 : 7 . Найдите отношение образующей первого конуса к образующей второго конуса, если радиус
первого конуса относится к радиусу второго как 15 : 7 .

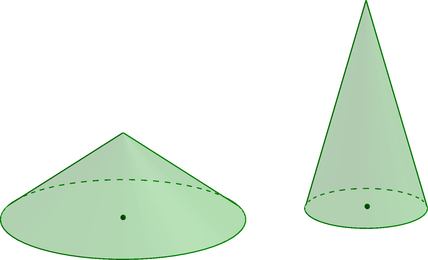
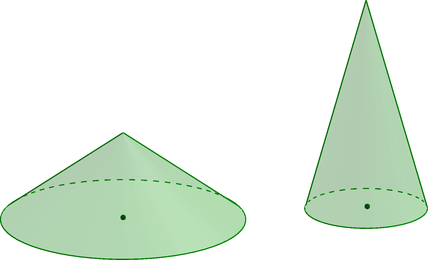
Даны два конуса. Радиус второго конуса в 3 раза больше радиуса первого конуса, а высота второго конуса в 6 раз меньше высоты
первого конуса. Найдите объем первого конуса, если объем второго конуса равен 18.

Показать ответ и решение

Объем конуса с высотой и радиусом основания вычисляется по формуле V = 1πR2h.
3 Следовательно, объем первого конуса
относится к объему второго конуса как

1 2 ( )2
V1= V1= 31π-R12h1 = R1- ⋅ h1
18 V2 3π R2h2 R2 h2

Так как радиус второго в 3 раза больше радиуса первого, то Так как высота второго в 6 раз меньше высоты первого,
то Следовательно,

( )2
V1= R1-- ⋅ 6h2= 1 ⋅6= 2 ⇒ V1 = 2⋅18= 12
18 3R1 h2 9 3 3

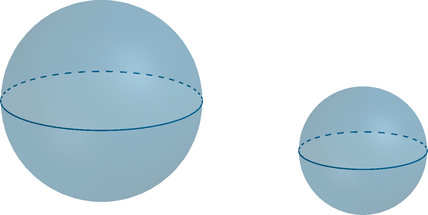
Объем первого шара равен равен 54. Найдите объем второго шара, если его радиус в 3 раза меньше радиуса первого
шара.

Показать ответ и решение

Объем шара радиуса ищется по формуле 4 3
V = 3 πR . Следовательно, объем первого шара относится к объему второго
как

4 3 ( )3
54= V1 = 3π-R1= R1-
V2 V2 43π R32 R2

Так как радиус второго шара в 3 раза меньше радиуса первого шара, то следовательно,

( )3
54 = 3R2- = 27 ⇒ V2 = 54 = 2
V2 R2 27

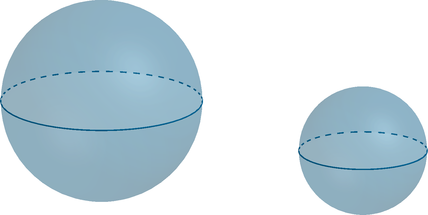
Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в 343
раза больше объема второго шара?

Показать ответ и решение

Объем шара радиуса ищется по формуле 4
V = --πR3
3 . Следовательно, объем первого шара относится
к объему второго как

4 3 ( )3 √ ----
343-= V1-= -3πR-1= R1- ⇒ R1- = 3343 = 7.
1 V2 43πR32 R2 R2

Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Радиус первого шара равен 6, а радиус второго шара равен 2. Во сколько раз объем первого шара больше объема второго
шара?

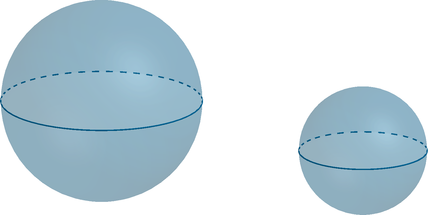
Показать ответ и решение

4 3 ( )3
V1 = 3π-⋅6-= 6 = 27
V2 43π ⋅23 2

Следовательно, объем первого шара в 27 раз больше объема второго шара.

Показать ответ и решение

Пусть – объём шара, ограниченного первой сферой. Так как радиус в два раза больше, чем
радиус , то .

следовательно, .

Источник

Понятие шарового сегмента

Если пересечь шар какой-либо плоскостью, то он разделиться на две части, каждая из которых и будет представлять собой шаровой сегмент. Иногда его также называют сферическим сегментом.

Онлайн-калькулятор объема шарового сегмента

Меньший из этих сегментов принято называть сферическим кругом. Если же центр сферы лежит на плоскости, пересекающей шар, то он делится на два равных полушара.

Формула объема шарового сегмента

Объем данного тела можно вычислить несколькими способами. Первая формула такова:

1. Объем шарового сегмента

V=13⋅π⋅h2⋅(3⋅R−h)V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)

hh —высота шарового сегмента;
RR — радиус шара.

Альтернативная формула:

2. Объем шарового сегмента

V=16⋅π⋅h⋅(3⋅r2+h2)V=frac{1}{6}cdotpicdot hcdot(3cdot r^2+h^2)

hh —высота шарового сегмента;
rr — радиус основания шарового сегмента.

Вторую формулу можно получить из первой, если использовать связь между RR, hh и rr:

R=r2+h22⋅hR=frac{r^2+h^2}{2cdot h},

получаемую с помощью теоремы Пифагора для прямоугольного треугольника.

Ниже приведены примеры задач на нахождение объемов шарового сегмента.

Задача 1

Вычислите объем шарового сегмента, если известны его высота и радиус основания. Равны они, соответственно, 4 см4text{ см} и 8 см8text{ см}.

Решение

h=4h=4
r=8r=8

По второй формуле получаем:

V=16⋅π⋅h⋅(3⋅r2+h2)=16⋅π⋅4⋅(3⋅82+42)≈435.4 см3V=frac{1}{6}cdotpicdot hcdot(3cdot r^2+h^2)=frac{1}{6}cdotpicdot 4cdot(3cdot 8^2+4^2)approx435.4text{ см}^3

Ответ

435.4 см3.435.4text{ см}^3.

Задача 2

Рассмотрим предыдущую задачу, но проделаем вычисления по другой формуле. Для этого нам нужно найти радиус шара RR.

Решение

h=4h=4
r=8r=8

R=r2+h22⋅h=82+422⋅4=10R=frac{r^2+h^2}{2cdot h}=frac{8^2+4^2}{2cdot 4}=10

Объем сегмента:

V=13⋅π⋅h2⋅(3⋅R−h)=13⋅π⋅42⋅(3⋅10−4)≈435.4 см3V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)=frac{1}{3}cdotpicdot 4^2cdot(3cdot 10-4)approx435.4text{ см}^3

Исходя из полученных ответов можно сделать вывод, что данная формула справедлива, так как ответы полученные разными формулами совпадают.

Ответ

435.4 см3.435.4text{ см}^3.

Задача 3

Определить объем шарового сегмента, если площадь его поверхности равна 64 см64text{ см}, а высота – 5см5text {см}.

Решение

S=64S=64
h=5h=5

Для начала найдем радиус RR шара. Площадь поверхности шарового сегмента можно найти так:

S=2⋅π⋅R⋅hS=2cdotpicdot Rcdot h.

Найдем отсюда радиус RR шара:

R=S2⋅π⋅h=642⋅π⋅5≈2R=frac{S}{2cdotpicdot h}=frac{64}{2cdotpicdot 5}approx2

Объем шарового сегмента по формуле:

V=13⋅π⋅h2⋅(3⋅R−h)≈13⋅π⋅52⋅(3⋅2−5)≈26 см3V=frac{1}{3}cdotpicdot h^2cdot(3cdot R-h)approxfrac{1}{3}cdotpicdot 5^2cdot(3cdot 2-5)approx26text{ см}^3

Ответ

26 см3.26text{ см}^3.

Хотите заказать выполнение контрольной работы у опытного исполнителя? Оформите заказ на нашей бирже!

Источник

{V = pi h^2 Big( R – dfrac{1}{3} h Big) }

На странице содержится калькулятор и формула для расчета объема шарового сегмента. Введите радиус шара и высоту сегмента и тут же получите результат.

Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.

Формула объёма шарового сегмента

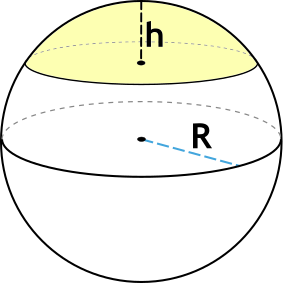
{V = pi h^2 Big( R – dfrac{1}{3} h Big)}

R – радиус шара

h – высота шарового сегмента

Примеры задач на нахождение объема шарового сегмента

Задача 1

Найдите обьем шарового сектора,если радиус шара равен 6см,а высота соответствующего сегмента составляет шестую часть диаметра шара.

Решение

Для решения задачи нам сначала необходимо найти высоту шарового сегмента. Помня о том, что диаметр – это два радиуса, получим, что диаметр шара составляет 2 • 6см = 12см. А так как высота шарового сегмента составляет шестую часть диаметра, то поделим 12см на 6 и получим высоту шарового сегмента 2см.

Теперь осталось применить формулу, подставив в нее значения и произвести вычисления.

V = pi h^2 Big( R – dfrac{1}{3} h Big) = pi cdot 2^2 cdot Big( 6 – dfrac{1}{3} 2 Big) = pi cdot 4 cdot dfrac{16}{3} = dfrac{64}{3} pi : см^3

Получившаяся дробь является неправильной, ее можно преобразовать в смешанную.

dfrac{64}{3} = 21dfrac{1}{3}

Итоговый ответ можно записать так 21dfrac{1}{3} pi : см^3 approx 67.02064 : см^3

Ответ: 21dfrac{1}{3} pi : см^3 approx 67.02064 : см^3

Осталось проверить ответ с помощью калькулятора .

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем сегмента шара, а также разберем пример решения задачи для закрепления теоретического материала.

Определение сегмента шара
Формулы для нахождения объема шарового сегмента
- Через радиус шара и высоту сегмента
- Через радиус основания сегмента и его высоту
Пример задачи

Определение сегмента шара

Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.

R – радиус шара;
r – радиус основания сегмента;
h – высота сегмента; это длина перпендикуляра от центра его основания (точка O₂) до точки на поверхности шара.

Формулы для нахождения объема шарового сегмента

Пояснения:

В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
Число π округленно равняется до 3,14.