Как найти объем выборки на примере – Сайт, где вы сможете решить свои вопросы

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

пример неправильного размера выборки, как опеределить размер выборки

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p – ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p – ∆; p + ∆) = (20% – 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ – ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ – ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Источник

Формула выборки — простая Приведенная ниже формула для расчета объема выборки используется в тех случаях, когда опрашиваемым (респондентам) задается только один вопрос, на который существует только два варианта ответа. Например: «Да» и «Нет», «Покупаю» и «Не покупаю», «Пользуюсь» и «Не пользуюсь». Конечно, данную формулу можно применять только при проведении простейших исследований. Если Вам нужно определить объем выборочной совокупности при проведении более масштабных исследований, например анкетирования, то следует использовать другие формулы.

Содержание:

формула с пояснениями;
пример расчета объема выборки;
нормированное отклонение (таблица);
область применения;
особенности формулы.

Простая формула для расчета объема выборки

Ниже приведена простая формула для расчета объема выборки для тех случаев когда на заданный вопрос возможны лишь два варианта ответа:

Формула выборки — простая

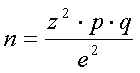
где: n – объем выборки;

z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности (доверительного интервала, доверительной вероятности).

Этот показатель характеризует вероятность попадания ответов в специальный доверительный интервал — диапазон, границам которого соответствует определенный процент определенных ответов на некоторый вопрос.

Можно сказать, что уровень доверительности выражает вероятность того, что респонденты генеральной совокупности ответят так же, как и представители анализируемой выборки.

На практике доверительный интервал при проведении маркетинговых исследований часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58.

Также существует специальная таблица «Значение интеграла вероятностей», используя которую можно найти значение z для различных доверительных интервалов. Сокращенный вариант такой таблицы приведен ниже;

p – вариация для выборки, в долях.

Вариация характеризует величину схожести / несхожести ответов респондентов на вопрос. По сути, p — вероятность того, что респонденты выберут той или иной вариант ответа.

Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;

q = 1 – p.

Можно сказать, что q — это вероятность того, что респонденты не выберут анализируемый вариант ответа (в нашем примере ответят «Нет»). Например, если p = 0,25, то q = 1 – 0,25 = 0,75;

e – допустимая ошибка, в долях.

Значение допустимой ошибки заранее определяют исследователь и заказчик маркетингового исследования.

Пример расчета объема выборочной совокупности

Маркетинговая компания получила заказ на проведение социологического исследования с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».

Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95% (одно из стандартных значений для маркетинговых исследований), тогда нормированное отклонение z = 1,96. Проведя предварительный анализ населения города, вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они — «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. исходя из требуемой заказчиком точности, допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.

Подставляем эти данные в формулу и считаем:

Расчет выборки

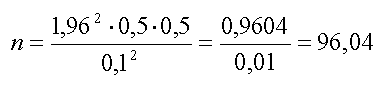
Округлив расчетное значение, получаем объем выборки n = 96 человек.

Следовательно, для проведения исследования с заданными параметрами (уровень доверительности, допустимая ошибка) компании необходимо опросить 96 человек.

Значение нормированного отклонения для различных доверительных интервалов

В таблице приведены некоторые значения нормированного отклонения (z) для важнейших уровней доверительности, или, иначе, доверительной вероятности (α):

α (%)	60	70	80	85	90	95	97	99	99,7
z	0,84	1,03	1,29	1,44	1,65	1,96	2,18	2,58	3,0

Конечно, в таблице приведены значения z только для основных уровней доверительности. Полную версию таблицы можно найти в интернете.

Область применения простой формулы выборки

При проведении простых исследований, когда нужно получить ответ всего на один простой вопрос. При этом шкала ответов, как правило, дихотомического характера. То есть предлагаются (или подразумеваются) варианты ответов по типу «Да» — «Нет», «Черное» — «Белое», «Куплю» — «Не куплю», и т. д. Иными словами возможны лишь два варианта ответа на заданный вопрос.

Особенности формулы расчета размера выборки

Для рассмотренной нами простой формулы определения объема выборки можно выделить несколько характерных особенностей:

перед тем, как рассчитывать объем выборки в данном случае желательно предварительно провести качественный анализ изучаемой генеральной совокупности. В частности установить степень схожести, близости изучаемых единиц совокупности в части их социальных, демографических, географических, иных характеристик. Также полезно провести пилотное (разведочное) исследование, чтобы установить приблизительную величину p;
нужно иметь в виду, что максимальная изменчивость (вариация ответов) соответствует значению p = 50%, так как тогда q = 50% и p × q = 0,5 × 0,5 = 0,25. Это наихудший случай, все другие значения p дадут изменчивость меньшего размера (например, при p = 80%, p × q = 0,8 × 0,2 = 0,16; а при p = 10%, p × q = 0,1 × 0,9 = 0,09). Впрочем, данный показатель влияет на объем выборки не очень сильно.

Также стоит отметить, что существует ряд иных формул для определения объема выборки в случаях с дихотомической шкалой ответов на единственный вопрос. Для более сложных маркетинговых исследований применяются другие формулы.

Источники

Голубков Е. П. Маркетинговые исследования: теория, методология и практика. – М.: Издательство «Финпресс», 1998.

Статья дополнена и доработана автором 10 дек 2020 г.

Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.

Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Формула выборки – простая // Сайт преподавателя экономики. [2020]. URL: https://galyautdinov.ru/post/formula-vyborki-prostaya (дата обращения: 19.05.2023).

Источник

Запуск рекламной кампании в маркетинге предполагает А/В-тестирование, однако не каждый проведенный тест будет показательным, а его результаты – значимыми для статистики. Одна из распространенных ошибок при проведении исследований – неправильное определение нормального размера выборки. Как следствие – запуск рекламы, которая не даст результатов, и зря потраченные деньги.

Что такое объем выборки

Объем выборки – это количество людей из общего числа целевой аудитории (ЦА) продукта или бренда, участвовавших в исследовании, или количество заполненных анкет, которые были учтены при подсчете результатов.

Что такое размер выборки

Выборка

Термин «выборка» говорит о том, что из всей совокупности участников опроса проводится оценка лишь части ответов.

В зависимости от параметров проекта, которые были указаны изначально, выборка может быть разной. Например, при случайной выборке респонденты выбираются из целевой совокупности случайным образом.

Зачем необходимо рассчитывать

Объем выборки определяют перед запуском количественных исследований в маркетинге (например, контент-анализа), чтобы узнать, какое число представителей ЦА должно поучаствовать в тестировании, и получить достоверные результаты. Если данных о объеме выборки нет, это может стать причиной того, что исследователь получит некорректные результаты.

Для качественных исследований объем выборки не определяют. Также он неактуален, если речь идет о проведении пилотных, т. е. предварительных исследований.

Основные понятия определения

В определении размера выборки участвуют различные параметры:

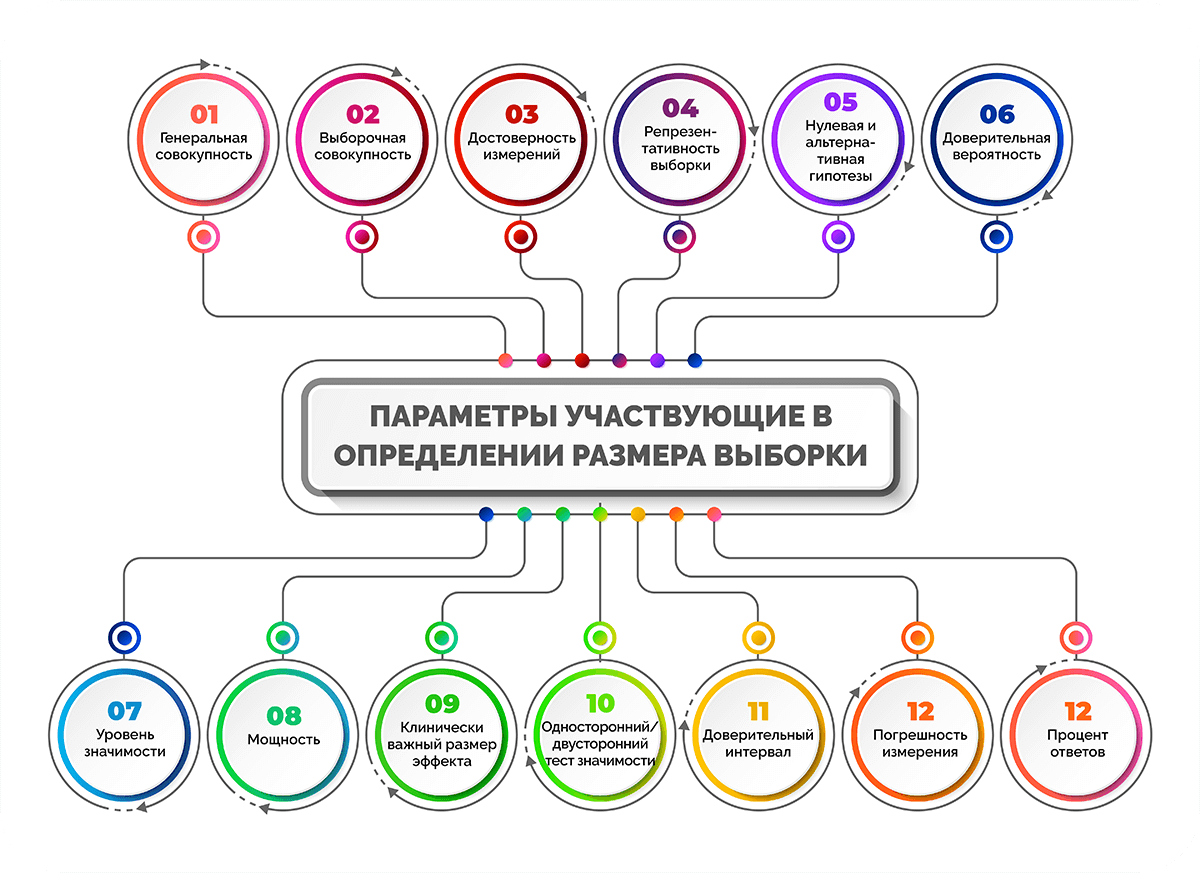
Параметры участвующие в определении размера выборки

Параметры

генеральная совокупность;
выборочная совокупность;
достоверность измерений;
репрезентативность выборки;
нулевая и альтернативная гипотезы;
доверительная вероятность;
уровень значимости;
мощность;
клинически важный размер эффекта;
односторонний / двусторонний тест значимости;
доверительный интервал;
погрешность измерения;
процент ответов.

Разберем, что означают основные из них.

Генеральная совокупность

Генеральной совокупностью называется общее количество объектов наблюдения, которые обладают определенными общими признаками (возраст, пол, оборот, численность, доход и пр.) и о которых будут сделаны заявления после обработки результатов исследования.

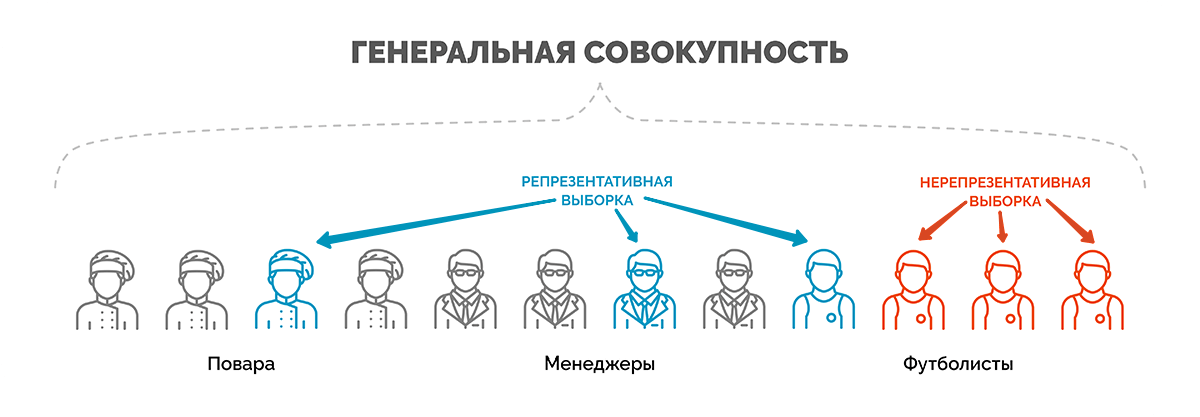
Генеральная совокупность

Пример

Объектами наблюдения могут быть люди, предприятия, домохозяйства, населенные пункты, отдельные малые социальные группы и т. д.

Если известно, что результаты опроса касаются всех жителей Москвы, то генеральная совокупность будет равна общей численности населения города, т. е. 13 млн человек (по данным 2021 года).

Оценивать свойства генеральный совокупностей, основываясь на выборочных методах, позволяет кривая нормального распределения.

Выборочная совокупность

Выборка или выборочная совокупность – это некоторая часть объектов из числа генеральной совокупности, отобранная для участия в исследовании с целью оценить распределение мнений и сделать итоговое заключение, которое будет распространяться на всю генеральную совокупность.

Характеристики выборочной совокупности должны корректно отражать параметры генеральной совокупности, т. е. обладать свойством репрезентативности. Только в данном случае заключение, сделанное исходя из результатов анализа выборки, будет с одинаковой вероятностью распространяться на представителей всей генеральной совокупности.

Выборка, состоящая из работников московских предприятий, не будет репрезентировать население города трудоспособного возраста и особенно все население столицы, т. к. не включает неработающих людей, женщин в декрете, удаленных сотрудников и т. д. Даже если мы будем увеличивать количество опрошенных работников столичных компаний, выборка все равно не сможет отразить характеристики генеральной совокупности, т. е. всего трудоспособного населения Москвы.

Погрешность измерений

Допустимая погрешность измерений – это процент возможной ошибки или отклонения результатов исследования, т. е. то значение, на которое истинный показатель может откланяться от значения, полученного в результате исследования.

Чем меньше погрешность, тем больше должна быть выборка.

Результаты опроса показали, что 60% опрощенных предпочитают делать покупки в сетевых магазинах. Предел погрешности 5% говорит о том, что в генеральной совокупности доля сторонников сетевых точек продаж может увеличиться или уменьшиться на 5% относительно уровня полученных 60%. Т. е. фактическое значение будет лежать в пределах значений от 55 до 65%.

Достоверность измерений

Уровень достоверности (надежности) измерений – это вероятность того, что полученные в результате исследования истинные результаты выбранного параметра генеральной совокупности находятся в пределах ее доверительного интервала (в примере выше это интервал 55-65%). Простыми словами, это степень уверенности в репрезентативности результатов.

Чем меньше доверительный интервал и выше заданный уровень достоверности, тем больше должна быть выборочная совокупность.

Если взять приведенный выше в статье пример с погрешностью в 5%, вы можете быть уверены в следующем: вероятность того факта, что от 55 до 65% людей предпочитают совершать покупки в сетевых магазинах, составляет не менее 95%.

Репрезентативность выборки

Под репрезентативностью понимают степень соответствия характеристик выборочной совокупности характеристикам генеральной совокупности, которые можно экстраполировать на всю популяцию.

выборка, состоящая на 100% из автомобилистов Санкт-Петербурга, не репрезентирует всех жителей Санкт-Петербурга;
выборка, состоящая только из российских фирм B2B с количеством сотрудников до 200 человек, не репрезентирует все компании страны, работающих в этом сегменте.

Исследование должно быть репрезентативным, если стоит задача по результатам количественного исследования сформировать представление о популяции в целом и правильно оценить ее. Если же исследование качественное или люди опрашиваются ради сбора мнений, предложений, идей, в этом случае репрезентативная выборка практически не играет роли.

Что влияет на результаты

Результаты тестирования могут изменяться под влиянием ряда факторов:

Факторы влияющие на результат

Факторы

количество вводных данных для анализа результатов;
правильность постановки гипотезы;
выбор той или иной метрики (показателя, переменных) для исследования;
количество тестируемых вариантов;
мощность исследования;
уровень статистической значимости;
стандартное отклонение (коэффициент) для количественных метрик;
клинически значимый эффект;
одно- / двусторонний тест значимости;
наличие парных данных в тестировании;
повторное измерение одних и тех же показателей;
равенство численности групп, участвующих в исследовании;
наличие иерархических данных.

Также расчет размера выборки может давать разные результаты, если анализ является:

рандомизированным и контролируемым;
рандомизированным и кластерным;
нерандомизированным экспериментом вмешательства;
исследованием эквивалентности;
исследованием распространенности;
обсервационным;
изучением специфичности и чувствительности теста.

Нерандомизированные тестирования взаимосвязей или различий предполагают задействования в маркетинговых исследованиях выборки гораздо большего размера, чтобы при анализе было не сложно учесть влияние третьих факторов.

Типы выборок

Различают два типа выборок: вероятностные и невероятностные или детерминированные. Каждая группа включает в себя виды. Разберем, какие из них входят в каждый тип.

Типы выборок

Типы

Вероятностные выборки:

Случайная или простой случайный отбор – предполагает полный список элементов (отбираются при помощи таблицы случайных чисел), равную вероятность доступности всех из них и однородную генеральную совокупность;
Механическая или систематическая – выступает в качестве разновидности случайной выборки, при этом упорядочивание происходит по тому или иному признаку, причем первый элемент отбирается случайно, затем с шагом n отбирается каждый последующий элемент;
Стратифицированная или районированная – выборка используется при неоднородной генеральной совокупности, которая разделяется на страты (группы), в каждой из которых выполняется случайный отбор пропорционально их доле в генеральной совокупности;
Серийная или кластерная, или гнездовая – единицами отбора выступают целые группы (гнезда или кластеры), которые могут попасть в выборку случайным образом, а все объекты внутри них подлежат сплошному исследованию.

Невероятностные (детерминированные) выборки:

Квотная выборка – формируется несколько групп объектов, в каждой из которых зачастую пропорционально доле в генеральной совокупности задается определенное число объектов, которые нужно исследовать;
Метод снежного кома – для формирования выборки каждый участник опроса предоставляет контакты своих знакомых; применяется для исследования труднодоступных групп респондентов;
Стихийная выборка или выборка «первого встречного» – ее состав и размер заранее неизвестен и зависит от активности людей, опрос проводится среди самых доступных респондентов (интернет-опросы, опросы в журналах и газетах, анкеты на самозаполнение и т. д.);
Выборка типичных случаев – для исследования отбираются отдельные представители генеральной совокупности, которым присуще среднее значение исследуемого признака.

Отбор в детерминированных выборках происходит не случайно, а по субъективным критериям: типичности, доступности, равного представительства каждой стороны и пр.

Расчет объема выборки

Расчет объема выборки – своего рода компромисс между требуемой мощностью исследования и возможностью реализовать его на практике с учетом имеющихся ресурсов и фокус-группы. При этом выбор метода расчета во многом определяется знаниями о параметрах и характеристиках изучаемых параметров.

Определить объем выборки можно двумя способами: по таблицам и с помощью формулы. Разберем эти методы.

По таблицам

Когда никаких данных о предстоящем исследовании нет, а сам эксперимент является инновационным, никто ранее ничего подобного не проводил и не предлагал решения, для определения объема выборки лучше выбрать табличный метод.

Ниже представлены различные методики. Выбор той или иной из них определяется имеющимися исходными данными или пожеланиями исследователя.

Таблица А. Определение объема выборки по методике К. А. Отдельновой

Уровень значимости	Уровень точности
Ориентировочное знакомство	Исследование средней точности	Исследование высокой точности
0,01	100	225	900
0,05	44	100	400

Объем выборки указан в абсолютных значениях.

Таблица Б. Методика определения размера выборки В. И. Паниотто

Размер генеральной совокупности	500	1000	2000	3000	4000	5000	10000	100000	∞
Объем выборки	222	286	333	350	360	370	385	398	400

Данные указаны в единицах.

Таблица В. Методика N. Fox для определения объема выборки

Процент допускаемой ошибки	Объем выборки в единицах
10	88
5	350
3	971
2	2188
1	8750

Таблица Г. Определение размера согласно способу K. Mitra, S. Das, M. Mandal

Величина различий между основной и контрольной группами	Уровень значимости	Мощность	Объем выборки
0,2	0,5	80	586
0,2	0,1	80	773
0,2	0,5	90	746
0,4	0,5	80	146
0,4	0,1	80	193
0,4	0,5	90	186
0,6	0,5	80	65
0,6	0,1	80	86
0,6	0,5	90	83

По формулам

Объем выборки, достаточный для проведения новых исследований, определяется следующими параметрами:

изменчивость признака;
уровень доверия;
размер эффекта.

Объем выборки всегда зависит от предполагаемой строгости эксперимента и изменчивости исследуемого признака.

Формула для оценки среднего значения размера выборки:

n = (z × σ / H)², где:

n – размер выборки;

z – доверительный уровень (при р = 0,05 z = 1,96);

σ – стандартное отклонение;

Н – допустимая ошибка в натуральных величинах.

Формула для оценки доли выборки:

Формула для оценки доли выборки

Где:

n – размер выборки;

z – доверительный уровень (при р = 0,05 z = 1,96);

p – доля признака (наибольшее значение достигается при р = 0,5);

H – допустимая ошибка в процентах.

Еще одна формула расчета объема выборки (чаще всего калькулятор размера выборки использует именно ее):

формула расчета объема выборки

Где:

n – размер выборки;

z – нормированное отклонение;

p – вариация для выборки;

q = 1 – р;

е – допустимая ошибка.

Нормированное отклонение (z) определяется по таблице, зная основные значения доверительной вероятности (α).

α, %	60	70	80	85	90	95	97	99	99,7
z	0,84	1,03	1,29	1,44	1,65	1,96	2,18	2,58	3,0

Последняя формула расчета имеет особенности.

Начинать считать размер выборки следует с проведения качественного анализа генеральной совокупности, чтобы выяснить степень схожести и близости исследуемых единиц совокупности относительно их географических, демографических, социальных и других характеристик.
Рекомендуется предварительно выполнить пилотное исследование с целью определения приблизительного значения р.
Если максимальная вариация р = 50%, то и значение q = 50%, что является наиболее худшим вариантом.

Пример расчета размера выборки

Маркетолог проводит исследование с целью определить, нужны ли компании визитки. Для этого промоутеру предстоит опросить потенциальных клиентов и задавать только один вопрос: «Вы пользуетесь визитками?». На что человек должен будет ответить «Да» или «Нет».

В таком случае размер выборки будет рассчитываться так. Принимаем, что уровень доверительности равен 95% (стандартное значение). При этом нормированное отклонение z составит 1,96. После предварительного анализа предположим, что 80% представителей генеральной совокупности дадут положительный ответ, а значит, р = 0,8. Соответственно, q = 1 – 0,8 = 0,2. Вероятность допустимой ошибки примем за 10%, т. е. e = 0,1. Теперь можно выполнить расчет.

Расчета размера выборки

Округлив значение, получаем размер выборки n = 62 человека. Соответственно, в опросе с заданными параметрами нужно задействовать 62 человека из числа целевой аудитории компании.

Подходы к определению размера выборки

Выделяют несколько подходов, которые позволяют установить объем выборки для проведения статистического исследования.

Подходы к определению размера выборки

Подходы

Арбитражный подход. Объем выборки составляет определенный процент от генеральной совокупности. Например, 10% от общего количество потребителей.
Традиционный подход. Выборка составляется на основе определенных норм, которые были выработаны в процессе проведенных ранее исследований. Подход игнорирует обстоятельства и условия, строгая логика отсутствует.
Затратный подход. Объем выборки определяется в зависимости от стоимости сбора информации и возможных затрат на материалы для проведения исследования.
Подход на основе использования доверительных интервалов. Размер выборки в этом случае рассчитывается по формуле, что обеспечивает высокую точность результата:
n = (p × q) / s², где:

n – размер выборки;
p – вероятность того, что нужное событие наступит, %;
q = 100% – p;
s – стандартное отклонение, которое соответствует доверительному уровню.

Ошибки выборки

Объем выборки при массовом исследовании определяется двумя факторами:

Точностью полученных данных или статистической погрешностью.
Размером и количеством подгрупп, на которые будет разбита выборка при проведении анализа.

При любом исследовании, которое предполагает выборочный опрос респондентов из генеральной совокупности, может присутствовать погрешность данных или ошибка выборки. Выделяют два ее типа:

случайная – обусловлена действием статистических законов, поэтому очень легко рассчитывается по формулам теории вероятности и математической статистики;
систематическая – является следствием неточностей при проектировании выборки, определить ее степень смещения, направление и размер практически невозможно.

При расчете размера выборки важно так собрать данные, чтобы вероятность систематической ошибки в результате работы была минимальной.

Расчет случайной ошибки выборки зависит от объема последней, а также от степени однородности данных (дисперсии). Принцип такой: чем меньше дисперсия, тем меньше ошибка. Для расчета чаще всего используют онлайн калькуляторы.

Также выделяют:

Ошибки первого рода – альфа-ошибка, при которой делается вывод о достоверности гипотезы, которая на самом деле неверна. Величина выбирается произвольно в диапазоне от 0 до 1, чаще всего это значение 0,05 или 0,01.
Ошибки второго рода – бета-ошибка, при которой тот факт, что гипотеза неверна, остается не выявленным. Значение, как правило, устанавливается на уровне 0,2.

Расчет доверительного интервала

Для расчета доверительного интервала применяются достаточно простые формулы, выбор которых зависит от доли выборки в составе генеральной совокупности.

Если выборка значительно меньше генеральной совокупности:

Если выборка меньше генеральной совокупности

Если выборка и генеральная совокупность сопоставимы:

выборка и генеральная совокупность сопоставимы

В обеих формулах:

Δ – предельная ошибка выборки в процентах;

z – нормированное отклонение или z-фактор;

p – доля респондентов с наличием признака, который исследуется;

q – доля респондентов без исследуемого признака;

n – размер выборки;

N – объем генеральной совокупности (сколько всего респондентов).

Доверительный интервал удобно рассчитывать с помощью онлайн-калькулятора, который использует те же формулы, что мы привели выше. Просто введите необходимые переменные, и система рассчитает результат.

Расчет статистической значимости

Определить этот показатель проще всего с помощью онлайн-сервиса. Калькулятор позволяет проверить, существует ли статистически значимая разница между долями признака, которые были получены из независимых выборок.

Расчет статистической значимости

Рассчитывать статистическую значимость можно только в том случае, если произведения (n × p) и (n × (1 – р)) превышают значение 5. При этом n – объем выборки, р – доля признака.

Часто задаваемые вопросы

Обычно размер выборки и ее статистическая значимость прямо пропорциональны, т. е. с ростом выборки получение случайных результатов сводится к минимуму. Важность статистической значимости зависит от определенной ситуации. Вот некоторые из них.

Ситуация	Важность статистической значимости
Опросы сотрудников	Важна, т. к. повышает всесторонность выводов по итогам опроса.
Опросы клиентов об уровне их удовлетворенности	Не имеет значения, т. к. важен каждый ответ независимо от того, положительный он или отрицательный.
Исследование рынка	Имеет решающее значение, т. к. помогает сделать вывод о целевом рынке.
Опросы об образовании	Важна, если нужно использовать результаты исследования при внесении изменений в учебном заведении. Не важна, если единственная цель применения – просто собрать обратную связь.
Здравоохранение	Помогает выявлять серьезные проблемы, делать выводы в исследованиях. Если же опрос проводится ради оценки удовлетворенности пациентов, то не имеет значения.
Опросы для развлечения	Не важна.

Заданный размер выборки нужен для получения оценок с желаемым уровнем точности, если речь идет об исследовании распространенности в популяции конкретной характеристики.

Мало просмотров.
Узкая тематика.
Низкий бюджет.
Высокий бюджет.

Чтобы правильно рассчитать размер выборки и провести показательное исследование с учетом выдвинутых требований:

наберитесь терпения и дождитесь, пока соберется требуемое количество респондентов;
будьте последовательны и показывайте рекламу только ЦА в определенное время;
устанавливайте высокий уровень достоверности при расчете выборки.

При определении объема выборки основную роль играет переменная исхода конкретного исследования. Если в расчет добавляются дополнительные важные переменные, то размер выборки должен позволять адекватно проанализировать их.

Это такое количество объектов исследования, которое позволит получить максимально точный и достоверный результат с предельно небольшой погрешностью. При этом его можно репрезентовать на более широкую аудиторию, в т. ч. по отношению к генеральной совокупности.

Заключение

Объем выборки – важный показатель, без которого невозможно провести адекватное исследование и сделать объективные выводы. Он отражает количество представителей целевой аудитории, которое будет принимать непосредственное участие в эксперименте, и требуется во всех случаях, когда стоит задача сделать определенные заключения по результатам опроса.

Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter

Источник

Содержание курса лекций “Статистика”

Выборочное наблюдение как источник статистической информации в изучении социально-экономических явлений и процессов

Тема 10 Выборочное наблюдение

Статистическая методология исследования массовых явлений различает, как известно, два способа наблюдения в зависимости от полноты охвата объекта: сплошное и несплошное. Разновидностью несплошного наблюдения является выборочное, которое в условиях рыночных отношений в России находит все более широкое применение. Переход статистики РФ на международные стандарты системы национального счетоводства требует более широкого применения выборки для получения и анализа показателей СНС не только в промышленности, но и в других секторах экономики.

Под выборочным наблюдением понимается несплошное наблюдение, при котором статистическому обследованию (наблюдению) подвергаются единицы изучаемой совокупности, отобранные случайным способом. Выборочное наблюдение ставит перед собой задачу ‑ по обследуемой части дать характеристику всей совокупности единиц при условии соблюдения всех правил и принципов проведения статистического наблюдения и научно организованной работы по отбору единиц.

К выборочному наблюдению статистика прибегает по различным причинам. На современном этапе появилось множество субъектов хозяйственной деятельности, которые характерны для рыночной экономики. Речь идет об акционерных обществах, малых и совместных предприятиях, фермерских хозяйствах и т.д. Сплошное обследование этих статистических совокупностей, состоящих из десятков и сотен тысяч единиц, потребовало бы огромных материальных, финансовых и иных затрат. Использование же выборочного обследования позволяет значительно сэкономить силы и средства, что имеет немаловажное значение.

Наряду с экономией ресурсов одной из причин превращения выборочного наблюдения в важнейший источник статистической информации является возможность значительно ускорить получение необходимых данных. Ведь при обследовании, скажем, 10% единиц совокупности будет затрачено гораздо меньше времени, а результаты могут быть представлены быстрее, и будут более актуальными. Фактор времени важен для статистического исследования особенно в условиях изменяющейся социально-экономической ситуации.

Реализация выборочного метода базируется на понятиях генеральной и выборочной совокупностей.

Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.

Отбор единиц в выборочную совокупность может быть повторным или бесповторным.

При повторном отборе попавшая в выборку единица подвергается обследованию, т.е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.

Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.

На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.

Например, при проведении маркетинговых исследований мы не можем сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.

При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами-изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.

При бесповоротном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.

Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).

Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения или ошибки репрезентативности позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.

Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.

Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия на рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.

При дальнейшем рассмотрении теории и методов выборочного наблюдения используются следующие общепринятые условные обозначения:

N ‑ объем (число единиц) генеральной совокупности;

n ‑ объем (число единиц) выборочной совокупности;

‑ генеральная средняя, т.е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т.п.);

‑ выборочная средняя,
т.е. среднее значение изучаемого признака по выборочной совокупности;

М ‑ численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского населения, численность сельского населения, количество бракованных изделий, число нерентабельных предприятий и т.п.);

р ‑ генеральная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т.п.); определяетcя как

m ‑ численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;

w ‑ выборочная доля, т.е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, в выборочной совокупности,

определяется как ;

‑ средняя ошибка выборки;

‑ предельная ошибка выборки;

‑ коэффициент доверия, определяемый в зависимости от уровня вероятности.

Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности, и в обратной зависимости ‑ от объема выборки.

Таким образом среднюю ошибку выборки можно представить как

Формула 10.1

(10.1)

При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время, между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:

Формула 10.2

(10.2)

В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки.

Учитывая, что при достаточно большом объеме выборки отношение близко к 1, формула средней ошибки повторной выборки принимает следующий вид:

Формула 10.3

(10.3)

Где ‑ дисперсия изучаемого признака по выборочной совокупности.

При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы.

Согласно теореме А.М. Ляпунова, вероятность той или иной величины предельной ошибки, при достаточно большом объеме выборочной совокупности, подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.

Значения интеграла Лапласа при различных величинах t табулированы и представлены в статистических справочниках.

При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения t:

Таблица 10.1 ‑ !!!Некоторые значения t

Вероятность, р_i.	0,683	0,866	0,954	0,988	0,997	0,999
Значение t	1,0	1,5	2,0	2,5	3,0	3,5

Например, если при расчете предельной ошибки выборки мы используем значение t=2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.

Теоретической основой для определения границ генеральной доли, т.е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции F(t) при заданном значении t.

Процесс подготовки и проведения выборочного наблюдения включает ряд последовательных этапов:

Определение цели обследования.
Установление границ генеральной совокупности.
Составление программы наблюдения и программы разработки данных
Определение вида выборки, процента отбора и метода отбора
Отбор и регистрация наблюдаемых признаков у отобранных единиц.
Насчет выборочных характеристик и их ошибок.
Распространение полученных результатов на генеральную совокупность.

В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора.

К наиболее распространенным на практике видам относятся:

собственно-случайная (простая случайная) выборка;
механическая (систематическая) выборка;
типическая (стратифицированная, расслоенная) выборка;
серийная (гнездовая) выборка.

Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.

Комбинированный отбор предполагает объединение нескольких видов выборки. Так, например, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.

Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом ‑ более мелкие и так до тех пор, пока не будут отобраны те единицы, которые подвергаются обследованию.

Многофазная выборка, в отличие от многоступенчатой, предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз – по более расширенной программе.

Собственно-случайная (простая случайная) выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.

Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или не включение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.

Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайных чисел.

Расчет ошибок позволяет решить одну из главных проблем организации выборочного наблюдения – оценить репрезентативность (представительность) выборочной совокупности.

Различают среднюю и предельную ошибки выборки. Эти два вида связаны следующим соотношением:

Формула 10.4

(10.4)

Величина средней ошибки выборки рассчитывается дифференцированно в зависимости от способа отбора и процедуры выборки.

Так, при собственно-случайном повторном отборе средняя ошибка определяется по формуле:

Формула 10.5

(10.5)

а при расчете средней ошибки собственно-случайной бесповторной выборки:

Формула 10.6

(10.6)

Расчет средней и предельной ошибок выборки позволяет определить возможные пределы, в которых будут находиться характеристики генеральной совокупности.

Например, для выборочной средней такие пределы устанавливаются на основе следующих соотношений:

Формула 10.7

(10.7)

где и ‑ генеральная и выборочная средняя соответственно;

‑ предельная ошибка выборочной средней.

Пример.

При проверке веса импортируемого груза на таможне методом случайной повторной выборки было отобрано 200 изделий. В результате был установлен средний вес изделия 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,997 определите пределы, в которых находится средний вес изделия в генеральной совокупности.

Решение. Рассчитаем сначала предельную ошибку выборки. Так как при р = 0,997, t = 3, она равна:

Определим пределы генеральной средней:

или

Вывод: Следовательно, с вероятностью 0,997 можно утверждать, что средний вес изделий в генеральной совокупности находится в пределах от 29,16 г. до 30,84 г.

Пример 2.

В городе проживает 250 тыс. семей. Для определения среднего числа детей в семье была организована 2%-ная случайная бесповторная выборка семей. По ее результатам было получено следующее распределение семей по числу детей:

Таблица 10.2 ‑ Распределение семей по числу детей в городе N

Число детей в семье

Количество

семей

1000

2000

1200

400

200

С вероятностью 0,954 определите пределы, в которых будет находиться среднее число детей в генеральной совокупности.

Решение. В начале на основе имеющегося распределения семей определим выборочные среднюю и дисперсию:

Таблица 10.3 ‑ Вспомогательная таблица для расчета среднего числа детей

Число детей

в семье, х;

Количество семей, f

1000

2000

1200

400

200

2000

2400

1200

800

1000

-1,5

-0,5

0,5

1,5

2,5

3,5

2,25

0,25

2,25

6,25

12,25

2250

500

300

900

1250

2450

Итого

5000

7400

–

7650

Вычислим теперь предельную ошибку выборки (с учетом того, что при р = 0,954 t = 2).

Следовательно, пределы генеральной средней:

Таким образом, с вероятностью 0,954 можно утверждать, что среднее число детей в семьях города практически не отличается от 1,5, т.е. в среднем на каждые две семьи приходится три ребенка.

Наряду с определением ошибок выборки и пределов для генеральной средней эти же показатели могут быть определены для доли признака.

В этом случае особенности расчета связаны с определением дисперсии доли, которая вычисляется так:

формула 10.8

(10.8)

где ‑ доля единиц, обладающих данным признаком в выборочной совокупности, определяемая как отношение количества соответствующих единиц к объему выборки.

Тогда, например, при собственно-случайном повторном отборе для определения предельной ошибки выборки используется следующая формула:

формула 10.9

(10.9)

Соответственно, при бесповторном отборе:

формула 10.10

(10.10)

Пределы доли признака в генеральной совокупности p выглядят следующим образом:

формула 10.11

(10.11)

Рассмотрим пример.

С целью определения средней фактической продолжительности рабочего дня в государственном учреждении с численностью служащих 480 человек, в январе 2009 г. было проведена 25%-ная случайная бесповторная выборка. По результатам наблюдения оказалось, что у 10% обследованных потери времени достигали более 45 мин. в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.

Решение. Определим объем выборочной совокупности:

n= 480 х 0,25 = 120 чел.

Выборочная доля w равна по условию 10%.

Учитывая, что при р = 0,683 t=1, вычислим предельную ошибку выборочной доли:

формула 10.10 решение

Пределы доли признака в генеральной совокупности:

формула 10.11 пример

Таким образом, с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6% до 12,4%.

Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.

Для определения необходимого объема собственно-случайной повторной выборки применяют следующую формулу:

формула 10.12

(10.12)

Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если мы получили, что необходимый объем выборки составляет 493,1 единицы, то обследовав 493 единицы мы не достигнем требуемой точности. Поэтому, для достижения желаемого результата обследованием должны быть охвачены 494 единицы.

С другой стороны, рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, если по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) мы вполне можем охватить больший объем, то включение в выборочную совокупность 500 или, например, 550 единиц только уменьшит значения полученных случайной и предельной ошибок.

При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:

формула 10.12 после 1 расчет

Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонный разговоров продолжительностью менее 1 минуты с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?

Для получения ответа на поставленный вопрос воспользуемся формулой (10.12) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:

формула 10.12 пример

Таким образом, обследованием должны быть охвачены не менее 2500 разговоров на предмет их продолжительности.

Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:

формула 10.13

(10.13)

Укажем на одну особенность формулы (10.13). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц.

Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.

Механическая выборка может быть применена в тех случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.). Для проведения отбора желательно, чтобы все единицы также имели порядковые номера от 1 до N.

Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей.

Так, если из совокупности в 500000 единиц предполагается отобрать 10000 единиц, то пропорция отбора составит

формула 10.13вставка после

Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы.

Например, при пропорции 1:50 (2%-ная выборка) отбирается каждая 50-я единица, при пропорции 1:20 (5%-ная выборка) – каждая 20-я единица и т.д.

Интервал отбора также можно определить как частное от деления 100% на установленный процент отбора.

Так, например при 2%-ном отборе интервал составит 50 (100%:2%), при 4%-ном отборе ‑ 25 (100%:4%). В тех случаях, когда результат деления получается дробным, сформировать выборку механическим способом при строгом соблюдении процента отбора не представляется возможным.

Например, по этой причине нельзя сформировать 3%-ную или 6%-ную выборки.

Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно из каждого интервала отбирать центральную или одну из двух центральных единиц.

Например, при 5%-ной выборке интервал отбора составит 20 единиц, тогда отбор целесообразно начинать с 10-й или с 11-й единицы. В первом случае в выборку попадут 10, 30, 50, 70 и с таким же интервалом последующие единицы; во втором случае – единицы с номерами 11,31,51,71 и т.д.

При механической выборке также может появиться опасность систематической ошибки, обусловленной случайным совпадением выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при переписи населения 1989 г. в ходе 25%-го выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.

Для определения средней ошибки механической выборки, а также необходимой ее численности, используются соответствующие формулы, применяемые при собственно-случайном бесповторном отборе(10.6 и 10.13). При этом, определив необходимую численность выборки и сопоставив ее с объемом генеральной совокупности, как правило, приходится производить соответствующее округление для получения целочисленного интервала отбора.

Например, в области зарегистрировано 12000 фермерских хозяйств. Определим, сколько из них нужно отобрать в порядке механического отбора для определения средней площади сельхозугодий с ошибкой ± 2 га. (Р=0,997). По результатам ранее проведенного обследования известно, что среднее квадратическое отклонение площади сельхозугодий составляет 8 га. Произведем расчет, воспользовавшись формулой (10.13).

формула 10.13 пример

С учетом полученного необходимого объема выборки (143 фермерских хозяйства) определим интервал отбора: 12000:143=83,9.

Определенный таким способом интервал всегда округляется в меньшую сторону, так как при округлении в большую сторону произведенная выборка не достигнет рассчитанного по формуле необходимого объема.

Следовательно, в нашем примере, из общего списка фермерских хозяйств необходимо отобрать для обследования каждое 83-е хозяйство. При этом процент отбора составит 1,2% (100% : 83).

Типический отбор целесообразно использовать в тех случаях, когда все единицы генеральной совокупности объединены в несколько крупных типических групп.. Такие группы также называют стартами или слоями, в связи с чем типический отбор также называют стратифицированным или расслоенным. При обследованиях населения в качестве типических групп могут быть выбраны области, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасли или подотрасли, формы собственности и т.п.

Рассматривать генеральную совокупность в разрезе нескольких крупных групп единиц имеет смысл только в том случае, если средние значения изучаемых признаков по группам существенно различаются. Например, с большой уверенностью можно предположить, что доходы населения крупного города будут в среднем выше доходов населения, проживающего в сельской местности; численность работников промышленного предприятия в среднем будет выше численности работников торгового или сельскохозяйственного предприятия; средний возраст студентов будет значительно меньше среднего возраста занятого населения и, тем более, пенсионеров. В то же время, нет никакого смысла при выделении типических групп ориентироваться на признак, не связанный или очень слабо связанный с изучаемым.

Отбор единиц в выборочную совокупность из каждой типической группы осуществляется собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. В то же время, в выделенных типических группах обследуются далеко не все единицы, а только включенные в выборку. Следовательно, на величине полученной ошибки будет сказываться различие между единицами внутри этих групп, т.е. внутригрупповая вариация. Поэтому, ошибка типической выборки будет определяться величиной не общей дисперсии, а только ее части – средней из внутригрупповых дисперсий.

При типической выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:

формула 10.14

(10.14)

Где N_i – объем i-ой группы. а n_i ‑ объем выборки из i-ой группы.

Пример. Предположим, общая численность населения области составляет 1,5 млн. чел., в том числе городское – 900 тыс. чел. и сельское – 600 тыс. чел. Если в ходе выборочного наблюдения планируется обследовать 100 тыс. жителей, то эта численность должна быть поделена пропорционально объему типических групп следующим образом:

формула 10.14пример

Средняя ошибка типической выборки определяется по формулам:

формула 10.15

(10.15)

формула 10.16 (10.16)

где – средняя из внутригрупповых дисперсий.

При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле:

формула 10.17

(10.17)

Где ‑ среднее отклонение признака в i-ой группе.

Cредняя ошибка такого отбора определяется следующим образом:

формула 10.18

(10.18)

формула 10.19

(10.19)

Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.

Таблица 10.4 ‑ Результаты обследования рабочих предприятия

Цех

Всего рабочих, человек

Обследовано, человек

Число дней временной нетрудоспособности за год

средняя

дисперсия

III

1000

1400

800

100

140

Рассмотрим оба варианта типической выборки на условном примере. Предположим, 10% бесповторный типический отбор рабочих предприятия, пропорциональный размерам цехов, проведенный с целью оценки потерь из-за временной нетрудоспособности, привел к следующим результатам (табл. 10.4)

Рассчитаем среднюю из внутригрупповых дисперсий:

пример к табл 10.4

Определим среднюю и предельную ошибки выборки (с вероятностью 0,954):

Рассчитаем выборочную среднюю:

пример к табл 10.4_3

С вероятностью 0,954 можно сделать вывод, что среднее число дней временной нетрудоспособности одного рабочего в целом по предприятию находится в пределах:

пример к табл 10.4_4

Воспользуемся полученными внутригрупповыми дисперсиями для проведения отбора пропорционального дифференциации признака. Определим необходимый объем выборки по каждому цеху:

пример к табл 10.4_5

пример к табл 10.4_6

С учетом полученных значений рассчитаем среднюю ошибку выборки:

пример к табл 10.4_7

В данном случае средняя, а следовательно, и предельная ошибки будут несколько меньше, что отразится и на границах генеральной средней.

Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.

Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:

формула 10.20

(10.20)

формула 10.21

(10.21)

Где r ‑ число отобранных серий; R ‑ общее число серий.

Межгрупповую дисперсию вычисляют следующим образом:

формула 10.22 (10.22)

где ‑ средняя i-й серии;

‑ общая средняя по всей выборочной совокупности.

Пример.

В области, состоящей из 20 районов, проводилось выборочное обследование урожайности на основе отбора серий (районов). Выборочные средние по районам составили соответственно 14,5 ц/га; 16 ц/га; 15,5 ц/га; 15 ц/га и 14 ц/га. С вероятностью 0,954 определите пределы урожайности во всей области.

Решение. Рассчитаем общую среднюю:

Межгрупповая (межсерийная) дисперсия равна:

Определим теперь предельную ошибку серийной бесповторной выборки (t = 2 при р = 0,954):

Вывод: Следовательно, урожайность будет с вероятностью 0,954 находиться в пределах:

Определение необходимого объема выборки

При проектировании выборочного наблюдения возникает вопрос о необходимой численности выборки. Эта численность может быть определена на базе допустимой ошибки при выборочном наблюдении, исходя из вероятности, на основе которой можно гарантировать величину устанавливаемой ошибки, и, наконец, на базе способа отбора.

Формулы необходимого объема выборки для различных способов формирования выборочной совокупности могут быть выведены из соответствующих соотношений, используемых при расчете предельных ошибок выборки. Приведем наиболее часто применяемые на практике выражения необходимого объема выборки:

– собственно-случайная и механическая выборка:

Формула 10.23

(10.23)

Формула 10.24

(10.24)

– типическая выборка:

Формула 10.25

(10.25)

Формула 10.26

(10.26)

– серийная выборка:

Формула 10.27

(10.27)

Формула 10.28

(10.28)

При этом в зависимости от целей исследования дисперсии и ошибки выборки могут быть рассчитаны для средней величины или доли признака.

Рассмотрим примеры определения необходимого объема выборки при различных способах формирования выборочной совокупности.

Пример.

В 100 туристических агентствах города предполагается провести обследование среднемесячного количества реализованных путевок методом механического отбора. Какова должна быть численность выборки, чтобы с вероятностью 0,683 ошибка не превышала 3 путевок, если по данным пробного обследования дисперсия составляет 225.

Решение. Рассчитаем необходимый объем выборки:

Пример.

С целью определения доли сотрудников коммерческих банков области в возрасте старше 40 лет предполагается организовать типическую выборку пропорциональную численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 12 тыс. чел., в том числе 7 тыс. мужчин и 5 тыс. женщин.

На основании предыдущих обследований известно, что средняя из внутригрупповых дисперсий составляет 1600. Определите необходимый объем выборки при вероятности 0,997 и ошибке 5%.

Решение. Рассчитаем общую численность типической выборки:

Вычислим теперь объем отдельных типических групп:

Вывод: Таким образом, необходимый объем выборочной совокупности сотрудников банков составляет 550 чел., в т.ч. 319 мужчин и 231 женщина.

Пример.

В акционерном обществе 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что межсерийная дисперсия доли равна 225. С вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.

Решение. Необходимое количество бригад рассчитаем на основе формулы объема серийной бесповторной выборки:

Содержание курса лекций “Статистика”

Контрольные задания

Самостоятельно проведите выборочное наблюдение и произведите соответствующие расчеты.

Источник

Download Article

Scientific studies often rely on surveys distributed among a sample of some total population. Your sample will need to include a certain number of people, however, if you want it to accurately reflect the conditions of the overall population it’s meant to represent. To calculate your necessary sample size, you’ll need to determine several set values and plug them into an appropriate formula.

1
Know your population size. Population size refers to the total number of people within your demographic. For larger studies, you can use an approximated value instead of the precise number.
- Precision has a greater statistical impact when you work with a smaller group. For instance, if you wish to perform a survey among members of a local organization or employees of a small business, the population size should be accurate within a dozen or so people.^[1]
- Larger surveys allow for a greater deviance in the actual population. For example, if your demographic includes everyone living in the United States, you could estimate the size to roughly 320 million people, even though the actual value may vary by hundreds of thousands.
2
Determine your margin of error. Margin of error, also referred to as “confidence interval,” refers to the amount of error you wish to allow in your results.^[2]
- The margin of error is a percentage the indicates how close your sample results will be to the true value of the overall population discussed in your study.
- Smaller margin of errors will result in more accurate answers, but choosing a smaller margin of error will also require a larger sample.
- When the results of a survey are presented, the margin of error usually appears as a plus or minus percentage. For example: “35% of people agree with option A, with a margin of error of +/- 5%”
  - In this example, the margin of error essentially indicates that, if the entire population were asked the same poll question, you are “confident” that somewhere between 30% (35 – 5) and 40% (35 + 5) would agree with option A.
Advertisement
3
Set your confidence level. Confidence level is closely related to confidence interval (margin of error). This value measures your degree of certainty regarding how well a sample represents the overall population within your chosen margin of error.^[3]
- In other words, choosing a confidence level of 95% allows you to claim that you 95% certain that your results accurately fall within your chosen margin of error.
- A larger confidence level indicates a greater degree of accuracy, but it will also require a larger sample. The most common confidence levels are 90% confident, 95% confident, and 99% confident.
- Setting a confidence level of 95% for the example stated in the margin of error step would mean that you are 95% certain that 30% to 40% of the total concerned population would agree with option A of your survey.
4
Specify your standard of deviation. The standard of deviation indicates how much variation you expect among your responses.
- Extreme answers are more likely to be accurate than moderate results.
  - Plainly stated, if 99% of your survey responses answer “Yes” and only 1% answer “No,” the sample probably represents the overall population very accurately.
  - On the other hand, if 45% answer “Yes” and 55% answer “No,” there is a greater chance of error.
- Since this value is difficult to determine you give the actual survey, most researchers set this value at 0.5 (50%). This is the worst case scenario percentage, so sticking with this value will guarantee that your calculated sample size is large enough to accurately represent the overall population within your confidence interval and confidence level.
5
Find your Z-score. The Z-score is a constant value automatically set based on your confidence level. It indicates the “standard normal score,” or the number of standard deviations between any selected value and the average/mean of the population.
- You can calculate z-scores by hand, look for an online calculator, or find your z-score on a z-score table. Each of these methods can be fairly complex, however.
- Since confidence levels are fairly standardized, most researchers simply memorize the necessary z-score for the most common confidence levels:
  - 80% confidence => 1.28 z-score
  - 85% confidence => 1.44 z-score
  - 90% confidence => 1.65 z-score
  - 95% confidence => 1.96 z-score
  - 99% confidence => 2.58 z-score

1
Look at the equation.^[4] If you have a small to moderate population and know all of the key values, you should use the standard formula. The standard formula for sample size is:
- Sample Size = ^{[z² * p(1-p)] / e²} / _{1 + [z² * p(1-p)] / e² * N}]
  - N = population size
  - z = z-score
  - e = margin of error
  - p = standard of deviation
2
Plug in your values. Replace the variable placeholders with the numerical values that actually apply to your specific survey.
- Example: Determine the ideal survey size for a population size of 425 people. Use a 99% confidence level, a 50% standard of deviation, and a 5% margin of error.
- For 99% confidence, you would have a z-score of 2.58.
- This means that:
  - N = 425
  - z = 2.58
  - e = 0.05
  - p = 0.5
3
Do the math. Solve the equation using the newly inserted numerical values. The solution represents your necessary sample size.
- Example: Sample Size = ^{[z² * p(1-p)] / e²} / _{1 + [z² * p(1-p)] / e² * N]}
  - = ^{[2.58² * 0.5(1-0.5)] / 0.05²} / _{1 + [2.58² * 0.5(1-0.5)] / 0.05² * 425]}
  - = ^{[6.6564 * 0.25] / 0.0025} / _{1 + [6.6564 * 0.25] / 1.0625]}
  - = 665 / 2.5663
  - = 259.39(final answer)

1
Examine the formula.^[5] If you have a very large population or an unknown one, you’ll need to use a secondary formula. If you still have values for the remainder of the variables, use the equation:
- Sample Size = [z² * p(1-p)] / e²
  - z = z-score
  - e = margin of error
  - p = standard of deviation
- Note that this equation is merely the top half of the full formula.
2
Plug your values into the equation. Replace each variable placeholder with the numerical values chosen for your survey.
- Example: Determine the necessary survey size for an unknown population with a 90% confidence level, 50% standard of deviation, a 3% margin of error.
- For 90% confidence, use the z-score would be 1.65.
- This means that:
  - z = 1.65
  - e = 0.03
  - p = 0.5
3
Do the math. After plugging you numbers into the formula, solve the equation. Your answer will indicate your necessary sample size.
- Example: Sample Size = [z² * p(1-p)] / e²
  - = [1.65² * 0.5(1-0.5)] / 0.03²
  - = [2.7225 * 0.25] / 0.0009
  - = 0.6806 / 0.0009
  - = 756.22 (final answer)

1
Look at the formula.^[6] Slovin’s formula is a very general equation used when you can estimate the population but have no idea about how a certain population behaves. The formula is described as:
- Sample Size = N / (1 + N*e²)
  - N = population size
  - e = margin of error
- Note that this is the least accurate formula and, as such, the least ideal. You should only use this if circumstances prevent you from determining an appropriate standard of deviation and/or confidence level (thereby preventing you from determining your z-score, as well).
2
Plug in the numbers. Replace each variable placeholder with the numerical values that apply specifically to your survey.
- Example: Calculate the necessary survey size for a population of 240, allowing for a 4% margin of error.
- This means that:
  - N = 240
  - e = 0.04
3
Do the math. Solve the equation using your survey-specific numbers. The answer you arrive at should be your necessary survey size.^[7]
- Example: Sample Size = N / (1 + N*e²)
  - = 240 / (1 + 240 * 0.04²)
  - = 240 / (1 + 240 * 0.0016)
  - = 240 / (1 + 0.384}
  - = 240 / (1.384)
  - = 173.41 (final answer)

Calculator, Practice Problems, and Answers

Add New Question

Question

If the total population size is not given in the problem, what formula will apply?

If the population size is not given, then a t-distribution formula is applicable.

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate sample size, first find the population size, or number of people taking your study, and margin of error, which is the amount of error you’ll allow in your results. Then, calculate your confidence level, which is how confident you are in percentage terms that your results will fall within your margin of error, and z-score, a constant value linked to your confidence level. Next, specify your standard of deviation, which is the amount of variation you expect in your results. Finally, plug your variables into the standard formula to figure out the sample size. To learn how to create a formula for unknown populations, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 299,714 times.

Reader Success Stories

“I recommend this to everyone who is on the same page I was until I found this article!”

Did this article help you?

Источник

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

Простая формула для расчета объема выборки

Пример расчета объема выборочной совокупности

Значение нормированного отклонения для различных доверительных интервалов

Область применения простой формулы выборки

Особенности формулы расчета размера выборки

Что такое объем выборки

Зачем необходимо рассчитывать

Основные понятия определения

Генеральная совокупность

Выборочная совокупность

Погрешность измерений

Достоверность измерений

Репрезентативность выборки

Что влияет на результаты

Типы выборок

Расчет объема выборки

По таблицам

По формулам

Пример расчета размера выборки

Подходы к определению размера выборки

Ошибки выборки

Расчет доверительного интервала

Расчет статистической значимости

Часто задаваемые вопросы

Заключение

Определение необходимого объема выборки

Calculator, Practice Problems, and Answers

References

About This Article

Reader Success Stories

Did this article help you?

Вам также может понравиться

Как найти карточку если потерял на улице

Как найти напряжение на катушке в цепи

Как найти синегнойную палочку

Добавить комментарий Отменить ответ