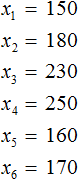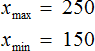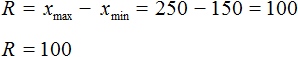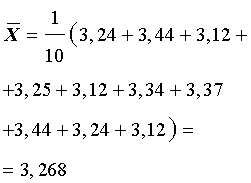Продолжаем изучать элементарные задачи по математике. Сегодня мы поговорим о статистике.
Статистика — это раздел математики в котором изучаются вопросы сбора, измерения и анализа информации, представленной в числовой форме. Происходит слово статистика от латинского слова status (состояние или положение дел).
Так, с помощью статистики мы можем узнать свое положение дел, касающихся финансов. С начала месяца можно вести дневник расходов и по окончании месяца, воспользовавшись статистикой, узнать сколько денег в среднем мы тратили каждый день или какая потраченная сумма была наибольшей в этом месяце либо узнать какую сумму мы тратили наиболее часто.
На основе этой информации можно провести анализ и сделать определенные выводы: следует ли в следующем месяце немного сбавить аппетит, чтобы тратить меньше денег, либо наоборот позволить себе не только хлеб с водой, но и колбасу.
Выборка. Объем. Размах
Что такое выборка? Если говорить простым языком, то это отобранная нами информация для исследования. Например, мы можем сформировать следующую выборку — суммы денег, потраченных в каждый из шести дней. Давайте нарисуем таблицу в которую занесем расходы за шесть дней
Выборка состоит из n-элементов. Вместо переменной n может стоять любое число. У нас имеется шесть элементов, поэтому переменная n равна 6
n = 6
Элементы выборки обозначаются с помощью переменных с индексами . Последний
элемент является шестым элементом выборки, поэтому вместо n будет стоять число 6.
Обозначим элементы нашей выборки через переменные
Количество элементов выборки называют объемом выборки. В нашем случае объем равен шести.
Размахом выборки называют разницу между самым большим и маленьким элементом выборки.
В нашем случае, самым большим элементом выборки является элемент 250, а самым маленьким — элемент 150. Разница между ними равна 100
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Средняя скорость движения
При изучении задач на движение мы определяли скорость движения следующим образом: делили пройденное расстояние на время. Но тогда подразумевалось, что тело движется с постоянной скоростью, которая не менялась на протяжении всего пути.
В реальности, это происходит довольно редко или не происходит совсем. Тело, как правило, движется с различной скоростью.
Когда мы ездим на автомобиле или велосипеде, наша скорость часто меняется. Когда впереди нас помехи, нам приходиться сбавлять скорость. Когда же трасса свободна, мы ускоряемся. При этом за время нашего ускорения скорость изменяется несколько раз.
Речь идет о средней скорости движения. Чтобы её определить нужно сложить скорости движения, которые были в каждом часе/минуте/секунде и результат разделить на время движения.
Задача 1. Автомобиль первые 3 часа двигался со скоростью 66,2 км/ч, а следующие 2 часа — со скоростью 78,4 км/ч. С какой средней скоростью он ехал?
Сложим скорости, которые были у автомобиля в каждом часе и разделим на время движения (5ч)
Значит автомобиль ехал со средней скоростью 71,08 км/ч.
Определять среднюю скорость можно и по другому — сначала найти расстояния, пройденные с одной скоростью, затем сложить эти расстояния и результат разделить на время. На рисунке видно, что первые три часа скорость у автомобиля не менялась. Тогда можно найти расстояние, пройденное за три часа:
66,2 × 3 = 198,6 км.
Аналогично можно определить расстояние, которое было пройдено со скоростью 78,4 км/ч. В задаче сказано, что с такой скоростью автомобиль двигался 2 часа:
78,4 × 2 = 156,8 км.
Сложим эти расстояния и результат разделим на 5
Задача 2. Велосипедист за первый час проехал 12,6 км, а в следующие 2 часа он ехал со скоростью 13,5 км/ч. Определить среднюю скорость велосипедиста.
Скорость велосипедиста в первый час составляла 12,6 км/ч. Во второй и третий час он ехал со скоростью 13,5. Определим среднюю скорость движения велосипедиста:
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
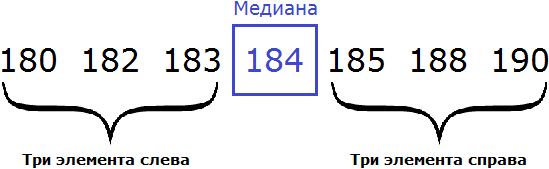
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Частота
Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.
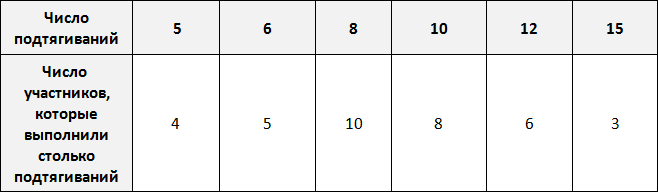
Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.
Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:
Такие таблицы называют таблицами частот.
Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.
Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:
4 + 5 + 10 + 8 + 6 + 3 = 36
Относительная частота
Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.
Относительная частота равна отношению частоты на общее число элементов выборки.
Вернемся к нашей таблице:
Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:
Выполним деление в этих дробях:
Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:
Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Содержание:
- формула с пояснениями;
- пример расчета объема выборки;
- нормированное отклонение (таблица);
- область применения;
- особенности формулы.
Простая формула для расчета объема выборки
Ниже приведена простая формула для расчета объема выборки для тех случаев когда на заданный вопрос возможны лишь два варианта ответа:
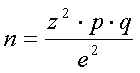
где: n – объем выборки;
z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности (доверительного интервала, доверительной вероятности).
Этот показатель характеризует вероятность попадания ответов в специальный доверительный интервал — диапазон, границам которого соответствует определенный процент определенных ответов на некоторый вопрос.
Можно сказать, что уровень доверительности выражает вероятность того, что респонденты генеральной совокупности ответят так же, как и представители анализируемой выборки.
На практике доверительный интервал при проведении маркетинговых исследований часто принимают за 95% или 99%. Тогда значения z будут соответственно 1,96 и 2,58.
Также существует специальная таблица «Значение интеграла вероятностей», используя которую можно найти значение z для различных доверительных интервалов. Сокращенный вариант такой таблицы приведен ниже;
p – вариация для выборки, в долях.
Вариация характеризует величину схожести / несхожести ответов респондентов на вопрос. По сути, p — вероятность того, что респонденты выберут той или иной вариант ответа.
Допустим, если мы считаем, что четверть опрашиваемых выберут ответ «Да», то p будет равно 25%, то есть p = 0,25;
q = 1 – p.
Можно сказать, что q — это вероятность того, что респонденты не выберут анализируемый вариант ответа (в нашем примере ответят «Нет»). Например, если p = 0,25, то q = 1 – 0,25 = 0,75;
e – допустимая ошибка, в долях.
Значение допустимой ошибки заранее определяют исследователь и заказчик маркетингового исследования.
Пример расчета объема выборочной совокупности
Маркетинговая компания получила заказ на проведение социологического исследования с целью выявить долю курящих лиц в населении города. Для этого сотрудники компании будут задавать прохожим один вопрос: «Вы курите?». Возможных вариантов ответа, таким образом, только два: «Да» и «Нет».
Объем выборки в этом случае рассчитывается следующим образом. Уровень доверительности принимается за 95% (одно из стандартных значений для маркетинговых исследований), тогда нормированное отклонение z = 1,96. Проведя предварительный анализ населения города, вариацию принимаем за 50%, то есть условно считаем, что половина респондентов может ответить на вопрос о том, курят ли они — «Да». Тогда p = 0,5. Отсюда находим q = 1 – p = 1 – 0,5 = 0,5. исходя из требуемой заказчиком точности, допустимую ошибку выборки принимаем за 10%, то есть e = 0,1.
Подставляем эти данные в формулу и считаем:
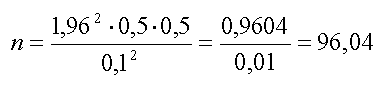
Округлив расчетное значение, получаем объем выборки n = 96 человек.
Следовательно, для проведения исследования с заданными параметрами (уровень доверительности, допустимая ошибка) компании необходимо опросить 96 человек.
Значение нормированного отклонения для различных доверительных интервалов
В таблице приведены некоторые значения нормированного отклонения (z) для важнейших уровней доверительности, или, иначе, доверительной вероятности (α):
| α (%) | 60 | 70 | 80 | 85 | 90 | 95 | 97 | 99 | 99,7 |
|---|---|---|---|---|---|---|---|---|---|
| z | 0,84 | 1,03 | 1,29 | 1,44 | 1,65 | 1,96 | 2,18 | 2,58 | 3,0 |
Конечно, в таблице приведены значения z только для основных уровней доверительности. Полную версию таблицы можно найти в интернете.
Область применения простой формулы выборки
При проведении простых исследований, когда нужно получить ответ всего на один простой вопрос. При этом шкала ответов, как правило, дихотомического характера. То есть предлагаются (или подразумеваются) варианты ответов по типу «Да» — «Нет», «Черное» — «Белое», «Куплю» — «Не куплю», и т. д. Иными словами возможны лишь два варианта ответа на заданный вопрос.
Особенности формулы расчета размера выборки
Для рассмотренной нами простой формулы определения объема выборки можно выделить несколько характерных особенностей:
- перед тем, как рассчитывать объем выборки в данном случае желательно предварительно провести качественный анализ изучаемой генеральной совокупности. В частности установить степень схожести, близости изучаемых единиц совокупности в части их социальных, демографических, географических, иных характеристик. Также полезно провести пилотное (разведочное) исследование, чтобы установить приблизительную величину p;
- нужно иметь в виду, что максимальная изменчивость (вариация ответов) соответствует значению p = 50%, так как тогда q = 50% и p × q = 0,5 × 0,5 = 0,25. Это наихудший случай, все другие значения p дадут изменчивость меньшего размера (например, при p = 80%, p × q = 0,8 × 0,2 = 0,16; а при p = 10%, p × q = 0,1 × 0,9 = 0,09). Впрочем, данный показатель влияет на объем выборки не очень сильно.
Также стоит отметить, что существует ряд иных формул для определения объема выборки в случаях с дихотомической шкалой ответов на единственный вопрос. Для более сложных маркетинговых исследований применяются другие формулы.
Источники
- Голубков Е. П. Маркетинговые исследования: теория, методология и практика. – М.: Издательство «Финпресс», 1998.
Статья дополнена и доработана автором 10 дек 2020 г.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.
Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Формула выборки – простая // Сайт преподавателя экономики. [2020]. URL: https://galyautdinov.ru/post/formula-vyborki-prostaya (дата обращения: 21.05.2023).
Запуск рекламной кампании в маркетинге предполагает А/В-тестирование, однако не каждый проведенный тест будет показательным, а его результаты – значимыми для статистики. Одна из распространенных ошибок при проведении исследований – неправильное определение нормального размера выборки. Как следствие – запуск рекламы, которая не даст результатов, и зря потраченные деньги.
Что такое объем выборки
Объем выборки – это количество людей из общего числа целевой аудитории (ЦА) продукта или бренда, участвовавших в исследовании, или количество заполненных анкет, которые были учтены при подсчете результатов.
Термин «выборка» говорит о том, что из всей совокупности участников опроса проводится оценка лишь части ответов.
В зависимости от параметров проекта, которые были указаны изначально, выборка может быть разной. Например, при случайной выборке респонденты выбираются из целевой совокупности случайным образом.
Зачем необходимо рассчитывать
Объем выборки определяют перед запуском количественных исследований в маркетинге (например, контент-анализа), чтобы узнать, какое число представителей ЦА должно поучаствовать в тестировании, и получить достоверные результаты. Если данных о объеме выборки нет, это может стать причиной того, что исследователь получит некорректные результаты.
Для качественных исследований объем выборки не определяют. Также он неактуален, если речь идет о проведении пилотных, т. е. предварительных исследований.
Основные понятия определения
В определении размера выборки участвуют различные параметры:
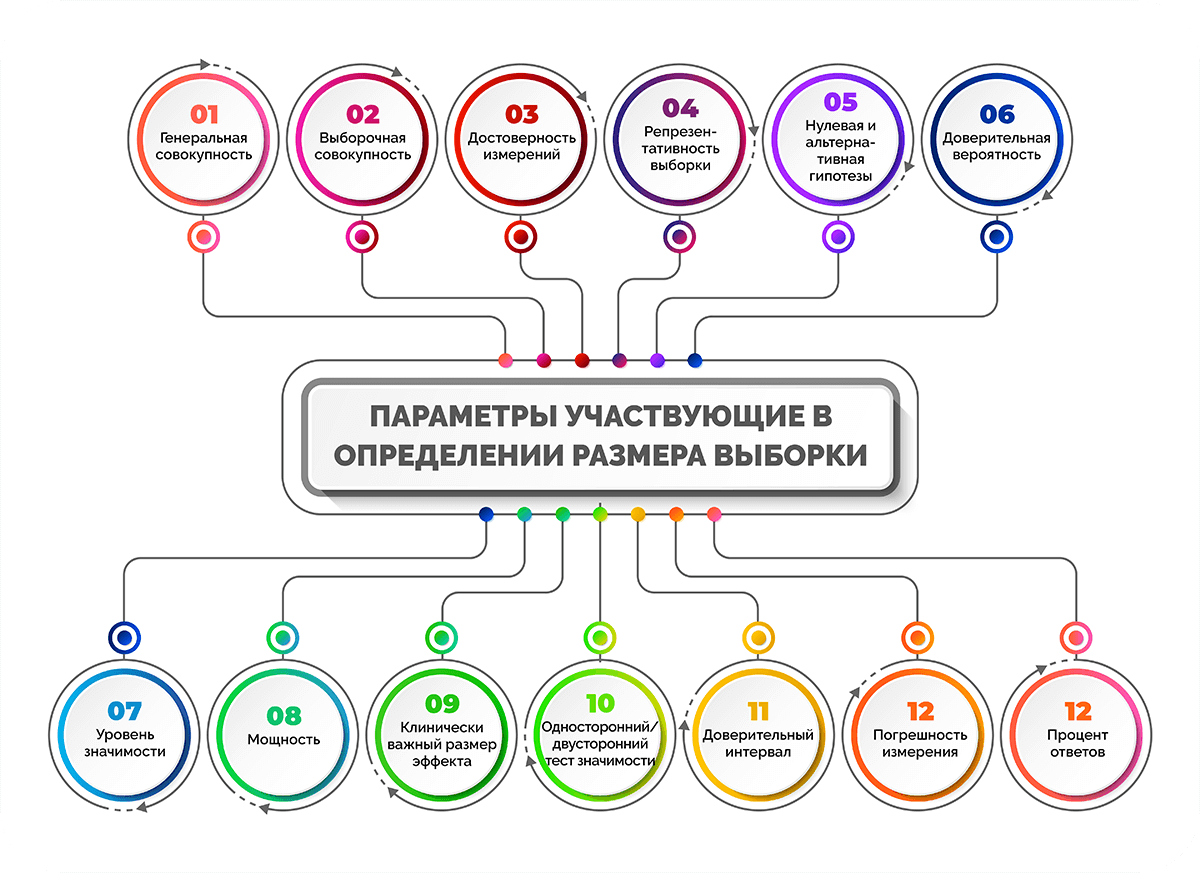
- генеральная совокупность;
- выборочная совокупность;
- достоверность измерений;
- репрезентативность выборки;
- нулевая и альтернативная гипотезы;
- доверительная вероятность;
- уровень значимости;
- мощность;
- клинически важный размер эффекта;
- односторонний / двусторонний тест значимости;
- доверительный интервал;
- погрешность измерения;
- процент ответов.
Разберем, что означают основные из них.
Генеральная совокупность
Генеральной совокупностью называется общее количество объектов наблюдения, которые обладают определенными общими признаками (возраст, пол, оборот, численность, доход и пр.) и о которых будут сделаны заявления после обработки результатов исследования.
Объектами наблюдения могут быть люди, предприятия, домохозяйства, населенные пункты, отдельные малые социальные группы и т. д.
Если известно, что результаты опроса касаются всех жителей Москвы, то генеральная совокупность будет равна общей численности населения города, т. е. 13 млн человек (по данным 2021 года).
Оценивать свойства генеральный совокупностей, основываясь на выборочных методах, позволяет кривая нормального распределения.
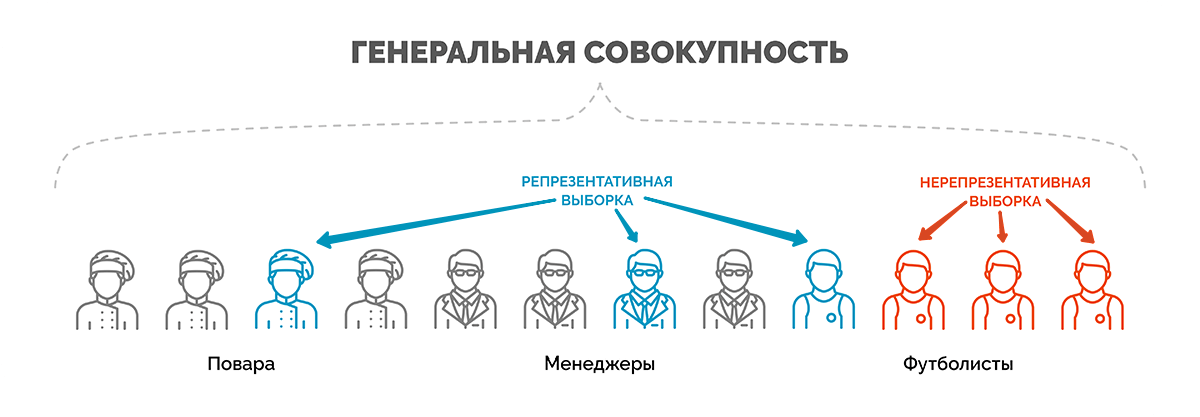
Выборочная совокупность
Выборка или выборочная совокупность – это некоторая часть объектов из числа генеральной совокупности, отобранная для участия в исследовании с целью оценить распределение мнений и сделать итоговое заключение, которое будет распространяться на всю генеральную совокупность.
Характеристики выборочной совокупности должны корректно отражать параметры генеральной совокупности, т. е. обладать свойством репрезентативности. Только в данном случае заключение, сделанное исходя из результатов анализа выборки, будет с одинаковой вероятностью распространяться на представителей всей генеральной совокупности.
Выборка, состоящая из работников московских предприятий, не будет репрезентировать население города трудоспособного возраста и особенно все население столицы, т. к. не включает неработающих людей, женщин в декрете, удаленных сотрудников и т. д. Даже если мы будем увеличивать количество опрошенных работников столичных компаний, выборка все равно не сможет отразить характеристики генеральной совокупности, т. е. всего трудоспособного населения Москвы.
Погрешность измерений
Допустимая погрешность измерений – это процент возможной ошибки или отклонения результатов исследования, т. е. то значение, на которое истинный показатель может откланяться от значения, полученного в результате исследования.
Чем меньше погрешность, тем больше должна быть выборка.
Результаты опроса показали, что 60% опрощенных предпочитают делать покупки в сетевых магазинах. Предел погрешности 5% говорит о том, что в генеральной совокупности доля сторонников сетевых точек продаж может увеличиться или уменьшиться на 5% относительно уровня полученных 60%. Т. е. фактическое значение будет лежать в пределах значений от 55 до 65%.
Достоверность измерений
Уровень достоверности (надежности) измерений – это вероятность того, что полученные в результате исследования истинные результаты выбранного параметра генеральной совокупности находятся в пределах ее доверительного интервала (в примере выше это интервал 55-65%). Простыми словами, это степень уверенности в репрезентативности результатов.
Чем меньше доверительный интервал и выше заданный уровень достоверности, тем больше должна быть выборочная совокупность.
Если взять приведенный выше в статье пример с погрешностью в 5%, вы можете быть уверены в следующем: вероятность того факта, что от 55 до 65% людей предпочитают совершать покупки в сетевых магазинах, составляет не менее 95%.
Репрезентативность выборки
Под репрезентативностью понимают степень соответствия характеристик выборочной совокупности характеристикам генеральной совокупности, которые можно экстраполировать на всю популяцию.
- выборка, состоящая на 100% из автомобилистов Санкт-Петербурга, не репрезентирует всех жителей Санкт-Петербурга;
- выборка, состоящая только из российских фирм B2B с количеством сотрудников до 200 человек, не репрезентирует все компании страны, работающих в этом сегменте.
Исследование должно быть репрезентативным, если стоит задача по результатам количественного исследования сформировать представление о популяции в целом и правильно оценить ее. Если же исследование качественное или люди опрашиваются ради сбора мнений, предложений, идей, в этом случае репрезентативная выборка практически не играет роли.
Что влияет на результаты
Результаты тестирования могут изменяться под влиянием ряда факторов:
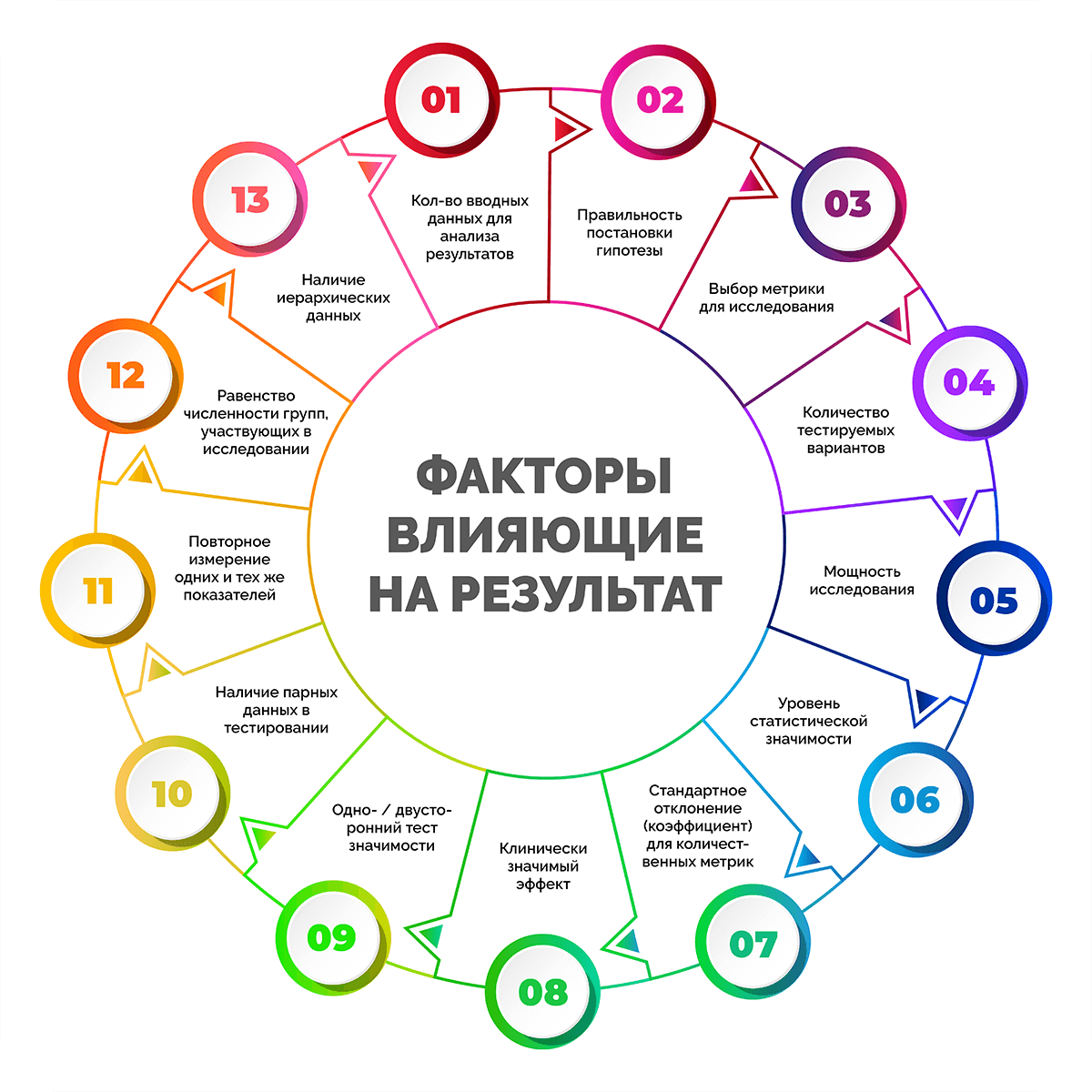
- количество вводных данных для анализа результатов;
- правильность постановки гипотезы;
- выбор той или иной метрики (показателя, переменных) для исследования;
- количество тестируемых вариантов;
- мощность исследования;
- уровень статистической значимости;
- стандартное отклонение (коэффициент) для количественных метрик;
- клинически значимый эффект;
- одно- / двусторонний тест значимости;
- наличие парных данных в тестировании;
- повторное измерение одних и тех же показателей;
- равенство численности групп, участвующих в исследовании;
- наличие иерархических данных.
Также расчет размера выборки может давать разные результаты, если анализ является:
- рандомизированным и контролируемым;
- рандомизированным и кластерным;
- нерандомизированным экспериментом вмешательства;
- исследованием эквивалентности;
- исследованием распространенности;
- обсервационным;
- изучением специфичности и чувствительности теста.
Нерандомизированные тестирования взаимосвязей или различий предполагают задействования в маркетинговых исследованиях выборки гораздо большего размера, чтобы при анализе было не сложно учесть влияние третьих факторов.
Типы выборок
Различают два типа выборок: вероятностные и невероятностные или детерминированные. Каждая группа включает в себя виды. Разберем, какие из них входят в каждый тип.
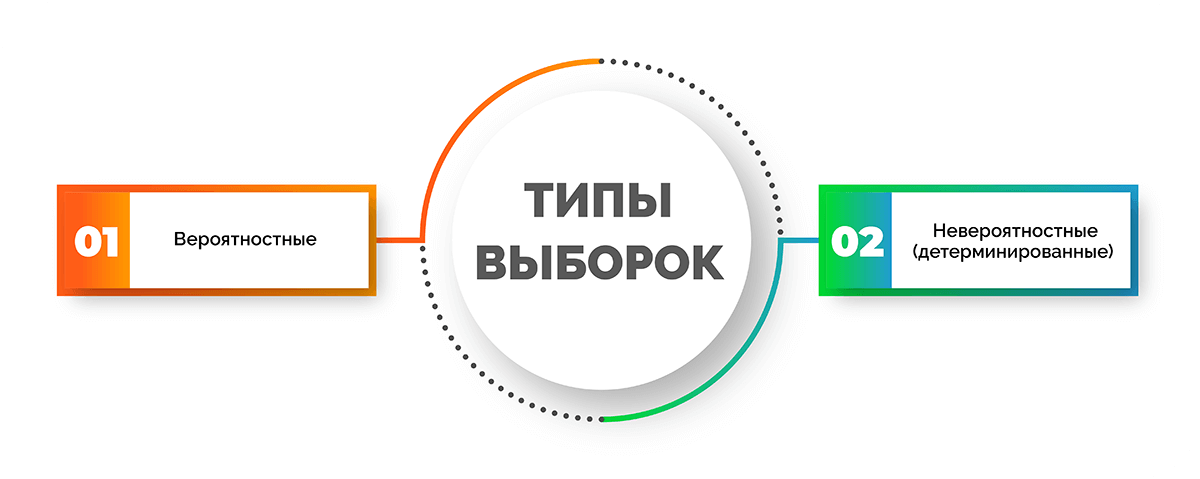
Вероятностные выборки:
- Случайная или простой случайный отбор – предполагает полный список элементов (отбираются при помощи таблицы случайных чисел), равную вероятность доступности всех из них и однородную генеральную совокупность;
- Механическая или систематическая – выступает в качестве разновидности случайной выборки, при этом упорядочивание происходит по тому или иному признаку, причем первый элемент отбирается случайно, затем с шагом n отбирается каждый последующий элемент;
- Стратифицированная или районированная – выборка используется при неоднородной генеральной совокупности, которая разделяется на страты (группы), в каждой из которых выполняется случайный отбор пропорционально их доле в генеральной совокупности;
- Серийная или кластерная, или гнездовая – единицами отбора выступают целые группы (гнезда или кластеры), которые могут попасть в выборку случайным образом, а все объекты внутри них подлежат сплошному исследованию.
Невероятностные (детерминированные) выборки:
- Квотная выборка – формируется несколько групп объектов, в каждой из которых зачастую пропорционально доле в генеральной совокупности задается определенное число объектов, которые нужно исследовать;
- Метод снежного кома – для формирования выборки каждый участник опроса предоставляет контакты своих знакомых; применяется для исследования труднодоступных групп респондентов;
- Стихийная выборка или выборка «первого встречного» – ее состав и размер заранее неизвестен и зависит от активности людей, опрос проводится среди самых доступных респондентов (интернет-опросы, опросы в журналах и газетах, анкеты на самозаполнение и т. д.);
- Выборка типичных случаев – для исследования отбираются отдельные представители генеральной совокупности, которым присуще среднее значение исследуемого признака.
Отбор в детерминированных выборках происходит не случайно, а по субъективным критериям: типичности, доступности, равного представительства каждой стороны и пр.
Расчет объема выборки
Расчет объема выборки – своего рода компромисс между требуемой мощностью исследования и возможностью реализовать его на практике с учетом имеющихся ресурсов и фокус-группы. При этом выбор метода расчета во многом определяется знаниями о параметрах и характеристиках изучаемых параметров.
Определить объем выборки можно двумя способами: по таблицам и с помощью формулы. Разберем эти методы.
По таблицам
Когда никаких данных о предстоящем исследовании нет, а сам эксперимент является инновационным, никто ранее ничего подобного не проводил и не предлагал решения, для определения объема выборки лучше выбрать табличный метод.
Ниже представлены различные методики. Выбор той или иной из них определяется имеющимися исходными данными или пожеланиями исследователя.
Таблица А. Определение объема выборки по методике К. А. Отдельновой
|
Уровень значимости |
Уровень точности |
||
|
Ориентировочное знакомство |
Исследование средней точности |
Исследование высокой точности |
|
|
0,01 |
100 |
225 |
900 |
|
0,05 |
44 |
100 |
400 |
Объем выборки указан в абсолютных значениях.
Таблица Б. Методика определения размера выборки В. И. Паниотто
|
Размер генеральной совокупности |
500 |
1000 |
2000 |
3000 |
4000 |
5000 |
10000 |
100000 |
∞ |
|
Объем выборки |
222 |
286 |
333 |
350 |
360 |
370 |
385 |
398 |
400 |
Данные указаны в единицах.
Таблица В. Методика N. Fox для определения объема выборки
|
Процент допускаемой ошибки |
Объем выборки в единицах |
|
10 |
88 |
|
5 |
350 |
|
3 |
971 |
|
2 |
2188 |
|
1 |
8750 |
Таблица Г. Определение размера согласно способу K. Mitra, S. Das, M. Mandal
|
Величина различий между основной и контрольной группами |
Уровень значимости |
Мощность |
Объем выборки |
|
0,2 |
0,5 |
80 |
586 |
|
0,2 |
0,1 |
80 |
773 |
|
0,2 |
0,5 |
90 |
746 |
|
0,4 |
0,5 |
80 |
146 |
|
0,4 |
0,1 |
80 |
193 |
|
0,4 |
0,5 |
90 |
186 |
|
0,6 |
0,5 |
80 |
65 |
|
0,6 |
0,1 |
80 |
86 |
|
0,6 |
0,5 |
90 |
83 |
По формулам
Объем выборки, достаточный для проведения новых исследований, определяется следующими параметрами:
- изменчивость признака;
- уровень доверия;
- размер эффекта.
Объем выборки всегда зависит от предполагаемой строгости эксперимента и изменчивости исследуемого признака.
Формула для оценки среднего значения размера выборки:
n = (z × σ / H)2, где:
n – размер выборки;
z – доверительный уровень (при р = 0,05 z = 1,96);
σ – стандартное отклонение;
Н – допустимая ошибка в натуральных величинах.
Формула для оценки доли выборки:
Где:
n – размер выборки;
z – доверительный уровень (при р = 0,05 z = 1,96);
p – доля признака (наибольшее значение достигается при р = 0,5);
H – допустимая ошибка в процентах.
Еще одна формула расчета объема выборки (чаще всего калькулятор размера выборки использует именно ее):
Где:
n – размер выборки;
z – нормированное отклонение;
p – вариация для выборки;
q = 1 – р;
е – допустимая ошибка.
Нормированное отклонение (z) определяется по таблице, зная основные значения доверительной вероятности (α).
|
α, % |
60 |
70 |
80 |
85 |
90 |
95 |
97 |
99 |
99,7 |
|
z |
0,84 |
1,03 |
1,29 |
1,44 |
1,65 |
1,96 |
2,18 |
2,58 |
3,0 |
Последняя формула расчета имеет особенности.
- Начинать считать размер выборки следует с проведения качественного анализа генеральной совокупности, чтобы выяснить степень схожести и близости исследуемых единиц совокупности относительно их географических, демографических, социальных и других характеристик.
- Рекомендуется предварительно выполнить пилотное исследование с целью определения приблизительного значения р.
- Если максимальная вариация р = 50%, то и значение q = 50%, что является наиболее худшим вариантом.
Пример расчета размера выборки
Маркетолог проводит исследование с целью определить, нужны ли компании визитки. Для этого промоутеру предстоит опросить потенциальных клиентов и задавать только один вопрос: «Вы пользуетесь визитками?». На что человек должен будет ответить «Да» или «Нет».
В таком случае размер выборки будет рассчитываться так. Принимаем, что уровень доверительности равен 95% (стандартное значение). При этом нормированное отклонение z составит 1,96. После предварительного анализа предположим, что 80% представителей генеральной совокупности дадут положительный ответ, а значит, р = 0,8. Соответственно, q = 1 – 0,8 = 0,2. Вероятность допустимой ошибки примем за 10%, т. е. e = 0,1. Теперь можно выполнить расчет.
Округлив значение, получаем размер выборки n = 62 человека. Соответственно, в опросе с заданными параметрами нужно задействовать 62 человека из числа целевой аудитории компании.
Подходы к определению размера выборки
Выделяют несколько подходов, которые позволяют установить объем выборки для проведения статистического исследования.
- Арбитражный подход. Объем выборки составляет определенный процент от генеральной совокупности. Например, 10% от общего количество потребителей.
- Традиционный подход. Выборка составляется на основе определенных норм, которые были выработаны в процессе проведенных ранее исследований. Подход игнорирует обстоятельства и условия, строгая логика отсутствует.
- Затратный подход. Объем выборки определяется в зависимости от стоимости сбора информации и возможных затрат на материалы для проведения исследования.
- Подход на основе использования доверительных интервалов. Размер выборки в этом случае рассчитывается по формуле, что обеспечивает высокую точность результата:
n = (p × q) / s2, где:
n – размер выборки;
p – вероятность того, что нужное событие наступит, %;
q = 100% – p;
s – стандартное отклонение, которое соответствует доверительному уровню.
Ошибки выборки
Объем выборки при массовом исследовании определяется двумя факторами:
- Точностью полученных данных или статистической погрешностью.
- Размером и количеством подгрупп, на которые будет разбита выборка при проведении анализа.
При любом исследовании, которое предполагает выборочный опрос респондентов из генеральной совокупности, может присутствовать погрешность данных или ошибка выборки. Выделяют два ее типа:
- случайная – обусловлена действием статистических законов, поэтому очень легко рассчитывается по формулам теории вероятности и математической статистики;
- систематическая – является следствием неточностей при проектировании выборки, определить ее степень смещения, направление и размер практически невозможно.
При расчете размера выборки важно так собрать данные, чтобы вероятность систематической ошибки в результате работы была минимальной.
Расчет случайной ошибки выборки зависит от объема последней, а также от степени однородности данных (дисперсии). Принцип такой: чем меньше дисперсия, тем меньше ошибка. Для расчета чаще всего используют онлайн калькуляторы.
Также выделяют:
- Ошибки первого рода – альфа-ошибка, при которой делается вывод о достоверности гипотезы, которая на самом деле неверна. Величина выбирается произвольно в диапазоне от 0 до 1, чаще всего это значение 0,05 или 0,01.
- Ошибки второго рода – бета-ошибка, при которой тот факт, что гипотеза неверна, остается не выявленным. Значение, как правило, устанавливается на уровне 0,2.
Расчет доверительного интервала
Для расчета доверительного интервала применяются достаточно простые формулы, выбор которых зависит от доли выборки в составе генеральной совокупности.
Если выборка значительно меньше генеральной совокупности:
Если выборка и генеральная совокупность сопоставимы:
В обеих формулах:
Δ – предельная ошибка выборки в процентах;
z – нормированное отклонение или z-фактор;
p – доля респондентов с наличием признака, который исследуется;
q – доля респондентов без исследуемого признака;
n – размер выборки;
N – объем генеральной совокупности (сколько всего респондентов).
Доверительный интервал удобно рассчитывать с помощью онлайн-калькулятора, который использует те же формулы, что мы привели выше. Просто введите необходимые переменные, и система рассчитает результат.
Расчет статистической значимости
Определить этот показатель проще всего с помощью онлайн-сервиса. Калькулятор позволяет проверить, существует ли статистически значимая разница между долями признака, которые были получены из независимых выборок.
Рассчитывать статистическую значимость можно только в том случае, если произведения (n × p) и (n × (1 – р)) превышают значение 5. При этом n – объем выборки, р – доля признака.
Часто задаваемые вопросы
Обычно размер выборки и ее статистическая значимость прямо пропорциональны, т. е. с ростом выборки получение случайных результатов сводится к минимуму. Важность статистической значимости зависит от определенной ситуации. Вот некоторые из них.
|
Ситуация |
Важность статистической значимости |
|
Опросы сотрудников |
Важна, т. к. повышает всесторонность выводов по итогам опроса. |
|
Опросы клиентов об уровне их удовлетворенности |
Не имеет значения, т. к. важен каждый ответ независимо от того, положительный он или отрицательный. |
|
Исследование рынка |
Имеет решающее значение, т. к. помогает сделать вывод о целевом рынке. |
|
Опросы об образовании |
Важна, если нужно использовать результаты исследования при внесении изменений в учебном заведении. |
|
Здравоохранение |
Помогает выявлять серьезные проблемы, делать выводы в исследованиях. Если же опрос проводится ради оценки удовлетворенности пациентов, то не имеет значения. |
|
Опросы для развлечения |
Не важна. |
Заданный размер выборки нужен для получения оценок с желаемым уровнем точности, если речь идет об исследовании распространенности в популяции конкретной характеристики.
- Мало просмотров.
- Узкая тематика.
- Низкий бюджет.
- Высокий бюджет.
Чтобы правильно рассчитать размер выборки и провести показательное исследование с учетом выдвинутых требований:
- наберитесь терпения и дождитесь, пока соберется требуемое количество респондентов;
- будьте последовательны и показывайте рекламу только ЦА в определенное время;
- устанавливайте высокий уровень достоверности при расчете выборки.
При определении объема выборки основную роль играет переменная исхода конкретного исследования. Если в расчет добавляются дополнительные важные переменные, то размер выборки должен позволять адекватно проанализировать их.
Это такое количество объектов исследования, которое позволит получить максимально точный и достоверный результат с предельно небольшой погрешностью. При этом его можно репрезентовать на более широкую аудиторию, в т. ч. по отношению к генеральной совокупности.
Заключение
Объем выборки – важный показатель, без которого невозможно провести адекватное исследование и сделать объективные выводы. Он отражает количество представителей целевой аудитории, которое будет принимать непосредственное участие в эксперименте, и требуется во всех случаях, когда стоит задача сделать определенные заключения по результатам опроса.
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Статистические исследования числовых рядов. Статистические характеристики числовых рядов
Очень часто из-за дороговизны или слишком большого числа наблюдений невозможно получить полной информации об объектах, событиях или наблюдениях. По этой причине информацию получают на основе анализа части всего множества объектов, событий или наблюдений, называемой рядом числовых данных, рядом выборочных данных или, просто, выборкой.
Выборка представляет собой конечный ряд чисел (выборочных данных), количество чисел в котором называют объемом выборки
Для обеспечения достоверности информации об объектах, событиях или наблюдениях, полученных на основе статистических исследований числовых рядов (анализа выборочных данных), отбор выборочных данных должен носить случайный характер и иметь достаточно большой объем, то есть выборка должны быть репрезентативной (представительной).
Статистические исследования числовых рядов (рядов чисел, рядов выборочных данных) удобно проводить в соответствии со следующей схемой, которую мы изложим на примере следующей выборки X :
| X = {3,24; 3,44; 3,12; 3,25; 3,12; 3,34; 3,37; 3,44; 3,24; 3,12} | (1) |
-
Определяем объем выборки (число чисел в числовом ряде).
В числовом ряде (1) десять чисел, поэтому объем выборки равен 10.
-
Вычисляем среднее арифметическое числового ряда X (среднее выборочное значение), которое обозначают
.
Для числового ряда (1)
-
Производим упорядочение числового ряда по возрастанию (ранжирование числовых данных). Полученный числовой ряд, который обозначим X1 , называют вариационным рядом.
Для числового ряда X вариационный ряд X1 имеет следующий вид:
X1 = {3,12; 3,12; 3,12; 3,24; 3,24; 3,25; 3,34; 3,37; 3,44; 3,44}
-
Вычисляем размах числового ряда X , то есть разность между наибольшим числом из числового ряда и наименьшим числом из числового ряда.
В числовом ряде X , как и в вариационном ряде X1 , число 3,44 является наибольшим числом, а число 3,12 является наименьшим числом. Поэтому размах числового ряда X равен
3,44 – 3,12 = 0,32
-
Вычисляем медиану числового ряда.
В случае, когда объем выборки (число членов числового ряда) – чётное число, медианой числового ряда является число, равное половине суммы двух чисел, стоящих в середине вариационного ряда.
Число членов ряда X равно чётному числу 10 , а в середине вариационного ряда X1 стоят числа 3,24 и 3,25 . Поэтому медиана числового ряда, которую обычно обозначают символом Me , равна
В случае, когда объем выборки (число членов числового ряда) –нечётное число, медианой числового ряда является число, стоящее в середине вариационного ряда.
Например, медианой числового ряда
{2; 3; 7; 9; 15}
является число 7 .
-
Составляем таблицу частот числового ряда.
Если взглянуть на числа (выборочные данные), составляющие вариационный ряд X1 , то можно заметить, некоторые числа повторяются, а другие встречаются лишь по одному разу. Это наблюдение приводит к следующему определению.
ОПРЕДЕЛЕНИЕ 1. Если выборочное данное встречается в вариационном ряде m раз, то число m называют частотой (абсолютной частотой) этого выборочного данного.
Воспользовавшись определением 1, сформируем для числового ряда X таблицу, содержащую две строки, которую называют таблицей частот (абсолютных частот) числового ряда. Для этого в первой строке таблицы запишем числа, составляющие вариационный ряд X1 , причем запишем числа в порядке возрастания и без повторений. Во второй строке таблицы запишем частоты (абсолютные частоты), соответствующие числам из первой строки таблицы.
ТАБЛИЦА ЧАСТОТ ЧИСЛОВОГО РЯДА
Числа, составляющие вариационный ряд (без повторений) 3,12 3,24 3,25 3,34 3,37 3,44 Частоты 3 2 1 1 1 2 Числа, составляющие вариационный ряд (без повторений) Частоты 3,12 3 3,24 2 3,25 1 3,34 1 3,37 1 3,44 2 ЗАМЕЧАНИЕ. Сумма частот, то есть сумма чисел, записанных во второй строке таблицы частот числового ряда, равна объему выборки (числу чисел в числовом ряде). В рассматриваемом случае это число 10 .
-
Составляем таблицу относительных частот (в процентах).
ОПРЕДЕЛЕНИЕ 2. Относительной частотой (в процентах) выборочного данного называют число процентов, которое составляет частота этого выборочного данного от всего объема выборки (количества членов числового ряда).
Для того, чтобы сформировать таблицу относительных частот числового ряда, заменим частоты, записанные во второй строке таблицы частот числового ряда, на соответствующие им относительные частоты. В результате получим следующую таблицу.
ТАБЛИЦА ОТНОСИТЕЛЬНЫХ ЧАСТОТ (В ПРОЦЕНТАХ)
Числа, составляющие вариационный ряд (без повторений) 3,12 3,24 3,25 3,34 3,37 3,44 Относительные частоты (%) 30% 20% 10% 10% 10% 20% Числа, составляющие вариационный ряд (без повторений) Относительные частоты (%) 3,12 30% 3,24 20% 3,25 10% 3,34 10% 3,37 10% 3,44 20% -
Находим моду числового ряда.
ОПРЕДЕЛЕНИЕ 3. Модой числового ряда называют выборочное данное с наибольшей частотой.
Из таблицы частот числового ряда видно, что модой числового ряда X является число 3,12 , поскольку его частота 3 является наибольшей. Очевидно, что и относительная частота этого выборочного данного является самой большой (30%) .
ЗАМЕЧАНИЕ. Объем выборки, среднее выборочное значение, размах, медиана и мода числового ряда являются одними из статистических характеристик числовых рядов.
Мода и медиана
Модой ряда чисел называется число, наиболее часто встречающееся в данном ряду.
Обратимся снова к нашему примеру со сборной по футболу:
Чему в данном примере равна мода? Какое число наиболее часто встречается в этой выборке?
Все верно, это число ( displaystyle 181), так как два игрока имеют рост ( displaystyle 181) см; рост же остальных игроков не повторяется.
Тут все должно быть ясно и понятно, да и слово знакомое, правда?
Перейдем к медиане, ты ее должен знать из курса геометрии. Но мне не сложно напомнить, что в геометрии медиана (в переводе с латинского- «средняя») — отрезок внутри треугольника, соединяющий вершину треугольника с серединой противоположной стороны.
Ключевое слово – СЕРЕДИНА. Если ты знал это определение, то тебе легко будет запомнить, что такое медиана в статистике.
Медианой ряда чисел с нечетным числом членов называется число, которое окажется посередине, если этот ряд упорядочить (проранжировать, т.е. расположить значения в порядке убывания или возрастания).
Медианой ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине, если этот ряд упорядочить.
Ну что, вернемся к нашей выборке футболистов?
Ты заметил в определении медианы важный момент, который нам еще здесь не встречался? Конечно, «если этот ряд упорядочить»!
Для того, чтобы в ряду чисел был порядок, можно расположить значения роста футболистов как в порядке убывания, так и в порядке возрастания. Мне удобней выстроить этот ряд в порядке возрастания (от самого маленького к самому большому).
Вот, что у меня получилось:
Так, ряд упорядочили, какой еще есть важный момент в определении медианы? Правильно, четное и нечетное количество членов в выборке.
Заметил, что для четного и нечетного количества даже определения отличаются? Да, ты прав, не заметить – сложно. А раз так, то нам надо определиться, четное у нас количество игроков в нашей выборке или нечетное?
Все верно – игроков ( displaystyle 11), значит, количество нечетное! Теперь можем применять к нашей выборке менее заковыристое определение медианы для нечетного количества членов в выборке.
Ищем число, которое оказалось посередине в нашем упорядоченном ряду:
Ну вот, чисел у нас ( displaystyle 11), значит, по краям остается по пять чисел, а рост ( displaystyle 183) см будет медианой в нашей выборке.
Не так уж и сложно, правда?
Частота и относительная частота
Частота представляет собой число повторений, сколько раз за какой-то период происходило некоторое событие, проявлялось определенное свойство объекта либо наблюдаемый параметр достигал данной величины.
То есть частота определяет то, как часто повторяется та или иная величина в выборке.
Разберемся на нашем примере с футболистами. Перед нами вот такой вот упорядоченный ряд:
Частота – это число повторений какой-либо величины параметра. В нашем случае, это можно считать вот так. Сколько игроков имеет рост ( 176)?
Все верно, один игрок. Таким образом, частота встречи игрока с ростом ( 176) в нашей выборке равна ( 1).
Сколько игроков имеет рост ( 178)? Да, опять же один игрок. Частота встречи игрока с ростом ( 178) в нашей выборке равна ( 1).
Задавая такие вопросы и отвечая на них, можно составить вот такую табличку:
Ну вот, все довольно просто. Помни, что сумма частот должна равняться количеству элементов в выборке (объему выборки).
То есть в нашем примере: ( 1+1+1+2+1+1+1+1+1+1=11)
Перейдем к следующей характеристике – относительная частота.
Относительная частота – это отношение частоты к общему числу данных в ряду. Как правило, относительная частота выражается в процентах.
Обратимся опять к нашему примеру с футболистами. Частоты для каждого значения мы рассчитали, общее количество данных в ряду мы тоже знаем ( left( n=11 right)) .
Рассчитываем относительную частоту для каждого значения роста и получаем вот такую табличку:
А теперь сам составь таблицы частот и относительных частот для примера с 9-классниками, решающими задачи.