Как найти объем выборки в экселе

Инструменты Excel для вычисления числовых характеристик выборки

Процедура «Описательные статистики » пакета «Анализ данных.

В процедуре автоматически вычисляются следующие числовые характеристики выборки:

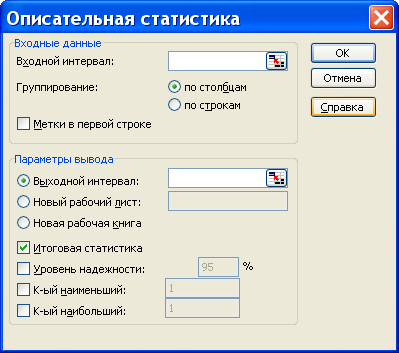
Для того чтобы выполнить вычисления, вводим в поле «Водной интервал» адреса ячеек, в которых записаны выборочные значения;

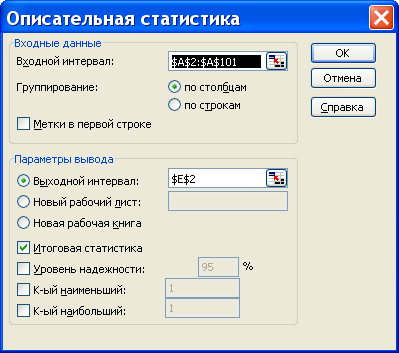
помечаем «Выходной интервал» и вводим в поле адрес первой ячейки, начиная с которой в листе Excel будет отображён резгультат; помечаем «Итоговая статистика»:

Результаты вычислений процедуры представлены в виде таблицы:

Источник

Как рассчитать распределения выборки в Excel

Выборочное распределение — это вероятностное распределение определенной статистики , основанное на множестве случайных выборок из одной совокупности .

В этом руководстве объясняется, как выполнить следующие действия с выборочными распределениями в Excel:

• Сгенерируйте выборочное распределение.
• Визуализируйте распределение выборки.
• Рассчитайте среднее значение и стандартное отклонение выборочного распределения.
• Рассчитайте вероятности относительно выборочного распределения.

Создание выборочного распределения в Excel

Предположим, мы хотим сгенерировать выборочное распределение, состоящее из 1000 выборок, в каждой из которых размер выборки равен 20 и происходит от нормального распределения со средним значением 5,3 и стандартным отклонением 9 .

Мы можем легко сделать это, введя следующую формулу в ячейку A2 нашего рабочего листа:

Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и перетащить формулу на 20 ячеек вправо и на 1000 ячеек вниз:

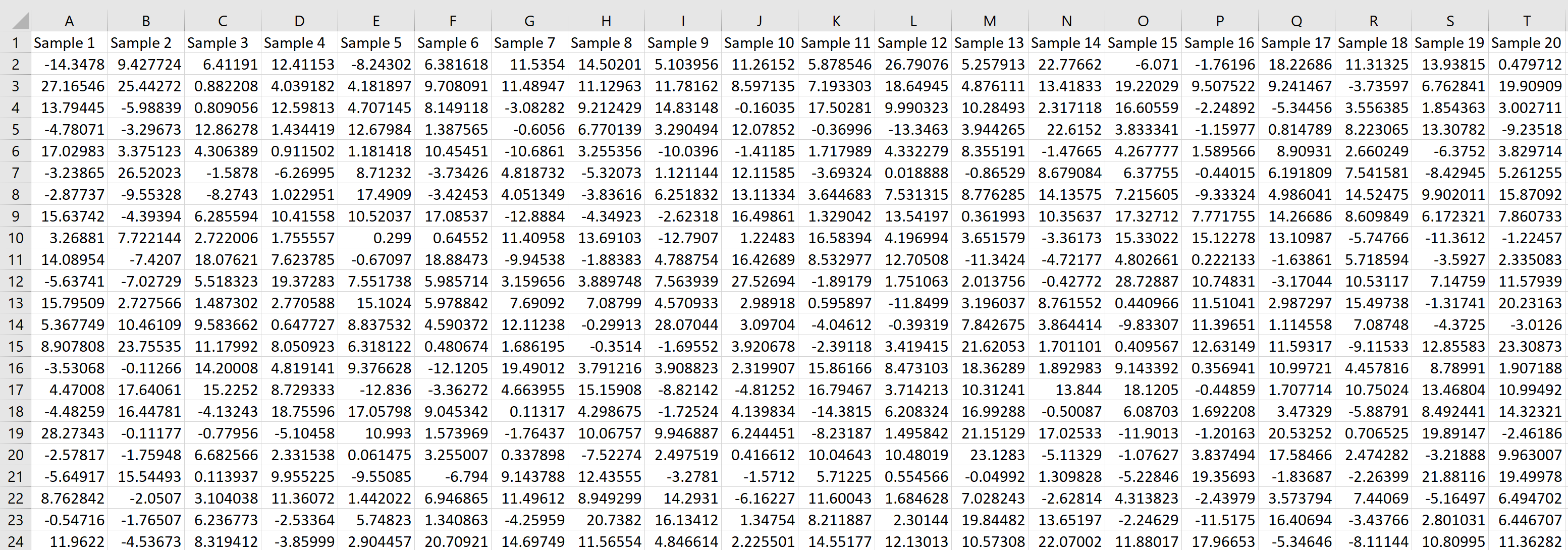
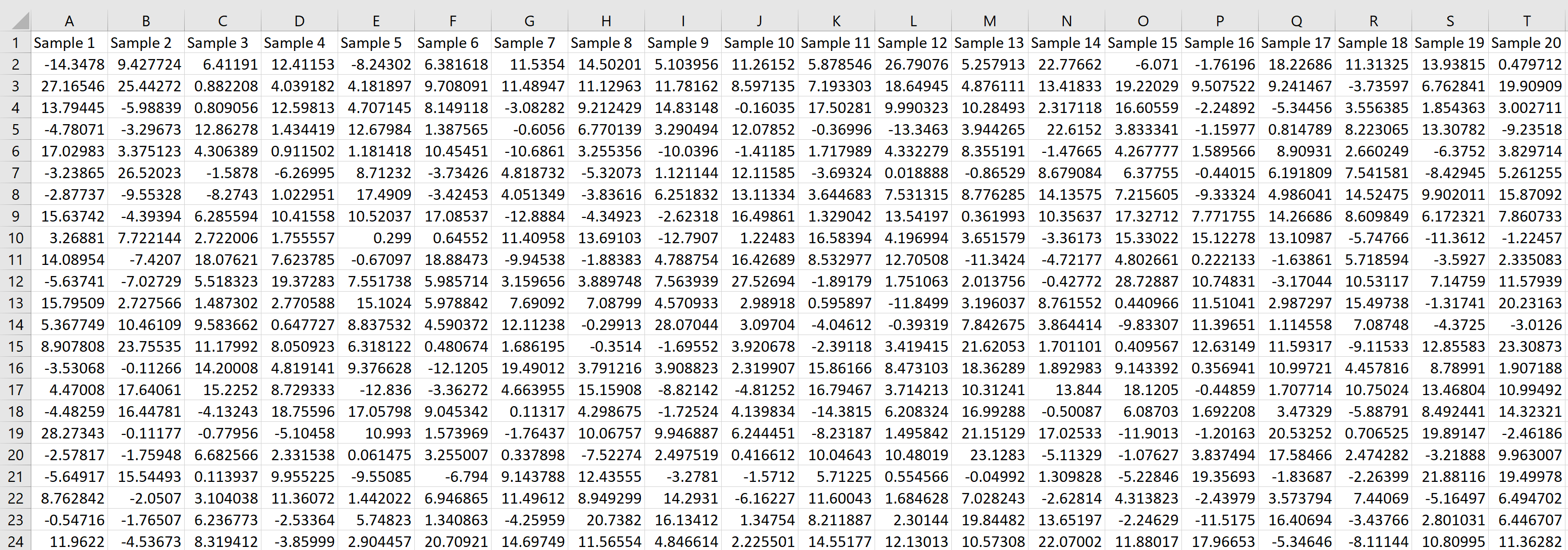
Каждая строка представляет выборку размера 20, в которой каждое значение получено из нормального распределения со средним значением 5,3 и стандартным отклонением 9.

Найдите среднее значение и стандартное отклонение

Чтобы найти среднее значение и стандартное отклонение этого выборочного распределения средних значений выборки, мы можем сначала найти среднее значение каждой выборки, введя следующую формулу в ячейку U2 нашего рабочего листа:

Затем мы можем навести указатель мыши на правый нижний угол ячейки, пока не появится крошечный + , и дважды щелкнуть, чтобы скопировать эту формулу в каждую другую ячейку в столбце U:

Мы видим, что первая выборка имела среднее значение 7,563684, вторая выборка имела среднее значение 10,97299 и так далее.

Затем мы можем использовать следующие формулы для расчета среднего значения и стандартного отклонения среднего значения выборки:

Теоретически среднее значение выборочного распределения должно быть 5,3. Мы видим, что фактическое среднее значение выборки в этом примере равно 5,367869 , что близко к 5,3.

И теоретически стандартное отклонение выборочного распределения должно быть равно s/√n, что будет равно 9/√20 = 2,012. Мы видим, что фактическое стандартное отклонение выборочного распределения составляет 2,075396 , что близко к 2,012.

Визуализируйте распределение выборки

Мы также можем создать простую гистограмму для визуализации выборочного распределения выборочных средних.

Для этого просто выделите все средние значения выборки в столбце U, щелкните вкладку « Вставка », затем выберите параметр « Гистограмма » в разделе « Диаграммы ».

В результате получается следующая гистограмма:

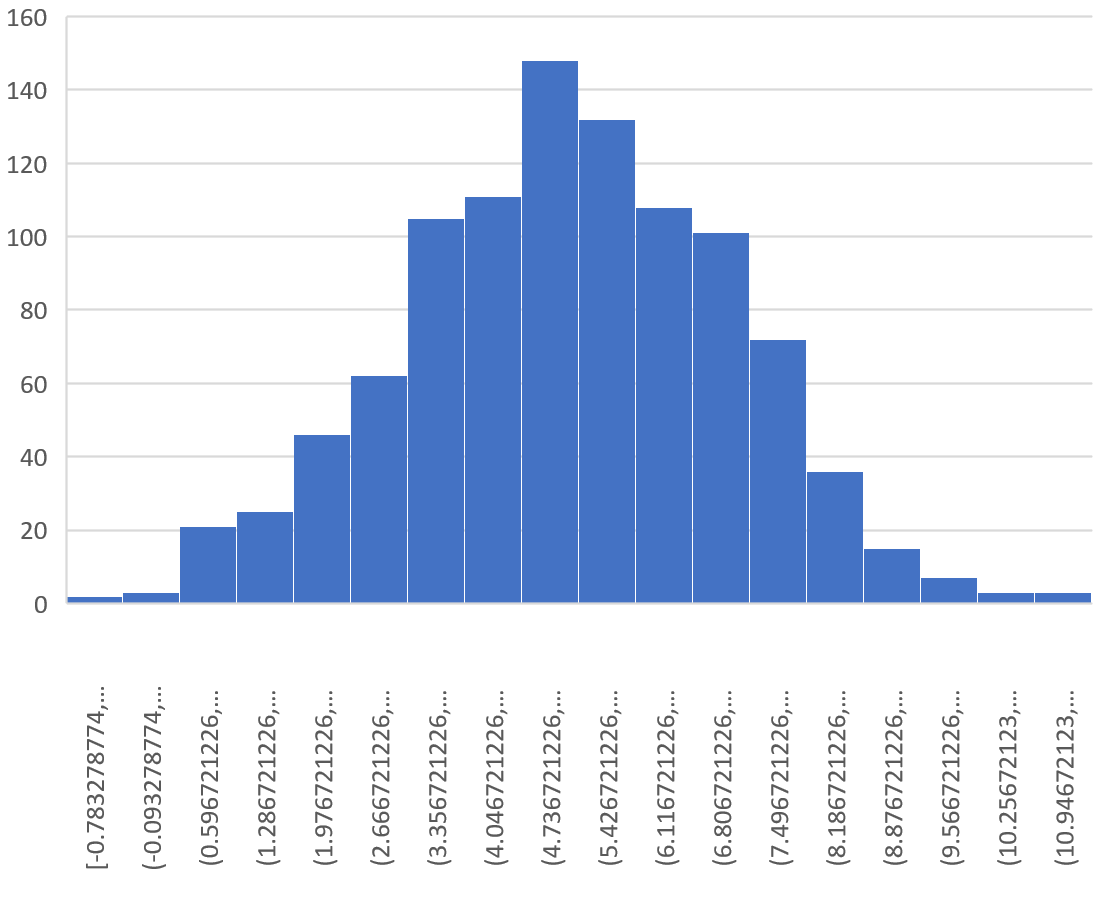
Мы видим, что распределение выборки имеет форму колокола с пиком около значения 5.

Однако из хвостов распределения мы можем видеть, что некоторые выборки имели средние значения больше 10, а некоторые — меньше 0.

Рассчитать вероятности

Мы также можем рассчитать вероятность получения определенного значения среднего значения выборки на основе среднего значения совокупности, стандартного отклонения совокупности и размера выборки.

Например, мы можем использовать следующую формулу, чтобы найти вероятность того, что среднее значение выборки меньше или равно 6, учитывая, что среднее значение генеральной совокупности равно 5,3, стандартное отклонение генеральной совокупности равно 9 и размер выборки равен:

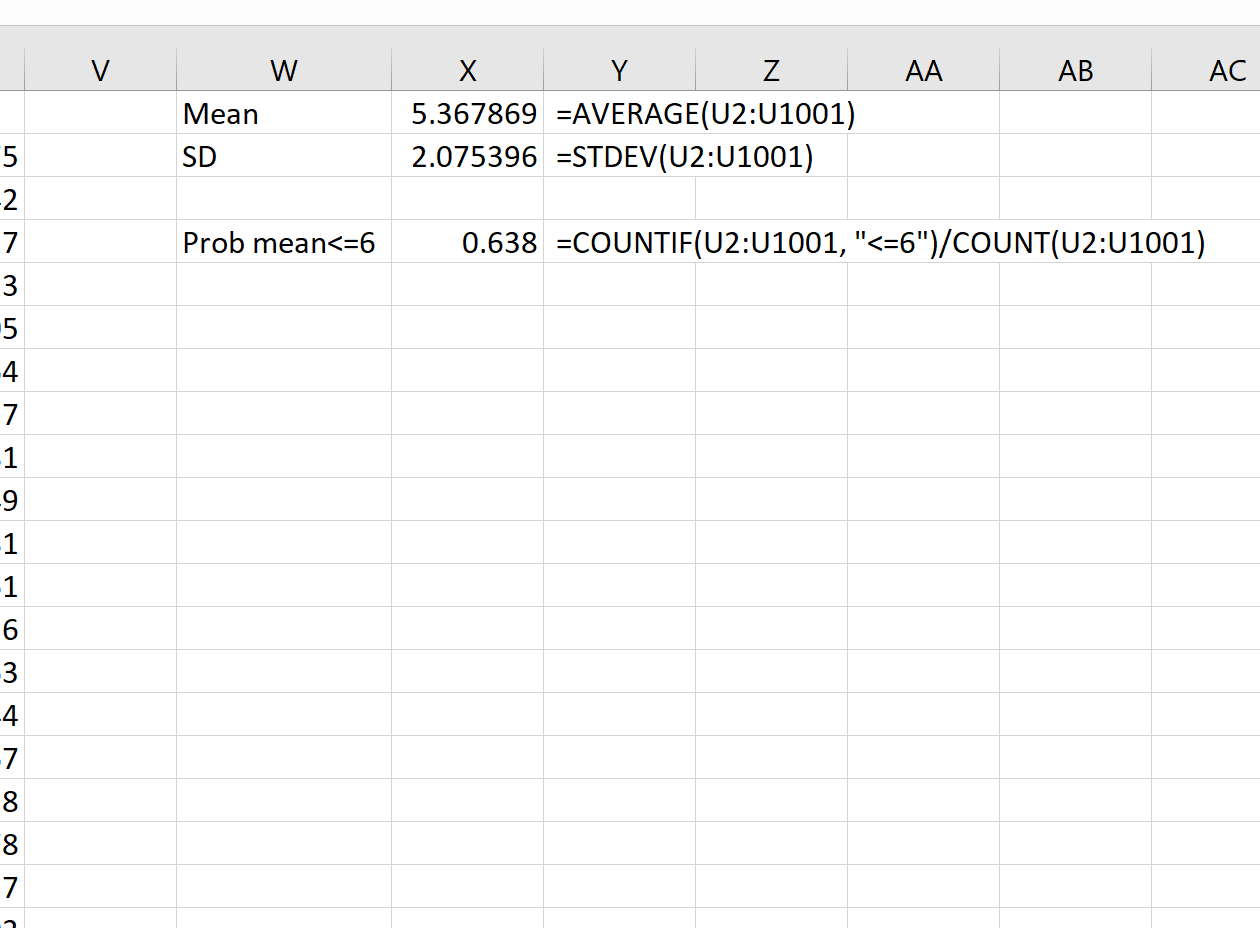
Мы видим, что вероятность того, что среднее значение выборки меньше или равно 6, составляет 0,638.

Это очень близко к вероятности, рассчитанной Калькулятором распределения выборки :

Источник

Б. Расчеты с использованием Мастера функций

Выше приведенные методы расчета статистических показателей неудобны, так как для каждого из них необходимо вручную прописывать формулы. Поэтому для удобства работы в программе Excel предусмотрен мастер функций, позволяющий вводить их в полуавтоматическом режиме и практически без ошибок. Многие статистические показатели выборки и параметры генеральной совокупности можно очень быстро определить с помощью функций, тем более что наименование большинства функций совпадает с наименованием статистических показателей.

В Листе 1 файла Книга1 в столбце введем, символ Х и значения глубины вспашки по 8-ми точкам. В ячейки с А10 по А17 впишем наименование статистических показателей, которые приведены в работе 1.

Для определения средней выборочной (средняя арифметическая) активизируем ячейку В10 (выделенная ячейка со знаком =), в этой ячейке будут отображаться результаты наших вычислений. Для вызова мастера функций необходимо нажать кнопкуВставка функциина стандартной панели инструментов или на строке формул нажать на «fx».

Появляется контекстное меню «Мастер функций – шаг 1 из 2, в категории выбрать «Статистические» (рис. 2.12. )

Рис.2.12. Лист с исходными данными и контекстным меню «Мастер функций»

После выбора категории « Статистические».в окне появляется перечень конкретных статистических функций, выбираемСРЗНАЧ, что означает среднюю по выборке (рис. 2.13 ).

Рис. 2.13. Выбор функции СРЗНАЧ

Далее открывается окно для выбора аргументов функции. В поле Число 1ставим курсор и мышкой выбираем диапазон значений глубины вспашкиВ2:В9, нажимаем клавишуОК, в строке формул автоматически появляется наименование функции и диапазон ячеек(=СРЗНАЧ(В2:В9), а в ячейкеВ10появляется в скобках этот же диапазон (рис. 2.14 )

Рис. 2.14. Диалоговое окно для выбора аргументов функции.

После нажатия клавиши ОКили щелчка мышки в ячейкеВ10появляется значение выборочной средней – средняя глубина вспашки –20,25 см. (рис. 2.15 )

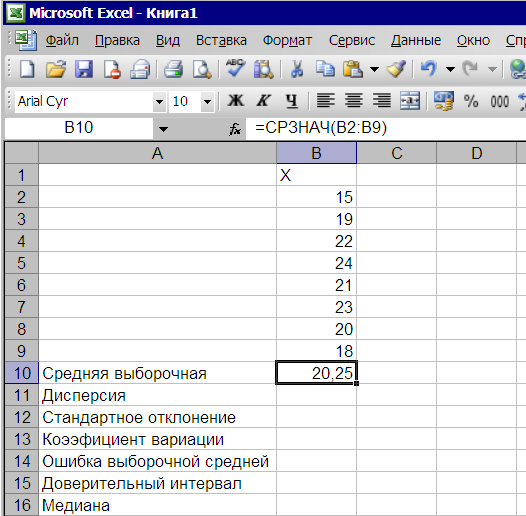
Рис.2.15. Средняя глубины вспашки – средняя выборочная – 20,25 см.

Находим объем выборки (n), который в Мастере функций называется счет (рис. 2.16)

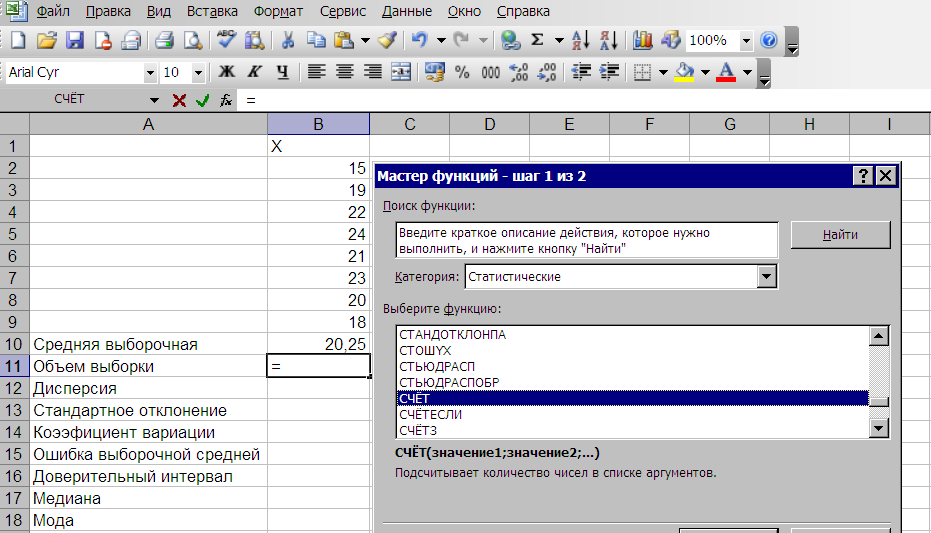
Рис.2.16. Диалоговое окно для нахождения объема выборки (счет)

Выбираем из списка функций ДИСП– дисперсия для выборки. Обратите внимание на то, что в списке имеетсяДИСПР – дисперсия для генеральной совокупности. При выборе конкретной дисперсии в подсказке указывается, что оценивает данная дисперсия (рис. 2.17 ).

Рис. 2.17. Диалоговое окно для выбора дисперсии

Для расчета дисперсии в поле Число 1ставим курсор и мышкой выбираем диапазон значений глубины вспашкиВ2:В9, нажимаем клавишуОК (рис.2.18)

Рис. 2.18. Выбор диапазона ячеек для определения дисперсии

Выбираем из списка функций СТАНДОТКЛОН– стандартное отклонение для выборки. Точно также как и для дисперсии в списке имеетсяСТАНДОТКЛОНП – стандартное отклонение для генеральной совокупности. При выборе конкретного стандартного отклонения в подсказке указывается, что оценивает данное стандартное отклонение (рис. 2.19 ).

Рис. 2.19. Диалоговое окно для выбора стандартного отклонения

В списке как математических, так и статистических функций нет такой функции с помощью, которой можно рассчитать коэффициент выборки (V), поэтому воспользуемся уже известной процедурой ручного набора формул.

Коэффициент вариации представляет собой отношение стандартного отклонения к выборочной средней, выраженной в %. Выделим ячейку для формулы коэффициента вариации В14, затем в строке формул пропишем формулу со ссылкой на ячейки, где находятся стандартное отклонение и выборочная средняя –(В13/В10*100)(рис. 2.20 )

В итоге получаем коэффициент вариации (V) = 14,3974%.

Рис. 2.20. Формула для определения коэффициента вариации

Расчет ошибки выборочной средней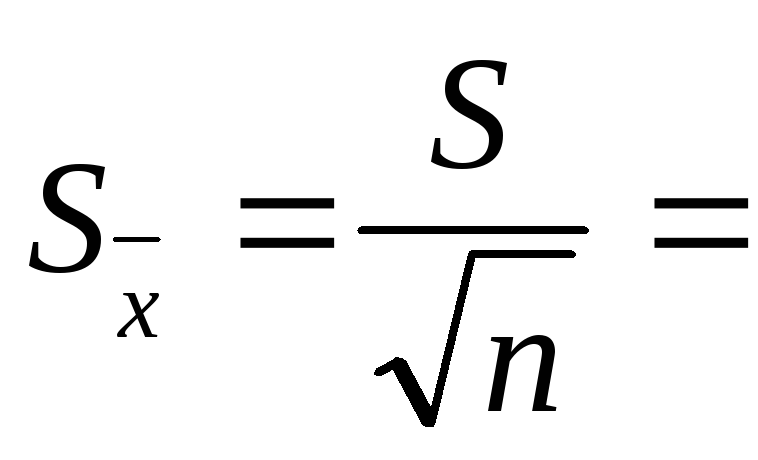

Так как в списке функций нет очень важного статистического показателя – ошибки выборочной средней (стандартная ошибка), рассчитаем этот важный показатель с помощью формул. Выделим ячейку для размещения формулы и получения готового результата В15 , затем в строке формул сначала вставим символ=и укажем следующую формулу:В13/КОРЕНЬ (В11). В ячейкеВ13 значение стандартного отклонения, в ячейкеВ11– объем выборки. После нажатия на клавишуEnter в ячейкеВ15получаем результат –1,0307764.(рис. 2.21)

Рис. 2.21. Расчет ошибки выборочной средней

Расчет предельной ошибки выборочной средней для нахождения доверительного интервала генеральной средней. Предельная ошибка выборочной средней представляет собой произведение критерия Стьюдента на ошибку выборочной средней (t ₀₅*S_x). Значение критерия Стьюдента зависит от числа степеней свободы (n – 1) .

В Мастере функций для нахождения предельной ошибки средней выборочной имеется функция, которая имеет странное название ДОВЕРИТ. Поместим курсор в ячейкуВ16 . затем из списка статистических функций выберем функциюДОВЕРИТ (рис. 2.22 ), нажимаем ОК.

Рис. 2.22. Выбор в меню функции ДОВЕРИТ (предельная ошибка средней)

В появившемся диалоговом окне вводим:

— в поле Альфа введем уровень значимости –0,05,

— в поле Станд_откл. – ссылку на ячейку, где находится стандартное отклонение или готовое значение (2,915),

— в поле Размер – объем выборки (8)

После нажатия на клавишу ОК получаем результат – предельная ошибка выборочной средней равна2,019 (рис. 2.23)

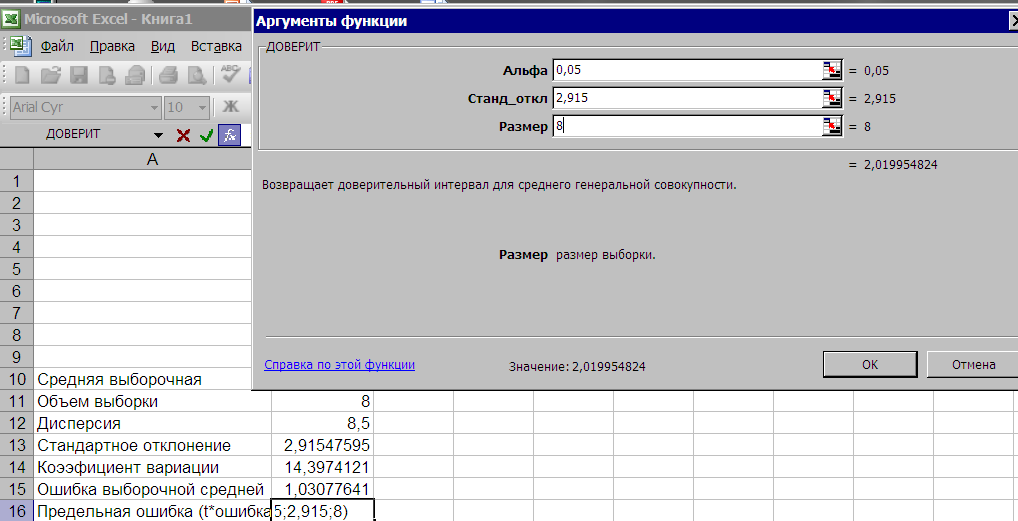
Рис. 2.23. Расчет предельной ошибки выборочной средней

95%-й доверительный интервал (ДИ) для генеральной средней ():

В ячейке А17вводим текст «Доверительный интервал», в ячейкуВ17 записываем значения ДИ следующим образом:20,25 ± 2.02(рис. 2.24 )

Для вычисления медианы – ячейка В18 выбираем функциюМЕДИАНА, в следующем окне указываем диапазонВ2:В9 и в итоге получаем значение –20,5

На рис. 2.24 показаны результаты расчета основных статистических показателей 50 клубней картофеля по массе, г. (Работа 2)

Рис. 2.24. Основные статистические показатели выборки — 50 клубней картофеля

Источник

Б. Расчеты с использованием Мастера функций

Выше приведенные
методы расчета статистических показателей
неудобны, так как для каждого из них
необходимо вручную прописывать формулы.
Поэтому для удобства работы в программе
Excel предусмотрен мастер функций,
позволяющий вводить их в полуавтоматическом
режиме и практически без ошибок. Многие
статистические показатели выборки и
параметры генеральной совокупности
можно очень быстро определить с помощью
функций, тем более что наименование
большинства функций совпадает с
наименованием статистических показателей.

В Листе 1 файла
Книга1 в столбце введем, символ Х и
значения глубины вспашки по 8-ми точкам.
В ячейки с А10 по А17 впишем наименование
статистических показателей, которые
приведены в работе 1.

Для определения
средней выборочной (средняя арифметическая)
активизируем ячейку В10 (выделенная
ячейка со знаком =), в этой ячейке будут
отображаться результаты наших вычислений.
Для вызова мастера функций необходимо
нажать кнопкуВставка функциина
стандартной панели инструментов или
на строке формул нажать на «fx».

Появляется
контекстное меню «Мастер функций –
шаг 1 из 2, в категории выбрать
«Статистические» (рис. 2.12. )

Рис.2.12. Лист с
исходными данными и контекстным меню
«Мастер функций»

После выбора
категории « Статистические».в окне
появляется перечень конкретных
статистических функций, выбираемСРЗНАЧ,
что означает среднюю по выборке (рис.
2.13 ).

Рис. 2.13. Выбор
функции СРЗНАЧ

Далее открывается
окно для выбора аргументов функции. В
поле Число 1ставим курсор и мышкой
выбираем диапазон значений глубины
вспашкиВ2:В9, нажимаем клавишуОК, в строке формул автоматически
появляется наименование функции и
диапазон ячеек(=СРЗНАЧ(В2:В9), а в
ячейкеВ10появляется в скобках этот
же диапазон (рис. 2.14 )

Рис. 2.14. Диалоговое
окно для выбора аргументов функции.

После нажатия
клавиши ОКили щелчка мышки в ячейкеВ10появляется значение выборочной
средней – средняя глубина вспашки –20,25 см. (рис. 2.15 )

Рис.2.15. Средняя
глубины вспашки – средняя выборочная
– 20,25 см.

Находим объем
выборки (n), который в
Мастере функций называется счет (рис.
2.16)

Рис.2.16. Диалоговое
окно для нахождения объема выборки
(счет)

Выбираем из списка
функций ДИСП– дисперсия для выборки.
Обратите внимание на то, что в списке
имеетсяДИСПР – дисперсия для
генеральной совокупности. При выборе
конкретной дисперсии в подсказке
указывается, что оценивает данная
дисперсия (рис. 2.17 ).

Рис. 2.17. Диалоговое
окно для выбора дисперсии

Для расчета
дисперсии в поле Число 1ставим
курсор и мышкой выбираем диапазон
значений глубины вспашкиВ2:В9, нажимаем
клавишуОК (рис.2.18)

Рис. 2.18. Выбор
диапазона ячеек для определения дисперсии

Выбираем из списка
функций СТАНДОТКЛОН– стандартное
отклонение для выборки. Точно также как
и для дисперсии в списке имеетсяСТАНДОТКЛОНП – стандартное отклонение
для генеральной совокупности. При выборе
конкретного стандартного отклонения
в подсказке указывается, что оценивает
данное стандартное отклонение (рис.
2.19 ).

Рис. 2.19. Диалоговое
окно для выбора стандартного отклонения

В списке как
математических, так и статистических
функций нет такой функции с помощью,
которой можно рассчитать коэффициент
выборки (V), поэтому
воспользуемся уже известной процедурой
ручного набора формул.

Коэффициент
вариации представляет собой отношение
стандартного отклонения к выборочной
средней, выраженной в %. Выделим ячейку
для формулы коэффициента вариации В14,
затем в строке формул пропишем формулу
со ссылкой на ячейки, где находятся
стандартное отклонение и выборочная
средняя –(В13/В10*100)(рис. 2.20 )

В итоге получаем
коэффициент вариации (V)
= 14,3974%.

Рис. 2.20. Формула
для определения коэффициента вариации

Расчет ошибки
выборочной средней

Так как в списке
функций нет очень важного статистического
показателя – ошибки выборочной средней
(стандартная ошибка), рассчитаем этот
важный показатель с помощью формул.
Выделим ячейку для размещения формулы
и получения готового результата В15 ,
затем в строке формул сначала вставим
символ=и укажем следующую формулу:В13/КОРЕНЬ (В11). В ячейкеВ13
значение стандартного отклонения, в
ячейкеВ11– объем выборки. После
нажатия на клавишуEnter
в ячейкеВ15получаем результат –1,0307764.(рис. 2.21)

Рис. 2.21. Расчет
ошибки выборочной средней

Расчет предельной
ошибки выборочной средней для нахождения
доверительного интервала генеральной
средней. Предельная ошибка выборочной
средней представляет собой произведение
критерия Стьюдента на ошибку выборочной
средней (t ₀₅*S_x). Значение критерия Стьюдента зависит
от числа степеней свободы (n
– 1) .

В Мастере функций
для нахождения предельной ошибки
средней выборочной имеется функция,
которая имеет странное название ДОВЕРИТ.
Поместим курсор в ячейкуВ16 .
затем из списка статистических функций
выберем функциюДОВЕРИТ (рис. 2.22
), нажимаем ОК.

Рис. 2.22. Выбор в
меню функции ДОВЕРИТ (предельная ошибка
средней)

В появившемся
диалоговом окне вводим:

– в поле Альфа введем уровень значимости –0,05,

– в поле Станд_откл.
– ссылку на ячейку, где находится
стандартное отклонение или готовое
значение (2,915),

– в поле Размер
– объем выборки (8)

После нажатия на
клавишу ОК получаем результат –
предельная ошибка выборочной средней
равна2,019 (рис. 2.23)

Рис. 2.23. Расчет
предельной ошибки выборочной средней

95%-й
доверительный интервал (ДИ) для генеральной
средней ():

В ячейке А17вводим текст «Доверительный интервал»,
в ячейкуВ17 записываем значения ДИ
следующим образом:20,25 ± 2.02(рис.
2.24 )

Для вычисления
медианы – ячейка В18 выбираем функциюМЕДИАНА, в следующем окне указываем
диапазонВ2:В9 и в итоге получаем
значение –20,5

На рис. 2.24 показаны
результаты расчета основных статистических
показателей 50 клубней картофеля по
массе, г. (Работа 2)

Рис. 2.24. Основные
статистические показатели выборки –
50 клубней картофеля

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Процедура «Описательные статистики » пакета «Анализ данных.

В процедуре автоматически вычисляются следующие числовые характеристики выборки:

Для того чтобы выполнить вычисления, вводим в поле «Водной интервал» адреса ячеек, в которых записаны выборочные значения;

помечаем «Выходной интервал» и вводим в поле адрес первой ячейки, начиная с которой в листе Excel   будет отображён резгультат; помечаем «Итоговая статистика»:

 

Результаты вычислений процедуры представлены в виде таблицы:

Столбец1
Среднее	120.10
Стандартная ошибка	0.22
Медиана	120.12
Мода	118.69
Стандартное отклонение	2.15
Дисперсия выборки	4.63
Эксцесс	0.21
Асимметричность	-0.16
Интервал	11.21
Минимум	114.46
Максимум	125.67
Сумма	12010.34
Счет	100

Здесь: «Асимметричность» – коэффициент асимметрии, «Интервал» – размах варьирования, «Счёт» – объём выборки.

Функция «Квартиль» для вычисления квартилей и межквартильного размаха

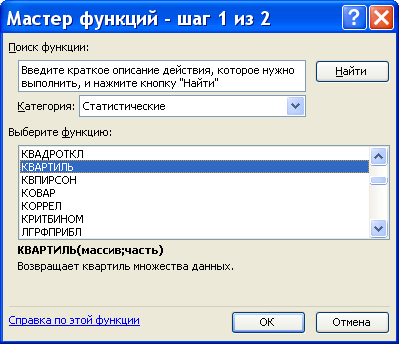
КВАРТИЛЬ(массив;часть)

Функция вычисляет (в зависимости от значения параметра «Часть»), выборочные значения верхней квартили («Часть» = 3)  или нижней квартили («Часть» = 13), медиану («Часть» = 2)  , наибольшее («Часть» = 4)  или наименьшее («Часть» = 03)   значения для выборки, определённой как «массив»..

Разделы: Математика

• Совершенствование умений и навыков нахождения статистических характеристик случайной величины, работа с расчетами в Excel;
• применение информационно коммутативных технологий для анализа данных; работа с различными информационными носителями.

1. Сегодня на уроке мы научимся рассчитывать статистические характеристики для больших по объему выборок, используя возможности современных компьютерных технологий.
2. Для начала вспомним:

– что называется случайной величиной? (Случайной величиной называют переменную величину, которая в зависимости от исхода испытания принимает одно значение из множества возможных значений.)

– Какие виды случайных величин мы знаем? (Дискретные, непрерывные.)

– Приведите примеры непрерывных случайных величин (рост дерева), дискретных случайных величин (количество учеников в классе).

– Какие статистические характеристики случайных величин мы знаем (мода, медиана, среднее выборочное значение, размах ряда).

– Какие приемы используются для наглядного представления статистических характеристик случайной величины (полигон частот, круговые и столбчатые диаграммы, гистограммы).

1. Рассмотрим, применение инструментов Excel для решения статистических задач на конкретном примере.

Пример. Проведена проверка в 100 компаниях. Даны значения количества работающих в компании (чел.):

1. Занести данные в EXCEL, каждое число в отдельную ячейку.

23	25	24	25	30	24	30	26	28	26
32	33	31	31	25	33	25	29	30	28
23	30	29	24	33	30	30	28	26	25
26	29	27	29	26	28	27	26	29	28
29	30	27	30	28	32	28	26	30	26
31	27	30	27	33	28	26	30	31	29
27	30	30	29	27	26	28	31	29	28
33	27	30	33	26	31	34	28	32	22
29	30	27	29	34	29	32	29	29	30
29	29	36	29	29	34	23	28	24	28

2. Для расчета числовых характеристик используем опцию Вставка – Функция. И в появившемся окне в строке категория выберем — статистические, в списке: МОДА

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_о = 29 (чел) – Фирм у которых в штате 29 человек больше всего.

Используя тот же путь вычисляем медиану.

Вставка – Функция – Статистические – Медиана.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили М_е = 29 (чел) – среднее значение сотрудников в фирме.

Размах ряда чисел – разница между наименьшим и наибольшим возможным значением случайной величины. Для вычисления размаха ряда нужно найти наибольшее и наименьшее значения нашей выборки и вычислить их разность.

Вставка – Функция – Статистические – МАКС.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наибольшее значение = 36.

Вставка – Функция – Статистические – МИН.

В поле Число 1 ставим курсор и мышкой выделяем нашу таблицу:

Нажимаем клавишу ОК. Получили наименьшее значение = 22.

36 – 22 = 14 (чел) – разница между фирмой с наибольшим штатом сотрудников и фирмой с наименьшим штатом сотрудников.

Для построения диаграммы и полигона частот необходимо задать закон распределения, т.е. составить таблицу значений случайной величины и соответствующих им частот. Мы ухе знаем, что наименьшее число сотрудников в фирме = 22, а наибольшее = 36. Составим таблицу, в которой значения x_iслучайной величины меняются от 22 до 36 включительно шагом 1.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni

Чтобы сосчитать частоту каждого значения воспользуемся

Вставка – Функция – Статистические – СЧЕТЕСЛИ.

В окне Диапазон ставим курсор и выделяем нашу выборку, а в окне Критерий ставим число 22

Нажимаем клавишу ОК, получаем значение 1, т.е. число 22 в нашей выборке встречается 1 раз и его частота =1. Аналогичным образом заполняем всю таблицу.

xi	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36
ni	1	3	4	5	11	9	13	18	16	6	4	6	3	0	1

Для проверки вычисляем объем выборки, сумму частот (Вставка – Функция – Математические — СУММА). Должно получиться 100 (количество всех фирм).

Чтобы построить полигон частот выделяем таблицу – Вставка – Диаграмма – Стандартные – Точечная (точечная диаграмма на которой значения соединены отрезками)

Нажимаем клавишу Далее, в Мастере диаграмм указываем название диаграммы (Полигон частот), удаляем легенду, редактируем шкалу и характеристики диаграммы для наибольшей наглядности.

Для построения столбчатой и круговой диаграмм используем тот же путь (выбирая нужный нам тип диаграммы).

Диаграмма – Стандартные – Круговая.

Диаграмма – Стандартные – Гистограмма.

4. Сегодня на уроке мы научились применять компьютерные технологии для анализа и обработки статистической информации.

Как рассчитать размер выборки в Excel — Вокруг-Дом — 2021

Table of Contents:

Microsoft Excel имеет десять основных статистических формул, таких как размер выборки, среднее значение, медиана, стандартное отклонение, максимум и минимум. Размер выборки — это число наблюдений в наборе данных, например, если опрашивающая компания опрашивает 500 человек, то размер выборки данных составляет 500. После ввода набора данных в Excel формула = COUNT вычислит размер выборки. , Размер выборки полезен для вычислений, таких как стандартные ошибки и уровни достоверности. Использование Microsoft Excel позволит пользователю быстро рассчитать статистические формулы, поскольку статистические формулы, как правило, длиннее и сложнее, чем другие математические формулы.

Excel облегчает сложные статистические вычисления.

Шаг 1

Введите данные наблюдений в Excel, по одному наблюдению в каждой ячейке. Например, введите данные в ячейки с A1 по A24. Это обеспечит вертикальный столбец данных в столбце А.

Шаг 2

Введите “= COUNT (” в ячейку B1.

Шаг 3

Выделите диапазон ячеек данных или введите диапазон ячеек данных после «(», введенного на шаге 2 в ячейку B1, затем завершите формулу знаком «)». Диапазон ячеек — это любые ячейки, в которых есть данные. В этом примере диапазон ячеек от A1 до A24. Формула в примере — это “= COUNT (A1: A24)”

Шаг 4

Нажмите «Enter», и размер ячейки появится в ячейке с формулой. В нашем примере ячейка B1 будет отображать 24, поскольку размер выборки будет 24.