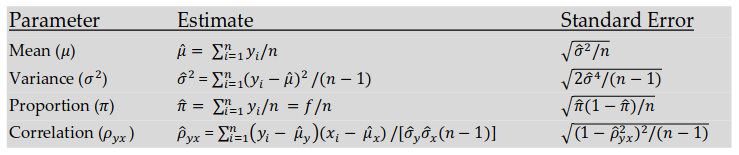Как найти объем выборки в нормальном распределении - Сайт, где вы сможете решить свои вопросы

Как определить размер выборки?

Время на прочтение
4 мин

Количество просмотров 55K

Статистика знает все. И Ильф и Е. Петров, «12 Стульев»

Представьте себе, что вы строите крупный торговый центр и желаете оценить автомобильный поток въезда на территорию парковки. Нет, давайте другой пример… они все равно этого никогда не будут делать. Вам необходимо оценить вкусовые предпочтения посетителей вашего портала, для чего необходимо провести среди них опрос. Как увязать количество данных и возможную погрешность? Ничего сложного — чем больше ваша выборка, тем меньше погрешность. Однако и здесь есть нюансы.

Теоретический минимум

Не будет лишним освежить память, эти термины нам пригодятся далее.

Популяция – Множество всех объектов, среди которых проводится исследования.
Выборка – Подмножество, часть объектов из всей популяции, которая непосредственно участвует в исследовании.
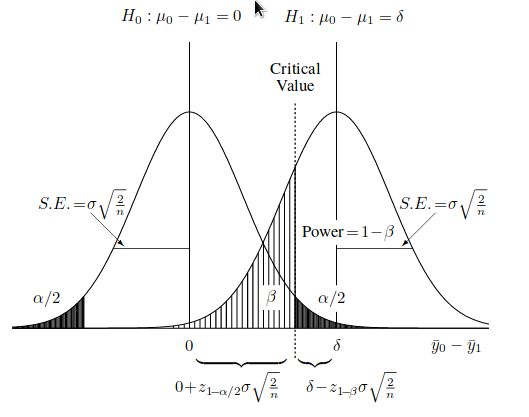
Ошибка первого рода — (α) Вероятность отвергнуть нулевую гипотезу, в то время как она верна.
Ошибка второго рода — (β) Вероятность не отвергнуть нулевую гипотезу, в то время как она ложна.
1 — β — Статистическая мощность критерия.
μ₀ и μ₁ — Средние значения при нулевой и альтернативной гипотезе.

Уже в самих определениях ошибки первого и второго рода имеется простор для дебатов и толкований. Как с ними определиться и какую выбрать в качестве нулевой? Если вы исследуете уровень загрязнения почвы или вод, то как сформулируете нулевую гипотезу: загрязнение присутствует, или нет загрязнения? А ведь от этого зависит объем выборки из общей популяции объектов.

Исходная популяция, также как и выборка может иметь любое распределение, однако среднее значение имеет нормальное или гауссово распределение благодаря Центральной Предельной Теореме.

Относительно параметров распределения и среднего значения в частности возможно несколько типов умозаключений. Первое из них называется доверительным интервалом. Он указывает на интервал возможных значений параметра, с указанным коэффициентом доверия. Так например 100(1-α)% доверительный интервал для μ будет таким (Ур. 1).

$hat{mu} pm t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

df — Степень свободы = n — 1, от английского «degrees of freedom».
$t_{{alpha/2};df}$ — Двусторонняя критическая величина, t-критерий Стьюдента.

Второе из умозаключений — проверка гипотезы. Оно может быть примерно таким.

H₀: μ = h
H₁: μ > h
H₂: μ < h

С доверительным интервалом 100(1-α) для μ можно сделать выбор в пользу H₁ и H₂ :

Если нижний предел доверительного интервала 100(1-α) < h, то тогда отвергаем H₀ в пользу H₂.
Если верхний предел доверительного интервала 100(1-α) > h, то тогда отвергаем H₀ в пользу H₁.
Если доверительного интервала 100(1-α) включает в себя h, то тогда мы не может отвергнуть H₀ и такой результат считается неопределенным.

Если нам нужно проверить значение μ для одной выборки из общей совокупности, то критерий обретет вид.

Где $t = (hat{mu} - h)/sqrtfrac{hatsigma^2}{n}$ .

Доверительный интервал, погрешность и размер выборки

Возьмем самое первое уравнение и выразим оттуда ширину доверительного интервала (Ур. 2).

$w = 2t_{{alpha/2};df}sqrt{frac{hatsigma^2}{n}}$

В некоторых случаях мы можем заменить t-статистику Стьюдента на z стандартного нормального распределения. Еще одним упрощением заменим половину от w на погрешность измерения E. Тогда наше уравнения примет вид (Ур. 3).

$E = z_{alpha/2}sqrt{frac{hatsigma^2}{n}}$

Как видим погрешность действительно уменьшается вместе с ростом количества входных данных. Откуда легко вывести искомое (Ур. 4).

$n = left[frac{z_{alpha/2}*sigma}{E}right]^2$

Практика — считаем с R

Проверим гипотезу о том, что среднее значение данной выборки количества насекомых в ловушке равно 1.

H₀: μ = 1
H₁: μ > 1

Насекомые	0	1	2	3	4	5	6
Ловушки	10	9	5	5	1	2	1

> x <- read.table("/tmp/tcounts.txt")
> y = unlist(x, use.names="false")
> mean(z);sd(z)
[1] 1.636364
[1] 1.654883

Обратите внимание, что среднее и стандартное отклонение практически равны, что естественно для распределения Пуассона. Доверительный интервал 95% для t-статистики Стьюдента и df=32.

> qt(.975, 32)
[1] 2.036933

и наконец получаем критический интервал для среднего значения: 1.05 — 2.22.

> μ=mean(z)
> st = qt(.975, 32)
> μ + st * sd(z)/sqrt(33)
[1] 2.223159
> μ - st * sd(z)/sqrt(33)
[1] 1.049568

В итоге, следует отбраковать H₀ и принять H₁ так как с вероятностью 95%, μ > 1.

В том же самом примере, если принять, что нам известно действительное стандартное отклонение — σ, а не ее оценка полученная с помощью случайной выборки, можно рассчитать необходимое n для данной погрешности. Посчитаем для E=0.5.

> za2 = qnorm(.975)
> (za2*sd(z)/.5)^2
[1] 42.08144

Поправка на ветер

На самом деле нет никаких причин, полагать, что нам будет известна σ (дисперсия), в то время как μ (среднее) нам еще только предстоит оценить. Из-за этого уравнение 4 имеет мало практической пользы, кроме особо рафинированных примеров из области комбинаторики, а реалистичное уравнение для n несколько сложнее при неизвестной σ (Ур. 5).

$n = 4tildesigma^2 (z_{alpha/2}/w)^2 + z^2_{alpha/2}/2$

Обратите внимание, что σ в последнем уравнении не с шапкой (^), а тильдой (~). Это следствие того, что в самом начале у нас нет даже оценочного стандартного отклонения случайной выборки — , и вместо нее мы используем запланированное — . Откуда же мы берем последнее? Можно сказать, что с потолка: экспертная оценка, грубые прикидки, прошлый опыт и т. д.

А что на счет второго слагаемого правой стороны 5-го уравнения, откуда оно взялось? Так как $z_{alpha/2} < t_{{alpha/2};df}$ , необходима поправка Гюнтера.

Помимо уравнений 4 и 5 есть еще несколько приблизительно-оценочных формул, но это уже заслуживает отдельного поста.

Использованные материалы

Sample sizes
Hypothesis testing

Источник

Объем выборки и репрезентативность

Планируем исследования и эксперименты

Если суп хорошо перемешать, то достаточно одной ложки, чтобы сделать вывод о вкусе всей кастрюли — Д.Гэллоп.

Для того, чтобы оценить любое явление, не обязательно изучать все объекты (генеральную совокупность). Для оценки здоровья человека не нужно анализировать всю кровь, достаточно небольшой пробирки. Чтобы понять настроения россиян можно не опрашивать 146 миллионов, а ограничиться несколькими тысячами. Оценка не сильно потеряет в точности.

По части судить о целом

О возможности судить о целом по части миру рассказал российский математик П.Л. Чебышев. «Закон больших чисел» простым языком можно сформулировать так: количественные закономерности массовых явлений проявляются только при

достаточном числе наблюдений

. Чем больше выборка, тем лучше случайные отклонения компенсируют друг друга и проявляется общая тенденция.

А.М. Ляпунов чуть позже сформулировал центральную предельную теорему. Она стала фундаментом для создания формул, которые позволяют рассчитать вероятность ошибки (при оценке среднего по выборке) и размер выборки, необходимый для достижения заданной точности.

Строгие формулировки:

Еще раз: чтобы корректно оценивать популяцию по выборке, нам нужна не обычная выборка, а репрезентативная выборка достаточного размера. Начнем с определения этого самого размера.

Как рассчитать объем выборки

Достаточный размер выборки зависит от следующих составляющих:

изменчивость признака (чем разнообразней показания, тем больше наблюдений нужно, чтобы это уловить);
размер эффекта (чем меньшие эффекты мы стремимся зафиксировать, тем больше наблюдений необходимо);
уровень доверия (уровень вероятности при который мы готовы отвергнуть нулевую гипотезу)

ЗАПОМНИТЕ
Объем выборки зависит от изменчивости признака и планируемой строгости эксперимента

Формулы для расчета объема выборки:

Формулы расчета объема выборки

Ошибка выборки значительно возрастает, когда наблюдений меньше ста. Для исследований в которых используется 30-100 объектов применяется особая статистическая методология: критерии, основанные на распределении Стьюдента или бутстрэп-анализ. И наконец, статистика совсем слаба, когда наблюдений меньше 30.

График зависимости ошибки выборки от ее объема при оценке доли признака в г.с.

Чем больше неопределенность, тем больше ошибка. Максимальная неопределенность при оценке доли — 50% (например, 50% респондентов считают концепцию хорошей, а другие 50% плохой). Если 90% опрошенных концепция понравится — это, наоборот, пример согласованности. В таких случаях оценить долю признака по выборке проще.

Репрезентативность

Репрезентативность — это степень соответствия характеристик выборки характеристикам генеральной совокупности. Только данные по репрезентативным выборкам можно экстраполировать на всю популяцию.

Репрезентативность достигается за счет случайного отбора. Случайный отбор — хорошо. Детерминированный отбор — плохо. Он искажает структуру выборки и как следствие результат измерений. Нельзя судить о среднем росте россиян по росту ста баскетболистов, которые тренируются во дворе вашего дома, просто потому что вам так удобно.

Идеальная выборка — это когда каждый человек имеет равную вероятность попасть в число опрошенных. Полностью случайный отбор трудно достижим (это очень дорого), но к нему нужно стремиться. Сам метод сбора данных может деформировать выборку (онлайн опросы отсекают пенсионеров, опрос по стационарным телефонам — экономических активных мужчин). Представьте, как будут различаться рейтинги, если провести электоральный опрос в «Вконтакте» и в бумажной газете «Лечебные письма».

Типы выборок

Существует методология, которая позволяет сократить детерминированность при формировании выборки и приблизиться к случайному отбору.

Стратифицированная выборка. Выделяются объективно существующие страты и из каждой страты отбираются единицы пропорционально их доле в генеральной совокупности. Например для опроса россиян страты могут быть определены пропорцией населения в регионах. После чего респонденты внутри каждого региона отбираются случайным образом.

Механический отбор. Все объекты сортируются по порядковым номерам, после чего осуществляется отбор с шагом n. Например, можно отсортировать телефонные номера потенциальных участников исследования и звонить каждому 100-му.

Серийная выборка (гнездовая, кластерная). Объективно существующие группы отбираются случайным образом. Объекты внутри групп обследуются полностью. Например вскрывается один контейнер продукции и каждый товар проверяется на брак.

Метод снежного кома. У каждого респондента запрашиваются контакты его знакомых, которые подходят под условия отбора. Условия случайности отбора грубо нарушается, но это один из способов провести исследование среди труднодостижимых групп. Как быть иначе, если ваша цель — опросить любителей стальных гоночных велосипедов выпущенных не позже 1987 года.

Стихийная выборка (выборка по удобству). Применяется, когда низкая цена получения данных — это главный приоритет. Для повышения качества стихийной выборки на неё накладываются квоты. Заранее рассчитываются пропорции признаков в выборке так, чтобы они соответствовали структуре генеральной совокупности. В социологии такими признаками служат пол, возраст, профессия, семейный статус, регион проживания…

Хотите систематизировать свои знания по аналитике?

Встречайте «Анализ данных для хулиганов»

Онлайн пособие о том, как создавать великолепные продукты и эффективно управлять маркетингом на основе данных⚡

Методики / Фреймворки / Шаблоны для скачивания

Источник

При планировании научного исследования представляет интерес получение оценки минимального объёма выборки. Как правило, объем выборки вычисляют для распределений случайных величин, близких к гауссовскому в соответствии со следующим выражением [1]:

Для случая негауссовского закона распределения в формуле [2] предложено другое выражение для оценки объема выборки:

Приведенные выше выражения применяются, в основном, при небольших объемах выборки (условно до 40-50) в случае оценивания выборочных моментов первого и второго порядков – среднего и дисперсии. При большом объеме выборки законы распределения выборочных среднего и дисперсии близки к гауссовскому, и оценка объема выборки может быть получена сравнительно просто из выражения для построения доверительного интервала.

Более подробно изучить этот вопрос помогут [3][4] и, конечно, наш курс математики для Data Science.

Список источников:
1 Койчубеков Б.К. Определение размера выборки при планирования научного исследования / Койчубеков Б.К., Сорокина М.А., Мхитарян К.Э. – Международный журнал прикладных и фундаментальных исследований. 2014. №4.
2 Дианов В.Н. Перспективные направления повышения надежности вычислительной техники и систем управления // Надежность. 2004. №3 (10). С. 33–47
3 Вентцель Е.С. Теория вероятностей. – М., 1964. – 576 с.
4 https://applied-research.ru/ru/article/view?id=5074

Источник

Поскольку
массовый опрос, анкетирование, как
количественный метод, основан на
применении теории вероятности, мы имеем
возможность в математических терминах
оценить достоверность и допустимые
погрешности каждого добросовестно
проведенного исследования.

Под
доверительным интервалом понимают
диапазон, в который попадет истинное
значение изучаемого параметра генеральной
совокупности при данном уровне
достоверности. Чем он меньше, тем больше
должна быть выборка.

Под,
уровнем достоверности понимают
вероятность того, что истинное значение
изучаемого параметра генеральной
совокупности попадет в доверительный
интервал. Чем выше задаваемый уровень
достоверности, тем больше должна быть
выборка.

Важная
задача маркетингового исследования –
вычисление таких статистик, как выборочное
среднее и выборочная доля, и применение
их для оценки соответствующих истинных
значений генеральной совокупности.
Процесс распространения результатов
оценки выборки на оценку генеральной
совокупности называется статистическим
заключением (statistical
inference).

На
практике создается одна выборка заданного
объема и по ней вычисляются выборочные
статистики (а именно, среднее и доля).
Теоретически, для того чтобы оценить
параметр изучаемой совокупности исходя
из статистики выборки, нужно изучить
каждую возможную выборку. Если бы все
возможные выборки создавались в
действительности, распределение
статистики являлось бы выборочным
распределением. Несмотря на то, что на
практике создается только одна выборка,
понятие выборочного распределения
очень важно. Это дает возможность
использовать теорию вероятности для
того, чтобы делать выводы относительно
значений совокупности.

Статистика
(statistic) – описание характеристики
выборки. Статистика выборки используется
для оценки параметров генеральной
совокупности.

Выборочное
распределение
(sampling distribution) – это распределение
значений выборочных статистик,
рассчитанных для каждой возможной
выборки, которая формируется из изучаемой
совокупности при определенном плане
выборочного наблюдения.

Важные
характеристики выборочного распределения
среднего и соответствующие характеристики
доли для больших выборок (30 и больше)
следующие.

Выборочное
распределение среднего для больших
выборок (n
= 30
и больше) можно свести к нормальному
распределению.
Среднее
значение по совокупности μ = сумма
элементов совокупности/количество
элементов

Стандартная
ошибка (standard
error) среднего или доли относится к
выборочному распределению среднего
или доли, а не к выборке или всей
совокупности. В случае, если генеральная
дисперсия (сумма квадратов отклонений
каждого элемента выборки от генерального
среднего / количество элементов
совокупности) известна, используются
следующие формулы для определения
стандартной (среднеквадратической)
ошибки:

Среднего: Доли:

Часто
среднеквадратичное отклонение изучаемой
совокупности неизвестно. Тогда
стандартная ошибка среднего может
только оцениваться.

,
тогда

Если
объем выборки составляет 10% или больше
от объема исследуемой совокупности,
применение формул стандартной ошибки
приведет к переоценке среднеквадратичного
отклонения среднего или доли совокупности,
Значит, его следует откорректировать,
применив коэффициент окончательной
коррекции совокупности. Тогда формула
стандартной ошибки будет выглядеть
следующим образом:

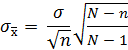
N
– объем генеральной совокупности, n
– объем выборки

Статистические
методы определения объема выборки

При
определении объема выборки следует
принимать во внимание многие качественные
факторы:

важность принимаемого
решения,
характер
исследования,
количество
переменных,
характер анализа,
объемы выборки,
которые использовались в подобных
исследованиях,
ограниченность
ресурсов.

Статистически
определенный объем выборки – это чистый
или конечный объем выборки, т.е. элементы
выборки, остающиеся после исключения
потенциальных респондентов, которые
не отвечают заданным критериям или не
закончили интервью. В зависимости от
коэффициентов охвата и завершенности
может потребоваться намного больший
объем исходной выборки. В коммерческих
маркетинговых исследованиях недостаток
времени, денег и хороших специалистов
может иметь решающее значение при
определении объема выборки.

Однако
профессиональный маркетолог должен
понимать статистические методы
определения объема выборки, основанные
на традиционном статистическом
заключении.

Этот
метод основан на создании доверительных
интервалов вокруг средних или долей
выборки.

Рассмотрим
понятие доверительного интервала. В
качестве примера предположим, что
исследователь провел простую случайную
выборку из 300 семей, чтобы оценить
ежемесячные расходы семьи на покупку
продуктов питания, и определил, что
средний ежемесячный расход семьи в
выборке равен 15000 рублей. Предыдущие
исследования показали, что стандартное
отклонение расходов в исследуемой
совокупности равно 9000 рублей.

Необходимо
найти интервал, в который попадал бы
определенный процент выборочных средних.
Предположим, необходимо определить
интервал вокруг среднего значения
совокупности, который включал бы 95%
выборочных средних, опираясь на выборку
из 300 семей. При нормальном распределении
95% наблюдений укладываются в ±1,96
среднеквадратических отклонений
среднего.

Для
того, чтобы вычислить доверительный
интервал, необходимо определить величину
Z,
в зависимости от выбранного уровня
достоверности. При уровне достоверности
95%, величина Z
составляет 1,96. Нет необходимости
пользоваться формулами, для вычисления
этой величины, т.к. существуют таблицы,
по которым легко вычислить Z
для любого уровня достоверности.

Следующий
шаг – вычисление доверительного
интервала, который устанавливается как

Для
начала вычислим стандартную ошибку
среднего. В нашем примере

Доверительный
интервал .= 15000±1.96*551 = 15000±1020

Таким
образом, 95%-ный доверительный интервал
находится в пределах от 16020 до 13980 рублей.
Другими словами, вероятность нахождения
истинного среднего значения наблюдаемой
совокупности в пределах от 16020 до 13980
рублей составляет 95%.

Метод,
использованный для создания доверительного
интервала, можно модифицировать так,
чтобы определить объем выборки с учетом
желательного доверительного интервала.

Предположим,
что необходимо рассчитать ежемесячные
расходы семьи на покупку продуктов
питания более точно, так, чтобы полученный
результат находился в пределах ±500
рублей от истинного среднего значения
исследуемой совокупности. Каким должен
быть объем выборки?

Ниже
приведен необходимый перечень действий,
которые необходимо выполнить.

Определите
степень точности. Это максимально
допустимое различие (D)
между выборочным средним и генеральным
средним. В нашем примере D
= ±500
рублей.
Укажите уровень
достоверности. Предположим, что
желательный уровень достоверности
95%.
Определите
значение z,
связанное
с данным уровнем достоверности,
воспользовавшись соответствующей
таблицей (см. табл. 2 в Приложении). При
95%-ном уровне достоверности вероятность
того, что среднее значение генеральной
совокупности выйдет за пределы
одностороннего интервала, равна 0,025
(0,05/2). Соответствующее значение z
составляет
1,96.
Определите
стандартное отклонение среднего
генеральной совокупности. Его можно
получить из вторичных источников или
рассчитать, проведя разведочное
исследование. Кроме того, стандартное
отклонение можно установить на основе
мнения исследователя. Например, диапазон
нормально распределенной переменной
примерно укладывается в шесть стандартных
отклонений (по три слева и справа от
среднего значения). Таким образом, можно
рассчитать среднеквадратичное
отклонение, разделив величину всего
диапазона на 6. Исследователь часто
может определить размеры диапазон,
исходя из собственного понимания
анализируемых явлений.
Определите объем
выборки, воспользовавшись формулой
стандартной ошибки среднего:

;
или

В
нашем примере 1245

Из
формулы объема выборки видно, что она
растет с ростом изменчивости генеральной
совокупности, а также с увеличением
уровня достоверности и степени точности,
с которой должны проводиться расчеты.
Объем выборки прямо пропорционален

,
поэтому, чем больше показатель изменчивости
генеральной совокупности, тем больше
объем выборки.

Аналогично,
более высокий уровень достоверности
предполагает большее значение z
и, следовательно, больший объем выборки.
Переменные и z
находятся
в числителе. Увеличение степени точности
достигается уменьшением значения D
и,
следовательно, увеличивает объем
выборки, поскольку D
находится
в знаменателе.

Если
объем выборки составляет 10% и больше
от объема генеральной совокупности,
то применяется окончательная коррекция
совокупности. Необходимый объем выборки
рассчитывается по формуле:

где n
–
объем выборки до применения окончательной
коррекции;

– объем выборки
после применения окончательной коррекции,

N
– объем генеральной совокупности.

После
всего выше сказанного, следует добавить,
что объем генеральной совокупности N
не
влияет на объем выборки напрямую, за
исключением случаев, когда применяется
коэффициент окончательной коррекции
совокупности. Например, если исследуемые
характеристики всех элементов совокупности
идентичны, то выборки, состоящей из
одного элемента, вполне достаточно,
чтобы рассчитать среднее. Это также
правильно, если совокупность состоит
из 50, 500, 5000 или 50000 элементов. В то же
время изменчивость характеристик
совокупности напрямую влияет на объем
выборки. Эта изменчивость учитывается
при вычислении объема выборки с помощью
дисперсии совокупности или дисперсии
выборки

Определение
объема выборки: доля

Если
изучаемая статистика является не
средним, а долей, то маркетолог определяет
объем выборки аналогичным образом.
Предположим, что исследователя интересует
установление доли семей, владеющих
дисконтной карточкой универмага. Порядок
действий будет следующим.

Укажите
степень точности. Предположим, желательная
степень точности такова, что допустимый
интервал установлен на уровне
Укажите
уровень достоверности. Предположим,
что желателен 95%-ный уровень достоверности.
Определите
значение z,
связанное
с данным уровнем достоверности. Как
объяснялось при расчете среднего, оно
составит z
= 1,96.
Определите
генеральную долю

.
Ее можно получить из вторичных источников,
в ходе экспериментального исследования
или на основе мнения исследователя.
Предположим, что на основе вторичных
данных исследователь делает предположение,
что 64% семей из изучаемой генеральной
совокупности обладают дисконтной
карточкой универмага. Следовательно,

= 0,64.
Определите
объем выборки с помощью формулы
стандартной ошибки доли:

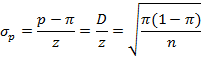
Следовательно,

В
нашем примере

355

Если
расчет

был неверным, то доверительный интервал
будет более или менее точным, чем
необходимо. Предположим, что по окончании
выборки рассчитывается значение доли
р,
равное
0,55. Затем повторно вычисляется
доверительный интервал, при этом

используется
для расчета неизвестного
,
а именно ,

где

В нашем
примере

Доверительный
интервал тогда равен 0,55±1,96 (0,0264) = 0,55
±0,052, что означает, что он шире, чем было
задано. Это объясняется тем, что
среднеквадратичное отклонение выборки
при
р
= 0,55
оказалось большим, чем предположительное
значение среднеквадратичного отклонения
совокупности, при

= 0,64.

В
приведенных выше примерах мы рассмотрели
оценку одного параметра. На практике,
как правило, маркетолог определяет не
один, а сразу несколько параметров
целевой совокупности. В таких случаях
расчет объема выборки должен проводиться
с учетом всех оцениваемых параметров.

Корректировка
статистически определенного объема
выборки

Статистически
определенный объем выборки представляет
собой конечный, или чистый объем выборки,
который необходимо получить, чтобы
обеспечить расчет параметров с желательной
степенью точности и заданным уровнем
достоверности. При проведении опросов
он выражается в количестве завершенных
интервью. Для получения конечного объема
выборки необходимо связаться с гораздо
большим количеством потенциальных
респондентов. Другими словами, начальный
объем выборки должен намного превышать
конечный, поскольку коэффициенты охвата
и завершенности обычно составляют
меньше 100%.

Коэффициентом
охвата (incidence rate) называется степень
наличия или процент людей, подходящих
для участия в исследовании. Коэффициент
охвата определяет, какое количество
контактов с людьми необходимо осуществить,
чтобы в итоге получить объем выборки,
соответствующий заданным критериям.
Предположим, что для исследования
характеристик моющих средств необходимо
создать выборку из женщин-глав семьи в
возрасте от 25 до 55 лет. Приблизительно
75% женщин в возрасте от 20 до 60 лет, к
которым можно обратиться – это
женщины-главы семьи в возрасте от 25 до
55 лет. Это означает, что, в среднем,
необходимо обратиться к 1,33 женщин, чтобы
получить одного подходящего респондента.
Дополнительные критерии для отбора
респондентов (например, каким образом
использовался продукт) увеличивают
необходимое количество контактов.
Предположим, что дополнительным критерием
является использование женщиной моющего
средства для пола в течение последних
двух месяцев.

Предполагается,
что 60% женщин, к которым обратятся
исследователи, будут соответствовать
этому критерию. Тогда коэффициент охвата
составит 0,75 х 0,60 = 0,45. Таким образом,
конечный объем выборки следует увеличить
на 2,22 (1/0,45).

Точно
так же при определении объема выборки
необходимо учитывать ожидаемые отказы
людей, соответствующих критериям
исследования. Коэффициент завершенности
(completion rate) указывает процент респондентов,
соответствующих критериям отбора,
которые полностью прошли интервью.
Например, если исследователь предполагает,
что коэффициент завершенности интервью
составит 80% от числа подходящих
респондентов, необходимое количество
контактов следует умножить на коэффициент
1,25. Применение коэффициентов охвата и
завершенности означает, что число
контактов с потенциальными респондентами,
т.е. начальный
объем
выборки, должно быть в 2,22 х 1,25 (или 2,77)
раз больше необходимого объема выборки.
В целом, при наличии с
отборочных
критериев со степенью охвата Q1,
Q2,
Q3,… Qc каждый,
коэффициент охвата = Ql
x
Q2
x
Q3
х
… Qc.

Т.о.,

На
величину коэффициента завершенности
влияет отсутствие ответов (ненаблюдение).
Две главные проблемы, которые необходимо
решать в связи с отсутствием ответов
(ненаблюдением) при проведении выборки
– это увеличение коэффициентов отклика
и корректировка на неполучение данных.

Ошибка
неполучения данных или ненаблюдения
возникает, когда некоторые потенциальные
респонденты, включенные в выборку, не
отвечают на вопросы исследования.
Неответившие респонденты отличаются
от ответивших по демографическим,
психологическим, поведенческим и
личностным параметрам, а также имеют
другую социальную установку и мотивацию.
Если неответившие респонденты отличаются
от ответивших по характеристикам,
которые исследуются в данном случае,
результаты выборки будут опасно смещены.
Высокий коэффициент отклика обычно
означает низкий коэффициент ошибки
ненаблюдения, но при этом не будет его
адекватным показателем. Коэффициенты
отклика сами по себе не указывают,
являются ли респонденты представителями
начальной выборки. Увеличение коэффициента
отклика может не привести к уменьшению
ошибки ненаблюдения, если дополнительные
респонденты не отличаются от тех, кто
уже ответил, но отличаются от тех, кто
еще не ответил.

Контрольные
вопросы и вопросы для самостоятельного
изучения

Приведите
характеристики выборочного распределения.
Что такое стандартная
ошибка среднего и доли?
Какие качественные
факторы необходимо учитывать при
определении объема выборки?
Что показывает
доверительный интервал?
В чем различие
между уровнем достоверности и степенью
точности?
Что такое коэффициент
охвата и коэффициент завершенности?
Каким образом определяется конечный
объем выборки?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Один из первых шагов при планировании количественного маркетингового исследования – определение объема выборки.

Калькулятор для расчета достаточного объема выборки
Калькулятор ошибки выборки для доли признака
Калькулятор ошибки выборки для среднего значения
Калькулятор значимости различий долей
Калькулятор значимости различий средних

1. Формула (даже две)

Бытует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с размером генеральной совокупности. Например, при опросах организаций (B2B).

Если речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная.

На рис.1. пример выборки 15000 человек (!) при опросе в муниципальном районе. Возможно, от численности населения взяли 10%?
Размер выборки никогда не рассчитывается как процент от генеральной совокупности!

Рис.1. Размер выборки 15000 человек, как реальный пример некомпетентности (или хуже).

В таких случаях для расчета объема выборки используется следующая формула:

где

n – объем выборки,
Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,
p – доля респондентов с наличием исследуемого признака,
q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует,
∆ – предельная ошибка выборки.

Доверительный уровень – это вероятность того, что реальная доля лежит в границах полученного доверительного интервала: выборочная доля (p) ± ошибка выборки (Δ). Доверительный уровень устанавливает сам исследователь в соответствии со своими требованиями к надежности полученных результатов. Чаще всего применяются доверительные уровни, равные 0,95 или 0,99. В маркетинговых исследованиях, как правило, выбирается доверительный уровень, равный 0,95. При этом уровне коэффициент Z равен 1,96.

Значения p и q чаще всего неизвестны до проведения исследования и принимаются за 0,5. При этом значении размер ошибки выборки максимален.

Допустимая предельная ошибка выборки выбирается исследователем в зависимости от целей исследования. Считается, что для принятия бизнес-решений ошибка выборки должна быть не больше 4%. Этому значению соответствует объем выборки 500-600 респондентов. Для важных стратегических решений целесообразно минимизировать ошибку выборки.

Рассмотрим кривую зависимости ошибки выборки от ее объема (Рис.2).

Рис.2. Зависимость ошибки выборки от ее объема при 95% доверительном уровне

Как видно из диаграммы, с ростом объема выборки значение ошибки уменьшается все медленнее. Так, при объеме выборки 1500 человек предельная ошибка выборки составит ±2,5%, а при объеме 2000 человек – ±2,2%. То есть, при определенном объеме выборки дальнейшее его увеличение не дает значительного выигрыша в ее точности.

ШПАРГАЛКА (скопируйте ссылку или текст)

Подходы к решению проблемы:

Случай 1. Генеральная совокупность значительно больше выборки:

Случай 2. Генеральная совокупность сопоставима с объемом выборки: (см. раздел исследований B2B)

где
n – объем выборки,

N – объем генеральной совокупности,

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня,

p – доля респондентов с наличием исследуемого признака,

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует, (значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования)

∆ – предельная ошибка выборки.

Например,

рассчитаем ошибку выборки объемом 1000 человек при 95% доверительном уровне, если генеральная совокупность значительно больше объема выборки:

Ошибка выборки = 1,96 * КОРЕНЬ(0,5*0,5/1000) = 0,031 = ±3,1%

При расчете объема выборки следует также учитывать стоимость проведения исследования. Например, при цене за 1 анкету 200 рублей стоимость опроса 1000 человек составит 200 000 рублей, а опрос 1500 человек будет стоить 300 000 рублей. Увеличение затрат в полтора раза сократит ошибку выборки всего на 0,6%, что обычно неоправданно экономически.

2. Причины «раздувать» выборку

Анализ полученных данных обычно включает в себя и анализ подвыборок, объемы которых меньше основной выборки. Поэтому ошибка для выводов по подвыборкам больше, чем ошибка по выборке в целом. Если планируется анализ подгрупп / сегментов, объем выборки должен быть увеличен (в разумных пределах).

Рис.3 демонстрирует данную ситуацию. Если для исследования авиапассажиров используется выборка численностью 500 человек, то для выводов по выборке в целом ошибка составляет 4,4%, что вполне приемлемо для принятия бизнес-решений. Но при делении выборки на подгруппы в зависимости от цели поездки, выводы по каждой подгруппе уже недостаточно точны. Если мы захотим узнать какие-либо количественные характеристики группы пассажиров, совершающих бизнес-поездку и покупавших билет самостоятельно, ошибка полученных показателей будет достаточно велика. Даже увеличение выборки до 2000 человек не обеспечит приемлемой точности выводов по этой подвыборке.

Рис.3. Проектирование объема выборки с учетом необходимости анализа подвыборок

Другой пример – анализ подгрупп потребителей услуг торгово-развлекательного центра (Рис.4).

Рис.4. Потенциальный спрос на услуги торгово-развлекательного центра

При объеме выборки в 1000 человек выводы по каждой отдельной услуге (например, социально-демографический профиль, частота пользования, средний чек и др.) будут недостаточно точными для использования в бизнес планировании. Особенно это касается наименее популярных услуг (Таблица 1).

Таблица 1. Ошибка по подвыборкам потенциальных потребителей услуг торгово-развлекательного центра при выборке 1000 чел.

Чтобы ошибка в самой малочисленной подвыборке «Ночной клуб» составила меньше 5%, объем выборки исследования должен составлять около 4000 человек. Но это будет означать 4-кратное удорожание проекта. В таких случаях возможно компромиссное решение:

увеличение выборки до 1800 человек, что даст достаточную точность для 6 самых популярных видов услуг (от кинотеатра до парка аттракционов);
добор 200-300 пользователей менее популярных услуг с опросом по укороченной анкете (см. Таблицу 2).

Таблица 2. Разница в ошибке выборки по подвыборкам при разных объемах выборки.

При обсуждении с исследовательским агентством точности результатов планируемого исследования рекомендуется принимать во внимание бюджет, требования к точности результатов в целом по выборке и в разрезе подгрупп. Если бюджет не позволяет получить информацию с приемлемой ошибкой, лучше пока отложить проект (или поторговаться).

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

КАЛЬКУЛЯТОР ДЛЯ РАСЧЕТА
ДОСТАТОЧНОГО ОБЪЁМА ВЫБОРКИ

Доверительный уровень:

Ошибка выборки (?):
%

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

РЕЗУЛЬТАТ

Один из важных вопросов, на которые нужно ответить при планировании исследования, — это оптимальный объем выборки. Слишком маленькая выборка не сможет обеспечить приемлемую точность результатов опроса, а слишком большая приведет к лишним расходам.

Онлайн-калькулятор объема выборки поможет рассчитать оптимальный размер выборки, исходя из максимально приемлемого для исследователя размера ошибки выборки.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке!
Формулы для других типов выборки отличаются.

Объем выборки рассчитывается по следующим формулам

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

Z – коэффициент, зависящий от выбранного исследователем доверительного уровня. Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень. Ему соответствует значение Z = 1,96.

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели соков и нектаров, постоянно проживающие в Москве и Московской области). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

p – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

q = 1 – p – доля респондентов, у которых исследуемый признак отсутствует. Значения p и q обычно принимаются за 0,5, поскольку точно неизвестны до проведения исследования. При этом значении размер ошибки выборки максимален. В данном калькуляторе значения p и q по умолчанию равны 0,5.

Δ– предельная ошибка выборки (для доли признака), приемлемая для исследователя. Считается, что для принятия бизнес-решений ошибка выборки не должна превышать 4%.

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании.

ПРИМЕР РАСЧЕТА ОБЪЕМА ВЫБОРКИ:

Допустим, мы хотим рассчитать объем выборки, предельная ошибка которой составит 4%. Мы принимаем доверительный уровень, равный 95%. Генеральная совокупность значительно больше выборки. Тогда объем выборки составит:

n = 1,96 * 1,96 * 0,5 * 0,5 / (0,04 * 0,04) = 600,25 ≈ 600 человек

Таким образом, если мы хотим получить результаты с предельной ошибкой 4%, нам нужно опросить 600 человек.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Доля признака (p):
%

РЕЗУЛЬТАТ

Зная объем выборки исследования, можно рассчитать значение ошибки выборки (или, другими словами, погрешность выборки).

Если бы в ходе исследования мы могли опросить абсолютно всех интересующих нас людей, мы могли бы быть на 100% уверены в полученном результате. Но ввиду экономической нецелесообразности сплошного опроса применяют выборочный подход, когда опрашивается только часть генеральной совокупности. Выборочный метод не гарантирует 100%-й точности измерения, но, тем не менее, вероятность ошибки может быть сведена к приемлемому минимуму.

Все дальнейшие формулы и расчеты относятся только к простой случайной выборке! Формулы для других типов выборки отличаются.

Ошибка выборки для доли признака рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели шоколада, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

n – объем выборки. Объем выборки – это количество людей, которые опрашиваются в исследовании. Существует заблуждение, что чем больше объем генеральной совокупности, тем больше должен быть и объем выборки маркетингового исследования. Это отчасти так, когда объем выборки сопоставим с объемом генеральной совокупности. Например, при опросах организаций (B2B). Если же речь идет об исследовании жителей городов, то не важно, Москва это или Рязань – оптимальный объем выборки будет одинаков в обоих городах. Этот принцип следует из закона больших чисел и применим, только если выборка простая случайная. ВАЖНО: если предполагается сравнивать какие-то группы внутри города, например, жителей разных районов, то выборку следует рассчитывать для каждой такой группы.

Δ– предельная ошибка выборки.

Таким образом, зная объем выборки исследования, мы можем заранее оценить показатель ее ошибки.
А получив значение p, мы можем рассчитать доверительный интервал для доли признака: (p – ∆; p + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ ДОЛИ ПРИЗНАКА:

Например, в ходе исследования были опрошены 1000 человек (n=1000). 20% из них заинтересовались новым продуктом (p=0,2). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * КОРЕНЬ (0,2*0,8/1000) = 0,0248 = ±2,48%

Рассчитаем доверительный интервал:

(p – ∆; p + ∆) = (20% – 2,48%; 20% + 2,48%) = (17,52%; 22,48%)

Таким образом, с вероятностью 95% мы можем быть уверены, что реальная доля заинтересованных в новом продукте (среди всей генеральной совокупности) находится в пределах полученного диапазона (17,52%; 22,48%).

Если бы мы выбрали доверительный уровень, равный 99%, то для тех же значений p и n ошибка выборки была бы больше, а доверительный интервал – шире. Это логично, поскольку, если мы хотим быть более уверены в том, что наш доверительный интервал «накроет» реальное значение признака, то интервал должен быть более широким.

КАЛЬКУЛЯТОР ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ

Доверительный уровень:

Объём выборки (n):

Объём генеральной совокупности (N):
(можно пропустить, если больше 100 000)

Среднее значение (x̄):

Стандартное отклонение (s):

РЕЗУЛЬТАТ

Ошибка выборки для среднего значения рассчитывается по следующим формулам.

1) если объем выборки значительно меньше генеральной совокупности:

(в данной формуле не используется показатель объема генеральной совокупности N)

2) если объем выборки сопоставим с объемом генеральной совокупности:

В приведенных формулах:

N – объем генеральной совокупности. Генеральная совокупность – это все люди, которые изучаются в исследовании (например, все покупатели мороженого, постоянно проживающие в Москве). Если генеральная совокупность значительно больше объема выборки (в сотни и более раз), ее размером можно пренебречь (формула 1).

s – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Δ– предельная ошибка выборки.

Зная среднее значение показателя x ̅ и ошибку ∆, мы можем рассчитать доверительный интервал для среднего значения:(x ̅ – ∆; x ̅ + ∆)

ПРИМЕР РАСЧЕТА ОШИБКИ ВЫБОРКИ ДЛЯ СРЕДНЕГО ЗНАЧЕНИЯ:

Например, в ходе исследования были опрошены 1000 человек (n=1000). Каждого из них попросили указать их примерную среднюю сумму покупки (средний чек) в известной сети магазинов. Среднее арифметическое всех ответов составило 500 руб. (x ̅=500), а стандартное отклонение составило 120 руб. (s=120). Рассчитаем показатель ошибки выборки по формуле 1 (выберем доверительный уровень, равный 95%):

∆ = 1,96 * 120 / КОРЕНЬ (1000) = 7,44

Рассчитаем доверительный интервал:

(x ̅ – ∆; x ̅ + ∆) = (500 – 7,44; 500 + 7,44) = (492,56; 507,44)

Таким образом, с вероятностью 95% мы можем быть уверены, что значение среднего чека по всей генеральной совокупности находится в границах полученного диапазона: от 492,56 руб. до 507,44 руб.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ ДОЛЕЙ

Доверительный уровень:

	Измерение 1	Измерение 2
Доля признака (p):	%	%
Объём выборки (n):

РЕЗУЛЬТАТ

Если в прошлогоднем исследовании вашу марку вспомнили 10% респондентов, а в исследовании текущего года – 15%, не спешите открывать шампанское, пока не воспользуетесь нашим онлайн-калькулятором для оценки статистической значимости различий.

Сравнивая два разных значения, полученные на двух независимых выборках, исследователь должен убедиться, что различия статистически значимы, прежде чем делать выводы.

Как известно, выборочные исследования не обеспечивают 100%-й точности измерения (для этого пришлось бы опрашивать всю целевую аудиторию поголовно, что слишком дорого). Тем не менее, благодаря методам математической статистики, мы можем оценить точность результатов любого количественного исследования и учесть ее в выводах.

В приведенном здесь калькуляторе используется двухвыборочный z-тест для долей. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Произведения n*p и n*(1-p), где n=размер выборки а p=доля признака, – не меньше 5.

В калькуляторе используются следующие вводные данные:

Доверительный уровень (или доверительная вероятность) – это вероятность того, что реальное значение измеряемого показателя (по всей генеральной совокупности) находится в пределах доверительного интервала, полученного в исследовании. Доверительный уровень выбирает сам исследователь, исходя из требований к надежности результатов исследования. В маркетинговых исследованиях обычно применяется 95%-й доверительный уровень.

Доля признака (p) – доля респондентов с наличием исследуемого признака. Например, если 20% опрошенных заинтересованы в новом продукте, то p = 0,2.

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

КАЛЬКУЛЯТОР ЗНАЧИМОСТИ РАЗЛИЧИЙ СРЕДНИХ

Доверительный уровень:

	Измерение 1	Измерение 2
Среднее значение (x̄):
Стандартное отклонение (s):
Объём выборки (n):

РЕЗУЛЬТАТ

Допустим, выборочный опрос посетителей двух разных ТРЦ показал, что средний чек в одном из них равен 1000 рублей, а в другом – 1200 рублей. Следует ли отсюда вывод, что суммы среднего чека в двух этих ТРЦ действительно отличаются?

В приведенном здесь калькуляторе используется двухвыборочный z-тест для средних значений. Для его применения должны соблюдаться следующие условия:

Обе выборки – простые случайные
Выборки независимы (между значениями двух выборок нет закономерной связи)
Генеральные совокупности значительно больше выборок
Распределения значений в выборках близки к нормальному распределению.

В калькуляторе используются следующие вводные данные:

Среднее значение ( ̅x) – среднее арифметическое показателя.

Стандартное отклонение (s) – выборочное стандартное отклонение измеряемого показателя. В идеале на месте этого аргумента должно быть стандартное отклонение показателя в генеральной совокупности (σ), но так как обычно оно неизвестно, используется выборочное стандартное отклонение, рассчитываемое по следующей формуле:

где, x ̅ – среднее арифметическое показателя, x_i– значение i-го показателя, n – объем выборки

Объем выборки (n) – это количество людей, которые опрашиваются в исследовании.

Результат расчетов – вывод о статистической значимости или незначимости различий двух измерений.

Вы можете подписаться на уведомления о новых материалах СканМаркет

Источник

Как определить размер выборки?

Теоретический минимум

Доверительный интервал, погрешность и размер выборки

Практика — считаем с R

Поправка на ветер

Использованные материалы

По части судить о целом

Как рассчитать объем выборки

Типы выборок

КАЛЬКУЛЯТОРЫ ДЛЯ РАСЧЕТА СТАТИСТИЧЕСКИХ ПОКАЗАТЕЛЕЙ И ОПРЕДЕЛЕНИЯ ЗНАЧИМОСТИ РАЗЛИЧИЙ:

Вам также может понравиться

Как найти свой антенный кабель

Как найти второй минимум в массиве

Как найти ячейку с минимальным значением

Добавить комментарий Отменить ответ