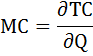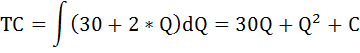Функция издержек фирмы ТС = Q2 – Q + 3, где Q – объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.
Решение:
По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.
Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.
Найдём предельные издержки фирмы по формуле:
МС =(TC)’= 2Q – 1
Найдём объём выпуска продукции, максимизирующий прибыль фирмы.
Цена по условию равна Р = 7.
Р = МС
7 = 2Q – 1
Q = 4
Задача №1. Расчёт экономической прибыли конкурентной фирмы
Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:
ТС = 140 + 10 × Q + 40 × Q2.
При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.
Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?
Решение:
Наличие в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.
Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:
Р = МС = МR = AR.
Определим функцию предельных издержек фирмы: найдём производную общих издержек.
МС = (ТС)’ = 10 + 80 × Q.
Приравняем эту функцию к цене равной 250.
10 + 80 × Q = 250
80 × Q = 240
Q = 3
Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:
П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 32) = 220 ден. ед.
В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.
Задача № 2. Определение рыночной цены и отраслевого выпуска продукции
В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями
ТС =Q3 — 36*Q2 + 384*Q,
где
Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.
Решение:
В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:
P = MC = MR = AR = minAC.
Найдём функцию средних издержек каждой фирмы по следующей формуле:
АС = ТС / Q = Q2 — 36*Q + 384
Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.
2*Q — 36 = 0
Q = 18
AC(18) = 182 — 36*18 + 384 = 60
Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.
Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:
Qотр. = 18*130 = 2340 тысяч штук
Задача № 3. Определение рыночной цены в долгосрочном периоде
Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q3 — 38*Q2 + 418*Q. Определите цену на этом рынке в долгосрочном периоде.
Решение:
В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.
Условие равновесия на рынке будет иметь вид:
Р = МС = МR = AR = min AC
Найдём средние затраты фирмы по формуле:
АС = ТС / Q = Q2 — 38*Q + 418
Определим минимум функции средних затрат. Для нахождения экстремума функции приравняем к нулю её производную:
АС’ = 2*Q — 38
2*Q — 38 = 0
Q = 19
При выпуске Q = 19 средние затраты будут равны:
АС = 192 — 38*19 + 418 = 57.
Таким образом, цена в долгосрочном периоде будет равна 57.
Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка
Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют
0,5*Q3 — 15*Q2 + 300*Q + 250 000.
При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?
Решение:
В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше минимума её средних переменных издержек: Р < min AVC.
Найдём переменные издержки фирмы, а точнее запишем функцию переменных издержек:
VC = 0,5*Q3 — 15*Q2 + 300*Q
Теперь определим функцию средних переменных издержек по формуле:
АVC = VC / Q = 0,5*Q2 — 15*Q + 300
Найдём экстремум этой функции, приравняв к нулю её производную.
Q — 15 = 0
Q = 15.
При объёме производства Q = 15 средние переменные издержки будут минимальными.
АVC(15) = 0,5*152 — 15*15 + 300 = 187,5
Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.
При Р < 187,5 фирме становится невыгодным работать на этом рынке в краткосрочном периоде.
Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы
Функция издержек фирмы ТС = Q2 — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.
Решение:
По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.
Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.
Найдём предельные издержки фирмы по формуле:
МС =(TC)’= 2Q — 1
Найдём объём выпуска продукции, максимизирующий прибыль фирмы.
Цена по условию равна Р = 7.
Р = МС
7 = 2Q — 1
Q = 4
Задача №6. Расчёт объёма производства в краткосрочном периоде
В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q2 + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.
Решение:
Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.
На рынке совершенной конкуренции предельный доход равен цене: MR = P.
Отсюда следует, что цена равна предельным издержкам: P = MC.
Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:
Функция предельных издержек будет иметь вид:
МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.
Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
Конкурентная фирма имеет общие затраты
ТС = 800 + 40*Q + 2*Q2
Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.
Определить цену на рынке и объём выпуска данной фирмы.
Решение:
Формула прибыли фирмы имеет вид:
П = TR — TC = P*Q — TC
По условию максимально возможная прибыль равна 1000.
P*Q — (800 + 40*Q + 2*Q2) = 1000
Найдём цену.
Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:
Р = МС = MR = AR
Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:
(40 + 4*Q)*Q — (800 + 40*Q + 2*Q2) = 1000
40*Q + 4*Q2 — 800 — 40*Q — 2*Q2 — 1000 = 0
2*Q2 = 1800
Q2 = 900
Q1,2 = ±30
Так как отрицательный корень экономического содержания не имеет, берём Q = 30.
Тогда цена будет равна:
Р = 40 + 4*30 = 160
Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде
Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:
Q3 – 16*Q2 + 400*Q.
а) При каком значении Q средние затраты достигают минимума?
б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?
Решение:
а) Найдём функцию средних затрат по формуле:
АС = ТС / Q = (Q3 – 16*Q2 + 400*Q) / Q = Q2 – 16*Q + 400
Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.
AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8
При Q = 8 средние затраты достигают минимума.
б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:
Р = МС = MR = minАС
Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:
minAC(Q=8) = 82 – 16*8 + 400 = 336
Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.
Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль
Спрос на продукцию конкурентной отрасли:
Qd = 55 – P
Предложение:
Qs = 2P – 5
Если у одной из фирм отрасли восходящий участок кривой предельных издержек:
МС = 3Q + 5
При каких цене и объёме производства фирма максимизирует прибыль?
Решение:
Найдём цену равновесия. Приравняем функцию спроса и предложения:
Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.
Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.
МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.
Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
Конкурентная фирма имеет предельные затраты:
МС = 30 + 2 × Q
при фиксированных затратах, равных 500 денежным единицам.
Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.
Определить цену на рынке и объём выпуска данной фирмы.
Решение:
Формула прибыли имеет вид:
П = TR – TC = P*Q – TC
Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.
где
С – константа, равная величине фиксированных затрат, которые по условию равны 500.
Таким образом функция общих затрат имеет вид:
ТС = Q2 +30*Q + 500
Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR
Воспользуемся тем, что:
Р = МС
По условию задачи:
МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q
Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.
(30 + 2 * Q) * Q – (Q2 +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40
Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.
Тогда рыночная цена будет равна:
Р = 30 + 2 * 40 = 110.
Как рассчитать оптимальный план производства, чтобы получить максимальную прибыль? Этот вопрос актуален для многих компаний. Интуитивное формирование плана производства может быть не таким эффективным, как расчет с помощью математических моделей.
Сравним эти способы на примере.
Компания производит шоколад трех сортов: белый, молочный и горький. У каждого — своя рецептура, но трудоемкость одинаковая. Цена каждого сорта разная, поэтому и прибыль на килограмм тоже отличается. Представим эти данные в виде таблицы:
| Ингредиент | Белый шоколад | Молочный шоколад | Горький шоколад |
| Какао-масло, кг | 0,4 | 0,4 | 0,4 |
| Сахар, кг | 0,3 | 0,4 | 0,2 |
| Сухое молоко, кг | 0,3 | 0,15 | 0 |
| Какао, кг | 0 | 0,15 | 0,3 |
| Прибыль, за 1 кг | 1 000 | 2 500 | 3 000 |
На складе имеются определенные запасы сырья:
- какао-масло — 20 кг;
- сахар — 15 кг;
- сухое молоко — 7 кг;
- какао — 12 кг.
Расчет плана производства интуитивным методом
План производства для первого вида продукции
Больше всего прибыли приносит горький шоколад. Рассчитаем, сколько шоколада этого сорта можно произвести из сырья на складе:
| Ингредиент | Требуется для производства 1 кг горького шоколада | Наличие сырья на складе, кг | Достаточно для объема производства горького шоколада, кг |
| Какао-масло, кг | 0,4 | 20 | 50 |
| Сахар, кг | 0,2 | 15 | 75 |
| Сухое молоко, кг | 0 | 7 | – |
| Какао, кг | 0,3 | 12 | 40 |
Объем производства ограничивает какао — его достаточно для производства только 40 килограммов шоколада.
Прибыль от горького шоколада = 40 х 3000 = 120 000 (руб.)
Рассчитаем количество сырья, которое потребуется для производства 40 килограммов горького шоколада. Для этого умножим количество ингредиента, нужного для производства одного килограмма, на 40.
Например, для производства одного килограмма горького шоколада нужно 16 килограммов какао-масла:
0,4 х 40 = 16 (кг)
Рассчитаем расход каждого ингредиента и внесем в столбец «Резерв сырья».
| Ингредиент | Требуется для производства 1 кг горького шоколада | Резерв сырья для производства 40 кг | Остаток на складе, с учетом резерва |
| Какао-масло, кг | 0,4 | 16 | 4 |
| Сахар, кг | 0,2 | 8 | 7 |
| Сухое молоко, кг | 0 | 0 | 7 |
| Какао, кг | 0,3 | 12 | 0 |
После производства горького шоколада на складе останутся продукты, их объем можно рассчитать как разницу между остатками на складе и резервом.
Остаток какао-масла = 20 – 16 = 4 (кг)
Такой же расчет проводим и для других ингредиентов и вносим данные по остаткам в последний столбец.
План производства для второго вида продукции
Так как все какао зарезервировано для производства горького шоколада, компания из остатков сырья может произвести только белый шоколад, при его приготовлении какао не используется.
Рассчитаем, сколько белого шоколада можно произвести из оставшихся ингредиентов:
| Ингредиент | Требуется для производства 1 кг белого шоколада | Остаток на складе, с учетом резерва, кг | Достаточно для объем производства белого шоколада, кг |
| Какао-масло, кг | 0,4 | 4 | 10 |
| Сахар, кг | 0,3 | 7 | 23 |
| Сухое молоко, кг | 0,3 | 7 | 23 |
| Какао, кг | 0 | 0 | – |
«Ограничивающим» ингредиентом выступает какао-масло. Из имеющегося количества можно сделать только 10 килограммов белого шоколада.
Прибыль от белого шоколада = 10 х 1000 = 10 000 (руб.)
Рассчитаем расход сырья на производство белого шоколада и остатки на складе.
| Ингредиент | Требуется для производства 1 кг белого шоколада | Резерв сырья для производства 10 кг | Остаток на складе, с учетом резерва |
| Какао-масло, кг | 0,4 | 4 | 0 |
| Сахар, кг | 0,3 | 3 | 4 |
| Сухое молоко, кг | 0,3 | 3 | 4 |
| Какао, кг | 0 | 0 | 0 |
Из остатков на складе произвести шоколад больше нельзя.
Общая прибыль составит 130 000 рублей.
120 000 + 10 000 = 130 000 (руб.)
Этот способ расчета достаточно трудоемкий и при большом ассортименте продукции и запасов может быть просто неприменим. Математическое моделирование плана производства позволит учесть больше переменных.
Антон Варламов, начальник производства CWS-group:
«Мы производим оборудование для моек самообслуживания. В производстве ориентируемся на спрос: в основном, начинаем сборку после заказа. Именно спрос является «толкающим» фактором.
Плюс этого способа — готовое оборудование не задерживается на складе, сразу отправляется клиентам. В процессе производства мы можем внести какие-то изменения и учесть просьбы заказчиков: сделать больше или меньше функций в пульте самообслуживания, подобрать нужную мощность аппаратов высокого давления.
Минус — мы упускаем часть прибыли из-за нерационального использования запасов. Что-то невостребованное лежит на складе, что-то приходится покупать срочно и переплачивать.
Но в текущей ситуации пока не видим возможности перехода на планирование производства»
Расчет плана производства методом математического моделирования
Для построения математической модели используется надстройка «Поиск решения» в Excel. Мы уже подготовили математическую модель, которую вы можете скачать на компьютер с установленным Excel и заполнить своими данными.
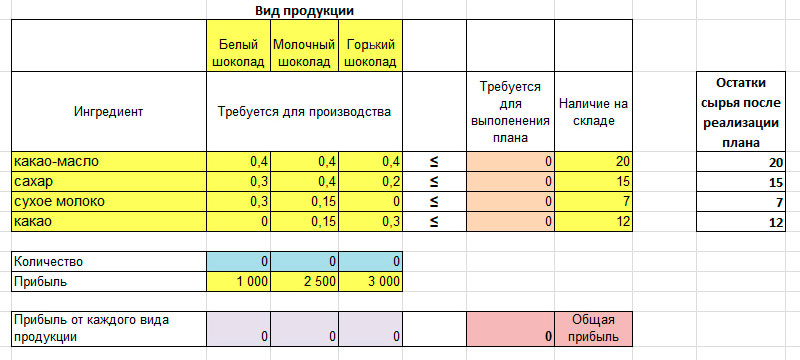
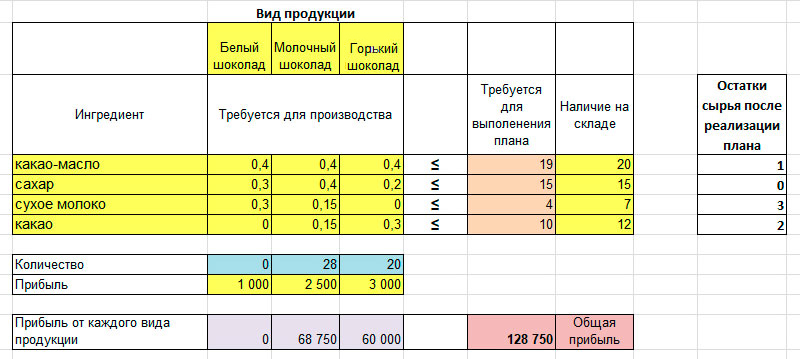
Таблица для производства шоколада выглядит так:
Желтые ячейки заполнены исходными данными из примера. Это прибыль по каждому виду продукции, расход ингредиентов и их наличие на складе.
Голубые ячейки будет изменять программа в процессе расчетов.
В оранжевых — расход сырья, нужного по плану производства. Он рассчитывается также, как и в первом способе, только не вручную, а автоматически. Для этого в ячейки введены нужные формулы.
В фиолетовых значение прибыли по сортам, рассчитывается по формуле:
Прибыль по сорту = Количество шоколада х Прибыль от сорта шоколада
Розовая — значение прибыли, максимум которой программа найдет в процессе расчета, она суммирует все прибыли по сортам.
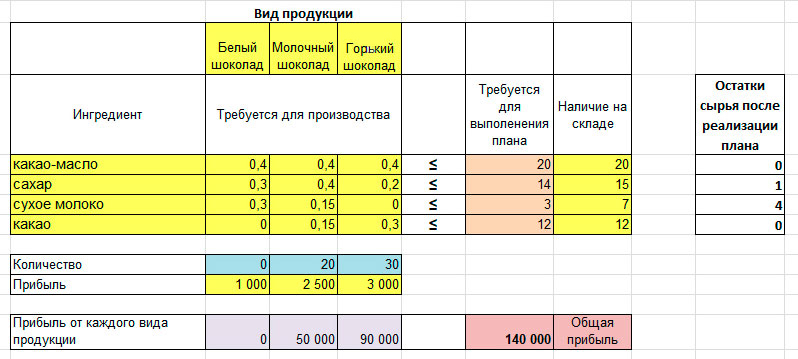
После нажатия «Поиск решения» система рассчитывает оптимальный план производства с максимальной прибылью:
План производства, рассчитанный этим способом, отличается от первого. Сокращено количество горького шоколада, поэтому остается больше сырья для производства молочного. Это позволяет увеличить прибыль со 130 тысяч рублей до 140 тысяч и более эффективно использовать складские запасы.
Изменение плана производства
Описанные методы не учитывают спрос, подразумевается, что будет продан весь произведенный шоколад. Но в математическую модель можно внести дополнительные ограничения.
Например, объем производства горького шоколада ограничить 20 килограммами, тогда программа посчитает новый план, но прибыль в нем будет меньше, чем в оптимальном:
Моделирование оптимального плана производства позволит один раз создать математическую модель и потом изменять параметры, оценивая изменение прибыли:
- Вводить ограничения по количеству производимой продукции: задать определенный объем или нужные пропорции. Например, чтобы объем производства горького шоколада был равен объему производства молочного.
- Менять ограничения по ресурсам, в зависимости от объема запасов.
- Проверить целесообразность введения новой продукции — будет ли увеличиваться или уменьшаться прибыль в этом случае.
- Изменять прибыль по видам продукции для более корректного ценообразования.
- Выявить слабые позиции в ассортименте и, возможно, отказаться от них.
В математической модели можно использовать не только ресурсы в натуральном выражении, как в нашем примере, но и в денежном. Это еще больше расширяет возможности ее применения, так как позволяет учесть расходы на оплату труда, электричество, время работы оборудования. Чем точнее исходные данные, тем точнее будет расчет плана производства. Компании, ведущие управленческий учет, тратят меньше времени на сбор данных для заполнения математической модели.
Резюмируем
Расчет оптимального плана производства позволяет компании заработать больше, используя ограниченные ресурсы. Создание модели плана производства в Excel экономит время и позволяет достаточно быстро оценить изменение прибыли при разных вариантах исходных данных.
-
Определение объема производства, максимизирующего прибыль (минимизирующего убытки): сопоставление валового дохода и валовых издержек.
Фирма в краткосрочном
периоде располагает фиксированными
мощностями. Следовательно, максимизировать
прибыль она может только изменяя объем
выпуска продукции (только путем изменения
переменных ресурсов).
Прибыль
– это разница между валовым доходом и
валовыми издержками. Объединим эти
данные.
Существует 2 подхода
к определению объема производства,
максимизирующего прибыль.
1) Сопоставление
валового дохода и валовых издержек.
2) Сопоставление
предельного дохода и предельных издержек.
1) Сопоставление валового дохода и валовых издержек.
Максимизация
прибыли.
График 8.2. Максимизация
прибыли.

Любое производство
за пределами Qk1
и Qk2
– убыточно: TC
> TR.
Внутри интервала – экономическая
прибыль.
Максимум прибыли
достигается в точке Qm
– там максимально расстояние между
кривыми TC
и TR,
следовательно максимальна и их разность.
Любой объем выпуска
Q<Qk1 следует увеличивать, Q>Qk2
– уменьшать.
Конкретизируем
условия равновесия.
;
.
В точке А (точка
на графике не обозначена – она
соответствует Объему выпуска Qm)
наклоны кривых совпадают: прибыль
максимальна тогда, когда фирма доведет
объем выпуска, при котором MR
= MC
– равновесия или правило макисмизации
прибыли. Действует
во всех рыночных структурах.
Минимизация
убытков.
Рынок установил
более низкую цену, при которой все уровни
производства убыточны:
.
Что произойдет?
Закроется ли фирма?
График 8.3(а).
Минимизация убытков.

1) Фирма не закроется,
если
,
т.ч.
.
Такие Q
лежат в интервале
.
В этом случае фирма покрывает не только
все переменные издержки, но и часть
постоянных. Естественно она выберет
некий объем выпуска
,
при котором расстояние между кривой
TVC
и TR
максимально (графически это определяется
путем проведения лини TR’,
касательно к TVC
– точка касания и соответствует искомому
объему выпуска
).
Длина отрезка
– величина покрываемых постоянных
издержек. При этом фирма несет убытки
в размере длины отрезка
,
но это лучше чем она бы закрылась и несла
убытки в размере длины отрезка
.
2) Закрытие фирмы.
График 8.3(б).
Минимизация убытков.

Рынок установил
еще более низкую цену, т.ч.:
(см. график 8.3(б))
Фирма будет нести
издержки при любых объемах выпуска Q
сверх постоянных, т.к. не покрывает всех
своих переменных издержек.
– величина издержек,
которые несет фирма сверх постоянных
(часть от переменных).
В данном случае
фирма будет минимизировать свои убытки
закрывшись: тогда она будет нести убытки
лишь в размере своих постоянных издержек.
2) Сопоставление предельного дохода и предельных издержек.
Т.е. сопоставление
сумм, которые каждая дополнительная
единица будет добавлять к валовому
доходу и валовым издержкам.
Уточним правило
максимизации прибыли при этом подходе.
График 8.4. Правило
максимизации прибыли.

Любую единицу
продукции Q1
< Qm
(имеются ввиду последние единицы
порождающие эти объемы выпуска) следует
производить: она добавляет больше к
валовому доходу, чем к валовым издержкам,
т.к. MR
> MC.
От производства
любой единицы продукции Q2
> Qm
следует отказаться, т.к. она добавляет
к валовому доходу меньше, чем валовым
издержкам, т.к. MR
< MC.
=>
Условие максимизации
прибыли: MR
= MC.
В условиях
совершенной конкуренции P
= MR
=> условие можно записать так:
MR(P)
= MC.
Далее будем
рассматривать этот частный случай
(рынок совершенной конкуренции).
Применим правило
максимизации прибыли и выясним какое
количество продукции будет производить
фирма при различных рыночных ценах.
Максимизация
прибыли.
График 8.4(а).
Максимизация прибыли.

Для анализа строим
ATC
& AVC.
Рынок установил
достаточно высокую цену:
.
OP1AQ1
– валовый доход.
OLKQ1
– валовые издержки.
Валовый доход
больше валовых издержек, следовательно
фирма получает экономическую прибыль
в размере площади: LP1AK.
График 8.3(б).

Рынок установил
более низкую цену
.
В соответствии с правилом максимизации
прибыли фирма доведет объем выпуска до
Q2.
Валовый
доход фирмы P2Q2
= площади фигуры OP3BQ2
= валовые издержки.
В данном случае
фирма покрывает все свои издержки и
несет прибыль в размере нормальной
прибыли, экономической прибыли здесь
нет.
P2
– стратегическая цена с точки зрения
максимизации прибыли.
Минимизация
убытков.
График 8.6(а).
Минимизация убытков.

Рынок установил
еще более низкую цену
.
По правилу
максимизации прибыли фирма доведет
свой объем выпуска да уровня Q3
(см. график).
Валовый доход:
P3Q3
= S[OP3CQ3].
Валовые издержки:
S[ONMQ3].
Q3M
> Q3C
=> фирма несет убытки в размере S[P3NMC]
– это предпочтительнее, чем если бы она
закрылась и понесла бы все свои постоянные
издержки в размере S[WNMC].
График 8.6(б).
Минимизация убытков.

Рынок установил
еще более низкую цену P4
= AVCmin.
В соответствии с правилом максимизации
прибыли фирма доведет свой объем выпуска
до Q4.
В данной
ситуции:
Валовый доход:
S[OP4AQ4].
Валовые издержки:
S[ONMQ4].
Фирма покрывает
только свои переменные издержки и несет
убытки в размере всех своих постоянных
издержек: S[P4NMA].
Точка А называется
точкой
бегства фирмы.
Фирме все равно
зарыться или производить данный объем
Q4.
Закрытие фирмы.
График 8.6(В). Закрытие
фирмы.

Рынок установил
еще более низкую цену P5
< AVCmin.
Помимо своих
постоянных издержек фирма не может
покрыть и часть переменных.
Валовый доход:
P5Q5
= S[OP5AQ5].
Валовые издержки:
S[OLCQ5].
Фирма будет
минимизировать убытки закрывшись, так
как тогда она будет нести убытки не в
размере S[P5LCA],
а только в размере своих постоянных
издержек: S[KLCB].
Вывод:
Фирма будет
максимизировать прибыль или минимизировать
убытки в краткосрочном периоде, доведя
свой объем выпуска до уровня, при котором
MR
= MC,
при условии, что
.
Кривая предложения
фирмы в краткосрочном периоде.
График 8.7. Кривая
предложения фирмы в краткосрочном
периоде.

Анализ объемов
производства фирмы при различных
рыночных ценах позволяет определить
функцию предложения фирмы в краткосрочном
периоде.
Кривая предложения
фирмы – это отрезок кривой предельных
издержек фирмы, лежащий выше средних
переменных издержек:

Соседние файлы в папке ЭТ
- #
- #
- #
- #
Татьяна Николаевна Таряник
Эксперт по предмету «Экономика»
Задать вопрос автору статьи
Определение 1
Оптимальный объем производства – это объем продукции, произведенной в установленные сроки с минимальными затратами и максимальной эффективностью, обеспечивающий выполнение обязательств по договорам.
Максимизация прибыли фирмы
Цель деятельность любого предприятия состоит в максимизации прибыли, которая представляет собой разницу между выручкой и суммарными расходами предприятия. Ниже представлена формула расчета прибыли предприятия:
П = TR – TC
Где П – прибыль, TR – выручка, TC – издержки.
Так как в функции выручки TR = P • Q рыночная цена совершенно неподконтрольна конкурентной фирме, то задачей последней является определение такого выпуска продукции, при котором прибыль будет максимальной.
Предприятие будет максимизировать прибыль при таком объеме выпуска, когда его предельный доход станет равен предельным издержкам, т.е. MR = MC.
Определение 2
Правило максимизации прибыли гласит, что предприятие, производящее продукцию в объеме, при котором MR = MC, будет получать максимально возможную прибыль при данных ценах. Таким образом, оптимальный объем производства представляет собой такой объем, при котором равны предельные издержки и предельный доход.
Равенство MR и MC – это условие максимизации прибыли для любого предприятия независимо от структуры рынка, в котором оно осуществляет свою деятельность.
Приведенное равенство MR и MC можно логически обосновать. С каждой дополнительной единицей выпуска предприятие получает дополнительный доход, но это требует и дополнительных затрат. Пока предельный доход будет превышать предельные затраты, дополнительные единицы выпуска будут увеличивать прибыль. Соответственно, при достижении равенства предельных затрат и предельного дохода прибыль будет максимальной. С дальнейшим увеличением выпуска, когда предельные затраты станут выше предельного дохода, прибыль будет снижаться.
«Оптимальный объем производства» 👇
Во всех своих решениях предприятие стремится достичь наилучших результатов, т.е. получить максимальную прибыль с минимальными затратами. Такое состояние предприятия называется состоянием равновесия.
Условие равновесия – это равенство предельных издержек, дохода и стоимости фактора:
MR = MC = P
Точка пересечения рыночной цены и кривой предельных издержек – это положение равновесия.
Рисунок 1. Равновесие производства. Автор24 – интернет-биржа студенческих работ
Левее точки Е, т.е. при MC , предприятию целесообразно наращивать производство, поскольку с каждой единицы продукции оно получает больше, чем расходует. Правее точки E, т.е. MC > MR, с каждой дополнительной единицы продукции предприятие несет убытки, поэтому наращивать производство не имеет смысла.
Методы определения оптимального объема производства
Как уже было отмечено, оптимальным объемом производства является такой объем, при котором обеспечивается выполнение заключенных соглашений и обязательств по производству товаров в установленные сроки с минимальными затратами.
Оптимальный производственный объем определяется при помощи одного из двух методов:
- С помощью метода сопоставления валовых показателей;
- С помощью метода сопоставления предельных показателей.
Использование данных методов сопровождается следующими допущениями:
- Предприятие производит и продает один товар;
- Цель предприятия состоит в максимизации прибыли за рассматриваемый период;
- Оптимизации подвергаются только лишь цена и объем производства, так как предполагается, что другие параметры деятельности неизменны;
- Объем производства в рассматриваемом периоде равняется объему реализации.
Несмотря на жесткие ограничения перечисленных допущений, использование данных методов в значительной степени увеличивает вероятность принятия правильных и рациональных решений.
Для наглядности рассмотрим на примерах определение оптимального производственного объема продукции с использованием двух перечисленных методов.
На рисунке 2 представлены исходные данные.
Рисунок 2. Исходные данные. Автор24 – интернет-биржа студенческих работ
Чтобы найти оптимальный объем продукции методом сопоставления валовых показателей, выполняют следующие действия в заданной последовательности:
- Определяют величину объема производства, при которой прибыль будет нулевой;
- Определяется объем производства, при котором прибыль максимальна.
Объем реализации товаров представлен на рисунке 3.
Рисунок 3. Объем реализации с максимальной прибылью. Автор24 – интернет-биржа студенческих работ
На основании данных таблицы можно сделать выводы:
- Прибыль будет нулевой при производстве и реализации от 30 до 40 тыс.шт. товара;
- Максимальная прибыль (1140 тыс.руб.) будет достигнута при производстве и реализации 90 тыс.шт. продукции, что в данном случае является оптимальным объемом производства.
Использование метода сопоставления предельных показателей дает возможность установить рентабельные пределы увеличения производства и продажи. Его основой является сопоставление предельного дохода и предельных издержек. Если предельный доход на единицу продукции будет выше величины предельных издержек, то рентабельно увеличивать производство и реализацию.
Вычисление оптимального объема производства товаров представлено на рисунке 4.
Рисунок 4. Определение оптимального производственного объема продукции при помощи метода сопоставления предельных показателей. Автор24 – интернет-биржа студенческих работ
Предельный доход на единицу продукции в данном случае – это рыночная цена одной единицы товара. Предельные издержки равны разнице последующих издержек и предыдущих издержек, поделенной на объем производства. Величина предельной прибыли равняется разнице предельного дохода и предельных издержек.
Из всего вышесказанного можно сделать такие выводы:
- Эффективно расширять объем производства товаров только до 90 тыс. шт.;
- Превышение объема производства 90 тыс. шт. при неизменной цене станет причиной снижения валовой прибыли, т.к. сумма дополнительных издержек будет больше суммы дополнительного дохода на одну единицу продукции.
Факторы, влияющие на оптимальный объем выпуска товаров
Важнейшим фактором управления производственными процессами является деление расходов на постоянные и переменные. Данное разделение позволяет прогнозировать прибыль на основании изменения расходов в зависимости от объема продаж, вычислять объем реализации для конкретной ситуации, который будет обеспечивать безубыточную деятельность. Эти действия позволят избежать многих ошибочных решений, принимаемых при калькулировании себестоимости.
Ключевым показателем в системе управления прибылью от реализации является маржинальный доход, который представляет собой разницу выручки от продаж и переменных расходов. Экономическая сущность маржинального дохода заключается в том, что он покрывает постоянные расходы. Если маржинальный доход выше постоянных расходов, то фирма имеет прибыль.
Маржинальный доход отражает вклад конкретного реализуемого продукта в прибыль компании. при помощи данного показателя менеджмент предприятия получает информацию об уровне рентабельности отдельного вида продукции в общих финансовых результатах.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме