Как найти объем зная силу трения

Обработка опытных данных

1. Определить объем
воды V, см³,
заполнения мерного бака. Размеры мерного
бака: а=19 см, b=44
см.

.

2. Определить расход
Q, зная время t,
с, заполнения объема воды V
в мерном баке по формуле:

.

3. Определить
скорости движения воды в трубе 2 зная,
что:

,

где

– площадь поперечного сечения трубы.

4. Определить
значение числа Рейнольдса

,

где
ν – кинематический
коэффициент вязкости воды,

.

5. Данные занести
в табл. 1 и построить график зависимости
h = ƒ(υ) в прямоугольных
координатах.

6. По графику
определить скорость υ_к в
момент перехода линейной зависимости
h=ƒ(υ) в криволинейную
и сравнить ее с величиной


полученной путем измерения как:

.

7. Вычислить Re_к
для υ_к определенной по
графику.

8. Привести пример
расчета.

ЛАБОРАТОРНАЯ
РАБОТА № 4

«Определение коэффициента гидравлического трения при движении жидкости в круглой трубе»

Цель работы:

Определить
коэффициент гидравлического трения

при ламинарном и турбулентном режимах
движения жидкости по трубопроводу.

Общие сведения

При движении
жидкости по прямому трубопроводу
постоянного сечения часть удельной
механической энергии затрачивается на
преодоление сил трения как внутри
жидкости, так и о стенки трубопровода
и носит название потерь напора по длине

.

Записывая уравнение
Бернулли для двух сечений потока, можно
определить потери удельной энергии на
участке между сечениями I-I
и II-II:

(1)

,
(2)

так как

.
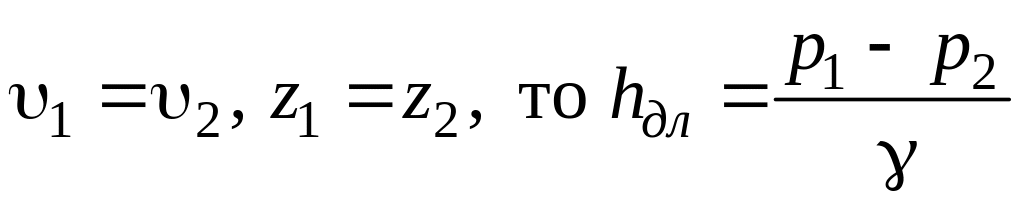
(3)

Отсюда следует,
что потери напора

можно определить по показаниям
пьезометров, установленных в рассматриваемых
сечениях.

Теоретически
потери напора по длине определяются по
формуле Дарси – Вейсбаха:

(4)

где L
– длина рассматриваемого участка
трубопровода;

d
– диаметр рассматриваемого участка;

– средняя скорость
движения жидкости;

– коэффициент
гидравлического трения (гидравлического
сопротивления);

g –
ускорение свободного падения, м/с².

Коэффициент
гидравлического трения

является функцией, зависящей как от
свойств жидкости (вязкости, плотности),
так и параметров трубопровода (диаметра,
шероховатости стенок) и условий течения
(средней скорости).

Из этих независимых
размерных величин можно получить два
безразмерных параметра, а именно:

1. Параметр
Рейнольдса:

(5)

2. Относительную
шероховатость:

,

то есть установить
зависимость:

.

При ламинарном
режиме движения жидкости

,
то есть

,
коэффициент гидравлического трения

зависит только от числа

,

.
Для определения коэффициента
гидравлического трения используют
формулу Стокса:

(6)

Для турбулентного
режима движения из-за сложности
происходящих при этом явлений расчетные
формулы для определения коэффициента
гидравлического трения могут быть
получены лишь при принятии определенных
гипотез с последующей проверкой
полученных результатов экспериментом.

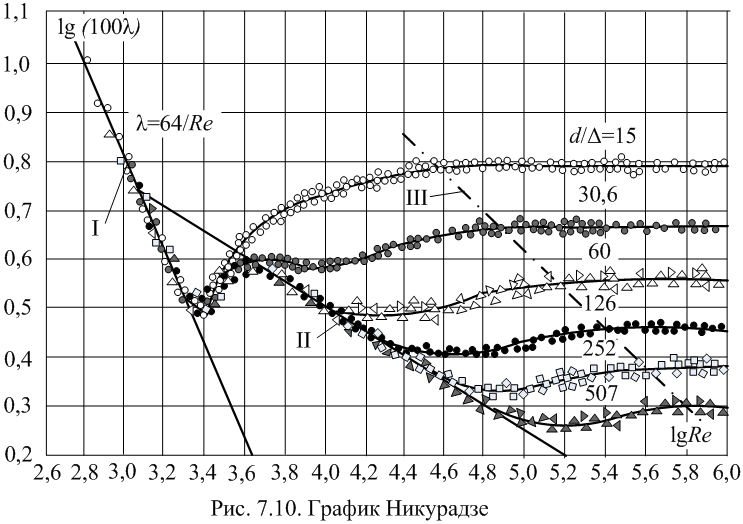
По наиболее
распространенной гипотезе Прандтля
турбулентный поток состоит из ядра
течения и ламинарного слоя, между
которыми находится переходная область
(рис.1).

П
ри
турбулентном режи­ме

различают четыре основные зоны чисел

:

Если

,
то режим течения называется «переходный
турбулентный» и коэффициент гидравлического
трения определяется по формуле Френкеля:

,
(7)

2. При относительно
небольших числах

–

– (

– относительная шероховатость внутренней
поверхности трубопровода), когда
ламинарный слой закрывает шероховатость
стенок трубопровода, возмущения,
возникающие при обтекании жидкостью
выступов шероховатости, быстро в нем
затухают и практически не сказываются
на коэффициенте гидравлического трения.
Эта зона турбулентного режима называется
«зоной гидравлически гладких труб». В
этом случае коэффициент гидравлического
трения определяется по формуле Блазиуса:

.
(8)

3. С увеличением
числа

ламинарный слой уменьшается. Когда его
толщина становится одного порядка с
высотой выступов шероховатости, то в
этой зоне коэффициент гидравлического
трения

зависит не только от числа

,
но и от шероховатости стенок:

.
Эта зона смешанного трения,

.
Коэффициент гидравлического трения
определяют по формуле Альтшуля:

.
(9)

4. Зона, в которой
число

называется зоной квадратичного
сопротивления (зона вполне шероховатых
труб). В этой зоне коэффициент
гидравлического трения

зависит только от относительной
шероховатости стенок:

и определяется по формуле Шифринсона:

.
(10)

Графически эти
зависимости отражены в графиках Никурадзе

(рис. 2).

Рис. 2. График Никурадзе

Для новых стальных
труб значение коэффициента λ может
находится также по номограмме Г.А. Мурина
(рис. 3).

Рис. 3. Номограмма Мурина

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Синтез наук – оружие познания XXI века

Продолжение. См. № 15, 17/05

К.Ю.Богданов,
школа № 1326, г. Москва. KBogdanov@mtu-net.ru

Элективный курс, 10–11 классы,
естественнонаучный профиль (136 ч, 2 ч/нед.)

Уроки 7–8. Всё о силе трения

С трением мы сталкиваемся на каждом
шагу, но без трения мы не сделали бы и шага.
Невозможно представить себе мир без сил трения. В
отсутствие трения многие кратковременные
движения продолжались бы бесконечно. Земля
сотрясалась бы от непрерывных землетрясений, т.к.
тектонические плиты постоянно сталкивались бы
между собой. Все ледники сразу же скатились бы с
гор, а по поверхности Земли носилась бы пыль от
прошлогоднего ветра. Как хорошо, что всё-таки
есть на свете сила трения! С другой стороны,
трение между деталями машин приводит к их износу
и дополнительным расходам. Приблизительные
оценки показывают, что научные исследования в
трибологии – науки о трении – могли бы сберечь
от 2 до 10% национального валового продукта.

Классический закон трения. Два самых
главных изобретения человека – колесо и
добывание огня – связаны с силой трения.
Изобретение колеса позволило значительно
уменьшить силу, препятствующую движению, а
добывание огня поставило силу трения на службу
человеку. Однако до сих пор учёные далеки от
полного понимания физических основ силы трения.
И вовсе не оттого, что людей с некоторых пор
перестало интересовать это явление. Первая
формулировка законов трения принадлежит
великому Леонардо (1519 г.), который утверждал, что
сила трения, возникающая при контакте тела с
поверхностью другого тела, пропорциональна силе
прижатия, направлена против направления
движения и не зависит от площади контакта. Этот
закон был заново открыт через 180 лет Г.Амонтоном,
а затем уточнён в работах Ш.Кулона (1781 г.). Амонтон
и Кулон ввели понятие коэффициента трения как
отношения силы трения к нагрузке, придав ему
значение физической константы, полностью
определяющей силу трения для любой пары
контактирующих материалов. До сих пор именно эта
формула:

Fтр = N,
         (1)

где Fтр – сила трения, N – составляющая
силы прижатия, нормальная к поверхности
контакта, а –
коэффициент трения, – является единственной
формулой, которую можно найти в учебниках по
физике.

В течение двух столетий
экспериментально доказанный закон (1) никто не
смог опровергнуть и до сих пор он звучит так, как
и 200 лет назад:

1. Сила трения прямо пропорциональна
нормальной составляющей силы, сжимающей
поверхности скользящих тел, и всегда действует в
направлении, противоположном направлению
движения.

2. Сила трения не зависит от величины
поверхности соприкосновения.

3. Сила трения не зависит от скорости
скольжения.

4. Сила трения покоя всегда больше силы
трения скольжения.

5. Сила трения зависит только от
свойств двух материалов, которые скользят друг
по другу.

Потираем руки и проверяем основной
закон трения. Сила трения – одна из
диссипативных сил. Другими словами, вся работа,
расходуемая на её преодоление, переходит в тепло.
Значения m, приводимые в инженерных справочниках,
позволяют оценивать этот нагрев в проектируемых
приборах и устройствах (см. таблицу). Ну а мы
попробуем найти количество выделяющейся
тепловой энергии, когда, разогреваясь, потираем
руки или разогреваем с их помощью охлаждённые
участки тела.

Пусть мы сжимаем ладони с силой 0,5 Н, и для трения кожи о
кожу составляет 0,5. Тогда сила трения, которую мы
преодолеваем при скольжении одной ладони по
поверхности другой, будет равна 0,25 Н. Если
считать, что, разогреваясь, мы за одну секунду
совершаем четыре движения ладони, и каждое из них
по 0,1 м, то мощность, расходуемая на преодоление
силы трения, составляет 0,1 Вт. За 10 с такого
разогрева в области контакта ладоней выделится 1
Дж тепловой энергии. Пусть всё тепло идёт на
разогрев участка поверхности кожи площадью 0,01 м²
и толщиной 0,001 м, который имеет массу около 10^–5
кг и удельную теплоёмкость, близкую к
теплоёмкости воды (4 кДж/(кг .  °С). Значит, наш
разогрев приведёт к нагреву этого участка на 25
°С. Видно, что оценка нагрева получилась явно
завышенной. Большая часть тепла от разогрева,
конечно, уходит в ткани, расположенные под кожей
и разносится по телу с кровотоком, но и
оставшейся части тепловой энергии оказывается
достаточно, чтобы поднять температуру кожи на
несколько градусов.

Тормозной путь. Две машины столкнулись
на перекрёстке. Повреждения небольшие, т.к.
каждый успел почти полностью затормозить перед
аварией. Поэтому и виноватым себя считать никто
не хочет. Приехавший инспектор решил, что виноват
тот, у кого длина тормозного пути – чёрного следа
от колёс – больше. Почему?

Пусть машина выезжала на перекрёсток
со скоростью , и
её водитель, увидев другую машину, стал
тормозить, оставив на дороге след длиной L. Если
считать, что к моменту столкновения вся
кинетическая энергия автомобиля перешла в
работу по преодолению силы трения (в тепло), то   где m – масса
автомобиля, а g – ускорение свободного падения.
Откуда следует, что длина тормозного пути
пропорциональна квадрату скорости автомобиля.
Значит, тот, кто подъезжал к перекрёстку с
большей скоростью, имеет и большую длину
тормозного пути. Так, например, для = 0,7 длина тормозного пути
30 м соответствует скорости движения 73 км/ч, что на
13 км/ч больше разрешённой скорости движения по
улицам города.

А почему все шины чёрные? Все
изготовители шин используют один и тот же
процесс – вулканизацию жидкой резины, при
котором одной из добавок служит угольная пудра. В
результате длинные молекулы жидкой резины
сшиваются между собой, что превращает её в
эластичный и прочный материал. Так как частички
угля чёрные и их относительно много (около 25% по
весу), то и резина становится чёрной. Чем больше
добавлять угольной пудры, состоящей практически
из одного углерода, тем более жёсткой, прочной и
менее прилипчивой будет резина.

Как нажимать на газ и тормоз, чтобы
быстрее разогнаться и остановиться? Некоторые
водители, увидев, что на светофоре зажёгся
зелёный свет, вдавливают педаль газа до самого
пола, пытаясь как можно быстрее набрать
максимальную скорость. Свидетели такого старта
слышат свист проскальзывающих относительно
дороги шин. Со стороны это выглядит,
действительно, очень впечатляюще. Но как на самом
деле? Неужели, для того чтобы машина приобрела
наибольшее ускорение, надо заставлять колёса
скользить по дорожному покрытию? Конечно, нет.

Известно, что движущей силой
автомобиля служит сила трения его колёс о
дорожное покрытие. Если резко нажать на педаль
газа, вызвав проскальзывание шин относительно
асфальта, то максимальное ускорение будет
пропорционально силе трения скольжения, которая
всегда меньше максимальной силы трения покоя.
Поэтому быстрее ускоряются не те, кто сжигает
резину покрышек, а те, кто использует силу трения
покоя (т.е. не допускает скольжения) в том
диапазоне, где она превышает силу трения
скольжения.

Резкое торможение, как и ускорение,
может привести к скольжению колёс по дорожному
покрытию, а значит, к уменьшению силы, тормозящей
автомобиль. Ведь тормозящей силой является тоже
сила трения. Поэтому, нажав очень резко на педаль
газа и допустив проскальзывание, мы увеличиваем
тормозной путь. Чтобы минимизировать тормозной
путь, в современных автомобилях устанавливают
систему ABS (Antilock Brake System), которая, препятствуя
скольжению колёс по дорожному покрытию,
трансформирует резкое нажатие на тормоз в
последовательность нескольких торможений.
Эффективность ABS-торможения особенно высока на
мокрых дорогах, когда максимальная сила трения
покоя может в несколько раз превышать силу
трения скольжения.

Зависимость силы трения, действующей
на тело, от силы, которая может привести или
приводит к движению тела для сухого и мокрого
дорожного покрытия

Для чего нужен рисунок на шинах
автомобиля? Если машина въезжает в лужу, а вода не
успевает выскочить из-под колеса, то сцепление с
дорогой теряется, и колесо может вращаться
вокруг оси, не испытывая трения. В этом случае
машина теряет движущую силу и становится
неуправляемой. Вот почему на покрышках
автомобильных шин находятся канавки, помогающие
воде выбираться из-под колеса, что помогает
резине шин даже в лужах быстро находить контакт с
покрытием дороги. Зимой большинство водителей
«обувают» свои машины в зимнюю резину. Если
ездить на летних покрышках зимой, то узкие
канавки быстро забьются снегом, а он,
превратившись в лёд, сделает из автомобиля
прекрасное средство для неуправляемого
скольжения по дорогам. Поэтому покрышки,
приспособленные для езды по заснеженным и
обледенелым дорогам, имеют широкие канавки и
гораздо большую поверхность контакта с дорожным
покрытием. Ну а если предстоит ехать по
бездорожью, то покрышки должны быть глубоко
рифлёными, т.к. грязь, имеющая большую вязкость,
просто не пролезет через канавки, когда будет
двигаться под весом наезжающего колеса.

Покрышки автомобильных шин,
предназначенные для летних (слева),
зимних (в середине) дорог и бездорожья (справа)

Гонки «Формулы-1» – война шин. Каждый
пилот гоночного болида хочет иметь хорошее
сцепление с дорогой, чтобы обеспечить быстрый
старт. Но это значит, что шины его автомобиля
должны хорошо прилипать к дорожному покрытию.
Ведь только тогда максимальная сила трения покоя
будет велика. Но такая прилипчивая шина всегда
будет оставлять на дороге след из частичек,
прилипших навсегда к дорожному покрытию. Другими
словами, износ шин с высоким сцеплением тоже
высок. Поэтому на гонках «Формулы-1» средний
ресурс шины около 200 км, в то время как у
обычных шин он может составлять несколько
десятков тысяч километров.

Шины гоночных болидов «Формулы-1» очень
широкие и совсем «лысые»

Известно, что автомобильные гонки
проходят на лысой резине или шинах с несколькими
очень неглубокими канавками. Канавки в шинах
гоночных машин не нужны, т.к. они увеличивают
сцепление с дорогой только тогда, когда она
мокрая. А при мокрой дороге гонки отменяют.

Для производства шин гоночных
автомобилей используется специальная липкая
резина. Поэтому сила трения этих шин на сухой
дороге растёт с увеличением площади контакта,
таким образом вступая в противоречие с
классическим законом, справедливым для трения
твёрдых и неэластичных поверхностей. Чтобы
обеспечить максимальную силу трения, шины колёс
гоночных автомобилей делают очень широкими (до
0,38 м), что также позволяет лучше рассеивать
тепло, образующееся при трении о дорожное
покрытие.

Чистая резина прилипает к дороге
лучше, чем грязная. Поэтому перед самым стартом
покрышки с помощью специальных устройств и
процедур нагревают до 80°С, очищая их поверхность,
обеспечивая хорошее прилипание к дорожному
покрытию. Кстати, шины гоночных автомобилей
иногда надувают азотом, т.к. влага, содержащаяся в
обычном воздухе, при нагревании шин испаряется и
увеличивает давление в колёсах, что создаёт
дополнительные трудности в управлении.

О чём поют колёса? Шум, издаваемый
колёсами автомобилей, – одна из основных проблем
больших городов. Огромные средства тратятся
ежегодно на борьбу с этим шумом, т.к. стоимость
одного километра звукопоглощающего барьера,
устанавливаемого вдоль шоссе, близка к миллиону
долларов. Есть несколько теорий возникновения
этого шума. В одной из них считается, что он
возникает из-за колебаний деформированных
участков внешней части покрышки, после того как
они распрямляются. Другая связывает появление
шума с отлипанием резины от дороги. Ну а самая
романтичная гипотеза объясняет шум тем, что
причиной всему воздух, двигающийся по канавкам
автомобильных покрышек, как по трубам органа, и
поэтому поющий.

Классики не всегда правы. Уже в XIX в.
стало ясно, что закон Амонтона–Кулона не даёт
правильного описания силы трения, а коэффициенты
трения отнюдь не являются универсальными
характеристиками. Прежде всего было отмечено,
что коэффициенты трения зависят не только от
того, какие материалы контактируют, но и от того,
насколько гладко обработаны контактирующие
поверхности. Выяснилось, например, что сила
трения в вакууме всегда больше, чем при
нормальных условиях.

Как отмечает лауреат Нобелевской
премии по физике (1965) Р.Фейнман в своих лекциях,
«…таблицы, в которых перечислены коэффициенты
трения “стали по стали, меди по меди” и прочее,
всё это сплошное надувательство, ибо в них этими
мелочами пренебрегают, а ведь они-то и определяют
значение .
Трение “меди о медь” и т.д. – это на самом деле
трение “о загрязнения, приставшие к меди”».

Можно, конечно, пойти по другому пути и,
изучая трение «меди по меди», измерять силы при
движении идеально отполированных и
дегазированных поверхностей в вакууме. Но тогда
два таких куска меди просто слипнутся, и
коэффициент трения покоя начнёт расти со
временем, прошедшим с начала контакта
поверхностей. По тем же причинам коэффициент
трения скольжения будет зависеть от скорости
(расти с её уменьшением). Значит, точно определить
силу трения для чистых металлов тоже невозможно.

Тем не менее для сухих стандартных
поверхностей классический закон трения почти
точен, хотя причина такого вида закона до самого
последнего времени оставалась непонятной. Ведь
теоретически оценить коэффициент трения между
двумя поверхностями никто так и не смог.

Как атомы трутся друг о друга? –
спрашиваем у учёных. Сложность изучения трения
заключается в том, что место, где этот процесс
происходит, скрыт от исследователя со всех
сторон. Несмотря на это, учёные уже давно пришли к
заключению, что сила трения связана с тем, что на
микроскопическом уровне (т.е. если посмотреть в
микроскоп) соприкасающиеся поверхности очень
шероховатые, даже если они отполированы. Поэтому
скольжение двух поверхностей друг по другу может
напоминать фантастический случай, когда
перевёрнутые Кавказские горы трутся, например, о
Гималаи.

Прежде думали, что механизм трения
несложен: поверхность покрыта неровностями, и
трение есть результат следующих друг за другом
циклов «подъём–спуск» скользящих частей. Но это
неправильно, ведь тогда не было бы потерь
энергии, а при трении расходуется энергия.
Поэтому более правильной можно считать
следующую модель трения. При скольжении трущихся
поверхностей микронеровности задевают друг за
друга, и в точках соприкосновения противостоящие
друг другу атомы сцепляются. При дальнейшем
относительном движении тел эти сцепки рвутся, и
возникают колебания атомов, подобные тем, какие
происходят при отпускании растянутой пружины. Со
временем эти колебания затухают, а их энергия
превращается в тепло, растекающееся по обоим
телам. В случае скольжения мягких тел возможно
также разрушение микронеровностей, так
называемое «пропахивание», в этом случае
механическая энергия расходуется на разрушение
атомарных связей.

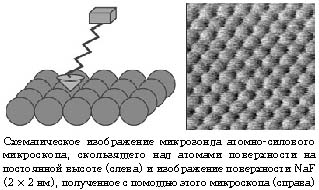
Таким образом, если мы хотим изучать
трение, нам надо ухитриться двигать песчинку,
состоящую из несколько атомов, вдоль поверхности
на очень маленьком расстоянии от неё, измеряя при
этом силы, действующие на эту песчинку со стороны
поверхности. Это стало возможным после
изобретения атомно-силового микроскопа (АСМ)
Г.Биннингом и Г.Рорером, которым в 1986 г. была
присуждена Нобелевская премия по физике.
Создание такого микроскопа, способного
чувствовать силы притяжения и отталкивания
между отдельными атомами, дало возможность
наконец «пощупать», что такое силы трения, открыв
новую область науки о трении – нанотрибологию.

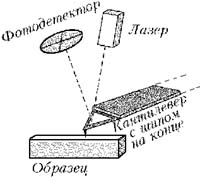Основой АСМ служит микрозонд, обычно
сделанный из кремния и представляющий собой
тонкую пластинку-консоль (её называют
кантилевером, от англ. cantilever – консоль, балка). На
конце кантилевера (длина 500 мкм, ширина 50 мкм,
толщина 1 мкм) делается очень острый шип (высота 10
мкм, радиус закругления 1–10 нм), оканчивающийся
группой из одного или нескольких атомов. При
перемещении микрозонда вдоль поверхности
образца остриё шипа приподнимается и опускается,
очерчивая микрорельеф поверхности, подобно
скользящей по грампластинке игле. На выступающем
конце кантилевера (над шипом) расположена
зеркальная площадка, на которую падает и от
которой отражается луч лазера. Когда шип
опускается и поднимается на неровностях
поверхности, отражённый луч отклоняется, и это
отклонение регистрируется фотодетектором.
Данные фотодетектора используются в системе
обратной связи, которая может обеспечивать либо
постоянное удаление шипа от поверхности образца,
либо постоянную силу давления острия на образец.

В первом случае пьезоэлектрический
преобразователь может регистрировать движение
кантилевера, прыгающего от одного атома
исследуемой поверхности к другому, строя таким
образом объёмный рельеф поверхности образца в
режиме реального времени. Разрешающая
способность таких микроскопов составляет
примерно 0,1–1 нм по горизонтали и 0,01 нм по
вертикали. Смещая зонд по горизонтали, можно
получить серию рельефов и с помощью компьютера
построить трёхмерное изображение.

С помощью АСМ с начала 1990-х гг.
проводятся систематические исследования силы
трения микрозондов при их скольжения вдоль
различных поверхностей и зависимости этих сил от
силы прижатия. Оказалось, что для обычно
используемых зондов, сделанных из кремния,
микроскопическая сила трения скольжения
составляет около 60–80% от прижимающей силы,
которая составляет не более 10 нН. Как и следовало
ожидать, сила трения скольжения растёт с
размером микрозонда, т.к. количество атомов,
одновременно его притягивающих, увеличивается.
Таким образом, сила трения скольжения микрозонда
зависит от площади его контакта с поверхностью,
что противоречит классическому закону трения.
Оказалось также, что сила трения скольжения не
становится нулевой при отсутствии силы,
прижимающей микрозонд к поверхности. Да это и
понятно, т.к. окружающие микрозонд атомы
поверхности так близко к нему расположены, что
притягивают его даже в отсутствие внешней силы
сжатия. Поэтому и основное предположение
классического закона – о прямой
пропорциональной зависимости силы трения от
силы сжатия – тоже не соблюдается в
нанотрибологии.

Однако все эти расхождения между
основным законом и данными нанотрибологии,
полученными с помощью АСМ, легко устраняются. При
увеличении силы, прижимающей скользящее тело,
увеличивается количество микроконтактов, а
значит, увеличивается и суммарная сила трения
скольжения. Поэтому никаких противоречий между
только что полученными данными и старым законом
нет.

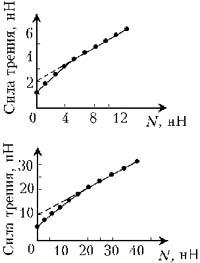
Зависимость силы трения скольжения
микрозонда от внешней силы N, прижимающей его к
графитовой поверхности. Радиус кривизны зонда 17
нм (вверху) и 58 нм (внизу). При малых N
зависимость нелинейная, а при больших
приближается к линейной (пунктир). Данные взяты
из статьи Х.Холшера и А.Шварца (2002)

Долгое время было принято считать, что,
принуждая одно тело скользить по другому, мы
ломаем малые неоднородности одного тела, которые
цепляются за неоднородности поверхности
другого, и для того, чтобы ломать эти
неоднородности, и нужна сила трения. Поэтому
старые представления часто связывают силу
возникновение силы трения с повреждением
микровыступов трущихся поверхностей, их так
называемым износом. Нанотрибологические
исследования с помощью АСМ и других современных
методик показали, что сила трения между
поверхностями может существовать даже тогда,
когда они не повреждаются. Причиной такой силы
трения служат постоянно возникающие и рвущиеся
адгезионные связи между трущимися атомами.

Почему лёд скользкий? Узнать, почему
можно скользить по льду, удалось учёным только
сейчас. А началось всё давным-давно, в 1849 г. Братья
Джеймс и Вильям Томсоны (последнему впоследствии
за большие заслуги было присвоен титул лорда
Кельвина) выдвинули гипотезу, согласно которой
лёд под нами плавится оттого, что мы на него
давим. И поэтому мы скользим уже не по льду, а по
образовавшейся плёнке воды на его поверхности.

Действительно, если увеличить
давление, то температура плавления льда
понизится. Происходит это вот почему. Известно,
что плотность льда меньше плотности воды, и
поэтому, когда лёд сжимают, он, «пытаясь»
уменьшить деформацию, вызванную ростом давления,
«понижает» температуру плавления. Это одно из
проявления так называемого принципа Ле Шателье:
внешнее воздействие, выводящее систему из
термодинамического равновесия, вызывает в ней
процессы, стремящиеся ослабить результаты этого
воздействия. Расчёты и эксперименты показали,
что для того, чтобы понизить температуру
плавления льда на один градус, необходимо
давление увеличить до 121 атм (1,22 МПа). Попробуем
посчитать, какое давление оказывает спортсмен на
лёд, когда скользит по нему на одном коньке
длиной 20 см и толщиной 0,3 см. Если считать, что
масса спортсмена 75 кг, то его давление на лёд
составит около 12 атм. Таким образом, стоя на
коньках, мы едва ли сможем понизить температуру
плавления льда больше, чем на 1 °С. Значит,
объяснить скольжение по льду в коньках и тем
более в обычной обуви, опираясь на принцип Ле
Шателье, невозможно, если за окном, например, –10
°С.

В 1939 г., когда стало ясно, что
понижением температуры плавления скользкость
льда не объяснить, Ф.Бауден и Т.Хьюз предположили,
что тепло, необходимое для плавления льда под
коньком, даёт сила трения. Однако эта теория не
могла объяснить, почему так тяжело бывает даже
стоять на льду, не двигаясь. С начала 1950-х гг.
учёные стали считать, что лёд скользкий из-за
тонкой плёнки воды, образующейся на его
поверхности в силу каких-то неизвестных причин.
Только в конце 1990-х гг. изучение того, как
рассеивает лёд рентгеновские лучи,
действительно показало, что его поверхность не
является упорядоченной кристаллической
структурой, а скорее похожа на жидкость.

Учёные объяснили это тем, что
расположенные на поверхности льда молекулы воды
находятся в особых условиях. Силы, заставляющие
их находиться в узлах гексагональной решётки,
действуют на них только снизу. Поэтому
поверхностным молекулам ничего не стоит
«уклониться от советов» молекул, находящихся в
решётке, и если это происходит, то к такому же
решению приходят сразу несколько поверхностных
слоёв молекул воды. В результате на поверхности
льда образуется плёнка жидкости, служащая
хорошей смазкой при скольжении.

Кстати, тонкие плёнки жидкости
образуются не только на поверхности льда, но и
многих других кристаллов. Толщина жидкой плёнки
увеличивается с ростом температуры, т.к. более
высокая тепловая энергия молекул вырывает из
гексагональных решёток больше поверхностных
слоёв. Наличие примесей (молекул, отличных от
воды) тоже мешает поверхностным слоям
образовывать кристаллические решётки. Поэтому
увеличить толщину жидкой плёнки можно, растворив
в ней какие-либо примеси, например, обычную соль.
Этим и пользуются коммунальные службы, когда
борются зимой с обледенением дорог и тротуаров.

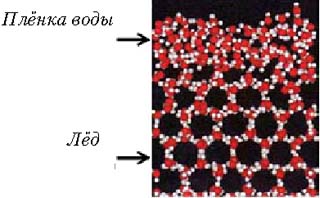
Схематическое изображение поперечного среза
льда. Беспорядочное расположение молекул воды на
поверхности соответствует плёнке жидкости, а
гексагональная структура в толще –
кристаллическому льду. Серые кружки – атомы
кислорода, белые – водорода

Трение качения – это совсем другое. В
идеальном случае, когда колесо, сделанное из
несжимаемого материала, по инерции катится по
гладкой недеформируемой поверхности, никакие
силы трения на это колесо не действуют. Колесо,
касаясь поверхности в одной точке, вращается
вокруг этой точки, потом точкой касания и центром
вращения становится другая точка и т.д. Так как
точка касания не движется относительно
поверхности, то и сила трения скольжения
отсутствует.

Однако в реальных условиях дорожное
покрытие, и материал, из которого сделан диск
колеса, не являются абсолютно жёсткими.
Рассмотрим сначала первый случай. Если поставить
колесо на мягкую поверхность, надавить сверху с
силой P и пытаться, вращая его, продвинуть вперёд
со скоростью v, то мы столкнёмся с силой
сопротивления качению Fк. Колесо деформирует
поверхность под собой так, что впереди
появляется бугорок, который всё время приходится
преодолевать. Горизонтальная составляющая сил
реакции этого бугорка и представляет собой силу
трения качения Fк. Вертикальные составляющие сил
сопротивления бугорка компенсируются силой
тяжести автомобиля. Так как высота бугорка
пропорциональна весу колеса (или укреплённого на
нём автомобиля), то и сила трения качения Fк тоже
пропорциональна весу автомобиля и силе реакции
со стороны дороги N : Fк = кN.

Качение несжимаемого колеса радиуса R
по несжимаемой поверхности. K – точка касания и
мгновенный центр вращения колеса с угловой
скоростью ,
результатом которого является движение центра
колеса О со скоростью

При качении мягкого колеса по твёрдой
дороге на переднюю часть соприкасающейся с
дорогой поверхности колеса всё время «наезжают».
Поэтому она сжимается больше, чем задняя, и сила
реакции от передней части колеса, направленная
противоположно движению, тоже больше. Сила
трения качения равна разности горизонтальных
составляющих сил реакции от передней и задней
частей колеса. Так как сжатие колеса
пропорционально весу машины (или силе реакции
опоры), то Fк = кN.

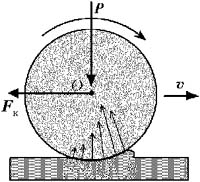
Возникновение силы трения при качении
твёрдого колеса по мягкой дороге

Силы трения качения определяются
жёсткостью материалов колеса и дорожного
покрытия. Чем больше жёсткость, тем меньше
величина трения качения. Поэтому, чтобы
сократить расходы на топливо, необходимо как
можно сильнее накачивать автомобильные колеса,
делая их более жёсткими. Достаточно пощупать
колёса грузовика, чтобы убедиться в этом. У
пассажирского автомобиля давление в колёсах
гораздо меньше, т.к. с жёсткими колёсами
пассажиры будут ощущать все неровности дороги. В
результате его шины больше деформируются, и
соответственно растёт сила трения качения.

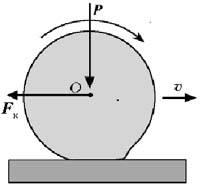
Возникновение силы трения при качении
мягкого колеса по жёсткой дороге. При качении
мягкого колеса деформация его передних участков
больше, что приводит к появлению горизонтальной
составляющей силы, действующей со стороны
дороги, и силы, тормозящей движение, – силы
трения качения

Сила, необходимая для преодоления
трения качения, пропорциональна весу автомобиля
и, вообще говоря, не зависит от скорости его
движения. Чтобы измерить эту силу, поместите
машину на горизонтальный участок дороги,
поставьте рычаг переключения скоростей в
нейтральное положение (отсоедините колёса от
двигателя) и выключите зажигание. После этого
привяжите к автомобилю трос, а к нему – пружинные
весы. Прикладывая к тросу силу, постарайтесь
сдвинуть машину с места и равномерно тянуть её.
Одновременно с этим ваш помощник должен смотреть
на показания весов и записывать их. Если нет
пружинных весов, можно использовать бытовые весы
для взвешивания человека. Такими весами можно
толкать машину, используя их в качестве
прокладки. Сила трения качения для автомобиля
массой 1000 кг в среднем составляет около 100 Н.

Для очень дальних перевозок построили железные
дороги, где железное колесо катится по железному
рельсу с очень малым коэффициентом трения
качения. Тормозят поезда медленно, но
эксплуатация их очень выгодна.

Приводим 2 варианта нахождения коэффициента трения — зная силу трения и массу тела или зная угол наклона. Для обоих вариантов вы найдете удобные калькуляторы и формулы для расчета.

Следует помнить, что коэффициент трения (μ) величина безразмерная, то есть не имеет единицы измерения.

Коэффициент трения зависит от качества обработки трущихся поверхностей, скорости движения тел относительно друг друга и материала соприкасающихся поверхностей. В большинстве случаев коэффициент трения находится в пределах от 0,1 до 0,5 (см. таблицу).

Через силу трения и массу

Формула для нахождения коэффициента трения по силе трения и массе тела:

<mu= dfrac<тр>>> , где μ — коэффициент трения, F_тр — сила трения, m — масса тела, g — ускорение свободного падения.

Через угол наклона

Формула для нахождения коэффициента трения по углу наклона поверхности:

<mu = tg(alpha)>, где μ — коэффициент трения, α — угол наклона поверхности скольжения.

Одной из наиболее интересных тем школьной программы по физике является «сила трения». Она достаточно доступна в понимании учащихся и быстро поддается осмыслению, так как её наличие можно проверить, не отходя от парты.

Стоит начать с определения самого понятия. Сила трения — есть итог сопротивления движению физических тел. Иными словами, она появляется, когда происходит относительное перемещение между взаимодействующими телами.

Различают по его области:

• Внешнее — зарождается при непосредственном движении действующих друг на друга тел,
• Внутреннее — возникает между частями одного предмета.

Основная формула силы трения

Ввиду отсутствия в природе абсолютно твердых тел сила трения существует постоянно, и его наличие разъясняют действием даже микроскопически шероховатых поверхностей между собой. Результат при умножении силы реакции опоры на коэффициент трения есть:

В СИ (международная система единиц) измеряется F тр. в Ньютонах (Н).

Нужно знать, что противоположно ходу движения направлена F тр., а N против силы тяжести и перпендикулярно поверхности. Безразмерная величина k не зависит от площади соприкасания тел, а зависит от степени шероховатости и типа материалов трущихся тел.

Необходимо иметь полное представление о физических величинах, участвующих в основной формуле. В первую очередь, F тр. это векторная величина, то есть она имеет направление. Следовательно, нужно знать направление и точку ее приложения. Приложена она в области соприкосновения поверхностей, а направлена против движения объекта.

Из названия нормальной реакции опоры понятно, что она показывает реакцию самой опоры, а возникает на молекулярном уровне. Направлена против силы, с которой предмет давит на поверхность.

Коэффициент пропорциональности k является связующим звеном между F тр. и силой нормальной реакции. Если k соответствует наибольшей F тр. пок., то в большинстве своих случаев он больше коэффициента скольжения.

Коротко о типах трения

Отличают такие разновидности, как:

Прилагая минимум F тр. пок., объект начнет свое движение. Она не определяется достаточно точно и зависит от приложенного усилия. Поразительно, но именно оно разгоняет тела. F тр. пок. не исчезает бесследно, после того, как привела в движение предмет, она превращается в F тр. , а, следовательно, не может бесконечно увеличиваться — есть верхний максимальный предел, равный по величине F тр. скольжения.

В названии «сила трения качения» скрыта суть самого явления. Она намного меньше трения скольжения и возникает во время качения одного тела по-другому, скорости их соприкосновения в точках касания одинаковы по направлению и значению.

Типы трения скольжения различают по физике взаимодействия:

1. Вязкое. Появляется, когда взаимодействующие тела разделены между собой слоем жидкости, газа или иного смазочного материала различного размера. F тр. пок. отсутствует. Абсолютная величина этой силы сопротивления зависит от скорости: прямо пропорциональна скорости при малых скоростях движение и прямо пропорциональна ее квадрату при больших.
2. Сухое. Дополнительным смазочным материалом соприкасающиеся тела не разделены. Может возникать даже при отсутствии относительного движения предметов. Особый пример — F тр. покоя . Существует вид сухого взаимодействия с сухой смазкой, как пример, со слоем графитового порошка.
3. Граничное. Одновременное содержание и слоев, и частей отличных по природе.
4. Смешанное. Имеются участки частичной смазки.

Формула выглядит следующим образом:

Использовались такие физические величины, как, μ — коэффициент трения скольжения, N — сила реакции опоры.

Также можно вывести формулу через массу:

где N = mg, g — свободного падения.

Формула коэффициента пропорциональности μ

В формуле, описывающей процесс приложения F тр. к любому телу, принимает участие коэффициент пропорциональности. Он выражается исключительно числами и почти при любых обстоятельствах меньше единицы. Это величина, зависящая от материала взаимодействующих объектов и от степени обработки их поверхностей.

Данную формулу можно вывести через массу и ускорение свободного падения:

μ =Fmg, где замена N происходит ранее описанным способом.

Трение повинуется третьему закону Ньютона, так как является разновидностью взаимодействия. А конкретно, если F тр. действует на один из объектов, то такая же в точности сила по модулю, но устремленная противоположно оказывает воздействие и на второе тело. Все силы противодействия возникают как результат молекулярного и атомного взаимодействия трущихся тел.

В заключение приведены слова Шарля Гийом (1861−1938): «Вообразим, что трение может быть устранено совершенно. Тогда никакие тела, будь они величиною с каменную глыбу или малы, как песчинка, никогда не удержатся одно на другом: все будет скользить и катиться, пока не окажется на одном уровне. Не будь трения, Земля представляла бы шар без неровностей, подобно жидкому».

Видео

Это видео поможет вам понять, что такое сила трения.

Ответ или решение 1

Силу трения тела можно рассчитать по формуле:

Fтр. = μ * N, где Fтр. — действующая сила трения ( Fтр. = 100 Н ), μ — коэффициент трения ( μ = 0,2 ), N — сила реакции опоры ( для горизонтальной поверхности N = Fт = m * g, где m — масса тела ( m = 10 кг ), g — ускорение свободного падения ( принимаем g = 10 м/с² ) ).

Выразим и вычислим коэффициент трения:

Fтр. = μ * N = μ * Fт = μ * m * g.

μ = Fтр. / ( m * g ) = 100 / ( 10 * 10 ) = 1.