{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
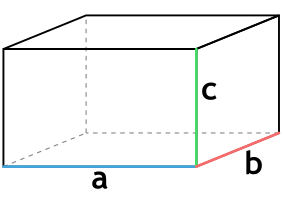
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
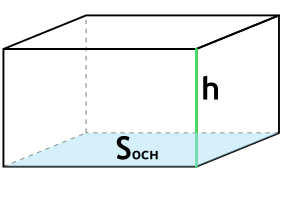
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
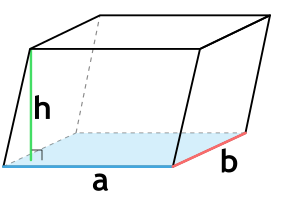
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
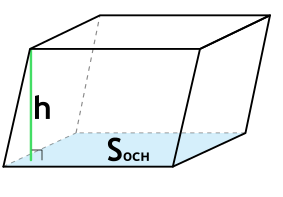
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер “a”, “b”, “c” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
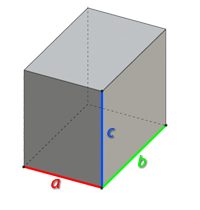
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку “Рассчитать”
Округлить результат до
знаков после запятой
Рассчитать
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.
Введите а — длину прямоугольника в мм (миллиметрах):
Введите b — ширину прямоугольника в мм (миллиметрах):
Введите h — толщину прямоугольника в мм (миллиметрах):
Как рассчитать объем прямоугольника?
Если прямоугольник имеет толщину, то фактически это параллелепипед. Объем параллелепипед в общем случае рассчитывается по формуле:
V = a x b х h
V — объем параллелепипеда . Объем прямоугольника имеющего толщину (высоту).
a — длина прямоугольника основания параллелепипеда
b — ширина прямоугольника основания параллелепипеда
h — высота параллелепипеда. Толщина прямоугольника.
Объем в миллиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vмм3 = aмм х bмм х hмм
Vмм3 — объем в миллиметрах кубических (мм3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в сантиметрах кубических прямоугольника имеющего толщину (параллелепипед):
Vсм3 = aмм х bмм х hмм / 1 000
Vсм3 — объем в сантиметрах кубических (см3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в метрах кубических прямоугольника имеющего толщину (параллелепипед):
Vм3 = aмм х bмм х hмм / 1 000 000 000
Vм3 — объем в метрах кубических (м3).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Объем в литрах прямоугольника имеющего толщину (параллелепипед):
Vл = aмм х bмм х hмм / 1 000 000
Vл — объем в литрах (л).
aмм — длина прямоугольника в миллиметрах (мм).
bмм — ширина прямоугольника в миллиметрах (мм).
hмм — толщина прямоугольника в миллиметрах (мм).
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
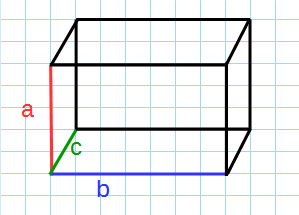
Формула объема параллелепипеда через его ребра:
a,b,c – ребра параллелепипеда.
Через стороны и высоту
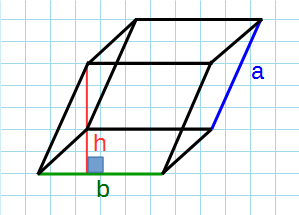
Формула объема параллелепипеда:
a,b – ребра параллелепипеда; h – высота параллелепипеда.
Сегодня Бим, Бом и ребята изучают объем геометрических фигур, геометрическую фигуру — прямоугольный параллелепипед, а также как найти объем прямоугольного параллелепипеда, и какие существуют единицы измерения объема.
Содержание статьи:
Объем геометрических фигур
Определение. Объем — это сколько места занимает фигура в пространстве.
Сегодня в цирке выходной. Бом прогуливает своих питомцев в парке, Бим помогает Бому.
— Вот я перед прогулкой зашел в магазин “Товары для животных” и купил специальные конфеты для твоих обезьянок, — обрадовал друга Бим. — Посмотри в какой объемной упаковке конфеты! Здесь можно измерить и длину, и ширину, и высоту коробки. А ведь раньше мы измеряли только длину и ширину донышка коробки.
— А ну-ка дай посмотреть! — попросил Бом. — Какая интересная коробка! Смотри, ее можно раскрыть с разных сторон.
— Ну да, — ответил Бим. — Ты только осторожнее, старайся открыть так, чтобы конфеты можно было вынуть только сверху. А то вдруг они разлетятся по всему парку! Попробуй тогда найди их все, да еще ведь и непонятно, сколько их там!
— Да, раньше мы рассматривали только плоские фигуры, — задумался Бом. — А у этой коробки могут быть три разных донышка, смотря с какой стороны ее открывать. И что же тогда в ней донышком называть? И как считать, сколько конфет в нее может поместиться? Вот если у донышка есть длина и ширина, но коробочка еще и высокая, то получается, что у нее и высота есть?
— Смотри, вон гуляют Коля, Вася и Оля! Может они нам объяснят?
Ребята тоже увидали Бима и Бома, да еще и с обезьянками. Как тут не подойти! Все радостно поздоровались друг с другом.
— Ой, какие обезьянки! — закричали дети.
Оля достала из сумочки банан:
— Можно угостить обезьянок? — спросила девочка.
— Конечно можно, — ответил Бом.
— Ой, у тебя, Оля, сумочка похожа на вот эту коробочку, у нее есть донышко, но она высокая. Значит, у сумочки тоже есть длина, ширина и высота. — удивился Бим. — Как же такие фигуры называются?
— Такие фигуры называются объемными, — ответил Вася. — Мы видим предметы вокруг нас: деревья, людей, машины, сумки, животных и еще очень много других предметов и у всех у них есть длина, ширина и высота.
— Люди договорились между собой, что такие предметы называются объемными, — добавил Коля, — и ввели понятие объема, то есть, сколько места занимает фигура в пространстве. Также решили, как измерять объем, — и ввели единицы измерения объема.
Объем прямоугольного параллелепипеда
Прямоугольный параллелепипед
Определение. Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
Объяснение продолжила Оля:
— Проще всего вычислить объем прямоугольного параллелепипеда. Прямоугольный параллелепипед — это геометрическая фигура, у которой внизу и вверху два одинаковых прямоугольника, соответствующие вершины прямоугольников соединяются отрезками. Эти отрезки перпендикулярны сторонам прямоугольников в верхнем и нижнем основаниях. Таких точек 8: 4 снизу и 4 сверху. В каждой такой точке получается 3 прямых угла и 3 отрезка.
Вот, посмотрите: на коробке тоже всего таких точек 8, из них 4 снизу на донышке и 4 сверху на крышечке. Эти 8 точек называют вершинами параллелепипеда. 12 линий (4 вверху, 4 внизу и 4 по бокам), которые соединяют вершины параллелепипеда называют ребрами, ребра образуют 6 прямоугольников (2 основания — донышко и крышечка, и 4 боковые стороны), которые называются гранями параллелепипеда.
Находим объем прямоугольного параллелепипеда
Правило. Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
Дальше объяснял Вася:
— Для того чтобы вычислить объем прямоугольного параллелепипеда, надо измерить длину двух прилегающих сторон прямоугольников (a, b) в основании и измерить длину ребра соединяющего нижнее и верхнее основания — это высота параллелепипеда (h). И потом перемножить длину этих сторон.
V = a × b × h (куб. ед. дл.).
— Давайте измерим объем вашей коробки и объем Олиной сумки, — предложил Коля.
Мальчик достал из портфеля угольник и начал прикладывать его по очереди к каждому углу коробки:
— Видно, что все углы прямые, — сделал вывод Коля. — Значит у нас прямоугольный параллелепипед. Длина и ширина сторон основания 5 см и 4 см:
a = 5 см, b = 4 см.
Высота параллелепипеда, то есть, длина отрезка, соединяющего верхнее и нижнее основания, — равна 6 см:
h = 6 см.
Значит, объем параллелепипеда равен
V = a × b × h, V = 5 × 4 × 6 = 120 (куб. см).
— Теперь измерим объем моей сумки-портфеля, — продолжила Оля. — Смотрим: все углы прямые, значит — можем воспользоваться формулой для объема прямоугольного параллелепипеда. Здесь у нас:
длина 30 см = 3 дм, ширина 20 см = 2 дм, высота 40 см = 4 дм.
Объем равен
V = 3 × 2 × 4 = 24 куб. дм.
Единицы измерения объема.
Единицами измерения объема являются:
1 куб. мм, 1 куб. см, 1 куб. дм, 1 куб. м, 1 куб. км,1 л.
— А в каких еще единицах измеряют объем? — поинтересовался Бим.
— Кроме кубических сантиметров и кубических дециметров, объем измеряют еще в кубических метрах, кубических миллиметрах, кубических километрах и в литрах, — ответил Вася. — Один литр равен объему куба (прямоугольный параллелепипед, у которого все стороны одинаковые) со стороной в 1 дм.
1 л = 1 куб. дм.
Кстати, Оля! Получается, что объем твоей сумки равен 24 л.
— При вычислении объема все три измерения — длина, ширина и высота, — должны быть записаны в одинаковых единицах измерения длины: или в миллиметрах, или в сантиметрах, или в дециметрах, или в метрах, или в километрах, — заметил Коля. Затем применяют формулу вычисления объема прямоугольного параллелепипеда:
V = a × b × h (куб. ед. дл.).
Если надо, то числа раздробляют, а уже после вычисления объем укрупняют. Есть специальные таблицы для перевода одних единиц измерения объема в другие единицы измерения объема.
Таблицы перевода единиц измерения объема
1 куб. см = 1000 куб. мм
1 куб. дм = 1000 куб. см
1 куб. дм = 1000 000 куб. мм
1 куб. дм = 1л
1 куб. м = 1000 000 000 куб. мм
1 куб. м = 1000 000 куб. см
1 куб. м = 1000 куб. дм
1 куб. м = 1000 л
1 куб. км = 1018 куб. мм
1 куб. км = 1015 куб. см
1 куб. км = 1012 куб. дм
1 куб. км = 109 куб. м
— Давайте теперь запишем для ребят вопросы, — подытожил Бом:
- Что такое объем?
- Что такое прямоугольный параллелепипед?
- Как найти объем прямоугольного параллелепипеда?
- Единицы измерения объема — это?
И ответы:
- Объем — это количество места, которое занимает фигура в пространстве.
- Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
- Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
- Единицы измерения объема — это:
1 куб. мм, 1 куб.см, 1 куб.дм, 1 куб. м , 1 куб.км,1 л.
Заключение
— Бим, пойдем отведем обезьянок в цирк, — поглядел на часы Бом. — Им пора обедать. Спасибо, ребята! Вы нам с Бимом помогли разобраться, что такое объем, что такое прямоугольный параллелепипед, найти объем прямоугольного параллелепипеда, узнать единицы измерения объема. До встречи в цирке!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются!)))