Рассмотрим
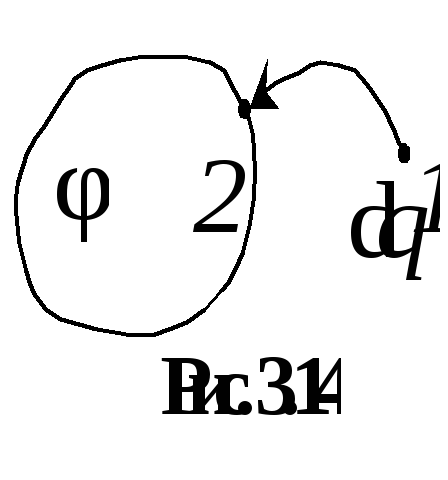
процесс зарядки уединенного проводника.
Чтобы его заряд достиг величины Q,
будем сообщать проводнику заряд порциями
dq,
перенося их из бесконечно удаленной
точки 1
на поверхность проводника в точку 2
(рис. 3.14). Для передачи проводнику новой
порции заряда
![]() внешние силы должны совершить работу
внешние силы должны совершить работу
против сил электрическогополя
:
![]() .
.
Поскольку проводник уединенный (точка1
бесконечно далека от проводника), то
![]() .
.
Потенциал точки2
равен потенциалу проводника .
Поэтому
![]() .
.
Если проводнику передан зарядq,
то его потенциал
![]() .
.
Полная работа внешних сил по зарядке
проводника до значения зарядаQ
будет равна
![]() .
.
Согласно
закону сохранения энергии, работа
внешних сил по зарядке проводника
увеличивает энергию создаваемого
электростатического поля, т.е. проводник
запасает определенную энергию:
![]() .
.
(3.13)
Рассмотрим
процесс зарядки конденсатора от источника
ЭДС. Источник в процессе зарядки переносит
заряды с одной пластины на другую, причем
сторонние силы источника совершают
работу по увеличению энергии конденсатора:
![]() ,
,
где
Q
– заряд конденсатора после зарядки.
Тогда энергия электрического поля,
созданного конденсатором, определится
как
![]() .
.
(3.14)
Выражение
(3.14) позволяет записать величину энергии
электростатического поля двумя способами:
![]() и
и
![]() .
.
Сопоставление
двух соотношений позволяет задать
вопрос: что является носителем
электрической энергии? Заряды (первая
формула) или поле (вторая формула)? Оба
записанных равенства прекрасно
согласуются с результатами экспериментов,
т.е. расчет энергии поля можно одинаково
правильно вести по обеим формулам.
Однако такое наблюдается только в
электростатике, т.е. когда осуществляется
расчет энергии поля неподвижных зарядов.
При рассмотрении теории электромагнитного
поля в дальнейшем (гл. 8) мы увидим, что
электрическое поле может создаваться
не только неподвижными зарядами.
Электростатическое поле – это частный
случай электромагнитного поля,
существующего в пространстве в виде
электромагнитной волны. Его энергия
распределена в пространстве с определенной
плотностью. Введем понятие объемной
плотности энергии поля
следующим образом.
Преобразуем
последнее равенство (3.14) для случая
плоского конденсатора, воспользовавшись
связью разности потенциалов и напряженности
однородного поля:
![]() ,
,
где
![]() – объем конденсатора, т.е. объем части
– объем конденсатора, т.е. объем части
пространства, в котором создано
электрическое поле.
Объемной
плотностью энергии поля
называется отношение энергии поля,
заключенного в малом объеме пространства
к этому объему:
![]() .
.
(3.15)
Следовательно,
энергию однородного электрического
поля можно рассчитать так:
![]() .
.
Сделанный
вывод можно распространить на случай
неоднородного поля таким образом:
![]() ,
,
(3.16)
где![]() – такой элементарный объем пространства,
– такой элементарный объем пространства,
в пределах которого поле можно считать
однородным.
Для
примера рассчитаем энергию электрического
поля, созданного уединенным металлическим
шаром радиусом R,
заряженным зарядом Q,
и находящимся в среде с относительной
диэлектрической проницаемостью .
Повторив рассуждения примера из п.2.5,
получим модуль напряженности поля в
виде функции
![]() :
:

Тогда
выражение для объемной плотности энергии
поля примет вид:


Поскольку
напряженность поля зависит только от
радиальной координаты, то она будет
практически постоянна в пределах тонкого
сферического слоя с внутренним радиусом
r
и толщиной
![]() (рис.
(рис.
3.15). Объем этого слоя![]() .
.
Тогда энергия поля определится так:
![]() .
.
Аналогичный
результат мы бы получили, если бы
вычисляли энергию заряженного шара по
формуле (3.13), воспользовавшись (3.6):
![]() .
.
Однако
следует помнить, что такой способ
неприменим, если необходимо найти
энергию электрического поля, заключенную
не во всем объеме поля, а лишь в его
части. Также метод расчета по формуле
(3.13) нельзя использовать при определении
энергии поля системы, для которой
неприменимо понятие “емкость”.
Соседние файлы в папке Шпоргалки
- #
- #
- #
- #
- #
- #
Объемная плотность энергии магнитного и электрического полей
Содержание:
- Электрическое поле и его свойства
- Плотность энергии электрического и магнитного полей
- Формула объемной плотности энергии
- Единицы измерения плотности энергии
Электрическое поле и его свойства
Заряженные тела окружены особой средой, которая представляет собой электрическое поле. С его помощью осуществляется электрическое взаимодействие.
Электрическое поле — физическое поле, окружающее любой электрический заряд и оказывающее силовое воздействие на другие заряды, отталкивая или притягивая их.
Причинами возникновения электрического поля служат:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- электрические заряды;
- магнитные поля, которые изменяются с течением времени.
Электрические и магнитные поля принято рассматривать в качестве проявления обобщенного электромагнитного поля. Данное понятие связано с проявлением какого-либо из четырех фундаментальных взаимодействий природного характера.
Изучение и применение свойств электрических полей имеет большое значение в развитии физики как науки. На основе электрических полей разрабатывают электротехническое оборудование. С точки зрения атомной физики и химии, электрическое поле является силой удержания атомного ядра и электронов в атомах.
За счет данной силы формируются химические связи между атомами, что приводит к образованию молекул. Путем практического применения электрических полей удается обнаружить движения с помощью емкостных методик. Явление активно используют в диагностике и терапии в медицинской сфере.
У электрического поля есть математическое определение, согласно которому оно представляет собой векторное поле, связывающее с любой точкой в пространстве силу (электростатическую или кулоновскую) на единицу заряда, приложенную к бесконечно малому положительному пробному заряду, покоящемуся в этой точке.
В системе СИ единица измерения электрического поля: Вольт на метр (В/м), что в точности эквивалентно Ньютону на Кулон (Н/Кл).
Электрическое поле обладает следующими свойствами:
- Существует вне зависимости от сознания наблюдателей, то есть является материальным.
- Находится в области, окружающей заряды. Обнаружить электрическое поле можно, действуя на тестовый заряд.
- Непрерывное распределение в пространстве и ослабевание в процессе удаления от заряда.
- Скорость распространения электрического поля в вакуумной среде соответствует скорости света, то есть равна (с= 3∙10 ^{8} м/с.)
С целью раскрытия смысла понятия «электрического поля» можно рассмотреть основные его характеристики.
Напряженность — силовая характеристика электрического поля.
Напряженность, как векторная величина, обозначается Е и измеряется в Ньютонах на Кулон (Н/Кл), либо Вольтах на метр (В/м).
Найти напряженность можно по формуле:
Источник: spadilo.ru
Силовые линии — линии, касательные к которым совпадают с вектором напряженности.
Свойства силовых линий:
- направление аналогично направлению вектора напряженности;
- густота силовых линий определяет силу электрического поля;
- начало линий напряженности совпадает с положительными зарядами, а конец — с отрицательными зарядами или бесконечностью;
- однородным называют поле с параллельными силовыми линиями.
Электрические заряды, которые являются причиной образования электрических полей, описывают с помощью закона Гаусса. Электрические поля могут быть сформированы за счет изменения магнитных полей. В этом случае работает закон электромагнитной индукции Фарадея.
Перечисленные закономерности позволяют определить поведение электрического поля в вакуумной среде. С другой стороны, магнитное поле представляет собой функцию электрического поля. Можно выявить связь между уравнениями для обоих полей. В результате будут образованы уравнения Максвелла, описывающие магнитное и электрическое поля в виде функции зарядов и токов.
При рассмотрении частного случая стационарного состояния, то есть при наличии стационарных зарядов и токов, можно наблюдать исчезновение индуктивного эффекта Максвелла–Фарадея. Получается пара уравнений.
Формула 1
Закон Гаусса:
(displaystyle nabla cdot mathbf {E} ={frac {rho }{varepsilon _{0}}})
Формула 2
Закон Фарадея без индукционного члена:
(displaystyle nabla times mathbf {E} =0)
Если объединить записанные закономерности, они будут эквивалентны закону Кулона: частица с электрическим зарядом (q_{1} ) в точке ({displaystyle {boldsymbol {x}}_{1}}) (радиус-вектор) действует с силой на частицу с зарядом (q_{0}) в точке ({displaystyle {boldsymbol {x}}_{0}}).
Формула 3
Закон Кулона:
({displaystyle {boldsymbol {F}}={1 over 4pi varepsilon _{0}}{q_{1}q_{0} over ({boldsymbol {x}}_{1}-{boldsymbol {x}}_{0})^{2}}{hat {boldsymbol {r}}}_{1,0}})
где ({displaystyle {boldsymbol {r}}_{1,0}}) — единичный вектор в направлении от точки ({displaystyle {boldsymbol {x}}_{1}}) в точку ({displaystyle {boldsymbol {x}}_{0}}),
(varepsilon _{0} )— электрическая постоянная.
В том случае, когда среда, в которой находятся заряды, является непустой, электрическую проницаемость вакуума (varepsilon _{0}) нужно заменить диэлектрической проницаемостью (varepsilon). При одинаковых знаках зарядов (q_{0}) и (q_{1}) сила обладает положительным значением. Ее направление от другого заряда указывает на отталкивание частиц друг от друга. При разных знаках зарядов сила отрицательна, а частицы притягиваются.
Формула 4
С целью упрощения вычисления кулоновской силы на любом заряде в точке ({displaystyle {boldsymbol {x}}_{0}}), данное выражение допустимо разделить на (q_{0}), оставив выражение, которое зависит только от другого заряда:
({displaystyle {boldsymbol {E}}({boldsymbol {x}}_{0})={{boldsymbol {F}} over q_{0}}={1 over 4pi varepsilon _{0}}{q_{1} over ({boldsymbol {x}}_{1}-{boldsymbol {x}}_{0})^{2}}{hat {boldsymbol {r}}}_{1,0}}.)
({boldsymbol {E}}({boldsymbol {x}}_{0}) )— электрическое поле в точке ({displaystyle {boldsymbol {x}}_{0}},) которое создано точечным зарядом (q_{1}). Рассматриваемая сила является векторной функцией, равной кулоновской силе на единицу заряда, испытываемой положительным точечным зарядом в точке ({displaystyle {boldsymbol {x}}_{0}}).
Данная формула позволяет определить, какова величина и направление электрического поля в какой-либо точке ({displaystyle {boldsymbol {x}}_{0}} )пространства, за исключением места расположения самого заряда ({displaystyle {boldsymbol {x}}_{1}}), где поле становится бесконечным. Таким образом, уравнение определяет векторное поле.
Анализируя записанное уравнение можно сделать вывод: электрическое поле, создающее точечный заряд, в любом месте имеет направление от заряда в том случае, когда он положительный. Если заряд отрицательный — поле направлено в его сторону. Можно также заметить уменьшение величины поля пропорционально обратному квадрату расстояния от заряда.
Формула 5
Кулоновская сила, которая действует на заряд величиной q в какой-либо точке пространства, определяется, как произведение заряда и электрического поля в этой точке:
({displaystyle {boldsymbol {F}}=q{boldsymbol {E}}})
Уравнения Максвелла линейны. По этой причине для электрических полей характерен принцип суперпозиции. Согласно данной закономерности, полное электрическое поле в точке от распределенных в пространстве зарядов соответствует векторной сумме электрических полей, которые образованы в рассматриваемой точке отдельными зарядами.
Принцип суперпозиции используют, чтобы рассчитать поле, которое создано множественными точечными зарядами. В том случае, когда заряды ({displaystyle q_{1},q_{2},…,q_{n}}) не перемещаются, находясь в точках (x = {-b pm sqrt{b^2-4ac} over 2a}),(mathbf {x} _{2}),…(mathbf {x} _{n}), в отсутствии токов справедлив принцип суперпозиции. Согласно ему, результирующее поле представляет собой сумму полей, сформированных каждой частицей. Величину можно описать с помощью закона Кулона.
Формула 6
Запись результирующего поля с помощью закона Кулона:
({displaystyle {boldsymbol {E}}({boldsymbol {x}})={boldsymbol {E}}_{1}({boldsymbol {x}})+{boldsymbol {E}}_{2}({boldsymbol {x}})+{boldsymbol {E}}_{3}({boldsymbol {x}})+cdots ={1 over 4pi varepsilon _{0}}{q_{1} over ({boldsymbol {x}}_{1}-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}_{1}+{1 over 4pi varepsilon _{0}}{q_{2} over ({boldsymbol {x}}_{2}-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}_{2}+{1 over 4pi varepsilon _{0}}{q_{3} over ({boldsymbol {x}}_{3}-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}_{3}+cdots })
({displaystyle {boldsymbol {E}}({boldsymbol {x}})={1 over 4pi varepsilon _{0}}sum _{k=1}^{N}{q_{k} over ({boldsymbol {x}}_{k}-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}_{k}},)
где ({displaystyle {boldsymbol {{hat {r}}_{k}}}} )— единичный вектор, направленный от точки ({displaystyle {boldsymbol {x}}_{k}}) в точку ({boldsymbol {x}}).
С помощью принципа суперпозиции можно выполнить расчет электрического поля от непрерывного распределения ({displaystyle rho ({boldsymbol {x}})}) (где ( rho) — плотность заряда в кулонах на кубический метр).
Формула 7
С учетом заряда ({displaystyle rho ({boldsymbol {x}}’)dV}) в каждом небольшом объеме пространства (dV) в точке ({displaystyle {boldsymbol {x}}’}) в виде точечного заряда, электрическое поле ({displaystyle d{boldsymbol {E}}({boldsymbol {x}})} ) в точке ({boldsymbol {x}}) можно определить таким образом:
({displaystyle d{boldsymbol {E}}({boldsymbol {x}})={1 over 4pi varepsilon _{0}}{rho ({boldsymbol {x}}’)dV over ({boldsymbol {x}}’-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}’},)
где ({displaystyle {hat {boldsymbol {r}}}’} )— это единичный вектор, направленный от ({displaystyle {boldsymbol {x}}’}) к ({boldsymbol {x}}).
Формула 8
Рассчитать полное электрическое поле можно с помощью суммы вкладов от всех малых объемов. При этом нужно воспользоваться методом интегрирования по объему распределения заряда ({displaystyle rho (x’)}):
({displaystyle {boldsymbol {E}}({boldsymbol {x}})={1 over 4pi varepsilon _{0}}iiint limits _{V},{rho ({boldsymbol {x}}’)dV over ({boldsymbol {x}}’-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}’})
Формула 9
Такие же формулы применимы в случае поверхностного заряда с непрерывным распределением заряда ({displaystyle sigma ({boldsymbol {x}})}), где (sigma) является плотностью заряда в кулонах на квадратный метр:
({displaystyle {boldsymbol {E}}({boldsymbol {x}})={1 over 4pi varepsilon _{0}}iint limits _{S},{sigma ({boldsymbol {x}}’)dA over ({boldsymbol {x}}’-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}’})
Формула 10
Уравнение для линейных зарядов с непрерывным распределением заряда ({displaystyle lambda ({boldsymbol {x}})}), где lambda представляет собой плотность заряда в кулонах на метр, имеет следующий вид:
({displaystyle {boldsymbol {E}}({boldsymbol {x}})={1 over 4pi varepsilon _{0}}int limits _{P},{lambda ({boldsymbol {x}}’)dL over ({boldsymbol {x}}’-{boldsymbol {x}})^{2}}{hat {boldsymbol {r}}}’})
В том случае, когда рассматривается статичная система с магнитными полями, стабильными во времени, согласно закону Фарадея, электрическое поле является потенциальным. При этом допустимо задать электрический потенциал или функцию (Phi.) В результате:
({displaystyle mathbf {E} =-nabla Phi })
Общий случай электрического поля недопустимо описывать без учета магнитного поля. При зависимости от вектора магнитного потенциала A, определенного как:
({displaystyle mathbf {B} =nabla times mathbf {A} }),
допустимо записать электрический потенциал ( {displaystyle Phi } ) в виде:
({displaystyle mathbf {E} =-nabla Phi -{frac {partial mathbf {A} }{partial t}}},)
где ({displaystyle nabla Phi } —) градиент электрического потенциала;
({displaystyle {frac {partial mathbf {A} }{partial t}}} )— частная производная от A по времени.
Формула 11
Из рассмотренного уравнения можно получить закон индукции Фарадея:
({displaystyle nabla times mathbf {E} =-{frac {partial (nabla times mathbf {A} )}{partial t}}=-{frac {partial mathbf {B} }{partial t}}})
Плотность энергии электрического и магнитного полей
Энергия электромагнитного поля — энергия, которая заключена в электромагнитном поле.
В рамках данного понятия можно рассматривать частные случаи чистого электрического и чистого магнитного поля. Рассмотреть энергию электромагнитного поля допустимо с помощью его характеристик.
Формула 12
Работа A электрического поля E, которая совершается для перемещения заряда Q, схожа по смыслу с механической работой:
({displaystyle A=int F(x),dx=int Qcdot E(x),dx=Qcdot U,})
где (U=int E,dx) — разность потенциалов, или напряжение.
Формула 13
Чаще всего при решении примеров рассматривают непрерывный перенос заряда за определенное время между точками с конкретной разностью потенциалов U(t). В результате уравнение для определения работы принимает следующий вид:
({displaystyle A=int U(t),dQ=int U(t)I(t),dt,})
где (I(t)={dQ over dt}) — сила тока.
Формула 14
Мощность P, которая характеризует электрический ток на отрезке цепи, равна производной от работы A по времени. Формула для расчета мощности:
({displaystyle P(t)={frac {dA}{dt}}=U(t)cdot I(t),})
Согласно закону Ома:
(U=Icdot R)
Электрическая мощность, которая выделяется на сопротивлении R, определяется, как:
({displaystyle P=I(t)^{2}cdot R,})
Формула мощности с учетом напряжения принимает следующий вид:
({displaystyle P={{U(t)^{2}} over R}.})
Таким образом, работа (выделившаяся теплота) представляет собой интеграл мощности по времени:
({displaystyle A=int P(t),dt=int I(t)^{2}cdot R,dt=int {{U(t)^{2}} over R},dt.})
Примечание
Если рассматривать электрическое и магнитное поля, можно прийти к выводу, что их энергия пропорциональна квадрату напряженности поля. Определение «энергия электромагнитного поля» не совсем соответствует действительности. Ему на замену в физике нередко употребляют термин плотности энергии электромагнитного поля (в заданной точке пространства). Общая величина энергии поля является интегралом плотности энергии по всему пространству.
В системе СИ:
({displaystyle u={frac {mathbf {E} cdot mathbf {D} }{2}}+{frac {mathbf {B} cdot mathbf {H} }{2}}.})
В вакуумной среде и микрополях:
({displaystyle u={varepsilon _{0}E^{2} over 2}+{B^{2} over {2mu _{0}}}=varepsilon _{0}{frac {E^{2}+c^{2}B^{2}}{2}}={frac {E^{2}/c^{2}+B^{2}}{2mu _{0}}},})
где E — напряженность электрического поля;
B — магнитная индукция;
D — электрическая индукция;
H — напряженность магнитного поля;
с — скорость света;
(varepsilon _{0} )— электрическая постоянная;
(mu _{0}) — магнитная постоянная.
В системе СГС:
({displaystyle u={frac {mathbf {E} cdot mathbf {D} +mathbf {B} cdot mathbf {H} }{8pi }}.})
Формула 15
Энергия электромагнитного поля в колебательном контуре:
({displaystyle W={frac {CU^{2}}{2}}+{frac {LI^{2}}{2}},})
где U — электрическое напряжение в цепи;
C — электроемкость конденсатора;
I — сила тока;
L — индуктивность катушки или витка с током.
В том случае, когда речь идет об электромагнитной волне, плотность потока энергии определяют с помощью вектора Пойнтинга S (в русской научной литературе можно встретить понятие вектор Умова–Пойнтинга).
Формула 16
В системе СИ вектор Пойнтинга определяют, как:
({mathbf S}={mathbf E}times {mathbf H})
В результате вектор Пойнтинга равен векторному произведению напряженностей электрического и магнитного полей. Направление вектора совпадает с перпендикулярами к векторам E и H. Данное условие соответствует свойству поперечности электромагнитных волн.
С другой стороны, формулу для плотности потока энергии можно адаптировать для случая стационарных электрических и магнитных полей:
({displaystyle mathbf {S} =mathbf {E} times mathbf {H}.})
Формула объемной плотности энергии
Конденсатор представляет собой двухполюсник, значение емкости которого может быть постоянным или переменным, а проводимость обладает малыми значениями.
Конденсатор является устройством, предназначенным для накопления заряда и энергии электрического поля, и пассивным электронным компонентом. Единицами измерения емкости конденсатора являются фарады.
Принято выражать энергию заряженного конденсатора с помощью величин, являющихся характеристиками электрического поля в пространстве между обкладками.
Энергия плоского конденсатора:
Емкость плоского конденсатора:
В результате:
Таким образом, напряженность поля в конденсаторе и разность потенциалов между его обкладками связаны формулой:
С другой стороны, объем конденсатора равен:
С учетом (overrightarrow{D} ) и (overrightarrow{E}:)
Таким образом:
Объемная плотность энергии электрического поля:
Объемная плотность энергии — величина, равная энергии единицы объема поля.
В случае изотропного диэлектрика объемная плотность энергии:
Исходя из записанных уравнений, можно сделать вывод о том, что плотность энергии поля с определенной напряженностью, образованного в среде с конкретной проницаемостью, прямо пропорциональна квадрату напряженности поля.
Энергия поля конденсатора с зарядом q на его обкладке определяется с помощью величины заряда и емкости конденсатора:
Энергия электрического поля может быть определена при известной силовой характеристике поля:
В том случае, когда поле является однородным:
(W=const)
Между обкладками плоского конденсатора действует сила притяжения. Известно, что:
(F=Eq)
Одна пластина создает поле, напряженность которого равна:
С другой стороны:
(q=sS)
В таком случае:
Источник: edu.tltsu.ru
Записанное выражение не согласуется с опытом. Причина заключается в том, что кроме «электрической силы» на обкладки со стороны диэлектрика (имеется виду жидкий или газообразный диэлектрик) действуют еще механические силы, стремящиеся их раздвинуть. Опытным путем доказано, что роль носителя энергии играет поле.
В электростатике поле и заряды невозможно отделить друг от друга. С другой стороны, электрические поля, которые изменяются по времени, могут существовать обособлено, независимо от возбудивших их зарядов, и могут распространяться в пространстве в виде электромагнитных волн, способных переносить энергию.
Единицы измерения плотности энергии
Единицами измерения объемной плотности энергии электрического поля являются (Дж/м^{3}). Джоуль на кубический метр соответствует объемной плотности энергии электрического поля, для которого энергия 1 Дж равномерно распределена по объему (1 м^{3}).
Тема: Найти объёмную плотность энергии электрического поля (Прочитано 5223 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Найти объёмную плотность энергии электрического поля, создаваемого заряженной металлической сферой радиусом 5 см на расстоянии 5 см от её поверхности, если поверхностная плотность заряда на ней 2 мкКл/м2. Сделать рисунок.

Записан
Решение.
Объёмная плотность энергии электрического поля создаваемого заряженной металлической сферой определяется по формуле:
[ omega =frac{varepsilon cdot {{varepsilon }_{0}}cdot {{E}^{2}}}{2} (1). ]
где: ε = 1 – диэлектрическая проницаемость воздуха, ε0 = 8,854∙10-12 Ф/м – электрическая постоянная.
Е – напряженность электрического поля в точке:
[ E=frac{kcdot q}{varepsilon cdot {{(R+r)}^{2}}} (2). ]
k = 9∙109 Н∙м2/Кл2.
q – заряд на поверхности сферы:
q = σ∙S (3), S = 4∙π∙R2 (4), q = σ∙4∙π∙R2 (5).
Подставим (5) в (2), (2) в (1) определим объёмную плотность энергии электрического поля создаваемого заряженной металлической сферой.
[ begin{align}
& omega =frac{varepsilon cdot {{varepsilon }_{0}}}{2} cdot {{(frac{kcdot sigma cdot 4cdot pi cdot {{R}^{2}}}{varepsilon cdot {{(R+r)}^{2}}} )}^{2}} (6). \
& omega =frac{8,854cdot {{10}^{-12}}}{2}cdot {{(frac{9cdot {{10}^{9}}cdot 2cdot {{10}^{-6}}cdot 4cdot 3,14cdot 25cdot {{10}^{-4}}}{{{10}^{-2}}})}^{2}}=14,14cdot {{10}^{-3}}. \
end{align}
]
ω = 14,14∙10-3 Дж/м3.
« Последнее редактирование: 24 Июля 2015, 07:28 от alsak »

Записан
Исходя из опытов, заряженный конденсатор имеет запас энергии.
Энергия заряженного конденсатора равняется работе внешних сил, которая необходима для его зарядки.
Его заряжение представляется как последовательный перенос малых порций заряда ∆q>0 с одной обкладки на другую, как изображено на рисунке 1.7.1 Одна из них заряжается положительным зарядом, другая – отрицательным. Процесс производится при уже имеющемся некотором заряде q, тогда как между обкладками существует разность потенциалов U=qC, а при переносе ∆q внешние силы совершают работу ∆A=U∆q=q∆qC.
Нахождение энергии We конденсатора с емкостью С и с зарядом Q производится с помощью интегрирования в переделах от 0 до Q. Формула примет вид:
We=A=Q22C.
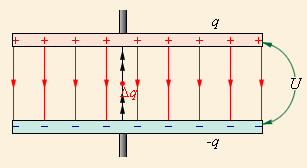
Рисунок 1.7.1. Процесс зарядки конденсатора.
Энергия заряженного конденсатора
Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:
We=Q22C=CU22=QU2.
Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:
Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.
Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.
Объемная плотность электрической энергии
Напряженность однородного поля плоского конденсатора равняется E=Ud, его емкость – C=ε0εSd.
Отсюда следует, что We=C·U22=ε0·ε·S·E2·d22d=ε0·ε·E22V, где V=Sd обозначает объем пространства между обкладками с наличием электрического поля. Данное соотношение приводит к формуле следующей физической величины.
Физическая величина We=ε0·ε·E22 – это электрическая энергия на единицу объема пространства, в котором создается электрическое поле. Ее называют объемной плотностью данной электрической энергии.
Энергия поля конденсатора, создаваемая любыми распределениями электрических зарядов в пространстве, находится путем интегрирования We по всему объему, в котором было создано электрическое поле.
Электрическое поле вызывает перемещение свободных зарядов и может выполнять работу, а это значит, что оно обладает энергией. Согласно теории близкодействия, вся энергия взаимодействия заряженных тел сконцентрирована в электрическом поле этих тел.
Электрическая энергия наэлектризованного проводника
Чтобы зарядить проводник, надо выполнить работу против кулоновских сил отталкивания между одноименно заряженными частицами. Для уточнения этого тезиса предположим, что процесс зарядки отдельного тела осуществляется последовательным переносом на него порций dqdq заряженных частиц из бесконечности, где потенциал Ф0=0Ф_0 = 0. При этом работой переноса первой порции можно пренебречь, но в дальнейшем для увеличения заряда тела на dqdq надо выполнить все большую работу dA=dqφdA = dqφ, где φφ соответствующее промежуточное значение потенциала проводника. Принимая q=Сφq = Сφ, получаем
dA=СφdφdA = Сφdφ
Общая работа при электризации проводника от потенциала 00 до φφ составляет
A=C∫0φφdφ=Cφ22A=Cintlimits_{0}^{varphi }{varphi d}varphi =frac{C{{varphi }^{2}}}{2}
По закону сохранения энергии работа электризации расходуется на увеличение энергии заряженного проводника. Итак, электрическую энергию наэлектризованного проводника определяют так:
We=Cφ22=qφ2=q22C{{W}_{e}}=frac{C{{varphi }^{2}}}{2}=frac{qvarphi }{2}=frac{{{q}^{2}}}{2C}
где q,φ,Сq, φ, С – заряд, потенциал и электроемкость проводника.
Поскольку с заряженным проводником связывается электрическое поле, точнее можно сказать, что данная формула выражает энергию электрического поля.
Энергия заряженного конденсатора
Выразим эту энергию через напряженность ЕЕ поля. Для этого применим формулу к заряженному плоскому конденсатору, поле которого однородное и локализовано, а энергия
We=CU22{{W}_{e}}=frac{C{{U}^{2}}}{2}
Подставив в уравнение значения емкости и напряжения, найдем формулу для определения энергии поля заряженного конденсатора
We=ε0εE22Sd{{W}_{e}}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}Sd
Плотность энергии электрического поля
Поскольку Sd – объем поля между обмотками, плотность энергии электрического поля
we=WeSd=ε0εE22{{w}_{e}}=frac{{{W}_{e}}}{Sd}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}
Учитывая, что D=ε0εED = ε_0εΕ, окончательно получим
we=ε0εE22=ED2=D22ε0ε{{w}_{e}}=frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}=frac{ED}{2}=frac{{{D}^{2}}}{2{{varepsilon }_{0}}varepsilon }
Зная объемную плотность энергии we, можно определить общую энергию произвольного электрического поля. Если поле неоднородно, то его можно разделить на бесконечно малые объемы, в пределах которых оно остается однородным. Тогда полная энергия электрического поля в объеме VV составит
We=∫Vwedv=∫Vε0εE22dv{{W}_{e}}=intlimits_{V}{{{w}_{e}}dv=}intlimits_{V}{frac{{{varepsilon }_{0}}varepsilon {{Epsilon }^{2}}}{2}dv}
Согласно энергии электрического поля по теории относительности можно определить массу поля, а именно:
me=Wec2m_e = frac{W_e}{c^2}
где сс – скорость света.
Итак, электрическое поле характеризуется напряженностью ЕЕ, потенциалом φφ, энергией WeW_e (или плотностью энергии wew_e) и массой mem_e.

