Как найти объемную плотность энергии конденсатора

III. Основы электродинамики

Тестирование онлайн

• Энергия конденсатора. Основные понятия

• Энергия конденсатора

Энергия заряженного конденсатора

Энергия определяется по формуле

Объемная плотность энергии конденсатора

Энергию конденсатора можно определить как

Объемная плотность энергии определяется как

Энергия
заряженного конденсатораравна
работе внешних сил, которую необходимо
затратить, чтобы зарядить конденсатор.

Процесс
зарядки конденсатора можно представить
как последовательный перенос достаточно
малых порций заряда Δq > 0 с одной
обкладки на другую. При этом одна
обкладка постепенно заряжается
положительным зарядом, а другая –
отрицательным. Поскольку каждая порция
переносится в условиях, когда на
обкладках уже имеется некоторый заряд
q, а между ними существует некоторая
разность потенциалов
,
при переносе каждой порции Δq внешние
силы должны совершить работу

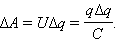
(С – емкость)

Энергия We
конденсатора емкости C, заряженного
зарядом Q, может быть найдена путем
интегрирования этого выражения в
пределах от 0 до Q:

Энергия
заряженного плоского конденсатора Eк
равна работе A, которая была затрачена
при его зарядке, или совершается при
его разрядке.

=Eк

Поскольку
напряжение на конденсаторе может быть
рассчитано из соотношения:

U=E*d,

где E- напряженность поля между обкладками
конденсатора,d- расстояние
между пластинами конденсатора, то
энергия заряженного конденсатора
равна:

где V- объем пространства между обкладками
конденсатора.

Энергия
заряженного конденсатора сосредоточена
в его электрическом поле.

Объемная
плотность энергии
электростатического поля (энергия
единицы объема)

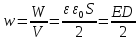
18. Электрический ток. Сила и плотность тока.

Ток —
направленное движение электрически
заряженных частиц. Величина тока
измеряется так называемой силой тока,
которая в системе СИ измеряется в
амперах.

Токбывает постоянный и переменный.
Постоянный ток — это ток, имеющий
постоянную величину. Переменный ток
периодически изменяет направление
своего движения по синусоиде с
определенной частотой, измеряемой в
герцах (Гц). Переменный ток высокой
частоты вытесняется на поверхность
проводника

Материал,
в котором течёт ток, называется
проводником

Сила тока
в проводнике — скалярная величина,
численно равная заряду, протекающему
в единицу времени через сечение
проводника. Обозначается буквой :I

I=q/t

Плотность
тока — векторная величина, имеющая
смысл силы тока, протекающего через
единицу площади. Например, при равномерном
распределении плотности jтока по сечениюSпроводника
|j|=I/S

19.Сторонние силы. Электродвижущая сила и напряжение.

Сторонние
силы –силы неэлектрической
природы, вызывающие перемещение
электрических зарядов внутри источника
постоянного тока.

Сторонними
считаются все силы отличные от кулоновских
сил.

Электродвижущая
сила

(эдс), физическая
величина, характеризующая действие
сторонних (непотенциальных) сил в
источниках постоянного или переменного
тока; в замкнутом проводящем контуре
равна работе этих сил по перемещению
единичного положительного заряда вдоль
контура.

ЭДС можно
выразить через напряжённость
электрического поля сторонних сил
(Eex). В замкнутом контуре (L) тогда ЭДС
будет равна:

где dl — элемент длины контура.

Напряжение
(разность потенциалов) между точками
A и B — это отношение работы электрического
поля при переносе пробного электрического
заряда из точки A в точку B к величине
пробного заряда.

Ф1-Ф2=U12

При этом
считается, что перенос пробного заряда
не изменяет распределения зарядов на
источниках поля.

Альтернативное
определение (для электростатического
поля) —

(интеграл от
проекции поля на траекторию между
точками AиBвдоль любой траектории, идущей изAвB)

Единицей
измерения напряжения в системе СИ
является Вольт.

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Исходя из опытов, заряженный конденсатор имеет запас энергии.

Энергия заряженного конденсатора равняется работе внешних сил, которая необходима для его зарядки.

Его заряжение представляется как последовательный перенос малых порций заряда ∆q>0 с одной обкладки на другую, как изображено на рисунке 1.7.1 Одна из них заряжается положительным зарядом, другая – отрицательным. Процесс производится при уже имеющемся некотором заряде q, тогда как между обкладками существует разность потенциалов U=qC, а при переносе ∆q внешние силы совершают работу ∆A=U∆q=q∆qC.

Нахождение энергии We конденсатора с емкостью С и с зарядом Q производится с помощью интегрирования в переделах от 0 до Q. Формула примет вид:

We=A=Q22C.

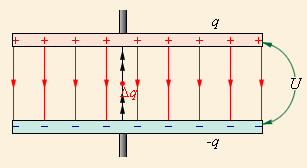
Рисунок 1.7.1. Процесс зарядки конденсатора.

Энергия заряженного конденсатора

Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:

We=Q22C=CU22=QU2.

Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:

Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.

Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.

Объемная плотность электрической энергии

Напряженность однородного поля плоского конденсатора равняется E=Ud, его емкость – C=ε0εSd.

Отсюда следует, что We=C·U22=ε0·ε·S·E2·d22d=ε0·ε·E22V, где V=Sd обозначает объем пространства между обкладками с наличием электрического поля. Данное соотношение приводит к формуле следующей физической величины.

Физическая величина We=ε0·ε·E22 – это электрическая энергия на единицу объема пространства, в котором создается электрическое поле. Ее называют объемной плотностью данной электрической энергии.

Энергия поля конденсатора, создаваемая любыми распределениями электрических зарядов в пространстве, находится путем интегрирования We по всему объему, в котором было создано электрическое поле.

Конденсаторы: плотность энергии поля

В этой статье представлены задачи на определение энергии конденсатора, плотности энергии поля, а также расчет выделившегося тепла.

Задача 1.

Емкость плоского воздушного конденсатора пФ, расстояние между пластинами м, напряжение на пластинах В. Определить: а) напряженность поля между пластинами; б) силу взаимодействия пластин; в) энергию поля конденсатора; г) объемную плотность энергии.

Запишем нужные нам соотношения:

Заряд можем посчитать сразу:

Заряд равен 180 нКл.

Также можно определить энергию конденсатора:

Энергия равна 18 мкДж.

Определим площадь пластин:

Тогда напряженность поля равна:

Сила взаимодействия пластин:

Таким образом, сила взаимодействия пластин 0,45 мН. Объемная плотность энергии:

Ответ: напряженность поля В/м, сила взаимодействия пластин 0,45 мН, энергия поля 18 мкДж, объемная плотность энергии Дж/м.

Задача 2.

Конденсатор, имеющий емкость мкФ, заряжен до разности потенциалов В. Какое количество теплоты выделится, если конденсатор замкнуть сопротивлением?

Если заряженный конденсатор замкнуть, то вся энергия, запасенная в нем, превратится в тепло на резисторе:

Ответ: энергия, а следовательно, и выделившееся тепло, равна 1 Дж.

Задача 3.

В импульсной фотовспышке лампа питается от конденсатора емкостью мкФ, заряженного до напряжения В. Найти энергию вспышки, среднюю ее мощность, если продолжительность разрядки мс.

Запасенная энергия выделяется в течение времени , следовательно, мощность

Ответ: энергия 36 Дж, мощность 15 кВт.

Задача 4.

Расстояние между пластинами плоского конденсатора с диэлектриком из парафинированной бумаги мм, а напряжение между пластинами В. Найти плотность энергии поля.

Ответ: 97 мДж/м.

Задача 5.

Во сколько раз изменится энергия поля заряженного конденсатора, если пространство между пластинами конденсатора заполнить маслом? Рассмотрите случаи: а) конденсатор отключен от источника напряжения; б) конденсатор остается присоединенным к источнику напряжения.

Если конденсатор отключен от питания, то он сохраняет заряд.

Так как диэлектрическая проницаемость масла и в нашей формуле стоит в знаменателе, то энергия уменьшится в раз, то есть в 2,2 раза.

Если конденсатор подключен к источнику питания, то , и

Видим, что в этом случае, наоборот, энергия увеличится в раз.