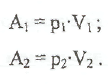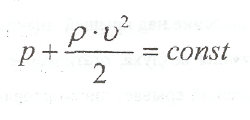Уравнение неразрывности и уравнение Бернулли.
Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.
Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.
Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.
Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.
Содержание статьи
Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.
Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υср .
Таким образом уравнение расхода для потока будет
υср – средняя скорость потока
F – площадь сечения потока.
Уравнение неразрывности потока жидкости
Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.
Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный
а через сечение 2-2 из него же вытекает объем, равный
Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.
Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.
Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки
Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что
т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.
Уравнение неразрывности струи жидкости. Уравнение Бернулли.
Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.
При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.
Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.
Если всё это записать в виде формулы, то
где W – приращение кинетической энергии = m * υ 2 / 2
ΣA – сумма работ действующих сил = P *ΔS
В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.
Теперь рассмотрим обе части этого выражения по порядку.
Приращение кинетической энергии ΔW
В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.
Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.
Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен
масса в этом случае получается равной
Подставляя все это в выражение для кинетической энергии получаем цепочку
ΔW = m * υ 2 2 / 2 – m * υ 2 1 / 2 = ρ * q * ΔТ * υ 2 2 / 2 – ρ * q * ΔТ * υ 2 1 / 2
Работа сил действующих на систему ΣA
Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести AТ равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.
Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.
Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.
Силы давления АД , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.
Суммарно работа сил давления будет
Подставляя в начальное уравнение
Полученные выражения для ΔW и ΣA получаем
Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые
Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:
Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2
В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.
Видео по теме уравнение неразрывности
Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.
Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.
Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.
Условие неразрывности струи
Течение жидкости характеризуется линиями тока. Это линии, касательные к которым совпадают с направлением вектора скорости частиц жидкости в данной точке (рис. 9.1). Часть пространства, ограниченная линиями тока, называется трубкой тока (на рис. 9.1 заштрихована). Если при течении жидкости линии тока непрерывны, то такое течение называется ламинарным (рис. 9.1).
Рис. 9.1. Линии тока при ламинарном течении
При определенных условиях в движущейся жидкости могут возникать завихрения, скорость ее частиц хаотически изменяется, линии тока претерпевают разрывы, изменяющиеся со временем. Такое движение жидкости называется турбулентным (рис. 9.2).
Рис. 9.2. Линии тока при турбулентном течении
Для установления связи между скоростью ламинарного течения жидкости и площадью поперечного сечения участка, через который она протекает, выделим в трубке тока участки с площадью поперечного сечения S± и S2 (рис. 9.3). В пределах этих сечений скорости частиц жидкости одинаковы, направлены перпендикулярно выделенным площадкам и равны по величине v± и v2 соответственно. Объемы жидкости V1 и V2, протекающей через выделенное сечение за одно то же время t, одинаковы, так как жидкость практически несжимаема. Это позволяет записать равенство
Уравнение (9.1) представляет собой условие неразрывности струи, утверждающее, что при ламинарном течении
Рис. 9.3. Условие неразрывности струи несжимаемой жидкости произведение площади сечения участка, через который она протекает, и ее скорости является постоянной величиной для данной трубки тока.
При течении жидкости различают ее линейную и объемную скорость. Линейная скорость (и) — это путь L, проходимый частицами жидкости в единицу времени: v = L/t (для равномерного течения). Объемная скорость (расход) Q — это объем жидкости V, протекающий через некоторое сечение за единицу времени t: Q = V/t. Объемная и линейная скорости течения жидкости связаны очевидным соотношением: Q = vS, где S — площадь поперечного сечения потока жидкости. Линейная скорость кровотока измеряется в м/с, а объемная — в м 3 /с, л/мин, мл/мин и др.
Условие неразрывности струи (9.1) выполняется и в реальной гемодинамике. Здесь формулировка этого условия звучит следующим образом: в любом сечении сердечно-сосудистой системы объемная скорость кровотока одинакова: Q = const.
Под площадью сечения сосудистой системы понимают суммарную площадь сечения кровеносных сосудов одного уровня ветвления. Так, в большом круге кровообращения первое (наименьшее по площади) сечение проходит через аорту, второе — через все артерии, на которые непосредственно разветвляется аорта, и т.д. Наибольшую площадь имеет сечение, соответствующее капиллярной сети.
Как следует из условия неразрывности струи, с увеличением площади сечения сосудистой системы скорость кровотока в ее соответствующих участках уменьшается. Так, в покое средняя линейная скорость кровотока в аорте составляет около 0,4-0,5 м/с, а в капиллярах — около 0,5 мм/с. Следовательно, сумма поперечных сечений всех функционирующих капилляров примерно в 800 раз больше площади сечения аорты.
Гидродинамика. Уравнение неразрывности движения жидкости.
Уравнение неразрывности потока демонстрирует закон сохранения массы: количество втекающей и вытекающей жидкости неизменно.
Проанализируем сечение 1 с площадью и скоростью движения частиц жидкости обозначим и1. Элементарный расход для него представлен соотношением:
Далее проанализируем сечение 2 в этой же струйке с площадью сечения и скоростью обозначим и2. Элементарный расход для него представлен соотношением:
Но согласно характерной особенности элементарной струйки притока и оттока жидкости через ее боковую поверхность не существует; на промежутке 1 – 2, которому свойственны постоянные размеры, отсутствуют пустоты и отсутствуют переуплотнения количества жидкости, протекающей в единицу времени сквозь сечения 1 и 2,будут одинаковыми, тогда:
Уравнение неразрывности для элементарной струйки – элементарный расход жидкости при установившемся движении величина одинаковая для всей элементарной струйки.
Проанализируем трубу с переменным живым сечением. Расход жидкости через трубу для всякого ее сечении постоянен, т.е. Q1=Q2= const, делаем вывод:
Значит, когда течение в трубе сплошное и неразрывное, то уравнение неразрывности станет:
Найдем отсюда скорость для выходного сечения:
Обратим внимание, что скорость возрастает обратно пропорционально площади живого сечения потока. Указанная обратная зависимость между скоростью и площадью выступает важным следствием уравнения неразрывности и нашла широкое применение. Так, к примеру, эта особенность используется пожарными при тушении пожара для формирования сильной и дальнобойной струи.
Что произойдет со скорость потока при сужении, когда диаметр напорной трубы d сузиться в два раза?
Площадь живого сечения трубы вычисляем на основе формулы w = πd 2 / 4. В этом случае соотношение площадей в формуле u2 = u1 w1 / w2 равняться 4.
Следовательно, в ситуации, когда диаметр трубы сужается в два раза – скорость потока возрастет в четыре раза. По аналогии, когда диаметр сузится в три раза – скорость увеличиться в девять раз.
[spoiler title=”источники:”]
http://studref.com/467417/meditsina/uslovie_nerazryvnosti_strui
http://www.calc.ru/Gidrodinamika-Uravneniye-Nerazryvnosti-Dvizheniya-Zhidkosti.html
[/spoiler]
Изучаем понятие объемной скорости и ее измерение
Объемная скорость — это физическая величина, которая характеризует количество жидкости, проходящей через определенную площадь за единицу времени. Она является одним из важнейших параметров при описании потока жидкости.
Для измерения объемной скорости необходимо знать скорость потока и площадь сечения, через которое проходит жидкость. Обычно объемная скорость обозначается буквой Q и выражается в кубических метрах в секунду (м³/с).
Измерение объемной скорости
Существует несколько методов для измерения объемной скорости, но наиболее распространенным является метод, основанный на измерении скорости потока и площади сечения.
Для измерения скорости потока используются различные датчики, такие как Пито-трубка, вихревые датчики и датчики Доплера. При измерении площади сечения могут использоваться такие методы, как прямоугольник, трапеция или круг.
После измерения скорости потока и площади сечения, объемная скорость может быть рассчитана с помощью формулы:
Q = V * S
где Q — объемная скорость (м³/с), V — скорость потока (м/с) и S — площадь сечения (м²).
Связь объемной скорости с другими характеристиками потока жидкости
Объемная скорость тесно связана с другими характеристиками потока жидкости, такими как расход жидкости и линейная скорость. Расход жидкости (Q) может быть рассчитан с помощью формулы:
Q = V * S
где Q — объемная скорость (м³/с), V — скорость потока (м/с) и S — площадь сечения (м²).
Линейная скорость (v) представляет собой скорость движения жидкости вдоль стенки трубы или канала и может быть рассчитана с помощью формулы:
v = Q / A
где A — периметр сечения (м).
Таким образом, зная объемную скорость и другие характеристики потока жидкости, можно рассчитать такие параметры, как расход жидкости и линейную скорость, что является важным для многих инженерных расчетов и проектирования трубопроводных систем.
Заключение
Объемная скорость является важной характеристикой потока жидкости, которая позволяет описывать количество жидкости, проходящей через определенную площадь за единицу времени. Измерение объемной скорости осуществляется на основе измерения скорости потока и площади сечения, и тесно связано с другими характеристиками потока жидкости, такими как расход жидкости и линейная скорость. Знание объемной скорости и других параметров потока жидкости является важным для многих инженерных расчетов и проектирования трубопроводных систем.
Важнейшими характеристиками потоков жидкости или газа (например при движении их в трубах) являются объемный расход и скорость потока.
Объем жидкости, проходящей через заданную площадь за единицу времени. Измеряется в системе СИ в кубических метрах в секунду (м3/с). Обычно обозначается символом QQ.
Скорость движения жидкости, которая численно равна отношению расхода жидкости Q к площади живого сечения.
Понятие расхода
Если через заданную площадь SS жидкость протекает с равномерно распределенной по площади скоростью VV под углом θθ к направлению скорости до перпендикуляра площади SS, то расход составит:
Q=V⋅S⋅cosθQ = V ⋅ S ⋅ cosθ
В частном случае, когда скорость потока перпендикулярна к площади SS, уравнение примет вид:
Q=V⋅SQ = V ⋅ S
Общий случай
Записанные выше уравнения обычно называют уравнениями непрерывности (для одномерных течений несжимаемой жидкости). Если скорость жидкости через заданную площадь неодинакова (или, если область не является плоской), то объемный расход потока жидкости может быть рассчитан с помощью интеграла по площади:
Q=∬Su⋅dωQ = ∬S u ⋅ dω,
где dωdω дифференциал поверхности, который записывается как:
dω=ndSdω = n dS,
где nn – единичный вектор нормали к поверхности; dSdS – дифференциал площади SS.
Полученное уравнение потока вектора скорости через поверхность SS является скалярной величиной. Физически поток вектора скорости представляет собой секундный объемный расход жидкости через поверхность SS.
Измерение скорости потока
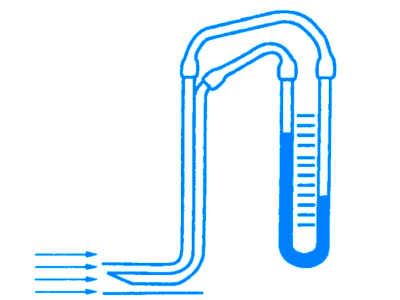
Для измерения скорости потока жидкости или газа используется прибор, предложенный французским ученым А. Пито (1695-1771). Этот прибор имеет две трубки: одну с отверстием напротив потока и вторую с отверстием, параллельным потоку:
Трубки соединены с дифференциальным манометром:
В отверстии первой трубки скорость жидкости или газа равна нулю, а в отверстии второй скорость потока сохраняется. Применив уравнение Бернулли для частиц потока в отверстиях трубок, получим:
p1=ρv22+p2{{p}_{1}}=frac{rho {{v}^{2}}}{2}+{{p}_{2}}
Составляющую ρv2/2ρv^2/2, имеющую размерность давления, называют динамическим давлениям, а составляющую р2р^2 – статичным.
Из уравнения определим скорость потока:
v=2(p1−p2)ρv=sqrt{frac{2({{p}_{1}}-{{p}_{2}})}{rho }}
Здесь ρρ – плотность вещества в потоке; (р1р_1 – р2р_2) находят по разнице высот жидкости в манометре. Согласно данной формуле можно проградуировать манометр в трубке Пито для измерения скорости потока.
Трубку Пито используют для измерения скорости кораблей и самолетов.
Скорость истечения жидкости из бака
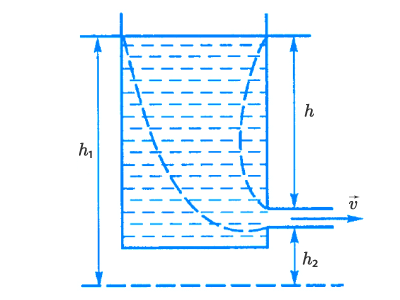
Найдем скорость истечения жидкости из бака:
Для этого выделим в жидкости трубку потока (показанную штриховой линией) и применим к ее сечениям (взятых на поверхности жидкости в баке, и в отверстии утечки) уравнение Бернулли. Если при этом учесть, что давления в обоих сечениях одинаковы и равны атмосферному, а скорость в сечении на поверхности жидкости в баке приравнять к нулю, то получим:
ρgh1=ρv22+ρgh2rho g{{h}_{1}}=frac{rho {{v}^{2}}}{2}+rho g{{h}_{2}}
Отсюда находим vv – скорость истечения жидкости из бака:
v=2g(h1−h2)v=sqrt{2g({{h}_{1}}-{{h}_{2}})}
Поскольку h1−h2=hh_1 – h_2 = h – высота уровня жидкости в баке над отверстием истечения, окончательно:
v=2ghv=sqrt{2gh}
Эту формулу вывел итальянский ученый Э. Торричелли (1608-1647) в 1641 Из нее следует, что скорость истечения жидкости (идеальной) из сосуда такова, какова была бы скорость приобретенная телом, свободно падая с высоты hh.
Цилиндрический сосуд высотой hh = 70 см с площадью дна SS = 600 см2 заполнено водой. В дне сосуда образовалось отверстие S1S_1 = 1 см2. За какое время вытечет вода из сосуда?
Приняв во внимание, что скорость истечения воды из сосуда со временем меняется, поскольку меняется уровень воды, определим сначала ее объем утечки за время dtdt:
dV=S1vdtdV = S_1vdt
где v=2ghv=sqrt{2gh} (hh – уровень воды в заданный момент времени); поэтому:
dV=S12ghdtdV={{S}_{1}}sqrt{2gh}dt
Этот объем утечки можно выразить через снижение уровня воды:
dV=−SdhdV = -Sdh
Если приравнять выражения и разделить переменные, то получим дифференциальное уравнение:
dhh=−S1S2gdtfrac{dh}{sqrt{h}}=-frac{{{S}_{1}}}{S}sqrt{2g}dt
Интегрируя обе части этого уравнения, получаем:
2h=−S1S2gdt+C2sqrt{h}=-frac{{{S}_{1}}}{S}sqrt{2g}dt+C
Найдем постоянную интегрирования. Поскольку при tt = 0, h=h0h = h_0, получим:
Тогда равенство примет вид:
h0−h=S12g2Stsqrt{{{h}_{0}}}-sqrt{h}=frac{{{S}_{1}}sqrt{2g}}{2S}t
В случае полного вытекания воды (hh = 0) равенство примет вид:
t=2SS1h02gt=frac{2S}{{{S}_{1}}}sqrt{frac{{{h}_{0}}}{2g}}
Подставив значения из условия получим
tt = 227 с.
Тест по теме «Скорость потока»
2.Течение
жидкости. Линейная и объемная скорости,
соотношение между ними. Уравнение
неразрывности струи. Закон Бернулли,
его практическое значение.
Основной
характеристикой любого движения является
его скорость. Выделяют 2 разных скорости.
Скорость
перемещения самих частиц жидкости (или
плывущих вместе с жидкостью мелких тел
– например, эритроцитов в крови) обозначают
v и называют линейной скоростью. V=x/t.
Объём
V жидкости, протекающей в данном потоке
(в трубе, в русле реки, в кровеносном
сосуде и т.п.) за единицу времени. Эту
величину называют объёмной скоростью
и обозначают Q.
Между
линейной скоростью v и объёмной скоростью
Q существует простая связь. Рассмотрим
трубку с площадью поперечного сечения
S.
Выделим
поперечный слой жидкости, который в
момент времени t = 0 занимает положение
1. Через некоторое время t он переместится
в положение 2, отстоящее на расстояние
x= v*t. При этом через трубку пройдёт объём
жидкости V = S*x . Объёмная скорость
жидкости Q при этом будет равна Q
=v/t=s*x/t. Но x/t=v, тогда
Q
= S*V
В
реальных жидкостях всегда существуют
силы трения. В отличие от твёрдых тел,
где силы трения действуют между двумя
разными телами, в жидкостях силы трения
возникают внутри жидкости (между разными
её слоями). Поэтому трение в жидкостях
называют внутренним трением или
вязкостью.
Термин
„идеальная жидкость” подразумевает,
что при движении такой жидкости не
происходит диссипация энергии (переход
механической, энергии в тепло). Считалось,
что таких жидкостей не существует, но
в 1938 году академик П Л.Капица обнаружил,
что при температурах, очень близких к
абсолютному нулю, подобными свойствами
обладает жидкий гелий (Капица назвал
такое поведение гелия «сверхтекучестью».
Хотя
во всех остальных случаях движение
жидкости обязательно сопровождается
диссипацией энергии, понятие идеальной
жидкости (как, например, и понятие
идеального газа) имеет большое практическое
значение, потому что во многих случаях
формулы, выведенные для идеальной
жидкости, можно без больших ошибок
применять для движения реальных жидкостей
и газов. Наиболее интересным примером
является теорема Бернулли, Рассмотрим
горизонтальную трубку переменного
сечения, по которой течёт жидкость или
газ.
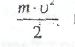
видеть, что кинетическая энергия жидкости
а правой части трубки больше, чем в
левой, потому что линейная скорость
жидкости справа больше, чем слева. Откуда
взялось это увеличение энергии ? Оно
произошло потому, что сила давления Кл
при перемещении какого-то объема жидкости
V производит некоторую работу А. По общей
формуле
но
сила давления
равна
самому давлению р, умноженному на площадь
S, то есть
. Отсюда
В
левой части трубки соответственно, в
правой части трубки
Разность работ слева и справа есть
но
мы уже несколько раз говорили, что через
любое сечение неразветвлённой трубки
проходит одинаковый объём жидкости, то
10
есть
V, =V2- Обозначая объём просто V и вынося
его за скобку, получим:
Так
как мы считаем жидкость идеальной
(потерь энергии нет), то разность работ
равна приросту кинетической энергии;
Если
разделить это равенство на объём, то
справа вместо массы будет стоять
плотность:
Перенося
члены с индексом 1 влево, а с индексом 2
направо,
получаем:
Члены
р и
соединены знаком „плюс”; отсюда
следует, что
их
размерность одинакова, то есть величина
тоже
имеет
смысл
давления. Её называют динамическим
давлением, а член р – статическим
давлением. Сумма статического и
динамического давлений, стоящая в
формуле называется полным давлением;
Так
как при выводе мы положения сечений 1
и 2 взяли произвольно,- то из равенства
(4) следует, что во всем потоке жидкости
или газа полное давление (то есть сумма
статического и динамического давлений)
есть величина постоянная:
Это
положение и, соответственно, формулы
(4) и (5) и принято называть теоремой.
Бернулли.
Статическое
давление – это то давление, которое
движущаяся жидкость оказывает на стенки
трубки. Его можно измерить, если плоскость
отверстия трубки манометра расположить
параллельно линиям тока жидкости
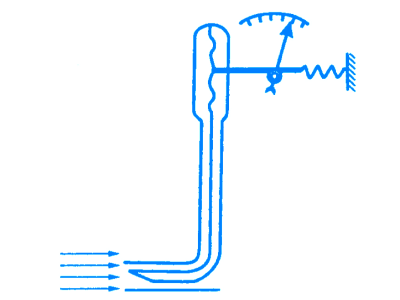
(рисунок 4-а). Если же плоскость отверстия
трубки-манометра будет перпендикулярна
линям тока, (рис. 4-6), то манометр покажет
полное давление. При расположении
манометра, как показано на рис. 4-в, мы
будем измерять разность между полным
и статическим давлениями, то есть
динамическое давление.
Из
теоремы Бернулли следует, что там, где
скорость жидкости или газа больше,
статическое давление меньше, и
наоборот.
From Wikipedia, the free encyclopedia
|
|
This article needs attention from an expert on the subject. The specific problem is: Lacks treatment of compressible flow. See the talk page for details. |
| Volume flow rate | |
|---|---|
|
Common symbols |
Q, V̇ |
| SI unit | m3/s |
| Dimension |  |
In physics and engineering, in particular fluid dynamics, the volumetric flow rate (also known as volume flow rate, or volume velocity) is the volume of fluid which passes per unit time; usually it is represented by the symbol Q (sometimes V̇). It contrasts with mass flow rate, which is the other main type of fluid flow rate. In most contexts a mention of rate of fluid flow is likely to refer to the volumetric rate. In hydrometry, the volumetric flow rate is known as discharge.
Volumetric flow rate should not be confused with volumetric flux, as defined by Darcy’s law and represented by the symbol q, with units of m3/(m2·s), that is, m·s−1. The integration of a flux over an area gives the volumetric flow rate.
The SI unit is cubic metres per second (m3/s). Another unit used is standard cubic centimetres per minute (SCCM). In US customary units and imperial units, volumetric flow rate is often expressed as cubic feet per second (ft3/s) or gallons per minute (either US or imperial definitions). In oceanography, the sverdrup (symbol: Sv, not to be confused with the sievert) is a non-SI metric unit of flow, with 1 Sv equal to 1 million cubic metres per second (260,000,000 US gal/s);[1][2] it is equivalent to the SI derived unit cubic hectometer per second (symbol: hm3/s or hm3⋅s−1). Named after Harald Sverdrup, it is used almost exclusively in oceanography to measure the volumetric rate of transport of ocean currents.
Fundamental definition[edit]
Volumetric flow rate is defined by the limit:[3]
That is, the flow of volume of fluid V through a surface per unit time t.
Since this is only the time derivative of volume, a scalar quantity, the volumetric flow rate is also a scalar quantity. The change in volume is the amount that flows after crossing the boundary for some time duration, not simply the initial amount of volume at the boundary minus the final amount at the boundary, since the change in volume flowing through the area would be zero for steady flow.
IUPAC[4] prefers the notation 


Useful definition[edit]
Volumetric flow rate can also be defined by:
where:
- v = flow velocity
- A = cross-sectional vector area/surface
The above equation is only true for flat, plane cross-sections. In general, including curved surfaces, the equation becomes a surface integral:
This is the definition used in practice. The area required to calculate the volumetric flow rate is real or imaginary, flat or curved, either as a cross-sectional area or a surface. The vector area is a combination of the magnitude of the area through which the volume passes through, A, and a unit vector normal to the area, 
.
The reason for the dot product is as follows. The only volume flowing through the cross-section is the amount normal to the area, that is, parallel to the unit normal. This amount is:
where θ is the angle between the unit normal 
These results are equivalent to the dot product between velocity and the normal direction to the area.
When the mass flow rate is known, and the density can be assumed constant, this is an easy way to get 
Where:
- ṁ = mass flow rate (in kg/s).
- ρ = density (in kg/m3).
[edit]
In internal combustion engines, the time area integral is considered over the range of valve opening. The time lift integral is given by:
where T is the time per revolution, R is the distance from the camshaft centreline to the cam tip, r is the radius of the camshaft (that is, R − r is the maximum lift), θ1 is the angle where opening begins, and θ2 is where the valve closes (seconds, mm, radians). This has to be factored by the width (circumference) of the valve throat. The answer is usually related to the cylinder’s swept volume.
Some key examples[edit]
- In cardiac physiology: the cardiac output
- In hydrology: discharge
- List of rivers by discharge
- List of waterfalls by flow rate
- Weir § Flow measurement
- In dust collection systems: the air-to-cloth ratio
See also[edit]
- Flow measurement
- Flowmeter
- Mass flow rate
- Orifice plate
- Poiseuille’s law
- Stokes flow
References[edit]
- ^ “Glossary”. Ocean Surface Currents. University of Miami Rosenstiel School of Marine and Atmospheric Science. Retrieved 2019-04-15.
- ^ “Sverdrups & Brine”. Ecoworld. Archived from the original on 20 January 2011. Retrieved 12 August 2017.
- ^ Engineers Edge, LLC. “Fluid Volumetric Flow Rate Equation”. Engineers Edge. Retrieved 2016-12-01.
- ^ International Union of Pure and Applied Chemistry ; https://iupac.org
- ^ “Volume flow rate, qv”. The IUPAC Compendium of Chemical Terminology. 2014. doi:10.1351/goldbook.V06642.
- ^ “Mass flow rate, qm”. The IUPAC Compendium of Chemical Terminology. 2014. doi:10.1351/goldbook.M03720.
- ^ “Heat, q, Q”. The IUPAC Compendium of Chemical Terminology. 2014. doi:10.1351/goldbook.H02752.