Формулы объема геометрических фигур
Объем геометрической фигуры
– количественная характеристика пространства, занимаемого телом или веществом. Объём тела или вместимость сосуда определяется его формой и линейными размерами.
Объем куба
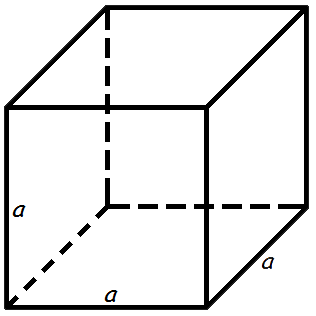
Объем куба равен кубу длины его грани.
Формула объема куба:
V = a3
где V – объем куба,
a – длина грани куба.
Объем призмы
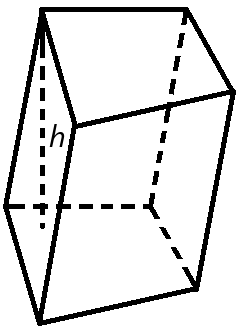
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы:
V = So h
где V – объем призмы,
So – площадь основания призмы,
h – высота призмы.
Объем параллелепипеда
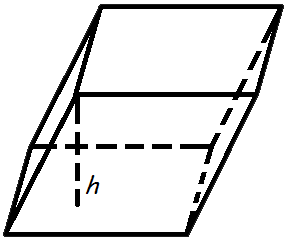
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда:
V = So · h
где V – объем параллелепипеда,
So – площадь основания,
h – длина высоты.
Объем прямоугольного параллелепипеда
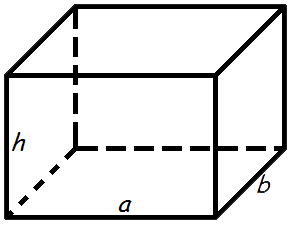
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда:
V = a · b · h
где V – объем прямоугольного параллелепипеда,
a – длина,
b – ширина,
h – высота.
Объем пирамиды
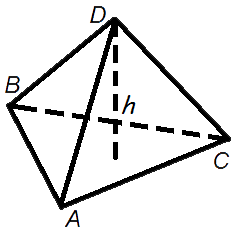
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды:
где V – объем пирамиды,
So – площадь основания пирамиды,
h – длина высоты пирамиды.
Объем правильного тетраэдра
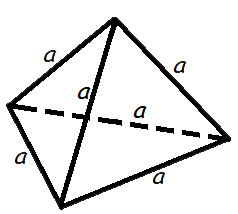
Формула объема правильного тетраэдра:
где V – объем правильного тетраэдра,
a – длина ребра правильного тетраэдра.
Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
V = π R2 h
V = So h
где V – объем цилиндра,
So – площадь основания цилиндра,
R – радиус цилиндра,
h – высота цилиндра,
π = 3.141592.
Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.
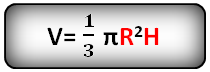
Формулы объема конуса:
где V – объем конуса,
So – площадь основания конуса,
R – радиус основания конуса,
h – высота конуса,
π = 3.141592.
Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.
Формула объема шара:
где V – объем шара,
R – радиус шара,
π = 3.141592.

a – сторона куба
Формула объема куба, (V):


a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
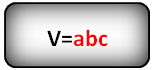

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

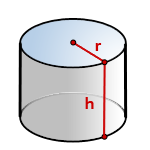
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

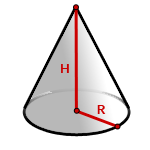
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
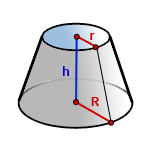
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

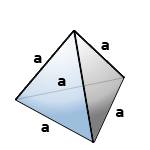
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
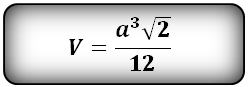
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
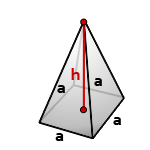
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
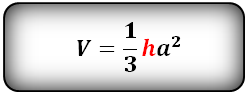
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
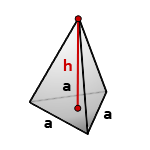
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
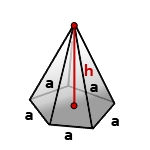
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
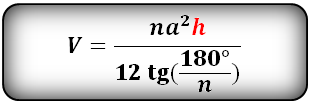
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
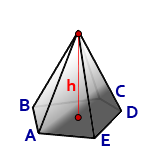
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
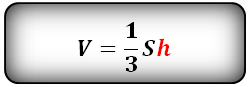
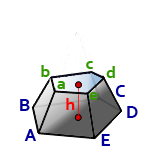
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
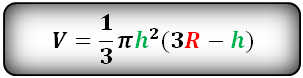
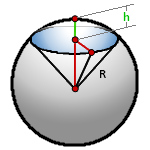
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

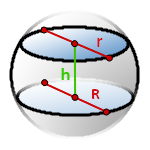
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
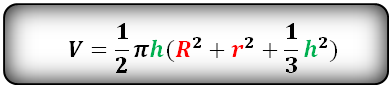
Приветствую Вас, уважаемые гости и подписчики моего канала!
Сегодня, хотел бы свою статью посвятить царице наук, а именно – математике! Являясь отцом двоих детей, я постоянно помогаю им с домашкой (домашними работами), в том числе и с математикой. Дочери в школе задали на лето около сотни задач, и, проверяя очередную, наткнулся в учебнике на интересный параграф, который называется в честь двух великих математиков: Формула Ньютона-Симпсона.
На самом же деле, она относится к высшей математике, а именно к приемам численного интегрирования, но благодаря своей простоте, проходят ее и в школьном курсе. С помощью одной единственной универсальной формулы Ньютона-Симпсона можно вычислять как площади фигур, так и объемы различных тел.
Формула выглядит следующим образом:
Если вычисляются объемы тел, то в качестве “b” берутся площади оснований и сечений, если же вычисляются площади, то “b” это длины оснований и отрезка по центру.
b1 – это длина или площадь нижнего основания;
b2 – это длина отрезка посередине фигуры или площадь сечения по центру тела;
b3 – это длина или площадь верхнего основания;
Проще на примерах…
1. Объемы
Итак, предположим нам требуется вычислить объем конуса или пирамиды. Геометрия нам говорит, что объем этих фигур равен:
V = (S*h)/3, где S – площадь основания, h – высота.
По формуле Ньютона-Симпсона это представляется так:
V=(Н/6)*(b1 + 4b2 + b3) или (Н/6)*(b1 + 4*(b1/4) + 0) = Н*b1/3.
Как вы видите формула Симпсона, путем преобразования, превращается в стандартную формулу, изучаемую в школе. Все то же самое можно проделать с цилиндром, призмой или шаром, а также с усеченными вариантами пирамиды и конуса.
В случаях с цилиндром и призмой, по формуле Ньютона-Симпсона у вас будет выведена формула объема, равная произведению высоты на основание b1, а в случае с шаром, получится реальная формула нахождения объема сферы: 4/3 *π*r³.
Уже за счет того, что формула применима для нахождения объемов самых известных геометрических фигур, она достойна называться универсальной. Кроме объема, как я уже ранее писал, с помощью нее можно вычислять и площади.
2. Площади
Итак…
Площадь любой произвольной трапеции:
S = h/6 * (b1 + 4(b1+b3)/2 + b3) = h/2 * (b1+b3)
Площадь треугольника:
S = h/6 * (b1 + 4(b1/2) + 0) = 1/2 *b*h
Площадь параллелограмма или правильного четырехугольника:
S = h/6 * (b1 + 4b1 + b1) = b*h
Что и требовалось доказать!
Формула очень проста и интересна, если Ваши детки не проходили ее в школе, считаю, что стоит им рассказать и показать.
А на этом всё, с Вами был Роман, канал “Строю для Себя”…
Всего доброго!
Многие сложные детали (конструкции) можно представить совокупностью различных элементов, объем которых можно вычислить, воспользовавшись набором online-калькуляторов с данной страницы.
Представлены программы для расчета объемов фигур, базисом которых является квадрат или прямоугольник, а также имеющих в основании окружность: цилиндра, конуса и шаровых элементов.
В конструкторской работе при различных расчетах возникает потребность использования значений объема элементарных фигур: параллелепипеда, куба, призмы и пр. В частности это может иметь место при расчете заполнения вагонов и платформ упакованной в транспортную тару готовой продукцией. Такой расчет требует учета многих факторов, в том числе боковой ветровой нагрузки, смещения центра тяжести и пр.
Если неправильно рассчитать объем тары подлежащего отгрузке упакованного товара, можно не вместить в вагон заявленное количество изделий. В результате предприятие потерпит убытки. Онлайн калькуляторы нашего сайта позволят избежать проблемных ситуаций. Расчеты объемов различных фигур выполняются с большой точностью.
Статьи
Среднее общее образование
Геометрия
Математика
Объемы геометрических тел
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
01 апреля 2019
Объемы геометрических тел
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
Определение объема
Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:
- V сохраняется при движениях.
- V удовлетворяет принципу Кавальери.
- Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
- Объем прямоугольного параллелепипеда V = abc.
Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.
В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.
Примеры
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
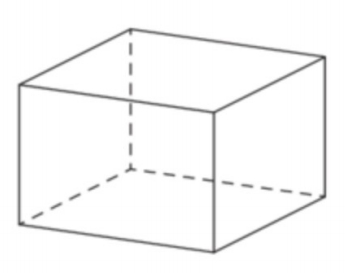
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
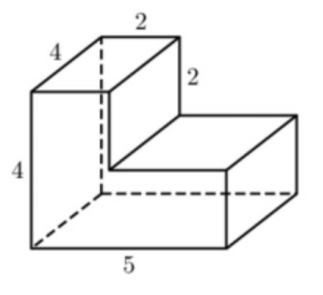
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Разберем, как можно вычислять объемы изучаемых в школе фигур.
Объем призмы
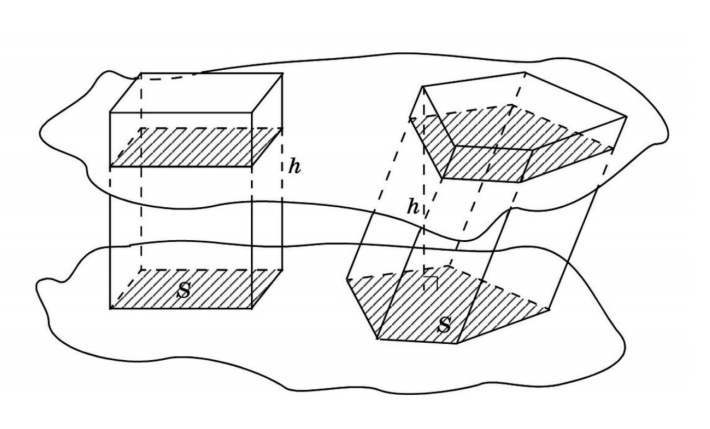
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф2) поместим прямоугольный параллелепипед (Ф1), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:
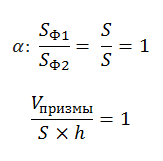
V Sосн h

Математика. Геометрия. Углублённый уровень. 11 класс. Задачник.
Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике.
Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.
Купить
Объем пирамиды
Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.
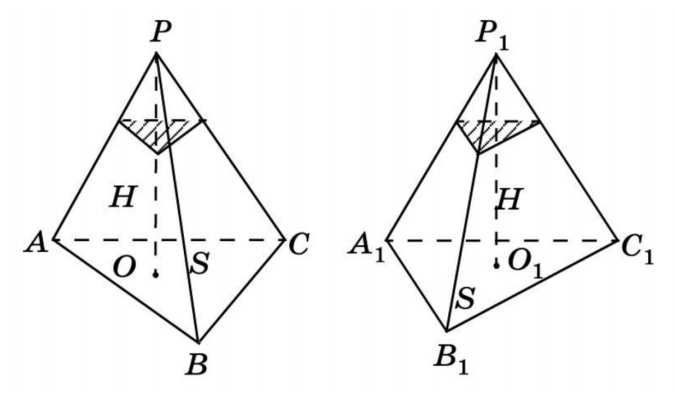
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V 1/V2 = 1 <=> V1 = V2
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:
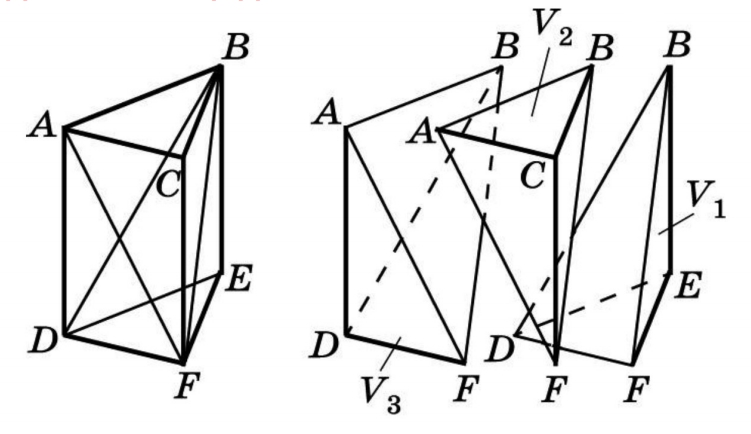
V1 = V2
V2 = V3
Vпризмы S h = 3V
V = 1/3 Sh
Объем цилиндра
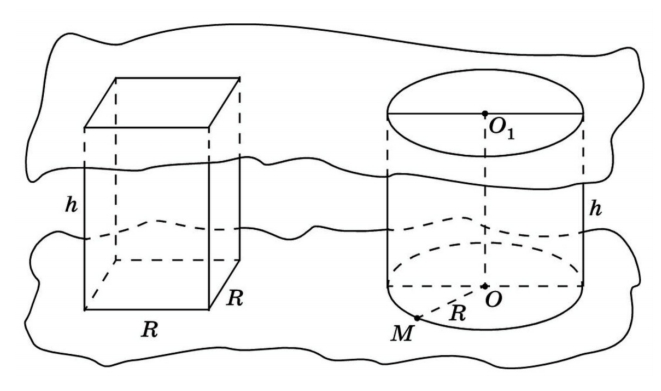
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

Vцил = πh × R2
Объем конуса
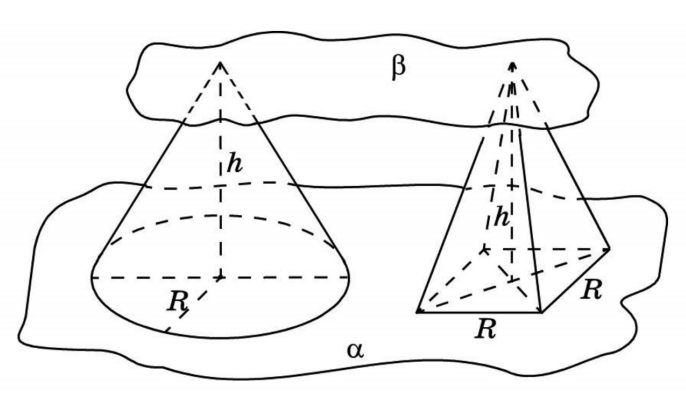
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.
SФ1/SФ2 = π

Vконуса = 1/3 πR2 h
Объем шара
Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.
Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.
Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR2. Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x2. Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R2 — x2).
Заметим, что: πR2 + πR2 — πR2 = πR2
Vцил = πR2 × R = πR3 = 1/3 R3 π + Vшара
Vшара = 4/3 πR3
Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.
#ADVERTISING_INSERT#
