Как найти область допустимого значения в дроби

        В предыдущем уроке мы с вами освоили основной принцип решения любых дробных уравнений. Это — ликвидация дробей. Кто читал, тот понял, что ничего сложного в этом нет.

        Однако, даже в самых простых (казалось бы!) дробных уравнениях нас может поджидать сюрприз не из приятных. С ним, с сюрпризом, надо разобраться! Разберёмся?)

Основная проблема в решении дробных уравнений.

        Сейчас мы с вами научимся обходить одну из самых коварных ловушек на ЕГЭ и контрольных! Попадаются в неё все — и троечники и отличники. Я специально поставил её в самое примитивное уравнение, чтобы с ней (с ловушкой) хорошенько разобраться. Но для начала посмотрим, попадёте вы в неё или нет.)

        Допустим, надо решить вот такое нехитрое уравнение:

        

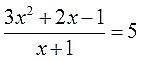
        Дело уже привычное и знакомое. Умножаем всё уравнение на знаменатель (х+1) и получаем:   

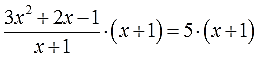
        Напоминаю, что со скобками (х+1) работаем целиком, как будто бы это одно число! Производим умножение:

        

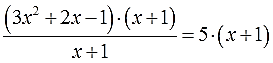
        Сокращаем знаменатель и избавляемся от дроби:

        

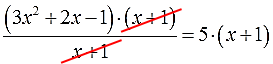
        3x² + 2x — 1 =  5(x+1)

        Раскрываем оставшиеся скобки, переносим всё влево, приводим подобные:

        3x² + 2x — 1 =  5x + 5

        3x² – 3x — 6 = 0

        Делим всё уравнение на 3 и получаем:

        х² — х — 2 = 0

        Отлично. Самое обычное квадратное уравнение. Решаем и получаем два корня:

        х₁ = -1

        х₂ = 2

        Предположим, в задании на ЕГЭ сказано записать в ответ меньший из корней, если корней более одного. Что писать будем?)

        Если вы решили, что ответ -1, то вы попали в ловушку. И задание вам не засчитают, да. Зря старались. Правильный ответ был 2… Два, а не минус один.

        Так в чём же дело? А вы попробуйте проверку сделать. Подставьте каждый из найденных иксов в исходное уравнение. И, если при х=2 у вас всё славненько срастётся, получится тождество 5=5, то при х=-1 получится деление на ноль! Чего делать нельзя категорически. Нет такой операции ни в природе, ни в математике…

        Что это значит? Это значит, что х=-1 — так называемый посторонний корень. Или лишний корень. Он не является корнем нашего дробного уравнения и в ответе никак не учитывается. Ибо его подстановка даёт бессмыслицу. Его мы просто отбрасываем. Окончательный корень один.

        А именно: х=2.

        Так, стоп, что-то тут не так! Нам же говорили, что всё уравнение можно умножать на одно и то же выражение! Это же тождественное преобразование!

        Да, тождественное. Я не спорю. Но при одном маленьком ограничении, которое многие попросту игнорируют. А именно — выражение, на которое умножаем (делим), отлично от нуля! А скобочка (х+1) при х=-1 обращается в ноль! Так что всё честно.

        И что нам теперь делать? Совсем не умножать? Тогда мы вообще ничего не решим! Каждый раз проверку делать? Это с ума сойдёшь. Особенно, если уравнение навороченное.

        Нет, мы с вами пойдём красивым и элегантным путём. Обратимся за помощью к трём волшебным буквам! Догадались? Да! Это ОДЗ! Область Допустимых Значений.

Что же такое ОДЗ?

        Это такие значения икса, которые могут быть в принципе. Или которые разрешены для данного примера.

        Например, в уравнении

        

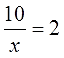
        мы ещё пока не знаем, чему равен икс, верно? Мы уравнение пока не решили. Но зато мы железно знаем, что икс не может равняться нулю ни в коем случае! На ноль делить нельзя. На любое другое число — целое, дробное, отрицательное, иррациональное — ради бога. А вот на ноль — никак. Стало быть, в этом примере ОДЗ:

        х — любое число, кроме нуля.

        Зато все остальные иксы — абсолютно безопасны. Хоть 41, хоть -17, хоть -1,3 — весь бесконечный набор чисел.

        Идея ясна?

        Как записывать ОДЗ? Как работать с ОДЗ?

        Тоже легко. На первом этапе всегда внимательно осматриваем исходный пример и ищем опасные места. Что значит опасные места?

        Это места, где возможны запретные действия. Действия, которые при каких-то иксах могут оказаться недопустимыми с точки зрения математики. В нашей теме такое действие всего одно — деление. Нельзя делить на ноль. Есть ещё запреты в корнях чётной степени, в логарифмах и в тригонометрии. Их мы тоже рассмотрим в соответствующих уроках.

        Как только опасные места найдены, рядышком с примером выписываем условия, которые не приводят к бессмыслице. После этого, глядя на эти условия, вычисляем запретные иксы. И исключаем их из ОДЗ. Вот и всё.

        Я специально акцентирую внимание на словах “исходный пример”. Любое преобразование (сокращение, приведение подобных и т.п.) может изменить ОДЗ, и мы можем получить неверный ответ.

        Важно! Для поиска ОДЗ мы не решаем пример! Мы решаем всего лишь маленькие кусочки примера для нахождения запретных иксов.

        “Многа букаффф”, да. Но на практике вся процедура выглядит до ужаса элементарно.

        Итак, берём наше уравнение:

        

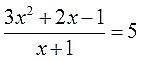
        Ничего пока что не трогаем, а внимательно осматриваем исходное уравнение. Осмотрев, мы сразу замечаем операцию деления на х+1.

        Это потенциально опасная операция: при каких-то значениях икса выражение х+1 может оказаться равным нулю. На который делить нельзя. Поэтому обезопасим себя вот такой записью:

        х+1 ≠ 0

        х ≠ -1

        Во-о-т. Минус один категорически не подходит нам в качестве ответа. Это и будет ОДЗ для нашего уравнения. Все иксы, кроме минус единички.

        На практике запись и нахождение ОДЗ обычно оформляют так:

        

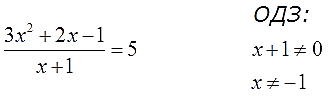
        Иногда ОДЗ записывают и в другой форме, через промежутки. Вот так:

        x ∈ (-∞; -1) U (-1; +∞)

        Читается эта запись так: “Икс принадлежит интервалу от минус бесконечности до минус единицы (не включая), и от минус единицы (не включая) до плюс бесконечности.”

        Перевод с математического на человеческий: “Икс — любое число, кроме минус единицы.”

        Вот и всё. Как только мы себя обезопасили такой записью, дальше мы имеем полное право делать с уравнением всё что хотим — переносить члены, домножать, сокращать… Вот и домножаем всё уравнение на (х+1). Дробь-то убирать всё равно надо! Это по-прежнему будет не совсем тождественным преобразованием, но все вредные последствия от нарушения тождественности мы исключим по ОДЗ.

        Умножаем:

        3x² + 2x — 1 =  5(x+1)

        Как вы думаете, в какой же момент мы с вами попали в ловушку элементарного примера? Как раз в момент домножения всего уравнения на знаменатель дроби! Знаменатель исчез, и вместе с ним исчезли и соответствующие ограничения на иксы. Бесследно. И для нового уравнения, без дроби, на икс уже не накладывается никаких запретов! Любым может быть икс…

        В математике это явление называется расширение ОДЗ.

        Но теперь мы уже с вами народ бдительный. Исходные ограничения (х≠-1) мы записали и сохранили.

        Поэтому дальше спокойно решаем уравнение безо всяких дробей и получаем два корня:

        х₁ = -1

        х₂ = 2

        А вот теперь стыкуем наши результаты и условия ОДЗ. И видим в наших кандидатах на ответ один из иксов в качестве запретного! Минус один. Это означает, что в окончательный ответ его включать нельзя. Это посторонний корень, появившийся в процессе решения без нашего желания.

        Да, это законный корень нашего вспомогательного квадратного уравнения, но никак не корень исходного дробного уравнения!

        Стало быть, минус единицу мы безжалостно вычёркиваем и в ответ не включаем. Вот и всё.)

        А в других уравнениях прошлого урока? Там что, нет ОДЗ? Есть, разумеется. Есть деление на икс — есть и ОДЗ.

        В первом уравнении:

        

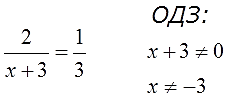
        Во втором уравнении:

        

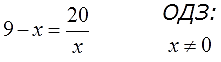
        И так далее.

        Я специально в тех примерах ничего не сказал про ОДЗ. Чтобы вас не перегрузить раньше времени.) В всех уравнениях прошлого урока (и домашнего задания к нему) ОДЗ никак не сказывалась на ответе. Так бывает. Но в заданиях ОГЭ и ЕГЭ ОДЗ в 99% случаев влияет на ответ! Так что мы с ОДЗ дружить будем. И во всех темах, где это необходимо, мы будем про ОДЗ вспоминать. Чтобы не упасть лицом в грязь.)

        Итак, про ОДЗ поговорили. Убедились, что работать с ней тоже совсем не сложно. Теперь можно перейти и к общему алгоритму решения любого дробного уравнения.

Решаем дробные уравнения по алгоритму!

        Для успешного решения любого дробного уравнения необходимо выполнить (правильно) пять пунктов:

        1. Разложить знаменатели всех дробей на множители (если требуется). До упора. Переписать уравнение с учётом этого факта.

        2. Найти ОДЗ, записать рядышком с уравнением и временно (до конца решения) забыть про неё.

        3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.

        4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Найти решения (кандидаты в ответ).

        5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.

        А теперь, вооружившись таким мощным супероружием, как ОДЗ, и общим алгоритмом, разберём очередной пример. Супердетально разберём!

        Решить уравнение:

        

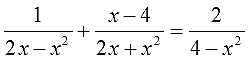
        Решаем строго по пунктам. Выполняем пункт первый:

        1. Разложить все знаменатели на множители (если требуется). До упора. Переписать пример с учётом этого факта.

        Знаменатели наших дробей НЕ разложены на множители. Вот и приступаем. Вынесение общего множителя за скобки и формула разности квадратов — мощные штуки.)

        2x — x² = x(2-x)

        2x + x² = x(2+x)

        4 — x² = 2² — x² = (2-x)(2+x)

        Вот так. А теперь переписываем уравнение с учётом наших разложений:

        

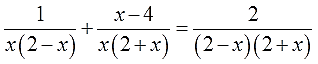
        Готово. Все знаменатели разложены до упора.) Можно приступать ко второму пункту.

        2. Найти ОДЗ, записать рядышком с примером и временно (до конца решения) забыть про неё.

        Итак, начинаем осматривать исходный пример на наличие опасных операций.

        Внимание! Ничего не трогаем и не решаем! Не складываем дроби, не приводим подобные, не сокращаем!!!

        Подобные преобразования запросто могут изменить ОДЗ, что может привести к неверному ответу! Оно нам надо?! Ещё раз напоминаю: ДО поиска ОДЗ с исходным примером мы не делаем НИЧЕГО! Кроме разложения на множители. Оно — безопасно и даже полезно.)

        Берём и именно осматриваем исходный пример. И замечаем три опасных места: каждая из дробей таит в себе возможное деление на ноль.

        Вот и пишем:

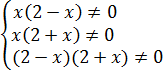
        Знак системы (фигурная скобка) здесь не зря поставлен. Она означает, что все три условия должны выполняться одновременно! Мы ведь ОДЗ записываем не для каждой дроби по отдельности, а для всего примера целиком.)

        Ну и как? Нашли ОДЗ? Не-а…)

        Мы записали кусочек примера, записали три требования, которые должны выполняться железно. Но этого мало. Нужно ещё найти иксы, которые обеспечивают эти железные требования. ОДЗ ведь к иксам относится, а не к кусочкам примера…

        Как же найти значения иксов, которые не превращают знаменатели дробей в ноль? Их же очень много? Очень просто! Мы поступим элегантно. Найдём иксы, которые наоборот, превращают знаменатели дробей в ноль. Это и будут запретные иксы.

        Вот и решаем эти неравенства методом “от противного”. То есть, делаем из неравенств уравнения:

        x(2-x) = 0

        x(2+x) = 0

        (2-x)(2+x) = 0

        Именно из этих трёх уравнений мы и будем искать запретные иксы. Уравнения очень простые: произведение равно нулю, когда хотя бы один из множителей равен нулю. Вот и приравниваем (в уме или на черновике) каждый множитель к нулю.

        Для первого уравнения получаем: x₁ = 0;  x₂ = 2.

        Вспомнив, что это запретные иксы, получим:

        х ≠ 0;  x ≠ 2.

        Точно так же решаем и два оставшихся уравнения.

        Для второго уравнения получаем:

        x ≠ 0;  x ≠ -2.

        И, наконец, для третьего уравнения получаем:

        x ≠ 2;  x ≠ -2.

        Видно, что некоторые запретные значения иксов повторяются. Разумеется, для окончательной записи ОДЗ мы их не будем дублировать. Итого ОДЗ для нашего уравнения будет выглядеть вот так:

        ОДЗ:

        

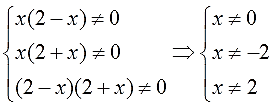
        Видите, насколько полезно предварительно раскладывать знаменатели на множители! В уме ОДЗ ищется! Поэтому эта процедура и стоит первым пунктом в алгоритме.)

        Можно приступать к третьему пункту.

        3. Сообразить, на что надо умножить обе части уравнения, чтобы все дроби исчезли полностью.

        И тут разложение на множители тоже здорово играет на руку!

        Понятно, что для ликвидации первой дроби, надо её домножать на x(2-x), вторую — на x(2+x) и третью – на (2-x)(2+x).

        Но чтобы сразу сократить все дроби, надо скомбинировать такое выражение, которое одинаково хорошо делится и на х(2-х), и на х(2+х), и на (2-х)(2+х).

        Вот оно, это выражение:

        х(2-x)(2+x)

        Как же я до него додумался? Очень просто: составил произведение всех неповторяющихся множителей всех знаменателей. Чтобы ничего не забыть и лишнего не взять.) Приступаем к четвёртому пункту:

        4. Выполнить это самое умножение и решить новое уравнение, уже безо всяких дробей. Получить решения (кандидаты в ответ).

        Итак, умножаем:

        

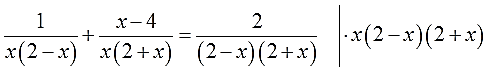
        И снова, чтобы не заплутать в трёх соснах, используем скобки:

        

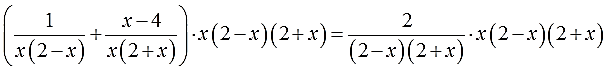
        Производим умножение. Большие скобки раскрываем, малые — не трогаем!

        

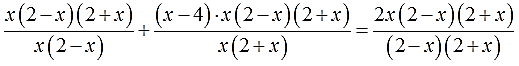
        Сокращаем все дроби:

        

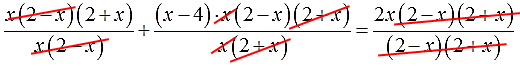
        2 + x + (x-4)(2-x) = 2x

        Всё. От дробей избавились. Как обычно, раскрываем оставшиеся скобки, приводим подобные и собираем все члены слева:

        2 + x + 2x — x2 — 8 + 4x — 2x = 0

        –х² + 5x — 6 = 0

        Помним, что минус впереди крайне неудобен, посему умножаем всё на (-1):

        x² — 5x + 6 = 0

        Решаем простенькое квадратное уравнение и получаем корни:

        x₁ = 2

        x₂ = 3

        Нашли кандидатов в ответ. Самое время вспомнить про ОДЗ. Про самый последний пункт:

        5. Вспомнить про ОДЗ и состыковать найденные решения с условиями ОДЗ. Те решения, которые не входят в ОДЗ, безжалостно выбросить. Записать окончательный ответ.

Итак, наши решения:

        x₁ = 2

        x₂ = 3

        Условия ОДЗ:

        

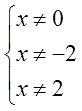
        Сопоставляем и… Оп-па! А ведь двойка — запретное значение! Нас не проведёшь! ОДЗ — штука жёсткая. В отвал двойку!

        Окончательный ответ: х = 3.

        Именно так и решаются все дробные уравнения. В пять шагов. Зачем же я распинался, рассказывая целый урок про избавление от дробей, затем ещё пол-урока про ОДЗ? Мог бы сразу дать общий алгоритм и соответствующий пример!

        На этот вопрос отвечу так. Если бы вы знали, сколько народу спотыкается на применении тупо заученного алгоритма! А уж при малейшем отклонении от шаблона простой пример становится вообще нерешаемым… Если понимать смысл, то шанс решить есть всегда. Понимание всегда побеждает механическую память.)

        Вот, собственно, и всё, что я хотел сказать. И напоследок очередная порция примеров для самостоятельного решения.

        Решить уравнения:

        

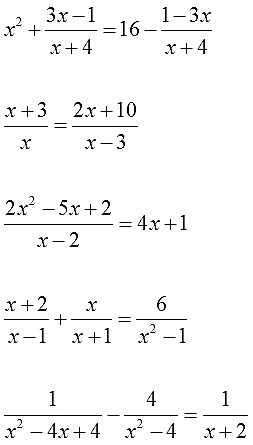
        Ответы (по традиции, в беспорядке):

        x = 3

        x = -1

        x = 4

        x₁ = -1;  x₂ = -9

        x = -2

        Всё совпало! Поздравляю! У вас иксов побольше будет? Хм… Про ОДЗ не забыли, случаем? Кое-какие корни выбрасывать надо! ОДЗ учли, а всё равно не выходит? Да-а-а… Проблемка. Такие уравнения надо уметь решать: слишком уж они популярны во многих темах математики. Особенно — в текстовых задачках! Но не отчаивайтесь!

        Перечитайте этот и предыдущий уроки ещё раз и прогуляйтесь по смежным темам: разложение на множители, квадратные уравнения, линейные уравнения и (особенно!) тождественные преобразования уравнений. И всё получится. Я в вас верю!)

Область допустимых значений функции

О чем эта статья:

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.

Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c).

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных — недопустимые.

Подставим значения переменных в выражение

На ноль делить нельзя.

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Пример 2

Рассмотрим выражение

ОДЗ такого выражения выглядит следующим образом: ( – ∞; 3) ∪ (3; +∞).

Читать запись нужно вот так:
Область допустимых значений переменной x для выражения — это числовое множество ( – ∞; 3) ∪ (3; +∞).

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.

Мы не можем вычислить значение выражения, если:

• требуется извлечение квадратного корня из отрицательного числа;
• присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.

ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.

Это значит, что мы может сказать, что ОДЗ переменной a в выражении — пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Запомните

• Если число входит в ОДЗ, то около числа ставим квадратные скобки.
• Если число не входит в ОДЗ, то около него ставятся круглые скобки.

Например, если х > 6, но х

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

• расширить ОДЗ
• никак не повлиять на ОДЗ
• сузить ОДЗ

Рассмотрим каждый случай в отдельности.

Пример 7

Рассмотрим выражение a + 4/a – 4/a

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.

ОДЗ для a — это R — множество всех вещественных чисел.

Преобразование расширило ОДЗ — добавился ноль.

Пример 8

Рассмотрим выражение a 2 + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование.

После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ.

Пример 9

Рассмотрим выражение

ОДЗ a определяется неравенством (a – 1) * (a – 4) ≥ 0.

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

ОДЗ переменной a для этого выражения определяется неравенствами:
a – 1 ≥ 0
a – 4 ≥ 0

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Область допустимых значений (ОДЗ): теория, примеры, решения

Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.

В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.

Допустимые и недопустимые значения переменных

Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.

Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.

Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.

Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.

Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.

То есть отсюда следует полное определение

Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.

Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.

Для примера рассмотрим выражение вида 1 x – y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 – 1 + 2 = 1 1 = 1 . Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 – 2 + 1 = 1 0 .

Что такое ОДЗ?

Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.

Область ОДЗ – это множество значений, допустимых для данного выражения.

Рассмотрим на примере выражения.

Если имеем выражение вида 5 z – 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.

Если имеется выражения вида z x – y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.

Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .

Как найти ОДЗ? Примеры, решения

Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.

Существуют выражения, где их вычисление невозможно:

• если имеется деление на ноль;
• извлечение корня из отрицательного числа;
• наличие отрицательного целого показателя – только для положительных чисел;
• вычисление логарифма отрицательного числа;
• область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
• нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ – 1 ; 1 ] .

Все это говорит о том, как важно наличие ОДЗ.

Найти ОДЗ выражения x 3 + 2 · x · y − 4 .

Решение

В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.

Ответ: x и y – любые значения.

Найти ОДЗ выражения 1 3 – x + 1 0 .

Решение

Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.

Ответ: ∅ .

Найти ОДЗ заданного выражения x + 2 · y + 3 – 5 · x .

Решение

Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.

Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .

Определить ОДЗ выражения вида 1 x + 1 – 1 + log x + 8 ( x 2 + 3 ) .

Решение

По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 – 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:

x + 1 – 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1

Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .

Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )

Почему важно учитывать ОДЗ при проведении преобразований?

При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.

• могут не влиять на ОДЗ;
• могут привести в расширению или дополнению ОДЗ;
• могут сузить ОДЗ.

Рассмотрим на примере.

Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.

Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.

Рассмотрим пример с наличием подкоренного выражения.

Если имеется x – 1 · x – 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x – 1 · x – 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x – 1 ≥ 0 , x – 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .

Нужно избегать преобразований, которые сужают ОДЗ.

Рассмотрим пример выражения x – 1 · x – 3 , когда х = – 1 . При подстановке получим, что – 1 – 1 · – 1 – 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x – 1 · x – 3 , тогда при вычислении получим, что 2 – 1 · 2 – 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.

Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.

Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.

Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.

При наличии логарифмов дело обстоит немного иначе.

Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.

При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.

Уравнения, часть С

Теория к заданию 13 из ЕГЭ по математике (профильной)

Уравнения, часть $С$

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, – правой частью уравнения.

Схема решения сложных уравнений:

1. Перед решением уравнения надо для него записать область допустимых значений (ОДЗ).
2. Решить уравнение.
3. Выбрать из полученных корней уравнения то, которые удовлетворяют ОДЗ.

ОДЗ различных выражений (под выражением будем понимать буквенно – числовую запись):

1. Выражение, стоящее в знаменателе, не должно равняться нулю.

2. Подкоренное выражение, должно быть не отрицательным.

3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.

4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.

Логарифмические уравнения

Для решения логарифмических уравнений необходимо знать свойства логарифмов: все свойства логарифмов мы будем рассматривать для $a > 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

4. При умножении двух логарифмов можно поменять местами их основания

6. Формула перехода к новому основанию

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

Можно выделить несколько основных видов логарифмических уравнений:

Представим обе части уравнения в виде логарифма по основанию $2$

Если логарифмы по одинаковому основанию равны, то подлогарифмические выражения тоже равны.

Т.к. основания одинаковые, то приравниваем подлогарифмические выражения

Перенесем все слагаемые в левую часть уравнения и приводим подобные слагаемые

Проверим найденные корни по условиям $table< x^2-3x-5>0; 7-2x>0;$

При подстановке во второе неравенство корень $х=4$ не удовлетворяет условию, следовательно, он посторонний корень

• Метод замены переменной.

В данном методе надо:

Решите уравнение $log_<2>√x+2log_<√x>2-3=0$

1. Запишем ОДЗ уравнения:

$table< х>0,text”так как стоит под знаком корня и логарифма”; √х≠1→х≠1;$

2. Сделаем логарифмы по основанию $2$, для этого воспользуемся во втором слагаемом правилом перехода к новому основанию:

3. Далее сделаем замену переменной $log_<2>√x=t$

4. Получим дробно – рациональное уравнение относительно переменной t

Приведем все слагаемые к общему знаменателю $t$.

Дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю.

5. Решим полученное квадратное уравнение по теореме Виета:

6. Вернемся в п.3, сделаем обратную замену и получим два простых логарифмических уравнения:

Прологарифмируем правые части уравнений

Приравняем подлогарифмические выражения

Чтобы избавиться от корня, возведем обе части уравнения в квадрат

7. Подставим корни логарифмического уравнения в п.1 и проверим условие ОДЗ.

Первый корень удовлетворяет ОДЗ.

$<table 16 >0; 16≠1;$ Второй корень тоже удовлетворяет ОДЗ.

• Уравнения вида $log_x+log_x+c=0$. Такие уравнения решаются способом введения новой переменной и переходом к обычному квадратному уравнению. После того, как корни уравнения будут найдены, надо отобрать их с учетом ОДЗ.

Дробно рациональные уравнения

• Если дробь равна нулю, то числитель равен нулю, а знаменатель не равен нулю.
• Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно-рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

1. Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. Найти общий знаменатель дробей, входящих в уравнение;
3. Умножить обе части уравнения на общий знаменатель;
4. Решить получившееся целое уравнение;
5. Исключить из его корней те, которые не удовлетворяют условию ОДЗ.

• Если в уравнении участвуют две дроби и числители их равные выражения, то знаменатели можно приравнять друг к другу и решить полученное уравнение, не обращая внимание на числители. НО учитывая ОДЗ всего первоначального уравнения.

Показательные уравнения

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

4. При возведении в степень произведения в эту степень возводится каждый множитель

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

6. При возведении любого основания в нулевой показатель степени результат равен единице

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

8. Радикал (корень) можно представить в виде степени с дробным показателем

Виды показательных уравнений:

1. Простые показательные уравнения:

а) Вида $a^=a^$, где $а >0, a≠1, x$ – неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием ($а >0, a≠1$) равны только тогда, когда равны их показатели.

b) Уравнение вида $a^=b, b>0$

Для решения таких уравнений надо обе части прологарифмировать по основанию $a$, получается

2. Метод уравнивания оснований.

3. Метод разложения на множители и замены переменной.

• Для данного метода во всем уравнении по свойству степеней надо преобразовать степени к одному виду $a^$.
• Сделать замену переменной $a^=t, t > 0$.
• Получаем рациональное уравнение, которое необходимо решить путем разложения на множители выражения.
• Делаем обратные замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^=t$, решаем его и результат записываем в ответ.

По свойству степеней преобразуем выражение так, чтобы получилась степень 2^x.

Сделаем замену переменной $2^x=t; t>0$

Получаем кубическое уравнение вида

Умножим все уравнение на $2$, чтобы избавиться от знаменателей

Разложим левую часть уравнения методом группировки

Вынесем из первой скобки общий множитель $2$, из второй $7t$

Дополнительно в первой скобке видим формулу разность кубов

Далее скобку $(t-1)$ как общий множитель вынесем вперед

Произведение равно нулю, когда хотя бы один из множителей равен нулю

Решим первое уравнение

Решим второе уравнение через дискриминант

Получили три корня, далее делаем обратную замену и получаем три простых показательных уравнения

4. Метод преобразования в квадратное уравнение

• Имеем уравнение вида $А·a^<2f(x)>+В·a^+С=0$, где $А, В$ и $С$ – коэффициенты.
• Делаем замену $a^=t, t > 0$.
• Получается квадратное уравнение вида $A·t^2+B·t+С=0$. Решаем полученное уравнение.
• Делаем обратную замену с учетом того, что $t > 0$. Получаем простейшее показательное уравнение $a^=t$, решаем его и результат записываем в ответ.

Способы разложения на множители:

• Вынесение общего множителя за скобки.

Чтобы разложить многочлен на множители путем вынесения за скобки общего множителя надо:

1. Определить общий множитель.
2. Разделить на него данный многочлен.
3. Записать произведение общего множителя и полученного частного (заключив это частное в скобки).

Разложить на множители многочлен: $10a^<3>b-8a^<2>b^2+2a$.

Общий множитель у данного многочлена $2а$, так как на $2$ и на «а» делятся все члены. Далее найдем частное от деления исходного многочлена на «2а», получаем:

Это и есть конечный результат разложения на множители.

Применение формул сокращенного умножения

1. Квадрат суммы раскладывается на квадрат первого числа плюс удвоенное произведение первого числа на второе число и плюс квадрат второго числа.

2. Квадрат разности раскладывается на квадрат первого числа минус удвоенное произведение первого числа на второе и плюс квадрат второго числа.

3. Разность квадратов раскладывается на произведение разности чисел и их сумму.

4. Куб суммы равен кубу первого числа плюс утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа плюс куб второго числа.

5. Куб разности равен кубу первого числа минус утроенное произведение квадрата первого на второе число плюс утроенное произведение первого на квадрат второго числа и минус куб второго числа.

6. Сумма кубов равна произведению суммы чисел на неполный квадрат разности.

7. Разность кубов равна произведению разности чисел на неполный квадрат суммы.

Метод группировки

Методом группировки удобно пользоваться, когда на множители необходимо разложить многочлен с четным количеством слагаемых. В данном способе необходимо собрать слагаемые по группам и вынести из каждой группы общий множитель за скобку. У нескольких групп после вынесения в скобках должны получиться одинаковые выражения, далее эту скобку как общий множитель выносим вперед и умножаем на скобку полученного частного.

Разложить многочлен на множители $2a^3-a^2+4a-2$

Для разложения данного многочлена применим метод группировки слагаемых, для этого сгруппируем первые два и последние два слагаемых, при этом важно правильно поставить знак перед второй группировкой, мы поставим знак + и поэтому в скобках запишем слагаемые со своими знаками.

Далее из каждой группы вынесем общий множитель

После вынесения общих множителей получили пару одинаковых скобок. Теперь данную скобку выносим как общий множитель.

Произведение данных скобок – это конечный результат разложения на множители.

С помощью формулы квадратного трехчлена.

Если имеется квадратный трехчлен вида $ax^2+bx+c$, то его можно разложить по формуле

$ax^2+bx+c=a(x-x_1)(x-x_2)$, где $x_1$ и $x_2$ – корни квадратного трехчлена

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/vyrazhenija/oblast-dopustimyh-znachenij-odz/

http://examer.ru/ege_po_matematike/teoriya/logarifmicheskie_i_pokazatelnue_uravneniya

[/spoiler]

В этой статье я подробно расскажу о том, что такое область допустимых значений (ОДЗ) выражения, опишу, как её искать, приведу несколько примеров с поиском ОДЗ выражений, содержащих дроби, корни чётных степеней и логарифмы.

Что такое ОДЗ выражения

Область допустимых значений выражения (ОДЗ выражения) – это множество значений переменной, при которых выражение имеет смысл.

Хочу заострить внимание читателя на некоторых ключевых моментах определения:

Во-первых, аббревиатура ОДЗ употребляется вместе с термином выражение, то есть термин “ОДЗ выражения” является более правильным, чем “ОДЗ“, но почему-то в устной речи школьников, репетиторов и учителей чаще можно услышать именно второй (“менее правильный”) вариант.

Во-вторых, ОДЗ выражения – это множество. Поэтому формально следующая запись является некорректной:

Дело в том, что запись “х >= 5” НЕ является множеством, а является предикатом (то есть высказыванием, содержащим переменную). Другими словами, выше записано следующее: “утверждение – это множество”. Но утверждение это не множество. Утверждение – это один математический объект, а множество – другой. Более корректная запись выглядит так:

Здесь всё записано корректно: “множество – это множество”. На ЕГЭ к таким тонкостям не придираются и баллы не снимают, но строгое отношение к терминам позволит быстрее и глубже разобраться в теме. Поэтому запоминаем, что ОДЗ выражения – это множество!

Как искать ОДЗ выражений

Поиск ОДЗ выражений обычно проводят в том случае, если выражение содержит дроби, корни чётных степеней или логарифмы. При этом используют следующие правила поиска ОДЗ выражений:

Эти правила не описывают поиск ОДЗ выражений, содержащих тригонометрических функции и степени. Про поиск ОДЗ выражений с тригонометрическими функциями и степенями будет отдельная статья.

Примеры поиска ОДЗ выражений

Ниже представлены 3 картинки с поиском ОДЗ выражений. Используйте стрелочки справа и слева, чтобы листать изображения:

Если вам понравилась статья, не забудьте поставить палец вверх. Если остались вопросы – задавайте их в комментариях. Спасибо за внимание!

Определение и примеры алгебраических дробей

Рациональные выражения делятся на целые и дробные выражения.

                         

Вычисление значения алгебраической дроби и две основные задачи на дроби

Рассмотрим первую типовую задачу: вычисление значения рациональной дроби при различных значениях входящих в нее переменных.

Пример 1. Вычислить значение дроби  при а) , б) ,    в)

Решение. Подставим значения переменных в указанную дробь: а) , б) , в)  – не существует (т. к. на ноль делить нельзя).

Ответ: а) 3; б) 1; в) не существует.

Как видим, возникает две типовые задачи для любой дроби: 1) вычисление дроби, 2) нахождение допустимых и недопустимых значений буквенных переменных.

Определение. Допустимые значения переменных – значения переменных, при которых выражение имеет смысл. Множество всех допустимых значений переменных называется ОДЗ или область определения.

Допустимые (ОДЗ) и недопустимые значения переменных в дробях с одной переменной

Значение буквенных переменных может оказаться недопустимым, если знаменатель дроби при этих значениях равен нулю. Во всех остальных случаях значение переменных являются допустимыми, т. к. дробь можно вычислить.

Пример 2. Установить, при каких значениях переменной не имеет смысла дробь .

Решение. Чтобы данное выражение имело смысл, необходимо и достаточно, чтобы знаменатель дроби не равнялся нулю. Таким образом, недопустимыми будут только те значения переменной, при которых знаменатель будет равняться нулю. Знаменатель дроби , поэтому решим линейное уравнение:

.

Следовательно, при значении переменной  дробь не имеет смысла.

Ответ: -5.

Из решения примера вытекает правило нахождения недопустимых значений переменных – знаменатель дроби приравнивается к нулю и находятся корни соответствующего уравнения.

Рассмотрим несколько аналогичных примеров.

Пример 3. Установить, при каких значениях переменной не имеет смысла дробь.

Решение. .

Ответ. .

Пример 4. Установить, при каких значениях переменной не имеет смысла дробь .

Решение..

Встречаются и другие формулировки данной задачи – найти область определения или область допустимых значений выражения (ОДЗ). Это означает – найти все допустимые значения переменных. В нашем примере – это все значения, кроме . Область определения удобно изображать на числовой оси.

Для этого на ней выколем точку , как это указано на рисунке:

Рис. 1

Таким образом, областью определения дроби будут все числа, кроме 3.

Ответ..

Пример 5. Установить, при каких значениях переменной не имеет смысла дробь .

Решение..

Изобразим полученное решение на числовой оси:

Рис. 2

Ответ..

Графическое представление области допустимых (ОДЗ) и недопустимых значений переменных в дробях

Пример 6. Установить, при каких значениях переменных не имеет смысла дробь .

Решение.. Мы получили равенство двух переменных, приведем числовые примеры:  или  и т. д.

Изобразим это решение на графике в декартовой системе координат:

Рис. 3. График функции 

Координаты любой точки, лежащей на данном графике, не входят в область допустимых значений дроби.

Ответ. .

Случай типа “деление на ноль”

В рассмотренных примерах мы сталкивались с ситуацией, когда возникало деление на ноль. Теперь рассмотрим случай, когда возникает более интересная ситуация с делением типа .

Пример 7. Установить, при каких значениях переменных не имеет смысла дробь .

Решение..

Получается, что дробь не имеет смысла при . Но можно возразить, что это не так, потому что: .

Может показаться, что если конечное выражение равно 8 при , то и исходное тоже возможно вычислить, а, следовательно, имеет смысл при . Однако, если подставить  в исходное выражение, то получим  – не имеет смысла.

Ответ..

Чтобы подробнее разобраться с этим примером, решим следующую задачу: при каких значениях  указанная дробь равна нулю?

 (дробь равна нулю, когда ее числитель равен нулю) . Но необходимо решить исходное уравнение с дробью, а она не имеет смысла при , т. к. при этом значении переменной знаменатель равен нулю. Значит, данное уравнение имеет только один корень .

Правило нахождения ОДЗ

Таким образом, можем сформулировать точное правило нахождения области допустимых значений дроби: для нахождения ОДЗ дроби необходимо и достаточно приравнять ее знаменатель к нулю и найти корни полученного уравнения.

Мы рассмотрели две основные задачи: вычисление значения дроби при указанных значениях переменных и нахождение области допустимых значений дроби.

Рассмотрим теперь еще несколько задач, которые могут возникнуть при работе с дробями.

Разные задачи и выводы

Пример 8. Докажите, что при любых значениях переменной дробь .

Доказательство. Числитель – число положительное. . В итоге, и числитель, и знаменатель – положительные числа, следовательно, и дробь является положительным числом.

Доказано.

Пример 9. Известно, что , найти .

Решение. Поделим дробь почленно . Сокращать на  мы имеем право, с учетом того, что  является недопустимым значением переменной для данной дроби.

Ответ..

На данном уроке мы рассмотрели основные понятия, связанные с дробями. На следующем уроке мы рассмотрим основное свойство дроби.

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Фестиваль педагогических идей (Источник).
2. Старая школа (Источник).

Домашнее задание

1. №4, 7, 9, 12, 13, 14. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Запишите рациональную дробь, областью определения которой является: а) множество , б) множество , в) вся числовая ось.
3. Докажите, что при всех допустимых значениях переменной  значение дроби  неотрицательно.
4. Найдите область определения выражения . Указание: рассмотреть отдельно два случая: когда знаменатель нижней дроби равен нулю и когда знаменатель исходной дроби равен нулю.

Целые рациональные уравнения

Если в уравнении нет переменной (x) в знаменателе, то такое уравнение называется целым. Или, другими словами, нигде в уравнении нет деления на переменную.
Метод решения целых рациональных уравнений сильно зависит от того, какой степени перед вами уравнения.

Степень уравнения – это максимальная степень у переменной (x).

Например, уравнение (x^2+5x-1=0) будет второй степени, так как есть (x^2).
Пример уравнения первой степени: (5x-1=17);
Уравнение третьей степени: (5x^3-3x^2=0);
Уравнение четвертой степени: (7x^4-5x^2+x-5=0);
И т.д.

Основной алгоритм решения целых уравнений:

• Если есть скобки, раскрываем их;
• Перекидываем все слагаемые в левую часть так, чтобы в правой части остался только (0). Не забываем при этом менять знак этих слагаемых;
• Приводим подобные слагаемые;
• Если получилось уравнение первой степени (в уравнении есть только (x)), то решаем его так (линейные уравнения);
• Если получилось уравнение второй степени (в уравнении есть (x^2)), то оно решается вот так (квадратные уравнения).
• А вот если в преобразованном уравнении получились члены (x^3) или большей степени, то придется применять нестандартные методы решения. Например, замена переменной, группировка, схема Горнера и т.д.

Чаще всего уравнения после преобразований будут сводиться к уравнениям первой (линейные уравнения) и второй (квадратные уравнения) степени.

Разберем примеры целых рациональных уравнений:

Пример 1
$$-4(-7+6x)=-9x-5;$$
Первым делом раскрываем скобки:
$$28-24x=-9x-5;$$
Перекидываем все слагаемые из правой части в левую:
$$28-24x+9x+5=0;$$
Поменяем слагаемые местами, чтобы удобнее было приводить подобные слагаемые:
$$-24x+9x+5+28=0;$$
$$-15x+33=0;$$
Получили линейное уравнение. Чтобы его решить, перекидываем свободный член (тот, что без (x)) в правую часть:
$$-15x=-33;$$
И поделим уравнение слева и справа на (-15):
$$x=frac{-33}{-15};$$
$$x=frac{11}{5}=2,2;$$
Ответ: (x=2,2.)

Важно отметить, то, что уравнение линейное, стало видно сразу после раскрытия скобок: у нас же не было степени у (x)-ов. Поэтому разумно было сразу решать его как линейное: перенести все слагаемые с (x) в левую часть, а все числа в правую. Так бы получилось немного короче.

Пример 2
$$4*(x+1)^2-2(x+3)=(2x-5)^2;$$
Тут сразу и не скажешь, какой степени уравнение. На первый взгляд кажется, что квадратное, но давайте раскроем скобки, воспользовавшись формулами сокращенного умножения:
$$4*(x^2+2x+1)-2x-6=4x^2-20x+25;$$
$$4*x^2+8x+4-2x-6=4x^2-20x+25;$$
Перекинем все в левую часть, не забывая поменять знак:
$$4*x^2+8x+4-2x-6-4x^2+20x-25=0;$$
Поменяем местами слагаемые, чтобы было проще приводить подобные:
$$4x^2-4x^2+8x-2x+20x+4-6-25=0;$$
$$26x-27=0;$$
Как видите, все квадраты сократились, и уравнение превратилось в линейное:
$$26x=27;$$
$$x=frac{27}{26};$$
Ответ: (x=frac{27}{26}.)

Пример 3
$$frac{x}{6}+frac{x}{12}+x=-frac{35}{4};$$
Домножим уравнение слева и справа на (12). Почему именно на (12)? Потому что в уравнении есть дроби с знаменателями (6), (12) и (4), на все эти числа (12) можно разделить:
$$12*(frac{x}{6}+frac{x}{12}+x)=12*(-frac{35}{4});$$
$$12*frac{x}{6}+12*frac{x}{12}+12*x=12*(-frac{35}{4});$$
$$2x+x+12x=-3*35;$$
$$15x=-105;$$
$$x=frac{-105}{15}=-7;$$
Ответ: (x=-7.)

Подробнее про линейные уравнения можно почитать в отдельной статье.

Пример 4
$$(x-1)^2=2x^2-6x-31;$$
Раскроем скобки:
$$x^2-2x+1=2x^2-6x-31;$$
$$x^2-2x+1-2x^2+6x+31=0;$$
$$x^2-2x^2-2x+6x+1+31=0;$$
$$-x^2+4x+32=0;$$
После приведения подобных слагаемых в уравнении остался (x^2), а значит перед нами квадратное уравнение, которое можно решить через дискриминант:
$$a=-1; quad b=4; quad c=32;$$
$$D=b^2-4ac=4^2-4*(-1)*32=16+128=144=12^2;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-4+12}{2*(-1)}=frac{8}{-2}=-4;$$
$$x_1=frac{-b-sqrt{D}}{2a}=frac{-4-12}{2*(-1)}=frac{-16}{-2}=8;$$
Ответ: (x=-4; qquad x=8.)

Подробнее про квадратные уравнения можно почитать здесь.

Методы решения уравнений третьей степени и старше

Не существует универсального удобного метода решения уравнений третьей степени или выше, как, например, квадратные уравнения, которые легко решаются через дискриминант, даже думать не надо.

Есть несколько методов, которые полезно знать: замена переменной, метод группировки, деление многочлена на многочлен, схема Горнера и т.д. Метод замены переменной заслуживает отдельного урока, поэтому про него мы подробно поговорим здесь. Сейчас мы обсудим метод группировки.

Метод группировки

Метод группировки слагаемых можно использовать и для решения квадратных уравнений, и, вообще говоря, для уравнений любой степени. Но проблема этого метода в том, что далеко не всегда удается его применить, и приходится использовать другие методы. Однако, если на экзамене вам не повезло, и попалось уравнение, которое сводится к уравнению 3й степени или старше, то в большинстве случаев оно будет решаться именно группировкой. Поэтому знать этот метод нужно обязательно.

Разберем метод группировки на примере кубического уравнения:

Пример 5
$$2x^3+4x^2-8x-16=0;$$
Посмотрите внимательно на уравнение, в нем 4 слагаемых, сгруппируем их попарно: первое слагаемое со вторым, а третье с четвертым:
$$(2x^3+4x^2)+(-8x-16)=0;$$

И вынесем общий множитель (2x^2) из первой пары, и (-8) из второй:

$$2x^2(x+2)-8(x+2)=0;$$
Теперь вместо 4-х слагаемых у нас всего два, но и у них есть общий множитель ((x+2)), который можно вынести за скобки:
$$(x+2)(2x^2-8)=0;$$
Произведение двух множителей (в нашем случае двух скобок) равно нулю, когда хотя бы один из множителей равен (0):
$$x+2-0 qquad Rightarrow qquad x_1=-2;$$
$$2x^2-8=0 qquad Rightarrow qquad 2x^2=8 qquad Rightarrow qquad x^2=frac{8}{2} qquadRightarrow $$
$$Rightarrow qquad x^2=4 qquad Rightarrow qquad x_{2,3}=pm 2;$$
Получилось три значения (x), но корень (x=-2) дублируется, поэтому исходное кубическое уравнение будет иметь 2 решения:
Ответ: (x=-2, quad x=2.)

Общий алгоритм разложения на множители:

1. Объединяем слагаемые в группы, как правило, в пары, но иногда это могут быть и тройки;
2. В каждой группе (паре) выносим общий множитель за скобки;
3. Если в скобках в каждой паре получилось одинаковое выражение, то опять выносим общий множитель в виде одинакового выражения внутри этих скобок за «большие» скобки.
4. Если в результате шагов (1) и (2) в каждой паре получились разные выражения в скобках, то нужно вернуться на шаг (1), поменять местами слагаемые и сгруппировать их в группы другим способом.

Попробуем решить уравнение четвертой степени:

Пример 6
$$4x^4+12x^3+6x^2+18x=0;$$
Опять сгруппируем слагаемые по парам: первое со вторым, а третье с четвертым:
$$(4x^4+12x^3)+(6x^2+18x)=0;$$
Вынесем общий множитель в каждой паре:
$$4x^3(x+3)+6x(x+3)=0;$$
Ура, в скобках получились одинаковые выражения ((x+3)), вынесем их за скобки:
$$(x+3)(4x^3+6x)=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
$$x+3=0 qquad qquad 4x^3+6x=0;$$
Первое уравнение имеет корень (x_1=-3), а второе выпишем отдельно и решим:
$$4x^3+6x=0;$$
Здесь тоже есть общий множитель (x), но это уже не группировка, а обычное вынесение общего множителя за скобки:
$$x(4x^2+6)=0;$$
$$x_2=0 qquad 4x^2+6=0;$$
Из уравнения (4x^2+6=0) выразим (x^2:)
$$4x^2=-6;$$
$$x^2=frac{-6}{4}=frac{-3}{2};$$
Но (x^2) никогда не может равняться отрицательному числу! Что бы вы не возвели в квадрат, всегда получите неотрицательное число. Поэтому последнее уравнение не будет иметь корней.
Осталось опять всего лишь два корня:
Ответ: (x_1=-3; qquad x_2=0.)

Дробно-рациональные уравнения

Если в уравнении есть деление на выражение, зависящее от переменной (x), то такое уравнение будет называться дробно-рациональным. Например, уравнения:
$$frac{1}{x}+3=x;$$
$$x+frac{20}{x+6}=6;$$
$$frac{x^2-3x-2}{x^2-3x+2}+frac{x^2-3x+16}{x^2-3x}=0;$$
все будут дробно-рациональными.

А уравнение
$$frac{x^2-3x}{5}+frac{x-7}{2}=1;$$
уже не будет дробно-рациональным, несмотря на то, что есть деление, но в знаменателе стоят обыкновенные числа, там нет переменной (x).

С тем, что такое дробно-рациональные уравнения, надеюсь, разобрались, теперь поговорим про алгоритм решения таких уравнений.

В общем виде дробно-рациональное уравнение выглядит так:
$$frac{P(x)}{Q(x)}=0;$$
где (P(x)) и (Q(x)) – целые рациональные выражения;

Схему решения можно записать в виде:
$$ begin{cases}
P(x)=0, \
Q(x) neq 0.
end{cases}$$

Простыми словами, решение дробно-рационального уравнения сводится к нахождению корней целого рационального уравнения (P(x)=0). И проверке того, чтобы найденные корни удовлетворяли неравенству (Q(x)neq0).

Пример 7
$$frac{x^2-5x+6}{x-3}=0;$$
Согласно приведенной выше схеме (P(x)=x^2-5x+6=0), а (Q(x)=x-3neq 0).
Или можно запомнить, что дробь равна нулю только тогда, когда числитель равен нулю. А делить на ноль в математике запрещено, поэтому еще и знаменатель не должен равняться нулю.
Приравниваем числитель к нулю:
$$x^2-5x+6=0;$$
$$D=(-5)^2-4*1*6=25-24=1;$$
$$x_1=frac{-(-5)+sqrt{1}}{2}=frac{5+1}{2}=3;$$
$$x_2=frac{-(-5)-sqrt{1}}{2}=frac{5-1}{2}=2;$$
И не забываем проверить, чтобы при найденных корнях знаменатель не был равен нулю:
$$x-3 neq 0;$$
При (x_1=3) знаменатель обращается в нуль, поэтому этот корень нам не подходит.
Ответ: (x_1=2.)

Рассмотрим более сложное уравнение:

Пример 8
$$frac{10}{x+6}=-frac{5}{3};$$
Чтобы решить такое уравнение, необходимо привести его к стандартному виду:
$$frac{P(x)}{Q(x)}=0;$$
Для этого переносим (-frac{5}{3}) в левую часть уравнения, не забываем, что (-frac{5}{3}) превращается в (+frac{5}{3}):
$$frac{10}{x+6}+frac{5}{3}=0;$$

Приводим дроби к общему знаменателю. Общим знаменателем здесь будет: (3*(x+6)). Поэтому домножаем числитель и знаменатель первой дроби на (3), а вторую дробь на ((x+6)):
$$frac{3*10}{3*(x+6)}+frac{5*(x+6)}{3*(x+6)}=0;$$
$$frac{30}{3*(x+6)}+frac{5*x+30}{3*(x+6)}=0;$$
Так как теперь знаменатели у дробей одинаковые, то можно сложить их числители и представить в виде одной большой дроби:
$$frac{30+5x+30}{3(x+6)}=0;$$
$$frac{60+5x}{3(x+6)}=0;$$
Получили стандартный вид дробно-рационального уравнения.

Дробь может быть равна нулю только в одном случае: если ее числитель равен нулю!

Иногда нулю еще пытаются приравнять знаменатель, но знаменатель не может быть равен нулю. Знак дроби – это то же самое, что и знак деления, а делить на ноль в математике категорически запрещено. Именно поэтому знаменатель дроби никак не может быть равен нулю.

Возвращаемся к нашему уравнению и приравниваем числитель к нулю:
$$60+5x=0;$$
$$5x=-60;$$
$$x=-12;$$
В качестве проверки подставим найденный корень в исходное уравнение:
$$frac{10}{x+6}=-frac{5}{3} quad Rightarrow quad frac{10}{-12+6}=-frac{5}{3} quad Rightarrow $$
$$Rightarrow quad frac{10}{-6}=-frac{5}{3} quad Rightarrow quad -frac{5}{3}=-frac{5}{3};$$
Получилось верное равенство, значит (x=-12) действительно будет корнем нашего уравнения.
Ответ: (x=-12.)

Алгоритм решения

• Переносим все слагаемые в левую часть, чтобы в правой части уравнения был 0, не забывая при этом менять знак;
• Приводим к общему знаменателю;
• Упрощаем получившееся выражение в числителе дроби: раскрываем скобки, приводим подобные слагаемые;
• Дробь равна нулю, когда числитель равен нулю. Поэтому избавляемся от знаменателя и приравниваем числитель к нулю;
• В результате вышеперечисленных действий дробно-рациональное уравнение сводится к целому рациональному уравнению;
• Решаем целое рациональное уравнение и проверяем найденные корни, чтобы при подстановке их в знаменатель, не получался ноль.

Посмотрим, как работает алгоритм на примерах:

Пример 9
$$frac{9}{x-11}+frac{11}{x-9}=2;$$
Перекидываем двойку в левую часть уравнения и приводим дроби к общему знаменателю ((x-11)(x-9)). Для этого в первой дроби домножаем числитель и знаменатель на ((x-9)), вторую дробь на ((x-11)), а (2-ку) мы всегда можем представить в виде дроби: (frac{2}{1}), и тоже приводим к знаменателю ((x-11)(x-9)):
$$frac{9*(x-9)}{(x-11)(x-9)}+frac{11*(x-11)}{(x-9)(x-11)}-frac{2(x-11)(x-9)}{(x-11)(x-9)}=0;$$
Получилось немного страшновато, но ничего: складываем дроби, раскрываем в числителе все скобки и приводим подобные слагаемые. Знаменатель при этом не трогаем.
$$frac{9(x-9)+11(x-11)-2(x-11)(x-9)}{(x-9)(x-11)}=0;$$
$$frac{9x-81+11x-121-2(x^2-9x-11x+99)}{(x-9)(x-11)}=0;$$
$$frac{9x-81+11x-121-2x^2+18x+22x-198}{(x-9)(x-11)}=0;$$
$$frac{-2x^2+60x-400}{(x-9)(x-11)}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-2x^2+60x-400=0;$$
$$D=60^2-4*(-2)*(-400)=3600-3200=400;$$
$$x_1=frac{-60+sqrt{400}}{2*(-2)}=frac{-60+20}{-4}=10;$$
$$x_2=frac{-60-sqrt{400}}{2*(-2)}=frac{-60-20}{-4}=20;$$
Подставив оба корня в исходное уравнение, аналогично тому, как мы это делали в примере №7, можно убедиться в правильности найденных корней.
Ответ: (x_1=10 quad x_2=20.)

Пример 10
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{4-9x^2};$$
Когда вы видите в знаменателе формулы сокращенного умножения, общий множитель или группировку, то нужно обязательно ими воспользоваться, чтобы разложить многочлен в знаменателе на множители перед тем, как приводить к общему знаменателю.

Замечаем у дроби справа в знаменателе формулу разности квадратов (a^2-b^2=(a-b)(a+b):)
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{(2-3x)(2+3x)};$$
Перекидываем в левую часть уравнения:
$$frac{x}{3x+2}+frac{5}{3x-2}-frac{3x^2+6x}{(2-3x)(2+3x)}=0;$$
Приведем все дроби к общему знаменателю ((2-3x)(2+3x)):

• У первой дроби в знаменателе поменяем слагаемые местами (от перемены мест слагаемых сумма не меняется ((3x+2=2+3x)) и домножим ее числитель и знаменатель на ((2-3x)).
• У второй дроби в знаменателе стоит ((3x-2)), а нам надо ((2-3x)). Поэтому домножим числитель и знаменатель на (-1) и на ((2+3x)).
• С третьей дробью делать ничего не нужно. У нее и так нужный нам знаменатель.

$$frac{x(2-3x)}{(2+3x)(2-3x)}+frac{5*(-1)*(2+3x)}{(3x-2)*(-1)*(2+3x)}-frac{3x^2+6x}{(2-3x)(2+3x)}=0;$$
$$frac{x(2-3x)}{(2-3x)(2+3x)}+frac{-5*(2+3x)}{(2-3x)(2+3x)}-frac{3x^2+6x}{(2-3x)(2+3x)}=0;$$
Складываем дроби и раскрываем скобки:
$$frac{x(2-3x)-5*(2+3x)-(3x^2+6x)}{(2-3x)(2+3x)}=0;$$
Обратите внимание, что я всегда беру числитель в скобки, когда складываю дроби. Тем самым я показываю, что минус перед дробью действует на каждое слагаемое в числителе.

Это одна из самых распространенных ошибок. Будьте внимательны.
$$frac{2x-3x^2—10-15x—3x^2-6x}{(2-3x)(2+3x)}=0;$$
$$frac{-6x^2—19x-10}{(2-3x)(2+3x)}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$-6x^2-19x-10=0;$$
Для удобства умножим все уравнение на (-1):
$$6x^2+19x+10=0;$$
$$D=19^2-4*6*10=361-240=121;$$
$$x_1=frac{-19+sqrt{121}}{2*6}=frac{-19+11}{12}=frac{-8}{12}=-frac{2}{3};$$
$$x_2=frac{-19-sqrt{121}}{2*6}=frac{-19-11}{12}=frac{-30}{12}=-frac{5}{2};$$

Подставим корень (x_1=-frac{2}{3}) в исходное уравнение:
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{4-9x^2};$$
$$frac{-frac{2}{3}}{3*left(-frac{2}{3}right)+2}+frac{5}{3*left(-frac{2}{3}right)-2}=frac{3left(-frac{2}{3}right)^2+6left(-frac{2}{3}right)}{4-9left(-frac{2}{3}right)^2};$$

Оказывается, что мы не cможем это посчитать, так как в знаменателе получается ноль, а делить на ноль нельзя. В таком случае говорят, что найденный корень не подходит, и в ответ мы его не записываем. А если подставить (-frac{5}{2}), то все будет нормально.

Ответ:(x=-frac{5}{2}.)

Область допустимых значений. ОДЗ

Примеры выше показали нам, что не всегда найденные значения (x) будут корнями исходного уравнения.

Почему так происходит?

Когда мы решаем уравнение, мы преобразовываем его: переносим слагаемые из одной части уравнения в другую, приводим к общему знаменателю, считаем подобные слагаемые, избавляемся от знаменателя и т.д. Эти преобразования меняют вид нашего уравнения. В новом измененном уравнении «исчезает» информация, например, о том, что в нем раньше был знаменатель.

Поэтому мы подставляли найденные (x) в ИСХОДНОЕ уравнение, чтобы проверить, действительно ли они являются корнями, и не нарушаются ли правила математики, такие, как деление на ноль.

Но решений в уравнении может быть много, да и само уравнение может быть большим и сложным. Подставлять туда каждый найденный корень и проверять, действительно ли он является корнем исходного уравнения, может быть проблематично.

Чтобы не заниматься трудоемкой подстановкой, лучше всего находить область значений (x) (еще ее называют область определения), при которых не нарушаются правила математики для исходного уравнения. И уже на этой области (x) искать корни: если найденный корень лежит в разрешенной области, значит он может быть корнем, а если нет, то выкидываем его.

Разрешенная область значений (x) называется «областью допустимых значений», сокращенно ОДЗ. Чтобы найти ОДЗ в дробно-рациональных уравнениях, нужно приравнять к нулю все знаменатели исходного уравнения и решить получившееся уравнения. Другими словами, ищем такие (x), при которых возникает запрещенное деление на ноль в исходном уравнении. Все (x), не являющиеся корнями этих уравнений, и будут нашей областью допустимых значений.

Найдем ОДЗ уравнения из примера №9:
$$frac{x}{3x+2}+frac{5}{3x-2}=frac{3x^2+6x}{4-9x^2};$$
Выписываем все знаменатели и находим (x), при которых они не равны нулю:
$$ begin{cases}
3x+2 neq 0, \
3x-2 neq 0, \
(2-3x)(2+3x) neq 0.
end{cases}$$

Третье неравенство в системе сводится к первым двум, поэтому его можно исключить из рассмотрения.
$$ begin{cases}
x neq -frac{2}{3}, \
x neq frac{2}{3}.
end{cases}$$

Решив неравенства, мы получили, что (x) может принимать любые значения, кроме (frac{2}{3}) и (-frac{2}{3}). Это и есть ОДЗ.

Напомню, что в примере №9 у нас получились корни (x_1=-frac{2}{3}) и (x_2=-frac{5}{2}). Соотносим их с найденным ОДЗ и видим, что корень (x_1=-frac{2}{3}) не подходит. Для этого нам не понадобилось подставлять его в исходное уравнение, как мы делали при решении.

Алгоритм решения дробно-рациональных уравнений с использованием ОДЗ

• Находим ОДЗ. Для этого выписываем все знаменатели и приравниваем их к нулю;
• Решаем дробно-рациональное уравнение: перекидываем все в левую часть, приводим к общему знаменателю, приводим подобные слагаемые, избавляемся от знаменателя и решаем получившееся целое рациональное уравнение;
• Проверяем, чтобы найденные корни удовлетворяли ОДЗ. Если не удовлетворяют, то отбрасываем их.

Пример 11
$$frac{2x^2+7x+3}{x^2-9}=1;$$
Начинаем решение с ОДЗ:
$$x^2-9 neq 0;$$
Разность квадратов:
$$(x-3)(x+3) neq 0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
$$x-3 neq 0 Rightarrow x neq 3;$$
$$x+3 neq 0 Rightarrow x neq -3;$$
ОДЗ нашли, приступаем к решению самого уравнения:
$$frac{2x^2+7x+3}{x^2-9}-1=0;$$
Приводим к общему знаменателю (x^2-9), для этого единицу представим в виде дроби ((1=frac{1}{1})) и домножим ее на (x^2-9):
$$frac{2x^2+7x+3}{x^2-9}-frac{1*(x^2-9)}{1*(x^2-9)}=0;$$
$$frac{2x^2+7x+3-(x^2-9)}{x^2-9}=0;$$
$$frac{2x^2+7x+3-x^2+9}{x^2-9}=0;$$
$$frac{x^2+7x+12}{x^2-9}=0;$$
$$x^2+7x+12=0;$$
$$D=7^2-4*1*12=49-48=1;$$
$$x_1=frac{-7+1}{2}=frac{-6}{2}=-3;$$
$$x_2=frac{-7-1}{2}=frac{-8}{2}=-4;$$

Сверяем найденные корни с ОДЗ ((x neq pm 3)) и видим, что корень (x_1=-3) не удовлетворяет ОДЗ.
Ответ: (x=-4.)

Пример 12
$$frac{x^2-6x+8}{x-1}-frac{x-4}{x^2-3x+2}=0;$$
Всегда начинаем решать с ОДЗ:
$$ begin{cases}
x-1 neq 0, \
x^2-3x+2 neq 0.
end{cases}$$

$$ begin{cases}
x neq 1, \
x neq 2.
end{cases}$$

Чтобы привести к общему знаменателю, разложим квадратный многочлен в знаменателе второй дроби на множители:
$$frac{x^2-6x+8}{x-1}-frac{x-4}{(x-1)(x-2)}=0;$$
Теперь видно, что общий знаменатель: ((x-1)(x-2)). Домножим первую дробь на ((x-2)):
$$frac{(x^2-6x+8)*(x-2)}{(x-1)*(x-2)}-frac{x-4}{(x-1)(x-2)}=0;$$
Если перемножить скобки в числителе, то получится многочлен третьей степени. Решать уравнение третьей степени не хочется, поэтому попробуем упростить нашу задачу: разложим на множители многочлен (x^2-6x+8=(x-2)(x-4)):
$$frac{(x-2)(x-4)*(x-2)}{(x-1)*(x-2)}-frac{x-4}{(x-1)(x-2)}=0;$$
$$frac{(x-2)^2(x-4)-(x-4)}{(x-1)(x-2)}=0;$$
Дробь равна нулю, когда числитель равен нулю:
$$(x-2)^2(x-4)-(x-4)=0;$$
Вынесем общий множитель: скобку ((x-4)):
$$(x-4)((x-2)^2-1)=0;$$
$$(x-4)(x^2-4x+4-1)=0;$$
$$(x-4)(x^2-4x+3)=0;$$
Произведение равно нулю, когда хотя бы один из множителей равен нулю:
$$x-4=0 Rightarrow x_1=4;$$
$$x^2-4x+3=0;$$
$$D=(-4)^2-4*1*3=16-12=4;$$
$$x_2=frac{-(-4)+sqrt{4}}{2}=frac{4+2}{2}=3;$$
$$x_3=frac{-(-4)-sqrt{4}}{2} =frac{4-2}{2}=1;$$
Проверяем, чтобы найденные корни удовлетворяли ОДЗ ((x neq 1; quad x neq 2)) и видим, что корень (x_3=1) не подходит.
Ответ: (x_1=4, qquad x_2=3.)

Чтобы научиться решать большинство уравнений из школьной программы необходимо также знать метод замены переменной. Это очень важный метод, который используется для решения некоторых рациональных и дробно-рациональных уравнений, и не только, поэтому он заслуживает того, чтобы поговорить о нем в отдельной статье, очень рекомендую.