Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
- – она определена в этой точке и ее некоторой
-окрестности;
- – существуют конечные лево- и правосторонние пределы от функции в этой точке и они равны между собой, т.е.
– предел функции в точке 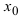
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 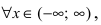
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 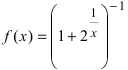
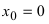
Решение:
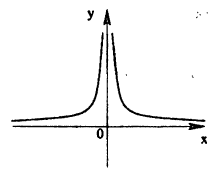
Нарисуем график функции в окрестности нуля (Рис. 64): 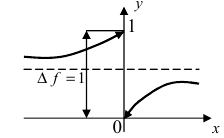
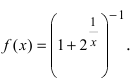
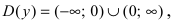
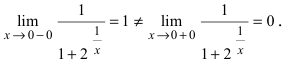
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция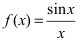
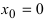
Решение:
В точке 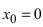
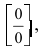
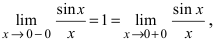
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 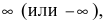
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 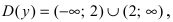
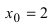
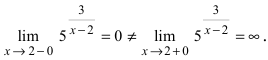
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 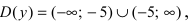
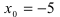
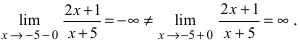
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 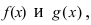
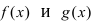
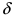
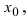
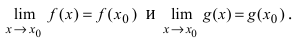
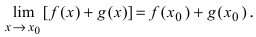
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 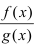
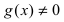
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
- Заказать решение задач по высшей математике
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 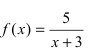
Из рисунка видно, что график функции 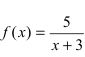
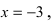
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 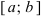
Определение: Замкнутый интервал 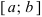
Приведем без доказательства свойства непрерывных функций на сегменте 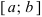
Теорема: Если функция 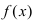
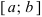
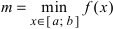
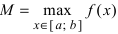
Пример:
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 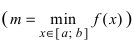
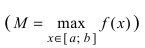
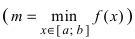
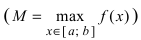
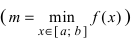
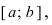
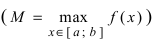
Тб. Если функция 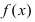
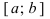
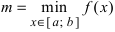
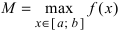
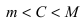
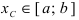
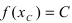
Пример:
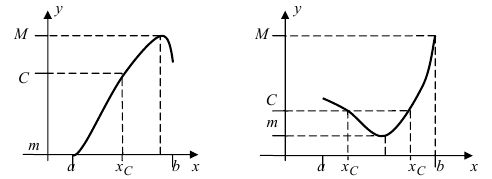
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 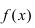
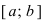
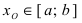
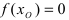
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Формула Тейлора и ее применение
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
Непрерывность функции и точки разрыва
- Приращение аргумента и приращение функции
- Непрерывность функции в точке
- Непрерывность функции на промежутке
- Односторонние пределы
- Классификация точек разрыва
- Точки разрыва первого рода
- Точки разрыва второго рода
- Алгоритм исследования функции на непрерывность
- Примеры
п.1. Приращение аргумента и приращение функции
Приращением аргумента называют разность $$ triangle x= x-x_0 $$ где x – произвольное число, которое мало отличается от начальной точки (x_0). Приращение аргумента может быть как положительным, так и отрицательным.
Приращением функции называют соответствующую разность $$ triangle y=f(x)-f(x_0) $$ Приращение функции может быть как положительным, так и отрицательным.
Например:
 |
Пусть (y=3x-1) (x_0=1, x=1,1 ) Тогда begin{gather*} triangle x=x-x_0=0,1\ triangle y=(3x-1)-(3x_0-1)=\ =3(x-x_0 )=3triangle x=0,3 end{gather*} В данном случае приращение функции всегда в 3 три раза больше приращения аргумента. |
п.2. Непрерывность функции в точке и на промежутке
Функция (y=f(x)) непрерывна в точке (x_0), если в этой точке малому приращению аргумента (triangle x=x-x_0) соответствует малое приращение функции (triangle y=f(x)-f(x_0)): $$ lim_{triangle xrightarrow 0}triangle y=lim_{xrightarrow x_0}triangle y=0 $$
На «языке ε-δ» определение непрерывности будет следующим:
Функция (y=f(x)) непрерывна в точке (x_0), если для любого (varepsilongt 0) существует такое (delta(varepsilon)gt 0), что для любого (x, |x-x_0|ltdelta) выполняется (|f(x)-f(x_0)|ltvarepsilon:) $$ forall varepsilongt 0 existsdelta=delta(varepsilon)gt 0: forall x, |x-x_0|ltdeltaRightarrow |f(x)-a|ltvarepsilon $$
ε-δ определение непрерывности похоже на ε-δ определение предела функции, с той разницей, что модуль (|x-x_0|) может быть равен 0 для непрерывной функции, т.е. сама точка (x_0) входит в δ-окрестность.
Проанализируем предел приращения функции: begin{gather*} lim_{triangle xrightarrow 0}triangle y= lim_{triangle xrightarrow 0}left(f(x)-f(x_0)right)= lim_{triangle xrightarrow 0}f(x)-lim_{triangle xrightarrow 0}f(x_0)=\ =lim_{triangle xrightarrow 0}f(x)-f(x_0) end{gather*} т.к. (f(x_0)) – величина постоянная и от (triangle x) не зависит.
Для непрерывной функции: $$ lim_{triangle xrightarrow 0}triangle y =0 Leftrightarrow lim_{triangle xrightarrow 0}f(x)-f(x_0)=0Leftrightarrow lim_{triangle xrightarrow 0}f(x)=f(x_0) $$ Учитывая, что (triangle xrightarrow 0Leftrightarrow x-x_0rightarrow 0Leftrightarrow xrightarrow x_0)
получаем (lim{xrightarrow x_0}f(x)=f(x_0).)
Функция (y=f(x)) непрерывна в точке (x_0), если существует предел функции в этой точке и он равен значению функции в точке: $$ lim{xrightarrow x_0}f(x)=f(x_0) $$
Все три представленных определения непрерывности функции в точке эквивалентны.
Существуют и другие эквивалентные определения. Мы дадим ещё одно из них дальше, в этом же параграфе.
п.3. Непрерывность функции на промежутке
Промежуток – это интервал, отрезок, луч и т.п. (см. §16 справочника для 8 класса).
Функция (y=f(x)) непрерывна на промежутке, если она непрерывна в каждой точке этого промежутка.
График непрерывной функции – это непрерывная линия.
Кроме непрерывности, эта линия еще и «плавная», без «заломов».
При наличии заломов функция называется кусочно-непрерывной.
п.4. Односторонние пределы
Односторонний предел – это предел числовой функции при приближении к предельной точке с определенной стороны (слева или справа).
Обозначение односторонних пределов: begin{gather*} lim_{xrightarrow x_0 -0}f(x)=a – text{левый предел}\ lim_{xrightarrow x_0 +0}f(x)=b – text{правый предел} end{gather*}
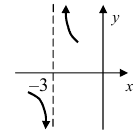
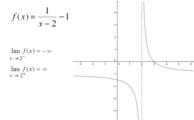
Рассмотрим гиперболу (y=frac{1}{x-2}).
 |
У этой гиперболы две асимптоты (y=0) и (x=2). Точка (x_0=2) не входит в область определения. Если мы будем приближаться к (x_0=2) слева, начав, например с 1,5, мы будем постепенно опускаться по ветке гиперболы на минус бесконечность. Т.е., левый предел: $$ lim_{xrightarrow 2-0}frac{1}{x-2}=-infty $$ |
Если же мы будем приближаться к (x_0=2) справа, начав, например с 2,5, мы будем постепенно подниматься по ветке гиперболы на плюс бесконечность. Т.е., правый предел: $$ lim_{xrightarrow 2+0}frac{1}{x-2}=+infty $$ Левый и правый пределы в точке (x_0=2) для данной гиперболы не равны: $$ lim_{xrightarrow 2-0}frac{1}{x-2} ne lim_{xrightarrow 2+0}frac{1}{x-2} $$
Теперь рассмотрим параболу (y=x^2-2)
Областью определения параболы является вся числовая прямая (xinmathbb{R})
 |
В этом случае, если приближаться к (x_0=2) слева, мы получаем: $$ lim_{xrightarrow 2-0}(x^2-2)=2 $$ И если приближаться (x_0=2) справа, мы тоже получаем: $$ lim_{xrightarrow 2+0}(x^2-2)=2 $$ Левый и правый пределы равны: $$ lim_{xrightarrow 2-0}(x^2-2) =lim_{xrightarrow 2+0}(x^2-2) $$ |
Функция (y=f(x)) непрерывна в точке (x_0), если одновременно выполняются следующие три условия:
1) точка (x_0) принадлежит области определения функции (xin D);
2) левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ 3) предел функции в точке (x_0) равен значению функции в этой точке: $$ lim_{xrightarrow x_0}f(x)=f(x_0) $$
Это еще одно определение непрерывности, которым удобно пользоваться на практике.
п.5. Классификация точек разрыва
Точка (x_0) будет точкой разрыва для функции (y=f(x)), если выполняется хотя бы одно из условий:
1) точка (x_0) не принадлежит области определения функции (xnotin D);
2) левый и правый пределы в точке (x_0) не равны или бесконечны: $$ lim_{xrightarrow x_0 -0}f(x) nelim_{xrightarrow x_0 +0}f(x) text{или} lim_{xrightarrow x_0 -0}f(x) =lim_{xrightarrow x_0 +0}f(x)=pminfty $$ 3) предел функции в точке (x_0) не совпадает со значением функции в этой точке: $$ lim_{xrightarrow x_0}f(x)ne f(x_0) $$
| Точки разрыва | 1-го рода Односторонние пределы существуют и конечны |
Устранимые Односторонние пределы равны между собой, но не равны (f(x_0)) |
| Неустранимые (скачок) Односторонние пределы не равны между собой |
||
| 2-го рода Хотя бы один из односторонних пределов бесконечен или не существует |
п.6. Точки разрыва первого рода
Устранимые точки разрыва 1-го рода
Левый и правый пределы в точке (x_0) равны и конечны: $$ lim_{xrightarrow x_0 -0}f(x)=lim_{xrightarrow x_0 +0}f(x)=lim_{xrightarrow x_0}f(x)=aneinfty $$ НО:
либо точка (x_0) НЕ принадлежит области определения функции (xnotin D);
либо предел НЕ равен значению функции в точке (x_0): (lim_{xrightarrow x_0}f(x)ne f(x_0))
Например:
 |
(y=frac{x^2-4}{x-2}, x_0=2) Эта функция эквивалентна системе $$ y=frac{x^2-4}{x-2} Leftrightarrow begin{cases} y=x+2\ xne 2 end{cases} $$ При этом (lim_{xrightarrow 2-0}(x+2)=lim_{xrightarrow 2+0}(x+2)=4) В точке (x_0=2notin D) функция имеет устранимый разрыв. |
Разрыв можно устранить (функцию можно «склеить»), отдельно задав «гладкое» значение в особой точке: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} $$ В таком случае система станет эквивалентна всей прямой, т.е. станет непрерывной функцией: $$ y= begin{cases} frac{x^2-4}{x-2}, xne 2\ 4, x=2 end{cases} Leftrightarrow y=x+2 $$
Неустранимые точки разрыва 2-го рода (скачок)
Левый и правый пределы в точке (x_0) конечны, но не равны: $$ begin{cases} lim_{xrightarrow x_0 -0}f(x)=aneinfty\ lim_{xrightarrow x_0 +0}f(x)=bneinfty\ ane b end{cases} $$ Такой разрыв также называют скачком.
Величина скачка рассчитывается по формуле: $$ triangle y=lim_{xrightarrow x_0 +0}f(x)- lim_{xrightarrow x_0 -0}f(x)=b-a $$
Например:
 |
(y= begin{cases} x+1, xlt 2\ 3-x^2, xgeq 2 end{cases} , x_0=2) Односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}f(x)= lim_{xrightarrow 2-0}(x+1)=3\ lim_{xrightarrow 2+0}f(x)= lim_{xrightarrow 2+0}(3-x^2)=-1 end{gather*} Пределы не равны, но конечны. Функция в точке (x_0=2) делает скачок вниз. Величина скачка: $$ triangle y=-1-3=-4 $$ |
п.7. Точки разрыва второго рода
В точках разрыва 2-го рода хотя бы один из односторонних пределов бесконечен или не существует.
Например:
 |
(y=e^frac1x, x_0=0)
(x_0=0ne D) – точка не входит в ОДЗ Точка (x_0=0) – точка разрыва второго рода. |
На практике, при моделировании реальных процессов, разрывы 2-го рода в функциональных зависимостях встречаются довольно часто. Их положено заботливо анализировать и тщательно обходить, выбирая рабочие участки характеристических кривых, – чтобы «система не пошла в разнос».
п.8. Алгоритм исследования функции на непрерывность
На входе: функция (y=f(x))
Шаг 1. Найти ОДЗ функции, определить точки и промежутки, не принадлежащие ОДЗ.
Шаг 2. Составить множество точек, в которое входят точки и границы промежутков, не принадлежащие ОДЗ, а также – для кусочно-непрерывных функций – точки сшивания. Полученное множество состоит из точек, подозрительных на разрыв.
Шаг 3. Исследовать каждую из точек, подозрительных на разрыв, с помощью односторонних пределов. Если разрыв обнаружен, определить тип разрыва.
На выходе: список точек разрыва и тип разрыва для каждой точки.
п.9. Примеры
Пример 1. Исследуйте функцию на непрерывность:
a) ( y=frac{x+3}{x-1} )
ОДЗ: (x-1ne 0Rightarrow xne 1)
(x_0=1notin D) – точка не входит в ОДЗ, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 1-0}frac{x+3}{x-1}=frac{1-0+3}{1-0-1}=frac{4}{-0}=-infty\ lim_{xrightarrow 1+0}frac{x+3}{x-1}=frac{1+0+3}{1+0-1}=frac{4}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_0=1) – точка разрыва 2-го рода.
б) ( y=frac{x}{sqrt{x+2}-2} )
ОДЗ: ( begin{cases} x+2geq 0\ sqrt{x+2}-2ne 0 end{cases} Rightarrow begin{cases} xgeq -2\ sqrt{x+2}ne 2 end{cases} Rightarrow begin{cases} xgeq -2\ xne 2 end{cases} )
(x_0=-2) – левая граница ОДЗ
(x_1=2notin D)- точка не входит в ОДЗ
Точки (x_0) и (x_1) – подозрительные на разрыв
Исследуем (x_0=-2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} – text{предел не существует}\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{-2+0}{sqrt{-2+0+2}-2}=frac{-2}{-2}=1 end{gather*} Один из односторонних пределов не существует.
Точка (x_0=-2) – точка разрыва 2-го рода.
Исследуем (x_1=2). Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 2-0}frac{x}{sqrt{x+2}-2} =frac{2-0}{sqrt{2-0+2}-2}=frac{2}{-0}=-infty\ lim_{xrightarrow 2+0}frac{x}{sqrt{x+2}-2}=frac{2+0}{sqrt{2+0+2}-2}=frac{2}{+0}=+infty end{gather*} Односторонние пределы не равны и бесконечны.
Точка (x_1=2) – точка разрыва 2-го рода.
в) ( y=frac{tgx}{3x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{tgx}{3x}=frac13lim_{xrightarrow -0}frac{tgx}{x}=frac13cdot 1=frac13\ lim_{xrightarrow +0}frac{tgx}{3x}=frac13lim_{xrightarrow +0}frac{tgx}{x}=frac13cdot 1=frac13 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
г) ( y= begin{cases} x+1, xlt 3\ x^2+3, xgeq 3 end{cases} )
ОДЗ: (xinmathbb{R})
(x_0=3)- точка сшивания, подозрительная на разрыв.
Найдем односторонние пределы: begin{gather*} lim_{xrightarrow 3-0}y=lim_{xrightarrow 3-0}(x+1)=3+1=4\ lim_{xrightarrow 3+0}y=lim_{xrightarrow 3+0}(x^2+3)=3^2+3=12 end{gather*} Односторонние пределы конечны, но неравны.
Точка (x_0=3) – точка разрыва 1-го рода, неустранимый разрыв (скачок).
Величина скачка: (lim_{xrightarrow 3+0}y-lim_{xrightarrow 3-0}y=12-4=8)
Пример 2. Доопределите функцию в точке разрыва так, чтобы она стала непрерывной в этой точке:
a) ( y=frac{2x^3-x^2}{7x} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{2x^3-x^2}{7x}=frac{x^2(2x-1)}{7x}=frac{x(2x-1)}{7}) $$ y=frac{2x^3-x^2}{7x}Leftrightarrow y= begin{cases} frac{x(2x-1)}{7}\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}frac{x(2x-1)}{7}=0, lim_{xrightarrow +0}frac{x(2x-1)}{7}=0 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=0).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{2x^3-x^2}{7x}, xne 0\ 0, x=0 end{cases} $$ б) ( y=frac{1-cos4x}{x^2} )
ОДЗ: (xne 0)
(x_0=0notin D)- точка не входит в ОДЗ, подозрительная на разрыв.
Упростим выражение: (frac{1-cos4x}{x^2}=frac{2sin^2 2x}{x^2}=frac{2sin^2 2x}{frac{(2x)^2}{4}}=8left(frac{sin2x}{2x}right)^2) $$ y=frac{1-cos4x}{x^2}Leftrightarrow y= begin{cases} 8left(frac{sin2x}{2x}right)^2\ xne 0 end{cases} $$ Найдем односторонние пределы: begin{gather*} lim_{xrightarrow -0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8, lim_{xrightarrow +0}8left(frac{sin2x}{2x}right)^2=8cdot 1=8 end{gather*} Односторонние пределы конечны и равны.
Точка (x_0=0) – точка разрыва 1-го рода, устранимый разрыв.
Доопределить функцию нужно значением предела в точке разрыва: (y(0)=8).
Доопределенная непрерывная функция: $$ y= begin{cases} frac{1-cos4x}{x^2}, xne 0\ 8, x=0 end{cases} $$
Непрерывность функции:
Непрерывные функции, точки разрыва и их классификация, действия над непрерывными функциями, свойства функций, непрерывных на сегменте.
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если:
- функция определена в точке x₀ и в некоторой ее окрестности, содержащей эту точку;
- функция имеет предел при х → x₀;
- предел функции при х → x₀ равен значению функции в точке x₀:
(10.1)
Если в точке x₀ функция непрерывна, то точка x₀ называется точкой непрерывности функции.
Пример:
Исследовать на непрерывность функцию 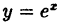
Решение:
Чтобы доказать, что функция 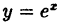
Таким образом, доказано, что функция 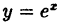
Замечание:
Формулу (10.1) можно записать в виде
(10.2)
так как 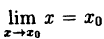
Введем понятие непрерывности функции в точке х₀ справа и слева.
Если, существует 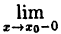
Так как ∆x = x-x₀, a ∆y = f(x)-(x₀), то условие (10.1) равносильно следующему:
Определение:
Функция у = f(x) называется непрерывной в точке х₀, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции
(10.3)
Пример:
Показать, что функция у = х³ непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y.
∆y= (x+∆x)³-x³ = x³+3x²∆x+3x∆x²+∆x³-x³ = 3x²∆x+3x∆x²+∆x³.
Используя теоремы о пределе суммы и произведения функции, получим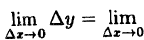
Следовательно, функция у = х³ непрерывна при — ∞< х < ∞.
Точки разрыва функции и их классификация
Определение:
Точка х₀ называется точкой разрыва функции у = f(x), если она принадлежит области определения функции или ее границе и не является точкой непрерывности.
Так, например, функция 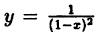
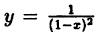
Определение:
Точка разрыва x₀ функции у = f(x) называется точкой устранимого разрыва, если существуют оба односторонних предела в точке x₀ и они равны, т. е.
Пример:
Исследовать на непрерывность функцию
Решение:
В точке x=-1 функция не определена, так как, выполнив подстановку, получаем неопределенность 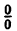
Таким образом, при x = -1 данная функция имеет устранимый разрыв.
Он будет устранен, если положить, что при x = -1 ⇒ у =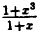
Определение:
Если в точке x₀ односторонние пределы слева и справа существуют, но не равны, точка x₀ называется точкой разрыва I рода.
Пример:
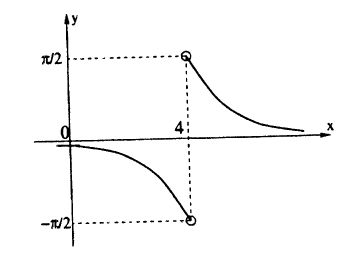
Исследовать на непрерывность функцию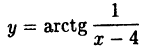
Решение: Вычислим односторонние пределы функции в точке ее разрыва х = 4.
Предел слева —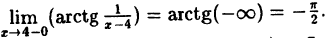
Предел справа — 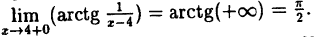
Пределы слева и справа существуют, но не равны, следовательно, точка x = 4 для данной функции — точка разрыва I рода (точка скачка).
Определение:
Точки разрыва, не являющиеся точками разрыва I рода, называются точками разрыва II рода.
В точках разрыва II рода не существует хотя бы один из односторонних пределов. Функция 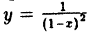
Действия над непрерывными функциями
Теорема:
Непрерывность суммы, произведения и частного непрерывных функций. Если функции ϕ(x) и ψ(x) непрерывны в точке Хо, то их сумма и произведение также непрерывны в точке x₀. Если, кроме того, знаменатель в рассматриваемой точке не равен нулю, то частное непрерывных функций есть функция непрерывная.
Докажем непрерывность произведения.
Дано: непрерывность функций в точке x₀: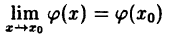
Доказать, что f(x) — ϕ(x) ∙ ψ(x) есть функция непрерывная в точке x₀, т. е. 
Доказательство:



Можно строго доказать, что все основные элементарные функции непрерывны при всех значениях х, для которых они определены.
Например, степенная у = xⁿ, показательная у = 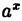
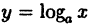
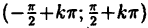
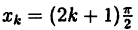
Теорема:
Непрерывность сложной функции. Если функция и = ϕ(x) непрерывна в точке x₀, а функция у = f(u) непрерывна в точке и₀ = ϕ(x₀), то сложная функция у = f [ϕ(x)] непрерывна в точке x₀.
Без доказательства.
В заключение этого раздела рассмотрим два предела, которые нам понадобятся в дальнейшем.
Пример:
Вычислить
Решение:
Заметим, что при х → 0 числитель и знаменатель одновременно стремятся к нулю, т.е. имеет место неопределенность вида 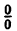
Так как данная логарифмическая функция непрерывна в окрестности точки х = 0, то можно перейти к пределу под знаком функции (

но 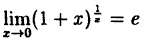
Следовательно,
(10.4)
В частности, при а = е
(10.5)
Таким образом, у = ln( 1 + х) и у = х — эквивалентные бесконечно малые функции при х → 0.
Пример:
Вычислить
Решение:
Здесь мы имеем дело с неопределенностью вида 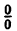
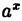
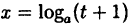
Так как на основании результата, полученного в предыдущем примере, 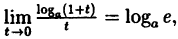
(10.6)
В частности, если а = е, имеем
т.е. у = 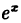
Свойства функций, непрерывных на сегменте
Определение:
Функция у = f(x) непрерывна на сегменте [а, b], если она непрерывна во всех внутренних точках Этого сегмента, а на концах сегмента (в точках a и b) непрерывна соответственно справа и слева.
Теорема:
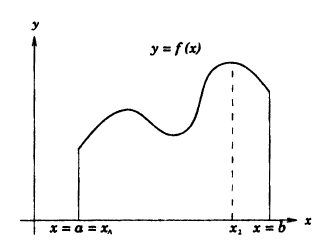
Если функция у = f(x) непрерывна на сегменте [а, b], то она достигает на этом сегменте своего наибольшего и(или) наименьшего значения.
Простым доказательством этой теоремы, является геометрическая иллюстрация функции у = f(x) на рисунке 91. Непрерывная на сегменте [α, b] функция достигает наименьшего своего значения в точке х = x₁= а, а наибольшего значения в точке х₂.
Следствие:
Если функция у = f(x) непрерывна на сегменте [a, b], то она ограничена на этом сегменте.
Действительно, если по теореме 10.3 функция достигает на сегменте наибольшего M и наименьшего т значений, то имеет место неравенство m ≤ f(x) ≤ M для всех значений функции на рассматриваемом сегменте. Т. е. |f(x)| ≤ M и, следовательно, функция у = f(x) ограничена на сегменте [а, b].
Теорема:
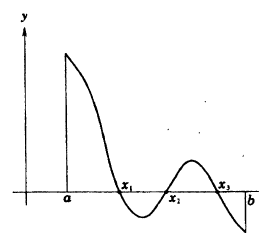
Теорема Больцано-Коши. Если функция у = f(x) непрерывна на сегменте [а, b] и на ее концах принимает значения разных знаков, то внутри этого сегмента найдется, по крайней мере, одна тонка С, в которой функция равна нулю.
Геометрический смысл теоремы заключается в следующем: если точки графика функции у = f(x), соответствующие концам сегмента [a, b], лежат по разные стороны от оси ОХ, то этот график хотя бы в одной точке сегмента пересекает ось OX. На данном рисунке 92 это три точки x₁, x₂, x₃.
Теорема:
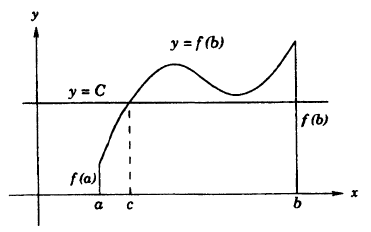
О промежуточных значениях функции. Если функция у = f(x) непрерывна на сегменте [α, b] и f(α) = A и f(b) = В, то для любого числа С, заключенного между A и B, найдется внутри этого сегмента такая точка с, что f(c) = С.
Из графика на рисунке 93 видно, что непрерывная функция, переходя от одного значения к другому, обязательно проходит через все промежуточные значения.
Теорема:
О непрерывности обратной функции.) Если функция у = f(x) непрерывна на сегменте [а, b] в возрастает (убывает) на этом сегменте, то обратная функция х = f⁻¹(y) на соответствующем сегменте оси OY существует и является также непрерывной возрастающей (убывающей) функцией.
Эту теорему мы принимаем без доказательства.
Решение на тему: Непрерывная функция
Пример:
Показать, что функция у = 4x² непрерывна в точке х = 2.
Решение:
Для этого необходимо показать, что в точке х = 2 выполняется все три условия непрерывности функции:
1) функция у = 4х² определена в точке х = 2 ⇒ f(2) = 16;
2) существует 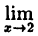
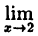
3) этот предел равен значению функции в точке х = 2
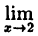
Пример:
Показать, что функция у = sin x непрерывна для любого значения аргумента х.
Решение:
Найдем приращение функции ∆y, используя формулы тригонометрических тождеств
Так как 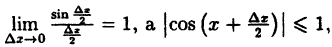
Следовательно, функция у = sin x непрерывна при -∞ < х < ∞.
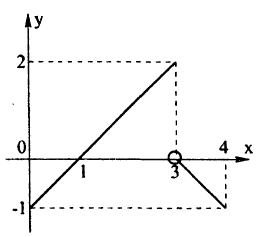
Пример:
Исследовать на непрерывность функцию
Решение:
Эта функция (рис. 94) определена во всех точках сегмента [0,4] и ее значение при х = 3 ⇒ у = 2. Функция терпит разрыв, так как она не имеет предела при х → 3 :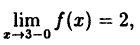
Следовательно, точка х = 3, точка разрыва первого рода. При этом в граничных точках исследуемого сегмента [0,4], функция f(x) непрерывна справа (х = 0) и непрерывна слева (х = 4).
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 5 функция не определена, т.к., выполнив подстановку, получаем неопределенность вида 0/0. Легко доказать, что
Следовательно, точка х = 5 точка устранимого разрыва.
Пример:
Исследовать на непрерывность функцию
Решение:
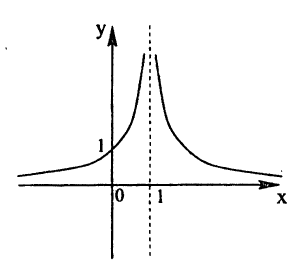
В точке х = 0 функция (рис. 95) терпит разрыв, так как она не определена в этой точке. Пределы функции слева и справа от точки х = 0 равны ∞. Следовательно, точка х = 0 для данной функции является точкой разрыва второго
Пример:
Исследовать на непрерывность функцию
Решение:
В точке х = 0 функция терпит разрыв 1-го рода, так как односторонние пределы существуют в этой точке, но не равны:
предел слева
предел справа
Пример:
Исследовать на непрерывность функцию 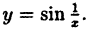
Решение:
Функция 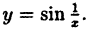
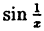
Пример:
Исследовать на непрерывность функцию
Решение:
Функция 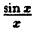
Если доопределить функцию 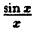
f(х) =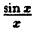
Доопределив функцию в точке х = 0, мы устранили разрыв.
Непрерывность функций
Смотрите также:
Предмет математический анализ
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Непрерывность функции
4 раздела
от теории до практики
1 пример
Примеры решения задач
видео
Примеры решения задач
-
Понятие непрерывности функции.
Начать изучение
-
Точки разрыва.
Начать изучение
-
Свойства функций, непрерывных в точке.
Начать изучение
-
Локальные свойства непрерывной функции.
Начать изучение
-
Непрерывность суммы, произведения и частного.
Начать изучение
-
Непрерывность сложной функции.
Начать изучение
-
Свойства функций, непрерывных на отрезке.
Начать изучение
-
Ограниченность непрерывной на отрезке функции.
Начать изучение
-
Достижимость точных граней.
Начать изучение
-
Промежуточные значения.
Начать изучение
-
Существование и непрерывность функции, обратной для непрерывной и строго монотонной функции.
Начать изучение
Понятие непрерывности функции.
Определение 1
Функция (f(x)), определенная в некоторой окрестности точки (a), называется непрерывной в точке (a), если
$$
displaystyle lim_{xrightarrow a}f(x)=f(a)label{ref1}
$$
Таким образом, функция (f) непрерывна в точке (a), если выполнены следующие условия:
- функция (f) определена в некоторой окрестности точки (a), то есть существует число (delta_0>0) такое, что (U_{delta_{0}}(a)subset D(f));
- существует (displaystyle lim_{xrightarrow a}f(x)=A);
- (A=f(a)).
Определение непрерывности функции (f(x)) в точке (a), выраженное условием eqref{ref1}, можно сформулировать с помощью неравенств (на языке (varepsilon-delta)), с помощью окрестностей и в терминах последовательностей соответственно в виде
- (forall varepsilon>0 existsdelta>0:quadforall x:|x-a| < deltarightarrow|f(x)-f(a)| < varepsilon,)
- (forall varepsilon>0 existsdelta>0:quadforall xin U_{delta}(a)rightarrow f(x)in U_{varepsilon}(f(a)),)
- (displaystyleforall{x_{n}}: lim_{nrightarrowinfty}x_{n}=arightarrowlim_{nrightarrowinfty}f(x_{n})=f(a).)
Следует обратить внимание на то, что в определении непрерывности функции, в отличие от определения предела, рассматривается полная, а не проколотая окрестность точки (a), и пределом функции является значение этой функции в точке (a).
Назовем разность (x-a) приращением аргумента и обозначим (Delta x), а разность (f(x)-f(a)) — приращением функции, соответствующим данному приращению аргумента (Delta x), и обозначим (Delta y). Таким образом,
$$
Delta x=x-a,;Delta y=f(x)-f(a)=f(a+Delta x)-f(a).nonumber
$$
При этих обозначениях равенство eqref{ref1} примет вид
$$
lim_{Delta xrightarrow 0}Delta y=0.nonumber
$$
Таким образом, непрерывность функции в точке означает, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Пример 1
Показать, что функция (f(x)) непрерывна в точке (a), если:
- (f(x)=x^3, a=1);
- (f(x)=displaystyle frac{1}{x^{2}}, aneq 0);
- (f(x)=sqrt{x}, a>0);
- (f(x)=displaystyle left{begin{array}{lc}xsinfrac1x,&xneq0,\0,&x=0,end{array}right.a=0)
Решение
- (triangle)Если (xrightarrow 1), то по свойствам пределов (S 10, (11)) получаем (x^3rightarrow 1), то есть для функции (f(x)=x^3) в точке (x=1) выполняется условие eqref{ref1}. Поэтому функция (x^3) непрерывна в точке (x=1).
- Если (xrightarrow a), где (aneq 0), то, используя свойства пределов (S 10), получаем (displaystyle frac{1}{x}rightarrowfrac{1}{a},;displaystyle frac{1}{x^{2}}rightarrowfrac{1}{a^{2}}), то есть Функция (displaystyle frac{1}{x^{2}}) непрерывна в точке (x=a,;(aneq 0)).
- Так как (displaystyle |sqrt{x}-sqrt{a}|=frac{|x-a|}{sqrt{x}+sqrt{a}}), то отсюда получаем (0leq|sqrt{x}-sqrt{a}|;<;displaystylefrac{|x-a|}{sqrt{a}}). Следовательно, (sqrt{x}-sqrt{a}rightarrow 0) при (xrightarrow a). Это означает, что функция (sqrt{x}) непрерывна в точке (a), где (a>0).
- Функция (f) определена на (mathbb{R}), и при любом (xinmathbb{R}) выполняется неравенство (0leq|f(x)-f(0)|=|f(x)|leq|x|), так как (left|sin{frac{1}{x}}right|leq1) при (xneq 0). Следовательно, (displaystyle lim_{xrightarrow 0}f(x)=f(0)=0), то есть функция (f) непрерывна в точке (x=0.quadblacktriangle)
По аналогии с понятием предела слева (справа) вводится понятие непрерывности слева (справа). Если функция (f) определена на полуинтервале ((a-delta,a]) и (displaystyle lim_{xrightarrow a-0}f(x)=f(a)), то есть(f(a-0)=f(a)), то эту функцию называют непрерывной слева в точке (a).
Аналогично, если функция (f) определена на полуинтервале ([a,a+delta)) и (f(a+0)=f(a)), то эту функцию называют непрерывной справа в точке (a).
Например, функция (f(x)=[x]) непрерывна справа в точке (x=1) и не является непрерывной слева в этой точке, так как (f(1-0)=0,;f(1+0)=f(1)=1).
Очевидно, функция непрерывна в данной точке тогда и только тогда, когда она непрерывна как справа, так и слева в этой точке.
Точки разрыва.
Будем предполагать, что функция (f) определена в некоторой проколотой окрестности точки (a).
Точку (a) назовем точкой разрыва функции (f), если эта функция либо не определена в точке (a), либо определена, но не является непрерывной в точке (a).
Следовательно, (a) — точка разрыва функции (f), если не выполняется по крайней мере одно из следующих условий:
- (ain D(f));
- существует конечный (displaystyle lim_{xrightarrow a}f(x)=A);
- (A=f(a)).
Определение 2
Если (a) — точка разрыва функции (f), причем в этой точке существуют конечные пределы слева и справа, то есть (displaystyle lim_{xrightarrow a-0}f(x)=f(a-0)) и (displaystyle lim_{xrightarrow a+0}f(x)=f(a+0)), то точку (a) называют точкой разрыва первого рода.
Замечание 1
Если (x=a) — точка разрыва первого рода функции (f(x)), то разность (f(a+0)-f(a-0)) называют скачком функции в точке (a). В случае когда (f(a+0)=f(a-0)), точку (a) называют точкой устранимого разрыва. Полагая (f(a)=f(a+0)=f(a-0)=A), получим функцию
$$
f(x)=left{begin{array}{l}f(x),;если;xneq a,\A,;если;x=a,end{array}right.nonumber
$$
непрерывную в точке (a) и совпадающую с (f(x)) при (xneq a). В этом случае говорят, что функция доопределена до непрерывности в точке (a).
Пусть (x=a) — точка разрыва функции (f), не являющаяся точкой разрыва первого рода. Тогда ее называют точкой разрыва второго рода функции (f). В такой точке хотя бы один из односторонних пределов либо не существует, либо бесконечен.
Например, для функции (f(x)=displaystyle xsin{frac{1}{x}}) точка (x=0) — точка разрыва первого рода. Доопределив эту функцию по непрерывности, получим функцию
$$
overline{f}(x)=left{begin{array}{ll}
xsin{frac{1}{x}},;если;xneq 0,\
0,;если;x=0,
end{array}right.nonumber
$$
непрерывную в точке (x=0), так как
$$
lim_{xrightarrow 0}xsinfrac{1}{x}=0.nonumber
$$
Для функций (displaystyle sin{frac{1}{x}}) и (displaystyle frac{1}{x^2}) точка (x=0) — точка разрыва второго рода.
Теорема 1
Если функция (f) определена на отрезке ([a,b]) и монотонна, то она может иметь внутри этого отрезка точки разрыва только первого рода.
Доказательство
(circ) Пусть (x_0) — произвольная точка интервала ((a,b)). Функция (f) имеет в точке (x_{0}) конечные пределы слева и справа. Если, например, (f) — возрастающая функция, то
$$
f(x_{0}-0)leq f(x_{0})leq f(x_{0}+0),nonumber
$$
где (f(x_{0}-0)) и (f(x_{0}+0)) — соответственно пределы функции (f) слева и справа в точке (x_{0}).
В том случае, когда (f(x_{0}-0)neq f(x_{0}+0)) , точка (x_{0}) является точкой разрыва первого рода функции (f); если же (f(x_{0}-0)=f(x_{0}+0)), то точка (x_{0}) есть точка непрерывности функции (f). Аналогичное утверждение справедливо и для убывающей функции.(bullet)
Свойства функций, непрерывных в точке.
Локальные свойства непрерывной функции.
Свойство 1
Если функция (f) непрерывна в точке (a), то она ограничена в некоторой окрестности этой точки, то есть
$$
existsdelta>0quadexists C>0:;forall xin U_{delta}(a)rightarrow|f(x)|leq Cnonumber
$$
Свойство 2
Если функция (f) непрерывна в точке (a), причем (f(a)neq 0), то в некоторой окрестности точки (a) знак функции совпадает со знаком числа (f(a)), то есть
$$
existsdelta>0:quadforall xin U_{delta}(a)rightarrow operatorname{sign} f(x)=operatorname{sign} f(a).nonumber
$$
(circ) Эти утверждения следуют из свойств пределов. (bullet)
Непрерывность суммы, произведения и частного.
Свойство 3
Если функции (f) и (g) непрерывны в точке (a), то функции (f+g), (fg) и (f/g) (при условии (g(a)neq 0)) непрерывны в точке (a).
(circ) Это утверждение следует из определения непрерывности и свойств пределов. (bullet)
Непрерывность сложной функции.
Напомним, что такое сложная функция.
Пусть функции (y=varphi(x)) и (z=f(y)) определены на множествах (X) и (Y) соответственно, причем множество значений функции (varphi) содержится в области определения функции (f). Тогда функция, которая принимает при каждом (xin X) значение (F(x)=f(varphi(x))), называется сложной функцией или суперпозицией (композицией) функций (varphi) и (f).
Теорема 2
Если функция (z=f(y)) непрерывна в точке (y_0), а функция (y=varphi(x)) непрерывна в точке (x_0), причем (y_0=varphi(x_0)), то в некоторой окрестности точки (x_0) определена сложная функция (f(varphi(x_0))), и эта функция непрерывна в точке (x_0).
Доказательство
(circ) Пусть задано произвольное число (varepsilon>0). В силу непрерывности функции (f) в точке (y_0) существует число (rho=rho(varepsilon)>0) такое, что (U_rho(y_0)subset D(f)) и
$$
forall yin U_rho(y_0)rightarrow f(y)in U_{varepsilon}(z_{0}),label{ref2}
$$
где (z_{0}=f(y_{0})).
В силу непрерывности функции (varphi) в точке (x_{0}) для найденного в eqref{ref2} числа (rho>0) можно указать число (delta=delta_{rho}=delta(varepsilon)>0) такое, что
$$
forall xin U_delta(x_0)rightarrow phi (x)in U_rho (y_0).label{ref2′}
$$
Из условий eqref{ref2} и eqref{ref2′} следует, что на множестве (U_delta(x_0)) определена сложная функция (f(varphi(x))), причем
$$
forall xin U_delta(x_0)rightarrow f(y)=f(varphi(x))in U_{varepsilon}(z_{0}),nonumber
$$
где (z_0=f(varphi(x_0))=f(y_{0})), то есть
$$
forall varepsilon>0;exists delta>0:quad forall хin U_delta(x_0)rightarrow f(varphi(х))in U_varepsilon(varphi(x_0)).nonumber
$$
Это означает, в силу определения непрерывности, что функция (f(varphi(x))) непрерывна в точке (x_0). (bullet)
Замечание 2
Соответствие между окрестностями точек (x_0, y_0, z_0) представлено на рис. 11.1. По заданному числу (varepsilon>0) сначала находим (rho>0), а затем для чисел (rho>0) находим (delta>0).
Свойства функций, непрерывных на отрезке.
Функцию (f(x)) называют непрерывной на отрезке ([a,b]), если она непрерывна в каждой точке интервала ((a,b)) и, кроме того, непрерывна справа в точке (a) и непрерывна слева в точке (b).
Ограниченность непрерывной на отрезке функции.
Теорема 3
(Теорема Вейерштрасса)
Если функция (f) непрерывна на отрезке ([a,b]), то она ограничена, то есть
$$
exists C>0:forall xin[a, b]rightarrow|f(x)|leq C.label{ref3}
$$
Доказательство
(circ) Предположим противное, тогда
$$
forall C>0;exists x_{C}in [a,b]:;|f(x_{C})|>C.label{ref4}
$$
Полагая в этом выражении (C=1,2ldots,n,ldots,) получим, что
$$
forall ninmathbb{N}quadexists x_{n}in[a,b]:;|f(x_{n})|>n.label{ref5}
$$
Последовательность (x_n) ограничена, так как (aleq x_{n}leq b) для всех (ninmathbb{N}). По теореме Больцано-Вейерштрасса из нее можно выделить сходящуюся подпоследовательность, то есть существуют подпоследовательность (x_{n_k}) и точка (xi) такие, что
$$
lim_{krightarrowinfty}x_{n_{k}}=xi,label{ref6}
$$
где в силу условия eqref{ref5} для любого (kinmathbb{N}) выполняется неравенство
$$
aleq x_{n_{k}}leq b.label{ref7}
$$
Из условий eqref{ref6} и eqref{ref7} следует, что (xiin [а,b]) а из условия eqref{ref6} в силу непрерывности функции (f) в точке (xi) получаем
$$
displaystyle lim_{krightarrowinfty}f(x_{n_{k}})=f(xi).label{ref8}
$$
С другой стороны. утверждение eqref{ref5} выполняется при всех (ninmathbb{N}) и, в частности, при (n=n_k;(k=1,2,ldots)), то есть
$$
|f(x_{n_{k}})|>n_{k},nonumber
$$
откуда следует, что (displaystyle lim_{krightarrowinfty}f(x_{n_{k}})=infty), так как (n_{k}rightarrow +infty) при (krightarrowinfty). Это противоречит равенству eqref{ref8}, согласно которому последовательность ({f(x_{n_{k}})}) имеет конечный предел. По этому условие eqref{ref4} не может выполняться, то есть справедливо утверждение eqref{ref3}. (bullet)
Замечание 3
Теорема Вейерштрасса неверна для промежутков, не являющихся отрезками. Например, функция (f(x)=displaystyle frac{1}{x}) непрерывна на интервале ((0,1)), но не ограничена на этом интервале. Функция (f(x)=x^{2}) непрерывна на (mathbb{R}), но не ограничена на (mathbb{R}).
Достижимость точных граней.
Теорема 4
(Теорема Вейерштрасса)
Если функция (f) непрерывна на отрезке ([a,b]), то она достигает своей точной верхней и нижней грани, то есть
$$
existsxiin[a,b]:quad f(xi)=sup_{xin [a,b]} f(x),label{ref9}
$$
$$
existswidetilde{xi}in[a,b]:quad f(widetilde{xi})= displaystyle inf_{xin [a,b]} f(x).label{ref10}
$$
Доказательство
(circ) Так как непрерывная на отрезке функция (f(x)) ограничена (теорема 3), то есть множество значений, принимаемых функцией (f) на отрезке ([a,b]), ограничено, то существуют (displaystyle sup_{xin[a,b]}f(x)) и (displaystyle inf_{xin[a,b]}f(x)).
Докажем утверждение eqref{ref9}. Обозначим (M=displaystyle sup_{xin[a,b]}f(x)). В силу определения точной верхней грани выполняются условия
$$
forall хin [a,b]rightarrow f(x)leq M,label{ref11}
$$
$$
forallvarepsilon>0;exists x(varepsilon)in[a,b]:quad f(x(varepsilon))>M-varepsilon.label{ref12}
$$
Полагая (varepsilon=displaystyle frac{1}{2}, displaystyle frac{1}{3},ldots,frac{1}{n},ldots), получим в силу условия eqref{ref12} последовательность({x_n}), где (x_n=displaystyle xleft(frac1nright)), такую, что для всех (ninmathbb{N}) выполняются условия
$$
x_nin [a,b],label{ref13}
$$
$$
f(x_{n})>M-displaystyle frac{1}{n}.label{ref14}
$$
Из соотношений eqref{ref11}, eqref{ref13} и eqref{ref14} следует, что
$$
forall ninmathbb{N}rightarrow M-frac{1}{n};<;f(x_{n})leq M,nonumber
$$
откуда получаем
$$
lim_{xrightarrowinfty}f(x_{n})=M.label{ref15}
$$
Как и в теореме 3, из условия eqref{ref13} следует, что существуют подпоследовательность ({x_{n_k}}) последовательности ({x_n}) и точка (xi) такие, что
$$
lim_{krightarrowinfty}x_{n_k}=xi,quad где xiin[a,b].nonumber
$$
В силу непрерывности функции (f) в точке (xi)
$$
lim_{krightarrowinfty} f(x_{n_{k}})=f(xi).label{ref16}
$$
С другой стороны, ({f(x_{n_{k}})}) — подпоследовательность последовательности ({f(x_{n})}), сходящейся, согласно условию eqref{ref15}, к числу (М). Поэтому
$$
lim_{krightarrowinfty}f(x_{n_{k}})=M.label{ref17}
$$
В силу единственности предела последовательности из eqref{ref16} и eqref{ref17} заключаем, что (f(xi)=M=displaystyle sup_{xin [a,b]}f(x)). Утверждение eqref{ref9} доказано. Аналогично доказывается утверждение eqref{ref10}. (bullet)
Замечание 4
Теорема 4 неверна для интервалов: функция, непрерывная на интервале, может не достигать своих точных граней. Например, функция (f(x)=x^{2}) не достигает на интервале (0,1) своей точной нижней грани, равной нулю, и точной верхней грани, равной единице.
Промежуточные значения.
Теорема 5
(теорема Коши о нулях непрерывной функции)
Если функция (f) непрерывна на отрезке [a,b] и принимает в его концах значения разных знаков, то есть (f(a)f(b);<;0), то на отрезке [a,b] имеется хотя бы один нуль функции (f), то есть
$$
exists cin[a,b]:; f(c)=0.label{ref18}
$$
Доказательство
(circ) Разделим отрезок ([a,b]) пополам. Пусть (d) — середина этого отрезка. Если (f(d)=0), то теорема доказана, а если (f(d)neq 0), то в концах одного из отрезков ([a,d], [d,b]) функция (f) принимает значения разных знаков. Обозначим этот отрезок (Delta_{1}=[a_{1},b_{1}]). Пусть (d_{1}) — середина отрезка (Delta_1). Возможны два случая:
- (f(d_{1})=0), тогда теорема доказана;
- (f(d_{1})neq 0), тогда в концах одного из отрезков ([a_{1},d_{1}],;[d_{1},b_{1}]) функция (f) принимает значения разных знаков; такой отрезок обозначим (Delta_{2}=[a_{2},b_{2}]).
Продолжая эти рассуждения, получим:
-
- либо через конечное число шагов найдется точка (cin [a,b]) такая, что (f(c)=0); тогда теорема доказана;
- либо существует последовательность отрезков ({Delta_n}) такая, что (f(a_{n})f(b_{n});<;0) для всех (ninmathbb{N}), где (Delta_n=[a_{n},b_{n}]).
Во втором случае последовательность отрезков является стягивающейся (S 6,п.4), так как (Delta_nsubsetDelta_{n-1}) для любого (ninmathbb{N}) и
$$
b_{n}-a_{n}=displaystyle frac{b-a}{2^{n}}.label{ref19}
$$
По теореме Кантора существует точка (c), принадлежащая всем отрезкам последовательности ({Delta_n}), то есть
$$
exists c:;forall ninmathbb{N}rightarrow сin [a_{n},b_{n}]subset[a,b].label{ref20}
$$
Докажем, что
$$
f(с)=0.label{ref21}
$$
Предположим, что равенство eqref{ref21} не выполняется. Тогда либо (f(с)>0), либо (f(с);<;0). Пусть, например, (f(с)>0). По свойству сохранения непрерывной функцией знака (п.3 а))
$$
existsdelta>0:quad хin U_delta(c)rightarrow f(x)>0.label{ref22}
$$
С другой стороны, из неравенства eqref{ref19} следует, что (b_{n}-a_{n}rightarrow 0) при (nrightarrowinfty), и поэтому
$$
exists n_0inmathbb{N}:quad b_{n_{0}}-a_{n_{0}};<;delta.label{ref23}
$$
Так как (cinDelta_{n_0}) в силу условия eqref{ref20}, то из eqref{ref23}следует, что (Delta_{n_0}subset U_{delta}(c)) и согласно условию eqref{ref22} во всех точках отрезка (Delta_{n_0}) функция (f) принимает положительные значения. Это противоречит тому, что в концах каждого из отрезков (Delta_n) функция (f) принимает значения разных знаков.
Полученное противоречие доказывает, что должно выполняться условие eqref{ref21}. (bullet)
Замечание 5
Теорема 5 утверждает, что график функции (y=f(x)), непрерывной на отрезке ([a,b]) и принимающей в его концах значения разных знаков, пересекает ось (Ox) (рис. 11.2) хотя бы в одной точке отрезка ([a,b]).
Теорема 6
(теорема Коши о промежуточных значениях)
Если функция (f) непрерывна на отрезке ([a,b]) и (f(a)neq (b)), то для каждого значения (C), заключенного между (f(a)) и (f(b)), найдется точка (xiin [a,b]) такая, что (f(xi)=C).
Доказательство
(circ) Обозначим (f(a)=A, f(b)=B). По условию (Аneq В). Пусть, например, (A < B). Нужно доказать, что
$$
forall Cin[A,B] existsxiin[a,b]: f(xi)=C.label{ref24}
$$
Если (C=A), то утверждение eqref{ref24} выполняется при (xi=a), а если (C=B), то eqref{ref24} имеет место при (xi=b). Поэтому достаточно рассмотреть случай (A < C < B).
Пусть (varphi(х)=f(x)-C), тогда (varphi(a)=A-C < 0, varphi(b)=B-С>0) и по теореме 5 найдется точка (xiin [a,b]) такая, что (varpi(xi)=0), то есть (f(xi)=C). Утверждение eqref{ref24} доказано. (bullet)
Следствие
Если функция (f) непрерывна на отрезке ([a,b], m=displaystyle inf_{xin[a,b]} f(x), M=displaystyle sup_{xin[a,b]} f(x)), то множество значений, принимаемых функцией (f) на отрезке ([a,b]), есть отрезок ([m,M]).
(circ) Для всех (xin[a,b]) выполняется неравенство (mleq f(x)leq M), причем согласно теореме 4 функция (f) принимает на отрезке ([a,b]) значения, равные (m) и (М). Все значения из отрезка ([m,M]) функция принимает по теореме 6. Отрезок ([m,M]) вырождается в точку, если (f(x)=const) на отрезке ([a,b]). (bullet)
Существование и непрерывность функции, обратной для непрерывной и строго монотонной функции.
Ранее мы уже рассматривали понятие обратной функции. Докажем теорему о существовании и непрерывности обратной функции.
Теорема 7
Если функция (y=f(x)) непрерывна и строго возрастает на отрезке ([a,b]), то на отрезке ([f(a),(b)]) определена функция (x=g(y)), обратная к f, непрерывная и строго возрастающая.
Доказательство
(circ) Существование обратной функции. Обозначим (A=f(a),;B=f(b)). Так как f — возрастающая функция, то для всех (хin [a,b]) выполняется неравенство (Aleq f(x)leq B), где (A= displaystyle inf_{xin[a,b]} f(x),;B=sup_{xin[a,b]}f(x)), и в силу непрерывности f (следствие из теоремы 6) множество значений функции (E(f)=[A,B]).
Согласно определению обратной функции (S 9,п. 9) нужно доказать, что для каждого (у_0in [A,В]) уравнение
$$
f(x)=y_{0}label{ref25}
$$
имеет единственный корень (x=x_{0}), причем (x_0in [a,b]).
Существование хотя бы одного корня уравнения eqref{ref25} следует из теоремы 6. Докажем, что уравнение eqref{ref25} имеет на отрезке ([a,b]) единственный корень.
Предположим, что наряду с корнем (x=x_{0}) уравнение eqref{ref25} имеет еще один корень (x=widetilde{x}_{0}), где (widetilde{x}_{0}neq x_0); тогда (f(widetilde{x_0})=y_{0},;widetilde x_0in[a,b]).
Пусть, например, (widetilde{x}_0>x_0). Тогда в силу строгого возрастания функции (f) на отрезке ([a,b]) выполняется неравенство (f(widetilde{x}_0)>f(x_{0})). С другой стороны, (f(widetilde{x}_0)=f(x_0)=y_{0}). Отсюда следует, что неравенство (widetilde{x}_0>x_{0}) не может выполняться. Следовательно, (widetilde{x}_0=x_0). Существование обратной функции доказано, то есть на отрезке ([A,В]) определена функция (x=f^{-1}(y)=g(y)), обратная к (f), причем ((g)=[a,b]) и
$$
g(f(x))=x,quad xin[a,b],quad f(g(y))=y,quad uin [A,B].label{ref26}
$$
Монотонность обратной функции. Докажем, что (g(y)) — строго возрастающая на отрезке [A,В] функция, то есть
$$
forall;y_{1},;y_{2}in [A,B]:quad y_{1};<;y_{2}rightarrow g(y_{1});<;g(у_2).label{ref27}
$$
Предположим противное; тогда условие eqref{ref27} не выполняется, то есть
$$
exists;widetilde{y}_{1},widetilde{y}_{2}in [A,B]:;widetilde{y}_{1};<;y_2rightarrow g(widetilde{y}_1geq g(widetilde{y}_2).label{ref28}
$$
Обозначим (widetilde{x}_1=g(widetilde{y}_1),;widetilde{x}_2=g(widetilde{y}_2)), тогда (widetilde{x}_1,widetilde{x}_2in [a,b],;widetilde{x}_1geqwidetilde{x}_{2}) в силу eqref{ref28} и (f(widetilde{x}_{1})=widetilde{y}_{1},;f(widetilde{x}_{2})=widetilde{y}_{2}) согласно равенству eqref{ref26}.
Так как (f) — строго возрастающая функция, то из неравенства (widetilde{X}_1geqwidetilde{x}_2) следует неравенство (f(widetilde{x}_{1})geq f(widetilde{x}_{2})), то есть (widetilde{y}_{1}geqwidetilde{y}_{2}), что невозможно, так как (widetilde{y}_1;<;widetilde{y}_{2}) в силу eqref{ref28}. Таким образом, утверждение eqref{ref28} не может выполняться, и поэтому (g(y)) — строго возрастающая функция.
Непрерывность обратной функции. Пусть (y_0) — произвольная точка интервала ((A,B)). Докажем, что функция (g) непрерывна в точке (y_{0}). Для этого достаточно показать, что справедливы равенства
$$
g(y_{0}-0)=g(y_{0}),quad g(y_{0}+0)=g(y_{0}),label{ref29}
$$
где (g(y_{0}-0)) и (g(y_{0}+0)) — пределы функции (g) соответственно слева и справа в точке (y_0).
По теореме о пределах монотонной функции (S 10) пределы функции (g) слева и справа в точке (y_{0}) существуют и выполняются неравенства
$$
g(y_{0}-0)leq g(y_{0})leq g(y_{0}+0).label{ref30}
$$
Пусть хотя бы одно из равенств eqref{ref29} не выполняется, например, (g(y_0-0)neq g(y_0)), тогда
$$
g(y_0-0) < g(y_0).label{ref31}
$$
Так как для всех (yin[A,y_{0})) выполняется неравенство (aleq g(у)leq g(y_0-0)), где (g(у_0-0)=displaystyle sup_{Aleq y;<;y_0}g(y)), а при всех (yin [y_0,B]) справедливо неравенство (g(y_0)leq g(y)leq b), то из условия eqref{ref31} следует, что интервал (Delta=(g(y_0-0),g(y_{0}))) не принадлежит множеству значений функции (g). Это противоречит тому, что все точки отрезка ([a,b]), в том числе и точки интервала (Delta), принадлежат множеству E(g). Итак, первое из равенств eqref{ref29} доказано. Аналогично доказывается справедливость второго из равенств eqref{ref29}.
Тем же способом устанавливается, что функция (g) непрерывна справа в точке (A) и непрерывна слева в точке (B). (bullet)
Замечание 6
Если функция (f) непрерывна и строго убывает на отрезке ([a,b]), то обратная к ней функция (g) непрерывна и строго убывает на отрезке ([f(b),f(a)]).
Замечание 7
Аналогично формулируется и доказывается теорема о функции (g), обратной к функции (f), для случаев, когда функция (f) задана на интервале (конечном либо бесконечном) и полуинтервале.
Если функция (f) определена, строго возрастает и непрерывна на интервале ((a,b)), то обратная функция (g) определена, строго возрастает и непрерывна на интервале ((A,B)), где
$$
A=lim_{xrightarrow a+0}f(x),quad B=lim_{xrightarrow b-0}f(x).nonumber
$$
Эта статья — о непрерывной числовой функции. О непрерывных отображениях в различных разделах математики см. непрерывное отображение.
Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.
График непрерывной функции является непрерывной линией.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой.
Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Вариацию этого понятия для функций комплексной переменной см. в статье Комплексный анализ.
Определение[править | править код]
Пусть 

Существует несколько эквивалентных определений непрерывности функции в точке 
- Комментарий: По сравнению с определением предела функции по Коши в определении непрерывности нет требования, обязывающего все значения аргумента
удовлетворять условию
, то есть быть отличными от а.
Функция 

В этом случае говорят, что функция 



Точки разрыва[править | править код]
Запрос «Точка разрыва» перенаправляется сюда; см. также другие значения.
Если условие, входящее в определение непрерывности функции, в некоторой точке нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если 










Классификация точек разрыва в R¹[править | править код]
Классификация разрывов функций 


Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. К точкам разрыва первого рода относят устранимые разрывы и скачки.
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. К точкам разрыва второго рода относят полюса и точки существенного разрыва.
-
Устранимый разрыв
-
Разрыв типа «скачок»
-
Особая точка типа «полюс». Если доопределить функцию для x=2 — получится разрыв «полюс».
-
Точка существенного разрыва
Устранимая точка разрыва[править | править код]
Если предел функции существует и конечен, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то точка 

Если «поправить» функцию 

Точка разрыва «скачок»[править | править код]
Разрыв «скачок» возникает, если
.
Точка разрыва «полюс»[править | править код]
Разрыв «полюс» возникает, если один из односторонних пределов бесконечен.
или
.[источник не указан 2709 дней]
Точка существенного разрыва[править | править код]
В точке существенного разрыва хотя бы один из односторонних пределов вообще отсутствует.
Классификация изолированных особых точек в Rn, n>1[править | править код]
Для функций 

Понятие «скачок» отсутствует. То, что в 
Свойства[править | править код]
Локальные[править | править код]
Глобальные[править | править код]
- Теорема о равномерной непрерывности: функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Теорема Вейерштрасса о функции на компакте: функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции
, непрерывной на отрезке
, является отрезок
где минимум и максимум берутся по отрезку
.
- Если функция
непрерывна на отрезке
и
то существует точка
в которой
.
- Теорема о промежуточном значении: если функция
непрерывна на отрезке
и число
удовлетворяет неравенству
или неравенству
то существует точка
в которой
.
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке
непрерывна в том и только в том случае, когда область её значений является отрезком с концами
и
.
- Если функции
и
непрерывны на отрезке
, причем
и
то существует точка
в которой
Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры[править | править код]
Элементарные функции[править | править код]
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом[править | править код]
Функция 
непрерывна в любой точке 

Функция знака[править | править код]
Функция
называется функцией знака.
Эта функция непрерывна в каждой точке 
Точка 
,
в то время как в самой точке функция обращается в нуль.
Функция Хевисайда[править | править код]
Функция Хевисайда, определяемая как
является всюду непрерывной, кроме точки 

Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
Функция Дирихле[править | править код]
Функция
называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция разрывна в каждой точке, поскольку в сколь угодно малой окрестности любой точки имеются как рациональные, так и иррациональные числа.
Функция Римана[править | править код]
Функция
называется функцией Римана или «функцией Тома».
Эта функция непрерывна на множестве иррациональных чисел (


Во всех же рациональных точках она разрывна.
Вариации и обобщения[править | править код]
Равномерная непрерывность[править | править код]
Функция 







Каждая равномерно непрерывная на множестве 
Полунепрерывность[править | править код]
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
Между непрерывностью и полунепрерывностью имеется следующая связь:
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
Односторонняя непрерывность[править | править код]
Функция 



Непрерывность почти всюду[править | править код]
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция 

В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Примечания[править | править код]
Литература[править | править код]
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
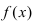
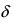 -окрестности;
-окрестности;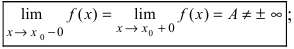
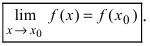
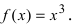
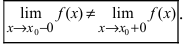
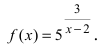
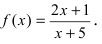
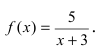
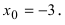
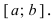
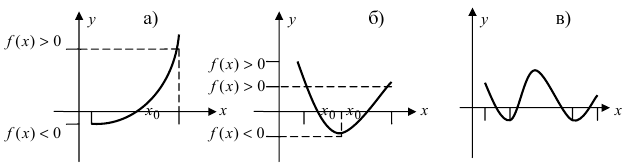
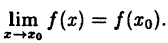
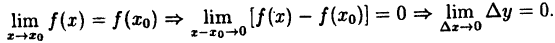
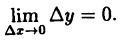

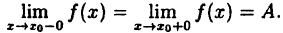
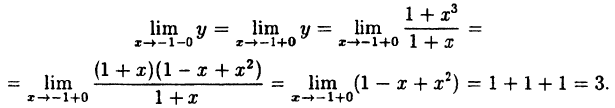
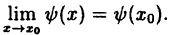
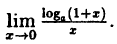
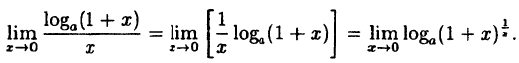
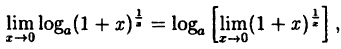
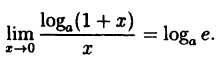
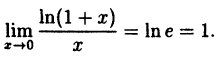
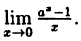
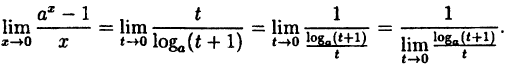
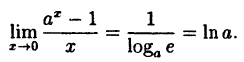
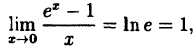
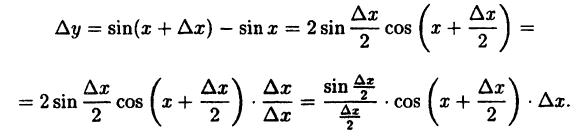
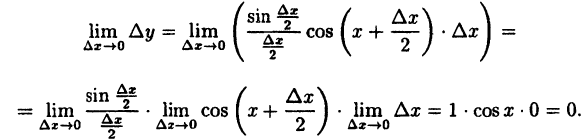
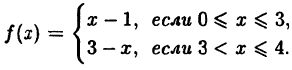
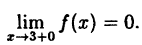
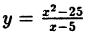
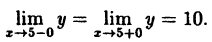
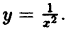
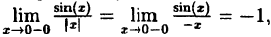
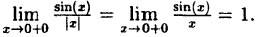
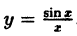
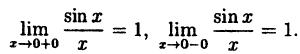















![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
![{displaystyle [min f, max f],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1898c8713b2f4013a0d3ba76e37ade6435ba3630)





















