Область определения функции
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.
Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции. Чтобы получить ответ, укажите функцию, для которой Вы хотите найти область определения. Основные примеры ввода функций и переменных для данного калькулятора указаны ниже.
Примеры функций: sqrt(16-ln(x^2))/sin(x)) или (5x^7+4x^6-3)/((3+2x-x^2)x^4)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Главная » Примеры решения задач » Онлайн калькулятор
Найти область определения функции |
||
|
Калькулятор для нахождения области определения функции онлайн (бесплатно). Правила ввода функции как на обычном калькуляторе. Найти область значения функции
Основные константы
Основные функции
модуль x: abs(x)
|
||
Поможем с решением ваших задач и контрольных! |
||
Категория: Онлайн калькулятор | Просмотров: 622816 | Добавил: Admin | Теги: онлайн калькулятор | Рейтинг: 3.3/78 |
Похожие материалы:
- Решение логарифмических уравнений
- Решение дифференциальных уравнений
- Решение квадратных уравнений
- Решение кубических уравнений
- Исследовать функцию, построить график
- Решение тригонометрических уравнений
- Найти неопределенный интеграл
- Сходимость рядов
- Найти предел функции
- Найти производную функции
| Всего комментариев: 0 | |
Калькулятор
Инструкция
Примечание: π записывается как pi; корень квадратный как sqrt().
Шаг 1. Введите данные.
Шаг 2. Нажмите кнопку “Найти”.
Шаг 3. Получите результат.
В калькулятор нужно вводить только латинские буквы.
Что такое область определения функции
Какую бы функцию мы не взяли, везде есть зависимая переменная и независимая. Значения зависимой переменной зависят от независимой. Например, возьмём функцию . Здесь
является независимой переменной, а
– зависимой. Иными словами говорится, что
– это функция от
. Все допустимые значения независимой переменной
– это область определения функции. А допустимые значения зависимой переменной
– область значения функции.
Область существования функции
Данный сервис используется для нахождения области определения функции в онлайн режиме.
Например, найти область определения функции ln(x2-1).
Примечание: число “пи” (π) записывается как pi; корень квадратный как sqrt, например, sqrt(3); arcsin ≡ asin
В таблице приведены области существования наиболее распространенных функций.
| ln(x) | x > 0 | 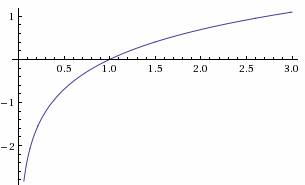 |
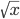 |
x ≥ 0 | 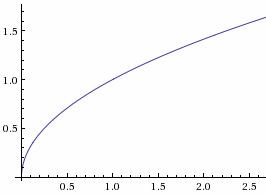 |
| tgx | 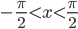 |
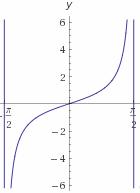 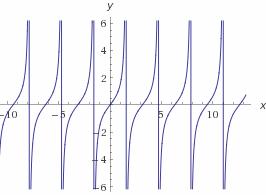 |
| ctgx | 0 < x< π | 
|
| arcsinx | -1 ≤ x ≤ 1 |  |
| arccosx | -1 ≤ x ≤ 1 |  |
Пример. Требуется найти область определения функции, для этого нужно знать области определения элементарных функций.
Найдем область определения 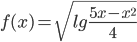 . Функция определена при тех значениях x, для которых
. Функция определена при тех значениях x, для которых 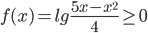 . Это неравенство будет выполнено, если
. Это неравенство будет выполнено, если 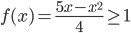 , т.е.
, т.е. x2–5x+4≤0. Решая это неравенство методом интервалов, находим область определения – промежуток [1;4]. Зная f(x), можно найти ![]() и т.д.
и т.д.
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки

Примеры
-
y=frac{x^2+x+1}{x}
-
f(x)=x^3
-
f(x)=ln (x-5)
-
f(x)=frac{1}{x^2}
-
y=frac{x}{x^2-6x+8}
-
f(x)=sqrt{x+3}
-
f(x)=cos(2x+5)
-
f(x)=sin(3x)
- Показать больше
Описание
Изучите функции шаг за шагом
functions-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Functions
A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…
Read More
Введите Задачу
Сохранить в блокнот!
Войти






![sqrt[n]{x}](https://upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png)




























