Учет области значений модуля при решении уравнения
23 мая 2014
Очень часто в уравнениях под знаком модуля стоят довольно сложные конструкции, которые было бы крайне затруднительно раскрывать, а затем решать «напролом». Для таких случаев существует множество приемов и замечаний, позволяющих значительно ускорить вычисления.
Одним из таких приемов является учет области значений модуля (учителя называют это решение методом следствий). Суть его можно описать одним простым предложением: «Сумма неотрицательных чисел равна нулю тогда и только тогда, когда каждое из этих чисел равно нулю».
Сегодня мы продолжаем изучать конструкции, содержащие знак модуля функции и переходим уже к более сложным конструкциям, когда ихдва, либо само уравнение содержит нестандартную функцию.
Немного теории
Для начала вспомним определение модуля: модулем числа $x$ называется либо само это число (при условии, что оно неотрицательное), либо минус это число, если оно отрицательно:
[left| x right|=left{ begin{align}& x,xge 0 \& -x,x<0 \end{align} right.]
Данная запись является алгебраическим определением, потому что здесь используется только алгебраическая терминология и никак не привлекается геометрия. И именно это определение позволяет нам заключить следующий факт: модуль числа всегда неотрицателен:
[left| x right|ge 0]
Именно поэтому его иногда еще называют абсолютным значением, т.е. расстоянием от 0 до этого числа на числовой прямой. И именно тот факт, что модуль функции всегда является неотрицательным числом, позволяет решить целый класс задач, которые иначе решались бы весьма проблематично.
Решаем реальные задачи
Пример № 1
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Чтобы решить такое выражение, давайте для начала вспомним, как решается простейшая конструкция с модулем, т.е уравнение вида $left| f right|=g$.
Решаются она довольно просто. Рассматривается два случая: в первом случае $f$ неотрицательно — в этом случае модуль функции снимается без всяких изменений и получается, что $f$ равно $g$. А во втором случае $f$ отрицательно — в этом случае модуль раскрывается со знаком «минус», как мы уже знаем из определения. Запишем совокупность систем:
[left| f right|=g=>left[ begin{align}& left{ begin{align}& fge 0 \& f=g \end{align} right. \& left{ begin{align}& f<0 \& -f=g \end{align} right. \end{align} right.]
Но все это работает только при условии, что модуль функции в выражении один, а у нас сегодня сразу два. Что делать в такой ситуации?
Давайте заметим, что при сложении двух модулей возникает выражение, значение которого 0. Но, с другой стороны, мы можем записать следующее:
[left| x-{{x}^{3}} right|ge 0]
[left| {{x}^{2}}+x-2 right|ge 0]
В этом случае сумма вышеописанных двух элементов также будет давать некое число (назовем его $k$), которое больше или равняется 0. При этом от нас требуется, чтобы оно строго равнялось 0. А это значит, что нас устроит только тот вариант, когда каждый из модулей равен 0, т.е. мы можем записать:
[left| x-{{x}^{3}} right|=0]
[left| {{x}^{2}}+x-2 right|=0]
Другими словами, сумма двух чисел, каждое из которых не меньше 0, дает в сумме ноль только в том случае, когда каждое из них равняется 0, т.е. требования должны выполняться одновременно. Поэтому запишем систему:
[left{ begin{align}& left| x-{{x}^{3}} right|=0 \& left| {{x}^{2}}+x-2 right|=0 \end{align} right.]
Модуль функции равен 0, когда подмодульное выражение равно 0, т.е:
[left{ begin{align}& x-{{x}^{3}}=0 \& {{x}^{2}}+x-2=0 \end{align} right.]
Давайте решим каждое из полученных выражений отдельно. Решаем первое:
[xleft( {{1}^{2}}-{{x}^{2}} right)=0]
[xleft( 1-x right)left( 1+x right)=0]
[{{x}_{1}}=0]
[{{x}_{2}}=1]
[{{x}_{3}}=-1]
При трех таких значениях тождество обнуляется.
Теперь разберемся со вторым выражением. Будем решать его при помощи формулы Виета:
[{{x}^{2}}+x-2=0]
[left( x+2 right)left( x-1 right)=0]
[{{x}_{1}}=-2]
[x=1]
А теперь вспоминаем, что мы решаем систему уравнений, т.е. нужно из первого и из второго наборов выбрать корни, которые принадлежат каждому из этих наборов. Очевидно, что такой корень только один — $x=1$.
Итого решением первого выражения является единственный корень $x=1$.
Как видите, такое решение оказалось существенно проще стандартного подхода. Здесь достаточно просто заметить,что сумма двух неотрицательных чисел равняется 0 только тогда, когда каждое из этих чисел имеет значение 0.
Пример № 2
Переходим ко второй конструкции:
[left| x-2 right|=-{{x}^{6}}]
На первый взгляд, можно сказать, что данная конструкция является простейшим уравнением. И, строго говоря, оно хорошо решается по выше записанной формуле, т.е. переходом от выражения с модулем функции к совокупности двух систем. Однако нас смущает степенная функция — степень слишком большая. Поэтому давайте заметим, что функция $fleft( x right)={{x}^{6}}$ является не просто четной, но и еще неотрицательной на всей числовой оси. А это значит, что $-{{x}^{6}}$ всегда будет либо отрицательной, либо равняться 0. Однако с другой стороны от знака равенства у нас стоит модуль функции — а он всегда неотрицателен. Это значит что, слева значение больше или равно нулю, а справа — меньше или равно. И от нас требуется узнать, когда эти значения друг другу тождественны. Очевидно, что такими они могут быть только тогда, когда каждое из них равняется 0, потому что в противном случае они будут лежать по разные стороны от разделяющего 0, т.е. $left| x-2 right|$ будет постоянно отклоняться вправо, а $-{{x}^{6}}$ — влево. Поэтому наше выражением может быть переписано следующим образом:
[left{ begin{align}& left| x-2 right|=0 \& -{{x}^{6}}=0 \end{align} right.]
Давайте решим эти конструкции:
[left{ begin{align}& x-2=0 \& {{x}^{6}}=0 \end{align} right.]
Решаем каждое из этих выражений:
[left{ begin{align}& x=2 \& x=0 \end{align} right.]
Мы получаем, что корень должен быть одновременно равен и 2 и 0. Это невозможно, поэтому решением данного выражения является пустое множество. Пусть вас не смущают подобные ответы при решении задач с модулями. Как и при работе с любыми другими функциями, накладывающими ограничения на область определения или значения в рамках задачи, в процессе решения сложных выражений с модулями функции вполне может оказаться, что этих решений просто не существует.
Ключевые моменты
- Сумма двух неотрицательных чисел равна нулю тогда, когда каждое из этих чисел равно нулю. В результате уравнение, которое само по себе далеко не тривиальное, разбивается на систему из двух отдельных уравнений, каждое из которых решается существенно проще.
- Тот факт, что модуль сам по себе является неотрицательным значением, можно использовать и иначе, например, когда с одной стороны стоит модуль функции (эта сторона неотрицательна), а с другой стороны — функция, которая меньше нуля или равна нулю. В этом случае все уравнение сводится к системе из двух уравнений, каждое из которых легко решается.
Как пример, второе вырадением может быть сведено к равенству первого вида следующим образом:
[left| x-2 right|+{{x}^{6}}=0]
Мы снова видим сумму двух функций, каждая из которых неотрицательна. Запомните этот прием, он очень эффективен при работе со всевозможными функциями, о которых точно известно, что они принимают лишнее отрицательное значение.
Смотрите также:
- Нестандартные уравнения с модулем
- Дробно-рациональные уравнения с модулем
- Тест к уроку «Что такое числовая дробь» (легкий)
- Сводный тест по задачам B15 (2 вариант)
- Как решать простейшие логарифмические уравнения
- Задача B4: вклад в банке и проценты
Область определения функции
Прежде чем перейти к изучению области определения функции внимательно изучите уроки
«Что такое функция в математике» и «Как решать задачи на функцию».
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
Вместо « x » (аргумента функции) в формулу « у = 2x » подставляем произвольные числовые значения и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу « у = 2x » и запишем результаты в таблицу.
| x | y = 2 x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
=
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
Вернемся к нашей функции « у = 2x » и найдем её область определения.
Посмотрим ещё раз на таблицу функции « y = 2x », где мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать, что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
В нашей функции « у = 2x » вместо « x » можно подставить любое число, поэтому область определения функции « у = 2x » — это любые действительные числа.
Запишем область определения функции « у = 2x » через математические обозначения.
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на математические символы. Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции « у = 2x ». Так как в функции
« у = 2x » нет ограничений для « x », заштрихуем всю числовую ось от минус бесконечности « −∞ » до плюс бесконечности « +∞ ».
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как « x ∈ R ».
Читается « x ∈ R » как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
« x ∈ R » одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
№ 233 (2) Мерзляк 8 класс
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x » в функции
« f(x) =
».
По законам математики из школьного курса мы помним, что на ноль делить нельзя. Иначе говоря, знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции « f(x) =
». Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
Получается, что « x » может принимать любые числовые значения кроме « −5 ». На числовой оси заштрихуем все доступные значения для « x ».
Число « −5 » отмечено «пустой» точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число « −5 » не входит в область определения функции, при записи ответа рядом с ним будет стоять круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке «Как записать ответ неравенства».
Запишем окончательный ответ для области определения функции
« f(x) =
».
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
№ 98 (5) Колягин (Алимов) 8 класс
Найти область определения функции:
Из урока «Квадратный корень» мы помним, что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
« у = √ 6 − x ». Подкоренное выражение
« 6 − x » должно быть больше или равно нулю.
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
Запишем полученный ответ, используя числовую ось и математические символы. Число « 6 » отмечено «заполненной» точкой на числовой оси, так как входит в область допустимых значений.
Правило для определения области определения функции
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
№ 242 (3) Мерзляк 8 класс
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции « f(x) = √ x + 3 +
» есть дробь «
», где « x » расположен в знаменателе. Запишем условие, что знаменатель « x 2 − 9 » не может быть равен нулю.
Решаем квадратное уравнение через формулу квадратного уравнения.
x1;2 =
x1;2 =
| −0 ± √ 0 2 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
Запомним полученный результат. Задаем себе второй вопрос. Проверяем, есть ли в формуле функции
« f(x) = √ x + 3 +
» корень четной степени. В формуле есть квадратный корень « √ x + 3 ». Подкоренное выражение « x + 3 » должно быть больше или равно нулю.
Решим линейное неравенство.
Объединим полученные ответы по обоим вопросам:
Объединим все полученные результаты на числовых осях. Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях. Обратим внимание, что числа « −3 » и « 3 » отмечены «пустыми» точками и не входят в итоговое решение.

промежутка « −3 » и « x > 3 », которые являются областью определения функции
« f(x) = √ x + 3 +
». Запишем окончательный ответ.
Примеры определения области определения функции
№ 101 Колягин (Алимов) 8 класс
Найти область определения функции:
Для поиска области определения функций задаем себе первый вопрос. Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
« y = 6 √ x + 5 √ 1 + x » нет дробей.
Задаем второй вопрос. Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени: « 6 √ x ». Степень корня — число « 6 ». Число « 6 » — чётное, поэтому подкоренное выражение корня « 6 √ x » должно быть больше или равно нулю.
В формуле функции « y = 6 √ x + 5 √ 1 + x » также есть корень пятой степени
« 5 √ 1 + x ». Степень корня « 5 » — нечётное число, значит, никаких ограничений на подкоренное выражение « 1 + x » не накладывается.
Получается, что единственное ограничение области определения функции
« y = 6 √ x + 5 √ 1 + x » — это ограничение подкоренного выражения « 6 √ x ».
Нарисуем область определения функции на числовой оси и запишем ответ.
№ 242 (4) Мерзляк 8 класс
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два. Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √ x + 2 ≠ 0 |
| x 2 − 7x + 6 ≠ 0 |
Обозначим их номерами « 1 » и « 2 » и решим каждое уравнение отдельно.
| √ x + 2 ≠ 0 (1) |
| x 2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
Если значение квадратного корня
« √ x + 2 ≠ 0 » не должно быть равно нулю, значит, подкоренное выражение
« x + 2 ≠ 0 » также не должно быть равно нулю.
Теперь решим уравнение под номером « 2 », используя формулу квадратного уравнения.
x1;2 =
x1;2 =
| −(−7) ± √ (−7) 2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
В формуле функции
« f(x) =
+
»
есть два корня « √ x − 4 » и « √ x + 2 ». Их подкоренные выражения должны быть больше или равны нулю.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
Объединим в таблицу ниже полученные ответы по обеим проверкам:
Результат проверки, что знаменатели дробей с « x » не равны нулю
Результат проверки, что подкоренные выражения должно быть больше или равны нулю
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет всем полученным условиям.
Источник
Область допустимых значений функции
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Источник
Область определения функции
Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох.
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
Чтобы обозначить область определения некоторой функции f, используют запись D(f). При этом нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
Константная функция — функция, которая для любого элемента из области определения возвращает одно и то же заданное значение. Множество значений такой функции состоит из одного единственного элемента.
Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Пример
Найти область определения функции:
Так как подкоренное выражение должно быть положительным, то решим неравенство x 2 + 4x + 3 > 0.
Разложим квадратный трёхчлен на множители:
Дискриминант положительный. Ищем корни:
Значит парабола a(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Область определения степенной функции
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
Рассмотрим несколько примеров.
Область определения показательной функции
Область определения показательной функции — это множество R.
Примеры показательных функций:
Область определения каждой из них (−∞, +∞).
Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
Область определения этих функций есть множество (0, +∞).
Пример
Укажите, какова область определения функции:
Составим и решим систему:
Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Источник
2
Математика
|
Объем | Codecademy
Scope
Переменные с областью видимости блока
Global Variables
Scope
function myFunction() { вар PizzaName = "Вольво"; // Код здесь может использовать pizzaName } // Код здесь не может использовать pizzaName
Область — это концепция, которая относится к тому, где можно получить доступ к значениям и функциям.
Различные области включают:
- Глобальная область (значение/функция в глобальной области может использоваться где угодно во всей программе)
- Файл или модуль область действия (доступ к значению/функции возможен только из файла)
- Область действия (видна только внутри функции),
- Кодовый блок область действия (виден только в кодовом блоке
{ .).. }
-
1
Область видимости
Важным понятием в программировании является область видимости . Область действия определяет, где можно получить доступ к переменным или на которые можно ссылаться. В то время как к некоторым переменным можно получить доступ из любой точки программы, другие переменные могут быть доступны…
Start
-
2
Блоки и область действия
Прежде чем мы поговорим о области действия, нам сначала нужно поговорить о блоках . Мы уже видели блоки, используемые ранее в функциях и операторах if. Блок — это код, находящийся внутри набора фигурных скобок {}. Blo…
Start
-
3
Global Scope
Scope — это контекст, в котором объявлены наши переменные. Мы думаем о области действия по отношению к блокам, потому что переменные могут существовать как вне, так и внутри этих блоков.
В global scope , varia…
Start
-
4
Block Scope
Следующий контекст, который мы рассмотрим, это block scope . Когда переменная определена внутри блока, она доступна только коду в фигурных скобках {}. Мы говорим, что эта переменная имеет область действия блока , потому что…
Начало
-
5
Загрязнение области
Может показаться хорошей идеей всегда делать ваши переменные доступными, но слишком много глобальных переменных могут вызвать проблемы в программа. Когда вы объявляете глобальные переменные, они переходят в _gl…
Start
-
6
Практика хорошего определения области видимости
Учитывая проблемы, связанные с глобальными переменными и загрязнением области видимости, мы должны следовать передовым методам для максимально узкой области видимости наших переменных, используя блочную область видимости.
Тщательное определение области видимости ваших переменных…
Начало
-
7
Обзор: область действия
На этом уроке вы узнали о области видимости и о том, как она влияет на доступность различных переменных. Давайте рассмотрим следующие термины: — Область относится к тому, где переменные могут быть доступны через…
Начало
-
Пришло время научиться бегло работать с функциями JavaScript. В следующем профессиональном проекте мы собираемся попрактиковаться в JavaScript, чтобы вы могли отточить свои навыки и чувствовать себя уверенно, применяя их в реальном мире.
Почему? Область видимости определяет видимость переменных и других ресурсов в вашем коде.
Что дальше? Марафонский бег, устранение ошибок, больше JavaScript. Ты получил это!
-
Область действия
Что такое глобальная переменная?
Глобальная переменная в Python с примерами [обновлено]
Python также использует переменные для хранения данных.
номер_класса = 4;
В приведенном выше примере переменная ‘class_number’ имеет значение 4; это целочисленный тип данных. И в отличие от других языков программирования, вам не нужно объявлять переменную без инициализации.
Что означает переменная область видимости в Python?
Область действия переменной означает область, в которой части программы могут получить доступ к переменной. В python есть четыре области видимости переменных:
.
- Местный
- Глобальный
- Корпус
- Встроенный
В этой статье вы познакомитесь с первыми двумя типами. Вы научитесь создавать переменные Python с локальной и глобальной областью видимости.
Что такое глобальная переменная в Python?
В мире программирования глобальная переменная в Python означает наличие области действия во всей программе, т.
Глобальная переменная в Python часто объявляется в начале программы. Другими словами, переменные, объявленные вне функции, называются глобальными переменными.
Вы можете получить доступ к глобальным переменным в Python как внутри, так и вне функции.
Синтаксис:
X = «sampleGlobalValue»
Защита fn1():
Как создавать глобальные переменные в Python?
Чтобы создать глобальную переменную в Python, вам нужно объявить переменную вне функции или в глобальной области.
Пример:
Выход:
Как получить доступ к глобальной переменной внутри и снаружи функции?
Пример:
Выход:
В приведенном выше примере вы видели глобальную переменную, объявленную и доступную как внутри, так и вне функции.
Итак, вы получаете доступ к значению как внутри, так и вне функции, и это нормально, но что произойдет, если вы попытаетесь изменить значение переменной глобальной области видимости внутри функции?
См.
Пример:
Выход:
Как видно, это выдает ошибку. Когда вы пытаетесь изменить значение глобальной переменной внутри функции, она выдает UnboundLocalError, потому что при изменении Python рассматривает x как локальную переменную, но x также не определен внутри функции (myfunc()).
Вот здесь и появляется ключевое слово Global. Вы увидите использование глобальных ключевых слов в следующих разделах.
Как создавать переменные с локальной областью действия в Python с примерами?
Область действия локальной переменной — это функция, в которой вы ее объявили. Чтобы получить доступ к переменной, вы должны вызвать соответствующую функцию. Например, вы можете создать локальную переменную, как показано ниже.
|
определение суперфункц() |
# определение функции |
|
х = фантастика |
# определение локальной переменной |
|
print(«Питон есть» + х) |
# доступ к локальной переменной |
|
суперфункция() |
# вызов функции |
Глобальное ключевое слово
Ключевое слово Global используется для изменения глобальной переменной за пределами ее текущей области действия и значения.
Обычно, когда вы создаете переменную внутри функции (локальную переменную), ее можно использовать только внутри этой функции. Вот где в игру вступает ключевое слово global, которое помогает создавать глобальные переменные внутри функции и которые могут быть доступны в глобальной области видимости.
Синтаксис:
Функция по умолчанию():
Глобальная переменная
Пример 1:
Используйте глобальное ключевое слово для создания переменной в глобальной области.
Выход:
Пример 2:
Используйте ключевое слово global, чтобы изменить значение глобальной переменной внутри функции.
Выход:
Вы увидели, что такое «глобальные» ключевые слова, их примеры и как использовать глобальные ключевые слова.
Давайте посмотрим Global во вложенных функциях.
Когда вы объявляете глобальную переменную ключевого слова внутри вложенной функции и когда вы изменяете глобальную переменную ключевого слова внутри вложенной функции, она будет отражена за пределами локальной области, поскольку она используется как глобальное ключевое слово.
Пример:
Давайте посмотрим пример для глобальных вложенных функций.
Выход:
Вы можете увидеть приведенный выше вывод для глобальных вложенных функций. Но, возможно, следующее краткое объяснение поможет лучшему пониманию.
Вы объявили глобальную переменную внутри функции inner(), которая вложена в функцию main().
До и после вызова функции inner() переменная ‘integ’ принимает значение локальной переменной main, т.е. ‘integ = 20’. Вне функции main() переменная ‘integ’ принимает значение глобального ключевого слова, объявленного внутри функция inner(), т.
Фундаментальные правила «глобального» ключевого слова следующие:
- Когда вы создаете переменную внутри функции, она по умолчанию находится в локальном контексте
- Когда вы создаете или определяете переменную вне функции, по умолчанию это глобальный контекст, здесь нет необходимости в глобальном ключевом слове
- Глобальные ключевые слова можно использовать для чтения или изменения глобальной переменной внутри функции
- Использование глобального ключевого слова вне функции бесполезно или не имеет никакого эффекта.
Как вы можете создавать переменные, используя глобальную область видимости в Python с примерами?
Вы можете создать переменную с глобальной областью действия, инициализировав ее вне всех функций в программе Python.
Создать глобальную переменную просто; вы можете сделать это следующим образом.
|
х = «замечательно» |
# определение глобальной переменной |
|
по определению Wonderfunc(): |
#объявление функции |
|
print(«Питон есть» + х) |
#доступ к глобальной переменной |
|
чудесная функция () |
# вызов функции |
Как использовать глобальные ключевые слова в Python с примерами?
Если вы используете переменную внутри функции, python считает, что вы имеете в виду локальную переменную. Поэтому используйте ключевое слово global, чтобы изменить глобальную переменную в функции Python.
В следующем примере показано использование глобальных ключевых слов в программе Python.
|
х = 5 |
#инициализация глобальной переменной |
|
защита жизни () |
# определение функции |
|
глобальных x |
#используя глобальное ключевое слово |
|
х = х + 2 |
#изменение глобальной переменной |
|
жизнь() |
# вызов функции |
|
печать(х) |
#доступ к глобальной переменной |
Локальные переменные
В следующем примере показана ошибка.
Пример 1: доступ к локальной переменной вне области видимости
|
дефлок() |
# определение функции loc() |
|
г = «местный» |
# локальное объявление y |
|
лок() |
# вызов функции loc() |
|
печать(г) |
# доступ к переменной y |
В приведенной выше программе вы пытаетесь получить доступ к ‘y’, определенному в функции loc().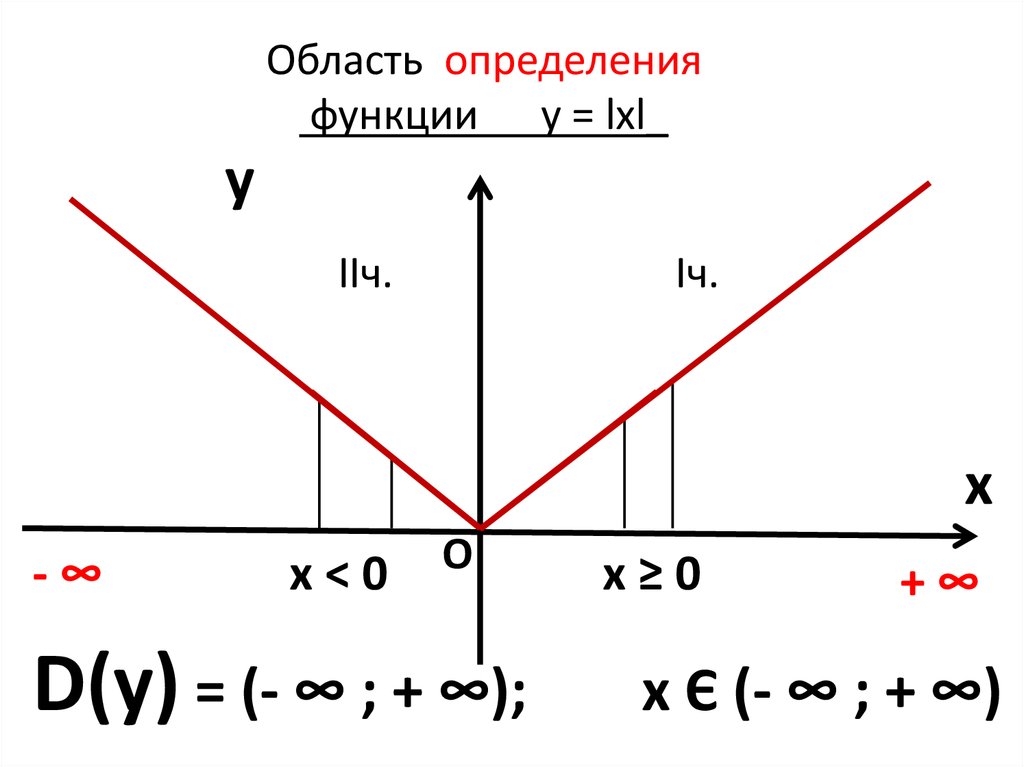
В следующем примере показано, как переписать приведенную выше программу.
Пример 2. Создание локальной переменной
|
деф лок() |
# определение функции |
|
г = «местный» |
# объявление локальной переменной |
|
печать(г) |
#локальный доступ к локальной переменной |
|
лок() |
# вызов функции |
Глобальные и локальные переменные
Поскольку вы не можете получить доступ к локальной переменной извне функции, не имеет значения, имеют ли глобальная и локальная переменные одно и то же имя. Ниже вы можете найти пример, где есть две переменные. Один глобальный, а другой локальный. Оба имеют одинаковое имя.
Пример 1: глобальная переменная и локальная переменная с одинаковым именем
|
х = 5; |
#инициализация глобальной переменной |
|
определение человека(): |
# определение функции man() |
|
х = 4 |
#инициализация локальной переменной |
|
print(«местный x:», x) |
# доступ к локальной переменной |
|
человек() |
# вызов функции человека |
|
print(«глобальный x:», x) |
# доступ к локальной переменной |
В приведенном выше примере функция печати в функции man() обращается к локальной переменной x со значением 4.
Разница между глобальными и локальными переменными
Давайте посмотрим пример того, как глобальные и локальные переменные ведут себя в одном и том же коде.
Пример:
Выход:
Объяснение:
Здесь, в приведенной выше программе, вы объявили x как глобальную переменную, а y как локальную переменную в той же программе. Затем он попытался изменить глобальную переменную, используя ключевое слово global в локальной функции и напечатав как gx, так и ly.
После вызова функции function1() значение gx стало глобальным. Когда вы попытались изменить как gx*2, он дважды напечатал «global». После этого вы напечатали локальную переменную ly, которая отображала значение локальной переменной, т. е. снова «local».
Разница между глобальными и нелокальными переменными
Когда переменная находится в локальной или глобальной области видимости, она называется нелокальной переменной.
Пример:
Выход:
Объяснение:
Из приведенной выше программы видно, что вложенной функцией является innerfn(). Внутри функции innerfn() вы видели использование ключевого слова nonlocal для создания нелокальной переменной. Функция innerfn() определена в области видимости externalfn(). Если вы вносите изменения в значение нелокальной переменной, они отражаются в локальной переменной.
В заключение, понимание области действия переменных Python необходимо для безошибочной программы. Вы можете получить доступ к глобальным переменным из любой точки программы. Однако вы можете получить доступ только к локальным переменным из функции. Кроме того, если вам нужно изменить глобальную переменную из функции, вам нужно объявить эту переменную глобальной. Вы можете сделать это, используя ключевое слово «global».
Ждете перехода в область программирования? Пройдите курс обучения Python и начните свою карьеру профессионального программиста Python 9.
0662
Заключение
Переменные являются одним из самых основных элементов языка программирования. Это уровень абстракции для ячеек памяти, содержащих фактическое значение. Глобальные, локальные и нелокальные типы переменных помогают программисту получить доступ к некоторым значениям полностью в области действия программы или к некоторым значениям, которые ограничены функцией.
В этой статье вы узнали, что такое глобальная переменная в Python, как определить глобальную переменную в Python, как объявить глобальную переменную в Python, что такое ключевое слово global, когда использовать ключевое слово global, разницу между global, локальные и нелокальные переменные вместе с некоторыми рабочими примерами.
Присоединяйтесь к учебному курсу Simplilearn Python, чтобы узнать больше по этой теме. Этот курс научит вас основам Python, условным операторам, операциям с данными, сценариям оболочки и Django. Этот сертификационный курс, который включает 38 часов смешанного обучения и 8 часов самостоятельного онлайн-обучения, подготовит вас к полноценной карьере профессионального программиста Python, предоставив вам практический опыт программирования.
Раскрытие модулей на ОДЗ
Раскрытие модулей на ОДЗ
При решении задач с модулями не всегда сразу возникает необходимость в применении метода интервалов или каких-либо других способов избавления от модулей. Иногда бывает достаточно провести анализ ОДЗ, и в результате по крайней мере часть модулей удаётся однозначно раскрыть. Рассмотрим три примера.
Пример №274.
Решить уравнение
Решение:
Очевидно, 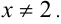
Но при 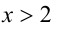
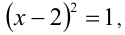
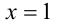
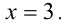
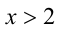
Пример №275.
Решить уравнение
Решение:
Заметим, что левая часть уравнения положительна (как сумма двух неотрицательных слагаемых, одновременно не обращающихся в нуль). Следовательно, 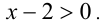
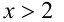
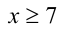
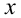
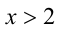
Пример №276.
Решение:
Очевидно,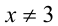
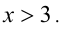
Видно, что при 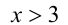
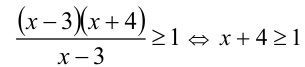
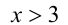
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Область допустимых значений функции
О чем эта статья:
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 0, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
ОДЗ такого выражения выглядит следующим образом: ( – ∞; 3) ∪ (3; +∞).
Читать запись нужно вот так:
Область допустимых значений переменной x для выражения — это числовое множество ( – ∞; 3) ∪ (3; +∞).
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
- требуется извлечение квадратного корня из отрицательного числа;
- присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении — пустое множество.
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Запомните
- Если число входит в ОДЗ, то около числа ставим квадратные скобки.
- Если число не входит в ОДЗ, то около него ставятся круглые скобки.
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
- расширить ОДЗ
- никак не повлиять на ОДЗ
- сузить ОДЗ
Рассмотрим каждый случай в отдельности.
Пример 7
Рассмотрим выражение a + 4/a – 4/a
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 8
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 9
Рассмотрим выражение
ОДЗ a определяется неравенством (a – 1) * (a – 4) ≥ 0.
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
ОДЗ переменной a для этого выражения определяется неравенствами:
a – 1 ≥ 0
a – 4 ≥ 0
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Область допустимых значений (ОДЗ): теория, примеры, решения
Любое выражение с переменной имеет свою область допустимых значений, где оно существует. ОДЗ необходимо всегда учитывать при решении. При его отсутствии можно получить неверный результат.
В данной статье будет показано, как правильно находить ОДЗ, использовать на примерах. Также будет рассмотрена важность указания ОДЗ при решении.
Допустимые и недопустимые значения переменных
Данное определение связано с допустимыми значениями переменной. При введении определения посмотрим, к какому результату приведет.
Начиная с 7 класса, мы начинаем работать с числами и числовыми выражениями. Начальные определения с переменными переходят к значению выражений с выбранными переменными.
Когда имеются выражения с выбранными переменными, то некоторые из них могут не удовлетворять. Например, выражение вида 1 : а , если а = 0 , тогда оно не имеет смысла, так как делить на ноль нельзя. То есть выражение должно иметь такие значения, которые подойдут в любом случае и дадут ответ. Иначе говоря, имеют смысл с имеющимися переменными.
Если имеется выражение с переменными, то оно имеет смысл только тогда, когда при их подстановке значение может быть вычислено.
Если имеется выражение с переменными, то оно не имеет смысл, когда при их подстановке значение не может быть вычислено.
То есть отсюда следует полное определение
Существующими допустимыми переменными называют такие значения, при которых выражение имеет смысл. А если смысла не имеет, значит они считаются недопустимыми.
Для уточнения вышесказанного: если переменных более одной, тогда может быть и пара подходящих значений.
Для примера рассмотрим выражение вида 1 x – y + z , где имеются три переменные. Иначе можно записать, как x = 0 , y = 1 , z = 2 , другая же запись имеет вид ( 0 , 1 , 2 ) . Данные значения называют допустимыми, значит, можно найти значение выражения. Получим, что 1 0 – 1 + 2 = 1 1 = 1 . Отсюда видим, что ( 1 , 1 , 2 ) недопустимы. Подстановка дает в результате деление на ноль, то есть 1 1 – 2 + 1 = 1 0 .
Что такое ОДЗ?
Область допустимых значений – важный элемент при вычислении алгебраических выражений. Поэтому стоит обратить на это внимание при расчетах.
Область ОДЗ – это множество значений, допустимых для данного выражения.
Рассмотрим на примере выражения.
Если имеем выражение вида 5 z – 3 , тогда ОДЗ имеет вид ( − ∞ , 3 ) ∪ ( 3 , + ∞ ) . Эта область допустимых значений, удовлетворяющая переменной z для заданного выражения.
Если имеется выражения вида z x – y , тогда видно, что x ≠ y , z принимает любое значение. Это и называют ОДЗ выражения. Его необходимо учитывать, чтобы не получить при подстановке деление на ноль.
Область допустимых значений и область определения имеет один и тот же смысл. Только второй из них используется для выражений, а первый – для уравнений или неравенств. При помощи ОДЗ выражение или неравенство имеет смысл. Область определения функции совпадает с областью допустимых значений переменной х к выражению f ( x ) .
Как найти ОДЗ? Примеры, решения
Найти ОДЗ означает найти все допустимые значения, подходящие для заданной функции или неравенства. При невыполнении этих условий можно получить неверный результат. Для нахождения ОДЗ зачастую необходимо пройти через преобразования в заданном выражении.
Существуют выражения, где их вычисление невозможно:
- если имеется деление на ноль;
- извлечение корня из отрицательного числа;
- наличие отрицательного целого показателя – только для положительных чисел;
- вычисление логарифма отрицательного числа;
- область определения тангенса π 2 + π · k , k ∈ Z и котангенса π · k , k ∈ Z ;
- нахождение значения арксинуса и арккосинуса числа при значении, не принадлежащем [ – 1 ; 1 ] .
Все это говорит о том, как важно наличие ОДЗ.
Найти ОДЗ выражения x 3 + 2 · x · y − 4 .
Решение
В куб можно возводить любое число. Данное выражение не имеет дроби, поэтому значения x и у могут быть любыми. То есть ОДЗ – это любое число.
Ответ: x и y – любые значения.
Найти ОДЗ выражения 1 3 – x + 1 0 .
Решение
Видно, что имеется одна дробь, где в знаменателе ноль. Это говорит о том, что при любом значении х мы получим деление на ноль. Значит, можно сделать вывод о том, что это выражение считается неопределенным, то есть не имеет ОДЗ.
Ответ: ∅ .
Найти ОДЗ заданного выражения x + 2 · y + 3 – 5 · x .
Решение
Наличие квадратного корня говорит о том, что это выражение обязательно должно быть больше или равно нулю. При отрицательном значении оно не имеет смысла. Значит, необходимо записать неравенство вида x + 2 · y + 3 ≥ 0 . То есть это и есть искомая область допустимых значений.
Ответ: множество x и y , где x + 2 · y + 3 ≥ 0 .
Определить ОДЗ выражения вида 1 x + 1 – 1 + log x + 8 ( x 2 + 3 ) .
Решение
По условию имеем дробь, поэтому ее знаменатель не должен равняться нулю. Получаем, что x + 1 – 1 ≠ 0 . Подкоренное выражение всегда имеет смысл, когда больше или равно нулю, то есть x + 1 ≥ 0 . Так как имеет логарифм, то его выражение должно быть строго положительным, то есть x 2 + 3 > 0 . Основание логарифма также должно иметь положительное значение и отличное от 1 , тогда добавляем еще условия x + 8 > 0 и x + 8 ≠ 1 . Отсюда следует, что искомое ОДЗ примет вид:
x + 1 – 1 ≠ 0 , x + 1 ≥ 0 , x 2 + 3 > 0 , x + 8 > 0 , x + 8 ≠ 1
Иначе говоря, называют системой неравенств с одной переменной. Решение приведет к такой записи ОДЗ [ − 1 , 0 ) ∪ ( 0 , + ∞ ) .
Ответ: [ − 1 , 0 ) ∪ ( 0 , + ∞ )
Почему важно учитывать ОДЗ при проведении преобразований?
При тождественных преобразованиях важно находить ОДЗ. Бывают случаи, когда существование ОДЗ не имеет место. Чтобы понять, имеет ли решение заданное выражение, нужно сравнить ОДЗ переменных исходного выражения и ОДЗ полученного.
- могут не влиять на ОДЗ;
- могут привести в расширению или дополнению ОДЗ;
- могут сузить ОДЗ.
Рассмотрим на примере.
Если имеем выражение вида x 2 + x + 3 · x , тогда его ОДЗ определено на всей области определения. Даже при приведении подобных слагаемых и упрощении выражения ОДЗ не меняется.
Если взять пример выражения x + 3 x − 3 x , то дела обстоят иначе. У нас имеется дробное выражение. А мы знаем, что деление на ноль недопустимо. Тогда ОДЗ имеет вид ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) . Видно, что ноль не является решением, поэтому добавляем его с круглой скобкой.
Рассмотрим пример с наличием подкоренного выражения.
Если имеется x – 1 · x – 3 , тогда следует обратить внимание на ОДЗ, так как его необходимо записать в виде неравенства ( x − 1 ) · ( x − 3 ) ≥ 0 . Возможно решение методом интервалов, тогда получаем, что ОДЗ примет вид ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) . После преобразования x – 1 · x – 3 и применения свойства корней имеем, что ОДЗ можно дополнить и записать все в виде системы неравенства вида x – 1 ≥ 0 , x – 3 ≥ 0 . При ее решении получаем, что [ 3 , + ∞ ) . Значит, ОДЗ полностью записывается так: ( − ∞ , 1 ] ∪ [ 3 , + ∞ ) .
Нужно избегать преобразований, которые сужают ОДЗ.
Рассмотрим пример выражения x – 1 · x – 3 , когда х = – 1 . При подстановке получим, что – 1 – 1 · – 1 – 3 = 8 = 2 2 . Если это выражение преобразовать и привести к виду x – 1 · x – 3 , тогда при вычислении получим, что 2 – 1 · 2 – 3 выражение смысла не имеет, так как подкоренное выражение не должно быть отрицательным.
Следует придерживаться тождественных преобразований, которые ОДЗ не изменят.
Если имеются примеры, которые его расширяют, тогда его нужно добавлять в ОДЗ.
Рассмотрим на примере дроби вида x x 3 + x . Если сократить на x , тогда получаем, что 1 x 2 + 1 . Тогда ОДЗ расширяется и становится ( − ∞ 0 ) ∪ ( 0 , + ∞ ) . Причем при вычислении уже работаем со второй упрощенной дробью.
При наличии логарифмов дело обстоит немного иначе.
Если имеется выражение вида ln x + ln ( x + 3 ) , его заменяют на ln ( x · ( x + 3 ) ) , опираясь на свойство логарифма. Отсюда видно, что ОДЗ с ( 0 , + ∞ ) до ( − ∞ , − 3 ) ∪ ( 0 , + ∞ ) . Поэтому для определения ОДЗ ln ( x · ( x + 3 ) ) необходимо производить вычисления на ОДЗ, то есть ( 0 , + ∞ ) множества.
При решении всегда необходимо обращать внимание на структуру и вид данного по условию выражения. При правильном нахождении области определения результат будет положительным.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/oblast-dopustimyh-znachenij-funkcii
http://zaochnik.com/spravochnik/matematika/vyrazhenija/oblast-dopustimyh-znachenij-odz/
[/spoiler]
Содержание:
- Примеры с решением
Как найти область определения функции? Давайте начнём с теории!
Совокупность всех рациональных и иррациональных чисел называется множеством действительных (или вещественных) чисел. Действительные числа можно изображать точками на числовой прямой.
Абсолютной величиной (или модулем) действительного числа 
Неравенство
равносильно неравенствам
Свойства абсолютной величины:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Переменной величиной называется величина, которая принимает различные числовые значения.
Совокупность всех числовых значений переменной величины называется областью изменения этой переменной. Различают следующие простейшие области изменения переменной 
- открытый промежуток или интервал
, т.е. совокупность всех чисел, заключенных между
и
:
(точки
и
исключены);
- замкнутый промежуток или сегмент
, т. е.
(точки
и
включены);
- полуинтервалы
т. е.
, и
т. е.
Переменная величина
называется функцией переменной величины
, если каждому значению
, которое она может принимать, соответствует единственное значение
. Переменная
называется независимой переменной или аргументом.
Функция обозначается одним из символов:

Для функции 

Функция и аргумент могут обозначаться и другими буквами, например 
Корнем (или нулем) функции 

Совокупность всех значений аргумента, при которых функция имеет определенные действительные значения, называется областью существования или областью определения функции.
Функция может быть задана табличным, графическим, аналитическим или другим способом.
Явной функцией называется функция, заданная формулой
Возможно вам будут полезны данные страницы:
Неявной функцией называется функция, заданная уравнением
не разрешенным относительно 
Функция, определенная в области

Функция называется нечетной, если для любого 
Функция называется периодической с периодом 

Если
функции своих аргументов, то функция
называется функцией от функции или сложной функцией.
Если уравнение 





Чтобы понять, что такое область определения функции, вам нужно знать область определения базовой элементарной функции.
Примеры с решением
Пример 1.
Найти область изменениях, если 
По определению абсолютной величины
поэтому соответственно получим неравенства
откуда
Следовательно, 

Прибавляя 2 ко всем частям неравенства, получим


Пример 2.
Найти область изменения 

По определению абсолютной величины
Из неравенств 


Следовательно, областью изменения переменной 
Пример 3.
Решить уравнение
Решение:
Рассмотрим три случая:
В первом случае
поэтому уравнение перепишется в виде
откуда 

Во втором случае

поэтому уравнение принимает вид
т. е. сводится к тождеству. Следовательно, уравнению удовлетворяют всех из отрезка [1,2].
В третьем случае получаем


откуда
, что противоречит условию
Таким образом, уравнению удовлетворяют все значения 
Пример 4.
Дана функция
Найти значения функции при значениях аргумента, равных соответственно среднему геометрическому и среднему арифметическому ее корней.
Решение:
Найдем корни, или нули, функции. Приравнивая функцию нулю, получим квадратное уравнение 

и среднее геометрическое
Подставляя найденные значения аргумента в выражение для 
Пример 5.
Доказать, что функция 
Решение:
Убедимся в том, что для данной функции выполняется условие (1.8). Подставляя 


Так как
то
Пример 6.
Доказать, что функция 
Решение:
Убедимся в том, что выполняется условие (1.9):
Пример 7.
Показать, что функция 
Решение:
Так как 


т. е. функция 
т.е. функция 



В самом деле
Пример 8.
Найти область определения функции
Решение:
Данная функция не определена для тех значений 




Другими словами, областью определения является совокупность трех интервалов: 
Замечание. Дробная рациональная функция 






Пример 9.
Найти область существования функции
Решение:
Функция представляет собой сумму двух функций. Вторая из них определена при всех 


лишь при тех значениях 
Это возможно, когда:
Рассмотрим первое условие: 






Переходим ко второму условию, которое перепишется так: 






Следовательно, это условие не выполнимо (не могут одновременно выполняться неравенства 

Таким образом, областью определения функции 


Замечание. Если функция содержит радикалы четной степени, то она определена лишь при тех значениях 
Пример 10.
Найти область определения функции
Решение:
Функция 





Пример 11.
Найти область определения функции
Решение:
Логарифмическая функция определена при положительных значениях своего аргумента, т. е. при 



Пример 12.
Найти 


Решение: По определению данных функций имеем 
Лекции:
- Разложить в ряд фурье
- Сектор шара и сегмент шара
- Тройной интеграл. Вычисление тройного интеграла
- Знаки тригонометрических функций
- Схема построения графика функции
- Метод Эйлера
- Производная функции
- Иррациональные выражения
- Метод вариации произвольных постоянных
- Сходимость ряда










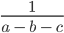
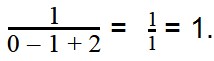
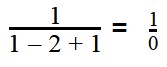
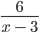
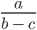
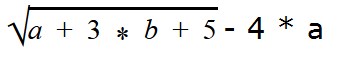

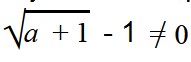
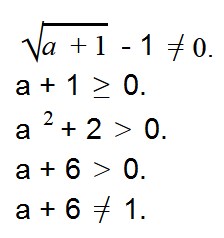
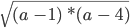
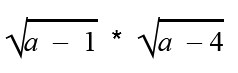











 Достоинство этого метода в его наглядности: на графике видна связь между величинами, входящими в условие задачи; чертеж помогает оценить реальность результата. Традиционные решения требуют больших временных затрат, что недопустимо в условиях сдачи экзаменов в форме ЕГЭ и ГИА. Графический способ экономит время.
Достоинство этого метода в его наглядности: на графике видна связь между величинами, входящими в условие задачи; чертеж помогает оценить реальность результата. Традиционные решения требуют больших временных затрат, что недопустимо в условиях сдачи экзаменов в форме ЕГЭ и ГИА. Графический способ экономит время.

 Решение уравнений и систем с параметрами, графическим способом.
Решение уравнений и систем с параметрами, графическим способом. В проекте представлено пособие для учащихся 7-9-х классов, в котором подобраны задания на решение уравнений и систем уравнений графическим способом.
В проекте представлено пособие для учащихся 7-9-х классов, в котором подобраны задания на решение уравнений и систем уравнений графическим способом. Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами.
Решение многих математических задач упрощается, если удается использовать графы. Представление данных в виде графа придает им наглядность и простоту. Многие математические доказательства также упрощаются, приобретают убедительность, если пользоваться графами.
 .. }
.. }  В global scope , varia…
В global scope , varia…  Тщательное определение области видимости ваших переменных…
Тщательное определение области видимости ваших переменных…  0662
0662

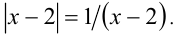
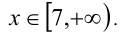
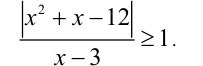
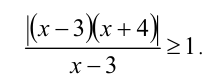
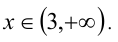





 , т.е. совокупность всех чисел, заключенных между
, т.е. совокупность всех чисел, заключенных между  и
и  :
: (точки
(точки  , т. е.
, т. е.  (точки
(точки  т. е.
т. е.  , и
, и  т. е.
т. е.  Переменная величина
Переменная величина называется функцией переменной величины
называется функцией переменной величины  , если каждому значению
, если каждому значению  , которое она может принимать, соответствует единственное значение
, которое она может принимать, соответствует единственное значение 



















 , что противоречит условию
, что противоречит условию 
























