Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
![]()
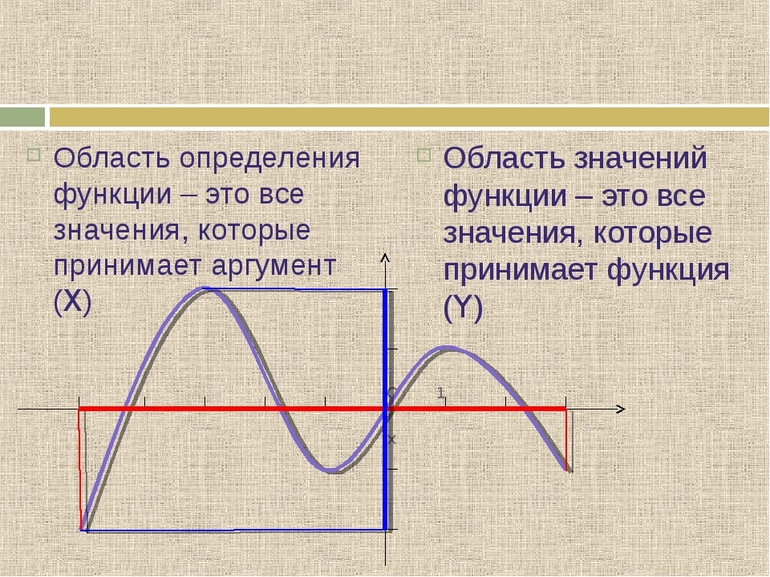
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
![]()
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
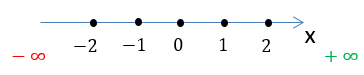
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
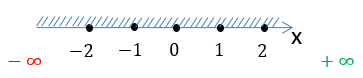
Запишем результат по правилам записи неравенств.

D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
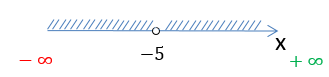
Запишем заштрихованную область на числовой оси через знаки неравенства.
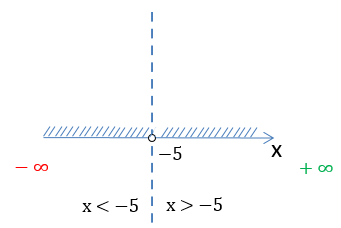
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».

x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
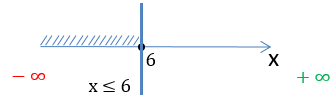
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
![]()
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
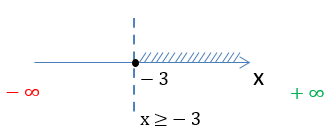
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
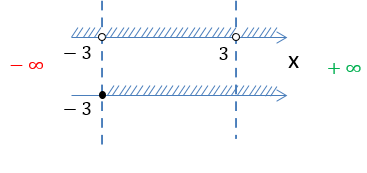
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
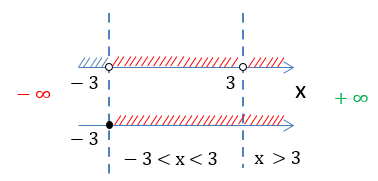
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
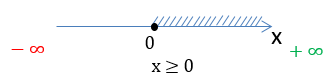
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
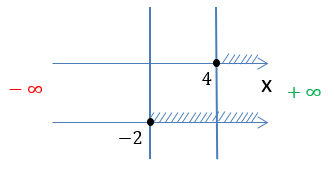
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
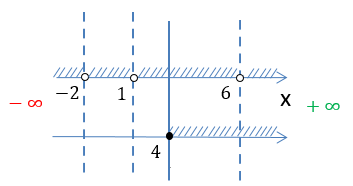
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев

Профиль
Благодарили: 0
Сообщений: 1

Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован

Профиль
Благодарили: 0
Сообщений: 1

Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая

Профиль
Благодарили: 0
Сообщений: 1

Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции

0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить

В этом вопросе следует разбираться, поскольку понятие не только встречается в школьной и университетской программах, но и широко применяется в науке и программировании (разработке программного обеспечения и прошивки контроллеров).
Общие сведения
Областью определения произвольной функции является множество значений переменных, от которых она зависит и принимает определенное значение. Встречаются функции с одной или несколькими переменными. Для простоты исследования нужно рассмотреть первый тип. Для того чтобы найти область определения и множество значений функции, необходимо использовать простые примеры. Специалисты рекомендуют применять метод изучения «от простого к сложному».

Первый раз этот термин упоминается в школьной программе. Книга «Алгебра и начало анализа» дает базовые знания в этой области. Однако она написана не для всех понятным языком.
Обучаемый часто ищет информацию в интернете. В некоторых случаях ученики занимаются поиском готовых решений, а это не совсем правильно, поскольку математические дисциплины пригодятся при поступлении в высшие учебные заведения. Исследование функции — естественный процесс, который встречается в различных дисциплинах.
Программирование на разных языках пользуется огромной популярностью. В нем нужны математические знания для написания некоторых программ и игр. В последних следует производить точные расчеты и описывать некоторые функции героя. Например, удар мечом подчиняется определенному математическому закону или функции. Для корректной ее работы и тестирования следует находить грамотно ее область определения.
Основные понятия
Область определения функции обозначается буквой «D». Кроме того, указывается ее имя D (f). Допускается также следующее обозначение «D (y)». Если необходимо ее найти для нескольких функций, можно изменить обозначение. Для сложного типа функций z = f (a, b, x, y) эта величина обозначается таким образом: D (z). Аргумент — независимая переменная, принимающая определенные значения.
Существуют также сложные функции, которые включают в число своих переменных и другие функции. Пример, z = f (x, k, l, w, y). В нем величины x, k, l являются переменными, а w и y — следующими функциями: w = 2 * x1 + 5 и y = 2 / (x2 — 6). Для каждого типа функции существует определенный алгоритм, по которому следует находить D (f). Он основывается на многолетнем опыте специалистов и придуман для оптимизации вычислений.
Важно уметь правильно определять тип функции, поскольку от этого зависит процесс выбора алгоритма. Для одних можно сразу определить D (f), для других — решить уравнение или неравенство, для третьих следует решить систему уравнений и т. д.
Можно воспользоваться специальными программными модулями. Простым примером программы является онлайн-калькулятор, позволяющий не только вычислить D (f), но и начертить ее график. Кроме того, D (f) записывается в виде множества значений.
Например, D (y) = [0, 157). Это значит следующее: областью определения функции вида y = 3*x / sqrt (156 — |x|) является множество чисел, которые находятся в интервале от 0 включительно (скобка «[“) до 157 не включительно.
Типы функций
Функций существует огромное разнообразие. Они бывают простыми и сложными. Первые в математических дисциплинах классифицируются на несколько типов: алгебраические, тригонометрические и трансцендентные. Алгебраические классифицируются на рациональные и иррациональные. Рациональные бывают целыми и дробными. Тригонометрические включают в свой состав все функции с sin, cos, tg, ctg и т. д. Трансцендентные делятся на степенные, показательные и логарифмические.
Рациональные целые — выражения полиномиального типа (линейные). Они без корней и степеней, дробей и логарифмов, а также без тригонометрических функций. Областью их определения является множество всех действительных чисел (Z) от бесконечно малого до бесконечно большого числа.
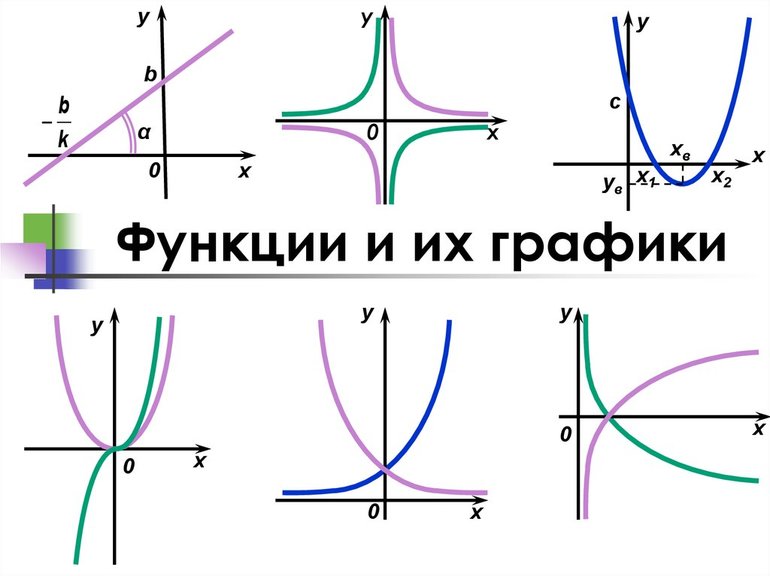
Дробный тип — функции, в числителе и знаменателе которых находится переменная. Для нахождения D (f) нужно исключить все значения переменных в нем, приводящие к 0. Если встречается тригонометрические функции, то нужно вычислить все значения, приводящие к отсутствию D (f) на определенном интервале. Этот тип функций может быть иррациональным, дробным, линейным, а также использоваться вместе со степенью и логарифмом.
К иррациональным функциям относят выражения, которые содержат переменную величину под корнем. Значение D (f) — все Z, кроме переменных, приводящих к отрицательным значениям выражений с четными степенями корней. D (f) степенной функции являются все действительные числа. Однако если степень представлена дробным выражением, то значения переменных не должны приводить к неопределенности (например, 4/0, т. к. на 0 делить нельзя). Для функций с натуральным логарифмом выражение, находящееся под ним, должно быть больше 0.
Правильное обозначение
Очень важно правильно обозначать D (f), поскольку это существенно влияет на результат. Это позволит избежать многих ошибок в любой сфере.
Следует руководствоваться такими правилами:
- Использовать скобку «[” и/или «]”, когда нужно указать принадлежность к множеству.
- Круглые скобки используются в двух случаях: указывание границы бесконечности и значения, которое не входит в интервал.
- Для объединения нескольких множеств нужно применять специальный символ «U».
- Допускается использование круглых и квадратных скобок в одном множестве.
Примером в первом случае является множество [0, 100]: от 0 включительно и до 100 не включительно. Во втором случае — (8, 10): значение, равное 9, поскольку 8 и 10 — нижняя и верхняя границы, не принадлежащие множеству.
Два предыдущих множества можно объединить: [0, 100] U (8, 10). Пример записи последнего случая следующий: (20, 50].
Алгоритмы определения
Для удобства определения D (f) необходимо применять специальные алгоритмы, которые упрощают операцию. Целая рациональная функция, как уже было описано ранее, имеет D (f), принадлежащую множеству Z (весь ряд действительных чисел). Кроме того, степенная функция также имеет D (f), которая соответствует Z.
Если функция является дробной, то следует использовать следующий алгоритм:

- Обратить внимание на знаменатель, который не должен быть равен 0.
- Выписать выражение знаменателя и решить его, приравнивая к 0.
- Записать интервал.
Если она представлена в виде четного корня, следует решить неравенство. Значение подкоренного выражения должно быть больше 0. В противном случае область определения под корнем не будет существовать (неопределенность).
Однако если корень нечетный, то D (f) — множество действительных чисел. Для функций с натуральным логарифмом (ln) значение выражения, которое находится под логарифмом, должно быть всегда больше 0. При отрицательных значениях ln «превращается» в неопределенность. Необходимо составить неравенство. Оно должно быть больше 0.
Для тригонометрических выражений синуса sin (x) и косинуса cos (x) множество всех Z является D (f). Однако для тангенса tg (x) и котангенса ctg (x) необходимо исключить значения переменной x = (Pi / 2) + Pi * k и x = Pi * k соответственно. В этих выражениях k является множеством действительных чисел.
Другие методы
Существуют также и другие методы определения D (f). Ее можно выяснить при помощи следующих инструментов: онлайн-калькулятора, специальных программ и построения графика. Первый способ позволяет довольно быстро найти необходимую величину. Но это не все его возможности. Можно с его помощью строить графики и находить все свойства функции.
Однако первый метод уступает второму, суть которого сводится к использованию специализированного программного обеспечения. В этом случае можно легко изобразить графики заданной функции, исследовать и найти ее основные свойства, а также D (f), представленных в виде функций. Например, зависимость амплитудных значений переменного электрического тока от времени.

В некоторых случаях можно найти D (f), построив ее график. Для этого следует подставить значение аргумента функции и получить ее значение. Построение таблицы зависимости значения функции от ее аргумента позволяет правильно построить графическое представление. Чтобы быстро строить графики, нужно знать их базовые виды: линейный, степенной (квадратичный, кубический и т. д. ), а также другие. Чем точнее графическая иллюстрация, тем легче определить D (f).
После заполнения таблицы значений следует приступать к построению графика. Для этого берутся точки с координатами из таблицы (x, y), и отмечаются на декартовой системе координат.
Затем их следует соединить. Получится график заданной функции, по которому не составит труда сделать определенные выводы.
Примеры решения
Теоретические знания необходимы, но некоторые люди делают огромную ошибку. Они не закрепляют их при помощи практики. Необходимо регулярно решать задачи на нахождения D (f), поскольку в этом случае набирается опыт. Наиболее простыми задачами считаются следующие: нахождения D (f) линейной, степенной, показательной и тригонометрической функций. Важным аспектом считается упрощение выражения. Для этого следует вспомнить также и формулы сокращенного умножения.
С дробными и иррациональными функциями могут возникнуть некоторые сложности, поскольку нужно решить уравнение или неравенство. Однако в последнем случае нельзя путать знак неравенства.
Для линейного вида
Нужно найти D (f) для y = 2*x — 3 * (x — 5). Для решения следует применить такой алгоритм:

- Упростить выражение.
- Определить D (f).
Для упрощения выражения следует раскрыть скобки. Конечно, это делать необязательно, поскольку ответ очевиден D (y) = (-бесконечность, +бесконечность). Но по правилам «хорошего тона» любое математическое выражение следует упрощать: y = 2 * x — 3 * x + 15 = – x + 15 = 15 — x. При решении следует правильно раскрывать скобки, а также следить за знаками. Малейшая ошибка может привести к значительному искажению графика.
В некоторых задачах следует также построить график функции. Для конкретного случая создается таблица зависимости значения «y» от аргумента. Не имеет смысла брать много значений «х», поскольку графиком является прямая. Известно, что необходимы только две точки для ее проведения. Подстановка количества значений «х», превышающих двух, является грубой и распространенной ошибкой.
Дробные и иррациональные
Пусть существует выражение вида y = 1 / [(x — 4) * (x + 4)]. Нужно определить D (f).
Решается задача таким способом:

- Приравнивается знаменатель к 0.
- Решается уравнение.
- Определяется интервал допустимых значений.
Нужно решить уравнение (x — 4) * (x + 4) = 0. Из него видно, что x1 = 4 и x2 = -4, поскольку эти значения «превращают» знаменатель в неопределенность. Следовательно, D (y) = (-бесконечность, -4) U (4, +бесконечность).
В случае с иррациональным выражением: y = sqrt[4 * sqr (x) — 12 * x + 9], нужно решить уравнение подкоренного выражения.
Для решения квадратного уравнения следует применить такой алгоритм:
- Записать неравенство: 4 * sqr (x) — 12 * x + 9 >= 0.
- Дискриминант: D = [(- b)^2] – (4 * a * c) = [(-12)^2] – (4 * 4 * 9) = 144 — 144 = 0.
- D = 0 — только одно решение.
- x = (-b) / (2 * a) >= 12 / (2 * 4) >= 12 / 8 >= 6 / 4 >= 1,5.
Множество чисел D (y) ограничивается следующим интервалом (-бесконечность, 1.5) U (1.5, +бесконечность).
Таким образом, для нахождения множества значений D (f) для конкретного выражения следует воспользоваться специальными алгоритмами. На первоначальном этапе исследования функции следует определить ее тип, поскольку это поможет избежать многих сложностей в процессе решения.
Содержание:
- Примеры с решением
Как найти область определения функции? Давайте начнём с теории!
Совокупность всех рациональных и иррациональных чисел называется множеством действительных (или вещественных) чисел. Действительные числа можно изображать точками на числовой прямой.
Абсолютной величиной (или модулем) действительного числа  называется неотрицательное действительное число, определяемое равенствами:
называется неотрицательное действительное число, определяемое равенствами: 
Неравенство

равносильно неравенствам

Свойства абсолютной величины:

По этой ссылке вы найдёте полный курс лекций по высшей математике:
Переменной величиной называется величина, которая принимает различные числовые значения.
Совокупность всех числовых значений переменной величины называется областью изменения этой переменной. Различают следующие простейшие области изменения переменной  :
:
- открытый промежуток или интервал
 , т.е. совокупность всех чисел, заключенных между
, т.е. совокупность всех чисел, заключенных между  и
и  :
: (точки
(точки  и
и  исключены);
исключены); - замкнутый промежуток или сегмент
 , т. е.
, т. е.  (точки
(точки  и
и  включены);
включены); - полуинтервалы
 т. е.
т. е.  , и
, и  т. е.
т. е.  Переменная величина
Переменная величина называется функцией переменной величины
называется функцией переменной величины  , если каждому значению
, если каждому значению  , которое она может принимать, соответствует единственное значение
, которое она может принимать, соответствует единственное значение  . Переменная
. Переменная  называется независимой переменной или аргументом.
называется независимой переменной или аргументом.
Функция обозначается одним из символов:
 и т. п.
и т. п.
Для функции  – значение, которое она принимает при
– значение, которое она принимает при  .
.
Функция и аргумент могут обозначаться и другими буквами, например  .
.
Корнем (или нулем) функции  называется значение аргумента
называется значение аргумента  , при котором функция равна нулю:
, при котором функция равна нулю:

Совокупность всех значений аргумента, при которых функция имеет определенные действительные значения, называется областью существования или областью определения функции.
Функция может быть задана табличным, графическим, аналитическим или другим способом.
Явной функцией называется функция, заданная формулой

Возможно вам будут полезны данные страницы:
Неявной функцией называется функция, заданная уравнением

не разрешенным относительно  .
.
Функция, определенная в области , называется четной, если для любого
, называется четной, если для любого  из области определения выполняется равенство
из области определения выполняется равенство

Функция называется нечетной, если для любого  выполняется равенство
выполняется равенство

Функция называется периодической с периодом  , если при любом
, если при любом  из области определения выполняется равенство
из области определения выполняется равенство

Если

функции своих аргументов, то функция

называется функцией от функции или сложной функцией.
Если уравнение  разрешимо относительно
разрешимо относительно  , т. е. существует функция
, т. е. существует функция  такая, что
такая, что  , то функция
, то функция  называется обратной по отношению к функции
называется обратной по отношению к функции  .
.
Чтобы понять, что такое область определения функции, вам нужно знать область определения базовой элементарной функции.

Примеры с решением
Пример 1.
Найти область изменениях, если  . Решение:
. Решение:
По определению абсолютной величины

поэтому соответственно получим неравенства

откуда

Следовательно,  , т. е.
, т. е.  меняется в интервале (-1,5). Этот пример можно решить и по-другому. На основании формул (1.2) и (1.3) можно записать
меняется в интервале (-1,5). Этот пример можно решить и по-другому. На основании формул (1.2) и (1.3) можно записать 
Прибавляя 2 ко всем частям неравенства, получим
 или
или  .
.
Пример 2.
Найти область изменения  , если
, если . Решение:
. Решение:
По определению абсолютной величины

Из неравенств  и
и  получаем
получаем  .
.
Следовательно, областью изменения переменной  является совокупность двух бесконечных интервалов:
является совокупность двух бесконечных интервалов: 
Пример 3.
Решить уравнение 
Решение:
Рассмотрим три случая: 
В первом случае

поэтому уравнение перепишется в виде

откуда  , что противоречит неравенству
, что противоречит неравенству  . В этом случае решений нет.
. В этом случае решений нет.
Во втором случае

поэтому уравнение принимает вид

т. е. сводится к тождеству. Следовательно, уравнению удовлетворяют всех из отрезка [1,2].
В третьем случае получаем
 или
или  ,
,
откуда
, что противоречит условию
Таким образом, уравнению удовлетворяют все значения  , для которых
, для которых 
Пример 4.
Дана функция 
Найти значения функции при значениях аргумента, равных соответственно среднему геометрическому и среднему арифметическому ее корней.
Решение:
Найдем корни, или нули, функции. Приравнивая функцию нулю, получим квадратное уравнение  , корни которого
, корни которого  Среднее арифметическое корней
Среднее арифметическое корней 
и среднее геометрическое 
Подставляя найденные значения аргумента в выражение для  , получаем соответственно
, получаем соответственно

Пример 5.
Доказать, что функция  является четной.
является четной.
Решение:
Убедимся в том, что для данной функции выполняется условие (1.8). Подставляя  вместо
вместо  в выражение для
в выражение для  , получим
, получим

Так как

то

Пример 6.
Доказать, что функция  является нечетной.
является нечетной.
Решение:
Убедимся в том, что выполняется условие (1.9):

Пример 7.
Показать, что функция  является периодической, и найги ее период.
является периодической, и найги ее период.
Решение:
Так как  т. е. функция
т. е. функция  имеет период
имеет период  ,
,

т. е. функция  имеет период
имеет период 

т.е. функция  имеет период
имеет период  , то функция
, то функция  имеет период, равный наименьшему кратному чисел
имеет период, равный наименьшему кратному чисел  , т.е.
, т.е. 
В самом деле 
Пример 8.
Найти область определения функции

Решение:
Данная функция не определена для тех значений  при которых знаменатель обращается в нуль (так как деление на нуль не имеет смысла). Приравнивая нулю знаменатель, получим
при которых знаменатель обращается в нуль (так как деление на нуль не имеет смысла). Приравнивая нулю знаменатель, получим , откуда
, откуда  . Итак, функция определена на всей действительной оси
. Итак, функция определена на всей действительной оси  , кроме точек
, кроме точек  .
.
Другими словами, областью определения является совокупность трех интервалов:  .
.
Замечание. Дробная рациональная функция  , где
, где  и
и  – полиномы соответственно степени
– полиномы соответственно степени  и
и  , определена для всех
, определена для всех  кроме нулей функции
кроме нулей функции  .
.
Пример 9.
Найти область существования функции

Решение:
Функция представляет собой сумму двух функций. Вторая из них определена при всех  , так как корень третьей степени существует при любом
, так как корень третьей степени существует при любом  . Первая функция
. Первая функция  определена
определена
лишь при тех значениях  , при которых подкоренное выражение неотрицательно (корень квадратный существует только для неотрицательных чисел). Итак, должно быть
, при которых подкоренное выражение неотрицательно (корень квадратный существует только для неотрицательных чисел). Итак, должно быть 
Это возможно, когда:
Рассмотрим первое условие:  , т.е.
, т.е.  или
или  и
и  , т.е.
, т.е.  или
или  и
и  . Таким образом, это условие выполняется, когда
. Таким образом, это условие выполняется, когда 
Переходим ко второму условию, которое перепишется так:  , т. е.
, т. е. или
или  и
и  , и
, и  , т. е.
, т. е.  или
или  .
.
Следовательно, это условие не выполнимо (не могут одновременно выполняться неравенства  ,
,  ).
).
Таким образом, областью определения функции  является совокупность двух сегментов:
является совокупность двух сегментов:

 Сумма двух функций определена там, где определено каждое слагаемое, поэтому исходная функция также определена в указанных двух сегментах (рис. 1.1).
Сумма двух функций определена там, где определено каждое слагаемое, поэтому исходная функция также определена в указанных двух сегментах (рис. 1.1).
Замечание. Если функция содержит радикалы четной степени, то она определена лишь при тех значениях  при которых подкоренные выражения неотрицательны.
при которых подкоренные выражения неотрицательны.
Пример 10.
Найти область определения функции
Решение:
Функция  определена при
определена при . Следовательно, данная функция определена только для тех значений
. Следовательно, данная функция определена только для тех значений  , для которых
, для которых  откуда
откуда  . Решив эти неравенства, получим
. Решив эти неравенства, получим  . Итак, функция определена на отрезке [-1,2].
. Итак, функция определена на отрезке [-1,2].
Пример 11.
Найти область определения функции 
Решение:
Логарифмическая функция определена при положительных значениях своего аргумента, т. е. при  , откуда
, откуда  или
или . Следовательно, данная функция определена при
. Следовательно, данная функция определена при  , т. е. в интервале (-2,2).
, т. е. в интервале (-2,2).
Пример 12.
Найти  и
и  , если
, если  .
.
Решение: По определению данных функций имеем  , поэтому
, поэтому 


Лекции:
- Разложить в ряд фурье
- Сектор шара и сегмент шара
- Тройной интеграл. Вычисление тройного интеграла
- Знаки тригонометрических функций
- Схема построения графика функции
- Метод Эйлера
- Производная функции
- Иррациональные выражения
- Метод вариации произвольных постоянных
- Сходимость ряда

