Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно разбираться в определенных понятиях и находить весомые аргументы и методы решения, что и предложено данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями, чтобы вам больше не нужно было определять все это онлайн.
Что значит найти область определения
После того как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Область определения и область значения можно найти и для кубического корня (куб. √), к примеру, для x+2.
Ограничение области определения
Область определения функции или ООФ рассматривается еще в школьном курсе алгебры. У действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально узнавать ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на сложение корня четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
При отсутствии хотя бы одного признака, область определения приходится искать другим образом (и это не с калькулятором). Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно иметь следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом, чтобы понимать понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Чтобы найти область определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1 является постоянной функцией, f2 является арктангенсом, f3 – логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x) – произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x) является -∞, +∞D(f)=D(f).
Естестввенным образом получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x – [0, +∞).
Области определения y=f(x) и y=−f(x) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2. В данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f) является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Найти область определения y=ln x2.
Решение
Алгоритм решения этого уравнения или функции следующий.
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Найти область определения функции y=(arcsin x)-12.
Решение
График решения следующий.
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3 – логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3 –это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4 – это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Действия с корнями
Корни в математике, в частности, функцию с корнем можно определить следующим образом:
y=n√x. N здесь — натуральное число, большее за единицу.
Область определения корня зависит от того, каков показатель: четный или нечетный.
Если n является четным числом (n=2m). Это значит, что область определения представляет собой множество всех неотрицательных действительных чисел.
Если показатель корня — нечетное число, большее за единицу (n=2m+1 и m принадлежит к n), то областью определения корня будет множество всех действительных чисел.
Также важным является вопрос, как складывать корни.
Сложение и вычитание корней возможно при условии наличия одинакового подкоренного выражения. К примеру, сложение и вычитание корней возможно 2√3 и 4√3. Можно ли складывать корни или вычитать в случае 2√3 и 2√5? Ответ — нет.
Как решать корни во втором случае? Вы можете упростить подкоренное выражение и привести их корни к одинаковому подкоренному выражению. После этого вы сможете как считать корни, так и вычитать корни.
К основным действиям с корнями относят:
- умножение корней;
- деление корней;
- корень минус корень или плюс.
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
К аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1 определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2 является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2 имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.
| Функция | Ее область определения |
|
Сумма, разность, произведение функций f1, f2,…, fn |
Пересечение множеств D(f1), D(f2), …, D(fn) |
|
Сложная функция y=f1(f2(f3(…fn(x)))) В частности, y=f1(f2(x)) |
Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1) x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
|
Прямая пропорциональность y=k·x |
R |
| Линейная y=k·x+b | R |
|
Обратная пропорциональность y=kx |
-∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C – число | D(f) |
|
Дробная y=f1(x)f2(x) В частности, если f1(x), f2(x) – многочлены |
Множество всех x, которые одновременно удовлетворяют условиям f2(x)≠0 |
| y=f(x)n, где n – четное | x∈D(f1), f(x)≥0 |
|
y=logf2(x)f1(x) В частности, y=logaf1(x) В частности, y=logf2(x)a |
x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1 x∈D(f1), f1(x)>0 x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Содержание
- Понятие и обозначение области определения функции
- Как найти области определения для основных элементарных функций
- Область определения постоянной функции
- Область определения функции с корнем
- Область определения степенной функции
- Область определения показательной функции
- Область определения логарифмической функции
- Область определения тригонометрических функций
- Область определения тригонометрических функций
- Области определения основных функций в табличном виде
Кубическая функция — это функция вида y=ax³, где a — число ( a≠0).
График кубической функции называется кубической параболой.
Для начала рассмотрим свойства и график кубической функции y=x³ (при a=1).
Свойства функция y=x³:
1) Область определения — множество действительных чисел:
2) Область значений — все действительные числа:
3) Функция имеет один нуль:
4) Точка O (0;0) делит кубическую параболу на две равные части, каждая из которых называется ветвью кубической параболы. Ветви кубической параболы симметричны относительно точки O — начала координат.
Отсюда следует, что противоположным значениям x соответствуют противоположные значения y: (- x)³= — x³ .
5) Функция возрастает на всей числовой прямой.
6) Промежутки знакопостоянства: функция принимает положительные значения при x∈(0;∞) (или y>0 при x>0);
функция принимает отрицательные значения при x∈(-∞;0) (или y
Эти точки отмечаем на координатной плоскости и строим кубическую параболу:
График функции y=ax³ при a≠1 ( a≠0) получают из графика функции y=x³ при помощи геометрических преобразований.
Функция y=x³ — один из частных случаев степенной функции
где α — любое действительное число.
В курсе алгебры из частных случаев степенной функции мы уже встречались с квадратичной функцией y=x² и функцией обратной пропорциональности
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Числовая функция с областью определения D – это соответствие значений переменной x некоторому числу y , которое находится в зависимых отношениях с x .
Используя это определение, охарактеризуем нужное нам понятие более четко:
Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Теперь рассмотрим, как правильно обозначать ее на письме. Ранее мы договорились, что для записи самих функций будем использовать маленькие латинские буквы, например, g , f и др. Чтобы указать на наличие функциональной зависимости, используется запись вида y = f ( x ) . Таким образом, функция f представляет собой некоторое правило, согласно которому каждому значению переменной x можно поставить в соответствие значение другой переменной y , которая находится в зависимых отношениях от x .
Возьмем для примера функцию y = x 2 . Можно записать ее как f ( x ) = x 2 . Это функция возведения в квадрат, которая ставит в соответствие каждому значению переменной x = x 0 некоторое значение y = x 0 2 . Так, если мы возьмем число 3 , то функция поставит ему в соответствие 9 , поскольку 3 2 = 9 .
Чтобы обозначить область определения некоторой функции f , используется запись D ( f ) . Однако нужно помнить, что у некоторых функций есть собственные обозначения, например, у тригонометрических. Поэтому в учебниках иногда встречаются записи вида D ( sin ) или D ( a r c sin ) . Их следует понимать как области определения синуса и арксинуса соответственно. Допустима и запись вида D ( f ) , где f – функция синуса или арксинуса.
Если мы хотим записать, что функция f определена на множестве значений x , то используем формулировку D ( f ) = X . Так, для того же арксинуса запись будет выглядеть как D ( a r c sin ) = [ − 1 , 1 ] (подробнее об области определения арксинуса мы расскажем далее.)
Как найти области определения для основных элементарных функций
Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y = x 2 и т.д., а их области определения указываются в качестве основных свойств.
В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.
Область определения постоянной функции
Вспомним формулу, которой задается постоянная функция: y = C , или f ( x ) = C . Переменная C может быть любым действительным числом.
Смысл функции в том, что каждому значению аргумента будет соответствовать значение, равное C , следовательно, областью определения данной функции будет множество всех действительных чисел. Обозначим его R .
Так, если у нас есть функция y = − 3 (или в другой записи f ( x ) = − 3 ), то ( D ( f ) = ( − ∞ , + ∞ ) или D ( f ) = R ) .
Если же мы возьмем функцию y = 7 3 , то для нее, как и для любой постоянной функции, область определения будет равна R .
Область определения функции с корнем
С помощью знака корня, или радикала, мы можем задать функцию извлечения квадратного корня y = x , либо в обобщенном виде функцию корня степени N , которую можно записать в виде формулы y = x n . В этих случаях n может быть любым натуральным числом, которое больше 1 .
Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.
- Возьмем сначала случай, когда n – четное число, т.е. n = 2 · m , где m ∈ N . Тогда областью определения станет множество всех неотрицательных действительных чисел: D 2 · m = [ 0 ; + ∞ ) .
- Если же n представляет из себя нечетное число, которое больше 1 , т.е. n = 2 · m + 1 , то областью определения будет множество всех действительных чисел: D 2 · m + 1 = ( — ∞ ; + ∞ ) .
Таким образом, область определения функций с корнем y = x , y = x 4 , y = x 6 – это числовое множество [ 0 , + ∞ ) , а функций y = x 3 , y = x 5 , y = x 7 – множество ( − ∞ , + ∞ ) .
Область определения степенной функции
Запись степенной функции выглядит как y = x a или f ( x ) = x a , где x является переменной, которая лежит в основании степени, и a представляет из себя определенное число в ее показателе. Мы берем область определения степенной функции в зависимости от значения ее показателя.
Перечислим возможные варианты.
- Допустим, что a будет положительным целым числом. Тогда областью определения степенной функции будет множество действительных чисел ( − ∞ , + ∞ ) .
- Если a является нецелым положительным числом, то D ( f ) = [ 0 , + ∞ ) .
- В случае, когда a относится к целым отрицательным числам, областью определения такой функции становится множество ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) .
- В остальных случаях, т.е. когда a будет отрицательным нецелым числом, область определения будет числовым промежутком ( 0 , + ∞ ) .
- Если a имеет нулевое значение, то такая степенная функция будет определена для всех действительных x , кроме нулевого. Это связано с неопределенностью 0 0 . Мы знаем, что любое число, кроме 1 , при возведении в нулевую степень будет равно 1 , тогда при a = 0 у нас получится функция y = x 0 = 1 , область определения которой ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) .
Поясним нашу мысль несколькими примерами.
Для функций y = x 5 , y = x 12 область определения представляет собой множество всех действительных чисел R , поскольку показатели степени являются целыми положительными числами.
Для степенных функций y = x 6 3 , y = x π , y = x 7 4 , y = x 2 3 будут определены на интервале [ 0 , + ∞ ) , поскольку показатели являются положительными, но не целыми числами.
3. Для функции y = x − 5 с целыми отрицательными показателями областью определения будет множество ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) .
4. Для степенных функций y = x — 19 , y = x — 3 e , y = x — 9 8 , y = x — 3 11 область определения будет представлять из себя открытый числовой луч ( 0 , + ∞ ) , т.к. их показателями являются нецелые отрицательные числа.
Область определения показательной функции
Такую функцию принято записывать как y = a x , причем переменная будет располагаться в показателе функции. Основанием степени здесь является число a , которое больше 0 и не равно 1 .
Область определения такой функции есть множество всех действительных чисел, т.е. R .
Например, если у нас есть показательные функции y = 1 4 x , y = e x , y = 13 x , y = 15 x , то они будут определены на промежутке от минус бесконечности до плюс бесконечности.
Область определения логарифмической функции
Функция логарифма задается как y = log a x , где a – основание, большее 0 и не равное 1 . Она определена на множестве всех положительных действительных чисел. Это можно записать как D ( log a ) = ( 0 , + ∞ ) , например, D ( ln ) = ( 0 , + ∞ ) и D ( l g ) = ( 0 , + ∞ ) .
Так, для логарифмических функций y = log 2 3 x , y = log 3 x , y = log 7 x , y = ln x областью определения будет множество ( 0 , + ∞ ) .
Область определения тригонометрических функций
Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.
- Формула y = sin x обозначает функцию синуса ( sin ) . Она будет определена на множестве всех действительных чисел. Можно записать, что D ( sin ) = R .
- Формула y = cos x означает функцию косинуса ( cos ) . Она также будет определена на множестве всех действительных чисел, т.е. D ( cos ) = R .
- Формула y = t g x означает функцию тангенса ( t g ) , а y = c t g x – котангенса. Областью определения тангенса будет множество всех действительных чисел, за исключением π 2 + π · k , k ∈ Z .
Областью определения котангенса будет также множество R , за исключением π · k , k ∈ Z .
Иными словами, если мы знаем, что x является аргументом функций тангенса и котангенса, то нужно помнить, что данные функции определены при x ∈ R , x ≠ π 2 + π · k , k ∈ Z и x ∈ R , x ≠ π · k , k ∈ Z .
Область определения тригонометрических функций
К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.
- Формула y = a r c sin x обозначает функцию арксинуса. Обычно она рассматривается на отрезке [ − 1 , 1 ] ] и обозначается arcsin. Промежуток [ − 1 , 1 ] и будет нужной нам областью определения данной функции. Можно записать, что D ( a r c sin ) = [ − 1 , 1 ] .
- Формула y = a r c cos x выражает функцию арккосинуса (обозначается a r c cos ). Она рассматривается на том же отрезке, что и арксинус. Следовательно, областью определения данной функции является [ − 1 , 1 ] , т.е. D ( a r c cos ) = [ − 1 , 1 ] .
- Функции y = a r c t g x и y = a r c c t g x означают арктангенс и арккотангенс. Они рассматриваются на множестве всех действительных чисел, значит, областью их определения является R . Можем записать, что D ( a r c t g ) = R и D ( a r c c t g ) = R .
Области определения основных функций в табличном виде
Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.
[ 0 ; + ∞ ) , если n — четное
— ∞ ; + ∞ , если n — нечетное
— ∞ ; + ∞ , если a > 0 , a ∈ Z
[ 0 ; + ∞ ) , если a > 0 , a ∈ R , a ∉ Z
— ∞ ; 0 ∪ 0 ; + ∞ , если a 0 , a ∈ Z
0 ; + ∞ , если a ∈ R , a ≠ Z
— ∞ ; 0 ∪ 0 , + ∞ , если a = 0
y = sin x y = cos x y = t g x y = c t g x
R R x ∈ R , x ≠ π 2 + π · k , k ∈ Z x ∈ R , x ≠ π · k , k ∈ Z
y = a r c sin x y = a r c cos x y = a r c t g x y = a r c c t g x
Подводя итоги статьи, следует отметить, что в рамках школьного курса изучаются не только основные элементарные функции, но и их различные сочетания. Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
Идёт приём заявок
Подать заявку
Для учеников 1-11 классов и дошкольников


- Колесник Марина АнатольевнаНаписать 3336 06.03.2018
Номер материала: ДБ-1293565
-
06.03.2018 576
-
06.03.2018 252
-
06.03.2018 179
-
06.03.2018 184
-
06.03.2018 778
-
06.03.2018 2666
-
06.03.2018 556
-
06.03.2018 1099
Не нашли то что искали?
Вам будут интересны эти курсы:
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
| Области определения функций | |
| Функиця | Ее область определения |
| Постоянная y = C | R |
| Корень y = x n | |
| Степенная y = x a | |
| Показательная y = a x | R |
| Логарифмическая y = log a x | 0 ; + ∞ |
Кубической
называется функция, заданная
формулой где а ≠ 0
I.
Частным случаем кубической функции является функция , здесь
a = 1, b
= c = d
= 0.
Графиком
кубической функции y
= x3
является кубическая парабола с вершиной в точке (0;0),
проходящая через точки (1;1), (-1;-1), (2;8), (-2;-8) (запомнить
эти точки), располагается в I
и III четвертях.
1) Область определения функции – множество всех
действительных чисел: D(y)=(−; +
).
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = (-x)3
= – x3 = – y(x). Значит, кубическая функция является нечётной, её график
симметричен относительно начала координат, т.е. точки (0;0).
4) Функция возрастает при х (−
; +
).
II.
Кубическая функция , здесь
a ≠ 0

кубической функции y
= ax3
является кубическая парабола с вершиной в точке (0;0),
проходящая через точки (1;1a),
(-1;-1a), (2;8a),
(-2;-8a)), располагается в I
и III четвертях, если a>0,
и во II и IV четвертях, если a<0.
1) Область определения функции – множество всех
действительных чисел: D(y)=(−; +
).
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x)3
= – ax3 = – y(x). Значит, кубическая функция является нечётной, её график
симметричен относительно начала координат, т.е. точки (0;0).
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
III.
Кубическая функция
Графиком
кубической функции является
кубическая парабола с вершиной в точке (m;0).
График функции получается
из графика функции смещением
вдоль оси Ox на m
единиц .
1) Область определения функции – множество всех
действительных чисел: D(y)=(−; +
)
.
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x – m)3 = – a(x + m)3 ≠
y(x) ≠ – y(x). Значит, данная
кубическая функция не является ни чётной, ни нечётной.
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
IV.
Кубическая функция
Графиком
кубической функции является
кубическая парабола с вершиной в точке (0; n).
График функции получается
из графика функции смещением
вдоль оси Oy на n
единиц .
1) Область определения функции – множество всех
действительных чисел: D(y)=(−; +
)
.
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x)3 + n = – ax3 + n ≠
y(x) ≠ – y(x). Значит,
данная кубическая функция не является ни чётной, ни нечётной.
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
V.
Кубическая функция

кубической функции является
кубическая парабола с вершиной в точке (m;
n). График функции получается
из графика функции смещением
вдоль оси Оx на
m единиц,
а вдоль оси Oy на n
единиц .
1) Область определения функции – множество всех действительных
чисел: D(y)=(−; +
)
.
2) Область значений функции – множество всех действительных
чисел: Е(y) = (−; +
).
3) y(-x) = a(-x)3 + n = – ax3 + n ≠
y(x) ≠ – y(x). Значит,
данная кубическая функция не является ни чётной, ни нечётной.
4) При a>0
функция возрастает при х (−
; +
).
При a<0,
функция убывает при х (−
; +
).
Кубическая парабола задается функцией y=x3
График кубической функции называется куби́ческой пара́болой. В литературе часто встречаются альтернативные определения кубической параболы как графика функции 
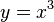
Перечислим основные свойства функции
1.Область определения – любое действительное число:.
2.Область значений – любое действительное число:.
3.Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием .
Производная кубической функции 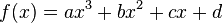
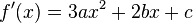





Кубическая функция
Кубическая функция — это функция вида y=ax³, где a — число (a≠0).
График кубической функции называется кубической параболой.
Для начала рассмотрим свойства и график кубической функции y=x³ (при a=1).
Свойства функция y=x³:
1) Область определения — множество действительных чисел:
D: x∈(-∞;∞).
2) Область значений — все действительные числа:
E: y∈(-∞;∞).
3) Функция имеет один нуль:
y=0 при x=0.
4) Точка O (0;0) делит кубическую параболу на две равные части, каждая из которых называется ветвью кубической параболы. Ветви кубической параболы симметричны относительно точки O — начала координат.
Отсюда следует, что противоположным значениям x соответствуют противоположные значения y: (-x)³= —x³.
5) Функция возрастает на всей числовой прямой.
6) Промежутки знакопостоянства: функция принимает положительные значения при x∈(0;∞) (или y>0 при x>0);
функция принимает отрицательные значения при x∈(-∞;0) (или y<0 при x<0).
Чтобы построить график кубической функции, возьмём несколько точек.
Берём точки с абсциссами x=0, x=±1, x=±2, x=±3 и находим соответствующие значения функции:
y=0³ =0; y=1³ =1; y=(-1)³ =-1; y=2³ =8; y=(-2)³ =-8.
Получили точки с координатами (0;0), (1; 1), (-1; -1), (2; 8), (-2; -8).
Удобно результаты вычислений оформлять в виде таблицы:
Эти точки отмечаем на координатной плоскости и строим кубическую параболу:
График функции y=ax³ при a≠1 (a≠0) получают из графика функции y=x³ при помощи геометрических преобразований.
Функция y=x³ — один из частных случаев степенной функции
где α — любое действительное число.
В курсе алгебры из частных случаев степенной функции мы уже встречались с квадратичной функцией y=x² и функцией обратной пропорциональности















