Урок 1. Функция. Область определения функции
Функция – одно из важнейших математических понятий.
Слово «функция» (от латинского function – совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 17 веке. Общее определение понятия функции было сформулировано в 19 веке.
Функцией называют такую зависимость переменной игрек от переменной икс, при которой каждому значению переменной икс соответствует единственное значение переменной игрек.
Переменную икс называют независимой переменной или аргументом функции. Переменную игрек называют зависимой переменной. Значения зависимой переменной называют значениями функции.
Если зависимость переменной игрек от переменной икс является функцией, то коротко это записывают так: y = f(x) (читают: «игрек равен эф от икс»). Символ эф от икс также обозначает значение функции, соответствующее значению аргумента икс.
В записи вида игрек равен эф от икс вместо эф используют и другие латинские (иногда греческие) буквы: ку, аш, пе, фи и другие.
Рассмотрим пример. Найдем значения функции эф для значений икс, равных двум целым четырем десятым и минус четырем. Для этого необходимо подставить значение аргумента икс в данную функцию. Получаем, что для значения икс, равного двум целым четырем десятым, значение функции равно одной целой семидесяти шести сотым. А для значения икс, равного минус четыре, значение функции равно двенадцати.
Все значения независимой переменной образуют область определения функции. Обозначают дэ от эф или дэ от игрек.
Рассмотрим пример.
Найдем область определения функций, заданных формулами:
1) Областью определения функции эф от икс является множество всех чисел.
2) Областью определения функции аш от икс является множество всех чисел, кроме минус трёх.
Функция может быть задана следующими способами: аналитически или формулой, таблицей и графически.
Вспомним, что графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.
С помощью графика функции мы можем находить значение функции в соответствующей точке: для аргумента икс равного двенадцати значение функции равно четырнадцати; или для аргумента икс равного минус шести значение функции равно одиннадцати.
Также по графику функции мы можем найти область определения функции. На первом графике видно, что областью определения является множество всех действительных чисел.
На втором графике область определения функции состоит из всех неотрицательных чисел.
-
1
-
2
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
![]()
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
![]()
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
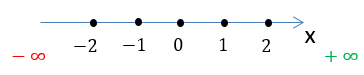
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
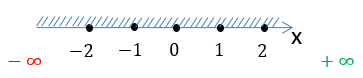
Запишем результат по правилам записи неравенств.

D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
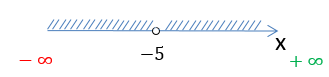
Запишем заштрихованную область на числовой оси через знаки неравенства.
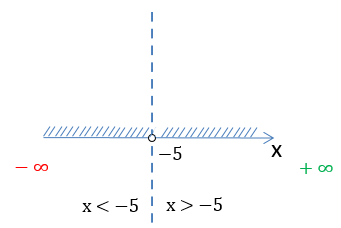
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».

x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
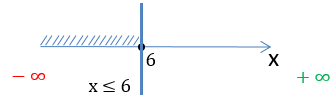
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
![]()
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
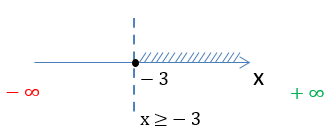
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
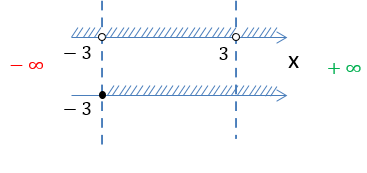
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
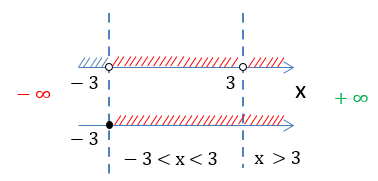
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
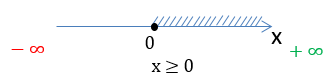
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
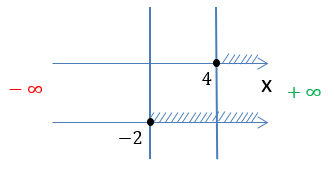
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
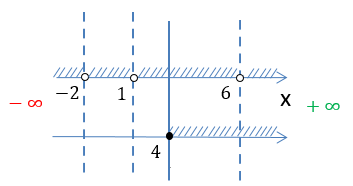
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев

Профиль
Благодарили: 0
Сообщений: 1

Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован

Профиль
Благодарили: 0
Сообщений: 1

Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая

Профиль
Благодарили: 0
Сообщений: 1

Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции

0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно разбираться в определенных понятиях и находить весомые аргументы и методы решения, что и предложено данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями, чтобы вам больше не нужно было определять все это онлайн.
Что значит найти область определения
После того как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Область определения и область значения можно найти и для кубического корня (куб. √), к примеру, для x+2.
Ограничение области определения
Область определения функции или ООФ рассматривается еще в школьном курсе алгебры. У действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально узнавать ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на сложение корня четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
При отсутствии хотя бы одного признака, область определения приходится искать другим образом (и это не с калькулятором). Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно иметь следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом, чтобы понимать понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Чтобы найти область определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1 является постоянной функцией, f2 является арктангенсом, f3 – логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x) – произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x) является -∞, +∞D(f)=D(f).
Естестввенным образом получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x – [0, +∞).
Области определения y=f(x) и y=−f(x) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2. В данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f) является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Найти область определения y=ln x2.
Решение
Алгоритм решения этого уравнения или функции следующий.
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Найти область определения функции y=(arcsin x)-12.
Решение
График решения следующий.
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3 – логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3 –это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4 – это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Действия с корнями
Корни в математике, в частности, функцию с корнем можно определить следующим образом:
y=n√x. N здесь — натуральное число, большее за единицу.
Область определения корня зависит от того, каков показатель: четный или нечетный.
Если n является четным числом (n=2m). Это значит, что область определения представляет собой множество всех неотрицательных действительных чисел.
Если показатель корня — нечетное число, большее за единицу (n=2m+1 и m принадлежит к n), то областью определения корня будет множество всех действительных чисел.
Также важным является вопрос, как складывать корни.
Сложение и вычитание корней возможно при условии наличия одинакового подкоренного выражения. К примеру, сложение и вычитание корней возможно 2√3 и 4√3. Можно ли складывать корни или вычитать в случае 2√3 и 2√5? Ответ — нет.
Как решать корни во втором случае? Вы можете упростить подкоренное выражение и привести их корни к одинаковому подкоренному выражению. После этого вы сможете как считать корни, так и вычитать корни.
К основным действиям с корнями относят:
- умножение корней;
- деление корней;
- корень минус корень или плюс.
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
К аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1 определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2 является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2 имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.
| Функция | Ее область определения |
|
Сумма, разность, произведение функций f1, f2,…, fn |
Пересечение множеств D(f1), D(f2), …, D(fn) |
|
Сложная функция y=f1(f2(f3(…fn(x)))) В частности, y=f1(f2(x)) |
Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1) x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
|
Прямая пропорциональность y=k·x |
R |
| Линейная y=k·x+b | R |
|
Обратная пропорциональность y=kx |
-∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C – число | D(f) |
|
Дробная y=f1(x)f2(x) В частности, если f1(x), f2(x) – многочлены |
Множество всех x, которые одновременно удовлетворяют условиям f2(x)≠0 |
| y=f(x)n, где n – четное | x∈D(f1), f(x)≥0 |
|
y=logf2(x)f1(x) В частности, y=logaf1(x) В частности, y=logf2(x)a |
x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1 x∈D(f1), f1(x)>0 x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
План-конспект урока алгебры в 9 «А» классе
По теме: «Функция. Область определения и область значений функции»
Дата проведения: 18.09.21
Цели урока:
Образовательные
- актуализация знаний о понятии функции, области определения и области значений функции;
- отработка знаний при решении задач;
- введение функциональной символики
Воспитательные
- воспитание ответственного отношения к учебному труду, настойчивости для достижения результатов.
Развивающие
- развитие умений абстрагировать и конкретизировать свойства изучаемых понятий;
- формирование навыков самоконтроля и самооценки.
Задачи урока:
- систематизировать и расширить представления о функциях;
- выработать умение находить значения функции по заданным значениям аргумента и обратно;
- выработать умение находить область определения и область значений функции;
- учить понимать и использовать функциональную символику при решении задач.
Оборудование:
- Компьютер с мультимедийным проектором, раздаточный материал (приложение 1), презентация.
Ход урока:
- Организационный момент
Приветствие учащихся. Настрой учащихся на работу. Отметить отсутствующих.
- Актуализация знаний
- Основное понятие урока сегодня – «Функция». Это слово вам знакомо? Что можете вспомнить по этой теме? Вспомните основные функции, изученные ранее. Приведите примеры известных вам функций.
- Откройте тетради, запишите дату и тему урока
Ответьте на вопросы:
- Какую зависимость называют функцией?
- Как читают запись y=f(x) ?
- Что называют аргументом функции?
- Что такое область определения функции?
- Что называют значением функции?
- Что называют областью значений функции?
(Учащиеся отвечают выборочно. Некоторые вопросы вызывают и учащихся затруднение, т. к. материал встречается впервые)
- Я вижу, что некоторые из вопросов вызвали трудности. Почему? Как будем решать эту проблему? (Предлагают обратиться к учебнику.)
- Правильно, нужно воспользоваться достоверными источниками, чтобы получить необходимую информацию. Изучите с.3 – 4 учебника и найдите ответы на вопросы, которые вызвали у вас затруднения.
(Учащиеся изучают материал)
- Изучение нового материала
Опр. Функцией называют такую зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.
- Переменную х называют независимой переменной или аргументом.
- Переменную у называют зависимой переменной.
Опр. Переменная у является функцией от переменной х
Опр. Значение зависимой переменной называют значениями функции
Если зависимость переменной у от переменной х является функцией, то записывается это так:
y=f(x)
Пример: функция задана формулой 

f(x)=
Найти значения функции f для значений х, равных 2,5 и -3
Опр. Все значения независимой переменной образуют область определения функции
Опр. Все значения, которые принимает зависимая переменная, образуют область значений функции.
Опр. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениями аргумента, а ординаты-соответствующим значениям функции.
Рассмотрим функции на рис.1,2,3,4,5
- Закрепление изученного материала
№1,№3,№4,№5,№6
- Самостоятельная работа
- Теперь вам будет предложен небольшой тест для проверки того, как вы поняли материал данного урока. (Приложение 1)
- Обменяйтесь вариантами теста, проверьте работы. Правильные ответы на слайде.
Давайте обсудим задания, которые вызывали затруднение. (Разбор заданий) - Желающие получить оценки за самостоятельную работу в журнал, сдайте листы с тестом.
- Подведение итогов
– Сегодня на уроке алгебры мы создали базу для усвоения целой группы следующих тем. Какие задачи мы решали сегодня на уроке?
– Где в обычной жизни мы с вами сталкиваемся с функциями?
– Оценки за урок:
- Домашнее задание
П.1, №2,№8
Определение:
Зависимость
переменной y
от
переменной x,
при которой каждому значению переменной x соответствует единственное
значение y,
называют функцией.
В
определении сказано, что только та зависимость является функцией, у которой
каждому значению аргумента соответствует единственное значение функции.
Рассмотрим
первый график. Видим, что одному значению x может соответствовать несколько
значений y.
Значит, данная зависимость не является функцией.
Обратимся
ко второму случаю. Какие бы значения аргумента мы не брали, каждому из них
соответствует только одно значение функции. Можно сказать, что эта зависимость
является функцией.
В
общем виде любую функцию можно записать так:
Например:
Понятно,
что функция может принимать различные значения в зависимости от значения
аргумента. Найдём значение каждой функции при заданном значении аргумента.
Вы
заметили, что в этом задании функции названы разными буквами. Действительно,
функцию можно называть любой буквой латинского алфавита.
Ранее
вами были изучены несколько важных функций. Вспомним их.
Сейчас
попробуем выяснить, как же получается график функции, и дадим определение этому
понятию.
Можно
записать её в таком виде:
Это
линейная функция, графиком как вы помните, является прямая. Для изображения прямой достаточно двух точек.
Получаем
точки с координатами (1;3) и (-1;-11).
Проведём
прямую через полученные точки.
Мы
изобразили график функции.
Определение:
Множество
всех точек координатной плоскости, абсциссы которых равны значениям аргумента,
а ординаты — значениям функции, называют графиком функции.
Все
значения аргумента, т.е. переменной x образуют область определения функции,
а все значения зависимой переменной, т.е. y, — область значений функции.
В
данном случае x и y могут быть любыми числами, т.е. областью определения и
областью значений является множество всех действительных чисел.
Потренируемся
находить область определения и область значений функции по её графику.
Область
определения можно находить не только по графику функции, но и по формуле, с
помощью которой задана функция.
