vieyostenil
Вопрос по алгебре:
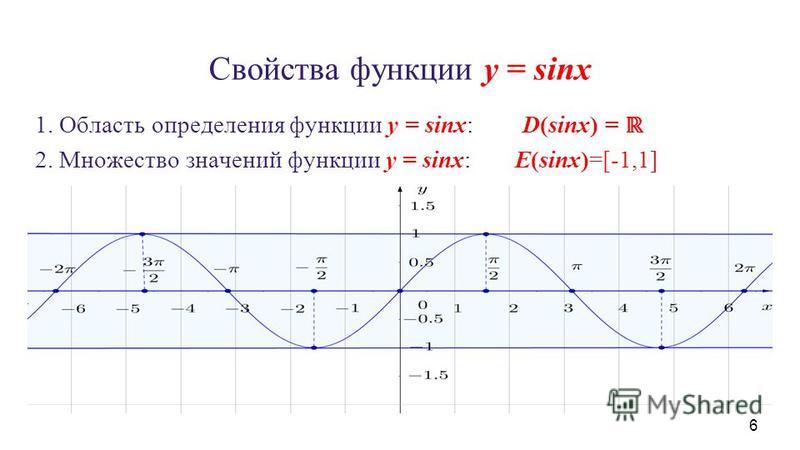
Найти область определения и множество значений функции y=2 cos x
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 2
xcostha
Область определения функции y=2cos x есть множество действительных чисел, т. е. R.
Область значений функции y=cos x есть отрезок [-1; 1], т. е. -1<= cos x <=1, тогда
-2<=2 cos x <=2, т. е.
это отрезок [-2; 2]
hamotho915
D(y)=R
|*2
E(y):[-2;]
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Алгебра.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Алгебра — раздел математики, который можно нестрого охарактеризовать как обобщение и расширение арифметики.
Ани Степанян
Ученик
(105),
на голосовании
12 лет назад
Голосование за лучший ответ
Irina Filippova
Мастер
(1224)
12 лет назад
D (y) = R (множество действительных чисел ) – область определения
E (y) = [-2 ; 2] – область значения
Виктория Агафоненкова
Ученик
(165)
12 лет назад
Д (у) = (- бесконечности; + бесконечности)
Е (у) =[-2;2]
Источник: я=)
Похожие вопросы
Найдите область определения и множество значений функции y = 2cosx.
Перед вами страница с вопросом Найдите область определения и множество значений функции y = 2cosx?, который относится к
категории Алгебра. Уровень сложности соответствует учебной программе для
учащихся 10 – 11 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.
Кто не видел белого медведя? В зоопарках он – обычный гость. Нет нужды описывать, каков он на вид. Напомним лишь, что у него только нос черный, сам медведь белый и зимой, и летом (а не как, скажем, песец или заяц-беляк – те лишь зимой белые). Подошвы лап у белого медведя густой шерстью поросли, а пальцы примерно на половину своей длины соединены плавательными перепонками.
Плавают и ныряют белые медведи отлично. Две минуты могут пробыть под водой, но погружаются в нее редко глубже двух метров. Далеко в открытом море не раз видели белых медведей, даже медведиц с медвежатами. Плывут со скоростью 5 километров в час, не беспокоясь, что ни земли, ни льдов нигде вблизи не видно.
Белый медведь и тюленей ловит не только на льду, украдкой к ним подползая. Обычный его прием, так сказать, атаки с моря такой: поблизости от лежбищ тюленей медведь осторожно, без плеска и шума, сползает в воду, плывет туда, где заметил тюленей. Затем он бесшумно ныряет и выныривает уже у самого лежбища, быстро карабкается на лед, отрезая тем самым тюленям путь к спасительной воде. По отвесным ледяным стенам медведь может прямо из воды выпрыгнуть на льдину, даже если высота ее над водой два метра.
Тюлени – главная охотничья добыча белого медведя весной. За год ловит и съедает он примерно 50 тюленей. Летом меню его более разнообразно. Ловит он рыбу на мелкой воде, на берегу – леммингов, песцов, лакомится яйцами птиц. Когда голоден, ест ягоды, водоросли, мхи, лишайник, грибы.
Белый медведь – самый могучий из сухопутных хищных зверей. Лев и тигр в сравнении с ним легковесы: средний вес медведиц 310 килограммов, медведей-самцов – 420 килограммов. Если медведь матерый и хорошо упитанный, то он может весить целую тонну!
Акимушкин И.И. Мир животных: Млекопитающие, или звери. – М., 1988 г
IV. Тест по русскому языку
1. В тексте про белых медведей больше всего предложений:
а) повествовательных; б) вопросительных
2. Восклицательное предложение находится:
а) в начале текста; б) в конце текста
3. Вопросительное предложение находится
а) в начале текста; б) в конце текста
4. Выпиши из второй части текста (из второго абзаца) первое предложение. Разбери его по членам предложения. Что ты можешь сказать о сказуемых? Они являются
а) родственными словами; б) однородными членами предложения
5. Что можно сказать о глаголах, которыми выражены сказуемые? Эти глаголы:
а) I спряжения; б) II спряжения
6. Эти глаголы стоят в форме:
а) настоящего времени; б) будущего времени; в) прошедшего времени
7. Эти глаголы стоят в форме:
а) единственного числа; б) множественного числа
8. Эти глаголы стоят в форме:
а) 1-го лица; б) 2-го лица; в) 3-го лица; г)нельзя определить лицо
9. Эти глаголы стоят в форме:
а) ж.р.; б) м.р.; в) ср.р.; г) нельзя определить род
10. Найди во второй части текста (во втором абзаце) все слова, которые являются родственными существительному, являющемуся подлежащим в первом предложении. Запиши их столбиком, поставив в начальную форму. У тебя получилось:
а) два слова; б) три слова
11. Найди во второй части текста (во втором абзаце) другую форму слова, которое является подлежащим в первом предложении. Выпиши такое словосочетание с формой этого слова, из которого можно определить его падеж. Этот падеж:
а) Р.п.; б) В.п.
Найти область определения функции y=3/sin(x/2)-2cos(x/2) — Учеба и наука
математика
область определения
тригонометрические функции
Лучший ответ по мнению автора |
|
|||||||||||||||
|
|
|
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Помогите с алгеброй.
Решено
Надо посчитать, сколько здоровья должно вытоге остаться у соперника что бы выполнить миссию
Помогите с алгеброй.
Решено
Площа чотирикутника дорівнює 126 , його ортогональною
проекцією є прямокутник, діагональ якого дорівнює √130 см ,а
одна зі сторін 9 см . Знайдіть кут між площинами чотирикутника
і прямокутник
Помогите решить математику
Свойства тригонометрических функций — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Базовый уровень Сложные задачи
1. 9 класс
Свойства тригонометрических
функций
2. Проверь себя.
Тригонометрический круг
90º π/2
180º π
90º π/2
0
180º π 2 чет. 1 чет.
360º 2π
270º 3π/2
3 чет.
4 чет.
270º 3π/2
Помните! π = 180 °
0
360º 2π
Какой четверти
принадлежит угол
5. Область определения функции
Областью определения
функции называют множество
всех допустимых значений
переменной x. Геометрически – это
проекция графика функции на ось
Ох.
D(y) = R
Синус, косинус
Функции непрерывны на R
Tангенс
D(y) = R, x ≠ π/2 + πn
x = π/2 + πn – вертикальная асимптота
tgx – определен при cosx ≠ 0
Котангенс
D(y) = R, x ≠ πn
x = πn – вертикальная асимптота
ctgx – определен при sinx ≠ 0
7. Множество значений функции
Множество значений функции
— множество всех значений,
которые функция принимает на
области определения.
Геометрически – это проекция
графика функции на ось Оy.
Множество значений
функций
-1 ≤ sin х ≤ 1, или |sinx | ≤1,
-1 ≤ cos х ≤ 1, или |cosx |≤1,
tgx € R, ctgx € R,
π/2
1
|sinx | ≤1
|cosx | ≤1
-1
π
1
2π
3π/2
-1
9. Свойства тригонометрических функций
10. Найди область определения функции y = 2sin(x + 3).
Найди область определения функции
y = 2sin(x + 3).
Область определения функции – это множество
всех значений аргумента, при котором
записанная формула функции имеет смысл.
Так как sinx имеет смысл при всех значений
переменной x, областью определения функции
y = 2sin(x + 3) является вся
числовая прямая, т.е. (–∞; +∞).
11. Найди сумму всех целых значений функции y = – 6 cosx + 1.
Найди сумму всех целых значений
функции y = – 6 cosx + 1.
Решение. Так как множество значений
функции y = cosx – промежуток [–1; 1], тогда:
–1 ≤ cosx ≤ 1,
–6 ≤ –6cosx ≤ 6,
–5 ≤ –6cosx + 1 ≤ 7,
т.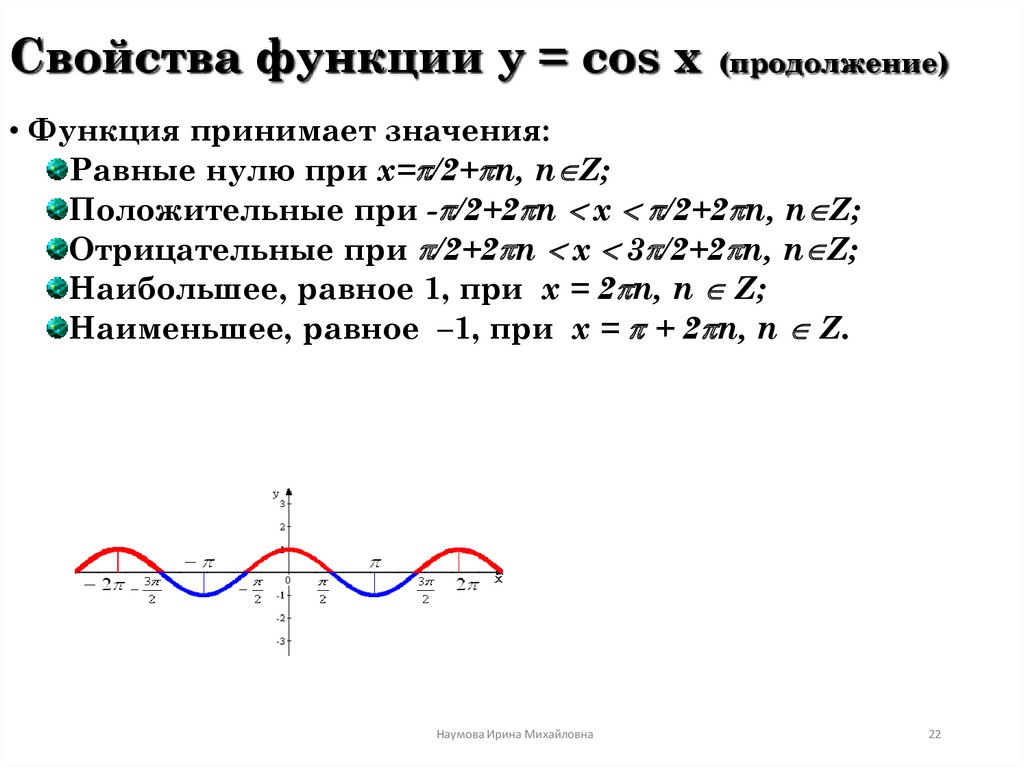 е. множество значений функции y = –6cosx + 1 –
е. множество значений функции y = –6cosx + 1 –
промежуток [–5; 7]. Этому промежутку
принадлежат следующие целые числа:
–5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7.
Найди сумму этих чисел:
(–5) + (–4) + (–3) + (–2) + (–1) + 0 + 1 + 2 + 3 +
4 + 5 + 6 + 7 = 13.
Ответ: 13.
12. Найди область значений функции y = 2cosx.
Найди область значений функции y = 2cosx.
Так как множество значений
функции y = cosx – промежуток
[–1; 1], тогда:
–1 ≤ cosx ≤ 1,
–2 ≤ 2cosx ≤ 2,
т.е. множество значений функции
y = 2cosx – промежуток [–2; 2].
Знаки по четвертям
Синус: знаки
соответствуют знакам по
оси У, косинус –по оси Х
Sin
Тангенс и котангенс в 1
четверти- плюс, далее знаки
чередуются
Tg, ctg
Cos
+
+
—
—
—
+
+
+
+
—
14. Рассмотрим примеры
у
ctg 240 » «
sin 20 » «
II
I
1
cos 70 » «
х
0
III
tg120 » «
sin( 45 ) » «
1
IV
tg( 130 ) » «
15.
 Четность и нечетность тригонометрических функцийsin( ) sin
Четность и нечетность тригонометрических функцийsin( ) sin
tg ( ) tg
ctg ( ) ctg
cos( ) cos
Если изменение знака
аргумента влечет за
собой и изменение
знака функции, то
функция называется
нечетной
Если изменение знака
аргумента не влечет
изменение знака
функции, то функция
называется четной
нечетные
Синус, тангенс, котангенс –функции
Минус у угла можно вынести за знак функции
Косинус – функция
четная
Минус у угла можно опустить
Примеры
1. sin ( – х) = — sin х
2. sin ( π/4 – х) =
—
sin ( х — π/4 )
3. tg (- π/6) = — tg π/6 = —
3
3
4. cos (-7π/3)= cos 7π/3 = cos (2π + π/3) = cos π/3 = ½
5. cos (-β) = cos β
6. ctg ( 2α — π/2) = — ctg (π/2 — 2α )
17. Рассмотрим примеры
cos (-120 )= cos 120
sin (-120 )=- sin 120
tg (-45 )=-tg 45
сtg (-60 )=-сtg 60
Период
это число,
при прибавлении
f(x +Т)
которого к аргументу значение функции не
изменяется.
Если Т – период, то Tn для n € Z тоже период.
–
=f(x)
Считается Т – наименьший период
Так как
sin, cos
f(x +Тn) = f(x),
Т=2π
то Tn можно опустить
tg, ctg
Примеры
1. sin 390º = sin (360º + 30º) = sin 30º = ½
2. sin 790º = sin (2∙360º + 30º) = sin 30º = ½
3
3. tg 210º = tg (180º + 30º) = tg 30º = 3
4. cos 7π/3= cos (2π + π/3) = cos π/3 = ½
5. cos (2π – β) = cos (-β) = cos β
6. sin (6π – 2α) = sin (-2α) = — sin 2α
Т=π
19. Рассмотрим примеры
Найдем
1)
cos 420 ,
cos1845 .
sin 1470 ,
1
cos 420 cos(60 360 ) cos 60 ;
2
2)
1
sin 1470 sin( 30 4 360 ) sin 30 ;
2
3)
2
cos 1845 cos( 45 5 360 ) cos 45
.
2
English
Русский
Правила
Как найти область определения и область значений функции
Область определения:
Пусть y = f(x) — функция.
Домен — это все действительные значения x, для которых определено y.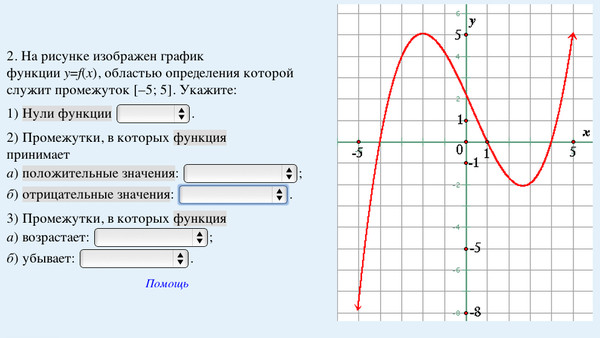
Если есть какое-либо значение x, для которого y не определено, мы должны исключить это конкретное значение из набора доменов.
Диапазон:
Пусть y = f(x) — функция.
Диапазон — все действительные значения y для данного домена (действительные значения x).
Давайте рассмотрим некоторые практические вопросы, чтобы понять, как найти домен и диапазон функции.
Вопрос 1:
Найдите домен 1 /(1 — 2SINX)
Решение:
1 — 2SIN X = 0
— 2SIN X = — 1
SIN SIN x = 1/2
sin x = sin π/6
Поскольку функция sin, область определения будет R — {nπ + (-1) n π/6}, n ∈ Z
Вопрос 2 :
Найдите наибольшую возможную область определения вещественной функции f(x) = √(4 — x
2 )/ √(x 2 — 9)
4 : 0 Решение
Приравняем числитель и знаменатель равными 0.
|
(4 — x 2 ) = 0 x 2 = 4 x = √4 x = ± 2 |
(x 2 — 9) = 0 x 2 = 9 x = √9 x = ± 3 |
(-∞, -3) (-3, -2) (-2, 2) (2, 3) (3, ∞)
Если x ∈ (-∞, -3)
f( -3,5) = √(4 — (-3,5) 2 )/ √((-3,5) 2 — 9)
= √(4 -12,25)/ √(12,25 0 0 0 2 9050 — 09) √(-8,25)/ √3,25
= Не определено
Следовательно, x ∉ (-∞, -3)
Если x ∈ (-3, -2)
f(-2,5) = √(4 — ( -2,5) 2 )/ √((-2,5) 2 — 9)
= √(4 -6,25)/ √(6,25- 9)
= Не определено
Следовательно, x ∉ (-3, -2)
Если x ∈ (-2, 2)
2 f(0) = √(4 — 0
2 )/ √(((0) 2 — 9)
= √4/ √(-9)
= Не определено
Отсюда (x 2 ≥ , 2)
Если x ∈ (2, 3)
f(2.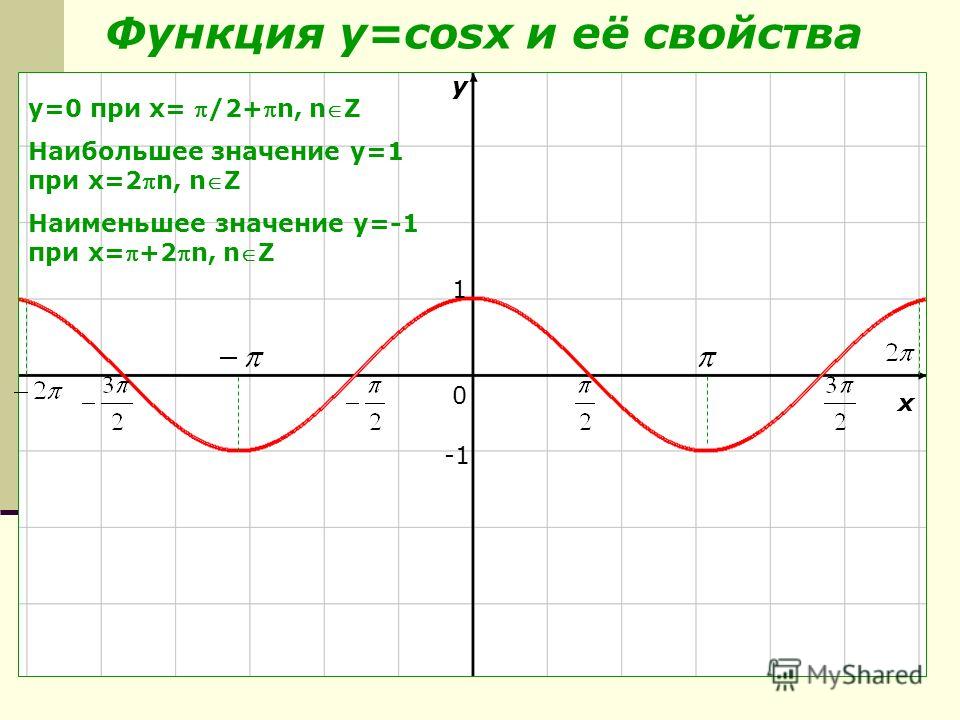 5) = √(4 — (2.5) 2 )/ √((2.5) 2 — 9)
5) = √(4 — (2.5) 2 )/ √((2.5) 2 — 9)
( = √ 6.25)/ √(6.25-9)
= Не определено
Отсюда x ∉ (2, 3)
Если x ∈ (3, ∞)
f(4) = √(4 — 4 2 )/ √(4) 2 — 9)
= √(4 — 16(1)/ 6 √ -9
= Не определено
Следовательно x ∉ (3, ∞).
Следовательно, ответ равен нулю
Вопрос 3 :
− 1)
Решение:
Диапазон для функции cos от -1 до 1
-1 ≤ cos x ≤ 1
-2 ≤ 2cos x ≤ 2
-2 — 1 ≤ 2cos x — 1 ≤ 2 — 1
-3 ≤ 2cos x — 1 ≤ 1
Выполним обратное уравнение, получим
-1/3 ≤ 1/(2cos x — 1) ≤ 1/1
-1/3 ≤ 1/(2cos x — 1) ≤ 1
(-∞, -1/3] U [1, ∞) — требуемый диапазон.
Вопрос 4 :
Покажите, что отношение xy = −2 является функцией для подходящей области. Найдите домен и диапазон функции.
Решение:
xy = −2
y = -2/x
Домен означает множество возможных значений x.
Домен — все действительные значения, за исключением 0.
Домен = R — {0}
x = -2/y
Диапазон означает набор возможных значений y.
Диапазон: все действительные значения, исключая 0.
Диапазон = R – {0}
Помимо приведенного выше материала, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Пожалуйста, присылайте свои отзывы на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Используйте график функции, чтобы ответить на следующие вопросы.
Математическое исчисление Предварительное исчисление Тригонометрия Предварительное исчисление Функции Trig Предварительное исчисление
Аэрин Х.
спросил 20/12/20
f ( x ) = cos( x ) на интервале [−2𝜋, 2𝜋]
0255 y = f ( x ).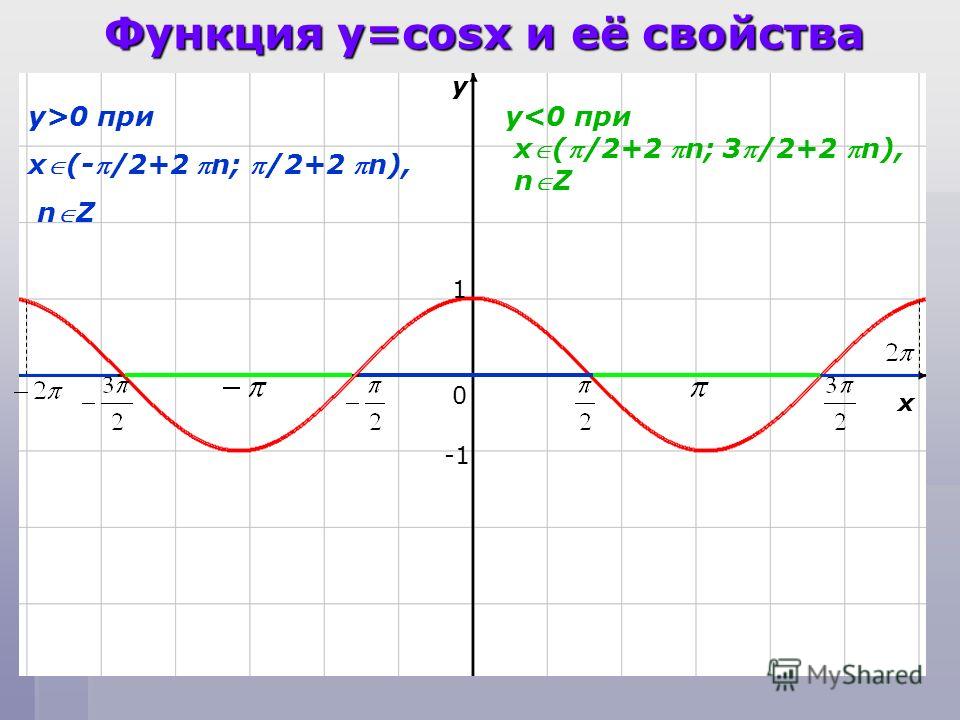 (Введите ответы в виде списка, разделенного запятыми.)
(Введите ответы в виде списка, разделенного запятыми.)
x =
(b) Найдите y -отрезки графика y = f ( x ).(Введите x ). ваши ответы в виде списка, разделенного запятыми.)
y =
(c) Найдите интервалы, на которых график y = f ( x ) возрастает, и интервалы, на которых график у = ж ( x ) уменьшается. (Введите ответы, используя обозначение интервала.)
в возрастающем:
в убывающем:
(d) Найдите относительные экстремумы графика
y = f ( x ). (Введите ваши ответы в виде списка упорядоченных пар, разделенных запятыми.)
относительные максимумы:
относительные минимумы
Подписаться
І
1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший
Новейшие
Самый старый
Автор:
ЛучшиеНовыеСамыеСтарые
Раймонд Б.
ответил 20.12.20
Репетитор
5
(2)
Математика, микроэкономика или уголовное правосудие
См. таких репетиторов
Смотрите таких репетиторов
точки пересечения x — это когда y = ноль
cosx=0, когда x = pi/2 + 2npi, где n = любое целое число, при котором x попадает в область значений -2pi
x=pi/2, 3pi/2 , -pi/2 и -3pi/2 или 90, 270, -90 и -270 градусов
или как точки они (3pi/2,0), (pi/2,0), (-pi/2, 0), и (-3pi/2,0)
только один отрезок y, y=1, или точка (0,1)
cosx=1, когда x=0
cosx увеличивается на интервалах (- p,0,) и (pi,2pi)
cosx убывает на интервалах (-2p,-pi) и (0,pi)
относительные или локальные и глобальные максимумы (-2pi,1), (0,1) и (2pi,1)
относительные или локальные и глобальные минимумы (-pi,-1), (pi,0)
Голосовать за
0
Понизить
Подробнее
Отчет
Джордж Ю.
ответил 20.12.20
Репетитор
5
(2)
Недавний выпускник Лиги плюща Математика, статистика, репетитор SAT
См. таких репетиторов
Смотрите таких репетиторов
а) пи/2, 3пи/2, -пи/2, -3пи/2
б) 1
в)
увеличение: (-пи, 0), (пи, 2пи)
уменьшение: ( 0, pi), (-2pi, -pi)
d)
относительные максимумы: (-2pi,1), (0,1), (2pi,1)
относительные минимумы: (-pi,-1 ), (пи,1)
Голосовать за
0
Понизить
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.