Определение 1. Пусть функцииfиg заданы на
множестве.Суммой функцийfиg называется
функция,
значение которой в точкеопределяется как сумма значений функцийfиg
в этой точке, то есть
.
Аналогично определяется разность
,
произведение
,
частное функций, если,
.
Определение 2. Пусть действительная
функцияf задана
на множествеХ, а действительная
функцияg – на
множестве.
Тогда существует композиция отображений,
которая является действительной
функцией, заданной на множествеХ и
называемой композицией действительных
функцийfиg
илисложной функцией.
Заметим, что сложную функцию
можно записать в виде цепочки функций
.
Переменнуюу в этом случае обычно
называютпромежуточной переменной.
Заметим также, что термин «сложная
функция» характеризует не сложность
функции, а способ ее задания. Например,
функцияили
– сложная функция, а тождественная ей
функцияуже не является сложной.
Пример 1. Если,
то,
.
Может получиться так, что множество
не является подмножеством множестваY. В этом случае сложная
функция определена лишь для техх,
для которых.
Пример 2. Пусть.
Тогда.
Здесьзадана на множестве
задана на
и
.
Сложная функциярассматривается
длях таких, что,
то есть.
Пример 3. Функциии
не определяют функции
,
так какопределена для
,
адля всех
.
Пример 4. (Решить самостоятельно).
Пустьи
.
Найти следующие функции и указать их
области определения:.
§ 10. Ограниченные и неограниченные функции. Монотонные функции
Определение 1. Функция,
заданная на множествеХ, называетсяограниченной сверху на этом
множестве, если существует числоМ,
такое, что.
Функция,
заданная на множествеХ, называетсяограниченной снизу на этом
множестве, если существует числоМ,
такое, что.
Функция,
заданная на множествеХ, называетсяограниченной на этом множестве,
если существуют числаи
,
такие, что.
Иными словами, функция
ограничена
на множествеХ, если на этом множестве
она ограничена и сверху, и снизу.
Например, функция
ограничена сверху на множествеR,
так как,
функцияограничена снизу наR,
так как,
функцияограничена наR, так
как.
Ограниченными являются также функциии
,
так как.
Свойства ограниченных функций:
1) если функции fиgограничены на множествеХ, то и
функциии
тоже ограничены на множествеХ;
2) если функция
ограничена сверху, то функция
ограничена снизу;
3) если функция
положительна
на множествеХи ограничена на нем
снизу положительным числом, то функцияограничена наХ.
Доказательство. 1) В силу ограниченности
функцийfиgна множествеХ найдутся числаи
,
и
,
такие, чтои
.
А тогдаи
– ограниченные наХ функции. Чтобы
доказать ограниченность функции,
положим.
Тогда имеют место неравенстваи
,
из которых следует, что,
а это и означает ограниченность функции.
2) В силу ограниченности функции f
сверху найдется числоМ, такое,
что.
Тогда,
что и означает ограниченность функцииснизу.
3) По условию
,
поэтомуограниченность функции
.
Например, функция
ограничена на множествеR
действительных чисел, так как.
Чтобы дать определение неограниченной
сверху или снизу функции, нужно
сформулировать отрицание соответствующей
части определения 1.
Определение 2. Функцияназываетсянеограниченной сверху
на множествеХ, если не существует
числаМ, такого, чтодля любого
,
то есть для любого числаМнайдется
число,
такое, что.
Функция
называетсянеограниченной снизу на
множествеХ, если для любого числаМнайдется число,
такое, что.
Докажем, например, что функция
неограниченна на множестве
сверху. Возьмем произвольное число
и покажем, что
,
такое, что.
Для этого, очевидно, достаточно взять
,
например,.
Если функция
ограничена на множествеХ, то
множествоограничено, поэтому имеет точную верхнюю
и точную нижнюю границы. Их обозначаюти
соответственно и называют точной
верхней границей и точной нижней границей
функциина множествеХ.
Определение 3. а) Функцияназываетсявозрастающей на
множествеХ, если большему значению
аргумента соответствует большее значение
функции, т.е.,
таких, что,
имеем.
б) Функция
называетсяубывающей на множествеХ, если
.
в) Функция
называетсянеубывающей на
множествеХ, если.
г) Функция
называетсяневозрастающей на
множествеХ, если.
Возрастающие, убывающие, неубывающие,
невозрастающие функции называются
монотонными, возрастающие и
убывающие –строго монотонными
функциями.
При исследовании функций на монотонность
полезны следующие утверждения.
Теорема.а) Если функцииf
иg возрастают
(убывают) на множествеХ, то и функцияf+g
возрастает (убывает) наХ.
б) Если
на множествеХ, то
наХ.
в) Если функции fиg неотрицательны
на множествеХи возрастают (убывают)
на этом множестве, то их произведениенаХ.
г) Если функция fположительна на множествеХи
возрастает (убывает), тонаХ.
д) Если функция
на множествеХ, а функция
на множестве
,
то функцияна множествеХ.
Доказательство. Докажем, например,
а) и д).
а) Пусть функции f иg возрастают
на множествеХ и,
причем.
Тогдаи поскольку неравенства одинакового
смысла можно складывать, то,
т.е. функцияf+g
возрастает.
д) Пусть функция
убывает на множествеХ, а функция
убывает на множестве
,
,
причем.
Тогдаи, так как
,
т.е. функциявозрастает на множествеХ.
Остальные утверждения теоремы доказать
самостоятельно.
Теорема доказана.
Отметим, что прибавление постоянной
величины к функции и умножение функции
на положительную постоянную величину
не меняет характера монотонности.
Пример. Докажем, что функциии
возрастают на промежутке
.
Доказательство. Функциявозрастает
на промежутке.
Тогда по свойству в)и
на
,
и
,
поэтому по свойству а) возрастает и
функция.
Для функции
доказательство проведем методом от
противного. Пусть.
Предположим противное, т.е. что.
Тогда, в силу возрастания функции,
,
т.е.,
что противоречит неравенству.
Из полученного противоречия следует,
что,
т.е. функциявозрастает на промежутке
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Композиция функций и функциональные уравнения
Школьный курс математики предполагает обучение учащихся различным методам решения задач на композицию функций, функциональные уравнения и неравенства. Однако, пожалуй впервые, в явном виде учащиеся общеобразовательных классов сталкиваются с понятием «композиция функций» в теме «Производная и ее применение» при выводе формулы производной сложной функции. Использование же этого понятия даже в достаточно простых задачах из других тем школьного курса вызывает у них большие трудности. Поэтому обращение авторов к данной теме является актуальным.
Наш опыт показывает, что и в ЕГЭ, и на олимпиадах разного уровня довольно часто встречаются задания на композицию функций, функциональные уравнения и неравенства, которые необходимо решать нетрадиционными способами, но в школьных учебниках не уделяется должного внимания методам их решения. Кроме того, при решении этих задач не подходит ни один стандартный (известный) алгоритм и учащимся приходится применять более широкий спектр теоретических знаний, проявлять сообразительность и умение рассуждать. Можно добавить, что они просто интересны, а решения некоторых из них необыкновенно красивы. Заметим, что такие задачи не выходят за рамки школьной программы, поскольку могут быть решены школьными методами. Поэтому изучение школьниками данной тематики улучшает закрепление пройденного материала, способствует развитию интереса к предмету, позволяет отработать различные способы решения задач при подготовке к ЕГЭ, олимпиадам разного уровня и вступительным испытаниям в вузы (в которых эти испытания сохранились).
Авторы настоящей статьи ставили перед собой цель познакомить заинтересованного читателя с основными подходами и методами решения задач, в которых фигурирует понятие сложной функции. Надеемся, что подобранный и систематизированный нами материал, а также максимально подробное его изложение будет полезно как учителям, так и школьникам.
Для начала напомним определение.
Пусть заданы две функции y = f(x) и x = g(t), причем область определения функции f содержит множество значений функции g. Тогда каждому числу t из области определения функции g соответствует значение x = g(t), принадлежащее области определения функции f, а ему, в свою очередь, соответствует число y = f(x).
Таким образом, каждому числу t из области определения функции g ставится в соответствие единственное число y из множества значений функции f, а это означает, что на области определения функции g задана функция, которую называют сложной функцией или композицией функций. При этом пишут y = f(g(x)).
Спонсор публикации статьи учебный центр “Стимул”. Центр предлагает Вам пройти учебные семинары для парикмахеров, семинары по парикмахерскому делу, косметологии, ногтевому сервису, организации туристического бизнеса, компьютерные курсы и другие. Профессиональная программа, квалифицированные преподаватели, доступные цены. Узнать подробнее о курсах в Ульяновске, цены и контакты Вы сможете на сайте, который располагается по адресу: http://www.stimul-kursy.ru/.
Пример 1. (Открытый банк заданий ЕГЭ-2010.) Найти
если
при | x | ≠ 2.
Решение. Функция g(x) определена при x ∈ (–∞; +∞); g(2 – x) — композиция функций g(x) и f(x) = 2 – x, а g(2 + x) — композиция g(x) и h(x) = 2 + x. Тогда
Отсюда получаем, что выражение
имеет смысл при всех | x | ≠ 2 и
Ответ: 1.
Пример 2. Дана функция f(x) = –x2 + 4x – 3. Решить уравнение f(2x + 3) = 4f(x – 2).
Решение. Опуская некоторые очевидные рассуждения и выкладки, получим для всех действительных x:
f(2x + 3) = –(2x + 3)2 + 4(2x + 3) – 3 = –4x2 – 4x,
f(x – 2) = –(x – 2)2 + 4(x – 2) – 3 = –x2 + 8x – 15.
Тогда уравнение f(2x + 3) = 4f(x – 2) примет вид:
Ответ:
Пример 3. Дана функция
Решить неравенство
2f(x + 3) < f(3x + 5).
Решение.
Тогда неравенство 2f(x + 3) < f(3x + 5) примет вид:
Поскольку 3x2 + 13x + 16 > 0 для всех действительных x, то последнее неравенство выполняется при x ∈ (–4; –2).
Ответ: (–4; –2).
Пример 4. (МИЭТ, 2004, № 9 из 11.) Найти значение f(f(1)), если
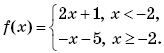
Решение. Найдем вначале f(1). Поскольку
1 ≥ –2, то f(1) = –1 – 5 = –6. Значит, f(f(1)) = f(–6). Так как –6 < –2, то f(–6) = 2∙(–6) + 1 = –11. Итак, f(f(1)) = –11.
Ответ: –11.
Пример 5. (МИЭТ, 2002, № 9 из 11.) Пусть
Решить неравенство f(g(x – 9)) ≥ f(4).
Решение. Поскольку
то
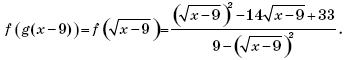
Так как f(4) = 1, то неравенство f(g(x – 9)) ≥ f(4) примет вид:
Пусть тогда t ≥ 0 и имеем систему:
Возвращаясь к переменной x, получим:
Ответ: [9; 18) (18; 25].
Пример 6. (Московская межвузовская олимпиада, 2009, № 5.) Пусть
Найти значение функции
в точке x = 4.
Решение. Установим вид функции
для первых трех натуральных значений n.
При
При
При
Возникает предположение, что
Докажем это утверждение методом математической индукции.
При n = 1, согласно условию задачи,
Утверждение истинно.
Пусть при n = k утверждение истинно, и функция
имеет вид:
Докажем, что при n = k + 1 функция
имеет вид:
Действительно,
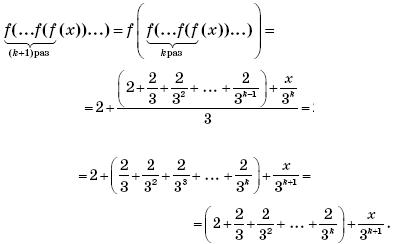
Что и требовалось доказать.
Итак,
при всех натуральных n. Следовательно, при
n = 2009:
В последнем соотношении выражение, заключенное в скобки, представляет собой сумму первых 2009 членов геометрической прогрессии со знаменателем
и первым членом, равным 2. Тогда
или
Подставляя в последнее соотношение x = 4, получим ответ:
Ответ: 3 + 3–2009.
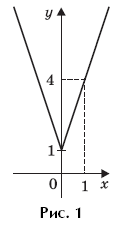
Пример 7. (МИЭТ, 2002, № 10 из 11.) Построить график функции y = 3| f(f(x)) | + 1, где
Решение. Выполним (по определению композиции функций) формальные преобразования:
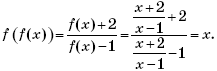
Найдем область определения функции f(f(x)):
Таким образом, функция y = 3∙| f(f(x)) | + 1 может быть представлена в виде:
График функции y = 3∙| f(f(x)) | + 1 изображен на рисунке 1.
Пример 8. (МИЭТ, 1999, № 7 из 11.) Изобразите на плоскости Oxy множество точек, координаты которых удовлетворяют условию
где f(x) = 1
– | x |.
Решение. Преобразуем уравнение, задающее на плоскости Oxy искомое множество точек:
Множество точек на плоскости Oxy, удовлетворяющих уравнению
очевидно, симметрично относительно координатных осей. Поэтому можно изобразить точки этого множества в первой координатной четверти, а затем окончательно достроить его, последовательно симметрично отразив относительно осей Ox и Oy. Итак, при x ≥ 0 и y ≥ 0 уравнение
примет вид
Тогда, раскрывая по определению модуль, получим:
Поскольку при 0 ≤ x < 1 значения
отрицательны, то в I координатной четверти нет точек, удовлетворяющих системе
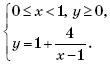
Множество точек на координатной плоскости, удовлетворяющих системе
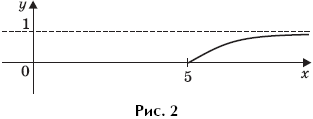
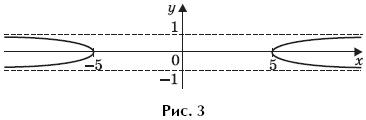
изображено на рисунке 2.
Окончательно, графическое изображение множества точек на плоскости Oxy, координаты которых удовлетворяют условию
показано на рисунке 3.
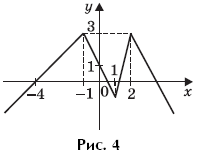
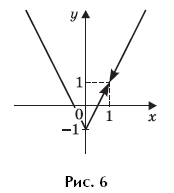
Пример 9. (МИЭТ, 1998, № 10 из 11.) Построить график функции y = f(f(x)), где
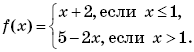
Решение. По определению композиции функций:
Формально возможны следующие четыре случая:
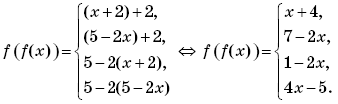
Найдем значения переменной x, при которых выполняется каждый из этих четырех случаев.
Первый случай выполняется, когда
Второй случай выполняется, когда
Третий случай выполняется, когда
Четвертый случай выполняется, когда
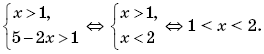
Таким образом,
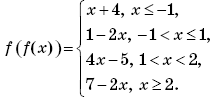
График функции y = f(f(x)) изображен на рисунке 4.
Пример 10. (МИЭТ, 2003, № 10 из 11.) Функция f(x) для каждого x равна наименьшему значению многочлена g(t) = t2
– 6t + 8 на отрезке [x + 1; x + 2]. Постройте график функции f(x).
Решение. Приведем функцию g(t) к виду:
g(t) = (t – 3)2 – 1.
Графиком функции g(t) является парабола, ветви которой направлены вверх, с вершиной в точке (3; –1). Значит, наименьшее значение функции g(t) на отрезке [x + 1; x + 2] будет равно –1, если 3 ∈ [x + 1; x + 2], то есть, записав систему неравенств
получим x ∈ [1; 2].
Если 3 [x + 1; x + 2], то наименьшее значение функции g(t) достигается на левом конце отрезка [x + 1; x + 2] (в случае 3 < x + 1) или на правом конце отрезка [x + 1; x + 2] (в случае
3 > x + 2).
Следовательно, если x > 2, то наименьшее значение функции g(t) на отрезке [x + 1; x + 2] будет равно
g(x + 1) = (x + 1 – 3)2 – 1 = (x – 2)2 – 1.
Если же x < 1, то наименьшее значение функции g(t) на отрезке [x + 1; x + 2] будет равно
g(x + 2) = (x + 2 – 3)2 – 1 = (x – 1)2 – 1.
Окончательно получим:
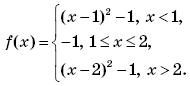
График функции f(x) изображен на рисунке 5.
Далее рассмотрим тип задач, в которых надо найти функцию, если задано некоторое уравнение, в котором в качестве неизвестной выступает сама функция. Такие уравнения называют функциональными уравнениями. В дальнейшем будем рассматривать функциональные уравнения, в которых искомые функции связаны с известными функциями одной переменной с помощью операции образования сложной функции. Отметим также, что функциональные уравнения можно рассматривать как выражение свойства, характеризующего тот или иной класс функций. Например, f(x) = f(–x) — уравнение четности, f(x + T) = f(x) —
уравнение периодичности и т.д.
Рассмотрим сначала задачи, в которых требуется найти значения функции, не заданной явно, но обладающей свойствами четности (нечетности), периодичности, или когда из данного функционального уравнения надо вывести (доказать) указанные свойства.
Пример 11. (МИЭТ, 2004, № 8 из 11.) Функция f(x) нечетная и периодическая с периодом
T = 10. Найти значение f(2004), если f(–4) = 1,5.
Решение. Воспользуемся вначале условием периодичности функции f(x). Тогда
f(2004) = f(4 + 10∙200) = f(4).
Поскольку функция f(x) нечетная, то
f(–x) = –f(x),
следовательно,
f(4) = –f(–4) = –1,5.
Ответ: –1,5.
Пример 12. (МИЭТ, 2005, № 10 из 11.) Известно, что f(x) нечетная периодическая функция с периодом 4 и f(x) = x4 – 2x3 при x ∈ [0; 2]. Вычислить сумму f(1) + f(2) + … + f(150).
Решение. f(0) = 0, f(1) = 14 – 2∙13 = –1,
f(2) = 24 – 2∙23 = 0. Поскольку f(x) нечетная функция, то f(–x) = –f(x), следовательно,
f(–1) = –f(1) = 1.
Так как f(x) — периодическая с периодом 4, то
f(3) = f(3 – 4) = f(–1) = 1,
f(4) = f(4 – 4) = f(0) = 0,
f(5) = f(5 – 4) = f(1) = –1,
f(6) = f(6 – 4) = f(2) = 0,
. . . . . . . . . . .
f(147) = f(–1 + 4∙37) = f(–1) = 1,
f(148) = f(0 + 4∙37) = f(0) = 0,
f(149) = f(1 + 4∙37) = f(1) = –1,
f(150) = f(2 + 4∙37) = f(2) = 0.
Таким образом получаем, что искомая сумма равна
f(1) + f(2) + (f(3) + f(4) + f(5) + f(6)) + … +
+ (f(147) + f(148) + f(150)) =
= –1 + 0 + (1 + 0 – 1 + 0) + … + (1 + 0 – 1 + 0) = –1.
Ответ: –1.
Пример 13. (МИЭТ, 1994, № 6 из 11.) Известно, что равенство f(x + 2) = –f(x) имеет место для всех действительных x. Доказать, что функция f(x) является периодической с периодом 4.
Решение. Пусть t = x + 2, тогда x = t – 2, и соотношение f(x + 2) = –f(x) примет вид
f(t) = –f(t – 2).
В последнем уравнении вместо переменной (буквы) t может выступать любая другая буква. Поэтому, заменив t на x, получим: f(x) = –f(x – 2). Подставим последнее выражение для f(x) в исходное уравнение и выполним преобразования:
f(x + 2) = –(–f(x – 2)) ⇔ f(x + 2) = f(x – 2).
Пусть u = x – 2, тогда x + 2 = u + 4, и соотношение f(x + 2) = f(x – 2) примет вид:
f(u + 4) = f(u) ⇔ (переобозначение: u ↔ x) ⇔ f(x + 4) = f(x).
Это означает, что функция f(x) является периодической с периодом 4.
Пример 14. (МИЭТ, 1999, № 9 из 11.) Функция f(x), определенная при всех значениях x и не равная 1 ни при каком значении x, удовлетворяет условию
Найти f(2000), если f(2) = 3.
Решение. Докажем, что функция f(x) является периодической и найдем ее период.
Пусть t = x + 2, тогда x = t – 2, и соотношение
примет вид
В последнем уравнении вместо переменной (буквы) t может выступать любая другая буква. Поэтому, заменив t на x, получим:
Подставим последнее выражение для f(x) в исходное соотношение и выполним преобразования:
Пусть u = x – 2, тогда x + 2 = u + 4, и соотношение
примет вид:
Пусть v = x + 4, тогда x = v – 4, и соотношение
Подставим последнее выражение для f(x) в уравнение
и выполним преобразования:
Пусть w = x – 4, тогда x + 4 = w + 8, и уравнение f(x + 4) = f(x – 4) примет вид:
f(w + 8) = f(w) ⇔ (переобозначение: w ↔ x)
⇔ f(x + 8) = f(x).
Таким образом, функция f(x) является периодической с периодом 8. Отсюда следует, что значение функции f(x) при x = 2000 будет равно значению f(x) при x = 8,
так как 2000 = 8∙249 + 8.
Найдем:
Следовательно, f(2000) = f(8) = 0,5.
Ответ: 0,5.
Пример 15. (МИЭТ, 2005, № 8 из 11.) Функция f(x) для всех x удовлетворяет равенству
f(x + 3) = x + 5 – f(x),
а при x ∈ [0; 3) задается формулой
f(x) = 1 + 6,5x – x2.
Найти f(100).
Решение. В функциональном уравнении
f(x + 3) = x + 5 – f(x)
сделаем замену t = x + 3. Тогда x = t – 3, и соотношение
f(x + 3) = x + 5 – f(x)
примет вид:
f(t) = t + 2 – f(t – 3) ⇔ (переобозначение: t ↔ x)
⇔ f(x) = x + 2 – f(x – 3).
Подставим последнее выражение для f(x) в уравнение f(x + 3) = x + 5 – f(x) и выполним преобразования:
f(x + 3) = x + 5 – (x + 2 – f(x – 3))
⇔ f(x + 3) = 3 + f(x – 3).
Пусть w = x – 3, тогда x + 3 = w + 6, и уравнение f(x + 3) = 3 + f(x – 3) примет вид:
f(w + 6) = 3 + f(w) ⇔ (переобозначение w ↔ x)
⇔ f(x + 6) = 3 + f(x).
Значит, функция f(x) является «почти периодической» с периодом 6. Причем при любом x значение функции f в точке x + 6 увеличивается на 3 по сравнению с ее значением в точке x. Поскольку 100 = 6∙16 + 4, то f(100) = 3∙16 + f(4) ⇔ f(100) = 48 + f(4).
Осталось вычислить f(4). Для этого воспользуемся соотношением f(x + 3) = x + 5 – f(x).
При x = 1 получим:
f(4) = 1 + 5 – f(1) ⇔ f(4) = 6 – f(1).
Найдем теперь f(1). Поскольку 1 ∈ [0; 3), то функция f(x) при x = 1 задается формулой
f(x) = 1 + 6,5x – x2.
Тогда
f(1) = 1 + 6,5∙1 – 12 = 6,5.
Таким образом,
f(100) = 48 + f(4) ⇔ f(100) = 48 + 6 – f(1) ⇔ f(100) = 54 – 6,5 ⇔ f(100) = 47,5.
Ответ: 47,5.
Функция f(x) называется решением данного функционального уравнения, если при подстановке ее в уравнение последнее превращается в тождество при всех значениях аргумента в области ее определения. Решить функциональное уравнение означает установить, имеет ли оно решения, и найти их, если таковые имеются.
Пример 16. (LXVIV Московская математическая олимпиада, окружной тур, 11-й класс, 2006, № 3.) Найти все такие функции f(x), что
f(2x + 1) = 4x2 + 14x + 7.
Решение. Пусть t = 2x + 1, тогда
Совершив замену переменной в уравнении
f(2x + 1) = 4x2 + 14x + 7,
получим:
В последнем соотношении для функции f(t) вместо переменной (буквы) t может выступать любая другая переменная (буква). Поэтому, заменив букву t на букву x, получим:
f(x) = x2 + 5x + 1.
Ответ: f(x) = x2 + 5x + 1.
Пример 17. (МИЭТ, 1995, № 11 из 11.) Найти f(x), если для всех x ≠ 0 имеет место соотношение
Решение. Предположим, что функция f(x), удовлетворяющая функциональному уравнению
существует. Тогда можно выполнить описанные ниже преобразования.
Пусть тогда
и исходное уравнение примет вид:
Получаем систему
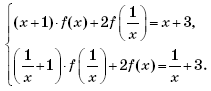
Из первого уравнения системы выразим
Подставим
во второе уравнение системы. Получим:
По условию x ≠ 0. Поэтому, умножив обе части последнего уравнения на 2x и приведя подобные члены, получим соотношение:
f(x)∙(x – 1)2 = (x – 1)2.
Отсюда следует, что f(x) = 1 при x ≠ 1. При x = 1
из исходного уравнения
получаем f(1) = 1.
Проверкой убеждаемся, что функция f(x) = 1 при всех x ≠ 0 удовлетворяет условию задачи.
Замечание. В условии данной задачи не было указано, что функция f(x), удовлетворяющая функциональному уравнению
существует. Предположив, что такая функция f(x) имеется, мы осуществили логический переход к следствию. Поэтому проверка в этой ситуации необходима.
Ответ: f(x) = 1, x ≠ 0.
Пример 18. (МГУ, ВМК, устный экзамен, 1997.) Существует ли линейная функция f(x), удовлетворяющая для всех x соотношению
f(x + 1) + f(2x) = (x + 1)2?
Решение. Функция f(x) является линейной тогда и только тогда, когда она может быть задана формулой f(x) = kx + b. Тогда
f(x + 1) = k(x + 1) + b,
f(2x) = k∙2x + b.
Следовательно, должны существовать такие единственные k и b, что для всех значений x будет выполняться равенство:
k(x + 1) + b + 2kx + b = (x + 1)2 ⇔
⇔ 3kx + (k + 2b) = x2 + 2x + 1.
Полученное равенство не может выполняться при любых значениях x (многочлен первой степени 3kx + (k + 2b) не при всех x может равняться многочлену второй степени x2 + 2x + 1). Это означает, что линейной функции, удовлетворяющей данным условиям, не существует.
Ответ: не существует.
Пример 19. (МГУ, экономический факультет, 1997, № 6.) Функция f(x) определена на всей числовой прямой, является нечетной, периодической с периодом 4, и на промежутке 0 ≤ x ≤ 2 ее значения вычисляются по правилу
f(x) = 1 – | x – 1 |.
Решить уравнение
2f(x)∙f(x – 8) + 5f(x + 12) + 2 = 0.
Решение. Раскроем модуль в выражении для функции f(x) на отрезке [0; 2]:
Так как функция f(x) — нечетная, то
По условию, функция f(x) — периодическая с периодом 4. Значит, f(x – 8) = f(x), f(x + 12) = f(x). Значит, исходное уравнение примет вид:
Найдем вначале решения последней совокупности на отрезке [–2; 2] (то есть на одном из полных периодов функции f(x)).
Если f(x) = –2, то:
при x ∈ [–2; –1] получим уравнение –x – 2 =
= –2, решением которого является x = 0, не удовлетворяющее условию x ∈ [–2; –1];
при x ∈ (–1; 1) получим x = –2, что не удовлетворяет условию x ∈ (–1; 1);
при x ∈ [1; 2] получим уравнение –x + 2 = –2, решением которого является x = 4, не удовлетворяющее условию x ∈ [1; 2].
Если f(x) = –0,5, то:
при x ∈ [–2; –1] получим уравнение –x – 2 = –0,5, решением которого является
x = –1,5, –1,5 ∈ [–2; –1];
при x ∈ (–1; 1) получим x = –0,5, –0,5 ∈ (–1; 1);
при x ∈ [1; 2] получим уравнение –x + 2 = –0,5, решением которого является x = 2,5, не удовлетворяющее условию x ∈ [1; 2].
Поскольку функция f(x) является периодической с периодом 4, то окончательно получим две серии решений уравнения
2f(x)∙f(x – 8) + 5f(x + 12) + 2 = 0:
x = –1,5 + 4k, k ∈ Z;
x = –0,5 + 4n, n ∈ Z.
Ответ: –1,5 + 4k, k ∈ Z; –0,5 + 4n, n ∈ Z.
Пример 20. (LXX Московская математическая олимпиада, окружной тур, 11-й класс, 2007, № 4.) Функция f(x) такова, что для любых положительных x и y выполняется равенство
f(xy) = f(x) + f(y). Найти f(2007), если
Решение. По условию f(1∙1) = f(1) + f(1), или f(1) = 2f(1). Значит, f(1) = 0. Кроме того, для всех положительных x выполнено:
Отсюда при x = 2007 получим:
Ответ: –1.
Пример 21. (МГУ, биологический факультет, 2005, № 7.) Функция f(x) такова, что для всех рациональных чисел x и y выполнено равенство f(x + y) = f(x) + f(y). Известно, что f(10) = –π. Найти
Решение. По условию f(0 + 0) = f(0) + f(0), или f(0) = f(0) + f(0). Значит, f(0) = 0. Кроме того,
f(0) = f(x – x), или 0 = f(x + (–x)). Отсюда получим:
f(x + (–x)) = f(x) + f(–x) ⇔ 0 = f(x) + f(–x).
Следовательно, f(–x) = –f(x). Значит,
Далее,
Таким образом,
Отсюда искомое значение
Ответ:
Пример 22. (LXXI Московская математическая олимпиада, окружной тур, 11-й класс, 2008, № 4.) Непрерывная функция f(x) такова, что для всех действительных x выполняется неравенство
Верно ли, что функция f(x) обязательно имеет точки экстремума?
Решение. При x = 0 получим:
Аналогично, при x = 1:
Так как непрерывная функция принимает одинаковые значения на концах отрезка [0; 1], то внутри этого отрезка существует хотя бы одна точка максимума или точка минимума.
Замечание. Если
для всех x ∈ [0; 1], то любая точка этого отрезка является точкой экстремума.
Ответ: да, верно.
В заключение статьи рассмотрим задачу C5 одного из вариантов ЕГЭ по математике 2009 года.
Пример 23. Решить уравнение
87cos x2 + (8 – 6x)4 = x8 + 87cos (8 – 6x).
Решение. Приведем исходное уравнение к виду
x8 – 87cos x2 = (8 – 6x)4 – 87cos (8 – 6x).
Введем непрерывную четную функцию
f(t) = t4 – 87cos t.
Найдем ее производную:
f ‘(t) = 4t3 + 87sin t.
При t ∈ (0; π)
f ‘(t) = 4t3 + 87sin t > 0 + 0 = 0,
при t ∈ [π; +∞)
f ‘(t) = 4t3 + 87sin t > 4π3 – 87 > 4∙33 – 87 = 4∙27 – 87 > 0.
Таким образом, f'(t) > 0 при t ∈ (0; +∞), следовательно, f(t) возрастает на промежутке [0; +∞). Значит, каждое свое значение функция принимает в точности в двух симметричных относительно
t = 0 точках (если t = 0, то исходное уравнение не имеет решений, так как при x2 = 0 не выполняется 8 – 6x = 0), а стало быть, исходное уравнение равносильно совокупности:
Ответ:
В заключение читателю предлагается подборка заданий для самостоятельного решения с ответами. Авторы не сомневаются, что решение этих задач поможет учащимся при подготовке к различным творческим и аттестационным испытаниям.
Задачи для самостоятельного решения
1. (МИЭТ, 2004, № 8 из 11.) Функция f(x) нечетная и периодическая с периодом T = 40. Найдите значение f(2004), если f(–4) = –4,5.
2. (МИЭТ, 2004, № 9 из 11.) Найдите значение f(f(1)), если
3. (МИЭТ, 2002, № 9 из 11.) Пусть
Решите неравенство f(4) ≤ g(f(x + 3)).
4. (МИЭТ, 2002, № 10 из 11.) Постройте график функции y = 2∙| f(f(x)) | – 1, где
5. (МИЭТ, 1999, № 7 из 11.) Изобразите на плоскости Oxy множество точек, координаты которых удовлетворяют условию
где f(x) = x – 2.
6. (МИЭТ, 1998, № 10 из 11.) Постройте график функции y = f(f(x)), где
7. (МИЭТ, 2003, № 10 из 11.) Функция f(x) для каждого x равна наибольшему значению многочлена g(t) = –t2 – 8t – 15 на отрезке [x – 3; x + 1]. Постройте график функции f(x).
8. Найдите f(x), если:
9. (МИЭТ, 1994, № 6 из 11.) Известно, что равенство
имеет место для всех действительных x. Докажите, что функция f(x) является периодической с периодом 2.
10. (МИЭТ, 1999, № 9 из 11.) Функция f(x), определенная при всех значениях x и не равная 0 ни при каком значении x, удовлетворяет равенству
Найдите f(2004), если f(8) = 5.
11. (МИЭТ, 2005, № 10 из 11.) Известно, что f(x) нечетная периодическая функция с периодом 6 и f(x) = 3x – x2 при x ∈ [0; 3]. Вычислите сумму
f(1) + f(2) + … + f(100).
12. (МИЭТ, 1995, № 11 из 11.) Найдите f(x), если для всех x имеет место соотношение
xf(x) + f(2 – x) = 2(x + 1).
13. (МИЭТ, 2005, № 8 из 11.) Функция f(x) для всех x удовлетворяет равенству
f(x + 4) = 2x – 1 – f(x),
а при x ∈ [0; 4) задается формулой f(x) = x2 – 3x.
Найдите f(135).
14. (МГУ, ВМК, устный экзамен, 1997.) Существует ли линейная функция f(x), удовлетворяющая для всех x соотношению
2f(x + 2) + f(4 – x) = 2x + 5?
15. (МГУ, химический факультет, 2001, № 7.) Функция f(x) для всех x удовлетворяет уравнению f(x + 1) = f(x) + 2x + 1. Найдите f(2001), если f(0) = 0.
16. (МГУ, биологический факультет, 2005, № 7.) Функция f(x) такова, что для всех рациональных чисел x и y выполнено равенство
f(x + y) = f(x)∙f(y). Известно, что f(4) = 16. Найдите f(–1,5).
17. (ЕГЭ-2009, задача С5.) Решите уравнение
x6 – | 7 – 6x |3 = 26cos x2 – 26cos (7 – 6x).
18. (ЕГЭ-2009, задача С5.) Решите уравнение
x6 – | 4x + 3 |3 = 25cos x2 – 25cos (4x + 3).
Ответы: 1. 4,5. 2. 9. 3. [8,5; 13) c (13; +∞).
4.
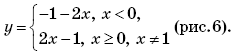
5.
6. 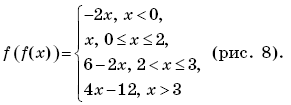
7. 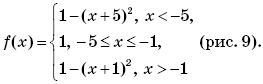
8. а) f(x) = x2 – 5x + 6;
б) f(x) = x2 – 14;
в) f(x) = x2 – 2, x ≠ 0;
г) f(x) = 12 – x2;
д)
е)
10. 0,8. 11. 2. 12. f(x) = 2.
13. 133. 14. Существует (и единственная!)
15. 20012.
Указание. Достаточно доказать, что функция f(x) удовлетворяет функциональному уравнению f(x + a) = f(x – a) + 4ax при любом натуральном a. Это можно сделать, например, с помощью метода математической индукции. Тогда, положив x = a, из уравнения
f(2a) = f(0) + 4a2 можно вычислить f(2000): f(2000) =
= 20002. Тогда получим f(2000 + 1) = f(2000) +
+ 2∙2000 + 1, или f(2001) = 20012. Замечание. Можно также доказать, что общее решение исходного функционального уравнения имеет вид f(x) = x2 + g(x), где g(x) — произвольная периодическая функция с периодом T = 1, определенная на всей числовой прямой. 16.
Указание. Установите вначале, что f(0) = 1. Затем, показав, что f(x) ≠ 0, докажите равенство
Выведите для всех натуральных n соотношение f(nx) = nn(x). Поскольку f(4) = f(8∙0,5) или 16 = f8(0,5), то
(Подумайте, почему f(x) > 0.) Тогда f(1,5) = f(3∙0,5). Замечание. Можно также доказать, что f(x) = 2x для рациональных x.
17.
Бардушин В. , Белов А., Прокофьев А. , Фадеичева Т.
В математике составная функция — это операция, при которой две функции порождают новую функцию. В некоторых источниках то же самое явление называется композицией функции.
Возьмем такой простой пример:
-
У нас есть две функции —
и
-
Вместе они порождают функцию
-
Составной функцией будет считаться
Как видите в примере выше, функция
применяется к функции
. Другими словами, одна функция применяется к результату другой функции.
Давайте посмотрим на математическое определение составной функции:
-
Пусть
и
— две функции
-
Тогда составная функция будет состоять из
и
— это обозначается как
-
Составная функция
определяется как функция
-
Функция
задается через
На рисунке ниже показано графическое представление составных функций:

Порядок функции является важным моментом при работе с композицией функций, потому что выражения
и
не равны между собой.
Это можно очень хорошо понять на примере. Представим машину, которая сначала запекает торт, а затем украшает его глазурью. Будем рассматривать эти действия как функции:
-
Запекание — функция
-
Украшение — функция
Машина будет производить торт, используя
— сначала печь, затем украшать. Но если функции поменять местами
, то машина сначала украсит сырой торт, а сожжет его в печке вместе со всеми украшениями. Такая перестановка действий не сработает, поэтому нам нужны оба домена.
Теперь рассмотрим, как обозначаются составные функции и их области:
-
Символ: В обозначении составных функций используется символ, похожий на маленький круг. Так это выглядит на практике —
-
Домен:
читается как «
от
от
». В композиции
домен функции
становится
-
Область: это множество всех значений, которые входят в функцию
-
Пример: Если
и
, то
от
от
Обратите внимание, что будет, если мы обратим операцию над функцией. Например, если мы возьмем
от
от
, то в итоге получим
.
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно разбираться в определенных понятиях и находить весомые аргументы и методы решения, что и предложено данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями, чтобы вам больше не нужно было определять все это онлайн.
Что значит найти область определения
После того как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Область определения и область значения можно найти и для кубического корня (куб. √), к примеру, для x+2.
Ограничение области определения
Область определения функции или ООФ рассматривается еще в школьном курсе алгебры. У действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально узнавать ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на сложение корня четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
При отсутствии хотя бы одного признака, область определения приходится искать другим образом (и это не с калькулятором). Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно иметь следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом, чтобы понимать понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Чтобы найти область определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1 является постоянной функцией, f2 является арктангенсом, f3 – логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x) – произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x) является -∞, +∞D(f)=D(f).
Естестввенным образом получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x – [0, +∞).
Области определения y=f(x) и y=−f(x) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2. В данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f) является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Найти область определения y=ln x2.
Решение
Алгоритм решения этого уравнения или функции следующий.
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Найти область определения функции y=(arcsin x)-12.
Решение
График решения следующий.
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3 – логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3 –это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4 – это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Действия с корнями
Корни в математике, в частности, функцию с корнем можно определить следующим образом:
y=n√x. N здесь — натуральное число, большее за единицу.
Область определения корня зависит от того, каков показатель: четный или нечетный.
Если n является четным числом (n=2m). Это значит, что область определения представляет собой множество всех неотрицательных действительных чисел.
Если показатель корня — нечетное число, большее за единицу (n=2m+1 и m принадлежит к n), то областью определения корня будет множество всех действительных чисел.
Также важным является вопрос, как складывать корни.
Сложение и вычитание корней возможно при условии наличия одинакового подкоренного выражения. К примеру, сложение и вычитание корней возможно 2√3 и 4√3. Можно ли складывать корни или вычитать в случае 2√3 и 2√5? Ответ — нет.
Как решать корни во втором случае? Вы можете упростить подкоренное выражение и привести их корни к одинаковому подкоренному выражению. После этого вы сможете как считать корни, так и вычитать корни.
К основным действиям с корнями относят:
- умножение корней;
- деление корней;
- корень минус корень или плюс.
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
К аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1 определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2 является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2 имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.
| Функция | Ее область определения |
|
Сумма, разность, произведение функций f1, f2,…, fn |
Пересечение множеств D(f1), D(f2), …, D(fn) |
|
Сложная функция y=f1(f2(f3(…fn(x)))) В частности, y=f1(f2(x)) |
Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1) x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
|
Прямая пропорциональность y=k·x |
R |
| Линейная y=k·x+b | R |
|
Обратная пропорциональность y=kx |
-∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C – число | D(f) |
|
Дробная y=f1(x)f2(x) В частности, если f1(x), f2(x) – многочлены |
Множество всех x, которые одновременно удовлетворяют условиям f2(x)≠0 |
| y=f(x)n, где n – четное | x∈D(f1), f(x)≥0 |
|
y=logf2(x)f1(x) В частности, y=logaf1(x) В частности, y=logf2(x)a |
x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1 x∈D(f1), f1(x)>0 x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
Конспект урока по математике
Преподаватель Дмитрива В.М.
Тема: Арифметические операции над функциями. Сложная функция (композиция). Понятие о непрерывности функции. Обратные функции. Область определения и область значений обратной функции. График обратной функции.
Цели:
образовательная: Ввести понятия: Арифметические операции над функциями. Сложная функция (композиция). Понятие о непрерывности функции. Обратные функции. Область определения и область значений обратной функции. График обратной функции.
развивающая: продолжить работу по развитию наблюдательности, умения сравнивать делать вывод;
воспитательная: формирование у обучающихся самостоятельности, трудолюбия, прививать чувства ответственности и сознательного отношения к изучаемому материалу.
Тип урока: Комбинированный урок.
Метод проведения: Сочетания фронтальной и индивидуальной работы с обучающимися.
Оборудование урока: Учебник, проектор, ПК, презентация.
ХОД УРОКА
1. Орг. момент: Приветствие группы, проверка дежурства, состояние кабинета, наличие студентов, готовность к занятиям.
Проверка наличия и ведения конспектов, домашнего задания; опрос.
2. Сообщение темы урока, постановка цели и задачи: Актуализация и мотивация познавательной деятельности студентов.
— Предположим, что у вас в кармане два яблока. Некто взял у вас одно яблоко. Сколько у вас осталось яблок?
— Два.
— Подумайте хорошенько. Буратино сморщился, — так здорово подумал.
— Два…
— Почему?
— Я же не отдам Некту яблоко, хоть он дерись!
к/ф «Золотой ключик, или приключения Буратино»
Всем нам хорошо известны основные арифметические операции: сложение, вычитание, умножение и деление. Сначала мы складывали и вычитали яблоки. Потом целые числа. Затем перешли к изучению операций над числами дробными. И вот наконец то пришла очередь операций над функциями. Да да, не удивляйтесь, функции, как и обычные числа можно складывать и вычитать, умножать и делить.
3. Изучение нового материала: Лекция.
Определение: Суммой функций f(x) и g(x) называется функция (f+g)(x), которая для каждого x из множества X принимает значение f(x)+g(x).
(f+g)(x)=f(x)+g(x), D(f+g)=D(f)∩D(g).
Аналогично определяется произведение функций: (f⋅g)(x)=f(x)⋅g(x),
D(f⋅g)=D(f)∩D(g).
Разность функций: (f−g)(x)=f(x)−g(x), D(f−g)=D(f)∩D(g).
Частное функций: (f/g)(x)=f(x)/g(x), D(fg)=D(f)∩D(g)∖Mg, Mg={x∈D(g):g(x)=0}.
Разумеется определения операций над функциями как всегда просты и понятны, но если они вызывают у вас некоторое смущение, то вы можете обратиться к примерам.
Прочитав определение определение суммы функций, мы задаем себе вполне логичный вопрос: «А что все это значит?» Давайте же разберемся, как будет выглядеть сложение функций на практике.
Пример:
Пусть у нас есть функция f(x) = 1 +
Тогда их сумма определяется как (f + g)(x) = f(x) + g(x) = (1 + 

Как видите, здесь нет ничего сложного. Основные проблемы начинаются при нахождении область определения результирующей функции. Говоря простым языком, область определения суммы функций является пересечением (общей частью) областей определения исходных функций.
Для нашего примера:
|
Функция |
Область определения |
|
f(x) = 1 + √x — 2 |
[2; +∞) |
|
g(x) = x — 1 |
(-∞ +∞) |
|
(f + g)(x) = x + √x — 2 |
[2; ∞)∩(-∞ +∞) = [2; ∞) |
Рассмотрим более сложный вариант.
Возьмем две функции
f(x) = 3√x и g(x) = √x
Тогда их произведение определяется как
(f*g)(x) = f(x).g(x) = (3√x)(√x) = 3x
Казалось бы, для области определения результирующей функции (f*g)(x) = 3x нет никаких ограничений, но
|
Функция |
Область определения |
|
f(x) = 3√x |
[0; +∞) |
|
g(x) = √x |
[0; +∞) |
|
(f.g)(x) = 3x, x ≥ 0 |
[0; +∞) ∩ [0; +∞) = [0; +∞) |
И напоследок самое простое, давайте расшифруем строку из определения деления функций:
(f/g)(x)=f(x)/g(x), D(fg)=D(f)∩D(g)∖Mg, Mg={x∈D(g):g(x)=0}.
Включаем переводчик….
Translate: Для f/g, область определения есть пересечение областей определения функций f и g кроме точек, где g(x) = 0
f(x)=x+100500
g(x)=x*√2+x, тогда
g(x)=0 при x=-2 и x=0
|
Функция |
Область |
|
f(x) = x+100500 |
(-∞ +∞) |
|
g(x) = x*√2+x |
[-2; +∞) |
|
(f/g)(x) = (x+100500)/(x*√2+x), |
(-2; 0) ∩ (0; +∞) |
|
Понятие о сложной функции |
|
Пример. Функцию z = |
|
Для записи композиции функций употребляется значок |
|
Пример. z = |
|
Взаимно обратные функции Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f. Если функция g является обратной для функции f, то и функция является обратной для функции g. Пару функций f и g называют взаимно обратными функциями. |
|
График обратной функции Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат – их значения, то эти графики будут симметричны друг другу относительно прямой у = х. |
|
Свойства взаимно обратных функций Отметим некоторые свойства взаимно обратных функций. |
Примеры нахождения обратных функций:
1) y=3x-8
1. x=3y-8, 2. 3y=x+8, 3. y=(x+8)/3.
2) y=11-5x
1. x=11-5y, 2. 5y=11-x, 3. y=(11-x)/5.
4. Закрепление изученного материала: Комментированное решение у доски: 

5. Подведение итогов урока: Вывод о достижении цели занятия.
6. Домашнее задание.
О.2 п. 1.6. № 1.58 (а, в), 1.59 (б) стр. 30
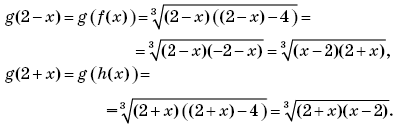
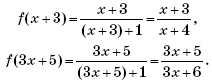
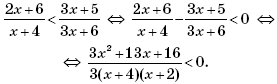
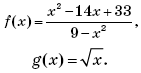
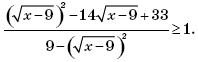
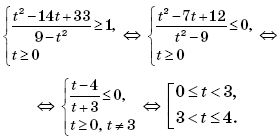
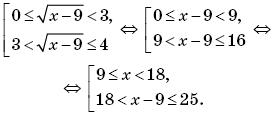
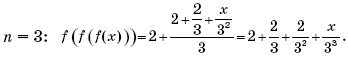
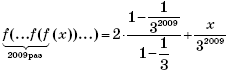
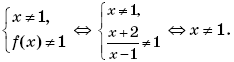
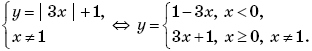
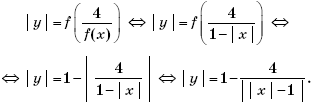
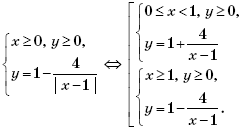
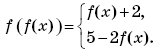
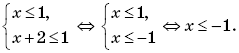
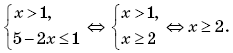
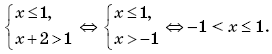
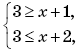
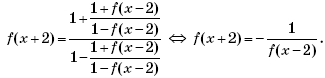
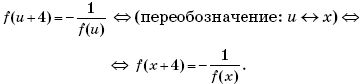
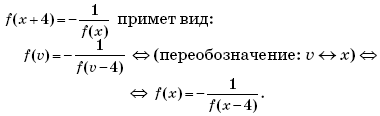
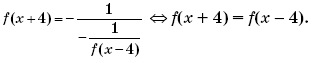
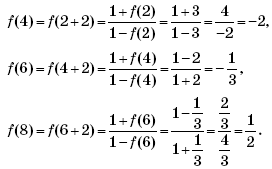
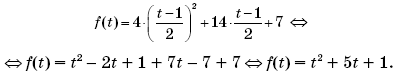
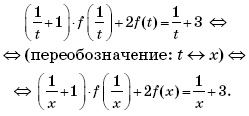
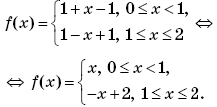
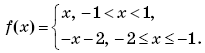
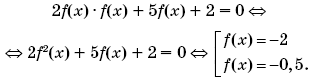
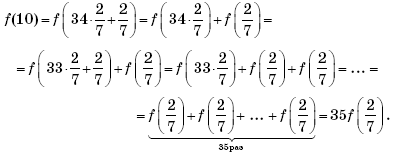
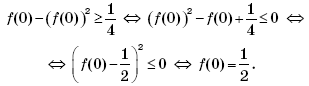
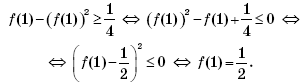
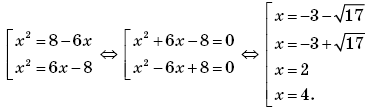
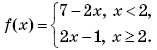
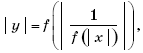
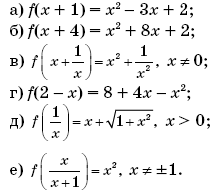
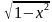 можно рассматривать как композицию функций y = 1 –
можно рассматривать как композицию функций y = 1 – 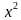 и z =
и z = 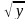 .
.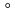 g означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е. (f
g означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е. (f 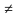 f
f 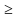 0, т. е. те, для которых число 1 –
0, т. е. те, для которых число 1 – 