Как найти область определения множество значений функции

Была ли эта статья полезной?

Всем привет! В этой статье мы познакомимся с функцией. Узнаем что такое область определения и область значений функции. А еще разберем линейную функцию и построим ее график.

Графиком функции называют множество всех точек координатной плоскости, абсциссы – x и ординаты – у.

Функцией называют зависимость переменной y от переменной x , при которой, каждому значению x соответствует единственное значение y.

x – аргумент, независимая переменная;

y – функция, которая зависит от аргумента x. Значения y называют значениями функции;

Область определения функции – это все значения x.

Область значения функции – это все значения y.

Когда функция задана формулой и её область определения не указана, то область определения функции будет состоять из всех значений аргумента(x), при которых функция имеет смысл.

Например областью определения функции f(x) = 3/x является множество всех чисел, кроме 0, потому что на 0 делить нельзя.

Линейная функция

Графиком функции kx + b является прямая.

Областью определения этой функции служит множество всех чисел.

Если k ≠ 0, то область значения функции – это множество всех чисел. Если же k = 0, то область значения состоит из одного числа равного b.

ДЗ:

Функция задана формулой f(x) = -4x + 10.

Найдите: f(-1), f(0), f(1/4).

Кто будет решать домашнее задание, пишите ваши ответы в комментариях. Для практики можно еще и график построить для каждого случая! И не забывайте подписаться на мой канал!

Исследование графика функции

На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

• область определения функции;
• область значений функции;
• нули функции;
• промежутки возрастания и убывания;
• точки максимума и минимума;
• наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.

Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.
Обозначается: D(f) или D(y).

На нашем рисунке область определения функции  — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок  — от самого нижнего до самого верхнего значения .

Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .

Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .

Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества  можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.

Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.

Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Для убывающей функции большему значению  соответствует меньшее значение . График идет вправо и вниз.

На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке  — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке  — точка минимума.

Точка  — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и  на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это  и .

А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен . Он достигается в точке .

Можно сказать, что экстремумы функции равны  и .

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке равно  и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.

Область значений функции, ее свойства и примеры решения

В данном материалы мы подробно рассмотрим значение функции. Определим основные методы ее вычисления. Изучим множество значений функции.

Подробно, разберем на примерах, методы нахождения функции.  Прежде, чем начать изучение материала, охарактеризуем основное определение значению функции.

Функции удобно изображать в виде графических прямых или кривых.

Понятие области определения функции

Функция задается тогда, когда любому значению, например x соответствует любое значение y. Независимой переменной называют значение х или по другому аргументом. Числовое значение y, как правило является зависимой переменной.

Данная зависимость между x и y в алгебре называют функциональной.  Записывают ее в виде функции y = f(x)

Другими словами, функция, это когда значения одной переменной зависят от значений другой переменной.

Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.

Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.

Например:

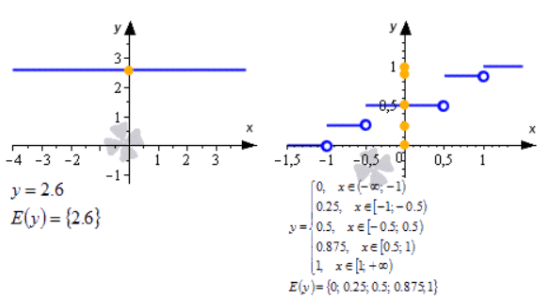
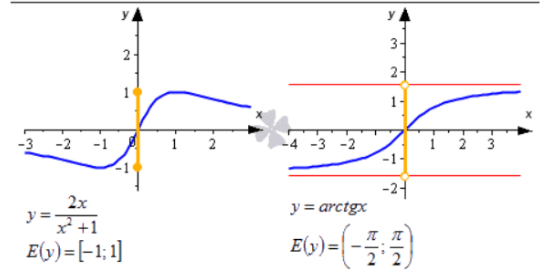
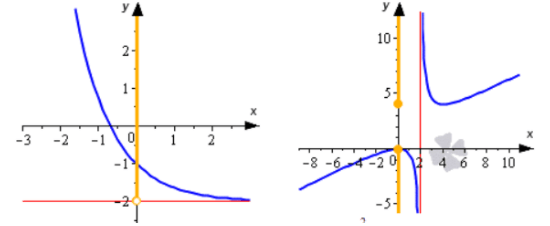
Область значений функции y = z² — это все значения, которые будут  больше либо равные нулю. В виде записи это выглядит следующим образом: f(у): у ≥ 0. Не все функции обозначаются одинаковыми формулировками, в основном D(f). Но тригонометрические функции обозначаются немного иначе. D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус. Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = x. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) =  [-1, 1]. Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.

Для указания множества чисел в определенном промежутке, необходимо выполнить следующие действия:

• назначается левая и правая границы, два числа через запятую или точку с запятой;
• ставится круглая или квадратная скобка; это зависит, входит ли граница в промежуток;
• круглая скобка, ставится, в том случае, если граница не входит в заданный промежуток;
• квадратная, в обратном случае.

Если у промежутка нет правой границы, записываем знак бесконечности или плюс бесконечности. Если отсутствует левая граница, записываем знак минус бесконечности.

В случае, если записывается множество, которое состоит из нескольких промежутков, ставится знак объединение. 

Рассмотрим на примерах

Все действительные числа от 1 до 9, можно выразить в следующей записи. [1;9]

Все положительные числовые значения, имеют следующий вид: (0; +);

Так как ноль, не является положительным число, то возле него ставится круглая скобка.

Область значения и определения функции

Область определения —  y(x) любые числовые значения аргумента x.

Чаще всего  область определения выражают как функцию D(y).

В математике существует две главных запрещенных (недопустимых) операции:

• деление любого числового значения на ноль;
• извлечение квадратного корня, из числа, которое имеет отрицательное значение.

При определении области функции, вступают в силу два основных ограничения:

• В функции может быть деление на любую переменную. Таким образом, знаменатель, будет равен нулю и получим недопустимое значение. В таком случае, принято считать областью определения все действительные числа.
• Функция имеет действие: как извлечение квадратного корня. Подкоренное выражение обязательно не должно быть отрицательным. Множество решений этого неравенства и будет областью определения функции.

Область определения постоянной функции

Постоянная функция записывается обычной формулой y = N, а именно f(x) = N, где N — любое действительное число. Иными словами, принято называть константа.

Область определения степенной функции

Степенная функция выглядит следующим образом: y = x^k, то есть, f(x) = x^k, где x — переменный показатель в основании степени, a — любое число в степени.

Область определения степенной функции, всегда имеет непосредственную зависимость, от значений показателя степени.

Рассмотрим основные моменты:

Если k — неотрицательное  целое число, то областью определения  данной функции является  множество любых, обязательно, действительных чисел: (-∞, +∞).

Когда  степенной показатель, является не целое число, то функция имеет следующий вид  D(f) = [0, +∞).

Когда k — отрицательное целое число, то область определения функции представляет собой (-∞, 0) ∪ (0, +∞).

Для остальных действительных отрицательных, a область определения степенной функции — числовой промежуток (0, +∞).

Если k равно нулю, то функция определена для всех чисел, кроме нуля. Так как ноль нельзя возвести в степень, а любое другое число в нулевой степени равно 1.

То есть, при k = 0, y =x0 = 1, на заданной области  определения (-∞, 0) ∪ (0, +∞).

Область определения показательной функции

Показательная функция записывается как: y=k^x

где значение x — показатель степени;

k — число, которое обязательно больше нуля и не равно единице.

Область определения показательной функции — это множество значений R.

Основные примеры показательных функций:

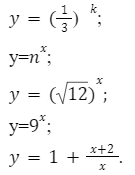
Область определения, для этих функций, записывается следующим образом: (−∞, +∞).

Область определения логарифмической функции

Логарифмическая функция выражается как: y=log n^k

Где значение n, имеет значение больше нуля и не менее единицы. Область определения логарифма и логарифмической функции — это  множество положительных значений и действительных чисел.

Рассмотрим на примере, характер решения задачи данной функции.

Пример №1

y=ln x, определить область определения натурального логарифма. D(y)=(0;+).

На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.

[y=ln x=frac{1}{x}]

Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.

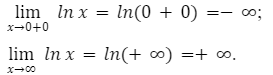
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.

Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.

Ответ: множество всех действительных чисел, это и есть область значений функции ln.

Область определения и множество значений функций косинус, синус, тангенс, котангенс

Множество значений всех действительных чисел, будет являться областью определения функций синус и косинус, и записываться следующим образом.

Функции являются ограниченными, как сверху, так и снизу.

y = sin x и y = cos x

Промежуток их действия сводится к неравенству -1 ≤ y ≤ 1

Областью определения функции тангенс tg x, является выражение [x neq frac{pi}{2}+pi k, k in z].

Областью определения функции y = сtg x  является множество чисел [x neq frac{pi}{2}, k in z].

На нижеприведенных примерах подробно расписано решение задач, при определении области функции, при заданных промежутках значений.

Пример №1

Определить область значения функции sin x

Данный вид функции относится к категории периодической. Ее период равняется 2π  

Определяем множество значений на следующем отрезке: (0;2π).

Пример №2

Необходимо определить область значения функции cos x.

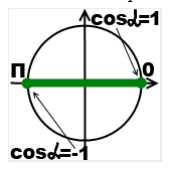
Наименьшее значение равно -1;

Минимальное значение косинуса равняется -1, потому что наименьшее значение х, на окружности стремится к этому значению и, следовательно, равняется -1.

Максимальное значение косинуса будет соответственно 1. Поскольку значение на окружности х имеет число 1.

Область значение, следовательно, будет от минус одно до плюс одного. [-1;1].

Применяем двойное неравенство и записывает следующее выражение:

[-1 leq cos 1 leq 1]

Область значения косинуса никогда не зависит от аргумента, только если сам аргумент выражен в виде сложного выражения. Где имеют место ограничения касающиеся области определения и области значения.

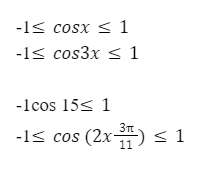
Таким образом, минимальное  значение cos x, cos (15α), cos(5-11x) и так далее, будет однозначно равняться -1;

Самым максимальным значением cos x, cos(4φ), cos(5х+3) равняется 1.

Область значений функции y=cos x — также промежуток [-1;1].

Область значения квадрата косинуса, будет промежуток от нуля до единицы [0;1]. Потому что число в четной степени, является не отрицательным.

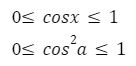
Аналогичным образом находим область значений модуля косинуса — промежуток [0;1]

[0 leq(cos alpha) leq 1]

Пример №3

y = tgx на определенном интервале [left(-frac{pi}{2} ; frac{pi}{1}right)].

Решение:

Из правил алгебры, известно, что производная тангенса имеет положительное значение. Соответственно функция будет иметь возрастающую характеристику.

Далее необходимо определить поведение функции, в заданных пределах.

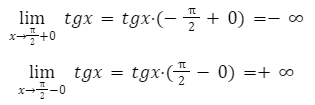
Выполнив решение, мы получаем рост значений от минус до плюс бесконечности. Решение будет сводится к следующему: множество решение заданной функции, будет множество всех действий функции.

Пример №4

[y=(arcsin x)=frac{1}{sqrt{1-x^{2}}}] на определенном интервале (-1;1).

Решение:

Для всех значений x производная будет положительной, в пределах от -1;1

Следовательно, область значения арксинуса равняется:

[
E=(arcsin x)=-frac{pi}{2} ; frac{pi}{2}
]

Пример №5

Разберем функцию 2sinx2-4, где значение х меньше либо равно значению 3. Необходимо вычислить область значений.

[frac{1}{x-3}] , где x > 3

Функция является для всех значений x определенной.

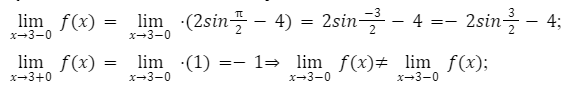
Наблюдаем недопустимый вид при значении аргумента − 3.

При приближении к данному аргументу функция стремится к [-2 sin frac{3}{2}-4]. При стремлении x к − 3 с правой стороны значения будут стремиться к − 1.

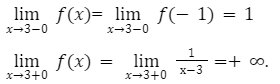
Наблюдается разрыв в точке 3. Когда функция стремится к данному разрыву ее числовые значения приближаются к -1. Минус бесконечность будет наблюдаться при стремлении к такой точке, но только с правой стороны.

Из этого следует вся область значений данной функции разбивается на три интервала. (-;−3], (−3 ;3], (3;+)(-;-3], (-3; 3], (3;+).

Первый интервал имеет функцию, следующего вида [y=2 sin frac{3}{2}-4]. Так как синус должен быть, меньше либо равен 1, или больше либо равен -1. Получаем следующие выражения:

[-1 leq sin frac{3}{2} leq 1] из этого следует [-2 leq 2 sin frac{3}{2} leq 2 Rightarrow-6 leq 2 sin frac{3}{2}-4 leq-2]

На промежутке -∞;-3, функция имеет следующие значения [-6;-2].

Функция y=-1, получается на полуинтервале (−3;3]. Следовательно, все значения будут сводится на данном интервале к одному числу, а именно -1.

Проанализируем второй промежуток (3;-+∞). Так как функция [y=frac{1}{x-3}] меньше нуля, она будет убывающей [y=frac{-1}{(x-) 2}<0]. Промежуток ее убывания будет от плюс бесконечности до нуля, однако значение ноль она не достигнет.

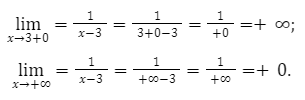
Если значение x больше значения 3, то большинство множеств функции будет в промежутке от нуля до +∞.

f(x)=-6;-2-1]∪(0;+∞).

Таблица областей определения функций

Составим таблицу, где покажем взаимосвязь области определения функции и самой функции.

Способы задания функции

Аналитический способ в виде формулы. К примеру:

y = x⁴-5x³+6x² ;

y = x²-3x³+6x² ;

y = x³-2x²+6x².

Таблица из множеств значений (x; y).

Графическим способом. Два значения (x; y) изображаются на координатной плоскости

Методы определения области значения функции

• определение значений сложных аргументов функции;
• способ оценки;
• использование свойств непрерывности и монотонности функции;
• применение производной значений;
• использование максимального и минимального значения функции;
• построение графика;
• вводные параметры;
• обратная функция и ее особенности.

Функции подразделяются на две категории:

• четные.
• нечетные

Области определения основных элементарных функций

Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.

На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x^y и другие.

А области их определения изучаем, как свойства.

Определения области значения функции x

На примерах рассмотрим, как определить области значений функции.

Первоначально, необходимо определить значения непрерывной функции y=f(x).

Известно, что функция непрерывная и достигает своих максимальных max f(x) и минимальных min f(x) значений, на разных периодах. Из этого следует отрезок, где находятся значения исходной функции. Тогда решение состоит в нахождении точек максимума и минимума.

Пример №1

Необходимо вычислить область значений уравнения

y = x⁴-5x³+6x² на отрезке [1;4 ][1;4].

Для решения задачи необходимо произвести следующие действия:

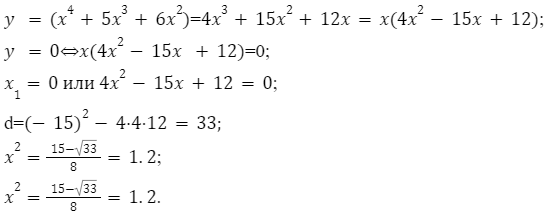
Следующим шагом будет определение значений функции в конечной и начальной точках.

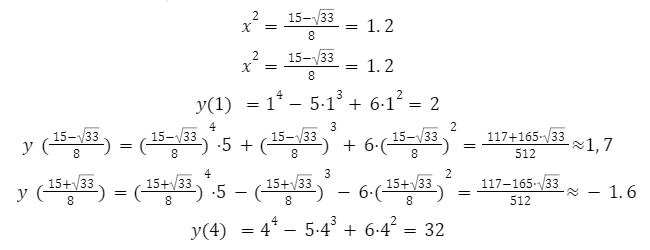
Ответ: [left(frac{117-165 cdot sqrt{33}}{512} ; 32right)].

Пример №2

Необходимо вычислить область значений уравнения

y = x⁴-7x³+5x² на отрезке [1;4] [1;4]

Для решения задачи необходимо произвести следующие действия:

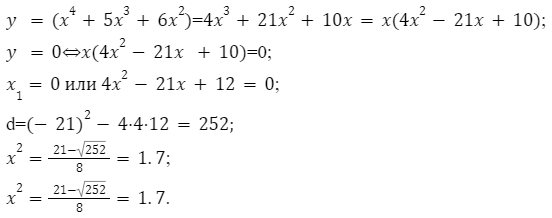
Следующим шагом будет определение значений функции в конечной и начальной точках.

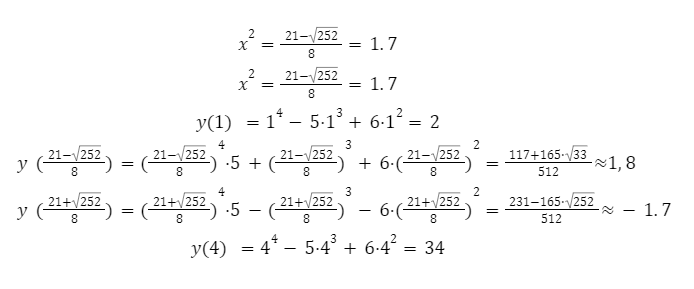
Ответ: [left(frac{231-165 cdot sqrt{33}}{512} ; 34right)].

Пример №3

На этом примере подробно рассмотрим, как вычисляются значения непрерывной функции y= f(x), в определенных промежутках.

Для этого, первоначально вычислим:

• наименьшее и наибольшее значение;
• определим промежуток возрастания и убывания функции;
• односторонние пределы;
• предел бесконечности.

Решение:

Для решения возьмем функцию [y=frac{1}{x^{2}-4}] и вычислим область значений на промежутке (-2;2).

Находим наименьшее и наибольшее значение функции на заданном отрезке.

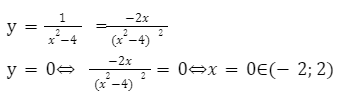
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.

А именно: [y=frac{1}{0^{2}-4}=-frac{1}{4}];

[-frac{1}{4}] — будет являться наибольшим значение заданной функции.

Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+2).

В алгебре иными словами эти значения называют односторонними пределами.

Решение выглядит следующим образом.

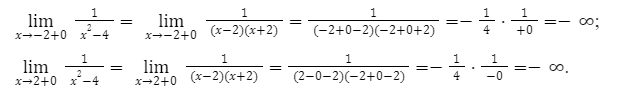
В конечном итоге мы получаем, что в пределах от -2 до 0, функции будут возрастать от -∞ до [-frac{1}{4}]. Если аргумент меняется, от 0 до то наоборот будет убывать к -∞.

Следовательно, необходимое множество значений будет на интервале -∞ до [-frac{1}{4}].

Ответ: [left(infty-frac{1}{4}right)].

Пример №4

Для решения возьмем функцию [y frac{1}{x^{2}-6}] и вычислим область значений на промежутке (-2;3).

Находим наименьшее и наибольшее значение функции на заданном отрезке.

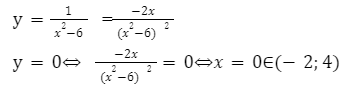
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.

А именно: [y(0)=frac{1}{0^{2}-6}=-frac{1}{6}];

[-frac{1}{6}] — будет являться наибольшим значение заданной функции.

Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+4).

В алгебре иными словами эти значения называют односторонними пределами.

Решение выглядит следующим образом.

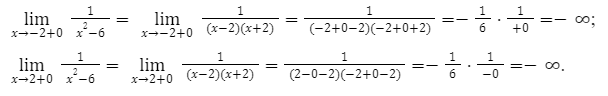
В конечном итоге мы получаем, что в пределах от -2 до 0, функции будут возрастать от -∞ до [-frac{1}{6}]. Если аргумент меняется, от 0 до то наоборот будет убывать к -∞.

Следовательно, необходимое множество значений будет на интервале -∞ до[-frac{1}{6}].

Ответ: (-∞ [-frac{1}{6}]).

Область определения функции y

Пример №1

Данная функция имеет определенное значение, только при положительных значениях. D(y) = (0;+).

Производная будет иметь следующий вид: [y=(ln x)=frac{1}{x}].

Так как функция имеет положительное значение, то всем промежутке будет наблюдаться ее возрастание. От -∞ до +∞.

Поэтому область значения — это множество всех натуральных значений.

Пример №2

У функции [y=frac{9}{z^{2}-1}];

Если значение z имеет положительное значение, то функция будет считаться определенной.

Вычислим наибольшее и наименьшее значение, а также промежутки возрастания и убывания.

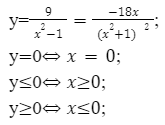
Если значение x будет больше, либо равным 0, то функция будет убывать. 

Если значение x будет меньше либо равным нулю, функция будет возрастать.

Затем рассмотрим поведение функции и ее значения на бесконечной прямой.

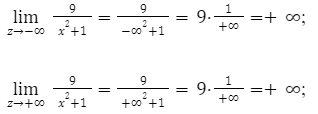
Вывод: если аргумент изменяется от -∞ до 0, тогда значение функции увеличиваются от 0 до 9. Когда значения аргумента меняются от 0 до+∞, значения функции будут уменьшаться от 9 до 0.

Пример №3

Определить область значений [y=frac{x}{x-2}];

По правилам математики. знаменатель не может равняться нулю. Поэтому: D(y)=(-∞;2)(+∞;2).

Определим множества на первом отрезке (-∞;2). На этом отрезке функция будет убывающей и значение отрицательным.

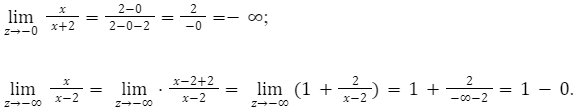
Функция асимметрично начнет приближаться к 1, когда аргумент будет изменяться к минус бесконечности.

Определим множества на втором отрезке (+∞;2). На этом отрезке функция будет также убывающей.

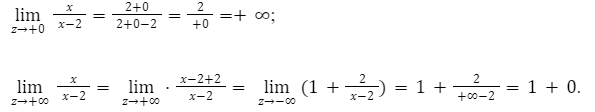
Вывод: E(y) = (∞;1)∪(1;∞).

Пример №4

Вычислить область значений функции [y=frac{2}{sqrt{2 x-1}}+3]

[y=2 cdot(2 x-1)^{-frac{1}{2}}+3]

Функцию и получаем следующий вид уравнения: [y=x^{-frac{1}{2}}];

Промежуток  значений будет следующим: (0;+∞);

[(2 x-1)^{-frac{1}{2}}>0]

В таком случае: [(2 x-1)^{-frac{1}{2}}>0 Rightarrow 2 cdot(2 x-1)^{-frac{1}{2}}>0 Rightarrow 2 cdot(2 x-1)^{-frac{1}{2}}+3>3]

Значит, E(y) = (3;+∞).

Пример №5

Определить область значений [y=frac{x}{x-2}];

По правилам математики. знаменатель не может равняться нулю. Поэтому: D(y)=(-∞;2)(+∞;2).

Определим множества на первом отрезке от минус бесконечности до двух (-∞;2). На этом отрезке функция будет убывающей и значение отрицательным.

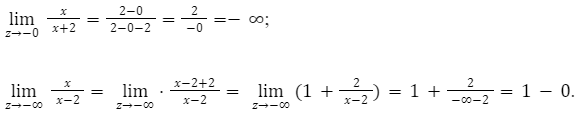
Функция ассиметрично начнет приближаться к 1, когда аргумент будет изменяться к минус бесконечности.

Определим множества на втором отрезке (+∞;2). На этом отрезке функция будет также убывающей

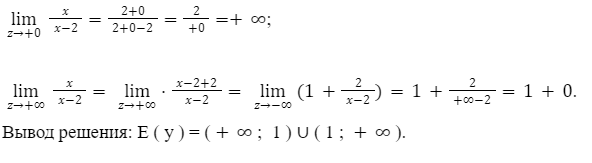
Вывод решения: E(y) = (+∞;1)∪(1;+∞).

Подводя итоги рассмотренного изученного материала стоит отметить следующие моменты:

Для вычисления и определения области значения функции, нужно обязательно знать основные правила математики.

Всегда помнить, что на ноль делить, ни в коем случае нельзя, это недопустимое действие. Число, из которого необходимо вычислить корень числа, также должно быть положительным.

Все основные законы определения области значения, очень удобно сводить в таблицу и пользоваться ею в процессе обучения.

Понятие функции является одним из основных в математике. Оно вводится следующим образом.

Пусть заданы два множества (X) и (Y). Если каждому элементу (x) из множества (X) поставлен в соответствие элемент (y=f(x)) множества (Y), то говорят, что на множестве (X) задана функция (f). При этом элемент (x) называется независимой переменной, а элемент (y) − зависимой переменной. В случае, когда (x и  y) являются действительными числами, функцию (y=f(x)) можно представить в виде графика в декартовой системе координат (Oxy).

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, то есть по оси абсцисс откладываются значения переменной (x), а по оси ординат откладываются значения переменной (y).

Область определения функции (D(y)) – это множество всех допустимых значений аргумента (x), при которых выражение, стоящее в правой части уравнения функции (y=f(x)), имеет смысл. Другими словами, это область допустимых значений выражения (f(x)).

Чтобы по графику функции (y=f(x)) найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений (x), на которых существует график функции.

Пример 1. Найти область определения функции: (y=sqrt{4x-x^3}).

Решение: Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством (4x-x^3ge0 Leftrightarrow x^3-4xle0 Rightarrow x(x-2)(x+2)le0).

Решая это неравенство с помощью метода интервалов, получим: (xin (-infty; -] cup [0;2]).

Ответ: (xin (-infty; -] cup [0;2]).

Множество значений функции (E(y)) – это множество всех значений, которые может принимать зависимая переменная (y).

Чтобы по графику функции (y=f(x)) найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений (y), на которых существует график функции.

Пример 2. Найти множество значений функции: (y = x^2 + 6x + 8).

Решение: Поскольку (y=x^2+6x+8=x^2+6x+9-1=(x+3)^2-1ge-1) и для каждого числа (yge-1) существуют решения уравнения (x^2 + 6x + 8 = y), определяемые формулой (x_{1,2}=-3pm sqrt{y+1}), то множеством значений функции (  y = x^2 + 6x + 8) будет множество ([-1;+infty)).

Ответ: (yin [-1;+infty)).

Обратная функция

Пусть задана функция (y=f(x)). Чтобы найти обратную для нее функцию, надо из уравнения (y=f(x)) выразить переменную (x) через (y) и затем поменять переменные местами. Обратную функцию часто обозначают в виде (y=f^{−1}(x)). Исходная и обратная функции симметричны относительно прямой (y=x).

Чтобы для данной функции (y = f(x)) найти обратную, надо:

1. В соотношении (y = f(x)) заменить (x) на (y), а (y) на (x):  (x = f(y)).
2. В полученном выражении (x=f(y)) выразить (y) через ( x).

Например, (y=3x-8: x=3y-8 Rightarrow 3y=x+8 Rightarrow y=frac{x+8}3).

Свойства взаимно обратных функций

Тождества. Пусть (f) и (g) – взаимно обратные функции. Это означает, что равенства (y = f(x)) и (x = g(y)) равносильны. Подставим одно из этих равенств в другое. Получим два тождества: (f(g(y)) = y) и (g(f(x)) = x).

Область определения. Пусть (f) и (g) – взаимно обратные функции. Область определения функции (f) совпадает с областью значений функции (g), и наоборот, область значений функции (f) совпадает с областью определения функции (g).

Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное верно и для убывающих функций.

Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой (y = x).