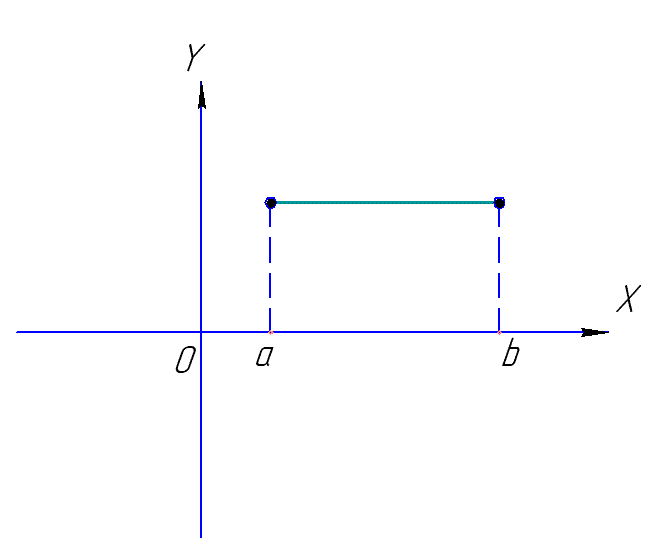
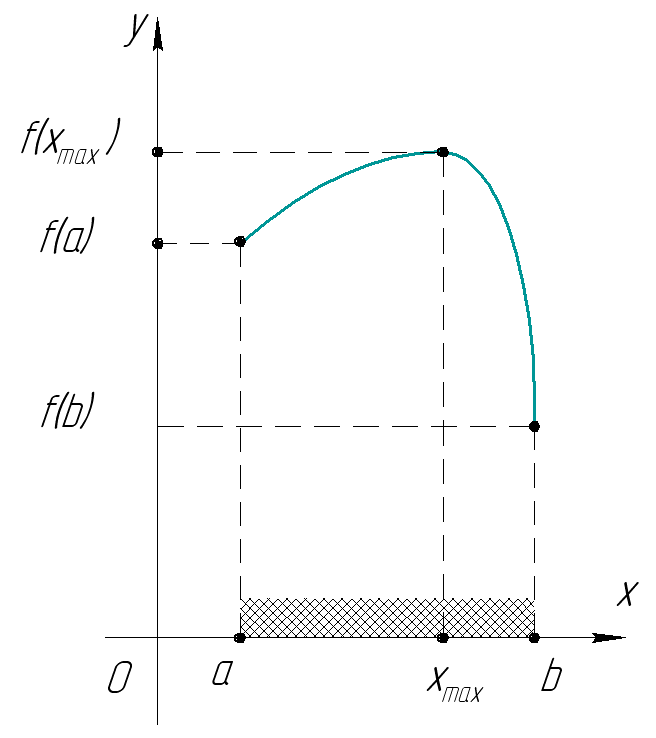
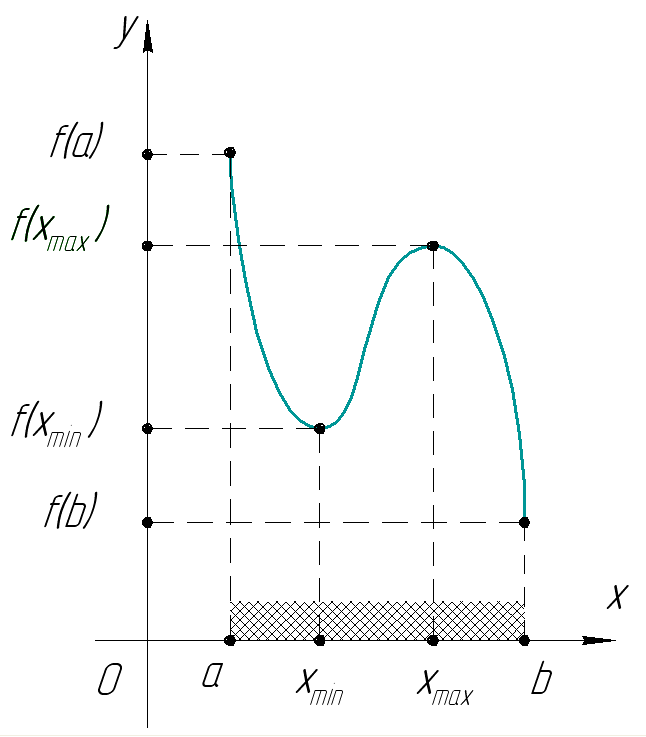
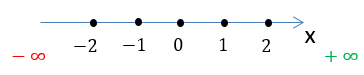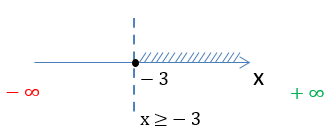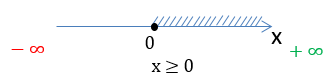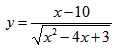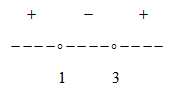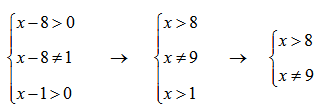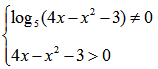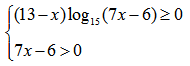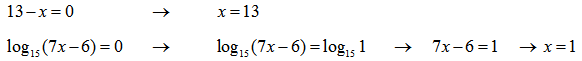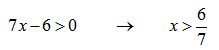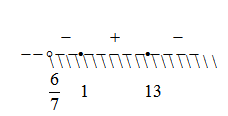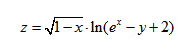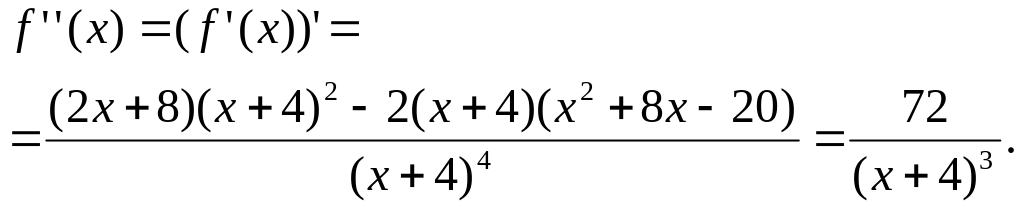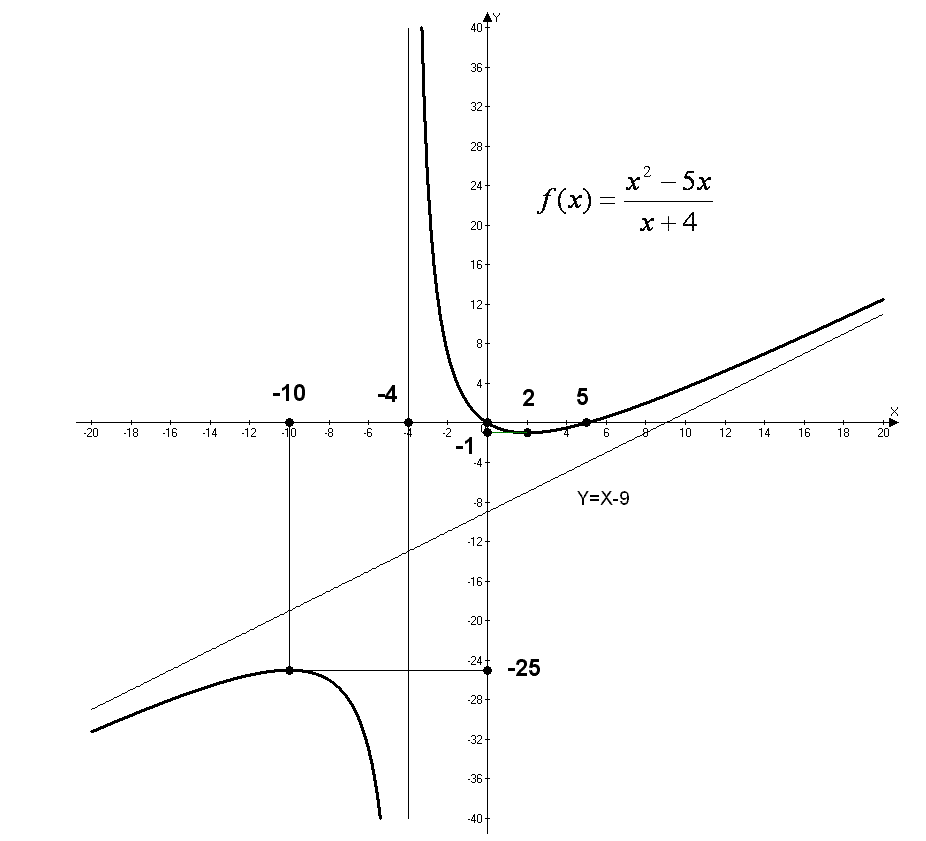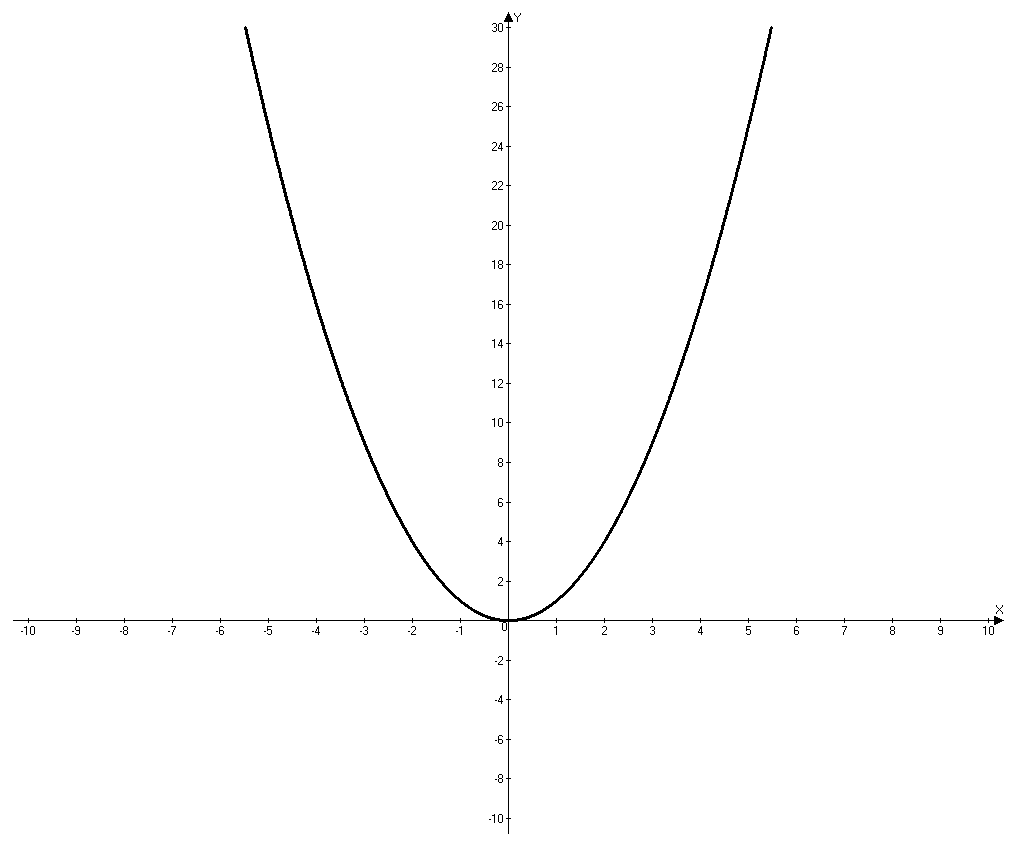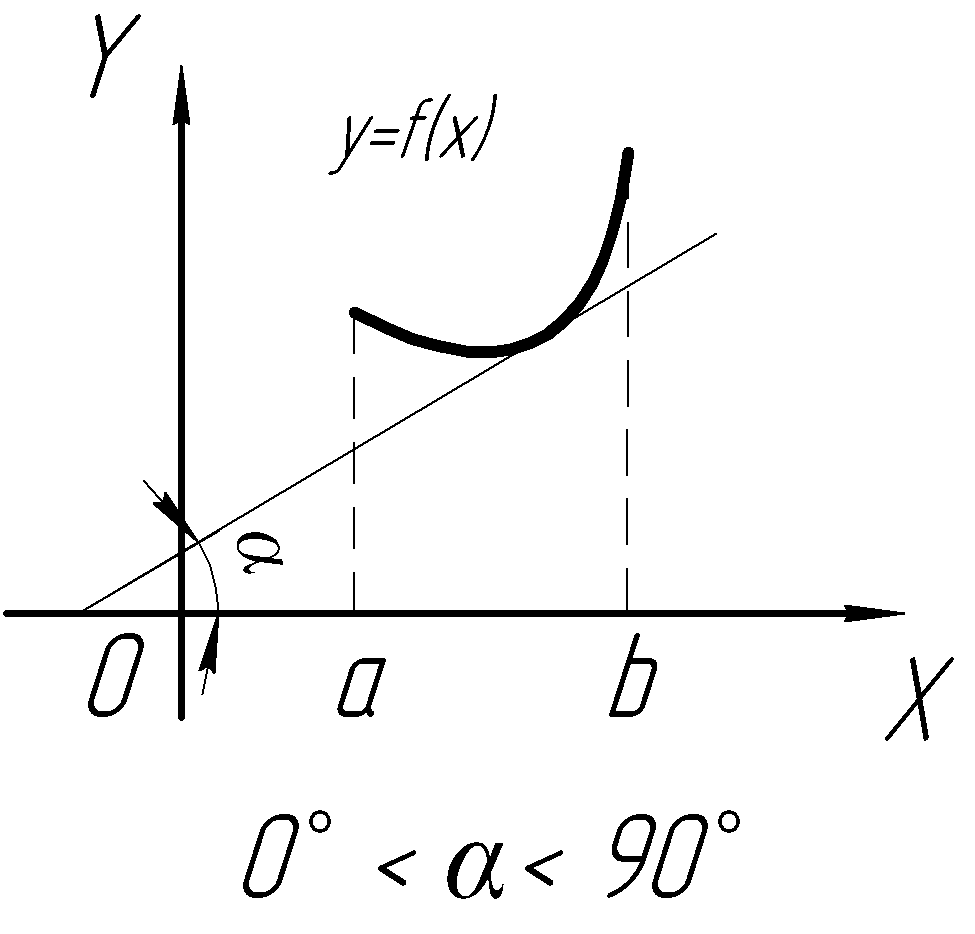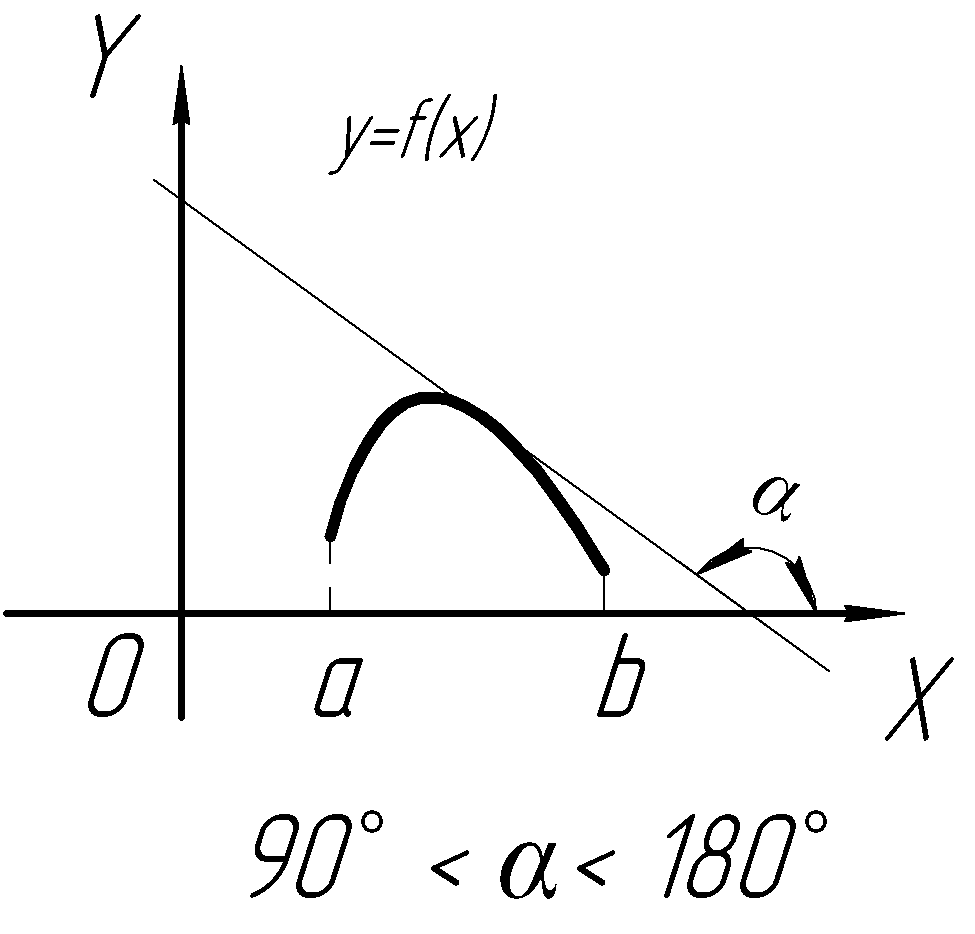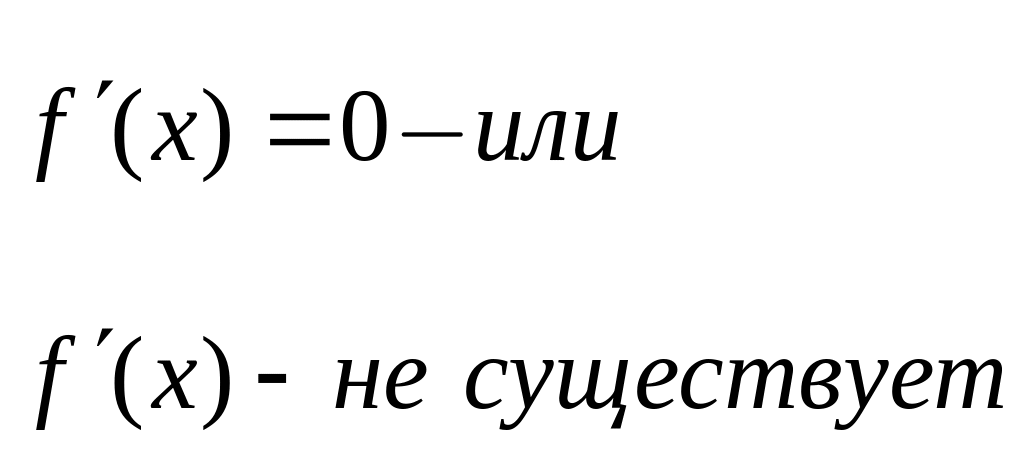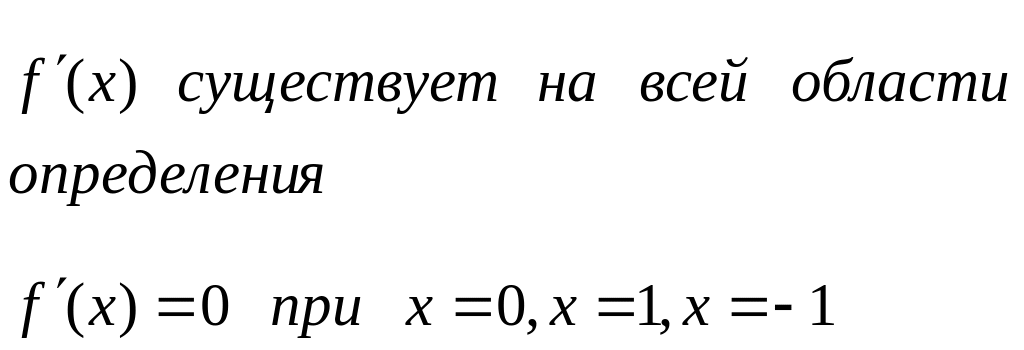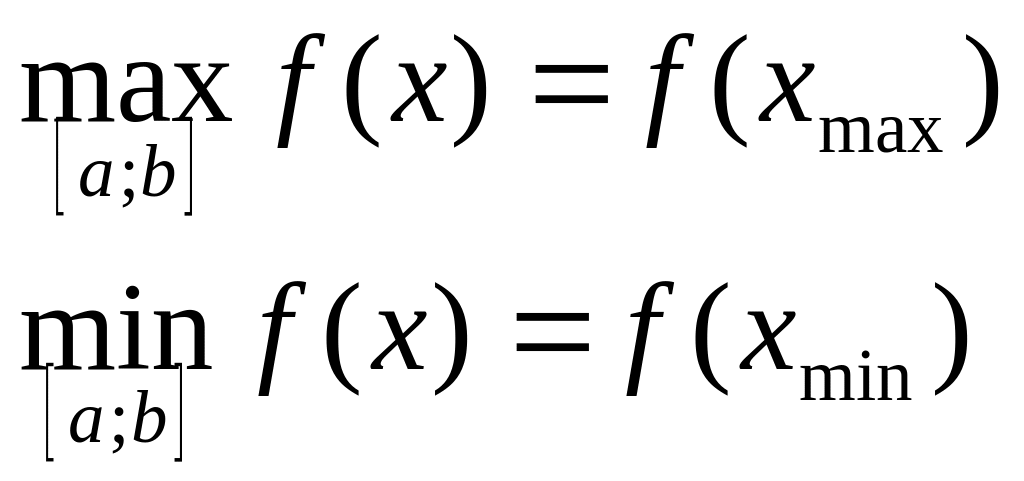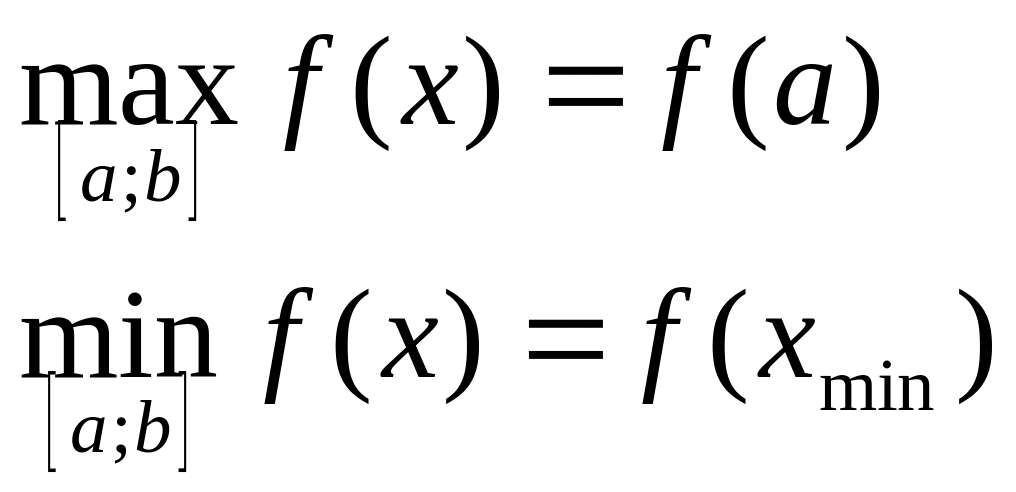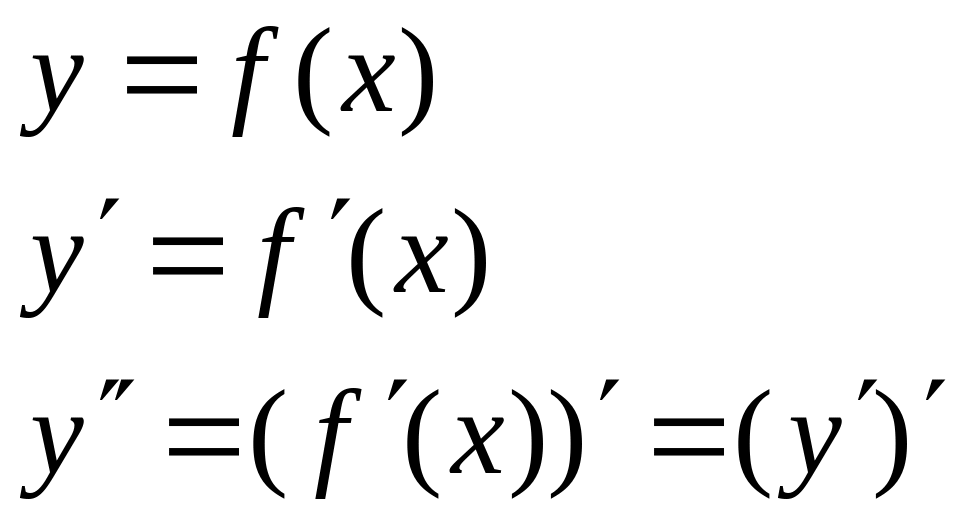Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
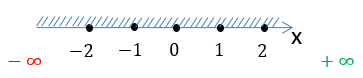
Запишем результат по правилам записи неравенств.
D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
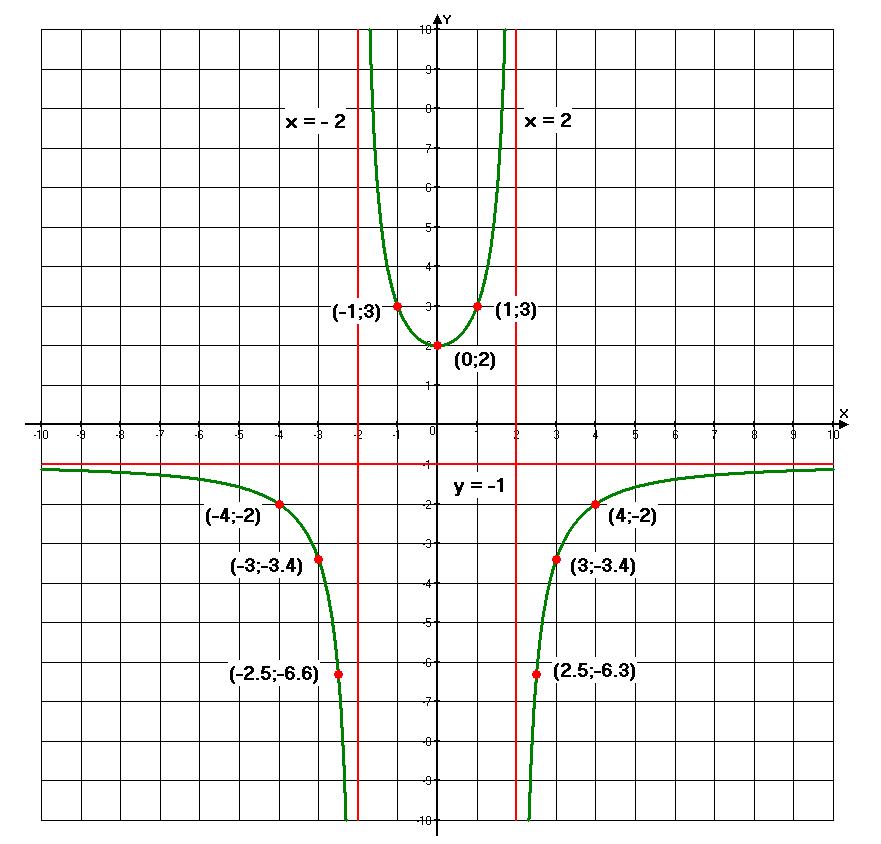
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
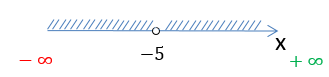
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».
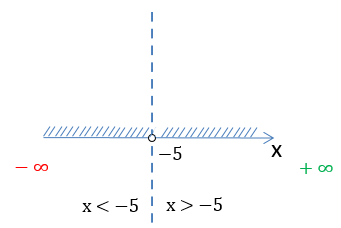
x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
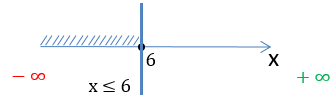
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
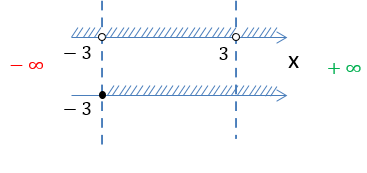
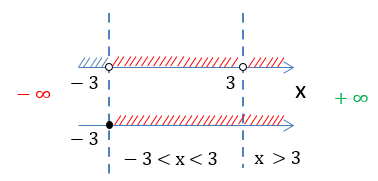
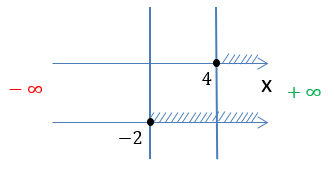
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
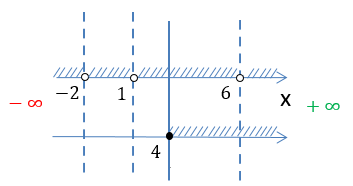
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции
0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Числовая функция с областью определения D – это соответствие значений переменной x некоторому числу y, которое находится в зависимых отношениях с x.
Используя это определение, охарактеризуем нужное нам понятие более четко:
Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Теперь рассмотрим, как правильно обозначать ее на письме. Ранее мы договорились, что для записи самих функций будем использовать маленькие латинские буквы, например, g, f и др. Чтобы указать на наличие функциональной зависимости, используется запись вида y=f(x). Таким образом, функция f представляет собой некоторое правило, согласно которому каждому значению переменной x можно поставить в соответствие значение другой переменной y, которая находится в зависимых отношениях от x.
Возьмем для примера функцию y=x2. Можно записать ее как f(x)=x2. Это функция возведения в квадрат, которая ставит в соответствие каждому значению переменной x=x0 некоторое значение y=x02. Так, если мы возьмем число 3, то функция поставит ему в соответствие 9, поскольку 32=9.
Чтобы обозначить область определения некоторой функции f, используется запись D(f). Однако нужно помнить, что у некоторых функций есть собственные обозначения, например, у тригонометрических. Поэтому в учебниках иногда встречаются записи вида D(sin) или D(arcsin). Их следует понимать как области определения синуса и арксинуса соответственно. Допустима и запись вида D(f), где f – функция синуса или арксинуса.
Если мы хотим записать, что функция f определена на множестве значений x, то используем формулировку D(f)=X. Так, для того же арксинуса запись будет выглядеть как D(arcsin)= [−1, 1] (подробнее об области определения арксинуса мы расскажем далее.)
Как найти области определения для основных элементарных функций
Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y=x2 и т.д., а их области определения указываются в качестве основных свойств.
В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.
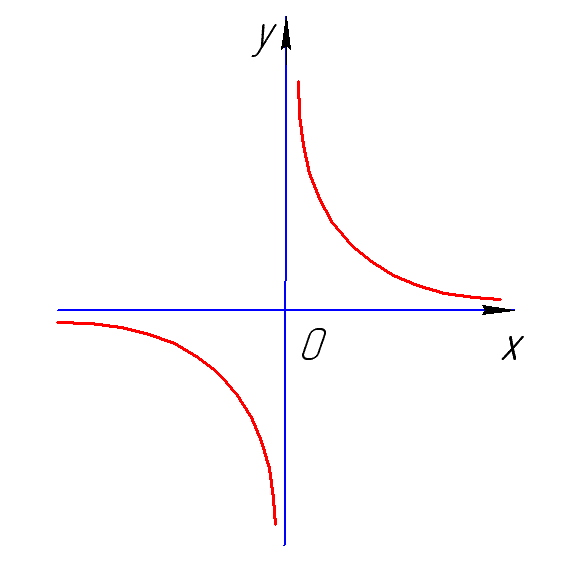
Область определения постоянной функции
Вспомним формулу, которой задается постоянная функция: y=C, или f(x)=C. Переменная C может быть любым действительным числом.
Смысл функции в том, что каждому значению аргумента будет соответствовать значение, равное C, следовательно, областью определения данной функции будет множество всех действительных чисел. Обозначим его R.
Так, если у нас есть функция y=−3 (или в другой записи f(x)=−3), то (D(f)= (−∞, +∞) или D(f)=R).
Если же мы возьмем функцию y=73, то для нее, как и для любой постоянной функции, область определения будет равна R.
Область определения функции с корнем
С помощью знака корня, или радикала, мы можем задать функцию извлечения квадратного корня y=x, либо в обобщенном виде функцию корня степени N, которую можно записать в виде формулы y=xn. В этих случаях n может быть любым натуральным числом, которое больше 1.
Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.
- Возьмем сначала случай, когда n – четное число, т.е. n=2·m, где m∈N. Тогда областью определения станет множество всех неотрицательных действительных чисел: D2·m=[0; +∞).
- Если же n представляет из себя нечетное число, которое больше 1, т.е. n=2·m+1, то областью определения будет множество всех действительных чисел: D2·m+1=(-∞; +∞).
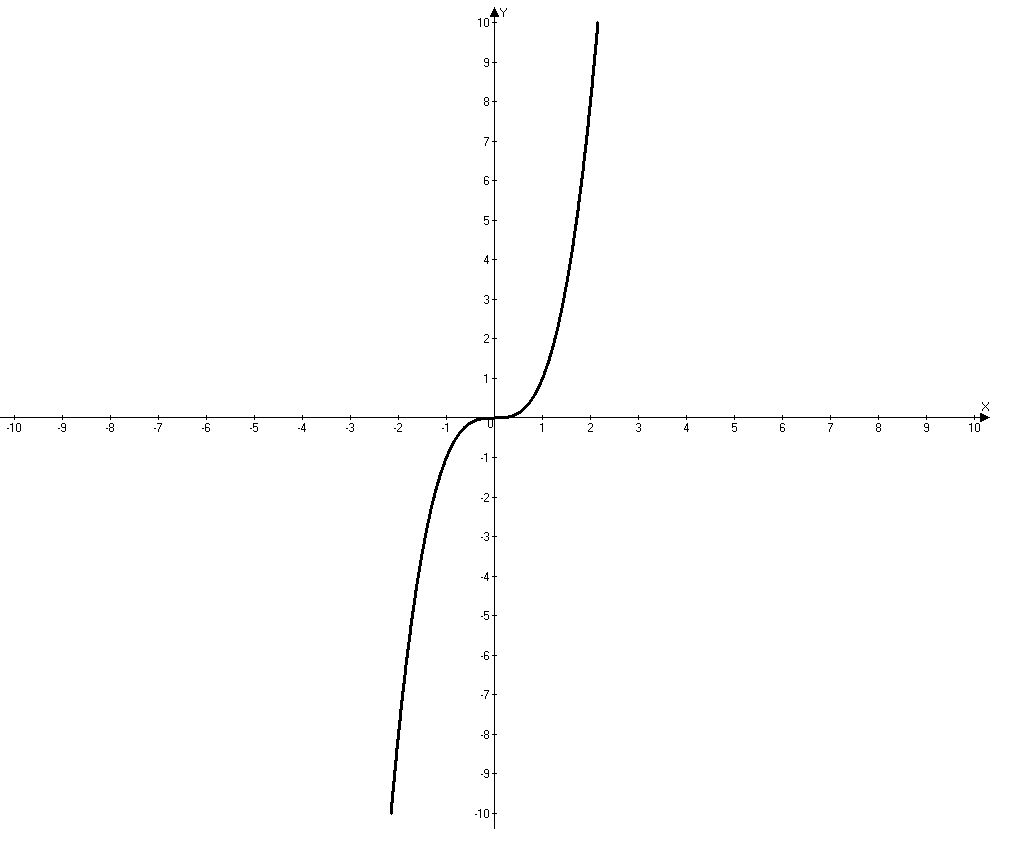
Таким образом, область определения функций с корнем y=x, y=x4, y=x6 – это числовое множество [0, +∞), а функций y=x3, y=x5, y=x7 – множество (−∞, +∞).
Область определения степенной функции
Запись степенной функции выглядит как y=xa или f(x)=xa, где x является переменной, которая лежит в основании степени, и a представляет из себя определенное число в ее показателе. Мы берем область определения степенной функции в зависимости от значения ее показателя.
Перечислим возможные варианты.
- Допустим, что a будет положительным целым числом. Тогда областью определения степенной функции будет множество действительных чисел (−∞, +∞).
- Если a является нецелым положительным числом, то D(f)= [0, +∞).
- В случае, когда a относится к целым отрицательным числам, областью определения такой функции становится множество (−∞, 0)∪(0, +∞).
- В остальных случаях, т.е. когда a будет отрицательным нецелым числом, область определения будет числовым промежутком (0, +∞).
- Если a имеет нулевое значение, то такая степенная функция будет определена для всех действительных x, кроме нулевого. Это связано с неопределенностью 00. Мы знаем, что любое число, кроме 1, при возведении в нулевую степень будет равно 1, тогда при a=0 у нас получится функция y=x0=1, область определения которой (−∞, 0) ∪ (0, +∞).
Поясним нашу мысль несколькими примерами.
Для функций y=x5, y=x12 область определения представляет собой множество всех действительных чисел R, поскольку показатели степени являются целыми положительными числами.
Для степенных функций y=x63, y=xπ, y=x74, y=x23 будут определены на интервале [0, +∞), поскольку показатели являются положительными, но не целыми числами.
3. Для функции y=x−5 с целыми отрицательными показателями областью определения будет множество (−∞, 0)∪(0, +∞).
4. Для степенных функций y=x-19, y=x-3e, y=x-98, y=x-311 область определения будет представлять из себя открытый числовой луч (0, +∞), т.к. их показателями являются нецелые отрицательные числа.
Область определения показательной функции
Такую функцию принято записывать как y=ax, причем переменная будет располагаться в показателе функции. Основанием степени здесь является число a, которое больше 0 и не равно 1.
Область определения такой функции есть множество всех действительных чисел, т.е. R.
Например, если у нас есть показательные функции y=14x, y=ex, y=13x, y=15x, то они будут определены на промежутке от минус бесконечности до плюс бесконечности.
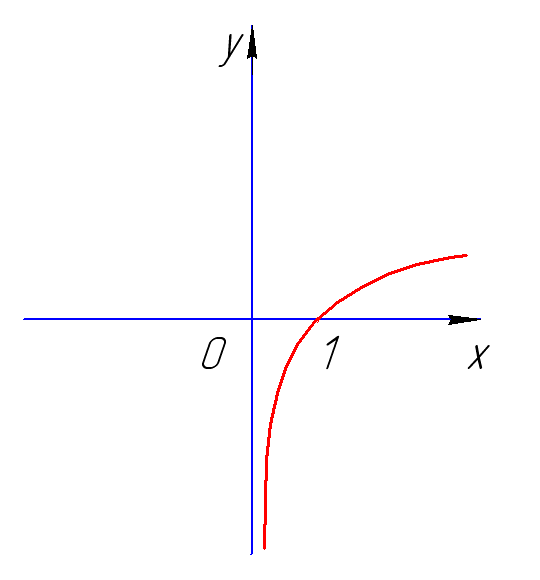
Область определения логарифмической функции
Функция логарифма задается как y=logax , где a – основание, большее 0 и не равное 1. Она определена на множестве всех положительных действительных чисел. Это можно записать как D(loga)=(0, +∞), например, D(ln)=(0, +∞) и D(lg)=(0, +∞).
Так, для логарифмических функций y=log23x, y=log3x, y=log7x, y=lnx областью определения будет множество (0, +∞).
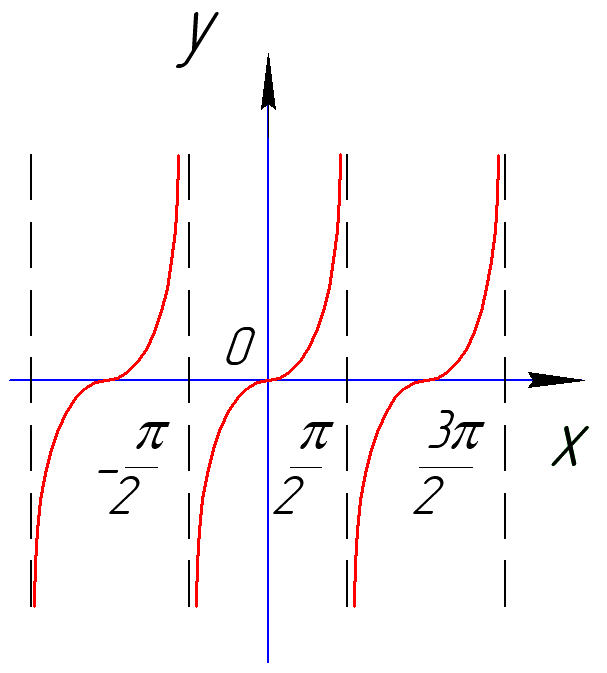
Область определения тригонометрических функций
Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.
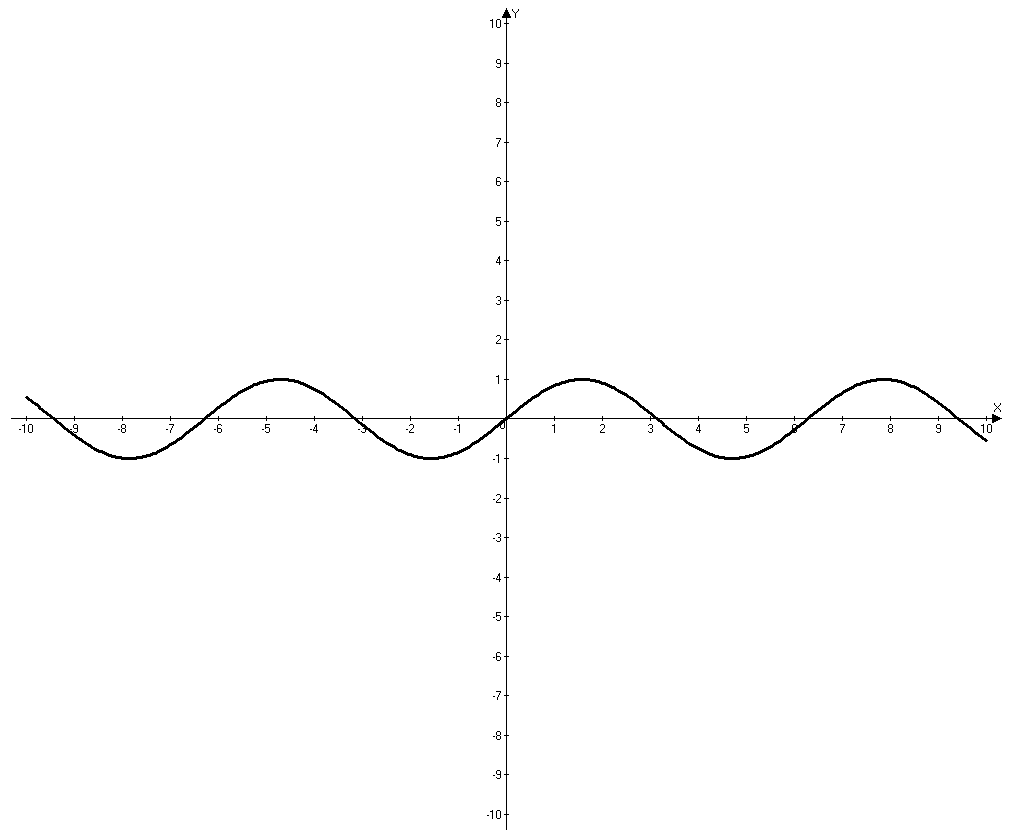
- Формула y=sin x обозначает функцию синуса (sin). Она будет определена на множестве всех действительных чисел. Можно записать, что D(sin)=R.
- Формула y=cos x означает функцию косинуса (cos). Она также будет определена на множестве всех действительных чисел, т.е. D(cos)=R.
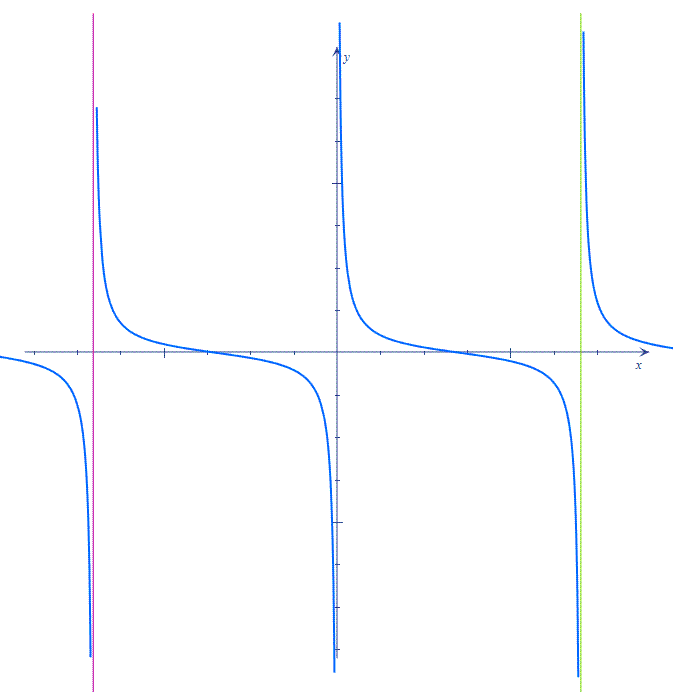
- Формула y=tg x означает функцию тангенса (tg), а y=ctg x– котангенса. Областью определения тангенса будет множество всех действительных чисел, за исключением π2+π·k, k∈Z.
Областью определения котангенса будет также множество R, за исключением π·k, k∈Z.
Иными словами, если мы знаем, что x является аргументом функций тангенса и котангенса, то нужно помнить, что данные функции определены при x∈R, x≠π2+π·k, k∈Z и x∈R, x≠π·k, k∈Z.
Область определения тригонометрических функций
К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.
- Формула y=arcsin x обозначает функцию арксинуса. Обычно она рассматривается на отрезке [−1, 1]] и обозначается arcsin. Промежуток [−1, 1] и будет нужной нам областью определения данной функции. Можно записать, что D(arcsin)=[−1, 1].
- Формула y=arccos x выражает функцию арккосинуса (обозначается arccos). Она рассматривается на том же отрезке, что и арксинус. Следовательно, областью определения данной функции является [−1, 1], т.е. D(arccos)=[−1, 1].
- Функции y=arctg x и y=arcctg x означают арктангенс и арккотангенс. Они рассматриваются на множестве всех действительных чисел, значит, областью их определения является R. Можем записать, что D(arctg)=R и D(arcctg)=R.
Области определения основных функций в табличном виде
Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.
| Области определения функций | |
| Функиця | Ее область определения |
| Постоянная y=C | R |
| Корень y=xn |
[0; +∞), если n – четное |
| Степенная y=xa |
-∞; +∞, если a>0, a∈Z |
| Показательная y=ax | R |
| Логарифмическая y=logax | 0; +∞ |
|
Тригонометрические y=sin xy=cos xy=tg xy=ctg x |
RRx∈R, x≠π2+π·k, k∈Zx∈R, x≠π·k, k∈Z |
|
Обратные тригонометрические y=arcsin xy=arccos xy=arctg xy=arcctg x |
-1; 1-1; 1RR |
Подводя итоги статьи, следует отметить, что в рамках школьного курса изучаются не только основные элементарные функции, но и их различные сочетания. Задачи такого типа встречаются очень часто. Области определения таких комбинированных функций указываются далеко не всегда. Авторы задач подразумевают, что в таких случаях областью определения функции можно считать множество таких значений аргумента, при которых она будет иметь смысл. Это позволяет нам приблизиться к ответу на вопрос, как именно вычисляется область определения функции в подобных случаях.
 |
Синонимы: область допустимых значений или сокращенно ОДЗ. Первое, с чем Вы сталкиваетесь при изучении различных функций или же при построении графиков – это область определения функции. Определение:Областью определения называется множество значений, которые может принимать x. Обозначение D(f).Как же это правило применить к заданной Вам функции? |
В математике имеется достаточно небольшое количество элементарных функций, область определения которых ограничена. Все остальные “сложные” функции – это всего лишь их сочетания и комбинации.
1. Дробная функция – ограничение на знаменатель.
2. Корень четной степени – ограничение на подкоренное выражение.
3. Логарифмы – ограничение на основание логарифма и подлогарифмическое выражение.
3. Тригонометрические tg(x) и ctg(x) – ограничение на аргумент.
Для тангенса:
Для котангенса:
4. Обратные тригонометрические функции.
| |
Пример нахождения области определения функции №1
Нахождение области определения любой линейной функции, т.е. функции первой степени:
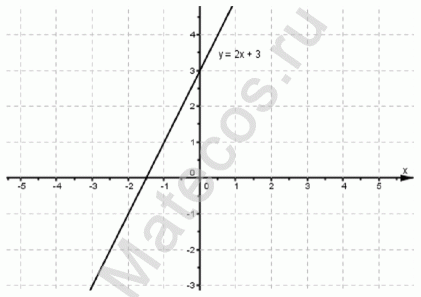
y = 2x + 3 – уравнение задает прямую на плоскости.
Посмотрим внимательно на функцию и подумаем, какие же числовые значения мы сможем подставить в уравнение вместо переменной х?
Попробуем подставить значение х=0
Так как y = 2·0 + 3 = 3 – получили числовое значение, следовательно функция существует при взятом значении переменной х=0.
Попробуем подставить значение х=10
так как y = 2·10 + 3 = 23 – функция существует при взятом значении переменной х=10 .
Попробуем подставить значение х=-10
так как y = 2·(-10) + 3 = -17 – функция существует при взятом значении переменной х=-10 .
Уравнение задает прямую линию на плоcкости, а прямая не имеет ни начала ни конца, следовательно она существует для любых значений х.
Заметим, что какие бы числовые значения мы не подставляли в заданную функцию вместо х, всегда получим числовое значение переменной y.
Следовательно, функция существует для любого значения x ∈ R или запишем так: D(f) = R
Формы записи ответа: D(f)=R или D(f)=(-∞:+∞)или x∈R или x∈(-∞:+∞)
Сделаем вывод:
Для любой функции вида y = ax + b областью определения является множество действительных чисел.
Пример нахождения области определения функции №2
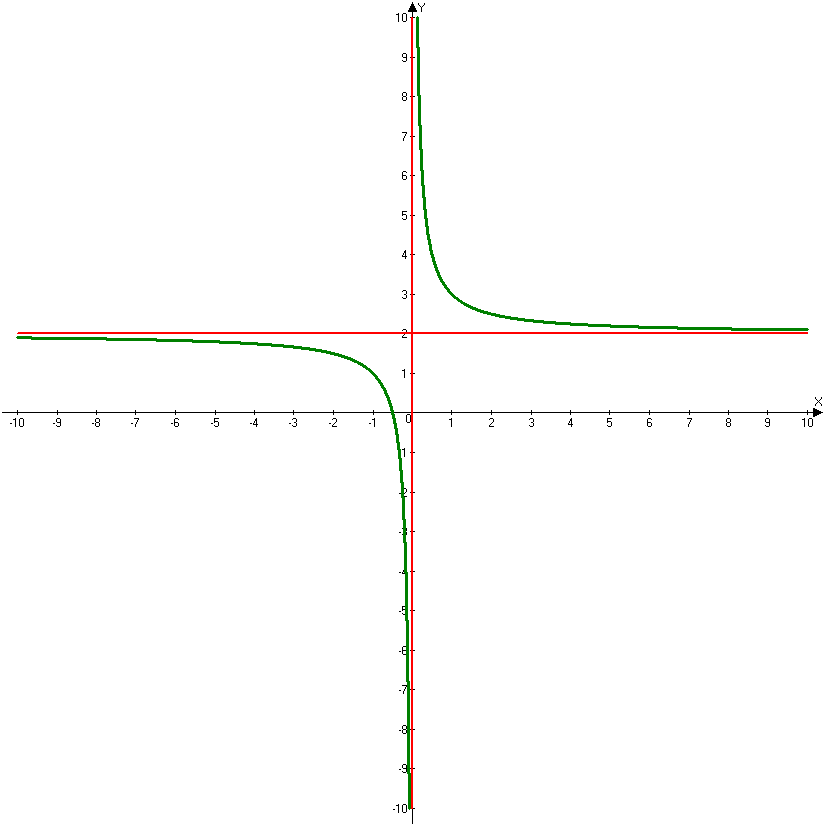
Задана функция вида:
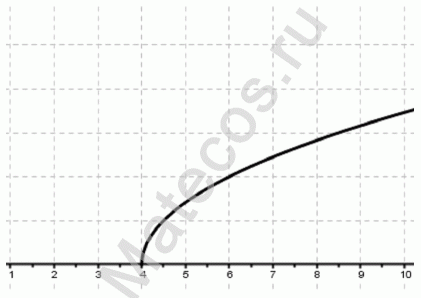
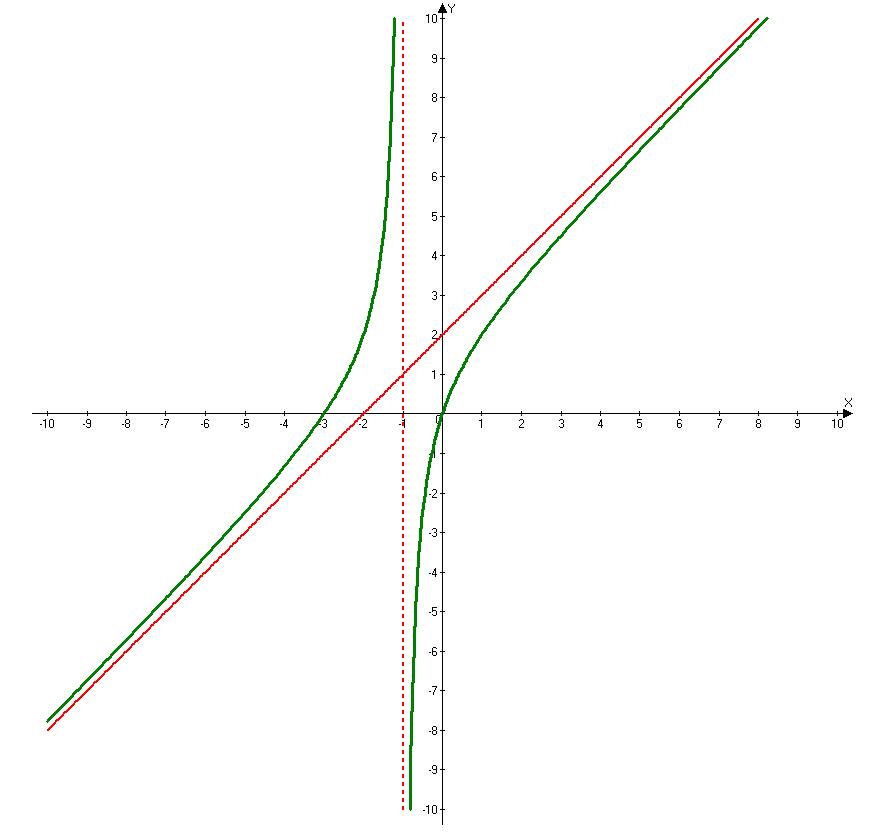
y = 10/(x + 5) – уравнение гиперболы
Имея дело с дробной функцией, вспомним, что на ноль делить нельзя. Следовательно функция будет существовать для всех значений х, которые не
обращают знаменатель в ноль. Попробуем подставить какие-либо произвольные значения х.
При х = 0 имеем y = 10/(0 + 5) = 2 – функция существует.
При х = 10 имеем y = 10/(10 + 5) = 10/15 = 2/3 – функция существует.
При х = -5 имеем y = 10/(-5 + 5) = 10/0 – функция в этой точке не существует.
Т.е. если заданная функция дробная, то необходимо знаменатель приравнять нулю и найти такую точку, в которой функция не существует.
В нашем случае:
x + 5 = 0 → x = -5 – в этой точке заданная функция не существует.
или
x + 5 ≠ 0 → x ≠ -5
Для наглядности изобразим графически:
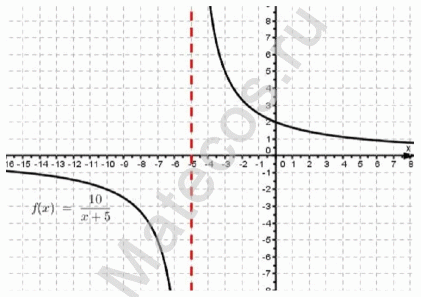
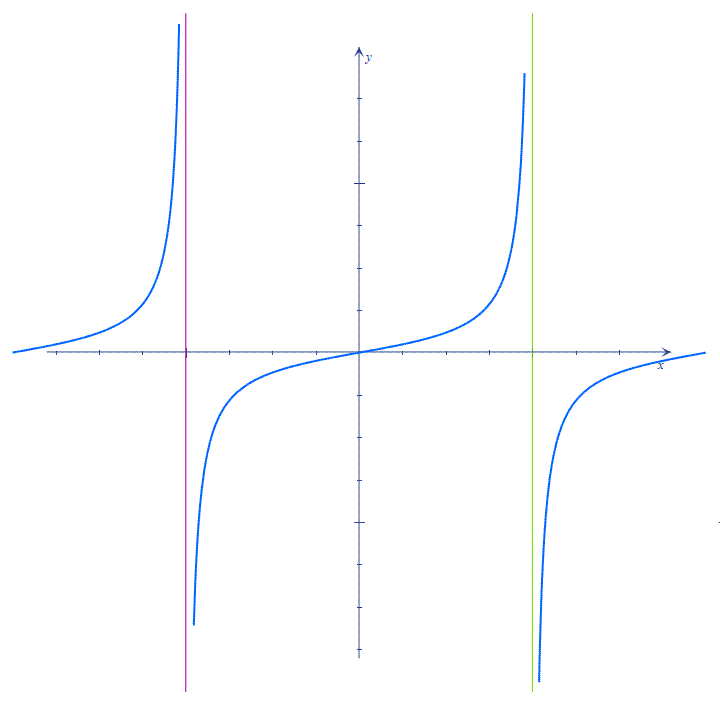
На графике также видим, что гипербола максимально близко приближается к прямой х = -5, но самого значения -5 не достигает.
Видим, что заданная функция существует во всех точках действительной оси, кроме точки x = -5
Формы записи ответа: D(f)=R{-5} или D(f)=(-∞;-5)∪ (-5;+∞) или x∈R{-5} или x∈(-∞;-5)∪(-5;+∞)
Вывод:
Если заданная функция дробная, то наличие знаменателя накладывает условие неравенства нулю знаменателя.
Пример нахождения области определения функции №3
Рассмотрим пример нахождения области определения функции с корнем четной степени:
Так как квадратный корень мы можем извлечь только из неотрицательного числа, следовательно, функция под корнем – неотрицательна.
2х – 8 ≥ 0
Решим простое неравенство:
2х – 8 ≥ 0 → 2х ≥ 8 → х ≥ 4
Заданная функция существует только при найденных значениях х ≥ 4 или D(f)=[4;+∞) или x∈[4;+∞).
На графике видим, что функция существует для найденных значений х : х ≥ 4 или D(f)=[4;+∞) или x∈[4;+∞).
При попытке подставить вместо х значения, отличные от найденных, под корнем получим отрицательное число, те в этих точках функция не существует.
Вывод:
Если заданная функция содержит квадратный корень (или корень любой четной степени), то обязательно накладывается условие неотрицательности (≥0) на подкоренное выражение. Если квадратный корень находится в знаменателе функции, у которой мы находим область определения, то на подкоренное выражение накладывается условие положительности (>0), так как знаменатель всегда должен быть отличен от нуля.
Пример нахождения области определения функции №4
Рассмотрим пример нахождения области определения функции с корнем четной степени в знаменателе:
В числителе имеем линейную функцию, область определения которой множество всех действительных чисел. (см. пример 1)
В знаменателе – квадратный корень, накладывает условие на подкоренное выражение, не забывая о том, что знаменатель всегда отличен от нуля.
Получим:
x2 – 4x + 3 > 0 → (x – 1)(x – 3) > 0
Решим строгое неравенство методом интервалов:
Видим, что функция положительна на следующих интервалах: x∈(-∞;1)∪(3;+∞)
Нашли такие значения переменной х, при которых функция существует – нашли ОДЗ функции.
Пример нахождения области определения функции №5
Рассмотрим пример нахождения области определения функции с корнем нечетной степени:
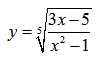
Имеем дело с корнем нечетной степени. Так как корень нечетной степени существует при любых значениях подкоренного выражения, то заданная дробная функция под корнем может принимать любые значения.
В числителе дробной функции – уравнение первой сnепени, которое существует при любых значениях переменной. Знаменатель любой дроби отличен от нуля. Следовательно, при нахождении ОДЗ заданного выражения имеем дело лишь с одним ограничением – ограничение на знаменатель дроби.
Получили ОДЗ: x∈(-∞;-1)∪(-1;1)∪(1;+∞)
Пример нахождения области определения функции №6
Рассмотрим пример нахождения области определения логарифма:
Простенький пример на область определения логарифмической функции.
Помним, что основание логарифма положительно и отлично от нуля. Подлогарифмическое выражение положительно:
Покажем на числовой прямой:
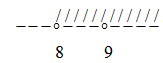
Получили ОДЗ: x∈(8;9)∪(9;+∞)
Пример нахождения области определения функции №7
Задана функция вида:
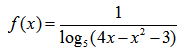
1 ограничение основывается на наложении ограничения на знаменатель дроби (отличен от нуля):
Второе ограничение — подлогарифмическое выражение положительно:
Т.е. для определения области определения заданной функции необходимо решить систему:
Необходимо решить каждое из ограничений системы по отдельности и пересечь получившиеся результаты.
Допускаю, что читатель самостоятельно может это проделать и перехожу к разбору следующего примера.
Пример нахождения области определения функции №8
Рассмотрим следующий пример:
Имеем дело с корнем четной степени, следовательно первое ограничение на подкоренное выражение:
Имеем дело с логарифмом, следовательно ограничение на подлогарифмическую функцию:
Таким образом для определения области определения исходной функции необходимо решить систему неравенств:
Каждое из неравенств решим по отдельности.
Первое неравенство будем решать методом интервалов: найдем корни каждого из выражений неравенства, вынесем их на координатную плоскость и расставим знаки неравенства в каждом из полученных интервалов.
Корни:
Второе неравенство:
Выносим на координатную прямую:
Объясню как расставлены знаки в каждом из интервалов:
Значения левее 6/7 нет смысла рассматривать, так как логарифм для этих значений не существует.
1-ый интервал: (6/7;1]
Основание логарифма больше единицы, следовательно функция возрастающая. В корне x=1 логарифм меняет свое значение с ” — ” на ” + “.
Наглядно покажу на графике:
Имеем: линейная функция (13 – x)
Пример нахождения области определения функции №9
Рассмотрим следующий пример:

Пример нахождения области определения функции №10
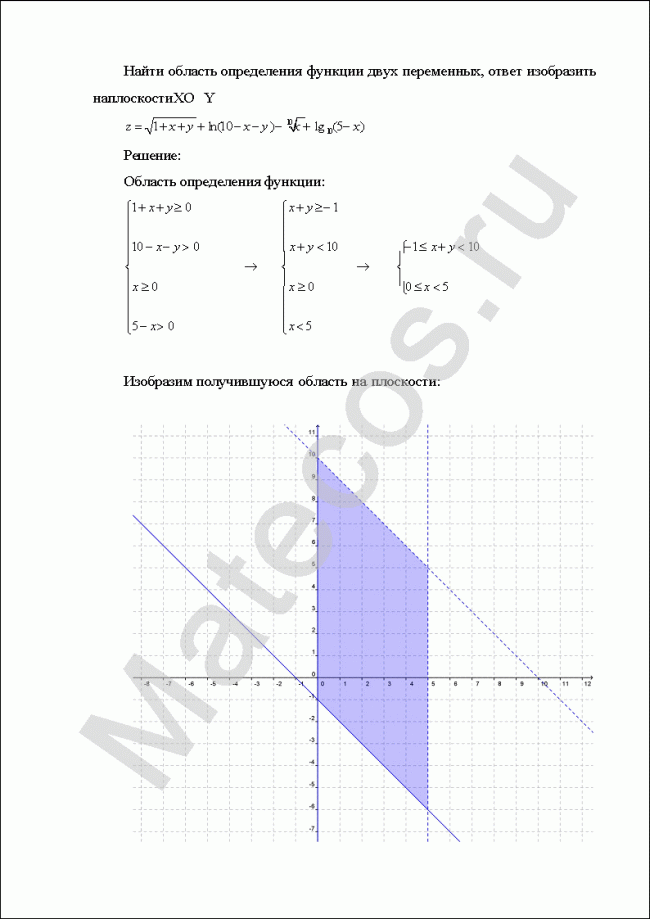
Найти область определения функции двух переменных, ответ изобразить на плоскости ХОY.
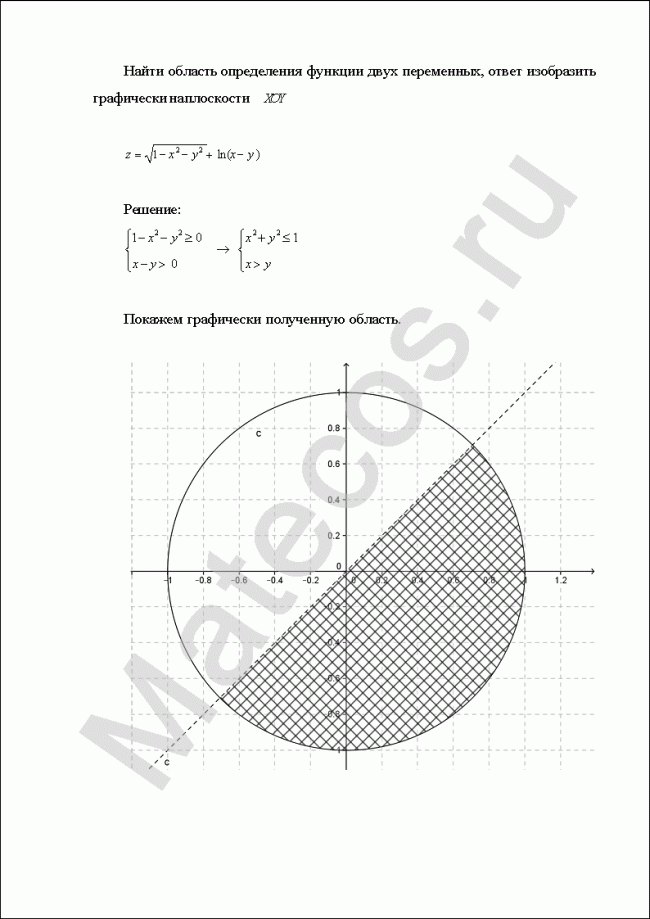
Пример нахождения области определения функции №11
Найти область определения функции двух переменных, ответ изобразить на плоскости ХОY.
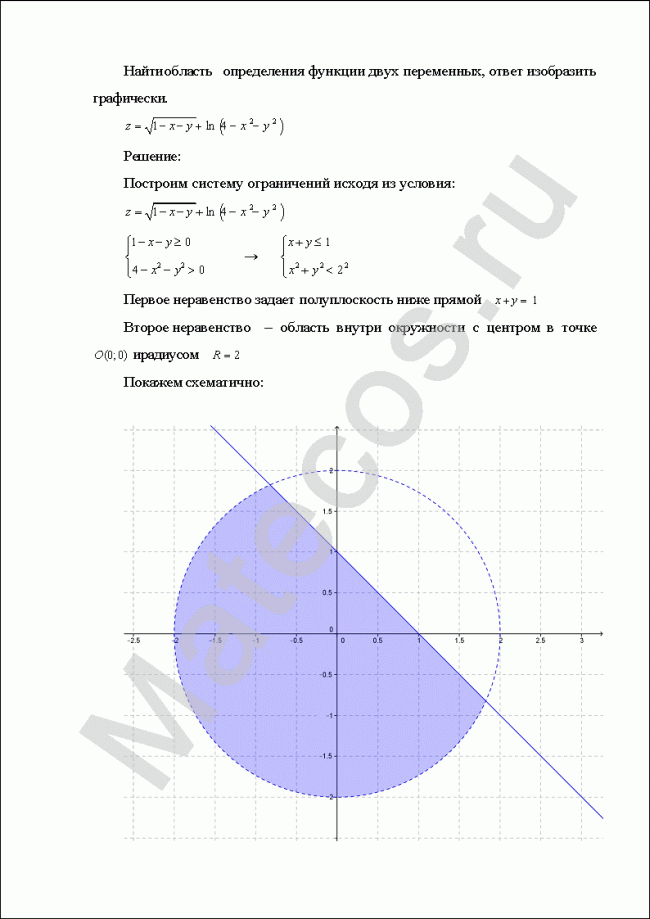
Пример нахождения области определения функции №12
Найти область определения функции двух переменных, ответ изобразить на плоскости ХОY.
Пример нахождения области определения функции №13
Найти область определения функции двух переменных, ответ изобразить на плоскости ХОY.
Все графике в этой статье были построены в Geogebra.
Подробно о построении графиков функции быстрым и удобным способом читать тут
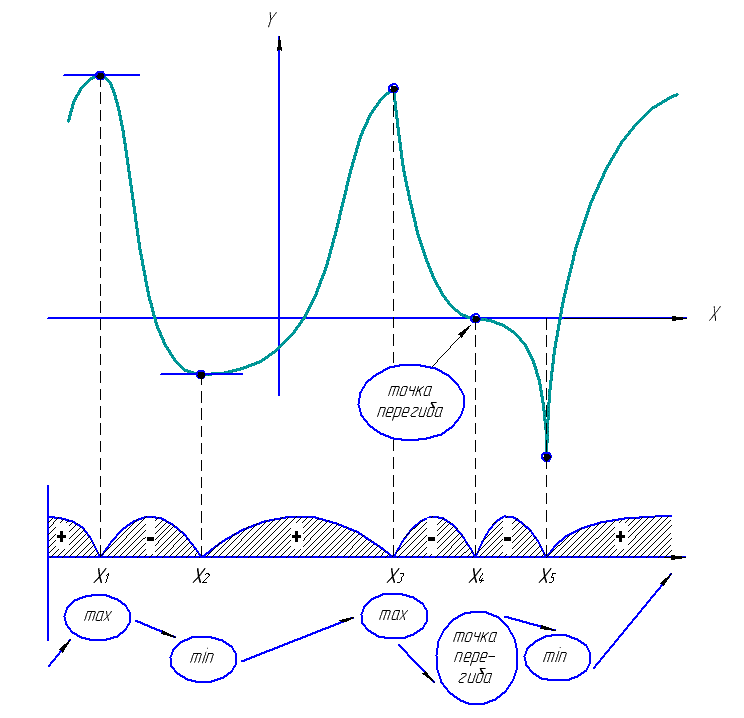
1. Область определения функции.
2. Четность, нечетность, периодичность.
3. Точки пересечения с осями координат.
4. Производная и критические точки.
5. Промежутки возрастания, убывания и
точки экстремума и значение функции в
этих точках.
6. Поведение функции на концах области
определения и асимптоты графика функции
(вертикальные, горизонтальные, и
наклонные)
7. Вторая производная и исследование
функции на выпуклость и вогнутость, и
нахождение точек перегиба.
8. Нахождение контрольных точек.
9. Построение графика по результатам
исследования.
Приложения.
Таблица
1. Как найти область определения функции.
Таблица
2. Четные и нечетные функции.
Таблица
3. Периодические функции.
Таблица
4. Применение производной к исследованию
функции.
Таблица
5. Асимптоты графика функции.
Таблица
6. Вторая производная и точки перегиба.
Примеры.
Пример
1. Исследовать
функцию
и построить график функции.
Пример
2. Исследовать
функцию
и построить график функции.
Пример
3. Исследовать
функцию
и построить график функции.
|
Схема исследования эскиза |
|||||||
|
Схема |
Пример |
||||||
|
1. Область определения функции (см. |
Область определения:
|
||||||
|
2. Четность, нечетность (табл. периодичность |
Функция ни четная, ни нечетная и не |
||||||
|
3. Точки пересечения с осями координат |
x = 0; y = 0 |
||||||
|
y = 0;
|
|||||||
|
4. Производная и критические точки |
|
||||||
|
|
|||||||
|
5. Промежутки возрастания, убывания |
|
||||||
|
6. Поведение функции на концах (табл. 5) |
П слева
При справа x
Так как
то при тогда
т.е. y |
||||||
|
7. Вторая производная и исследование |
П оскольку |
||||||
|
|
||||||
|
|
|
Как найти |
|||
|
№ |
Вид функции |
Ограничения
(f(x) существуют!) |
Формулировка |
|
1 |
|
|
Знаменатель дроби не равен нулю |
|
2 |
|
|
Под знаком корня четной степени может |
|
3 |
|
|
Под знаком логарифма может стоять |
|
4 |
(a |
|
В основании логарифма может стоять |
|
5 |
|
|
Под знаком котангенса может стоять (k – целое) |
|
6 |
|
|
Под знаком котангенса может стоять (k – целое) |
|
7 |
|
|
Под знаком арксинуса и арккосинуса |
|
8 |
|
||
|
9 |
|
||
|
а) |
x – любое число |
||
|
б) – |
|
||
|
в) – положитель-ное не целое число |
|
||
|
г) – отрицатель-ное не целое число |
|
Таблица 1
Таблица 2
|
Четные и нечетные |
|
|
Четная функция |
Нечетная функция |
|
Определение. Функция f
|
Определение. Функция f
|
|
Свойства |
Свойства |
|
График четной функции |
График нечетной функции |
|
Примеры четных функций |
Примеры нечетных функций |
|
|
|
|
|
|
Таблица 3
|
Периодические |
|||
|
Определение. |
|||
|
Свойства |
|||
|
1. Если число Т период функции f k*T |
|||
|
2. Если функция y=f(x) (A, b, k |
|||
|
3. Если функция y=f(x) |
|||
|
4. Для построения графика периодической влево и вправо |
|||
|
Примеры периодических функций |
|||
|
y=sin(x) T=2π
|
y=cos(x) T=2π
|
y=tg(x) T=π
|
y=ctg(x) T=π
|
|
y=sin(3x)
T=
|
y={x}- дробная часть х T=1
|
y=|cos(x)| T=π
|
y=3 T-любое число (Т≠0)
|
|
Практические приемы нахождения |
|||
|
1. Найти период каждой составляющей 2. Подобрать Пример: |
Таблица 4
|
Применение |
|||
|
Монотонность и постоянство функции |
|||
|
Достаточное возрастания |
Достаточное возрастания |
||
|
Если в каждой то функция ƒ(x) возрастает на |
|
Если в каждой то функция ƒ(x) убывает на |
|
|
З но возрастания Например, – возрастающая на
ее производная равна нулю. |
|||
|
Необходимое и достаточное условие |
|||
|
Функция |
|
Экстремумы (максимум и минимум) |
|
|
Точка максимума |
Точка минимума |
|
Определение Точка из области определения называется для найдется
( , т из этой окрестности выполняется
|
Определение Точка из области определения называется для найдется
– ( ) , такая, из этой окрестности выполняется
|
|
– точка максимума |
– точка минимума |
|
Точки максимума
Значения функции экстремумами |
|
|
-максимум |
-минимум |
|
Критические точки |
|
|
Определение. в |
|
|
Необходимое |
Достаточное |
|
В точках экстремума равна – точка экстремума |
Если функция непрерывна и , то – точка экстремума функции в знак меняется с «+» на «-» – точка максимума в знак меняется с «-» на «+» точка минимума |
|
Пример графика функции , ( |
|
|
|
|
|
Исследование функции на монотонность и экстремумы |
|
|
Схема |
Пример |
|
1. Найти область |
Область определения: Функция |
|
2. Найти производную |
|
|
3. Найти критические или не существует |
|
|
4. Отметить |
|
|
5. Относительно |
|
6. Записать |
возрастает при |
|
убывает |
|
|
Точки экстремума: Экстремумы: |
|
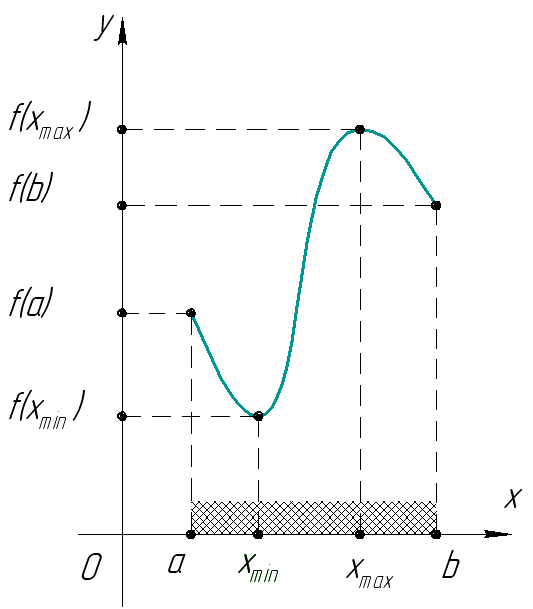
Наибольшее и наименьшее значение |
|||
|
Свойства |
|||
|
Если функция непрерывна |
|||
|
Примеры |
|||
|
|
|
|
|
|
|
|
|
|
|
Нахождение наибольшего и наименьшего непрерывной |
|||
|
Схема |
Пример Найти при |
||
|
1. Найти производную |
|
||
|
2. Найти критические ( |
|
||
|
3. Выбрать |
Заданному отрезку |
||
|
4. Вычислить |
|
||
|
5. Сравнить |
|
|
АСИМПТОТЫ ГРАФИКА ФУНКЦИИ |
||
|
Определение. к при |
||
|
Вертикальные асимптоты (х = а) |
||
|
асимптота Вертикальная |
||
|
Примеры |
||
|
|
|
|
|
О.О. При При X
|
О.О. При X
|
О.О. При (слева) y→+∞ При (справа) y→-∞ X –
|
Таблица 5.
|
Наклонные и |
|
|
1. |
|
|
Пример 1 |
Пример 2 |
|
При т.е.
– наклонная вертикальная |
При т.е.
– горизонтальная
вертикальная |
|
|
|
|
2. |
|
|
|
|
|
Для примера 1 |
Для примера 2 |
|
– наклонная |
– горизонтальная |
Таблица 6.
|
ВТОРАЯ ПРОИЗВОДНАЯ И ТОЧКИ ПЕРЕГИБА |
|
|
Понятие второй |
|
|
|
Пусть функция дифференцируема, то ее производную и (или |
|
Пример. |
|
|
Понятия |
|
|
Пусть функция определена Тогда |
|
|
|
Если в некоторой (кроме направлен |
|
|
Если в некоторой (кроме направлен |
|
|
Если точка оси абсцисс обладает тем свойством, переходит с одной стороны касательной называется точкой перегиба функции , – – точка В : кривая ниже касательной, а при |
|
Достаточные которая |
|||
|
Условие |
Условие |
||
|
Если в каждой |
|
Если в каждой график направлен |
|
|
Замечание:
Эти условия
Например, график хотя ее вторая производная |
|
||
|
Нахождение |
|||
|
Необходимое |
Достаточное |
||
|
В ее |
Если имеет и , |
||
|
Исследование на выпуклость, вогнутость и точки |
|||
|
Схема |
Пример. |
||
|
1. Найти область |
Область определения: Функция |
||
|
2. Найти вторую |
|
||
|
3. Найти внутренние или не |
|
||
|
|
|||
|
4. Отметить |
|
||
|
5. Записать |
В интервале направлен направлен Точки |
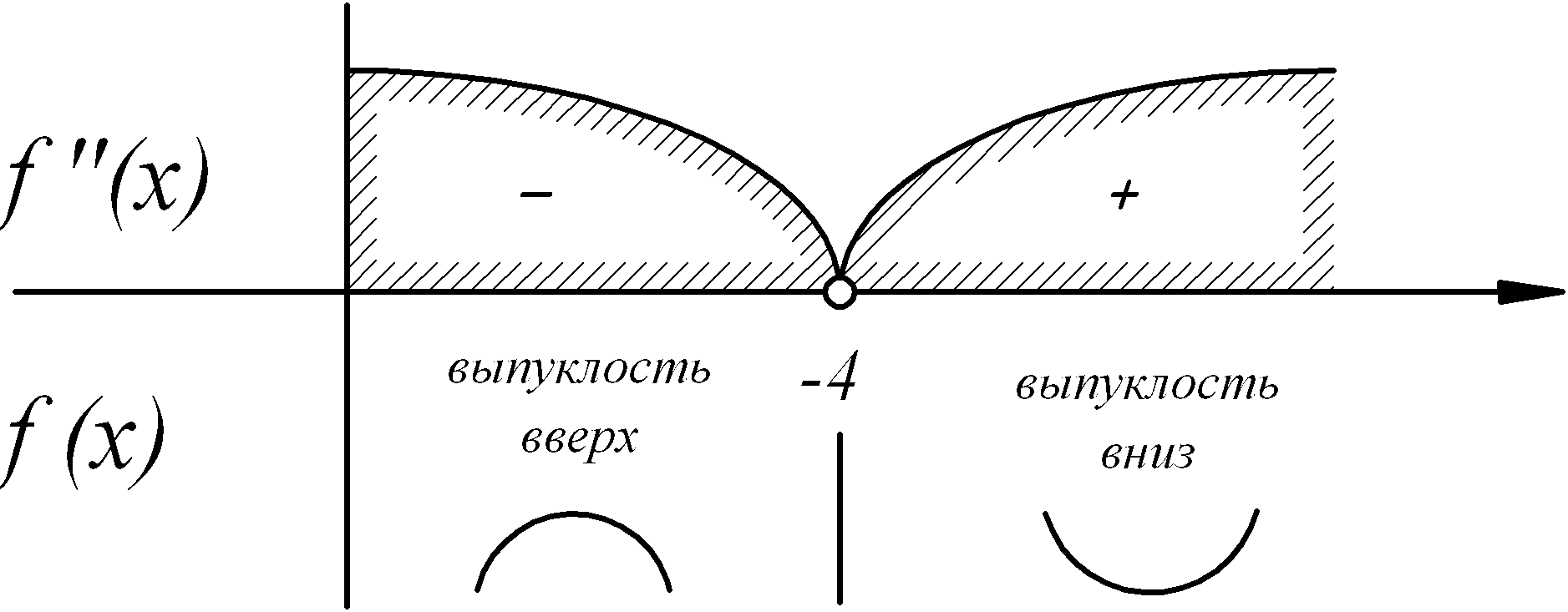
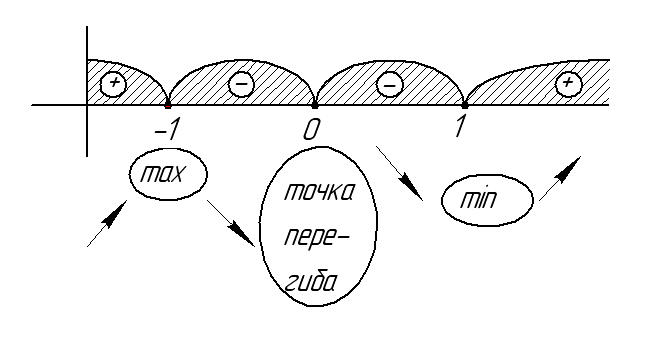
Пример 1:
Исследовать
функцию
и построить график функции.
Т.к. знаменатель
заданной функции не должен быть равен
нулю, то можем записать:
Функция определена
на трех указанных участках.
2.
Функция четная,
график функции симметричен оси OY.
Функция не
периодическая.
3. Точки пересечения с осями координат.
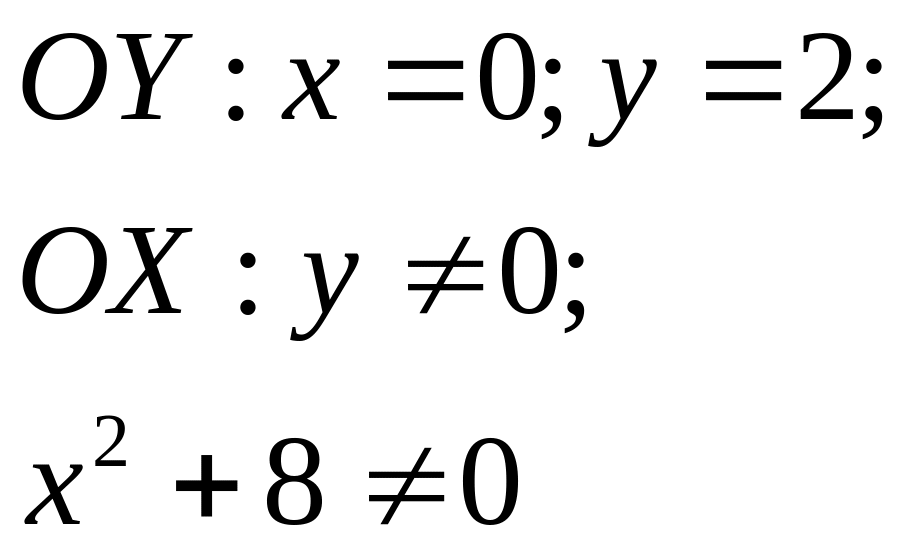
Точка пересечения
с осью OY
(0;2), точек пересечения с осью OX
нет.
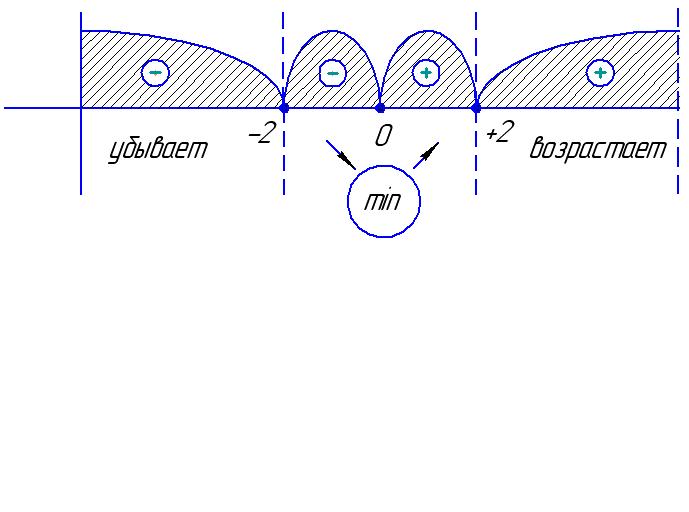
4. Производная и критические точки.

5. Промежутки
возрастания, убывания, точки экстремума.
На рисунке
представлено изменение знака первой
производной и поведение функции на
участках области определения.
Точка Х0(0;2)
– точка минимума функции.
6. Поведение
функции на концах области определения
и асимптоты.
При :
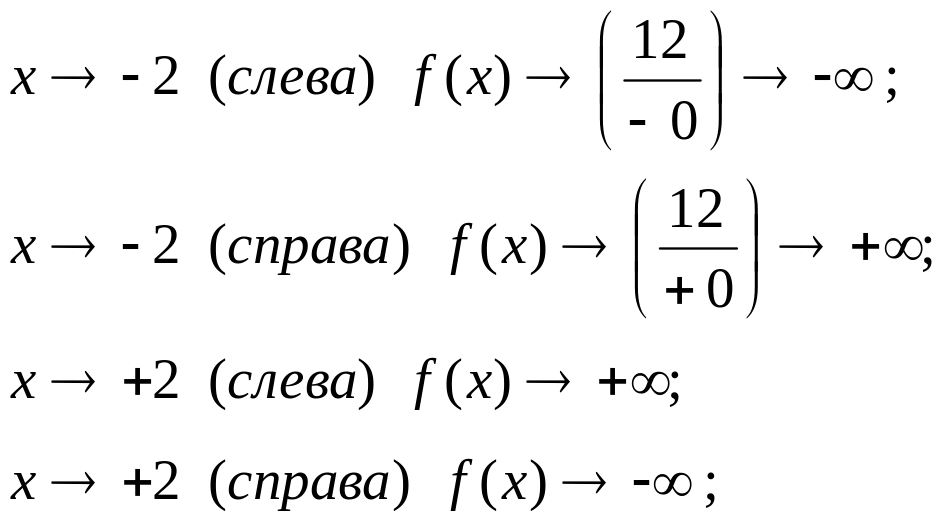
Следовательно, мы
имеем две вертикальные асимптоты
Наклонные и
горизонтальные асимптоты типа: y=kx+b
находим по формулам:

Уравнение асимптоты
примет вид: y=0*x-1=-1.
Горизонтальная
асимптота: Y=-1.
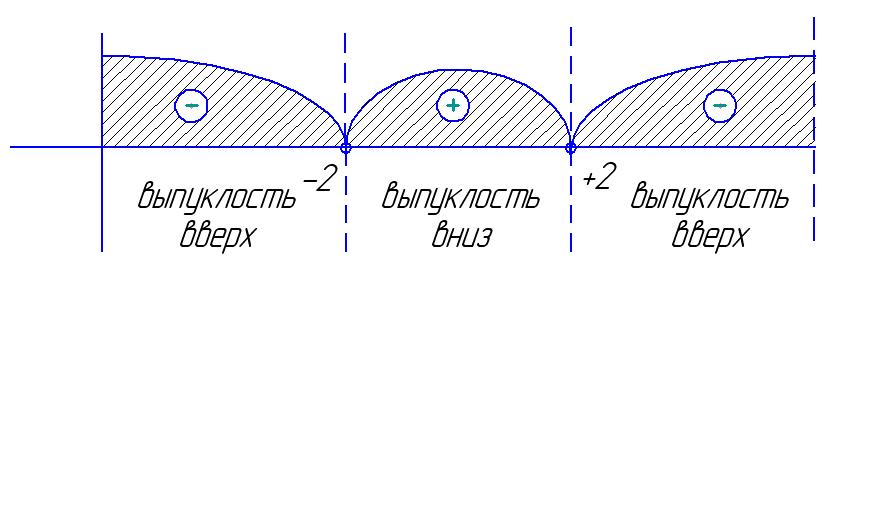
7. Вторая производная
и исследование функции на выпуклость
и вогнутость.

– не существует в
точках +2 и -2.
Знак производной
меняется в указанных точках.
На рисунке
представлено изменение знака второй
производной и поведение функции на
участках области определения.
8. Контрольные
точки.
Для более наглядного
представления поведения графика функции
определим значение функции в точках:

9. График функции
представлен на рисунке.
Красным цветом
отмечены асимптоты графика и найденные
по результатам исследования точки.
Пример 2:
Исследовать
функцию
и построить график функции.
1. Область определения функции:
Т.к. под знаком
логарифма может стоять только положительное
выражение, то можем записать следующее:
Функция определена
на указанном участке.
2.
Функция ни нечетная,
ни четная, не периодическая.
3. Точки пересечения с осями координат.
Точек пересечения
с осью OY
нет. Точка пересечения с осью ОХ: х=8.
4. Производная и критические точки.
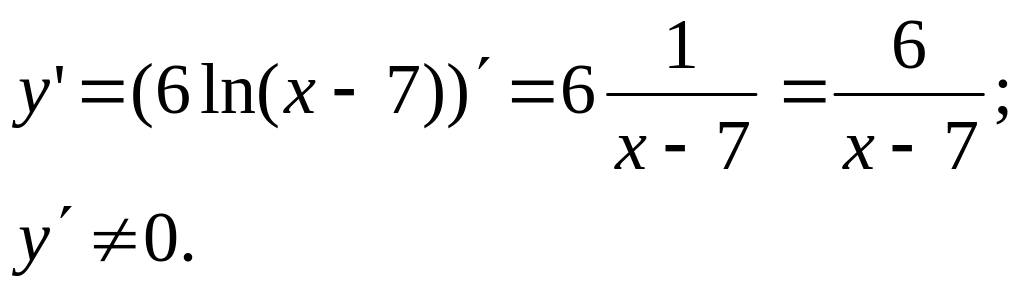
5. Промежутки
возрастания, убывания, точки экстремума.
На рисунке
представлено изменение знака первой
производной и поведение функции на
участках области определения.
точек экстремума
нет.
возрастает
на всей области определения
6. Поведение
функции на концах области определения
и асимптоты.
При :
Следовательно, мы
имеем вертикальную асимптоту
Наклонные и
горизонтальные асимптоты типа: y=kx+b
находим по формулам:

наклонных и
горизонтальных асимптот нет.
7. Вторая производная
и исследование функции на выпуклость
и вогнутость.

Вторая производная
не меняет знак на всей области определения.
выпуклость
вверх
8. Контрольные
точки.
Для более наглядного
представления поведения графика функции
определим значение функции в точках:
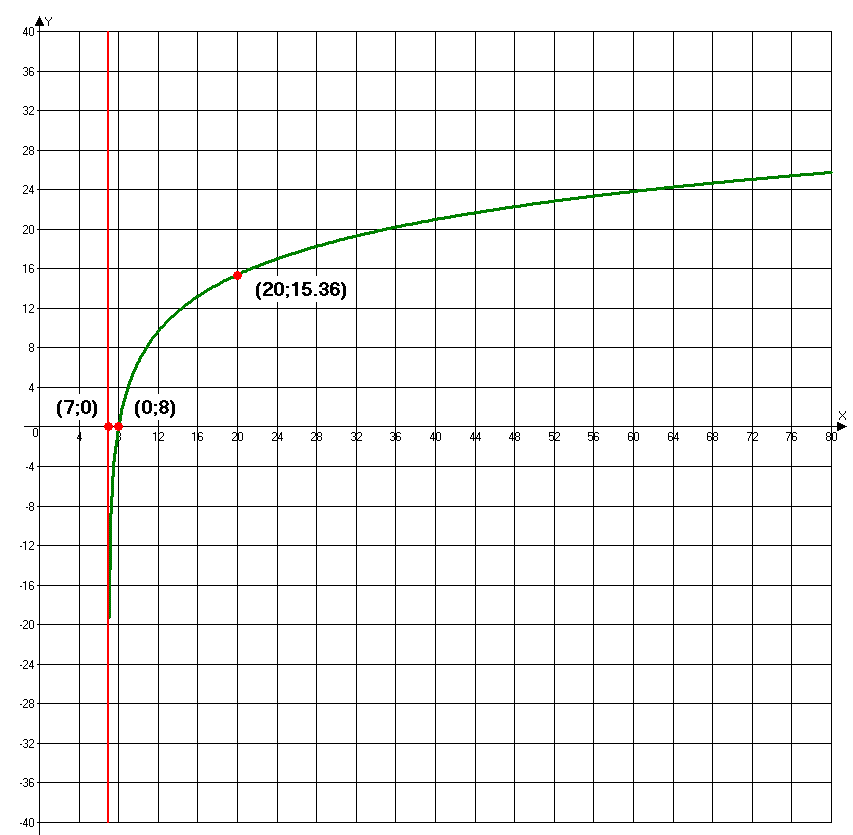
9. График функции
представлен на рисунке.
Красным цветом
отмечены асимптоты графика и найденные
по результатам исследования точи.
Пример 3:
Исследовать
функцию
и построить график функции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое функция? Представим себе машину, которая двигается по дороге из одного города в другой. Мы можем в каждый момент времени определить положение машины. То есть у нас есть множество различных моментов времени и множество точек, определяющих положение машины на дороге. При этом положение машины на дороге зависит от того, в какой момент времени мы определяем это положение. То есть одно множестве переменных величин зависит от другого множества, каждая отдельная переменная из одного множества зависит от переменной из другого множества. Зависимость одной переменной от другой называется функциональной зависимостью.
В этой статье мы рассмотрим что такое функция, дадим определения области определения функции и области ее значений, понятие графика функции.
Область определения и область значений функции
– значение функции в точке
.
Если область определения функции и область ее значений определены в множестве рациональных чисел, то функцию называют числовой.
Элементы множества еще называют значениями аргумента, а соответствующие им элементы
– значениями функции.
Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
Например, область определения функции, заданной формулой , состоит из всех чисел, кроме нуля.
Как найти область определения функции
Для того, чтобы найти область определения функции, мы должны определить – где функция будет существовать, при каких значениях аргумента. Приведем примеры:
Пример 1
Найти область определения функции
Зададимся вопросом – при каких значениях функция будет существовать? Очевидно, что функция существует, если знаменатель дроби не равен нулю. То есть
.
Для определения этого значения решим уравнение:
.
Находим, .
То есть функция не будет существовать при значении . Тогда областью определения функции (где она существует) – будут все значения
кроме 5. Через интервалы можно записать так:
.
Пример 2
Найти область определения функции .
Здесь функция определена при любых значениях аргумента. То есть D(f) – все числа.
Пример 3
Определить область определения функции
.
Выражение, стоящее под знаком квадратного корня, должно быть больше или равно нулю. Таким образом, мы можем записать:
Решим данное неравенство и получим: .
Тогда область определения функции будет интервал значений аргумента .
График функции
Графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. То есть график функции – это изображение на координатной плоскости множества пар
, связанных зависимостью
, где
.
Способы задания функции
Функция может быть задана аналитически в виде формулы , где переменная
– элемент множества значений аргумента, а переменная
– соответствующее значение функции.
Например, формула определяет некоторую функцию, где каждому значению переменной
, взятому из области определения функции, соответствует единственное значение переменной
.
Функция полностью определяется заданием множества пар
, где
принимает все значения из
, а
– соответствующие значения функции.
Однако не всякое множество точек координатной плоскости является графиком некоторой функции. Например, если мы рассмотрим следующий график, то увидим, что значению соответствуют три значения
, и, следовательно, такое соответствие не является функцией.
Для того, чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая, параллельная оси , пересекалась с указанным графиком не более чем в одной точке.
Монотонность функции
Функция называется возрастающей на данном числовом промежутке
, если большему значению аргумента
соответствует большее значение функции
. Это значит, что для любых
и
из промежутка
, таких, что
, выполнено неравенство
.
Функция называется убывающей на данном числовом промежутке
, если большему значению аргумента
соответствует меньшее значение функции
. Это значит, что для любых
и
из промежутка
, таких, что
, выполнено неравенство
.
Функция только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.
О монотонности функции можно судить по ее графику. Например, функция, график которой изображен ниже является монотонно возрастающей на всей числовой оси.
А вот эта функция является монотонно убывающей.
А теперь рассмотрим вот такой график функции – на ней функция убывает на промежутке и возрастает на промежутке
.
Пример
Докажите, что функция, заданная формулой , где
, возрастающая.
Решение: Пусть , где
и
. Тогда
.
Поскольку , то и
, а, значит,
. То есть большему значению аргумента соответствует большее значение функции, таким образом, функция
возрастающая на промежутке
.
Четные и нечетные функции
Пример 1
Доказать, что функция не является ни четной, ни нечетной.
Доказательство.
Областью определения данной функции является вся числовая прямая, то есть условие 1 выполнено. Проверяем условие 2.
Чтобы доказать, что функция не является четной, нам нужно доказать, что условие 2 для четной функции не выполняется, то есть что
.
Пусть , тогда
. Проверяем:
, а
, таким образом
. Функция не является четной. Одновременно, не выполняется и второе условие для нечетной функции, мы получили, что:
. То есть функция не является нечетной.
Пример 2
Определите четность или нечетность функции:
Решение: область определения данной функции – вся числовая ось, кроме точки (на ноль делить нельзя). Найдем
.
Получим: . Вынесем минус за скобки:
.
Отсюда выходит, что , то есть выполняется условие для нечетной функции. А, значит, функция
– нечетная функция.
Пример 3
Определить четность или нечетность функции:
.
Решение: Первое условие о симметричности области определения функции выполняется, так как область определения функции . Переменим знак
аргумента функции и упростим:
.
Получается, что . То есть функция
– четная.
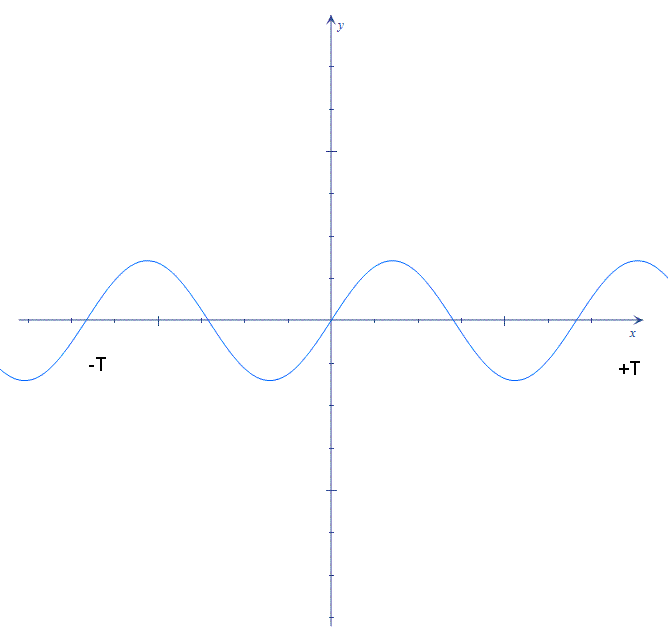
Периодические функции
Если – период функции, то
, где
,
, также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривается наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это обстоятельство используется при построении графиков.
Промежутки знакопостоянства и корни функции
Числовые промежутки, на которых функция сохраняет свой знак (то есть остается положительной или отрицательной), называются промежутками знакопостоянства функции.
О промежутках знакопостоянства функции можно сделать вывод, посмотрев на график функции. Например, возьмем график функции . Здесь
при
,
при
. В первом случае график расположен выше оси
, во втором – ниже ее.
Итак, мы с вами изучили что такое функция, определили когда функция является четной, а когда нечетной, способы задания функции, область определения функции и область ее значений. А также дали понятие периодической функции и корней функции. Выяснили, что называется промежутками знакопостоянства функции. Привели примеры.
Читайте еще похожие статьи: