Как найти область определения обратной тригонометрической функции

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика XVIII века Карла Шерфера и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: ${displaystyle sin ^{-1},{frac {1}{sin }},}$ но они не прижились^[1].
Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin⁻¹, cos⁻¹ для арксинуса, арккосинуса и т. п.^[2], — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.

Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, означает множество углов $left ( frac{pi}{6}, frac{5 pi}{6}, frac{13 pi}{6}, frac{17 pi}{6} dots ~ (30^circ, 150^circ, 390^circ, 510^circ dots) right )$ , синус которых равен 1/2 . Из множества значений каждой аркфункции выделяют её главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.

В общем случае при условии все решения уравнения можно представить в виде $x=(-1)^{n}arcsin alpha +pi n,~n=0,pm 1,pm 2,dots ~.$ ^[3]

Основное соотношение[править | править код]

$arcsin x+arccos x={frac {pi }{2}}$

$operatorname {arctg},x+operatorname {arcctg},x={frac {pi }{2}}$

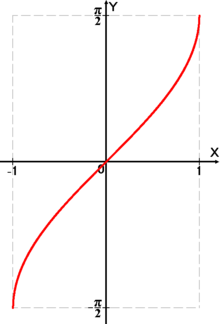
Функция arcsin[править | править код]

График функции

Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого ${displaystyle sin y=x,quad -{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}},quad |x|leqslant 1.}$

Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.

Свойства функции arcsin[править | править код]

Получение функции arcsin[править | править код]

Дана функция y=sin x . На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок , на котором функция y=sin x строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции y=sin x относительно прямой y=x .

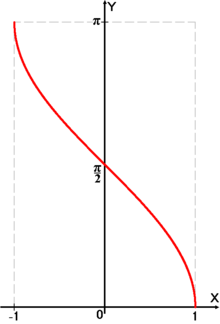
Функция arccos[править | править код]

График функции

Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого

Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.

Свойства функции arccos[править | править код]

Получение функции arccos[править | править код]

Дана функция y=cos x . На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок [0;pi ] , на котором функция y=cos x строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на отрезке [0;pi ] существует обратная функция , график которой симметричен графику функции y=cos x относительно прямой y=x .

Функция arctg[править | править код]

График функции

Аркта́нгенсом числа x называется такое значение угла выраженное в радианах, для которого ${displaystyle operatorname {tg} y=x,quad -{frac {pi }{2}}<y<{frac {pi }{2}}.}$

Функция определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.

Свойства функции arctg[править | править код]

Получение функции arctg[править | править код]

Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал , на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой y=x .

Функция arcctg[править | править код]

График функции

Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого

Функция определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго убывающей и всюду положительной.

Свойства функции arcctg[править | править код]

Получение функции arcctg[править | править код]

Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал (0;pi ) , на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на интервале (0;pi ) существует обратная функция , график которой симметричен графику функции относительно прямой y=x .

График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, ) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы

Функция arcsec[править | править код]

График функции

Арксе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого

Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.

Свойства функции arcsec[править | править код]

Функция arccosec[править | править код]

График функции

Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого

Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей.

Свойства функции arccosec[править | править код]

Разложение в ряды[править | править код]

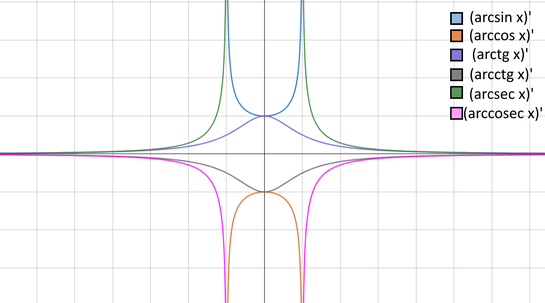
Производные от обратных тригонометрических функций[править | править код]

Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:

производные обратных тригонометрических функций

Функция	Производная	Примечание
	${frac {1}{{sqrt {1-x^{2}}}}}$	Доказательство Найти производную арксинуса можно при помощи взаимно обратных функций. После чего мы должны взять производную этих обеих функций. Теперь мы должны выразить производную арксинуса. ${displaystyle (arcsin(x))'={frac {1}{cos(arcsin(x))}}}$ Исходя из тригонометрического тождества( ${displaystyle sin^{2}x+cos^{2}x=1}$ ) — получаем. ${displaystyle (arcsin(x))'={frac {1}{pm {sqrt {1-sin^{2}(arcsin(x))}}}}}$ Для того, чтобы понять плюс должен стоять или минус взглянем какие значения. ${displaystyle D(cos(x))=[{frac {pi }{2}};-{frac {pi }{2}}]}$ Так как косинус находится в 2-й и 4-й четвертях то, получается что косинус положительный. ${displaystyle (arcsin(x))'={frac {1}{sqrt {1-sin^{2}(arcsin(x))}}}}$ Получается. ${displaystyle (arcsin(x))'={frac {1}{sqrt {1-x^{2}}}}}$
	$-{frac {1}{{sqrt {1-x^{2}}}}}$	Доказательство Найти производную арккосинуса можно при помощи данного тождества: ${displaystyle arcsin(x)+arccos(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arcsin(x)+arccos(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккосинуса. Получается. ${displaystyle (arccos(x))'=-{frac {1}{sqrt {1-x^{2}}}}}$
	${displaystyle {frac {1}{1+x^{2}}}}$	Доказательство Найти производную арктангенса можно при помощи взаимнообратной функции: Теперь находим производную обеих частей этого тождества. ${displaystyle {frac {1}{cos^{2}(arctg(x))}}cdot (arctg(x))'=1}$ Теперь мы должны выразить производную арктангенса: ${displaystyle (arctg(x))'=cos^{2}(arctg(x))}$ Теперь на помощь нам придет на помощь тождество( ${displaystyle cos(x)={frac {1}{sqrt {1+tg^{2}(x)}}}}$ ): ${displaystyle (arctg(x))'=({frac {1}{sqrt {1+tg^{2}(arctg(x))}}})^{2}}$ Получается. ${displaystyle (arctg(x))'={frac {1}{1+x^{2}}}}$
	${displaystyle -{frac {1}{1+x^{2}}}}$	Доказательство Найти производную арккотангенса можно при помощи данного тождества: ${displaystyle arctg(x)+arcctg(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arctg(x)+arcctg(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккотангенса. Получается. ${displaystyle (arcctg(x))'=-{frac {1}{1+x^{2}}}}$
	${displaystyle {frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	Доказательство Найти производную арксеканса можно при помощи тождества: ${displaystyle arcsec(x)=arccos({frac {1}{x}})}$ Теперь находим производную обеих частей этого тождества. ${displaystyle (arcsec(x))'=(arccos({frac {1}{x}}))'}$ ${displaystyle (arcsec(x))'=-{frac {1}{sqrt {1-{frac {1}{x^{2}}}}}}cdot (-{frac {1}{x^{2}}})}$ ${displaystyle (arcsec(x))'={frac {1}{x^{2}{sqrt {frac {x^{2}-1}{x^{2}}}}}}}$ ${displaystyle (arcsec(x))'={frac {1}{x^{2}{frac {sqrt {x^{2}-1}}{\|x\|}}}}}$ Получается. ${displaystyle (arcsec(x))'={frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$
	${displaystyle -{frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	Доказательство Найти производную арккосеканса можно при помощи данного тождества: ${displaystyle arccosec(x)+arcsec(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arccosec(x)+arcsec(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккосинуса. Получается. ${displaystyle (arccosec(x))'=-{frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$

Интегралы от обратных тригонометрических функций[править | править код]

Неопределённые интегралы[править | править код]

Для действительных и комплексных x:

${begin{aligned}int arcsin x,dx&{}=x,arcsin x+{sqrt {1-x^{2}}}+C,\int arccos x,dx&{}=x,arccos x-{sqrt {1-x^{2}}}+C,\int operatorname {arctg},x,dx&{}=x,operatorname {arctg},x-{frac {1}{2}}ln left(1+x^{2}right)+C,\int operatorname {arcctg},x,dx&{}=x,operatorname {arcctg},x+{frac {1}{2}}ln left(1+x^{2}right)+C,\int operatorname{arcsec} x,dx&{}=x,operatorname{arcsec} x-ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C,\int operatorname {arccosec},x,dx&{}=x,operatorname {arccosec},x+ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C.end{aligned}}$

Для действительных x ≥ 1:

${begin{aligned}int operatorname{arcsec} x,dx&{}=x,operatorname{arcsec} x-ln left(x+{sqrt {x^{2}-1}}right)+C,\int operatorname {arccosec},x,dx&{}=x,operatorname {arccosec},x+ln left(x+{sqrt {x^{2}-1}}right)+C.end{aligned}}$

См. также Список интегралов от обратных тригонометрических функций

Использование в геометрии[править | править код]

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.

В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол.
Так, если катет длины является противолежащим для угла alpha , то

Связь с натуральным логарифмом[править | править код]

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

${displaystyle {begin{aligned}arcsin z&{}=-iln(iz+{sqrt {1-z^{2}}})={frac {pi }{2}}-iln(z+{sqrt {z^{2}-1}})=-ioperatorname {arsh} ,iz,end{aligned}}}$

${displaystyle arccos(z)={dfrac {pi }{2}}+iln(iz+{sqrt {1-z^{2}}})=-ioperatorname {arch} (iz)}$

${displaystyle operatorname {arctg} (z)={dfrac {i}{2}}(ln(1-iz)-ln(1+iz))=-ioperatorname {arth} (iz)}$

${displaystyle operatorname {arcctg} (z)={dfrac {i}{2}}left(ln left({dfrac {z-i}{z}}right)-ln left({dfrac {z+i}{z}}right)right)=ioperatorname {arcth} (iz)}$

${displaystyle operatorname {arcsec}(z)=arccos left(z^{-1}right)={dfrac {pi }{2}}+iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right),}$

${displaystyle operatorname {arccosec} ,(z)=arcsin left(z^{-1}right)=-iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right).}$

См. также[править | править код]

Обратные гиперболические функции
Теорема Данжуа — Лузина

Примечания[править | править код]

Ссылки[править | править код]

Weisstein, Eric W. Обратные тригонометрические функции (англ.) на сайте Wolfram MathWorld.
Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: «Советская Энциклопедия», 1982. — [dic.academic.ru/dic.nsf/enc_mathematics/3612/%D0%9E%D0%91%D0%A0%D0%90%D0%A2%D0%9D%D0%AB%D0%95 Т. 3. — с. 1135].
Обратные тригонометрические функции — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1974. — Т. 18. — с. 225.
Обратные тригонометрические функции // Энциклопедический словарь юного математика / Савин А.П. — М.: Педагогика, 1985. — С. 220—221. — 352 с.
Построение графиков обратных тригонометрических функций онлайн
Онлайн калькулятор: обратные тригонометрические функции

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист.

Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым).

Список проблемных доменов

dic.academic.ru

Источник

– Здравствуйте,
ребята.

-Сегодняшний урок
я хотела бы начать с повторения свойств обратных тригонометрических функций.

-Скажите, что
называют арксинусом числа y₀? Сделайте соответствующую запись на доске.

– Почему функция y=arcsin x относится к обратным
тригонометрическим функциям?

– Каковы область
определения, множество значений и характер монотонности функции y = =arcsin x?

– Теперь повторим
определение арккосинуса числа y₀.

– Почему функция y=arccos x относится к обратным
тригонометрическим функциям?

– Каковы область
определения, множество значений и характер монотонности функции y = =arccos x?

– Ответьте мне на
те же вопросы, касающиеся чисел arctg y₀и arcсtg y₀ифункций y=arctg x и y=arcсtg.

-Что называют
арктангенсом числа y₀?

-Что называют
арккотангенсом числа y₀?

– Функции y=arctg x и y=arcctg x, как вам уже известно, также относят к обратным тригонометрическим
функциям. Обоснуйте этот факт.

– Опишите основные
свойства этих функций, то есть те свойства, которые мы уже установили для y=arcsin x и y=arccos
x.

– Как вы думаете,
для чего мы изучали все эти свойства?

– Верно. Запишите
в тетрадях тему нашего сегодняшнего занятия «Вычисление области определения и
множества значений функций, связанных с обратными тригонометрическими
функциями».

– Для начала
выполним задание № 670 под номером 1.

К доске идет Даша,
все остальные записывают задачу в рабочую тетрадь.

– Даша, прочитайте
задачу и выполните ее.

– Верно, теперь
выполним следующее задание, найдите область определения и множество значений
функции . На доске его будет выполнять Кирилл, а
все остальные в тетрадях.

– Кирилл, обратите
внимание на выражение, стоящее под знаком арксинуса.

– Какими
свойствами обладает данная функция? Каковы ее область определения и множество
значений?

– Как это можно
сделать?

– Молодец, Кирилл,
садитесь.

Обратите внимание,
в задачах такого типа, то есть в задачах на нахождение области определения и
множества значений функции вида

нужно исследовать функцию g(x), ее область определения и множество
значений.

-Решим еще одну
подобную задачу. Найдите множество значений функции .
На доске его будет выполнять Ира, а все остальные в тетрадях.

– Какую в данном
случае надо исследовать функцию прежде, чем переходить к непосредственному
нахождению множества значений функции ?

– Молодец, садитесь.

– Разделитесь на 3
группы, каждой группе я выдаю карточку с двумя заданиями. Сделав задания,
сначала вы отчитываетесь передо мной, а затем, при условии, что у вас нет
ошибок – перед всем классом. Того, кто будет предоставлять отчет мне и
классу, выберу я, причем мне будет отвечать один человек из группы, а
защищать работу перед классом – другой. Таким образом, 6 человек должны
сегодня получить хорошую оценку.

Домашнее задание к
следующему уроку найдите область определения и множество значений функции , Найдите множество значений функции.

А теперь приступим
к работе с карточками.

-Если | y₀|≤1, то
арксинусом y₀называют такое число x₀, что sin x₀= y₀и –π/2≤ x₀≤ π/2.

(x₀=arcsin y₀, -1≤ у₀≤1) (у₀= sin x₀, -π/2≤ x₀ ≤π/2)

– Функция y=arcsin x относится к обратным
тригонометрическим функциям, так как она является обратной к функции y=sin x, где –π/2≤x≤ π/2.

– Область
определения функции y=arcsin x –
отрезок [-1;1], множество ее значений – отрезок [-π/2; π/2], данная
функция монотонно возрастает на всей своей области определения.

-Если | y₀|≤1, то
арккосинусом y₀называют такое число x₀, что cos x₀= y₀и 0≤ x₀≤ π.

(x₀=arccos y₀, -1≤ у₀≤1) (у₀= cos x₀, 0≤ x₀ ≤π)

– Функция y=arccos x относится к обратным
тригонометрическим функциям, так как она является обратной к функции y=cos x, где 0≤x≤ π.

– Область
определения функции y=arccos x –
отрезок [-1;1], множество ее значений – отрезок [0; π], данная функция
монотонно убывает на всей своей области определения.

-Арктангенсом y₀называют такое
число x₀, что tg x₀= y₀и –π/2< x₀< π/2.

(x₀=arctg y₀, y₀ Î R) (у₀= tg x₀, -π/2< x₀ <π/2)

-Арккотангенсом y₀называют такое
число x₀, что ctg x₀= y₀и 0< x₀< π.

(x₀=arcctg y₀,
y₀ Î R) (у₀= ctg x₀, 0< x₀ <π)

-Функция y=arctg x относится к обратным тригонометрическим
функциям, поскольку является обратной к функции y=tg
x, где –π/2<x< π/2, а функция y=arcсtg x обратная
тригонометрическая, так как обратна к функции y=сtg
x, где 0<x< π.

– Область
определения функции y=arctg x – все
множество действительных чисел, множество ее значений – интервал (-π/2; π/2),
данная функция монотонно возрастает на всей своей области определения.

Область
определения функции y=arcсtg
x также все множество действительных чисел, множество ее
значений – интервал (0; π), данная функция монотонно убывает на всей своей
области определения.

-Вероятно, для
того чтобы решать такие задачи, выполнять такие упражнения, которые требуют
наличия знаний об обратных тригонометрических функциях и их свойствах.

выполняют

– Найдите область
определения функции . Для того чтобы найти область
определения данной функции нужно учесть, что область определения функции y=arcsin t – отрезок [-1;1]. В нашем случае
t=x-2, то есть

-1 ≤ x-2 ≤ 1.

Прибавим 2 ко всем
частям данного неравенства:

1 ≤ x ≤ 3.

Таким образом,
искомая область определения функции – отрезок [1;3].

Кирилл
записывает на доске .

– Это функция .

– Область
определения функции g(x) – множество
действительных чисел.

Для того чтобы
найти ее множество значений нужно для начала преобразовать выражение .

– Так как
коэффициенты, стоящие перед и равны 1, разделим и умножим данное
выражение на

Получаем ,

Так как множество
значений функции y=sin t – отрезок [-1;1],
то

умножим все части
данного неравенства на , тогда

Теперь прибавим , а затем разделим на :

Таким образом, мы
получили, что множество значений функции g(x) – это отрезок [1/2;1].

Учитывая, что
функция g(x) стоит под знаком
арксинуса и область определения функции y=arcsin t, делаем вывод о том, что областью определения функции является множество действительных чисел.

Далее учитывая,
что функция y=arcsin t монотонно
возрастает на всей своей области определения, из неравенства получаем, что .

Умножив все части
последнего неравенства на 6, получим искомое множество значений.

Ответ: D(f)=R, E(f)=[π;3π].

Ира записывает .

– Сначала надо
найти множество значений функции .

Учитывая то, что
модуль числа всегда неотрицателен, имеем:

умножим обе части
неравенства на 3, 3>0, тогда

Затем прибавим 4и разделим на 8, получаем

Учитывая область
определения функции y=arсcos
t, запишем .

Функция y=arcсos t является
убывающей, то

Ответ: E(f)=[0;1].

Источник

Понятие арктангенса
График и свойства функции y=arctgx
Уравнение tgx=a
Понятие арккотангенса
График и свойства функции y=arcctgx
Уравнение ctgx=a
Формулы преобразований аркфункци
Примеры

Определение тангенса и котангенса через отношение сторон прямоугольника и с помощью касательной к числовой окружности – см. §3 данного справочника.
Свойства функции y=tgx на всей области определения (xinmathbb{R}) – см. §6 данного справочника.
Свойства функции y=ctgx на всей области определения (xinmathbb{R}) – см. §7 данного справочника.
Определение и свойства взаимно обратных функций – см. §2 справочника для 9 класса.

п.1. Понятие арктангенса

В записи (y=tgx) аргумент x – это значение угла (в градусах или радианах), функция y – тангенс угла, действительное число в пределах от (-infty;) до (+infty). Т.е., по заданному углу мы находим тангенс.
Можно поставить обратную задачу: по заданному тангенсу найти угол. Но одному значению тангенса соответствует бесконечное количество углов. Например, если (tgx=1), то (x=fracpi4+pi k, kinmathbb{Z}); если (tgx=0), то (x=pi k, kinmathbb{Z}) и т.д.
Поэтому, чтобы построить однозначную обратную функцию, ограничим значения углов x главной ветвью тангенса: (-fracpi2leq xleq fracpi2) (правая половина числовой окружности, вся ось тангенсов).

Арктангенсом числа (a (ainmathbb{R})) называется такое число (xin[-fracpi2; fracpi2]), тангенс которого равен (a). $$ arctg a=x Leftrightarrow begin{cases} tgx=a\ -fracpi2leq xleq fracpi2 end{cases} $$

Например:

(arctgfrac{1}{sqrt{3}}=fracpi6, arctg(-sqrt{3})=-frac{pi}{3}, arctg1=fracpi4).

п.2. График и свойства функции y=arctgx

1. Область определения (xinmathbb{R}).
2. Функция ограничена сверху и снизу асимптотами (-fracpi2leq arctgxleq fracpi2).
Область значений (yinleft(-fracpi2; fracpi2right))
3. Функция стремится к максимальному значению (y_{max}=fracpi2 text{при} xrightarrow +infty)
Функция стремится к минимальному значению (y_{min}=-fracpi2 text{при} xrightarrow -infty)
Функция имеет две горизонтальные асимптоты (y=pmfracpi2).
4. Функция возрастает на всей области определения.
5. Функция непрерывна на всей области определения.
6. Функция нечётная: (arctg(-x)=-arctg(x)).

п.3. Уравнение tgx=a

На оси тангенсов каждому углу на числовой окружности в интервале (-fracpi2leq xleq fracpi2) соответствует одно действительное число.

Например:
1) Решим уравнение (tgx=frac{1}{sqrt{3}})
Числу (frac{1}{sqrt{3}}) на оси тангенсов соответствует угол (fracpi6) на числовой окружности, (arctgfrac{1}{sqrt{3}}=fracpi6).
Учитывая период тангенса (pi), получаем ответ:
(x=fracpi6+pi k)

2) Решим уравнение (tgx=2)
Числу (frac{1}{sqrt{3}}) на оси тангенсов соответствует угол (arctg2) на числовой окружности.
Учитывая период тангенса (pi), получаем ответ:
(x=arctg2+pi k)

В общем случае:

Уравнение (tgx=a) имеет решения $$ x=arctga+pi k, kinmathbb{Z}, ainmathbb{R} $$

п.4. Понятие арккотангенса

По аналогии с арктангенсом, арккотангенс определяется на главной ветви котангенса: (0lt xlt pi) (верхняя половина числовой окружности, вся ось котангенсов).

Арккотангенсом числа (a (ainmathbb{R})) называется такое число (xin(0;pi)), котангенс которого равен (a). $$ arcctg a=x Leftrightarrow begin{cases} ctgx=a\ 0lt xlt pi end{cases} $$

Например:

(arcctgfrac{1}{sqrt{3}}=fracpi3, arcctg(-sqrt{3})=-frac{pi}{6}, arcctg1=fracpi4).

п.5. График и свойства функции y=arcctgx

1. Область определения (xinmathbb{R}).
2. Функция ограничена сверху и снизу асимптотами (0lt arcctgxlt pi).
Область значений (yin(0;pi))
3. Функция стремится к максимальному значению (y_{max}=pi text{при} xrightarrow -infty)
Функция стремится к минимальному значению (y_{min}=0 text{при} xrightarrow +infty)
Функция имеет две горизонтальные асимптоты (y=0 text{и} y=pi).
4. Функция убывает на всей области определения.
5. Функция непрерывна на всей области определения.
6. Функция ни чётная, ни нечётная.

п.6. Уравнение ctgx=a

В общем случае:

Уравнение (ctgx=a) имеет решения $$ x=arcctga+pi k, kinmathbb{Z}, ainmathbb{R} $$

Часто уравнение (ctgx=a) преобразуют в уравнение (tgx=frac{1}{a}), и ищут его корни.
Например:
1) (ctgx=sqrt{3})
(x=fracpi6+pi k)
Можно также преобразовать уравнение в (tg x=frac{1}{sqrt{3}})
Получаем тот же ответ: (x=fracpi6+pi k)

2) (ctgx=2)
(x=arcctg2+pi k)
Можно также преобразовать уравнение в (tg x=frac{1}{2})
Получаем ответ: (x=arctgfrac12+pi k)
Очевидно, что (arcctg 2=arctgfrac{1}{2}) (см. ниже формулы для аркфункций).

п.7. Формулы преобразования аркфункций

Аркфункции от обратных тригонометрических функций

begin{gather*} arcsin(sinalpha)=alpha, alphainleft[-fracpi2;fracpi2right], arccos(cosalpha)=alpha, alphain[0;pi]\ arctg(tgalpha)=alpha, alphainleft(-fracpi2;fracpi2right), arcctg(ctgalpha)=alpha, alphain(0;pi) end{gather*}

Аркфункции отрицательных аргументов

begin{gather*} arcsin(-alpha)=-arcsinalpha, arccos(-alpha)=pi-arccosalpha\ arctg(-alpha)=-arctgalpha, arcctg(-alpha)=pi-arcctgalpha end{gather*}

Суммы аркфункций

begin{gather*} arcsinalpha+arccosalpha=fracpi2, arctgalpha+arcctgalpha=fracpi2 end{gather*}

Сводная таблица тригонометрических функций от аркфункций

	arcsin	arccos	arctg	arcctg
sin	begin{gather} a\ ain[-1;1] end{gather}	begin{gather} sqrt{1-a^2}\ ain[-1;1] end{gather}	begin{gather} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}	begin{gather} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}
cos	begin{gather} sqrt{1-a^2}\ ain[-1;1] end{gather}	begin{gather} a\ ain[-1;1] end{gather}	begin{gather} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}	begin{gather} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}
tg	begin{gather} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather}	begin{gather} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather}	begin{gather} a\ ainmathbb{R} end{gather}	begin{gather} frac{1}{a}\ ane 0 end{gather}
ctg	begin{gather} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather}	begin{gather} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather}	begin{gather} frac{1}{a}\ ane 0 end{gather}	begin{gather} a\ ainmathbb{R} end{gather}

Аркфункции, выраженные через другие аркфункции

arcsin
arccos	$$ arcsina= begin{cases} arccossqrt{1-a^2}, 0leq aleq 1\ -arccossqrt{1-a^2}, -1leq alt 0 end{cases} $$
arctg	$$ arcsina=arctgfrac{a}{sqrt{1-a^2}}, -1lt alt 1 $$
arcctg	$$ arcsina= begin{cases} arcctgfrac{sqrt{1-a^2}}{a}, 0lt aleq 1\ -arcctgfrac{sqrt{1-a^2}}{a}-pi, -1leq alt 0 end{cases} $$

arccos
arcsin	$$ arccosa= begin{cases} arcsinsqrt{1-a^2}, 0leq aleq 1\ pi-arcsinsqrt{1-a^2}, -1leq alt 0 end{cases} $$
arctg	$$ arccosa= begin{cases} arcctgfrac{sqrt{1-a^2}}{a}, 0lt aleq 1\ pi+arctgfrac{sqrt{1-a^2}}{a}, -1leq alt 0 end{cases} $$
arcctg	$$ arccosa=arcctgfrac{a}{sqrt{1-a^2}}, -1lt alt 1 $$

arctg
arcsin	$$ arctga=arcsinfrac{a}{sqrt{1+a^2}}, ainmathbb{R} $$
arccos	$$ arctga= begin{cases} arccosfrac{1}{sqrt{1+a^2}}, ageq 0\ -arccosfrac{1}{sqrt{1+a^2}}, alt 0 end{cases} $$
arcctg	$$ arctga=arcctgfrac{1}{a}, ane 0 $$

arcctg
arcsin	$$ arcctga= begin{cases} arcsinfrac{1}{sqrt{1+a^2}}, ageq 0\ pi-arcsinfrac{1}{sqrt{1+a^2}}, alt 0 end{cases} $$
arccos	$$ arcctga=arccosfrac{a}{sqrt{1+a^2}}, ainmathbb{R} $$
arctg	$$ arcctga=arctgfrac{1}{a}, ane 0 $$

п.8. Примеры

Пример 1. Найдите функцию, обратную арктангенсу. Постройте графики арктангенса и найденной функции в одной системе координат.

Для (y=arctgx) область определения (xinmathbb{R}), область значений (-fracpi2leq yleq fracpi2).
Обратная функция (y=tgx) должна иметь ограниченную область определения (-fracpi2leq xleq fracpi2) (главная ветвь) и область значений (yinmathbb{R}).
Строим графики:

Графики симметричны относительно прямой y=x.
Обратная функция найдена верно.

Пример 2. Решите уравнения:

a) (tg x=-1)
(x=fracpi4+pi k)

б) (ctgx=-1)
(x=frac{3pi}{4}+pi k)

Если решать через (tgx=-1)
(x=-fracpi4+pi k)

в) (tg x=-5)
(x=arctg(-5)+pi k=-arctg5+pi k)

г) (ctgx=3)
(x=arcctg3+pi k)

Если решать через (tgx=frac13)
(x=arctgfrac13+pi k)

Пример 3. Вычислите:
a) (2arccosleft(-frac12right)+arctg(-1)+arcsinfrac{sqrt{2}}{2}=2cdotfrac{2pi}{3}-fracpi4+fracpi4=frac{4pi}{3})
б) (arcsin1-arccosfrac{sqrt{3}}{2}-arctg(sqrt{-3})=arcsin1-fracpi3+fracpi3=arcsin1)
в) (arctg4+arcsin0-arccos1=arctg4+0-0=arctg4)
г) (5-2arccos0+arcsinfrac{sqrt{2}}{2}+3arccosfrac{sqrt{2}}{2}=5-2cdotfracpi2+fracpi4+3cdotfracpi4=5)

Пример 4. Постройте графики функций:
(a) y=arccosleft(frac{1}{x}right)+arccosleft(-frac{1}{x}right))
Сумма арккосинусов (arccosa+arccos(-a)=pi), где (-1leq aleq 1).
Получаем систему для определения ОДЗ: begin{gather*} -1leq frac{1}{x}leq 1Rightarrow 0leq frac{1}{x}+1leq 2Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{x+1}{x}leq 2 end{cases} Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{-x+1}{x}leq 0 end{cases} Rightarrow begin{cases} frac{x+1}{x}geq 0\ frac{x-1}{x}geq 0 end{cases} Rightarrow\ Rightarrow left[ begin{array}{l l} begin{cases} xgt 0\ x+1geq 0\ x-1geq 0 end{cases} \ begin{cases} xlt 0\ x+1leq 0\ x-1leq 0 end{cases} end{array} right. Rightarrow left[ begin{array}{l l} begin{cases} xgt 0\ xgeq 1 end{cases} \ begin{cases} xlt 0\ xleq -1 end{cases} end{array} right. Rightarrow xleq -1cup xgeq 1 end{gather*} Заметим, что используя модуль, тот же результат можно получить значительно быстрей: $$ -1leqfrac{1}{x}leq 1Leftrightarrow |frac{1}{x}|leq 1Leftrightarrow |x|geq 1 $$ Таким образом, ОДЗ – вся числовая прямая, кроме (xnotin(-1;1).) $$ y=arccosleft(frac{1}{x}right)+arccosleft(-frac{1}{x}right)Leftrightarrow begin{cases} y=pi\ xnotin (-1;1) end{cases} $$ Строим график:

(б) y=arcctg(sqrt{x})+arcctg(-sqrt{x}))
Сумма арккотангенсов (arcctga+arcctg(-a)=pi), где (ainmathbb{R})
ОДЗ ограничено требованием к подкоренному выражению: (xgeq 0)
$$ y=arcctgleft(sqrt{x}right)+arcctgleft(-sqrt{x}right)Leftrightarrow begin{cases} y=pi\ xgeq 0 end{cases} $$ Строим график:

Пример 5*. Запищите в порядке возрастания:
$$ arctgleft(fracpi4right), arcsinleft(fracpi4right), arctg1 $$

Способ 1. С помощью числовой окружности.

Отмечаем точку (fracpi4) на оси синусов (ось OY) и точки (fracpi4) и 1 на оси тангенсов (касательная к окружности).
На пересечении с числовой окружностью получаем искомые углы.
В порядке возрастания: $$ arctgleft(fracpi4right)lt underbrace{arctg1}_{=fracpi4} lt arcsinleft(fracpi4right) $$

Способ 2. Аналитический
Арктангенс – функция возрастающая: (fracpi4approx 0,79lt 1Rightarrow arctgleft(fracpi4right)lt arctg 1)
Сравним (arctg1=fracpi4=arcsinleft(frac{sqrt{2}}{2}right)) и (arcsinleft(fracpi4right))
(frac{sqrt{2}}{2} ? fracpi4) – возведем в квадрат обе части
(frac12 ? frac{pi^2}{16}Leftrightarrow 8 ? pi^2)
(8ltpi^2Rightarrowfrac{sqrt{2}}{2}ltfracpi4 Rightarrow arcsinleft(frac{sqrt{2}}{2}right)lt arcsinleft(fracpi4right)Rightarrow 1lt arcsinleft(fracpi4right))
Получаем: $$ arctgleft(fracpi4right)lt underbrace{arctg1}_{=fracpi4} lt arcsinleft(fracpi4right) $$

Пример 6*. Решите уравнения:

a) (arccosx=arctgx)
ОДЗ определяется ограничением для арккосинуса: (-1leq xleq 1)
Арккосинус ограничен (0leq arccosxleq pi), арктангенс (-fracpi2leq arctgxltfracpi2)
Т.к. по условию они равны, ограничение сужается до (0leq arctgxlt fracpi2) и (0leq arccos xlt fracpi2) $$ arccosx=arctgxLeftrightarrow begin{cases} x=cos(arctgx)\ -1leq xleq 1\ 0leq arctgxltfracpi2\ 0leq arccosxltfracpi2 end{cases} Leftrightarrow begin{cases} x=cos(arctgx)\ -1leq xleq 1\ 0leq x\ 0lt xleq 1 end{cases} Leftrightarrow begin{cases} x=cos(arctgx)\ 0lt xlt 1 end{cases} $$ Для решения можно воспользоваться готовой формулой для (cos(arctgx)).
Выведем её. Пуcть (arctgx=varphi). Тогда (x=tgvarphi) и $$ cos(arctgx)=cosvarphi=sqrt{frac{1}{1+tg^2varphi}}=sqrt{frac{1}{1+x^2}} $$ Получаем уравнение: $$ x=sqrt{frac{1}{1+x^2}}Rightarrow x^2=frac{1}{1+x^2}Rightarrow x^2(1+x^2)=1Rightarrow x^4+x^2-1=0 $$ $$ D=1+4=5, x^2=frac{-1pmsqrt{5}}{2} $$ Квадрат числа не может быть отрицательным. Остаётся корень (x^2=frac{sqrt{5}-1}{2})
Откуда (x=pmsqrt{frac{sqrt{5}-1}{2}})
По условию (0lt xlt 1). Получаем (x=sqrt{frac{sqrt{5}-1}{2}})
Ответ: (sqrt{frac{sqrt{5}-1}{2}})

б) (arccos^2x+arcsin^2x=frac{5pi^2}{36})
Используем формулу для суммы: (arccosx+arcsinx=fracpi2)
Получаем: begin{gather*} arccos^2x+left(fracpi2-arccosxright)^2=frac{5pi^2}{36}\ arccos^2x+frac{pi^2}{4}-pi arccosx+arccos^2x=frac{5pi^2}{36}\ 2arccos^2x-pi arccosx+frac{pi^2}{9}=0\ D=(-pi)^2-4cdot 2cdot frac{pi^2}{9}=pi^2-frac89pi^2=frac{pi^2}{9}\ arccosx=frac{pipmfracpi3}{4}Rightarrow left[ begin{array} {l l} arccosx_1=fracpi6\ arccosx_2=fracpi3 end{array} right. Rightarrow left[ begin{array} {l l} x_1=cosfracpi6=frac{sqrt{3}}{2}\ x_2=cosfracpi3=frac12 end{array} right. end{gather*} Ответ: (left{frac12; frac{sqrt{3}}{2}right})

в) (arcsinfrac{sqrt{3x+2}}{2}=arcctgsqrt{frac{2}{x+1}})
ОДЗ определяется ограничением для арксинуса: ( -1leq frac{sqrt{3x+2}}{2}leq 1)
Арксинус ограничен (-fracpi2leq arcsinfrac{sqrt{3x+2}}{2}leqfracpi2), арккотангенс (0leq arcctgsqrt{frac{2}{x+1}}ltpi)
Т.к. по условию они равны, ограничение сужается до (0leq arcctgsqrt{frac{2}{x+1}}ltfracpi2) и (0leq arcsinfrac{sqrt{3x+2}}{2}ltfracpi2). begin{gather*} arcsinfrac{sqrt{3x+2}}{2}=arcctgsqrt{frac{2}{x+1}}Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ -1leqfrac{sqrt{3x+2}}{2}leq 1\ 0leq arcsinfrac{sqrt{3x+2}}{2}ltfracpi2\ 0leq arcctgsqrt{frac{2}{x+1}}ltfracpi2 end{cases} Leftrightarrow\ Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ -1leqfrac{sqrt{3x+2}}{2}leq 1\ 0leq frac{sqrt{3x+2}}{2}lt 1\ 0leq sqrt{frac{2}{x+1}} end{cases} Leftrightarrow begin{cases} frac{sqrt{3x+2}}{2}=sinleft(arcctgsqrt{frac{2}{x+1}}right)\ 0leq frac{sqrt{3x+2}}{4}lt 1\ frac{4}{x+1}geq 0 end{cases} end{gather*} Для ОДЗ получаем: $$ begin{cases} 0leq 3x+2lt 4\ x+1gt 0 end{cases} Rightarrow begin{cases} -2leq 3x lt 2\ xgt -1 end{cases} Rightarrow begin{cases} -frac23leq x lt frac23\ xgt -1 end{cases} Rightarrow -frac23leq xltfrac23 $$ ОДЗ: (-frac23leq xlt frac23)
Выведем формулу для синуса арккотангенса.
Пусть (arcctgx=varphi Rightarrow x=ctgvarphi)
Тогда (sin(arcctgx)=sinvarphi=sqrt{frac{1}{1+ctg^2varphi}}=sqrt{frac{1}{1+x^2}})
Правая часть уравнения: $$ sinleft(arcctgsqrt{frac{2}{x+1}}right)= sqrt{frac{1}{1+left(sqrt{frac{2}{x+1}}right)}}= sqrt{frac{1}{1+frac{2}{x+1}}}=sqrt{frac{x+1}{x+3}} $$ Подставляем: begin{gather*} frac{sqrt{3x+2}}{2}=sqrt{frac{x+1}{x+3}}Rightarrow frac{3x+2}{4}=frac{x+1}{x+3}Rightarrow (3x+2)(x+3)=4(x+1)Rightarrow\ Rightarrow 3x^2+11x+6=4x+4Rightarrow 3x^2+7x+2=0\ D=49-4cdot 3cdot 2=25\ x=frac{-7pm5}{6}Rightarrow left[ begin{array} {l l} x_1=-2 – text{ не подходит по ОДЗ}\ x_2=-frac13 end{array} right. end{gather*} Ответ: (-frac13)

Источник

Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.

Сначала дадим определения.

Арксинусом числа а называется число $varphi in left[-frac{pi }{2} ;frac{pi }{2}right]$ , такое, что Или, можно сказать, что это такой угол varphi , принадлежащий отрезку $left[-frac{pi }{2}, ;frac{pi }{2}right]$ , синус которого равен числу а.

Арккосинусом числа а называется число , такое, что

Арктангенсом числа а называется число $varphi in left(-frac{pi }{2};frac{pi }{2}right)$ , такое, что

Арккотангенсом числа а называется число , такое, что

Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.

Помните, мы уже встречались с обратными функциями.

Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.

${(sqrt{a})}^2=a; sqrt{a}ge 0; age 0.$

Логарифм числа b по основанию a — такое число с, что $boldsymbol{a^c=b.}$

При этом

Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения x^2=5 — это sqrt{5} и Мы не смогли бы записать их без специального символа арифметического квадратного корня.

Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: 2^x=7. Решение этого уравнения — иррациональное число ${log}_27.$ Это показатель степени, в которую надо возвести 2, чтобы получить 7.

Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение $sinx = frac{1}{4}.$

Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна $frac{1}{4}.$ И ясно, что это не табличное значение синуса. Как же записать решения?

Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.

Угол, принадлежащий отрезку $left[-frac{pi }{2}, ;frac{pi }{2}right]$ , синус которого равен $frac{1}{4}$ — это арксинус одной четвертой. И значит, серия решений нашего уравнения, соответствующая правой точке на тригонометрическом круге, — это $arcsin frac{1}{4}+2 pi n,, nin Z.$

А вторая серия решений нашего уравнения — это $pi -arcsin frac{1}{4}+2 pi n,, nin Z.$

Подробнее о решении тригонометрических уравнений — здесь.

Осталось выяснить — зачем в определении арксинуса указывается, что это угол, принадлежащий отрезку $left[-frac{pi }{2}, ;frac{pi }{2}right]$ ?

Дело в том, что углов, синус которых равен, например, $frac{1}{4}$ , бесконечно много. Нам нужно выбрать какой-то один из них. Мы выбираем тот, который лежит на отрезке $left[-frac{pi }{2}, ;frac{pi }{2}right]$ .

Взгляните на тригонометрический круг. Вы увидите, что на отрезке $left[-frac{pi }{2}, ;frac{pi }{2}right]$ каждому углу соответствует определенное значение синуса, причем только одно. И наоборот, любому значению синуса из отрезка [-1;1] отвечает одно-единственное значение угла на отрезке $left[-frac{pi }{2}, ;frac{pi }{2}right]$ . Это значит, что на отрезке [-1;1] можно задать функцию принимающую значения от $-frac{pi }{2}$ до $frac{pi }{2}.$

Повторим определение еще раз:

Арксинусом числа a называется число $varphi in left[-frac{pi }{2}, ;frac{pi }{2}right]$ , такое, что

Обозначение: Область определения арксинуса — отрезок [-1;1]. Область значений — отрезок $left[-frac{pi }{2}, ;frac{pi }{2}right]$ .

Можно запомнить фразу «арксинусы живут справа». Не забываем только, что не просто справа, но ещё и на отрезке $left[-frac{pi }{2}, ;frac{pi }{2}right]$ .

Мы готовы построить график функции

Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.

Поскольку , следовательно, х лежит в пределах от -1 до 1.

Значит, областью определения функции y = arcsin x является отрезок [-1;1].

Мы сказали, что у принадлежит отрезку $left[-frac{pi }{2}, ;frac{pi }{2}right]$ . Это значит, что областью значений функции y = arcsin x является отрезок $left[-frac{pi }{2}, ;frac{pi }{2}right]$ .

Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями $x= -1; , x = 1, , y= -frac{pi}{2}$ и $y= frac{pi}{2} .$

Как всегда при построении графика незнакомой функции, начнем с таблицы.

По определению, арксинус нуля — это такое число из отрезка $[-frac{pi}{2} ; frac{pi}{2} ]$ , синус которого равен нулю. Что это за число? — Понятно, что это ноль.

Аналогично, арксинус единицы — это такое число из отрезка $[-frac{pi}{2} ; frac{pi}{2} ]$ , синус которого равен единице. Очевидно, это $frac{pi}{2} .$

Продолжаем: $arcsin frac{1}{2}$ — это такое число из отрезка $[-frac{pi}{2} ; frac{pi}{2} ]$ , синус которого равен $frac{1}{2}$ . Да, это $frac{pi}{6}.$

		$-frac{1}{2}$	0	$frac{1}{2}$
	$-frac{pi}{2}$	$-frac{pi}{6}$	0	$frac{pi}{6}$	$frac{pi}{2}$

Строим график функции

Свойства функции

1. Область определения

2. Область значений $E (y): y in left[-frac{pi }{2}, ;frac{pi }{2}right]$

3. , то есть эта функция является нечетной. Ее график симметричен относительно начала координат.

4. Функция монотонно возрастает. Ее наименьшее значение, равное – $frac{ pi }{2}$ , достигается при x=-1 , а наибольшее значение, равное $frac{pi}{2}$ , при x = 1.

5. Что общего у графиков функций y=sin x и ? Не кажется ли вам, что они «сделаны по одному шаблону» — так же, как правая ветвь функции y=x^2 и график функции , или как графики показательной и логарифмической функций?

Представьте себе, что мы из обычной синусоиды вырезали небольшой фрагмент от $-frac{pi}{2}$ до $frac{pi}{2}$ , а затем развернули его вертикально — и мы получим график арксинуса.

То, что для функции y=sin x на этом промежутке — значения аргумента, то для арксинуса будут значения функции. Так и должно быть! Ведь синус и арксинус — взаимно-обратные функции. Другие примеры пар взаимно обратных функций — это y = x^2 при xgeq 0 и , а также показательная и логарифмическая функции.

Напомним, что графики взаимно обратных функций симметричны относительно прямой y=x.

Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок

Арккосинусом числа a называется число , такое, что

Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке

Обозначение: Область определения арккосинуса — отрезок [-1;1]. Область значений — отрезок

Очевидно, отрезок [0;pi ] выбран потому, что на нём каждое значение косинуса принимается только один раз. Иными словами, каждому значению косинуса, от -1 до 1, соответствует одно-единственное значение угла из промежутка

Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:

Построим график функции

Нам нужен такой участок функции , на котором она монотонна, то есть принимает каждое свое значение ровно один раз.

Выберем отрезок . На этом отрезке функция монотонно убывает, то есть соответствие между множествами и взаимно однозначно. Каждому значению х соответствует свое значение у. На этом отрезке существует функция, обратная к косинусу, то есть функция у = arccosx.

Заполним таблицу, пользуясь определением арккосинуса.

Арккосинусом числа х, принадлежащего промежутку [-1; 1] , будет такое число y, принадлежащее промежутку [0;pi ] , что

Значит, , поскольку ;

, так как ;

$arccos 0 = frac{pi}{2}$ , так как $cos frac{pi}{2} = 0$ ,

$arccos frac{1}{2} = frac{pi }{3}$ , так как $cos frac{pi }{3} = 0$ ,

		$-frac{1}{2}$	0	$frac{1}{2}$
		$frac{2pi}{3}$	$frac{pi}{2}$	$frac{pi}{3}$	0

Вот график арккосинуса:

Свойства функции

1. Область определения

2. Область значений

Эта функция общего вида — она не является ни четной, ни нечетной.

4. Функция является строго убывающей. Наибольшее значение, равное , функция у = arccosx принимает при x=-1 , а наименьшее значение, равное нулю, принимает при x=1.

5. Функции и являются взаимно обратными.

Следующие — арктангенс и арккотангенс.

Арктангенсом числа a называется число $varphi in left(-frac{pi }{2}, ;frac{pi }{2}right)$ , такое, что

Обозначение: . Область определения арктангенса — промежуток Область значений — интервал $left(-frac{pi }{2}, ;frac{pi }{2}right)$ .

Почему в определении арктангенса исключены концы промежутка — точки $pm frac {pi}{2}$ ? Конечно, потому, что тангенс в этих точках не определён. Не существует числа a, равного тангенсу какого-либо из этих углов.

Построим график арктангенса. Согласно определению, арктангенсом числа х называется число у, принадлежащее интервалу $(-frac{pi}{2} ; frac{pi}{2} )$ , такое, что

Как строить график – уже понятно. Поскольку арктангенс — функция обратная тангенсу, мы поступаем следующим образом:

– Выбираем такой участок графика функции , где соответствие между х и у взаимно однозначное. Это интервал Ц На этом участке функция принимает значения от -infty до +infty.

Тогда у обратной функции, то есть у функции , область, определения будет вся числовая прямая, от -infty до +infty, а областью значений — интервал $(-frac{pi}{2} ; frac{pi}{2} ).$

Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.

, значит,

$tg frac{pi}{4} = 1$ , значит, $arctg 1 = frac{pi}{4}$

$tg (-frac{pi}{4}) = -1$ , значит, $arctg (-1) = - frac{pi}{4}.$

А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?

Мы можем задать себе вопрос: для какого числа из интервала $(-frac{pi}{2} ; frac{pi}{2} )$ значение тангенса стремится к бесконечности? — Очевидно, это $frac{pi}{2} .$

А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте $y=frac{pi}{2} .$

Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте $y= - frac{pi}{2} .$

На рисунке — график функции

Свойства функции

1. Область определения

2. Область значений $E (y): y in (-frac{pi}{2} ; frac{pi}{2} )$

3. Функция нечетная.

4. Функция является строго возрастающей.

5. Прямые $y= - frac{pi}{2}$ и $y= frac{pi}{2}$ — горизонтальные асимптоты данной функции.

6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке $(-frac{pi}{2} ; frac{pi}{2} )$

Аналогично, определим функцию арккотангенс и построим ее график.

Арккотангенсом числа a называется число , такое, что

График функции :

Свойства функции

1. Область определения

2. Область значений

3. Функция – общего вида, то есть ни четная, ни нечетная.

4. Функция является строго убывающей.

5. Прямые y= 0 и y= pi — горизонтальные асимптоты данной функции.

6. Функции и являются взаимно обратными, если рассматривать на промежутке

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Обратные тригонометрические функции и их графики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Уроки 32-33. Обратные тригонометрические функции

Цель: рассмотреть обратные тригонометрические функции, их использование для записи решений тригонометрических уравнений.

Ход уроков

I. Сообщение темы и цели уроков

II. Изучение нового материала

1. Обратные тригонометрические функции

Рассмотрение этой темы начнем со следующего примера.

Пример 1

Решим уравнение: a) sin x = 1/2; б) sin x = а.

а) На оси ординат отложим значение 1/2 и построим углы x1 и х2, для которых sin x = 1/2. При этом х1 + х2 = π, откуда х2 = π – x1. По таблице значений тригонометрических функций найдем величину х1 = π/6, тогда Учтем периодичность функции синуса и запишем решения данного уравнения: где k ∈ Z.

б) Очевидно, что алгоритм решения уравнения sin х = а такой же, как и в предыдущем пункте. Разумеется, теперь по оси ординат откладывается величина а. Возникает необходимость каким-то образом обозначить угол х1. Условились такой угол обозначать символом arcsin а. Тогда решения данного уравнения можно записать в виде Эти две формулы можно объединить в одну: при этом

Аналогичным образом вводятся и остальные обратные тригонометрические функции.

Очень часто бывает необходимо определить величину угла по известному значению его тригонометрической функции. Такая задача является многозначной – существует бесчисленное множество углов, тригонометрические функции которых равны одному и тому же значению. Поэтому, исходя из монотонности тригонометрических функций, для однозначного определения углов вводят следующие обратные тригонометрические функции.

Арксинус числа a (arcsin а) – такой угол а из промежутка , синус которого равен а, т. е.

Арккосинус числа a (arccos а) – такой угол а из промежутка [0; π], косинус которого равен а, т. е.

Арктангенс числа a (arctg а) – такой угол а из промежутка тангенс которого равен а, т. е. tg а = а.

Арккотангенс числа a (arcctg а) – такой угол а из промежутка (0; π), котангенс которого равен а, т. е. ctg а = а.

Пример 2

Найдем:

Учитывая определения обратных тригонометрических функций получим:

Пример 3

Вычислим

Пусть угол а = arcsin 3/5, тогда по определению sin a = 3/5 и . Следовательно, надо найти cos а. Используя основное тригонометрическое тождество, получим: Учтено, что и cos a ≥ 0. Итак,

Рассмотрим более подробно свойства обратных тригонометрических функций.

Свойства функции	Функция
у = arcsin х	у = arccos х	у = arctg х	у = arcctg х
Областьопределения	х ∈ [-1; 1]	х ∈ [-1; 1]	х ∈ (-∞; +∞)	х ∈ (-∞ +∞)
Область значений	y ∈ [-π/2; π/2]	y ∈ [0; π]	y ∈ (-π/2; π/2)	y ∈ (0; π)
Четность	Нечетная	Ни четная, ни нечетная	Нечетная	Ни четная, ни нечетная
Нули функции (y =0)	При х = 0	При х = 1	При х = 0	у ≠ 0
Промежутки знакопостоянства	у > 0 при х ∈(0; 1], у < 0 при х ∈[-1; 0)	у > 0 при х∈ [-1; 1)	у > 0 при х ∈(0; +∞), у < 0 при х ∈(-∞; 0)	у > 0 при x∈ (-∞; +∞)
Монотонность	Возрастает	Убывает	Возрастает	Убывает
Связь с тригонометрической функцией	sin у = х	cos у = х	tg у = х	ctg у = х
График	а	б	в	г

Приведем еще ряд типичных примеров, связанных с определениями и основными свойствами обратных тригонометрических функций.

Пример 4

Найдем область определения функции

Для того чтобы функция у была определена, необходимо выполнение неравенства которое эквивалентно системе неравенств Решением первого неравенства является промежуток х ∈ (-∞; +∞), второго – Этот промежуток и является решением системы неравенств, а следовательно, и областью определения функции

Пример 5

Найдем область изменения функции

Рассмотрим поведение функции z = 2х – х2 (см. рисунок).

Видно, что z ∈ (-∞; 1]. Учитывая, что аргумент z функции арккотангенса меняется в указанных пределах, из данных таблицы получим, что Таким образом, область изменения

Пример 6

Докажем, что функция у = arctg х нечетная. Пусть Тогдаtg а = -х или х = –tg а = tg(-a), причем Следовательно, – a = arctg х или а = –arctg х. Таким образом, видим, что т. е. у(х) – функция нечетная.

Пример 7

Выразим через все обратные тригонометрические функции

Пусть Очевидно, что Тогда Так как

Введем угол Так как то

Аналогично поэтому и

Итак,

Пример 8

Построим график функции у = cos(arcsin х).

Обозначим а = arcsin x, тогда Учтем, что х = sin а и у = cos а, т. е. x2 + у2 = 1, и ограничения на х (х ∈ [-1; 1]) и у (у ≥ 0). Тогда графиком функции у = cos(arcsin х) является полуокружность.

Пример 9

Построим график функции у = arccos(cos x).

Так как функция cos х изменяется на отрезке [-1; 1], то функция у определена на всей числовой оси и изменяется на отрезке [0; π]. Будем иметь в виду, что у = arccos(cos x) = х на отрезке [0; π]; функция у является четной и периодической с периодом 2π. Учитывая, что этими свойствами обладает функция cos x, теперь легко построить график.

Отметим некоторые полезные равенства:

Пример 10

Найдем наименьшее и наибольшее значения функции Обозначим тогда Получим функцию Эта функция имеет минимум в точке z = π/4, и он равен Наибольшее значение функции достигается в точке z = -π/2, и оно равно Таким образом, и

Пример 11

Решим уравнение

Учтем, что Тогда уравнение имеет вид: или откуда По определению арктангенса получим:

2. Решение простейших тригонометрических уравнений

Аналогично примеру 1 можно получить решения простейших тригонометрических уравнений.

Уравнение	Решение


tgx = а
ctg х = а

Пример 12

Решим уравнение

Так как функция синус нечетная, то запишем уравнение в виде Решения этого уравнения: откуда находим

Пример 13

Решим уравнение

По приведенной формуле запишем решения уравнения: и найдем

Заметим, что в частных случаях (а = 0; ±1) при решении уравнений sin х = а и cos х = а проще и удобнее использовать не общие формулы, а записывать решения на основании единичной окружности:

для уравнения sin х = 1 решения

для уравнения sin х = 0 решения х = πk;

для уравнения sin х = -1 решения

для уравнения cos х = 1 решения х = 2πk;

для уравнения cos х = 0 решения

для уравнения cos х = -1 решения

Пример 14

Решим уравнение

Так как в данном примере имеется частный случай уравнения, то по соответствующей формуле запишем решение: откуда найдем

III. Контрольные вопросы (фронтальный опрос)

1. Дайте определение и перечислите основные свойства обратных тригонометрических функций.

2. Приведите графики обратных тригонометрических функций.

3. Решение простейших тригонометрических уравнений.

IV. Задание на уроках

§ 15, № 3 (а, б); 4 (в, г); 7 (а); 8 (а); 12 (б); 13 (а); 15 (в); 16 (а); 18 (а, б); 19 (в); 21;

§ 16, № 4 (а, б); 7 (а); 8 (б); 16 (а, б); 18 (а); 19 (в, г);

§ 17, № 3 (а, б); 4 (в, г); 5 (а, б); 7 (в, г); 9 (б); 10 (а, в).

V. Задание на дом

§ 15, № 3 (в, г); 4 (а, б); 7 (в); 8 (б); 12 (а); 13 (б); 15 (г); 16 (б); 18 (в, г); 19 (г); 22;

§ 16, № 4 (в, г); 7 (б); 8 (а); 16 (в, г); 18 (б); 19 (а, б);

§ 17, № 3 (в, г); 4 (а, б); 5 (в, г); 7 (а, б); 9 (г); 10 (б, г).

VI. Творческие задания

1. Найдите область определения функции:

Ответы:

2. Найдите область значений функции:

Ответы:

3. Постройте график функции:

VII. Подведение итогов уроков

Источник

	arcsin	arccos	arctg	arcctg
sin	begin{gather} a\ ain[-1;1] end{gather}	begin{gather} sqrt{1-a^2}\ ain[-1;1] end{gather}	begin{gather} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}	begin{gather} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}
cos	begin{gather} sqrt{1-a^2}\ ain[-1;1] end{gather}	begin{gather} a\ ain[-1;1] end{gather}	begin{gather} frac{1}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}	begin{gather} frac{a}{sqrt{1+a^2}}\ ainmathbb{R} end{gather}
tg	begin{gather} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather}	begin{gather} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather}	begin{gather} a\ ainmathbb{R} end{gather}	begin{gather} frac{1}{a}\ ane 0 end{gather}
ctg	begin{gather} frac{sqrt{1-a^2}}{a}\ ain(-1;0)cup(0;1) end{gather}	begin{gather} frac{a}{sqrt{1-a^2}}\ ain(-1;1) end{gather}	begin{gather} frac{1}{a}\ ane 0 end{gather}	begin{gather} a\ ainmathbb{R} end{gather}

Основное соотношение[править | править код]

Функция arcsin[править | править код]

Свойства функции arcsin[править | править код]

Получение функции arcsin[править | править код]

Функция arccos[править | править код]

Свойства функции arccos[править | править код]

Получение функции arccos[править | править код]

Функция arctg[править | править код]

Свойства функции arctg[править | править код]

Получение функции arctg[править | править код]

Функция arcctg[править | править код]

Свойства функции arcctg[править | править код]

Получение функции arcctg[править | править код]

Функция arcsec[править | править код]

Свойства функции arcsec[править | править код]

Функция arccosec[править | править код]

Свойства функции arccosec[править | править код]

Разложение в ряды[править | править код]

Производные от обратных тригонометрических функций[править | править код]

Интегралы от обратных тригонометрических функций[править | править код]

Неопределённые интегралы[править | править код]

Использование в геометрии[править | править код]

Связь с натуральным логарифмом[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

п.1. Понятие арктангенса

п.2. График и свойства функции y=arctgx

п.3. Уравнение tgx=a

п.4. Понятие арккотангенса

п.5. График и свойства функции y=arcctgx

п.6. Уравнение ctgx=a

п.7. Формулы преобразования аркфункций

п.8. Примеры

Вам также может понравиться

Как просто найти площадь стен

Как мне найти свою пенсию

Как найти поваров сушистов

Добавить комментарий Отменить ответ