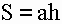В статье о Polygon мы видели, что ромб – четырехугольник с четырьмя параллельными сторонами равной длины. Противоположные углы ромба также равны.
Сходным образом, диагонали ромба пересекаются под прямым углом, и их длины всегда равны. Квадрат – это разновидность ромба, у которого все четыре угла – прямые. Иногда ромб называют ромбом, ромбом или ромбом.
В этой статье вы узнаете, как рассчитать площадь ромба, используя формулы трех областей ромба.
Как рассчитать площадь ромба?
Площадь ромба – это область, ограниченная четырьмя сторонами ромба..
Есть три способа найти площадь ромба.
В одну сторону это за счет использования высоты и стороны ромба. Второй способ влечет за собой использование стороны и угла, и последний метод предполагает использование диагонали.
Эти формулы для вычисления площади ромба известны как формулы площади ромба. Давайте взглянем.
Формула площади ромба
Мы можем найти площадь ромба разными способами. Мы увидим каждого из них по очереди ниже.
Площадь ромба с использованием высоты и основания
Если высота или высота и длина сторон ромба известны, площадь определяется по формуле;
Площадь ромба = основание × высота
A = b × h

Давайте посмотрим, чтобы понять это на примере:
Пример 1
Найдите площадь ромба со стороной 30 см и высотой 15 см.
Решение
A = b × h
= (30 х 15) см2
= 450 см2
Следовательно, площадь ромба 450 см.2.
Пример 2
Рассчитайте площадь ромба, показанного ниже.
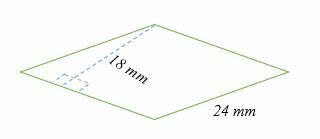
Решение
A = b × h
= (18 x 24) мм2
Пример 3
Если высота и площадь ромба 8 см и 72 см2, соответственно, найдите размеры ромба.
Решение
A = b × h
72 см2 = 8 см x b
Разделите обе стороны на 8.
72 см2/ 8 см = b
б = 9 см.
Следовательно, размеры ромба 9 см на 9 см.
Пример 4
Основание ромба в 3 раза плюс 1 больше высоты. Если площадь ромба 10 м2Найдите основание и высоту ромба.
Решение
Пусть высота ромба = x
и база = 3x + 1
A = b × h
10 м2 = х (3x + 1)
10 = 3x2 + х
3x2 + х – 10 = 0
Решите квадратное уравнение.
⟹ 3x2 + х – 10 = 3х2 + 6x – 5x – 10
⟹ 3х (х + 2) – 5 (х + 2)
⟹ (3х – 5) (х + 2) = 0
⟹ 3x – 5 = 0
⟹ х = 5/3
⟹ х + 2 = 0
х = -2
Теперь подставьте значение x.
Высота = x = 5/3 м
База = 3x + 1 = 3 (5/3) + 1 = 6 м
Итак, основание ромба 6 м, а высота 5/3 м.
Площадь ромба по диагоналям
Учитывая длину диагоналей, площадь ромба равна половине произведения диагоналей.
A = ½ × d1 × d2
Где D1 и г2 диагонали ромба.
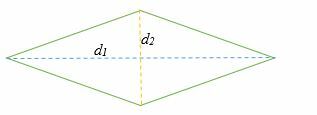
Пример 5
Две диагонали ромба – 12 см и 8 см. Рассчитайте площадь ромба.
Решение:
Пусть d1 = 12 см и d2 = 8 см.
A = ½ × d1 × d2
= (½ × 12 × 8) см2.
= 48 см2.
Пример 6
Рассчитайте длину стороны, если ее площадь составляет 24 см.2, диагональ 8 см, высота 3 см.
Решение
Пусть d1 = 8 см.
d2 =?
A = ½ × d1 × d2
24 см2 = ½ × 8 × d2
24 см2 = 4d2
Разделите обе стороны на 4, чтобы получить,
6 = d2
Следовательно, другая диагональ – 6 см.
Теперь рассчитайте длину сторон ромба.
A = b × h
24 см2 = 3 см x b
Разделите обе стороны на 3.
8 см = б.
Следовательно, длина сторон ромба равна 8 см.
Пример 7
Найдите диагонали ромба, показанного ниже, если его площадь составляет 3458 см.2.
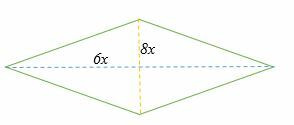
Решение
A = ½ × d1 × d2
3458 см2 = ½ * 6x * 8x
3458 см2 = 24x2
Разделите обе стороны на 24.
3,458 / 24 = х2
144 = х2
Найдите квадратный корень из обеих частей.
х = -12 или 12.
Длина не может быть отрицательным числом; поэтому подставляем только x = 12 в уравнения диагоналей.
6x = 6 * 12 = 72 см
8x = 8 * 12 = 96 см
Следовательно, длины диагоналей 72 см и 96 см.
Пример 8
Допустим, стоимость полировки пола составляет 4 доллара за квадратный метр. Найдите стоимость полировки пола в форме ромба, каждая из диагоналей которого составляет 20 м и 12 м.
Решение
Чтобы узнать стоимость полировки пола, умножьте коэффициент полировки на площадь пола в форме ромба.
A = ½ × 20 м × 12 м
= 120 м2
Стоимость покраски = 120 м.2 х 4 $ за м.
= $480
Площадь ромба с использованием длины сторон и включенного угла.
Площадь ромба равна квадрату длины стороны продукта и синусу угла между двумя сторонами.
Площадь ромба = b2 × Синус (A)
Где A = угол, образованный между двумя сторонами ромба.
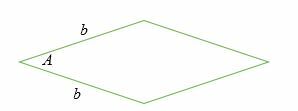
Пример 9
Найдите площадь ромба, стороны которого равны 8 см, а угол между двумя сторонами равен 60 градусам.
Решение
А = б2 × Синус (A)
= 82 x синус (60)
= 55,43 см2.
Практические вопросы
- Найдите длину диагонали ромба, если длина другой диагонали составляет 5 единиц, а площадь ромба составляет 30 квадратных единиц.
- Воздушный змей имеет более короткую диагональ длиной 16 единиц, более короткую сторону длиной 10 единиц и более длинную сторону длиной 17 см. Какова длина другой диагонали?
- Какая площадь у ромба с длиной сторон 18 см и диагональю 20 см?
Содержание:
- Формулы площади ромба:
- Формула периметра ромба:
Ромб – это четырёхугольник, у которого все стороны равны.
Ромб можно рассматривать как частный случай параллелограмма, у которого или две смежные стороны равны, или диагонали
взаимно перпендикулярны, или диагональ делит угол пополам. Ромб с прямыми углами называется квадратом.
Формулы площади ромба:
Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади ромба выражается числом заключающихся в него квадратных единиц.
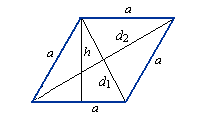
1) Площадь ромба равна произведению длины его стороны на высоту (a, h).
2) Площадь ромба равна половине произведения его диагоналей.
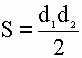
S – площадь ромба
a – длина основания ромба
h – длина высоты ромба
d1 – длина 1-ой диагонали
d2 – длина 2-ой диагонали
См. также: Программа для расчета площади ромба.
Формула периметра ромба:
Периметр геометрической фигуры – суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр ромба равен сумме 4-х длин его сторон или произведению
длины любой его стороны на четыре (так как у ромба длины всех сторон равны).
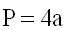
P – периметр ромба
a – длина стороны ромба
Остались вопросы?
Здесь вы найдете ответы.
Что понимается под высотой ромба?
Высота ромба представляет собой перпендикуляр, который опущен из одного из
его углов на сторону, противоположную данному углу.
Высота ромба, опущенная из одного его угла, делит противолежащую сторону
пополам. Как найти величины углов этого ромба?
Обозначим имеющийся ромб как ABCD. Из его угла В проведем высоту ВН, после
чего получим треугольник АВН с прямым углом. Известно, что длина всех
сторон ромба одинаковая, а длина АН равна половине длины АВ. Зная это и
используя теорему, которая является обратной теореме о 30-градусном угле,
можно провести доказательство того, что угол АВН равен 30 градусам.
Учитывая то, что сумма всех углов треугольника равна 180 градусом, можно
найти неизвестную величину третьего угла треугольника:
BAH=180-30-90=60 градусов.
Так, угол АВС равен:
ABC=180-60=120 градусов.
Как найти высоту ромба, если единственной величиной, которая известна,
является длина одной его стороны?
Известна формула площади (S) ромба, которая представляет собой
произведение длины его стороны (а) на высоту (h), проведенную к ней:
S = a*h.
Есть возможность выразить высоту из приведенной выше формулы. Она будет
равна отношению площади ромба к длине его стороны:
h = S/a.
Имеется треугольник с прямым углом и катетами длиной 3 см. и 4 см. Его
площадь аналогична площади ромба со стороной 5 см. Как найти высоту ромба?
Площадь (S) треугольника с прямым углом рассчитывается путем деления
пополам произведения длин его катетов. В данном случае она будет равна:
SΔ = 4*3/2 = 6 см.кв.
Площадь ромба определяется умножением длины его стороны на высоту,
проведенную к ней. Если принять высоту за х, и учесть, что площадь ромба
равна площади прямоугольного треугольника (6 см.кв.), то:
S = 5*x = 6 см.кв.
Отсюда можно найти значение х:
х = 6/5 = 1,2 см.
Ответ: высота ромба составляет 1,2 см.
Как найти высоту ромба при условии, что длины его диагоналей равны 6 см. и 8
см.?
Диагонали, проведенные в ромбе, делят эту фигуру на четыре треугольника,
которые являются равными. Длины катетов этих треугольников составляют 3
см. и 4 см. Такой вывод можно сделать на основании того, что в точке
пересечения диагоналей они делятся пополам. Гипотенуза (с) треугольников
представляет собой сторону ромба. Ее длина равна:
с = √(9+16) = √25 = 5 см.
Следовательно, сторона ромба также равна 5 см.
Площадь ромба высчитывается как произведение длин его диагоналей, деленное
пополам:
S = d1*d2/2 = 6*8/2 = 24 см. кв.
Известна также другая формула, используемая для вычисления площади ромба,
в которой длина его стороны (а) умножается на высоту(h):
S = a*h
Из данной формулы выражаем высоту:
h = S/a = 24/5 = 4,8 см.
Ответ: Высота ромба составляет 4,8 см.
Как найти высоту ромба при условии, что его диагонали равны d1 и d2, а длина
стороны – а?
Высоту ромба можно рассчитать, если его диагонали (d1 и d2)и сторона (а) –
известные величинами. В этом случае для определения неизвестной высоты
следует пользоваться приведенной ниже формулой:
h = (d1 * d2)/a
Площадь ромба составляет 60 см.кв., а его периметр равен 48 см. Как найти
высоту ромба в конкретном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а) и вычисляется по
следующей формуле:
Р = а+а+а+а
В данном случае периметр ромба равен 48 см., это значит, что:
а+а+а+а = 48 см.
Находим значение а:
а = 48/4 = 12 см.
Площадь ромба (S) является произведением длины его стороны (а) и высоты
(h), проведенной к этой стороне:
S = а*h
В задании сказано, что площадь ромба – 60 см.кв. Значит:
а*h=60
Находим неизвестную высоту:
h=60/а=60/12=5 см.
Ответ: Высота ромба – 5 см.
Как найти высоту ромба, зная о том, что его площадь составляет 48 см.кв., а
периметр – 32 см.?
Согласно формуле расчета периметра (Р) ромба, он равен сумме длин всех его
сторон (а) (Р=а+а+а+а). Известно, что все стороны ромба имеет одинаковую
длину. Из этого следует, что длина одной стороны будет равна ¼ части его
периметра:
а = Р/4 = 32/4 = 8 см.
Площадь (S) ромба можно высчитать путем умножения длины его стороны (а) на
высоту (h), проведенную к ней:
S = а* h
В конкретном случае:
48 = 8* h
Отсюда можем найти высоту (h), разделив площадь на длину стороны ромба:
H = 48/8 = 6 см.
Ответ: Высота ромба составляет 6 см.
Отношение длин диагоналей ромба выглядит как 10/24. Его периметр равен 52
см. Как найти высоту ромба в данном случае?
Периметр (Р) ромба равен сумме длин всех его сторон (а), длины которых
равны. Это значит:
Р = 4*а
По условию задачи:
52 = 4*а
Следовательно:
а = 52/13 = 13 см.
Предположим, что длина одной из диагоналей ромба равна 10х, тогда длина
второй его диагонали будет выглядеть как 24х. Отношение их длин можно
записать в следующем виде:
10х:24х=10:24
Доказано, что диагонали ромба взаимно перпендикулярны и в точке
пересечения они делятся пополам, при этом образуя четыре равных
треугольника с прямым углом.
Теорема Пифагора гласит, что сумма длин его катетов, возведенных во вторую
степень, равна длине гипотенузы, которая также возведена в квадрат:
с2 = а2 + b2
Для данной задачи это равенство записывается так:
(5х)²+(12х)²=13²
Отсюда видно, что:
169х²=169; следовательно, х2 = 1. Значит х тоже будет равен 1.
Длина диаметра, обозначенного как 10х, равна 10 см. (10*1), а длина
второго диаметра, который обозначен как 24х, равна 24 см. (24*1).
Площадь (S) ромба рассчитывается как:
S = d₁*d₂/2 или a·h
Из этого можно составить следующее уравнение:
d₁*d₂=2a*h
Выражаем h и получаем:
h= d₁*d₂/2*а=10·24:26=240/26=120/13 см.
Какая формула используется с целью вычисления высоты ромба?
Ромб имеет четыре высоты. Все они имеют равные длины. Вывод об этом можно
сделать, рассмотрев все треугольные фигуры, элементами которых являются
эти высоты. Есть возожность высчитать высоту ромба при помощи различных
параметров, которые могут быть указаны в условии конкретной задачи.
Предположим, что нам известна площадь (S) ромба и длина его стороны (а). В
этом случае высота ромба будет равна отношению его площади к длине высоты:
h = S/a.
Если же по условию задачи известны длины диагоналей ромба d1 и d2, а также
его сторона а, то высоту можно рассчитать так: h = (d1*d2 )/a.
В случае, когда известна длина стороны (а) ромба и угол А, находящийся
между смежными сторонами, то для расчета высоты ромба используется
следующая формула:
h = a*a*sin A /a = a*sin A.
Существуют также и другие варианты вычисления длины высоты ромба на
основании того, какие величины будут известны по условию задания. Однако
ключевыми параметрами, используя которые можно вычислить высоту ромба,
являются диагонали, длина любой его стороны и угол, образованный между
смежными сторонами.
В каком виде записываются формулы, используемые для определения площади
ромба?
Площадь ромба можно рассчитать одним из трех способов:
1. S = a² sin a, в которой α — образованный двумя сторонами угол, a —
сторона.
2. S = ah, или Длина стороны ромба, умноженная на его высоту.
3. S = (d1*d2)/2, в которой d1 и d2 – длины диагоналей фигуры.
На сторону ромба опущена высота, которая на 1,7 см. меньше ее длины.
Периметр фигуры составляет 32 см. Как в данном случае вычислить площадь
ромба?
Зная, чему равен периметр ромба, можно вычислить длину его стороны:
Р/4 = 8 см.
Известно, что высота данной фигуры меньше ее стороны на 1,7 см. Теперь
можем определить длину высоты:
h = 8-1,7 = 6,3 см.
Площадь ромба можно найти, умножив его сторону на высоту, которая на нее
опущена:
8 * 6,3 = 50,4 см².кв.
Ответ: S = 50,4 см. кв.
Известно, что диагонали ромба относятся как 4/3, а его сторона составляет 10
см. Как найти площадь ромба?
Если длины диагоналей фигуры относятся как 4/3, то их половины будут
относиться также:
(4d)²+(3d)²=10² = 16d²+9d² = 100
Отсюда:
25d²=100
d =2,
Значит:
d¹/2 = 4d = 8 см.
d²/2 = 3d = 6 см.
Теперь можно найти площадь:
S= 2*d¹/2*d²/2=2*8*6 = 96 см.кв.
Ответ: S ромба = 96 см.кв.
Как записывается формула расчета площади ромба через длины его диагоналей d1
и d2?
Площадь ромба можно описать как сумму площадей 2-х треугольных фигур,
основанием которых является одна диагональ, а вторая диагональ ромба
представляет собой сумму длин высот этих фигур. Диагонали ромба при
пересечении образуют угол в 90 градусов. На основании этого можно найти
площадь ромба следующим образом:
S = ½ d1*d2.
Как записать формулу вычисления площади ромба через диагонали?
Известно, что, пересекаясь, диагонали ромба образуют угол в 90 градусов и
в точке пересечения делятся пополам.
Для расчета площади ромба через диагонали нужно перемножить их длины, а
затем разделить полученное число на два:
S = ½ d1*d2.
Для примера можно рассмотреть ромб, одна диагональ которого равна 5 см., а
вторая – 4 см. Тогда его площадь будет равна:
S=1/2*5*4=10 см. кв.
Как выглядит формула для определения площади ромба?
S ромба возможно вычислить, перемножив длину одной из его сторон (а) и
высоту (h). Формула записывается так:
S=a*h.
См. также: Программа для расчета периметра ромба.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Rhombus is a special type of Parallelogram which is of huge importance. In a rhombus, all four sides are equal and opposite pairs of lines are congruent, also opposite angles in a rhombus are equal. Rhombus often gets confused with square but Rhombus is very different from the square. Why a rhombus is not considered a square is explained here. Area of the Rhombus is the space occupied by the boundaries of the Rhombus in 2-D space. Area of the Rhombus can be calculated using various methods some of which are discussed in this article.
What is Area of a Rhombus?
Area of the rhombus is considered as the space enclosed by the Rhombus in the 2-D plane. It depends on the dimensions of the rhombus. It is measured in square units, such as square meters, square centimeters, etc. Area of Rhombus is measured using the formulas listed below
Area of Rhombus Formula
Area of the rhombus can be found using various methods some of them are listed in the table below
| Formulas for finding the Area of Rhombus | |
|---|---|
| If Base and Height are given | A = b × h |
| If Diagonals are given | A = ½ × D × d |
| If Base and Interior angle is given | A = b2 × Sin(a) |
Where,
D = length of first diagonal
d = length of second diagonal
b = length of side of rhombus
h = height of rhombus
a = measure of an interior angle
Derivation of Area Formula for Rhombus
Let us consider a rhombus ABCD with O as the point of intersection of two diagonals AC and BD.
The area of rhombus will be
Area = 4 × area of △AOB
= 4 × (1/2) × AO × OB sq.units
= 4 × (1/2) × (1/2) d1 × (1/2) d2 sq.unit
= 4 × (1/8) d1 × d2
= 1/2 d1 × d2
Therefore, the area of a rhombus is A = 1/2 d1 × d2.
How to Find the Area of a Rhombus?
The area of a rhombus is the total space covered or enclosed by the rhombus on a two-dimensional plane. The area of the rhombus can be calculated by three different methods by using diagonal, using base and height, and using trigonometry.
Different methods for finding area of Rhombus are given below
Area of Rhombus using Diagonal
Area = (d1 × d2)/2 sq. units
Where,
d1 is the length of diagonal 1
d2 is the length of diagonal 2
Example 1: Find the area of a rhombus having diagonals 16 m and 18 m.
Solution:
Diagonal 1, d1 = 16 m
Diagonal 2, d2 = 18 m
Area of a rhombus, A = (d1 × d2) / 2
= (16 × 18) / 2
= 288 / 2
= 144 m2
Thus, the area of the rhombus is 144 m2
Area of Rhombus using Base and Height
Area of a Rhombus = b × h sq units
Where,
b is the length of any side of the rhombus
h is the height of the rhombus
Example 2: Find the area of a rhombus having base of 12 m and height is 16 m.
Solution:
Base, b = 12 m
Height, h = 16 m
Area, A = b × h
= 12 × 16 m2
A = 192 m2
Thus, the area of the rhombus is 192 m2
Area of Rhombus using Trigonometric Ratios
Area of a Rhombus = b2 × sin(A) sq. units
Where,
b is the length of any side of the rhombus
A is a measure of any interior angle
Example 3: Find the area of a rhombus if the length of its side is 12 m and one of its angles A is 60°
Solution:
Side = s = 12 m
Angle A = 60°
Area = s2 × sin (60°)
A = 144 × √3/2
A = 72√3 m2
Solved Examples on Area of Rhombus
Example 1: Calculate the area of a rhombus (using base and height) if its base is 5cm and height is 3cm.
Solution:
Given,
Base (b) = 5cm
height of rhombus(h) = 3cm
Now,’
Area of the rhombus(A) = b × h
= 5 × 3
= 15cm2
Example 2: Calculate the area of a rhombus (using diagonal) having diagonals equal to 4cm and 3cm.
Solution:
Given,
Length of diagonal 1 (d1) = 4cm
Length of diagonal 2 (d2) = 3cm
Now,
Area of Rhombus (A) = 1/2 d1 × d2
= 4 x3/2 = 6cm2
Example 3: Calculate the area of the rhombus (using trigonometry) if its side is 8cm and one of its angles A is 30 degrees.
Solution:
Side of the rhombus (b) = 8cm
angle (a) = 30 degrees
Now,
Area of the rhombus(A) = b2 × sin(a)
= (8) × sin(30)
= 64 × 1/2 = 32 cm2
Example 4: Calculate the base of a rhombus if its area is 25cm2 and height is 10cm.
Solution:
Given,
Area = 25 cm2
height of rhombus(h) = 10 cm
Now,
Area of the rhombus(A) = b × h
25 = b × 10
= 2.5 cm
FAQs on Area of Rhombus
Question 1: What do we mean by Rhombus?
Answer:
A rhombus is a type of quadrilateral whose opposite sides are parallel and equal. Also, the opposite angles of a rhombus are equal and the diagonals bisect each other at right angles.
Question 2: Give the Formula for finding the Area of a Rhombus.
Answer:
For finding the area of a rhombus, the given formula is used:
A = ½ × d1 × d2
where, d1 and d2 are diagonals of rhombus
Question 3: How to calculate the perimeter of a rhombus?
Solution:
The perimeter of a rhombus can be calculated by the formula
P= 4b units
where b is a side of the rhombus.
Question 4: How to Find the Area of a Rhombus When the Side and Height are Given?
Answer:
The area of a rhombus its height and side are given is calculated using
A = Base × Height sq units
Question 5: Can area of a rhombus be same as the area of a square?
Answer:
No, The area of a rhombus is not the same as the area of a square. The area of a square is the square of its side, whereas the area of a rhombus is the half the product of diagonal 1 and diagonal 2.
Question 6: Write the Difference between Area of Rhombus and Perimeter of Rhombus.
Answer:
Perimeter of a rhombus is the measure of its boundary and it is calculated by adding the length of all its sides i.e. Perimeter = 4 × sides, whereas area of Rhombus is the product of its base and height, i.e., Area = base × height.
Last Updated :
25 Aug, 2022
Like Article
Save Article

{S = a^2 cdot sin (alpha)}
На этой странице мы предлагаем вам 7 формул площади ромба. Для каждой формулы можно воспользоваться онлайн калькулятором и мгновенно получить результат, не прибегая к помощи обычного калькулятора
Содержание:
- калькулятор площади ромба
- формула площади ромба через сторону и угол
- формула площади ромба через сторону и высоту
- формула площади ромба через диагонали
- формула площади ромба через угол и диагональ из угла
- формула площади ромба через угол и противолежащую диагональ
- формула площади ромба ромба через радиус вписанной окружности и угол
- формула площади ромба через радиус вписанной окружности и сторону
- примеры задач
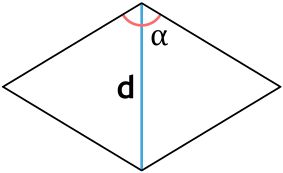
Формула площади ромба через сторону и угол
S = a^2 cdot sin (alpha)
a – сторона ромба
α – угол между сторонами ромба
Формула площади ромба через сторону и высоту
S = a cdot h
a – сторона ромба
h – высота ромба
Формула площади ромба через диагонали
S = dfrac{d_1 cdot d_2}{2}
d1 и d2 – диагонали ромба
Формула площади ромба через угол и диагональ из угла
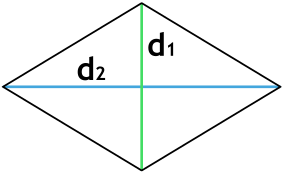
S = dfrac{d^2}{2} cdot \tg(dfrac{alpha}{2})
d – диагональ ромба
α – угол между сторонами ромба, из которого выходит диагональ
Формула площади ромба через угол и противолежащую диагональ
S = dfrac{d^2}{2} cdot ctg(dfrac{alpha}{2})
d – диагональ ромба, противоположная углу α
α – угол между сторонами ромба
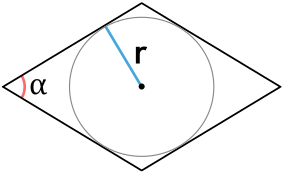
Формула площади ромба через радиус вписанной окружности и угол
S = dfrac{4r^2}{sin(alpha)}
r – радиус окружности
α – угол между сторонами ромба
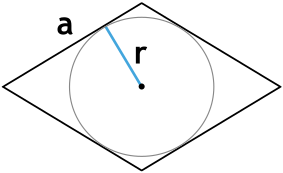
Формула площади ромба через радиус вписанной окружности и сторону
S = 2ar
r – радиус окружности
a – сторона ромба
Примеры задач на нахождение площади ромба
Задача 1
Найдите площадь ромба если его диагонали равны 34 и 4.
Решение
Для решения задачи воспользуемся формулой площади ромба через диагонали.
S = dfrac{d_1 cdot d_2}{2} = dfrac{34 cdot 4}{2} = 68 : см^2
Ответ: 68 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь ромба если его диагонали равны 4 и 6.
Решение
Задача аналогична предыдущей.
S = dfrac{d_1 cdot d_2}{2} = dfrac{4 cdot 6}{2} = 12 : см^2
Ответ: 12 см²
Проверим ответ на калькуляторе .
Задача 3
Найдите площадь ромба стороны которого равны 5, а высота равна 4.
Решение
Воспользуемся формулой площади ромба через высоту и сторону.
S = a cdot h = 5 cdot 4 = 20 : см^2
Ответ: 20 см²
Проверим полученный ответ на калькуляторе .
Ромб — это параллелограмм, в котором все стороны равны друг другу.
Онлайн-калькулятор площади ромба
Если стороны ромба образуют прямой угол, то получим квадрат.
Диагонали ромба пересекаются под прямым углом.
Диагонали ромба являются биссектрисами его углов.
Площадь ромба, как и площади большинства геометрических фигур, можно найти несколькими способами. Разберемся в их сути и рассмотрим примеры решений.
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной aa и высотой hh, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
aa — сторона;
hh — высота, опущенная на сторону aa.
Решим простой пример.
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба SS.
Решение
a=5a=5
h=2h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10 (см. кв.)
Ответ: 10 см. кв.
Формула площади ромба через диагонали
Здесь все так же просто. Нужно просто взять половину произведения диагоналей и получить площадь.
S=12⋅d1⋅d2S=frac{1}{2}cdot d_1cdot d_2
d1,d2d_1, d_2 — диагонали ромба.
Одна из диагоналей ромба равна 7 (см.), а другая в 2 раза больше первой. Найдите площадь фигуры.
Решение
d1=7d_1=7
d2=2⋅d1d_2=2cdot d_1
Найдем вторую диагональ:
d2=2⋅d1=2⋅7=14d_2=2cdot d_1=2cdot 7=14
Тогда площадь:
S=12⋅7⋅14=49S=frac{1}{2}cdot7cdot14=49 (см. кв.)
Ответ: 49 см. кв.
Формула площади ромба через две стороны и угол между ними
S=a2⋅sin(α)S=a^2cdotsin(alpha)
aa — сторона ромба;
αalpha — любой угол ромба.
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
a=10a=10
α=30∘alpha=30^{circ}
По формуле получаем:
S=a2⋅sin(α)=100⋅sin(30∘)=50S=a^2cdotsin(alpha)=100cdotsin(30^{circ})=50 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба по радиусу вписанной окружности и углу
S=4⋅r2sin(α)S=frac{4cdot r^2}{sin(alpha)}
rr — радиус вписанной окружности в ромб;
αalpha — любой угол ромба.
Найти площадь ромба, если угол между основаниями равен 60 градусов, а радиус вписанной окружности – 4 (см.).
Решение
r=4r=4
α=60∘alpha=60^{circ}
S=4⋅r2sin(α)=4⋅16sin(60∘)≈73.9S=frac{4cdot r^2}{sin(alpha)}=frac{4cdot 16}{sin(60^{circ})}approx73.9 (см. кв.)
Ответ: 73.9 см. кв.
Формула площади ромба по радиусу вписанной окружности и стороне
S=2⋅a⋅rS=2cdot acdot r
aa —сторона ромба;
rr — радиус вписанной окружности в ромб.
Возьмем условие из предыдущей задачи, но пусть вместо угла нам известна сторона ромба, равная 5 см.
Решение
a=5a=5
r=4r=4
S=2⋅a⋅r=2⋅5⋅4=40S=2cdot acdot r=2cdot5cdot4=40 (см. кв.)
Ответ: 40 см. кв.
Ищете того, кто сможеит помочь вам решить контрольную работу по геометрии? Наши эксперты окажут вам быструю и качественную помощь с выполнением работы!