Несобственные интегралы, зависящие от параметра. Равномерная сходимость
4 раздела
от теории до практики
10 примеров
Примеры решения задач
видео
Примеры решения задач
-
Равномерная сходимость несобственных интегралов по параметру.
Начать изучение
-
Признаки равномерной сходимости несобственных интегралов по параметру.
Начать изучение
-
Непрерывность, интегрируемость и дифференцируемость несобственного интеграла по параметру.
Начать изучение
-
Перестановка порядка интегрирования в том случае, когда оба интеграла несобственные.
Начать изучение
Равномерная сходимость несобственных интегралов по параметру.
Предположим, что выполнены следующие условия:
- (-infty < a < b leq +infty);
- функция (f(x, y)) определена на множестве пар ((x, y)), где (x in [a, b)), (y in Y), a (Y) есть известное множество параметров;
- для любого (xi in [a, b)) и для любого (y in Y) существует интеграл Римана
$$
intlimits_{a}^{xi} f(x, y) dx;nonumber
$$ - для любого (y in Y) интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится как несобственный, то есть на множестве (Y) определена функция
$$
Phi(y) = intlimits_{a}^{b} f(x, y) dx = lim_{xi rightarrow b-0} intlimits_{a}^{xi} f(x, y) dx.label{ref1}
$$
Если выполнены условия все вышеперечисленные условия, то будем говорить, что несобственный интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) (с особой точкой (b)) сходится на множестве (Y).
Таким образом, несобственный интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится на множестве (Y), если для любого (y in Y) и любого (varepsilon > 0) найдется число (b'(y, varepsilon) < b) такое, что для любого (xi in (b’, b)) выполнено неравенство
$$
left|intlimits_{a}^{b} f(x, y) dx-intlimits_{a}^{xi} f(x, y) dxright| = left|intlimits_{xi}^{b} f(x, y) dxright| < varepsilon.label{ref2}
$$
Аналогичным образом можно рассмотреть несобственный интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) с особой точкой (a), (-infty leq a < b). Если и точка (a), и точка (b) особые, то интеграл нужно разбить на сумму двух интегралов с одной особой точкой. Все три теоремы, которые мы доказывали ранее, вообще говоря, не переносятся на несобственные интегралы, зависящие от параметра, если не накладывать дополнительных ограничений на характер сходимости несобственного интеграла. Например, интеграл
$$
I(y) = intlimits_{0}^{+infty} ye^{-xy} dxlabel{ref3}
$$
сходится при (y geq 0). Очевидно, что (I(0) = 0). Пусть (y > 0). Тогда, полагая (xy = t), получаем, что (I(y) = 1). Следовательно, в точке (y = 0) функция (I(y)) разрывна, несмотря на то, что подынтегральная функция интеграла eqref{ref3} непрерывна на множестве (T = {(x, y): 0 leq x < +infty, 0 leq y leq 1}).
Определение.
Пусть несобственный интеграл (intlimits_{a}^{b} f(x, y) dx) сходится на множестве (Y). Этот несобственный интеграл сходится равномерно по параметру (y) на множестве (Y), если для любого (varepsilon > 0) существует (b’ in [a, b)) такое, что для любого (xi in [b’, b)) и для любого (y in Y) выполнено неравенство
$$
left|intlimits_{xi}^{b} f(x, y) dxright| < varepsilon.nonumber
$$
Пример 1.
Интеграл
$$
intlimits_{0}^{+infty} e^{-x} cos xy dxlabel{ref4}
$$
сходится равномерно по параметру у на интервале ((-infty, +infty) = mathbb{R}).
Решение.
(vartriangle) Для любого (varepsilon > 0) существует (b’ = displaystyleln frac{2}{varepsilon}) такое, что для любого (xi in [b’, +infty)) и любого (y in Y) выполняется неравенство
$$
left|intlimits_{xi}^{+infty} e^{-x} cos xy dxright| leq intlimits_{xi}^{+infty} e^{-x} dx = e^{-xi} leq e^{-b’} = frac{varepsilon}{2} < varepsilon.nonumber
$$
Следовательно, интеграл eqref{ref4} сходится равномерно по параметру (y) на интервале ((-infty, +infty)). (blacktriangle)
Определение.
Если интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится на множестве (Y), но не является равномерно сходящимся по параметру (y) на множестве (Y), то будем говорить, что интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится неравномерно по параметру (y) на множестве (Y).
В этом случае существует (varepsilon > 0) такое, что для любого (b’ in [a, b)) существует (xi in [b’, b)) и существует (y in Y), для которых выполняется неравенство
$$
left|intlimits_{xi}^{b} f(x, y) dxright| geq varepsilon.nonumber
$$
Пример 2.
Интеграл
$$
I_{y} = intlimits_{0}^{+infty} ye^{-xy} dxnonumber
$$
сходится неравномерно по параметру (y) на полуинтервале ([0, +infty)).
Решение.
(vartriangle) Возьмем (varepsilon = e^{-1}). Тогда для любого (b’ in (0, +infty)) существует (xi = b’) и (y = 1/b’) такие, что
$$
intlimits_{xi}^{+infty} ye^{-xy} dx = intlimits_{b’}^{+infty} ye^{-xy} dx = intlimits_{b’y}^{+infty} e^{-t} dt = intlimits_{1}^{+infty} e^{-t} dt = e^{-1} = varepsilon,nonumber
$$
и поэтому интеграл (displaystyle I_{y} = intlimits_{0}^{+infty} ye^{-xy} dx) сходится неравномерно по параметру (y) на множестве (Y = [0, +infty)). (blacktriangle)
Признаки равномерной сходимости несобственных интегралов по параметру.
Теорема 1.
(Признак Вейерштрасса равномерной сходимости несобственного интеграла по параметру).
Пусть для любого (y in Y) функция (f(x, y)) интегрируема по (x) на любом отрезке ([a, b’] subset [a, b)), и пусть на ([a, b)) существует функция (varphi(x)) такая, что для всех (y in Y) и всех (x in [a, b)) выполнено неравенство (|f(x, y)| leq varphi(x)), а несобственный интеграл (displaystyleintlimits_{a}^{b} varphi(x) dx) сходится.
Тогда интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на множестве (Y).
Доказательство.
(circ) Так как (displaystyleintlimits_{a}^{b} varphi(x) dx) сходится, то для любого (varepsilon > 0) найдется число (b in [a, b)) такое, что для всех (xi in [b’, b)) выполнено неравенство (displaystyleintlimits_{a}^{b} varphi(x) dx < varepsilon). Так как (intlimits_{a}^{b} f(x, y) dx) сходится абсолютно при любом (y in Y) по признаку сравнения, то для любого (xi in [b’, b)) и любого (y in Y) выполнено неравенство
$$
left|intlimits_{xi}^{b} f(x, y) dxright| leq intlimits_{xi}^{b} |f(x, y)| dx leq intlimits_{xi}^{b} varphi(x) dx < varepsilon,nonumber
$$
то есть интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на множестве (Y). (bullet)
Пример 3.
Интеграл
$$
intlimits_{0}^{+infty} frac{cos xy}{1+x^{2}} dxlabel{ref5}
$$
сходится равномерно по параметру (y) на интервале ((-infty, +infty)).
Решение.
(vartriangle) Так как (displaystylefrac{|cos xy|}{1+x^{2}} leq frac{1}{1+x^{2}}) и (displaystyleintlimits_{0}^{+infty} frac{dx}{1+x^{2}} = frac{pi}{2}), то по признаку Вейерштрасса интеграл eqref{ref5} сходится равномерно по параметру (y) на ((-infty, +infty)). (blacktriangle)
Докажем признак Дирихле равномерной сходимости для интегралов вида
$$
intlimits_{a}^{+infty} f(x, y) g(x, y) dx, y in Y.label{ref6}
$$
Теорема 2.
(Признак Дирихле равномерной сходимости несобственного интеграла по параметру).
Пусть:
-
- для любого (y in Y subset boldsymbol{R}^{n}) функции (f(x, y)), (g(x, y)) и (displaystylefrac{partial g}{partial x}(x, y)) непрерывны как функции (x) на полуинтервале ([a, +infty));
- функция (F(x, y)), являющаяся при любом (y in Y) первообразной по (x) функции (f(x, y)), ограничена при (y in Y), (x in [a, +infty));
- (displaystylefrac{partial g}{partial x}(x, y) leq 0) при (y in Y) и (x in [a, +infty));
- существует непрерывная на ([a, +infty)) функция (psi(x)) такая, что (displaystylelim_{x rightarrow +infty} psi(x) = 0) и (|g(x, y)| leq psi(x)) для (y in Y) и (x in [a, +infty)).
Тогда интеграл eqref{ref6} сходится равномерно по параметру (y) на множестве (Y).
Доказательство.
(circ) По признаку Дирихле несобственный интеграл eqref{ref6} сходится при любом (y in Y). Покажем, что он сходится равномерно по параметру (y) на множестве (Y).
Так как по условию 4) функция (psi(x) rightarrow 0) при (x rightarrow +infty), то для любого (varepsilon > 0) существует (a’ > a) такое, что для любого (xi in [a’, +infty)) выполнено неравенство
$$
psi(xi) < frac{varepsilon}{2C}label{ref7}
$$
где (C) есть постоянная, ограничивающая в силу условия 2) первообразную (F(x, y)).
Пусть (y in Y) и (xi in [a’, +infty)). Воспользовавшись формулой интегрирования по частям и тем, что (g(x, y) rightarrow 0) при (x rightarrow +infty), получаем
$$
intlimits_{xi}^{+infty} f(x, y) g(x, y) dx = F(xi, y) g(xi, y)-intlimits_{xi}^{+infty} F(x, y) frac{partial g(x, y)}{partial x} dx.label{ref8}
$$
Так как по условиям теоремы
$$
|F(x, y)| leq C,quad frac{partial g}{partial x}(x, y) leq 0,quad |g(x, y)| leq psi(x),nonumber
$$
то из eqref{ref8} и eqref{ref7} получаем, что для любого (xi in [a’, +infty)) выполнено неравенство
$$
left|intlimits_{xi}^{+infty} f(x, y) g(x, y) dxright| leq Cpsi(xi)+intlimits_{xi}^{+infty} Cleft|frac{partial g(x, y)}{partial x}right| dx =\= Cpsi(xi)-Cintlimits_{xi}^{+infty} frac{partial g(x, y)}{partial x} dx = Cpsi(xi)+Cg(xi, y) leq 2Cpsi(xi) < varepsilon.label{ref9}
$$
Из неравенства eqref{ref9} следует, что интеграл eqref{ref6} сходится равномерно по параметру (y) на множестве (Y). (bullet)
Замечание 2.
Если (+infty) — единственная особая точка сходящегося интеграла eqref{ref6}, то этот интеграл сходится равномерно по параметру (y) на множестве (Y) в том и только том случае, когда при любом (a’ > a) интеграл (displaystyleintlimits_{a’}^{+infty} f(x, y) g(x, y) dx) сходится равномерно по параметру (y) на множестве (Y).
Поэтому для справедливости утверждения теоремы 2 достаточно, чтобы условия 1)-4) выполнялись на некотором промежутке ([a’, +infty) subset [a, +infty)).
Пример 4.
Интеграл
$$
intlimits_{0}^{+infty} e^{-xy} frac{sin x}{x} dxlabel{ref10}
$$
сходится равномерно по параметру (y) при (y in [0, +infty)).
Решение.
(vartriangle) Так как функция (sin x) имеет ограниченную первообразную, а при (x geq 1), (y geq 0) выполнены следующие условия:
$$
frac{partial}{partial x} left(frac{e^{-yx}}{x}right) =-frac{e^{-yx}}{x^{2}}(1+xy) < 0, frac{e^{-yx}}{x} leq frac{1}{x}, lim_{x rightarrow +infty}frac{1}{x} = 0,nonumber
$$
то интеграл eqref{ref10} сходится равномерно по параметру (y) на множестве ([0, +infty)). (blacktriangle)
Теорема 3.
(Критерий Коши равномерной сходимости несобственного интеграла по параметру).
Для того чтобы несобственный интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходился равномерно по параметру (y) на множестве (Y), необходимо и достаточно, чтобы для любого (varepsilon > 0) существовало (b’ in [a, b)) такое, что для любых (xi, xi’ in [b’, b)) и для любого (y in Y) выполнялось неравенство
$$
left|intlimits_{xi}^{xi’} f(x, y) dxright| < varepsilon.label{ref11}
$$
Доказательство.
(circ) Необходимость. Пусть (intlimits_{a}^{b} f(x, y) dx) равномерно сходится по параметру (y) на множестве (Y). Тогда для любого (varepsilon > 0) существует (b’ in [a, b)) такое, что для любого (xi in [b’, b)) и для любого (y in Y) выполнено неравенство
$$
|intlimits_{xi}^{b} f(x, y) dx| < frac{varepsilon}{2}.label{ref12}
$$
Пусть (displaystylexi, xi’ in [b’, b)) и (y in Y). Используя неравенство eqref{ref12}, получаем
$$
left|intlimits_{xi}^{xi’} f(x, y) dxright| = left|intlimits_{xi}^{b} f(x, y) dx-intlimits_{xi’}^{b} f(x, y) dxright| leq \ leqleft|intlimits_{xi}^{b} f(x, y) dxright|+left|intlimits_{xi’}^{b} f(x, y) dxright| < frac{varepsilon}{2}+frac{varepsilon}{2} = varepsilon.nonumber
$$
Достаточность. Пусть для любого (varepsilon > 0) существует (b’ in [a, b)) такое, что для любых (xi, xi’ in [b’, b)) и любого (y in Y) выполнено неравенство eqref{ref11}. Тогда в силу критерия Коши сходимости несобственных интегралов (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится при (y in Y). Воспользуемся произвольностью (xi’) и перейдем в неравенстве eqref{ref11} к пределу при (xi’ rightarrow b-0).
Получаем, что для любого (xi in [b’, b)) и для любого (y in Y) выполнено неравенство (displaystyleleft|intlimits_{xi}^{b} f(x, y) dxright| leq varepsilon), из которого следует, что интеграл (intlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на множестве (Y). (bullet)
Применяя правило построения отрицания, получаем из критерия Коши полезное следствие.
Следствие.
Если существует (varepsilon_{0} > 0) такое, что для любого (b’ in [a, b)) существуют (xi_{0}, xi’_{0} in [b’, b)) и существует (y_{0} in Y) такие, что
$$
left|intlimits_{xi_{0}}^{xi’_{0}} f(x, y_{0}) dxright| geq varepsilon_{0},
$$
то интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) не сходится равномерно по параметру (y) на множестве (Y).
Пример 5.
Интеграл
$$
intlimits_{0}^{+infty} e^{-alpha x^{2}} dxlabel{ref14}
$$
сходится равномерно по параметру (alpha) на множестве ([alpha_{0}, +infty)), (alpha_{0} > 0), и сходится неравномерно на множестве ((0, +infty)).
Решение.
(vartriangle) Пусть (alpha geq alpha_{0} > 0). Так как (e^{-alpha x^{2}} leq e^{-alpha_{0} x^{2}}) и (displaystyleintlimits_{0}^{+infty} e^{-alpha x^{2}} dx) сходится, то по признаку Вейерштрасса интеграл eqref{ref14} сходится равномерно по параметру (alpha) на множестве ([alpha_{0}, +infty)).
Пусть теперь (alpha in (0, +infty)). Покажем, что на ((0, +infty)) интеграл eqref{ref14} сходится неравномерно. Воспользуемся следствием из критерия Коши. Возьмем (varepsilon_{0} = e^{-1}), для любого (b > 0) возьмем (xi_{0} = b), (xi’_{0} = b+1), (alpha_{0} = 1/(b+1)^{2}). Тогда
$$
intlimits_{xi_{0}}^{xi’_{0}} e^{-alpha_{0} x^{2}} dx = intlimits_{b}^{b+1} e^{-alpha_{0} x^{2}} dx geq e^{-alpha_{0} (b+1)^{2}} intlimits_{b}^{b+1} dx = e^{-1} = varepsilon_{0}nonumber
$$
и, следовательно, интеграл eqref{ref14} сходится неравномерно по параметру (alpha) на множестве ((0, +infty)). (blacktriangle)
Замечание 2.
Из теоремы 3 легко выводится следующее следствие: если (0 leq f(x, y) leq varphi(x, y)) при (x in [a, b)), (y in Y), (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится на множестве (Y), а интеграл (displaystyleintlimits_{a}^{b} varphi(x, y) dx) сходится равномерно по параметру (y) на множестве (Y), то и интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на множестве (Y).
Непрерывность, интегрируемость и дифференцируемость несобственного интеграла по параметру.
Теорема 4.
Пусть функция (f(x, y)) непрерывна на множестве ({(x, y): a leq x leq b, c leq y leq d}) и интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на отрезке ([c, d]).
Тогда (displaystyleintlimits_{a}^{b} f(x, y) dx) есть непрерывная функция параметра (y) на ([c, d]).
Доказательство.
(circ) Возьмем любое (varepsilon > 0). Так как (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на ([c, d]), то существует (b’ in [a, b)) такое, что для любого (y in [a, b]) выполнено неравенство
$$
left|intlimits_{b’}^{b} f(x, y) dxright| < frac{varepsilon}{3}.label{ref15}
$$
Так как интеграл (displaystyleintlimits_{a}^{b’} f(x, y) dx) является собственным, то в силу теоремы 1, § 71 этот интеграл есть непрерывная функция параметра (y) на ([c, d]). Пусть (y_{0} in [c, d]). Тогда найдется (delta > 0) такое, что для любого (y in [c, d]) такого, что (|y-y_{0}| < delta), имеет место неравенство
$$
left|intlimits_{a}^{b’} f(x, y) dx-intlimits_{a}^{b’} f(x, y_{0}) dxright| < frac{varepsilon}{3}.label{ref16}
$$
Тогда для любого (y in [c, d]) такого, что (|y-y_{0}| < delta), имеем в силу неравенств eqref{ref15} и eqref{ref16}
$$
left|intlimits_{a}^{b} f(x, y) dx-intlimits_{a}^{b} f(x, y_{0}) dxright| leq left|intlimits_{a}^{b’} f(x, y) dx-intlimits_{a}^{b’} f(x, y_{0}) dxright|+\+left|intlimits_{b’}^{b} f(x, y) dxright|+left|intlimits_{b’}^{b} f(x, y_{0}) dxright| < frac{varepsilon}{3}+frac{varepsilon}{3}+frac{varepsilon}{3} = varepsilon.nonumber
$$
Итак, интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) есть непрерывная функция параметра (y) в произвольной точке (y_{0} in [c, d]). (bullet)
Пример 6.
Доказать равенство
$$
lim_{y rightarrow +0} intlimits_{0}^{+infty} e^{-xy} frac{sin x}{x} dx = intlimits_{0}^{+infty} frac{sin x}{x} dx.label{ref17}
$$
Решение.
(vartriangle) Если функцию (displaystylefrac{sin x}{x}) доопределить при (x = 0) по непрерывности, считая, что при (x = 0) функция (frac{sin x}{x}) принимает значение, равное единице, то подынтегральная функция интеграла eqref{ref17} будет непрерывной на множестве ({(x, y): x geq 0, y geq 0}).
При рассмотрении примера 4 было показано, что интеграл eqref{ref10} сходится равномерно по параметру (y) на множестве ([0, +infty)). В силу теоремы 4 интеграл eqref{ref10} есть непрерывная функция параметра (y) на любом отрезке ([0, b]). В частности, эта функция непрерывна при (y = 0), поэтому должно быть выполнено равенство eqref{ref17}. (blacktriangle)
Теорема 5.
(Теорема о перестановке порядка интегрирования).
Пусть функция (f(x, y)) непрерывна на множестве ({(x, y): a leq x leq b, c leq y leq d}) и интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на ([c, d]).
Тогда справедлива формула
$$
intlimits_{c}^{d} dy intlimits_{a}^{b} f(x, y) dx = intlimits_{a}^{b} dx intlimits_{c}^{d} f(x, y) dy.label{ref18}
$$
Доказательство.
(circ) Так как интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится равномерно по параметру (y) на отрезке ([c, d]), то он будет на отрезке ([c, d]) непрерывной, а поэтому и интегрируемой функцией. Повторный интеграл в левой части формулы eqref{ref18} существует. Кроме того, в силу равномерной сходимости интеграла (displaystyleintlimits_{a}^{b} f(x, y) dx) на ([c, d]) для любого (varepsilon > 0) существует (b’ in [a, b)) такое, что для любого (xi in [b’, b)) и любого (y in Y) выполнено неравенство
$$
left|intlimits_{xi}^{b} f(x, y) dxright| < frac{varepsilon}{d-c}.label{ref19}
$$
Применяя теорему о перестановке порядка интегрирования в собственных интегралах, получаем равенство
$$
intlimits_{c}^{d} dy intlimits_{a}^{xi} f(x, y) dx = intlimits_{a}^{xi} dx intlimits_{c}^{d} f(x, y) dy.label{ref20}
$$
Покажем, что интеграл, стоящий в левой части равенства eqref{ref20}, при (xi in b-0) стремится к интегралу в левой части равенства eqref{ref18}. Действительно, в силу неравенства eqref{ref19}
$$
left|intlimits_{c}^{d} dy intlimits_{a}^{b} f(x, y) dx-intlimits_{c}^{d} dy intlimits_{a}^{xi} f(x, y) dxright| = \ = left|intlimits_{c}^{d} dy intlimits_{xi}^{b} f(x, y) dxright| leq intlimits_{c}^{d} left(left|intlimits_{xi}^{b} f(x, y) dxright|right) dy < frac{varepsilon}{d-c} intlimits_{c}^{d} dy = varepsilon.nonumber
$$
Итак, левая часть равенства eqref{ref20} имеет предел при (xi rightarrow b-0). Поэтому, правая часть этого равенства имеет предел при (xi rightarrow b-0). Переходя в равенстве eqref{ref20} к пределу, получаем формулу eqref{ref18}. (bullet)
Пример 7.
Вычислить интеграл Дирихле, доказав, что
$$
intlimits_{0}^{+infty} frac{sin x}{x} dx = frac{pi}{2}.label{ref21}
$$
Решение.
(vartriangle) Воспользуемся известной формулой
$$
intlimits_{0}^{+infty} e^{-xy} sin x dx = frac{1}{1+y^{2}}, y > 0.label{ref22}
$$
Интеграл eqref{ref22} сходится равномерно по параметру (y) на любом отрезке ([delta, N]), где (delta > 0). Это следует из признака Вейерштрасса равномерной сходимости, так как
$$
|e^{-xy} sin x dx| leq e^{-delta x},quad intlimits_{0}^{+infty} e^{-delta x} dx = frac{1}{delta}.nonumber
$$
Применяя теорему 5 и интегрируя равенство eqref{ref22}, получаем
$$
operatorname{arctg} N-operatorname{arctg} delta = intlimits_{0}^{+infty} dx intlimits_{delta}^{N} e^{-xy} sin x dy = intlimits_{0}^{+infty} dfrac{e^{-delta x}-e^{-Nx}}{x} sin x dx.label{ref23}
$$
Так как (|sin x| leq x) при (x geq 0), то
$$
left|intlimits_{0}^{+infty} dfrac{e^{-Nx}sin x}{x} dxright| leq intlimits_{0}^{+infty} e^{-Nx} dx = frac{1}{N}.nonumber
$$
Переходя к пределу при (N rightarrow +infty) в равенстве eqref{ref23}, получаем
$$
frac{pi}{2}-operatorname{arctg} delta = intlimits_{0}^{+infty} e^{-delta x} frac{sin x}{x} dx.
$$
Воспользовавшись равенством eqref{ref17} и переходя к пределу при (delta rightarrow +0), получаем выражение eqref{ref21} для интеграла Дирихле. (blacktriangle)
Теорема 6.
(Теорема о дифференцировании несобственного интеграла по параметру).
Пусть функции (f(x, y)) и (f_{y}(x, y)) непрерывны на множестве ({(x, y): aleq x < b, c leq y leq d}) и интеграл (displaystyleintlimits_{a}^{b} f_{y}(x, y) dx) сходится равномерно по параметру (y) на отрезке ([c, d]).
Тогда если интеграл (displaystyleintlimits_{a}^{b} f(x, c) dx) сходится, то интеграл (displaystyleintlimits_{a}^{b} f(x, y) dx) сходится на отрезке ([c, d]) и является на этом отрезке непрерывно дифференцируемой функцией параметра (y), причем
$$
frac{d}{dy} intlimits_{a}^{b} f(x, y) dx = intlimits_{a}^{b} f_{y}(x, y) dx.label{ref24}
$$
Доказательство.
(circ) Пусть (c leq y leq d). Рассмотрим интеграл (displaystyleintlimits_{a}^{b} f_{y}(x, eta) dx) при (eta in [c, y]).
По условию теоремы этот интеграл сходится равномерно по параметру (eta) на отрезке ([c, y]). В силу теоремы 5 законна перестановка порядка интегрирования
$$
intlimits_{c}^{y} deta intlimits_{a}^{b} frac{partial f}{partial y} f(x, eta) dx = intlimits_{a}^{b} dx intlimits_{c}^{y} frac{partial f}{partial y} f(x, eta) dx = intlimits_{a}^{b} f(x, y) dx+c_{0},label{ref25}
$$
где (c_{0} = -displaystyleintlimits_{a}^{b} f(x, c) dx).
Так как интеграл (displaystyleintlimits_{a}^{b} f(x, eta) dx) сходится равномерно по параметру (eta) на ([c, d]), то этот интеграл будет непрерывной функцией (eta) на этом отрезке, и интеграл, стоящий в левой части равенства eqref{ref25}, будет непрерывно дифференцируемой функцией параметра (y) на отрезке ([c, d]). Но тогда и (displaystyleintlimits_{a}^{b} f(x, y) dx) есть непрерывно дифференцируемая функция на ([c, d]). Дифференцируя обе части равенства eqref{ref25} по (y), получаем формулу eqref{ref24}. (bullet)
Пример 8.
Вычислить интегралы Лапласа
$$
I_{1} = intlimits_{0}^{+infty} frac{cos xy}{1+x^{2}} dx,quad I_{2}(y) = intlimits_{0}^{+infty} frac{xsin xy}{1+x^{2}} dx, y in boldsymbol{R}.nonumber
$$
Решение.
(vartriangle) Пусть (y geq delta > 0). Тогда оба интеграла сходятся равномерно по параметру (y) на ([delta, +infty)) в силу признака Дирихле: функции (cos xy) и (sin xy) имеют ограниченные первообразные, а функции (displaystylefrac{1}{1+x^{2}}) и (displaystylefrac{x}{1+x^{2}}) стремятся к нулю при (x rightarrow +infty), причем
$$
frac{d}{dx} left(frac{1}{1+x^{2}}right) = -frac{2x}{(1+x^{2})^{2}} leq 0,quad frac{d}{dx} left(frac{x}{1+x^{2}}right) = frac{1-x^{2}}{(1+x^{2})^{2}} leq 0nonumber
$$
при (x geq 1).
Дифференцируя (I_{1}(y)) по параметру, получаем
$$
frac{dI_{1}(y)}{dy} = -intlimits_{0}^{+infty} frac{xsin xy}{1+x^{2}} dx = -I_{2}(y), delta leq y < +infty.label{ref26}
$$
Дифференцирование по параметру законно, так как интеграл (I_{2}(y)) сходится равномерно по параметру (y) при (y in [delta, +infty)). Чтобы найти производную (I_{2}(y)), заметим, что при (y geq delta > 0)
$$
I_{2}(y) = intlimits_{0}^{+infty} frac{xsin xy}{1+x^{2}} dx = intlimits_{0}^{+infty} left(frac{1}{x}-frac{1}{x(1+x^{2})}right) sin xy dx =\= intlimits_{0}^{+infty} frac{sin xy}{x} dx-intlimits_{0}^{+infty} frac{xsin xy}{x(1+x^{2})} dx =\= intlimits_{0}^{+infty} frac{sin t}{t} dt-intlimits_{0}^{+infty} frac{xsin xy}{(1+x^{2})x} dx = frac{pi}{2}-intlimits_{0}^{+infty} frac{xsin xy}{(1+x^{2})x} dx.nonumber
$$
Применяя теорему 6, получаем
$$
frac{dI_{2}(y)}{dy} = -intlimits_{0}^{+infty} frac{cos xy}{1+x^{2}} dx = -I_{1}(y), y in [delta, +infty).label{ref27}
$$
Из формул eqref{ref26} и eqref{ref27} следует, что при (y in [delta, +infty))
$$
I’_{1}(y) = -I_{2}(y), I’_{2}(y) = -I_{1}(y), I″_{1}(y)-I_{1}(y) = 0.label{ref28}
$$
Решая это дифференциальное уравнение, получаем
$$
I_{1}(y) = C_{1}e^{-y}+C_{2}e^{y} mbox{при} y in [delta, +infty),label{ref29}
$$
где (C_{1}) и (C2) — произвольные постоянные.
Покажем, что (C_{2} = 0). Так как
$$
|I_{1}(y)| = left|intlimits_{0}^{+infty} frac{cos xy}{1+x^{2}} dxright| leq intlimits_{0}^{+infty} frac{|cos xy|}{1+x^{2}} dx leq intlimits_{0}^{+infty} frac{dx}{1+x^{2}} = frac{pi}{2},nonumber
$$
то (I_{1}(y)) есть ограниченная функция на ([delta, +infty)). Так как (e^{y}) — неограниченная функция на ([delta, +infty)), то в формуле eqref{ref29} нужно принять (C_{2} = 0).
Итак,
$$
I_{1}(y) = C_{1}e^{-y}, I_{2}(y) = -I’_{1}(y) = C_{1}e^{-y} mbox{при} y in [delta, +infty).label{ref30}
$$
Так как (delta) — произвольное положительное число, то из eqref{ref30} следует, что
$$
I_{1}(y) = C_{1}e^{-y} = I_{2}(y) mbox{при} y > 0.label{ref31}
$$
Замечая, что интеграл Лапласа (I_{1}(y)) есть четная функция на ((-infty, +infty)), а интеграл (I_{2}(y)) есть нечетная функция на ((-infty, +infty)), перепишем равенство eqref{ref31} в следующем виде:
$$
I_{1}(y) = C_{1}e^{-|y|}, I_{2}(y) = C_{1} operatorname{sign} ye^{-|y|} mbox{при} y neq 0.label{ref32}
$$
Для определения произвольной постоянной (C_{1}) воспользуемся тем, что интеграл Лапласа (I_{1}(y)) сходится равномерно по параметру (y) на ((-infty, +infty)) (пример 3). Поэтому (I_{1}(y)) есть непрерывная функция в точке (y = 0). Следовательно,
$$
frac{pi}{2} = intlimits_{0}^{+infty} frac{dx}{1+x^{2}} = I_{1}(0) = lim_{y rightarrow +0} I_{1}(y) = lim_{y rightarrow +0} C_{1}e^{-y} = C_{1}.nonumber
$$
Теперь формулы eqref{ref32} дают, что при любом (y in boldsymbol{R})
$$
intlimits_{0}^{+infty} frac{cos xy}{1+x^{2}} dx = frac{pi}{2}e^{-|y|},\ intlimits_{0}^{+infty} frac{xsin xy}{1+x^{2}} dx = frac{pi}{2} operatorname{sign} ye^{-|y|}.label{ref33}
$$
То, что формулы eqref{ref33} справедливы при (y = 0), проверяется непосредственно. (blacktriangle)
Перестановка порядка интегрирования в том случае, когда оба интеграла несобственные.
В теореме 5 была обоснована перестановка порядка интегрирования, когда внутренний интеграл несобственный, а внешний собственный. Сложнее обосновывать перестановку порядка интегрирования, когда оба интеграла несобственные.
Теорема 7.
Пусть функция (f(x, y)) непрерывна на множестве ({(x, y): a leq x leq b, c leq y leq d}) и выполнены следующие условия:
- несобственный интеграл (displaystyleintlimits_{a}^{b} |f(x, y)| dx) сходится равномерно по параметру у на любом отрезке ([c’, d’] subset (c, d));
- несобственный интеграл (displaystyleintlimits_{c}^{d} |f(x, y)| dy) сходится равномерно по параметру у на любом отрезке ([a’, b’] subset (a, b));
- один из двух повторных интегралов
$$
intlimits_{c}^{d} dy intlimits_{a}^{b} |f(x, y)| dx,quad intlimits_{a}^{b} dx intlimits_{c}^{d} |f(x, y)| dynonumber
$$
сходится.
Тогда сходятся оба повторных интеграла (displaystyleintlimits_{a}^{b} dx intlimits_{c}^{d} f(x, y) dy) и (displaystyleintlimits_{c}^{d} dy intlimits_{a}^{b} f(x, y) dx) и
$$
intlimits_{a}^{b} dx intlimits_{c}^{d} f(x, y) dy = intlimits_{c}^{d} dy intlimits_{a}^{b} f(x, y) dx.label{ref34}
$$
Доказательство.
- (circ) Пусть сначала (f geq 0) и существует повторный интеграл (displaystyleintlimits_{a}^{b} dx intlimits_{c}^{d} f(x, y) dy). Возьмем произвольный отрезок ([c’, d’] subset [c, d]). Тогда интеграл по отрезку ([c’, d’]) будет собственным и, применяя теорему 5, получаем
$$
intlimits_{c’}^{d’} dy intlimits_{a}^{b} f(x, y) dx = intlimits_{a}^{b} dx intlimits_{c’}^{d’} f(x, y) dy leq intlimits_{a}^{b} dx intlimits_{c}^{d} f(x, y) dy.label{ref35}
$$
Перестановка интегрирования законна, так как интеграл (displaystyleintlimits_{a}^{b} f_{y}(x, y) dx) сходится равномерно по параметру (y) на отрезке ([c’, d’] subset (x, d)). Последнее неравенство в формуле eqref{ref35} следует из неотрицательности (f) и существования повторного интеграла (displaystyleintlimits_{a}^{b} dx intlimits_{c}^{d} f(x, y) dy). Переходя в формуле eqref{ref35} к пределу при (d’ rightarrow d-0) и (c’ rightarrow c-0) и замечая, что в силу неотрицательности функции (f) интеграл в левой части неравенства eqref{ref35} есть возрастающая функция верхнего предела (d’) и убывающая функция нижнего предела (c’), получаем, что
$$
I_{2} = intlimits_{c}^{d} dy intlimits_{a}^{b} f(x, y) dx leq intlimits_{a}^{b} dx intlimits_{c}^{d} f_{y}(x, y) dy = I_{1}.label{ref36}
$$Проведя еще раз то же самое рассуждение, но для повторного интеграла (displaystyleintlimits_{c}^{d} dy intlimits_{a}^{b} f(x, y) dx), получим вместо неравенства eqref{ref36} неравенство (I_{1} leq I_{2}). Поэтому должно выполняться равенство eqref{ref34}. - Пусть теперь (f(x, y)) — знакопеременная вещественная функция. Представим ее в виде
$$
f = f^{+}-f^{-}, mbox{где} f^{+} = frac{|f|+f}{2}, f^{-} = frac{|f|-f}{2}, f^{+} geq 0, f^{-} geq 0.nonumber
$$
Очевидно, что (0 leq f^{+} leq |f|), (0 leq f^{-} leq |f|).Используя замечание 2 и признаки сравнения для несобственных интегралов, получаем, что для (f^{+}) и (f^{-}) выполнены условия теоремы. В силу первого пункта доказательства повторные интегралы от (f^{+}) и (f^{-}) равны. Поэтому равны и повторные интегралы от функции (f = f^{+}-f^{-}). (bullet)
Замечание 3.
Теоремы 4-7 остаются справедливыми и при замене функции (f(x, y)) на функцию (psi(x)f(x, y)), где функция (psi(x)) интегрируема по Риману на любом отрезке, лежащем в интервале ((a, b)).
Замечание 4.
Если (f(x, y) = varphi(x, y)+ipsi(x, y)) есть комплекснозначная функция, то
$$
|varphi(x, y)| leq |f(x, y)|, |psi(x, y)| leq |f(x, y)|.nonumber
$$
Все условия теоремы будут выполнены и для функций (varphi(x, y)) и (psi(x, y)), если (f(x, y)) удовлетворяет условиям теоремы 7. Поэтому оба повторных интеграла от каждой из этих функций существуют и равны. Следовательно, существуют и равны повторные интегралы от функции (f(x, y)).
Пример 9.
Вычислить интеграл Эйлера-Пуассона (интеграл вероятностей)
$$
I = intlimits_{0}^{+infty} e^{-t^{2}} dt.nonumber
$$
Решение.
(vartriangle) Сделаем замену переменной (t = xy), (y > 0). Тогда
$$
I = y intlimits_{0}^{+infty} e^{-x^{2}y^{2}} dx.nonumber
$$
Умножая это равенство на (e^{-y^{2}}) и интегрируя его от 0 до (+infty) по (y), получаем
$$
I^{2} = intlimits_{0}^{+infty} Ie^{-y^{2}} dy = intlimits_{0}^{+infty} dy intlimits_{0}^{+infty} ye^{-y^{2}(1+x^{2})} dx.label{ref37}
$$
Меняя порядок интегрирования, получаем
$$
I^{2} = intlimits_{0}^{+infty} dx intlimits_{0}^{+infty} ye^{-y^{2}(1+x^{2})} dy = -left.intlimits_{0}^{+infty} frac{e^{-y^{2}(1+x^{2})}}{2(1+x^{2})}right|_{0}^{+infty} dx = frac{1}{2} intlimits_{0}^{+infty} frac{1}{1+x^{2}} = frac{pi}{4},nonumber
$$
откуда
$$
I = intlimits_{0}^{+infty} e^{-x^{2}} dx = frac{sqrt{pi}}{2}.nonumber
$$
Для обоснования законности изменения порядка интегрирования применим теорему 7. Интеграл (displaystyleintlimits_{0}^{+infty} ye^{-y^{2}(1+x^{2})} dx) сходится равномерно по параметру (y) на любом отрезке ([c, d] subset (0, +infty)) по признаку Вейерштрасса, так как (|ye^{-y^{2}(1+x^{2})}| leq de^{-c^{2}(1+x^{2})}) а интеграл (displaystyleintlimits_{0}^{+infty} de^{-c^{2}(1+x^{2})} dx) сходится.
Аналогично доказывается, что интеграл (displaystyleintlimits_{0}^{+infty} ye^{-y^{2}(1+x^{2})} dx) сходится равномерно по параметру (x) на любом отрезке ([a, b] subset (0, +infty)). Повторный интеграл (intlimits_{0}^{+infty} ye^{-y^{2}(1+x^{2})} dx) сходится в силу равенства eqref{ref37}.
Пример 10.
Вычислить интегралы Френеля
$$
J_{1} = intlimits_{0}^{+infty} sin x^{2} dx, J_{2} = intlimits_{0}^{+infty} cos x^{2} dx.
$$
Решение.
(vartriangle) Выполняя замену переменной (y = x^{2}), получаем
$$
begin{array}{cc}
& J_{1} = frac{1}{2} intlimits_{0}^{+infty} frac{sin y}{sqrt{y}} dy = frac{1}{2} lim_{k rightarrow +0} intlimits_{0}^{+infty} e^{-ky} frac{sin y}{sqrt{y}} dy,\
& J_{2} = frac{1}{2} intlimits_{0}^{+infty} frac{cos y}{sqrt{y}} dy = frac{1}{2} lim_{k rightarrow +0} intlimits_{0}^{+infty} e^{-ky} frac{cos y}{sqrt{y}} dy.
end{array}label{ref38}
$$
При написании формул eqref{ref38} использована равномерная сходимость несобственных интегралов в правых частях равенств eqref{ref38} по параметру (k) при (k geq 0) (признак Дирихле).
Выполняя в интеграле Эйлера-Пуассона (displaystyleintlimits_{0}^{+infty} e^{-t^{2}} dt = frac{sqrt{pi}}{2}) замену переменной (t = xsqrt{y}), получаем
$$
intlimits_{0}^{+infty} sqrt{y} e^{-x^{2}y} dx = frac{pi}{2},quad frac{1}{sqrt{y}} = frac{2}{sqrt{pi}} intlimits_{0}^{+infty} e^{-x^{2}y} dx, y > 0.nonumber
$$
Подставляя выражение для (frac{1}{sqrt{y}}) в формулы eqref{ref38} и меняя порядок интегрирования, получаем
$$
J_{1} = frac{1}{pi} lim_{k rightarrow +0} intlimits_{0}^{+infty} dy intlimits_{0}^{+infty} e^{-y(k+x^{2})} sin y dx =\= frac{1}{sqrt{pi}} lim_{k rightarrow +0} intlimits_{0}^{+infty} dx intlimits_{0}^{+infty} e^{-y(k+x^{2})} sin y dy =\= frac{1}{sqrt{pi}} lim_{k rightarrow +0} intlimits_{0}^{+infty} dfrac{dx}{1+(k+x^{2})^{2}} =\= frac{1}{sqrt{pi}} intlimits_{0}^{+infty} frac{dx}{1+x^{4}} = frac{1}{sqrt{pi}} frac{pi}{2sqrt{2}} = frac{1}{2}sqrt{frac{pi}{2}}.nonumber
$$
Аналогично получаем
$$
J_{2} = frac{1}{sqrt{pi}} lim_{k rightarrow +0} intlimits_{0}^{+infty} dx intlimits_{0}^{+infty} e^{-y(k+x^{2})} cos y dy =\=frac{1}{sqrt{pi}} lim_{k rightarrow +0} intlimits_{0}^{+infty} dfrac{k+x^{2}}{1+(k+x^{2})^{2}} dx = frac{1}{sqrt{pi}} intlimits_{0}^{+infty} frac{x^{2}dx}{1+x^{4}} = frac{1}{2}sqrt{frac{pi}{2}}.nonumber
$$
Изменение порядка интегрирования при (k > 0) обосновывается при помощи теоремы 7, предельный переход при (k rightarrow +0) под знаком интеграла возможен в силу его равномерной сходимости по параметру (k) при (k in [0, +infty)) (признак Вейерштрасса). Интегралы (displaystyleintlimits_{0}^{+infty} frac{dx}{1+x^{4}}) и (displaystyleintlimits_{0}^{+infty} frac{x^{2}dx}{1+x^{4}}) вычислены нами ранее (примеры здесь и здесь). (blacktriangle)
Сегодня я подготовил для вас подробную статью о несобственных интегралах.
Определенные интегралы  , для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
, для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
С целью обобщения понятия интеграла рассмотрим:
1) определенные интегралы от непрерывных функций, но с бесконечными пределами интегрирования;
2) определенные интегралы с конечными пределами интегрирования, но от функций, имеющих бесконечный разрыв на промежутке интегрирования. Такие определенные интегралы называют несобственными.
1. Интегралы с бесконечными пределами.
Пусть функция f(x) определена на промежутке [a; +∞) и пусть f(x) интегрирована на любом отрезке [a; b] (b> a– произвольные действительные числа).
Определение 1.1. Предел  интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом:
интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом: 

Если предел (1.1) есть конечное число, то несобственный интеграл  называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл
называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл  называют расходящимся.
называют расходящимся.
Пример 1.1. Исследовать на сходимость интеграл

Решение. Вычислим определенный интеграл

Имеем

Следовательно, заданный интеграл сходится и он равен

Из рассмотренного следует, что вопрос о сходимости (расходимости) несобственных интегралов решается с помощью первоначальной функции для подынтегральной функции. Это обстоятельство сильно сужает круг практического использования понятия несобственного интеграла. В отдельных случаях вопрос о сходимости (расхождении) несобственного интеграла можно решить, не находя первообразной для подынтегральной функции. При этом пользуются так называемыми признаками сходимости несобственных интегралов. Простейшим признаком сходимости является признак сравнения.
Теорема 1.1. Пусть для всех x ≥ a функции f(x) и g(x) определены и выполняются неравенства 0 ≤ f(x) ≤ g(x). Тогда:

Для функции f(x), непрерывной на бесконечном промежутке -∞ < x ≤ b, определяется несобственный интеграл 

Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл  определяется равенством:
определяется равенством:

где с – произвольное действительное число.
2. Интегралы от неограниченных функций.
Пусть функция f(x) такая, что для произвольного малого ɛ>0 она определена, ограничена и интегрирована на отрезке [a+ɛ; b] и неограниченна на (a; b].
Определение 1.2. Предел определенного интеграла  при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом
при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом

Аналогично для функции f(x), определенной, непрерывной и интегрированной на отрезке [a; b- ɛ] и неограниченной на [a; b) обозначается несобственный интеграл:

Если пределы (1.4), (1.5) есть конечные числа, то несобственные интегралы называются сходящимися, а если эти пределы не существуют, то несобственные интегралы называются расходящимися.
В конце отметим, что для функции f(x), которая имеет на промежутке (a; b) точку с, в окрестности которой f(x) неограниченная, но является ограниченной и интегрированной на каждом из отрезков [a; c- ɛ] и [ñ + ɛ; b], интеграл определяется равенством.
Аналогично обозначается несобственный интеграл на отрезке [a; b] от функции, которая непрерывна на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.
Пример 1.2.Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение:

Решение.
а) функция 
ограничена и непрерывна, а потому и интегрируемая. Предельное значение

существует; таким образом,


ограничена и непрерывна, но

 расходится.
расходится.
Пример 1.3. Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение

Решение.

если α > 0, интеграл сходится; если α ≤ 0, то интеграл расходится;

если α > 1; если 0 < α ≤ 1, интеграл расходится как и при α = 1:

так и при 0 < α < 1:

Пример 1.4. Найти несобственный интеграл 
Решение. Функция  непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем
непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем

Поэтому данный интеграл сходится и равен 2√2.
Пример 1.5. Исследовать сходимость интегралы. Для сходящихся интегралов найти их значение:

Решение.

то есть, несобственный интеграл расходится

то есть, несобственный интеграл I2 сходится и равен  .
.
Пример 1.5. Исследовать на сходимость интегралы:

Решение.
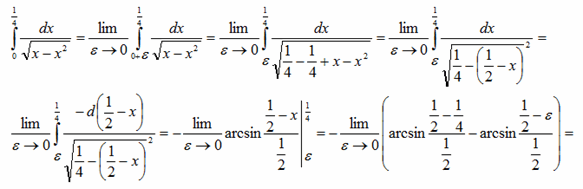
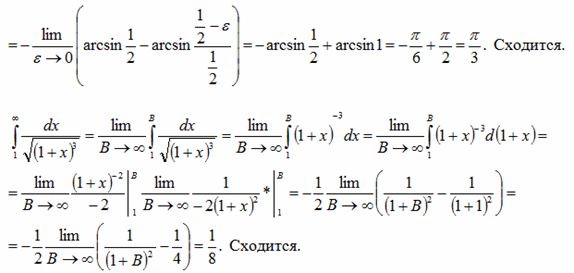
Если у Вас есть ко мне вопросы, или нужна помощь, консультация по решению несобственных интегралов, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Пример
1.
Исследовать сходимость интеграла

.
Функция
![]()
на
промежутке
![]()
имеет
одну особую точку
.
Воспользуемся
определением несобственного интеграла

–
не
существует
![]()
расходится.
Пример
2.
Исследовать сходимость и вычислить ( в
случае сходимости ) интеграл

.

Пример
3.
Исследовать сходимость

.
Заметим,
что так как подынтегральная функция
рациональна, то её первообразная
выражается элементарной функцией. Но
вычисление первообразной здесь громоздко
и для ответа на вопрос воспользуемся
не определением несобственного интеграла,
а признаком сравнения, так как
подынтегральная функция положительна.
Так как особой точкой является
,
интеграл
![]()
сходится
и

,
то
в силу признака сравнения исходный
интеграл сходится.
Пример
4.
Исследовать сходимость интеграла

.
Функция

имеет
на промежутке интегрирования две особые
точки
![]()
и
![]()
.
Следовательно
необходимо рассмотреть сходимость
каждого из
интегралов

и
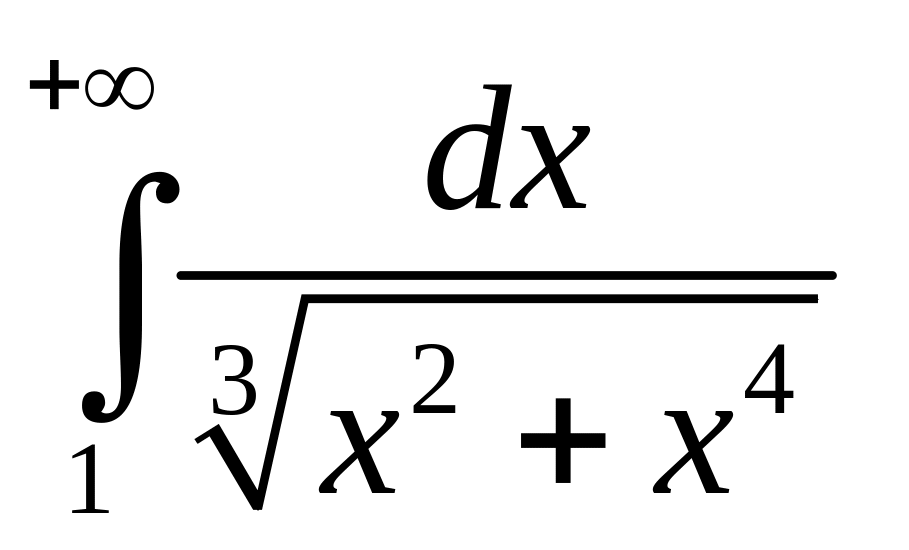
.
Воспользуемся
признаком сравнения

;

.
Так
как оба интеграла
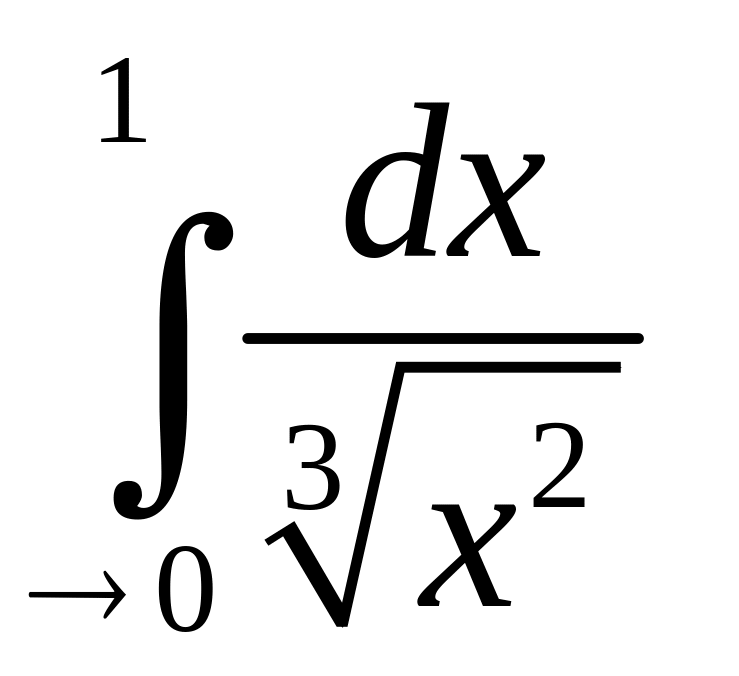
и

сходятся,
то сходится и исходный.
Пример
5.
Исследовать сходимость интеграла

.
Подынтегральная
функция имеет на промежутке
![]()
две
особые точки
и
![]()
.
Разобьем
наш интеграл на два

.
Так
как

и
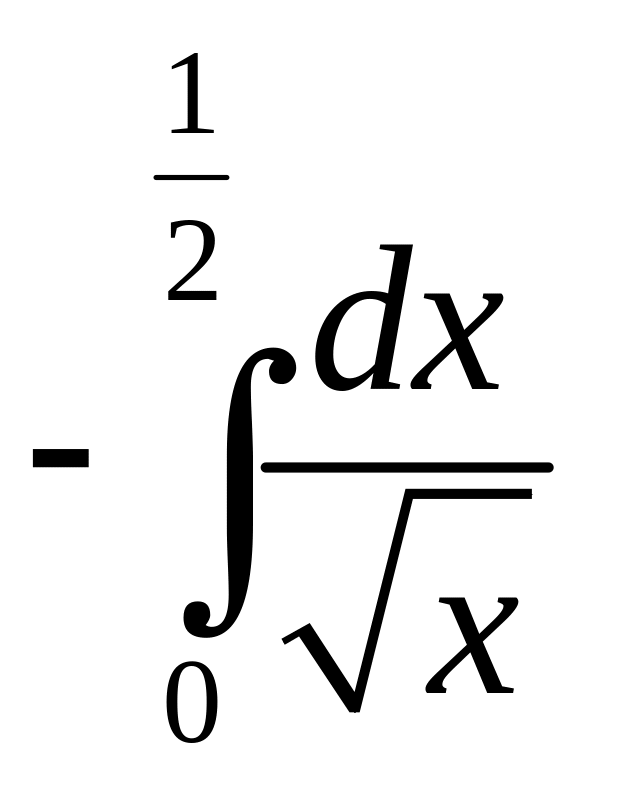
сходится,
то сходится

.
Так
как

и

расходится,
то

расходится.
Следовательно, исходный интеграл
расходится.
Пример
6.
Исследовать сходимость интеграла

.
Особая
точка
.
Так
как
![]()
при
,
то
при достаточно малых
![]()
имеет
место оценка
![]()

.
Подберём
так,
чтобы

.
Тогда
интеграл от «большей» функции
будет
сходится. По признаку сравнения
исходный
интеграл сходится.
Пример
7.
Исследовать абсолютную или условную
сходимость интеграла

.
Функция
![]()
имеет
на
одну
особую точку
,
является
знакопроизвольной. Исследуем сходимость
интеграла по признаку Дирихле.

-ограничена
на
,
функция
![]()
-монотонно
убывает слева в точке
,
так
как

при
![]()
и
![]()
.
Итак,
в силу признака Дирихле, интеграл
сходится.
Для
исследования абсолютной сходимости
данного интеграла воспользуемся оценкой
![]()
.
Имеем

.
Дословно
повторяя приведённые выше рассуждения,
получим, что интеграл

сходится. Так как
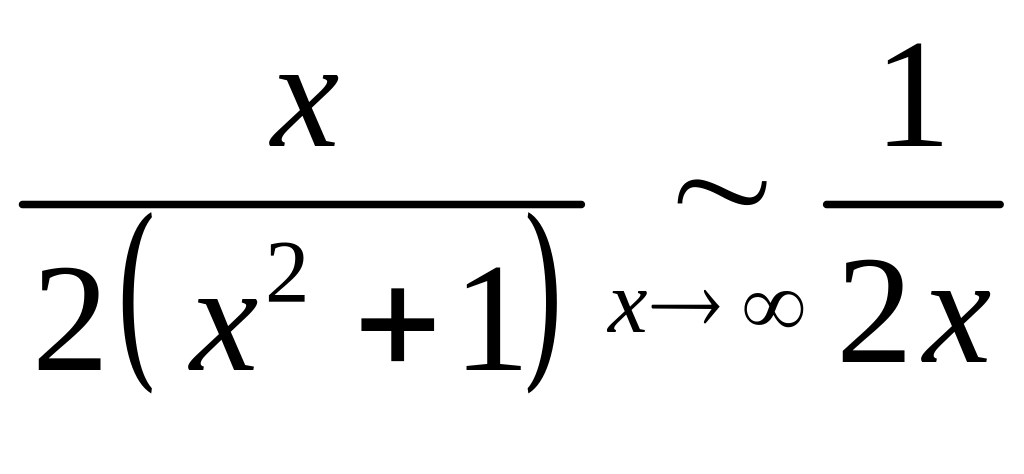
,
то
по признаку сравнения

расходится. Следовательно, интеграл
расходится
и
исходный интеграл сходится условно.
Пример
8.
Исследовать на сходимость несобственные
интегралы
а)
сходится.
б)
расходится.
в)
сходится.
г)
,
(где
![]()
,
так
как
![]()
при
достаточно большом значении
![]()
верна
оценка
![]()
)
Подберём
так,
чтобы
![]()
(тогда интеграл от «большей» функции
будет
сходящимся). При

данный
интеграл сходится.
д)
и интеграл от «меньшей» функции
расходится
исходный интеграл расходится.
е)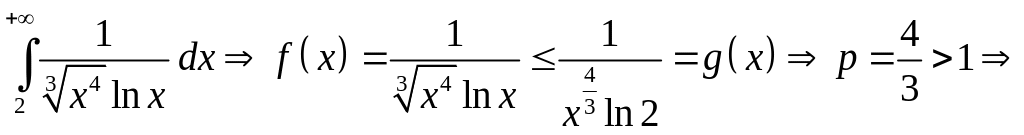
сходится.
«Большая»
функция
,
интеграл
от неё сходится
исходный интеграл сходится.
ж)
.
Подберём
так,
чтобы
![]()
(тогда
интеграл от «меньшей» функции
будет
расходящимся). При
![]()
данный интеграл расходится.
з)
.
Особая точка
,
так
как

.
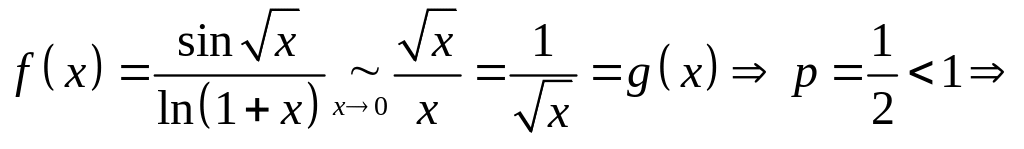
интеграл
сходится.
и)
.
Исследуем на сходимость каждый интеграл.

первый
интеграл сходится.

.
Исследуем
на сходимость интеграл

.
Сделаем
замену в интеграле
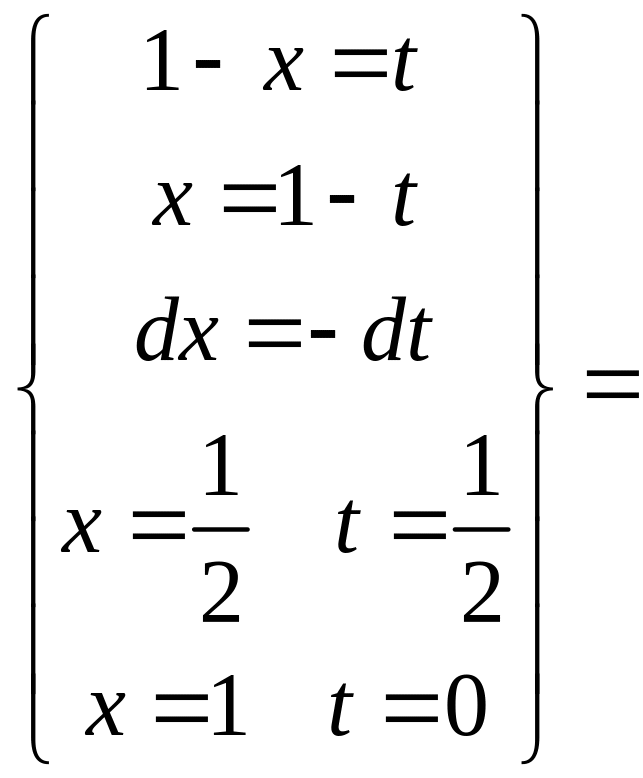

второй
интеграл сходится.
Следовательно,
исходный интеграл сходится.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Примеры исследования несобственных интегралов на сходимость
Пример 1 Исследовать на сходимость  . Вычислим интеграл по определению:
. Вычислим интеграл по определению:  .
.
Таким образом, данный интеграл сходится при a>1 и расходится при a£1.
Пример 2 Исследовать на сходимость ![]() . Вычислим интеграл по определению:
. Вычислим интеграл по определению: 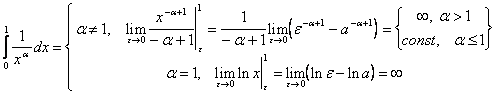 .
.
Таким образом, данный интеграл сходится при a<1 и расходится при a³1.
Пример 3 Исследовать на сходимость ![]() .
.
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два
 .
.
Сходимость первого интеграла I1 исследуем с помощью эквивалентной функции: ![]() ( т. к. n>0), а интеграл
( т. к. n>0), а интеграл![]() сходится при m>-1 (пример 2). Аналогично, для интеграла I2 :
сходится при m>-1 (пример 2). Аналогично, для интеграла I2 :
![]() , а интеграл
, а интеграл![]() сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.
сходится при m+n<-1 (пример2). Следовательно, исходный интеграл сходится при выполнении одновременно двух условий m>-1 и m+n<-1, и будет расходится при нарушении хотя бы одного из них.
Пример 4 Исследовать на сходимость ![]() .
.
Подынтегральная функция может быть бесконечно большой ( если m<0) при x стремящемся к 0, поэтому разобьем исходный интеграл на два:
![]() .
.
Так как arctgx »x при x®0, то интеграл I1 эквивалентен интегралу  , который сходится при m+1>-1 т. е. при m>-2 (пример1).
, который сходится при m+1>-1 т. е. при m>-2 (пример1).
Для подынтегральная функции в несобственном интеграле первого рода I2 подберем эквивалентную:
![]() т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
т. к. arctgx » p/2 при x® ¥. Следовательно, по второму признаку сравнения интеграл I2 будет сходится при m+n<-1, и расходится в противном случае.
Объединяя условия сходимости интегралов I1 и I2 получим условия сходимости исходного интеграла: m>-2 и m+n<-1 одновременно.
Замечание. В примерах 2-4 использовался 2 признак сравнения, который обеспечивает необходимые и достаточные условия сходимости, что позволяет, установив сходимость при некотором условии на значения параметров, не доказывать расходимость интеграла при нарушении полученных условий сходимости.
Пример 5 Исследовать на сходимость  .
.
Данный интеграл содержит особую точку 0, в которой подынтегральная функция может обращается в бесконечность при p<0, поэтому снова разобьем исходный интеграл на два:
![]() .
.
Интеграл I1 является несобственным интегралом второго рода, и подынтегральная функция эквивалентна при x®0 функции xp (e-x ®1 при x®0), т. е. I1 сходится при p>-1 (пример 1).
Интеграл I2 является несобственным интегралом первого рода. Подобрать функцию, эквивалентную подынтегральной функции, такую, чтобы она не содержала показательной функции, не удается. Поэтому использовать признак сравнения 2, как в предыдущих примерах, нельзя. Применим первый признак сравнения, для чего используем следующий известный факт:
![]() При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
При a>0 и любом p. Из этого, и того, что функция xpe-ax непрерывна, следует, что эта функция ограничена, т. е. существует такая константа M>0, что xpe-ax < M. Возьмем, например, a=1/2, и оценим интеграл I2 сверху:
 ,
,
Т. е. интеграл I2 сходится при любом p.
Таким образом, исходный интеграл сходится при p>-1.
Пример 6 Исследовать на сходимость ![]() .
.
Проведем замену переменной: t = lnx, и получим
 .
.
Разбиение интеграла на два произведено аналогично примеру 5. Интеграл I1 полностью эквивалентен интегралу I1 из примера 5 и, следовательно, сходится при q<1.
Рассмотрим интеграл I2 . При условии 1-p<0 этот интеграл полностью эквивалентен интегралу I2 в примере 5 (доказательство сходимости аналогично, а условие 1-p<0 нужно для выполнения ![]() и a=(1-p)/2. ).
и a=(1-p)/2. ).
Итак, I2 сходится при p>1. Однако, на этом исследование сходимости этого интеграла не закончено, так как использованный признак сходимости дает только достаточные условия сходимости. Поэтому нужно исследование сходимости при 1-p£0.
Рассмотрим случай p=1. Тогда интеграл I2 эквивалентен ![]() , который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
, который сходится при q>1 (заметим, что в этом случае интеграл I1 расходится) и расходится в противном случае.
При p<1 оценим интеграл I2 и покажем его расходимость. Для этого вспомним, что ![]() При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T–QE(1-P)T ³ M=const>0. Тогда для интеграла I2 справедлива оценка
При 1-p>0, и, следовательно, начиная с некоторого А>1 выполнено T–QE(1-P)T ³ M=const>0. Тогда для интеграла I2 справедлива оценка
 ,
,
Где интеграл в правой части расходится, что и доказывает расходимость интеграла I2 .
Суммируя полученные результаты, получаем что исходный интеграл сходится при q<1 и p>1, в противном случае интеграл расходится.
Пример 6 Исследовать на абсолютную и условную сходимость ![]() .
.
Разобьем исходный интеграл на два:
 .
.
Сходимость. Интеграл I1 эквивалентен  , т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
, т. е. сходится при p<2 (пример 1) , причем абсолютно, так как подынтегральная функция положительна на отрезке интегрирования.
Интеграл I2 сходится про признаку Дирихле-Абеля при p>0 т. к. первообразная sin(x) ограничена, а функция 1/xp монотонно стремится к нулю при x стремящемся к бесконечности.
Покажем, что при p£0 интеграл расходится. Воспользуемся для этого критерием Коши, а точнее его отрицанием
 .
.
Возьмем в качестве R1и R2 следующие величины: R1=2pk и R2=2pk+p/2, тогда
 , при p>0.
, при p>0.
Таким образом, интеграл сходится при 0<p<1.
Абсолютная сходимость Абсолютная сходимость интеграла I1 уже установлена, рассмотрим абсолютную сходимость I2 . Оценим интеграл сверху:
 , т. е. интеграл сходится при p>1.
, т. е. интеграл сходится при p>1.
Для доказательства расходимости при p£1 оценим интеграл снизу
 .
.
Разобьем последний интеграл от разности функций на разность интегралов
 .
.
Если оба интеграла сходятся, то и интеграл от разности сходится, если один из интегралов расходится, а другой сходится – то интеграл от разности расходится. В случае расходимости обоих интегралов сходимость интеграла от разности подлежит дальнейшему исследованию. Нас интересует второй из описанных случаев.
 расходится (пример 1) при p<1.
расходится (пример 1) при p<1.  сходится по признаку Дирихле-Абеля при 1>p>0 (см. Сходимость), следовательно интеграл
сходится по признаку Дирихле-Абеля при 1>p>0 (см. Сходимость), следовательно интеграл 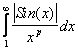 оценивается снизу расходящимся интегралом, т. е. расходится.
оценивается снизу расходящимся интегралом, т. е. расходится.
Случай p³1 нас не интересует, т. к. при этих значениях параметра интеграл ![]() расходится.
расходится.
Таким образом, исходный интеграл сходится абсолютно при 0<p<1, сходится условно при 1£p<2.
| < Предыдущая | Следующая > |
|---|
