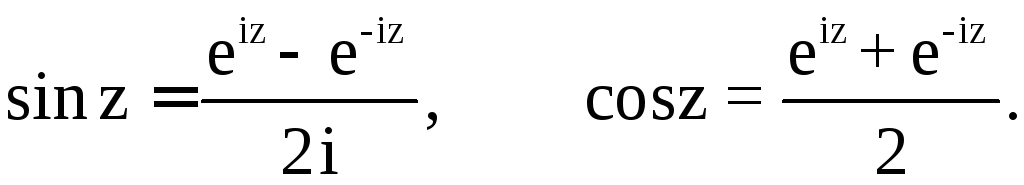Как найти область в комплексной плоскости

2.1. Кривые и области на комплексной плоскости

Областью
на комплексной плоскости называют
множество
точек, обладающее следующими свойствами:

вместе
с каждой точкой из
этому множеству принадлежит и достаточно
малый круг с центром в этой точке
(свойство открытости);

любые
две точки
можно соединить кривой, все точки которой
принадлежат(свойство связности).

Приведем
примеры кривых и областей на комплексной
плоскости.

1. Где
расположены точки
,
для которых,
если– фиксированное комплексное число,?

Решение.
Пусть
,.

Тогда

или
.

Это
уравнение окружности с центром в точке
и радиусом.

2. Где
расположены точки
,
для которых,
если,?

Решение.
Так как
,,
то

.

После
несложных преобразований получим
,
где,,.

Таким
образом, данное равенство определяет
прямую
.

3. Построить
линию
.

Решение.
Так как
,
то данное уравнение примет вид.
Это прямая, проходящая через точкупараллельно оси.

4. Неравенство
определяет верхнюю полуплоскость.

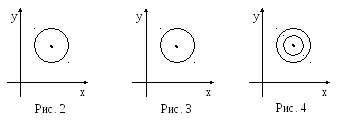
5. Неравенство
определяет круг с центром в точкеи радиусом(рис.2).

6. Неравенство
определяет круг с «проколотым» центром
и радиусом(рис.3).

7. Неравенство
определяет кольцо, ограниченное
окружностями с центром в точке
и радиусами
и(рис.4).

8.Решить:
а) систему уравнений; б), в) неравенства
(геометрически):

а)

б)
;

в)
.

Решение.
а) Перепишем
первое уравнение в виде
.
Множество решений этого уравнения
задаёт окружность радиусом 1 с центром
в точке(см. пример 1). Аналогично находим, что
решением уравненияявляется окружность радиусом 1 с центром
в точке (1+2i).
Решением нашей системы уравнений
являются точки пересечений этих
окружностей.

Запишем
z в алгебраической форме: z = x + yi.

Тогда

Отсюда,
вычитая из первого уравнения второе,
получим
x = 3/2 . Подставив это значение в первое
уравнение, найдём y:;,.
Таким образом, решениями нашей системы
являются числа,.

б) Представление
z
в алгебраической форме приводит нас к
неравенству x

y.
Решением этого неравенства является
замкнутая полуплоскость (заштриховано).

в) Перепишем
неравенство в виде

.

Решением
этого неравенства является кольцо с
центром в точке

(2,
-3i),
внутренний радиус которого равен 1, а
внешний равен 2 (см. пример 7).

Область
называется ограниченной, если существует
кругтакой, что.

Ограниченная
область называется односвязной, если
любую замкнутую кривую, лежащую в
,
можно непрерывно деформировать в точку,
оставаясь в области.
Примером односвязной области является
область на рис. 2. Области на рис. 3 и рис.
4 не являются односвязными.

Пусть
в области
комплексной плоскостиопределена комплекснозначная функция,
то есть каждой точкепоставлено в соответствие комплексное
число.
Эту функцию можно представить в виде.
Таким образом, комплекснозначную функцию
комплексного переменного можно
рассматривать как пару действительных
функций двух действительных переменных,
и многие свойства действительных функций
естественным образом переносятся на
функции комплексного переменного.

Примеры

Функция
.

Здесь
,.

Функция
.
Здесь,.

–многочлен
степени
с комплексными коэффициентами.

Рациональная
функция
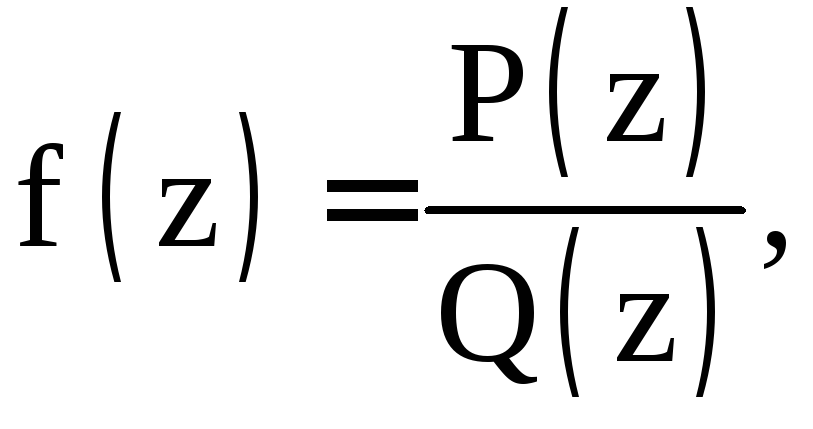
гдеи– многочлены.

Учитывая
формулы Эйлера, функции sin
z
и cos
z
для любого комплексного z
определим равенствами

Отметим,
что все формулы элементарной тригонометрии,
справедливые для действительных x,
остаются справедливыми и при всех
комплексных значениях z.
Кроме того, можно доказать, что уравнения
иимеют решения только прито есть только на действительной оси.
Следовательно, все решения уравнениянаходятся по формулеа все решения уравненияопределяются формулой

Функции
tgz
и ctg
z
для любого комплексного z
определим формулами

Функции
shz,
chz
и
для любого комплексногоz
определим равенствами

Из
определения видно, что
=Таким
образом, свойства функцийинепосредственно
вытекают из свойств функцийsinz,
cosz
и
Отметим
в частности, что все решения уравнениянаходятся по формулеа все решения уравненияопределяются формулой.
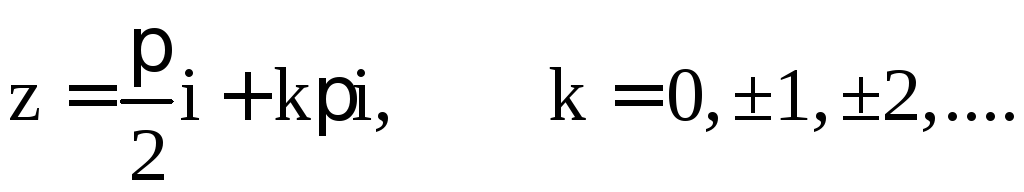
Кроме того, функцииинепрерывны на всей комплексной плоскости,
а функциянепрерывна при,
где

Соседние файлы в папке ТФКП

• #
• #

Областью в комплексной плоскости называется множество D точек этой плоскости, обладающее свойствами:

1) открытости – вместе с точкой из D этому множеству принадлежит и достаточно малая окрестность с центром в этой точке;

2) связности – любые две точки D можно соединить ломаной, целиком состоящей из точек D.

Примером области могут служить окрестности точек на комплексной плоскости. Под e-окрестностью точки z₀ понимают открытый круг радиуса e с центром в этой точке: |z – z₀| < e.

Область называется ограниченной (или конечной), если все ее точки можно поместить в круг достаточно большого конечного радиуса R. В противном случае область называется неограниченной (бесконечной).

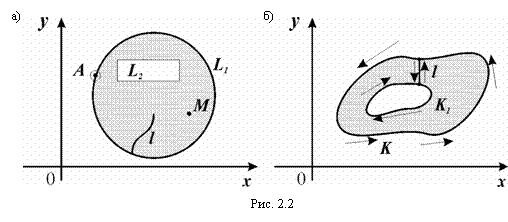
Граничной точкой области D называют такую, которая сама не принадлежит D, но в любой ее окрестности лежат точки этой области (рис. 2.2,а). Совокупность граничных точек области D называется границей этой области.

Например, для  e-окрестности точки z = i  является окружность  |z–i|=e. Так как z = x+iy,  то  |x + iy  –i| = e Þ = e Þ x² + (y – 1)² = e² – окружность радиуса e с центром в точке х = 0,  у = 1 комплексной плоскости.

Область с присоединенной к ней границей называют замкнутой и обозначают D. Будем в дальнейшем предполагать, что граница области состоит из конечного числа замкнутых линий, разрезов (дуг) и точек. Линии и разрезы, входящие в состав границы будем предполагать всегда кусочно-гладкими.

Область называется односвязной, если граница состоит из одной связной линии. Область называется многосвязной, если граница области состоит из нескольких связных частей, например: двухсвязной, трехсвязной и т.д. – по числу не связных между собой частей границы. На рис. 2.2,б – пример двухсвязной области.

Обход односвязной области считается положительным, если она остается по левую руку (контур обходится против хода часовой стрелки). На рис. 2.2,б сделан разрез l, а обход области изображен положительным (область в результате разреза стала односвязной).

Пример 1

Построить области:

а) ;        б) ;      в) ; г) .

Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или неограниченной, односвязной или многосвязной.

Решение:

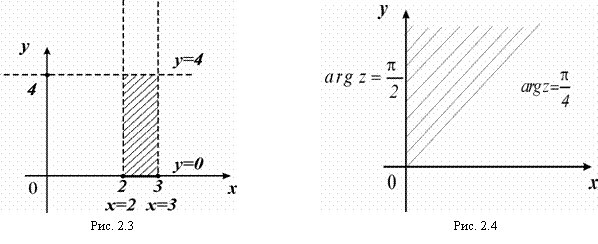
а)  поэтому получим: . Область (рис. 2.3) – замкнутая, ограниченная, односвязная.

б)  и  – лучи, выходящие из начала координат (рис. 2.4). Все точки, удовлетворяющие неравенству б) лежат внутри угла, образованного этими лучами, и на сторонах этого угла. Следовательно, область замкнутая, неограниченная, односвязная.

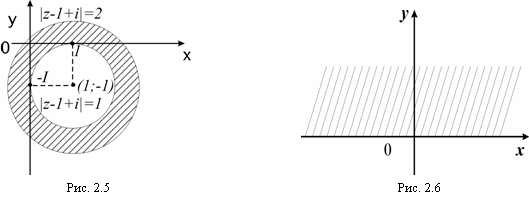
Неравенство  означает, что расстояние каждой точки z от точки  больше 1, но меньше 2. Поэтому областью есть кольцо (его внутренность), ограниченное концентрическими окружностями с центром в точке . Область – открытая, ограниченная, двухсвязная (рис. 2.5).

г) Неравенство  равносильно  или

,

или, возведя в квадрат обе части, получим:

х² + у² – 2у + 1 < х² + у² + 2у + 1.

Отсюда:  – верхняя полуплоскость (рис.

2.6).

Вывод: область у>0 – открытая, неограниченная, односвязная (рис. 2.4).

Определение. Кривая называется непрерывной, если она может быть задана параметрическими уравнениями:

,                                            (2.18)

в которых  – непрерывные функции на отрезке .

Например, окружность ;   дуга окружности           

;    дуга параболы  – непрерывные кривые;   гипербола  не является непрерывной, так как функции эти при    и    имеют точки разрыва.

С помощью комплексного переменного  параметрические уравнения кривой (2.18) можно записать в виде одного уравнения:     

.                                            (2.19)

Например, уравнение эллипса с полуосями a и b можно записать:

;

уравнение окружности радиуса R

;

единичной окружности:

;

уравнение окружности  с центром в точке  запишется так:

.

Задачи для упражнений

1) Построить в комплексной плоскости линии, точки которых удовлетворяют уравнениям:

а)    б)     в)    г)   д)     е)    ж) ;   з)

2) Построить на комплексной плоскости z области, заданные условиями:

а)                б)        в )

г)    д)

Указать, является ли каждая из этих областей открытой или замкнутой, ограниченной или нет, односвязной или многосвязной.

3) Какие кривые определяются следующими уравнениями:

а)     б)                           в) ;

г)            д)    е)

ж) .

Ответы:  а)    б)    в)    г)    д)

е)    ж)

1. КОМПЛЕКСНЫЕ ЧИСЛА, КОМПЛЕКСНАЯ ПЛОСКОСТЬ

Поле комплексных чисел. . Напомним, что комплексными называют числа вида , где  и  – действительные числа,  – мнимая единица. Число  называется действительной частью комплексного числа, число  – мнимой частью. Вводятся обозначения .

  Для комплексных чисел определяют арифметические действия:

Если  и , то

  В частности, если , то . Если  — действительное число, то . Иными словами с выражениями  поступают как с многочленами с переменной , при этом считаем, что . В частности, два числа  и считаются равными, если  и .

        Если  (т. е. ), то существует обратное к  число. Действительно, попробуем найти  в виде . Тогда должно выполниться равенство

  Вычисляя произведение, получим , откуда  и .

  В алгебре показывается, что множество комплексных числе с введенными операциями образует поле. Это, в частности, означает, что общие правила действий с комплексными числами такие же как и с вещественными. Это поле обозначается буквой С.

  Кроме арифметических операций в С вводится операция сопряжения:

.

  Легко проверяется, что и , .

  Множество действительных чисел рассматривается как множество всех тех комплексных чисел, для которых мнимая часть равна нулю. Для таких комплексных числе действия совпадают с обычными арифметическими.

  Заметим, что

                      (1.1)

  Комплексная плоскость. Комплексные числа естественно изображаются точками на плоскости. Если на плоскости выбрать прямоугольную систему координат и на оси абсцисс откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть, то этим устанавливается взаимно однозначное соответствие между комплексными числами и точками плоскости. Тем самым комплексному числу  ставится в соответствие точка с абсциссой  и ординатой . Точку плоскости можно еще описывать ее радиусом–вектором. Тогда становится ясным, что сложению комплексных чисел отвечает сложение радиусов-векторов, их изображающих.

  Легко видеть также, что точки  и  симметричны относительно оси абсцисс. Ось абсцисс теперь естественно называть действительной осью, поскольку на оси абсцисс лежат вещественные числа.

  Плоскость, точки которой отождествлены с комплексными числами, называется комплексной плоскостью. Обозначается она также, как поле комплексных чисел через С.

  Тригонометрическая форма комплексного числа. Комплексное число  иногда удобно записывать в следующей форме

,

где  вещественное число строго большее нуля, а  некоторое вещественное число. Такая форма записи называется тригонометрической.

  Величина  в силу периодичности функции  и  определяется с точностью до целого кратного . Она называется аргументом комплексного числа. Иногда, чтобы подчеркнуть многозначность, ее обозначают через , иногда пишут , помня, что она определяется с точностью до слагаемого вида , где  — целое.

Из равенства

 и                            (1.2)

следует, что . Это число называется модулем комплексного числа и обозначается . Геометрически модуль комплексного числа представляет собой расстояние от начала координат до точки с координатами  и , то есть длину радиуса-вектора, изображающего на плоскости число

  Равенство (1.1) теперь означает, что . Формулу для числа, обратного к можно записать в виде .

  Модуль обладает свойствами:

1.   (неравенство треугольника)

2. 

3.  .

  Свойства 1 и 3 геометрически очевидны, как только мы изобразим комплексные числа точками плоскости. Обоснование свойства 2 дается ниже.

  Рассмотрим вопрос о том, у всякого ли комплексного числа есть тригонометрическая форма и сколькими способами можно записать число в этой форме?

  Если на плоскости ввести систему полярных координат , то, как известно из курса аналитической геометрии, декартовы координаты  и  выражаются через полярные координаты по формулам

  ,

следовательно, любое комплексное число  имеет вид

  Значит  и . Иными словами аргумент комплексного числа -это угол, образованный радиусом-вектором, идущим из начала координат в точку а модуль – это длина этого радиуса-вектора. То есть для отыскания тригонометрической формы достаточно найти полярные координаты соответствующей точки на комплексной плоскости. Так как для начала координат (нуля) вторая полярная координата (угол) не определяется, то тригонометрическая форма нулевого комплексного числа не рассматривается.

  Если каким–то образом получены две тригонометрические формы одного числа, то есть

то очевидно . Поэтому, сокращая равные между собой  и , получим

,

или

 

Из тригонометрии известно, что отсюда следует

 для некоторого целого.

  Таким образом разные тригонометрические формы могут отличаться только своими аргументами, причем разные аргументы отличаются на слагаемое кратное .

  Для чего нужна тригонометрическая форма?

  Пусть  и  Тогда

  Таким образом при перемножении комплексных числе их модули перемножаются, а аргументы складываются:

 

(последнее равенство понимается с точностью до слагаемого , где  целое).

   В частности, при возведении числа в целую положительную степень, аргумент умножается на показатель степени:

Частным случаем этого равенства при  является замечательная формула Муавра

                         (1.3)

  Извлечение корней из комплексных чисел. Корнем -ой степени из комплексного числа  называется решение уравнения

.           (1.4)

  Основное преимущество от введения комплексных чисел состоит в том, что во множестве комплексных числе это уравнение всегда имеет решение, чего как известно, не было, когда мы находились во множестве вещественных чисел. Например, извлечь корень из отрицательного числа во множестве вещественных чисел невозможно. Покажем как можно решить уравнение (1.4).

Если , то решение, очевидно, равно нулю.

Если , рассмотрим число  в тригонометрической форме  Тогда

и поэтому

 и

для некоторого целого

  Следовательно, . Поэтому решение уравнения (1.4) равно

где  — любое целое число. На первый взгляд получается бесконечное множество корней, соответствующих бесконечному множеству целых чисел . На самом же деле, как известно, при разных  числа вида

повторяются при разных , и получается ровно  различных комплексных корней вида

при

  В частности при  получается ровно два корня.

  Множества на комплексной плоскости. Если  и  – точки на комплексной плоскости, то расстояние между ними равно длине вектора, соединяющего  и , то есть расстояние между ними равно .

  Окрестностью точки  радиуса  называется множество всех  для которых . Геометрически такая окрестность является открытым кругом с центром в  и радиусом . В дальнейшем окрестность точки  радиуса  будем обозначать через .

  Множество  называется открытым, если каждая его точка входит в него вместе с некоторой окрестностью. Дополнение к открытому множеству называется замкнутым.

  Открытое множество называется связным, если две любые его точки можно соединить ломаной, целиком лежацей в этом множестве.

  Открытое связное множество называется областью. Это понятие является основным для всего курса.

  Области часто описываются с помощью неравенств.

ПРИМЕРЫ

1.  Im z > 0 — верхняя полуплоскость без вещественной оси.

2.  0 < Re z < 1 — вертикальная бесконечная полоса, лежащая между прямыми x = 0 и x = 1, не включая эти прямые.

3.  |z — z0| < r — внутренность круга радиусом r с центром в z0.

4.   — внутренность кольца между окружностями  и .

5.   — внутренность прямого угла, биссектриса которого совпадает с положительной полуосью .

  Множество  называется ограниченным, если существует такое число , что  при всех . Геометрически это означает, что множество  лежит внутри некоторого круга с центром в начале координат. Из всех перечисленных выше примеров только круг из примера 3 является ограниченным множеством.

  РЕШЕНИЕ ТИПИЧНЫХ ПРИМЕРОВ

Найти действительную мнимую части следующих комплексных чисел:

; ; .

Решение:

Так как , то . Преобразуем следующим образом:

. Тогда .

Аналогичным образом преобразуем :

. Тогда ,

.

Найти модули и аргументы комплексных чисел:

; ; ; .

Решение:

. Находим . Отсюда . Таким образом . Для аналогично находим . Поэтому . . Тогда . . Следовательно, . Итак, ; .

Представить в тригонометрической форме число , считая .

Решение:

,

так как при . Имеем , где , . Таким образом, .

Вычислить, пользуясь формулой Муавра:

; .

Решение:

Представим число в тригонометрической форме: . По формуле Муавра

.

Найти все значения следующих корней:

; ; .

Решение:

1.  Запишем число в тригонометрической форме: . Тогда , следовательно, .

. Тогда , следовательно, . . Тогда , поэтому .

Определение 1. Областью в комплексной плоскости (Z) называется открытое связное множество.

Определение 2. Открытым называется множество, состоящее лишь из внутренних точек.

Определение 3. Точка Z Называется внутренней точкой множества, если она принадлежит ему вместе с некоторой своей окрестностью.

Определение 4. Под – окрестностью точки A понимается открытый круг радиуса с центром в точке A:

. (2.1)

Определение 5. Множество называется связным, если любые две его точки и можно соединить непрерывной кривой, все точки которой принадлежат этому множеству.

Определение 6. Область называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса R с центром в начале координат. Иначе она называется неограниченной.

Определение 7. Границей Г области D называется совокупность точек, не принадлежащих области D, но любая окрестность которых содержит точки, принадлежащие области D.

Определение 8. Область D вместе с границей Г называется замкнутой областью; обозначается это .

Определение 9. Ограниченная область называется односвязной областью, если ее граница состоит из одной связной линии; многосвязной областью, если ее граница состоит из нескольких связных линий. Связной называется линия, из любой точки которой можно перейти по ней в любую другую ее точку.

Определение 10. Говорят, что в области D определена функция , если поставлено в соответствие (по некоторому закону соответствия) одно (однозначная функция) или несколько (многозначная функция) значений W. Пусть . Тогда

. (2.2)

Функция комплексного переменного (ФКП) (2.2) не имеет графика: она соответствует заданию двух действительных функций переменных x и y:

; . (2.2¢)

Геометрический смысл ее состоит в осуществлении отображения точек комплексной плоскости (Z) на соответствующие точки комплексной плоскости (w) (формула (2.2¢)).

Пусть в плоскости (Z) кривая задана уравнением . Чтобы найти уравнение образа этой кривой в плоскости (w) при отображении с помощью функции , нужно исключить X и Y из уравнений

(2.3)

Если кривая задана параметрическими уравнениями или , то параметрические уравнения ее образа при отображении будут

(2.3¢)

Пример 1. Даны множества точек: a) ; б) ; в); г) . Какие из этих множеств являются областями?

Решение. В соответствии с определениями 1-9 заключаем, что множества – открытый круг с центром в точке –I радиуса 3, множество – открытое круговое кольцо с центром в начале координат, множество – открытый угол (см. рис.7) являются областями. Построив множество г):(см. рис.10) убеждаемся, что оно не является областью (не выполняется для него условие связности).

Пример 2. Найти действительную и мнимую часть функции .

Решение. Имеем +; отсюда ; .

Пример 3. В какую кривую отображается единичная окружность с помощью функции ?

Решение. Имеем . Исключая X и Y из уравнений ; ; , получим . Таким образом, окружность преобразуется при преобразовании в окружность в плоскости . Так как , то когда точка z описывает полную окружность , ее образ (точка W) описывает две полные окружности .

< Предыдущая		Следующая >