Как найти область значений функции arccos - Сайт, где вы сможете решить свои вопросы

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика XVIII века Карла Шерфера и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: ${displaystyle sin ^{-1},{frac {1}{sin }},}$ но они не прижились^[1].
Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin⁻¹, cos⁻¹ для арксинуса, арккосинуса и т. п.^[2], — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.

Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, означает множество углов $left ( frac{pi}{6}, frac{5 pi}{6}, frac{13 pi}{6}, frac{17 pi}{6} dots ~ (30^circ, 150^circ, 390^circ, 510^circ dots) right )$ , синус которых равен 1/2 . Из множества значений каждой аркфункции выделяют её главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.

В общем случае при условии все решения уравнения можно представить в виде $x=(-1)^{n}arcsin alpha +pi n,~n=0,pm 1,pm 2,dots ~.$ ^[3]

Основное соотношение[править | править код]

$arcsin x+arccos x={frac {pi }{2}}$

$operatorname {arctg},x+operatorname {arcctg},x={frac {pi }{2}}$

Функция arcsin[править | править код]

График функции

Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого ${displaystyle sin y=x,quad -{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}},quad |x|leqslant 1.}$

Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.

Свойства функции arcsin[править | править код]

Получение функции arcsin[править | править код]

Дана функция y=sin x . На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок , на котором функция y=sin x строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на отрезке существует обратная функция , график которой симметричен графику функции y=sin x относительно прямой y=x .

Функция arccos[править | править код]

График функции

Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого

Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.

Свойства функции arccos[править | править код]

Получение функции arccos[править | править код]

Дана функция y=cos x . На всей своей области определения она является кусочно-монотонной, и, значит, на всей числовой прямой обратное соответствие функцией не является. Поэтому рассмотрим отрезок [0;pi ] , на котором функция y=cos x строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на отрезке [0;pi ] существует обратная функция , график которой симметричен графику функции y=cos x относительно прямой y=x .

Функция arctg[править | править код]

График функции

Аркта́нгенсом числа x называется такое значение угла выраженное в радианах, для которого ${displaystyle operatorname {tg} y=x,quad -{frac {pi }{2}}<y<{frac {pi }{2}}.}$

Функция определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.

Свойства функции arctg[править | править код]

Получение функции arctg[править | править код]

Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал , на котором функция строго монотонно возрастает и принимает все значения своей области значений только один раз. Тогда на интервале существует обратная функция , график которой симметричен графику функции относительно прямой y=x .

Функция arcctg[править | править код]

График функции

Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого

Функция определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго убывающей и всюду положительной.

Свойства функции arcctg[править | править код]

Получение функции arcctg[править | править код]

Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим интервал (0;pi ) , на котором функция строго монотонно убывает и принимает все значения своей области значений только один раз. Тогда на интервале (0;pi ) существует обратная функция , график которой симметричен графику функции относительно прямой y=x .

График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, ) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы

Функция arcsec[править | править код]

График функции

Арксе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого

Функция непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.

Свойства функции arcsec[править | править код]

Функция arccosec[править | править код]

График функции

Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого

Функция непрерывна и ограничена на всей своей области определения. Она является строго убывающей.

Свойства функции arccosec[править | править код]

Разложение в ряды[править | править код]

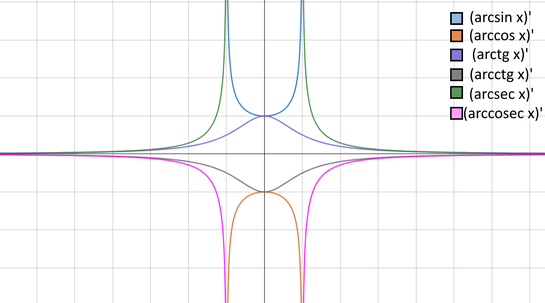
Производные от обратных тригонометрических функций[править | править код]

Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:

производные обратных тригонометрических функций

Функция	Производная	Примечание
	${frac {1}{{sqrt {1-x^{2}}}}}$	Доказательство Найти производную арксинуса можно при помощи взаимно обратных функций. После чего мы должны взять производную этих обеих функций. Теперь мы должны выразить производную арксинуса. ${displaystyle (arcsin(x))'={frac {1}{cos(arcsin(x))}}}$ Исходя из тригонометрического тождества( ${displaystyle sin^{2}x+cos^{2}x=1}$ ) — получаем. ${displaystyle (arcsin(x))'={frac {1}{pm {sqrt {1-sin^{2}(arcsin(x))}}}}}$ Для того, чтобы понять плюс должен стоять или минус взглянем какие значения. ${displaystyle D(cos(x))=[{frac {pi }{2}};-{frac {pi }{2}}]}$ Так как косинус находится в 2-й и 4-й четвертях то, получается что косинус положительный. ${displaystyle (arcsin(x))'={frac {1}{sqrt {1-sin^{2}(arcsin(x))}}}}$ Получается. ${displaystyle (arcsin(x))'={frac {1}{sqrt {1-x^{2}}}}}$
	$-{frac {1}{{sqrt {1-x^{2}}}}}$	Доказательство Найти производную арккосинуса можно при помощи данного тождества: ${displaystyle arcsin(x)+arccos(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arcsin(x)+arccos(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккосинуса. Получается. ${displaystyle (arccos(x))'=-{frac {1}{sqrt {1-x^{2}}}}}$
	${displaystyle {frac {1}{1+x^{2}}}}$	Доказательство Найти производную арктангенса можно при помощи взаимнообратной функции: Теперь находим производную обеих частей этого тождества. ${displaystyle {frac {1}{cos^{2}(arctg(x))}}cdot (arctg(x))'=1}$ Теперь мы должны выразить производную арктангенса: ${displaystyle (arctg(x))'=cos^{2}(arctg(x))}$ Теперь на помощь нам придет на помощь тождество( ${displaystyle cos(x)={frac {1}{sqrt {1+tg^{2}(x)}}}}$ ): ${displaystyle (arctg(x))'=({frac {1}{sqrt {1+tg^{2}(arctg(x))}}})^{2}}$ Получается. ${displaystyle (arctg(x))'={frac {1}{1+x^{2}}}}$
	${displaystyle -{frac {1}{1+x^{2}}}}$	Доказательство Найти производную арккотангенса можно при помощи данного тождества: ${displaystyle arctg(x)+arcctg(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arctg(x)+arcctg(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккотангенса. Получается. ${displaystyle (arcctg(x))'=-{frac {1}{1+x^{2}}}}$
	${displaystyle {frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	Доказательство Найти производную арксеканса можно при помощи тождества: ${displaystyle arcsec(x)=arccos({frac {1}{x}})}$ Теперь находим производную обеих частей этого тождества. ${displaystyle (arcsec(x))'=(arccos({frac {1}{x}}))'}$ ${displaystyle (arcsec(x))'=-{frac {1}{sqrt {1-{frac {1}{x^{2}}}}}}cdot (-{frac {1}{x^{2}}})}$ ${displaystyle (arcsec(x))'={frac {1}{x^{2}{sqrt {frac {x^{2}-1}{x^{2}}}}}}}$ ${displaystyle (arcsec(x))'={frac {1}{x^{2}{frac {sqrt {x^{2}-1}}{\|x\|}}}}}$ Получается. ${displaystyle (arcsec(x))'={frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$
	${displaystyle -{frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	Доказательство Найти производную арккосеканса можно при помощи данного тождества: ${displaystyle arccosec(x)+arcsec(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arccosec(x)+arcsec(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккосинуса. Получается. ${displaystyle (arccosec(x))'=-{frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$

Интегралы от обратных тригонометрических функций[править | править код]

Неопределённые интегралы[править | править код]

Для действительных и комплексных x:

${begin{aligned}int arcsin x,dx&{}=x,arcsin x+{sqrt {1-x^{2}}}+C,\int arccos x,dx&{}=x,arccos x-{sqrt {1-x^{2}}}+C,\int operatorname {arctg},x,dx&{}=x,operatorname {arctg},x-{frac {1}{2}}ln left(1+x^{2}right)+C,\int operatorname {arcctg},x,dx&{}=x,operatorname {arcctg},x+{frac {1}{2}}ln left(1+x^{2}right)+C,\int operatorname{arcsec} x,dx&{}=x,operatorname{arcsec} x-ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C,\int operatorname {arccosec},x,dx&{}=x,operatorname {arccosec},x+ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C.end{aligned}}$

Для действительных x ≥ 1:

${begin{aligned}int operatorname{arcsec} x,dx&{}=x,operatorname{arcsec} x-ln left(x+{sqrt {x^{2}-1}}right)+C,\int operatorname {arccosec},x,dx&{}=x,operatorname {arccosec},x+ln left(x+{sqrt {x^{2}-1}}right)+C.end{aligned}}$

См. также Список интегралов от обратных тригонометрических функций

Использование в геометрии[править | править код]

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.

В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол.
Так, если катет длины является противолежащим для угла alpha , то

Связь с натуральным логарифмом[править | править код]

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

${displaystyle {begin{aligned}arcsin z&{}=-iln(iz+{sqrt {1-z^{2}}})={frac {pi }{2}}-iln(z+{sqrt {z^{2}-1}})=-ioperatorname {arsh} ,iz,end{aligned}}}$

${displaystyle arccos(z)={dfrac {pi }{2}}+iln(iz+{sqrt {1-z^{2}}})=-ioperatorname {arch} (iz)}$

${displaystyle operatorname {arctg} (z)={dfrac {i}{2}}(ln(1-iz)-ln(1+iz))=-ioperatorname {arth} (iz)}$

${displaystyle operatorname {arcctg} (z)={dfrac {i}{2}}left(ln left({dfrac {z-i}{z}}right)-ln left({dfrac {z+i}{z}}right)right)=ioperatorname {arcth} (iz)}$

${displaystyle operatorname {arcsec}(z)=arccos left(z^{-1}right)={dfrac {pi }{2}}+iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right),}$

${displaystyle operatorname {arccosec} ,(z)=arcsin left(z^{-1}right)=-iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right).}$

См. также[править | править код]

Обратные гиперболические функции
Теорема Данжуа — Лузина

Примечания[править | править код]

Ссылки[править | править код]

Weisstein, Eric W. Обратные тригонометрические функции (англ.) на сайте Wolfram MathWorld.
Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: «Советская Энциклопедия», 1982. — [dic.academic.ru/dic.nsf/enc_mathematics/3612/%D0%9E%D0%91%D0%A0%D0%90%D0%A2%D0%9D%D0%AB%D0%95 Т. 3. — с. 1135].
Обратные тригонометрические функции — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1974. — Т. 18. — с. 225.
Обратные тригонометрические функции // Энциклопедический словарь юного математика / Савин А.П. — М.: Педагогика, 1985. — С. 220—221. — 352 с.
Построение графиков обратных тригонометрических функций онлайн
Онлайн калькулятор: обратные тригонометрические функции

Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист.

Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым).

Список проблемных доменов

dic.academic.ru

Источник

По определению арккосинуса числа для каждого

x∈−1;1

существует единственное число

y=arccosx

Поэтому на отрезке

−1;1

определена функция

y=arccosx,где−1≤x≤1.

Функция

y=arccosx

является обратной к функции

y=cosx,где0≤x≤π

График функции

y=arccosx

является симметричным графику функции

y=cosx,где0≤x≤π

, относительно прямой

y=x

Функция

y=arccosx

Основные свойства функции

y=arccosx

1. Область определения — отрезок

−1;1

2. Множество значений — отрезок

0;π

3. Функция

y=arccosx

убывает.

Источник

Как найти арккосинус: формула, свойства, функция

Получение функции arccos

Арккосинус некого числа «х» определяется, как значение угла «у» в радианах (не в градусах), для которого:

(cos y=x,qquad 0leqslant yleqslant pi ,|x|leqslant 1)

Рассмотрим понятие функции (y=cos x). Она обладает областью определения, в рамках которой, как и функция арксинуса, является кусочно-монотонной. По этой причине обратное соответствие, равное (y=arccos x,) нельзя посчитать за функцию.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В данном случае целесообразно проанализировать интервал убывания функции, на котором она принимает все свои значения: ([0;pi ]). Данный отрезок характеризуется строго монотонным убыванием функции (y=cos x), где она принимает все свои значения лишь однажды.

Таким образом, на отрезке ([0;pi ]) можно заметить обратную функцию (y=arccos x). График этой обратной функции является симметричным графику (y=cos x) на интервале ([0;pi ]) по отношению к первой прямой (y=x).

Свойства функции arccos

Функция arccos обладает следующими свойствами, которые можно использовать при математических и инженерных вычислениях. Данные свойства следует знать, чтобы решать задачи разной степени сложности:

(arccos(-x)=pi -arccos x). Функция является центрально-симметричной по отношению к точке (left(0;{frac {pi }{2}}right)). Данную функцию определяют, как индифферентную, то есть не относят к четным или нечетным. Это является ответом на вопрос о четности функции.
(arccos x>0), если при приведении обнаружено, что (-1leqslant x<1).
(arccos x=0) когда (x=1).
(arccos x={frac {pi }{2}}-arcsin x).
(arccos x=left{{begin{matrix}arcsin {sqrt {1-x^{2}}},qquad 0leqslant xleqslant 1\pi -arcsin {sqrt {1-x^{2}}},qquad -1leqslant x<0end{matrix}}right.)
(arccos x=operatorname {arcctg} {frac {x}{sqrt {1-x^{2}}}}).
(arccos x=left{{begin{matrix}operatorname {arctg},{frac {{sqrt {1-x^{2}}}}{x}},qquad 0<xleqslant 1\pi +operatorname {arctg},{frac {{sqrt {1-x^{2}}}}{x}},qquad -1leqslant x<0end{matrix}}right.)
(arccos x=2arcsin {sqrt {frac {1-x}{2}}}).
(arccos x=2arccos {sqrt {frac {1+x}{2}}}.)
(arccos x=2operatorname {arctg}{sqrt {frac {1-x}{1+x}}}).

График функции (y = arccosx)

Функция y=arccos x не прерывается и ограничивается на протяжении всей своей области определения. Данная функция строго убывает и не является отрицательной. Характеристики понятия функции arccos, которые используют при ее нахождении:

(cos(arccos x)=x, когда -1leqslant xleqslant 1 ) (от минус единицы до плюс единицы);
(arccos(cos y)=y, если 0leqslant yleqslant pi 😉
(D(arccos x)=[-1;1]) является областью определения;
(E(arccos x)=[0;pi ]) является областью множества значений.

Функцию (y=arccos x) можно изобразить графически. В результате нужный график принимает следующий вид:

Источник: ru.wikipedia.org

Основное соотношение

При решении задач принято использовать главные соотношения в виде формул. К примеру, уравнения:

(arcsin x+arccos x={frac {pi }{2}})

(operatorname {arctg},x+operatorname {arcctg},x={frac {pi }{2}})

Источник

Алгебра и начала математического анализа, 11 класс

Урок №6. Обратные тригонометрические функции.

Перечень вопросов, рассматриваемых в теме

Рассмотреть свойства арксинуса и арккосинуса;
Рассмотреть свойства арктангенса и арккотангенса;
Объяснять расположение промежутков монотонности;
Определять наибольшее и наименьшее значение функции;
Применять знания при решении задач.

Глоссарий по теме

Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения и множество значений .

Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения и множество значений

Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения и множество значений .

Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения и множество значений

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.

Дополнительная литература:

Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.

Открытые электронные ресурсы:

Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/

Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Актуализация знаний

Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен ? Первое, что хочется ответить, что это угол 60° или , но вспомнив о периоде косинуса, понимаем, что углов, при которых косинус равен , бесконечное множество. И такое множество значений углов, соответствующих данному значению тригонометрической функции, будет наблюдаться и для синусов, тангенсов и котангенсов, т.к. все они обладают периодичностью. Для внесения точности для каждой из обратных тригонометрических функций диапазон углов, которые она возвращает, выбран свой, и мы их рассмотрим отдельно.

Объяснение нового материала

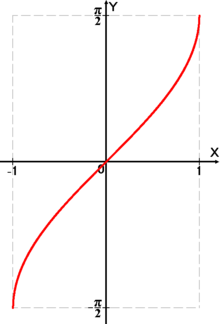
Рассмотрим свойства функции y=arcsin x и построим ее график.

Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).

Свойства	Функции y=arcsin х
E(f)
D(f)
Чётность	Нечётная, т.к. arcsin(-x)= – arcsin x
Промежутки монотонности	Возрастающая

Рис.1 График функции y=arcsin х

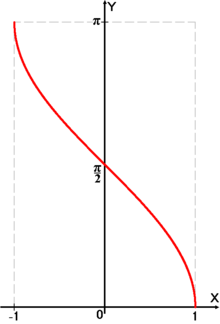
Рассмотрим свойства функции y=arcos x и построим ее график.

Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ).

Свойства	Функции y=arccos х
E(f)
D(f)
Чётность	Ни чётная, ни нечётная
Промежутки монотонности	Убывающая

Рис.2 График функции y=arccos х

Рассмотрим свойства функции y=arctgx и y=arcctgx и построим их графики.

Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ).

Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ).

Свойства	y=arctg х	y=arcctg х
E(f)	R	R
D(f)
Чётность	Нечётная	Нечётная
Промежутки монотонности	Возрастающая	Убывающая