Как найти область значения функции онлайн калькулятор – Сайт, где вы сможете решить свои вопросы

Областью значений
некоторой функции

называется множество, содержащее все значения которые могут получиться при подстановке в эту функцию всех допустимых значений аргумента
.
Область значений функции обозначается
.

Проиллюстрируем вышесказанное на конкретном примере. Рассмотрим функцию
,
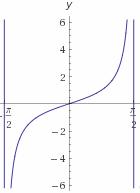
график которой изображён на рисунке.

График функции e^(-x^2)

Из графика нетрудно заметить, что какие бы значения аргумента

мы не подставляли бы в функцию
,
возвращаемое значение всегда будет находиться в диапазоне от

до
. Таким образом, область значений рассматриваемой функции от

до
.

Данный факт можно записать следующим образом:

Наш онлайн калькулятор построен на основе системы Wolfram Alpha. Калькулятор позволяет найти область определения практически любой функции.

Источник

Множество значений функции

Онлайн калькулятор поможет найти множество значений (область значений) функции — все значения, которые принимает функция в ее области определения. Другими словами, это те значения у, которые получаются при подстановке всех возможных значений х.

Теперь рассмотрим следующий вопрос: Как найти множество значений функции? Решение этой задачи с помощью онлайн калькулятора не составит труда, просто введите нужную функцию и получите ответ.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

Главная » Примеры решения задач » Онлайн калькулятор

Найти область значения функции

Калькулятор для нахождения области значения функции онлайн (бесплатно). Правила ввода функции как на обычном калькуляторе.

Найти область определения функции

Правила ввода функций:

Основные константы

Число $pi$ : Pi
Число $e$ : E
Бесконечность $infty$ : Infinity или inf

Основные функции

$left(a=operatorname{const} right)$

$x^{a}$ : x^a

модуль x: abs(x)

$sqrt{x}$ : Sqrt[x]
$sqrt[n]{x}$ : x^(1/n)
$a^{x}$ : a^x
$log_{a}x$ : Log[a, x]
$ln x$ : Log[x]
$cos x$ : cos[x] или Cos[x]
$sin x$ : sin[x] или Sin[x]
$operatorname{tg}x$ : tan[x] или Tan[x]
$operatorname{ctg}x$ : cot[x] или Cot[x]
$sec x$ : sec[x] или Sec[x]
$operatorname{cosec} x$ : csc[x] или Csc[x]
$arccos x$ : ArcCos[x]
$arcsin x$ : ArcSin[x]
$operatorname{arctg} x$ : ArcTan[x]

$operatorname{arccosec} x$ : ArcCsc[x]
$operatorname{ch} x$ : cosh[x] или Cosh[x]
$operatorname{sh} x$ : sinh[x] или Sinh[x]
$operatorname{th} x$ : tanh[x] или Tanh[x]
$operatorname{cth} x$ : coth[x] или Coth[x]
$operatorname{sech} x$ : sech[x] или Sech[x]
$operatorname{cosech} x$ : csch[x] или Csch[е]
$operatorname{areach} x$ : ArcCosh[x]
$operatorname{areash} x$ : ArcSinh[x]
$operatorname{areath} x$ : ArcTanh[x]
$operatorname{areacth} x$ : ArcCoth[x]
$operatorname{areasech} x$ : ArcSech[x]
$operatorname{areacosech} x$ : ArcCsch[x]
$operatorname{arcctg} x$ : ArcCot[x]
$operatorname{arcsec} x$ : ArcSec[x]

Поможем с решением ваших задач и контрольных!

Категория: Онлайн калькулятор | Просмотров: 198985 | Добавил: Admin | Теги: онлайн калькулятор | Рейтинг: 3.6/24

Похожие материалы:

Решение логарифмических уравнений
Решение дифференциальных уравнений
Решение квадратных уравнений
Решение кубических уравнений
Исследовать функцию, построить график
Решение тригонометрических уравнений
Найти неопределенный интеграл
Найти область определения функции
Сходимость рядов
Найти предел функции

Всего комментариев: 0

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

y=frac{x^2+x+1}{x}
f(x)=x^3
f(x)=ln (x-5)
f(x)=frac{1}{x^2}
y=frac{x}{x^2-6x+8}
f(x)=sqrt{x+3}
f(x)=cos(2x+5)
f(x)=sin(3x)
Показать больше

Описание

Изучите функции шаг за шагом

functions-calculator

Блог-сообщения, имеющие отношение к Symbolab

Functions

A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Область существования функции

Данный сервис используется для нахождения области определения функции в онлайн режиме.

Например, найти область определения функции ln(x²-1).

Примечание: число “пи” (π) записывается как pi; корень квадратный как sqrt, например, sqrt(3); arcsin ≡ asin

В таблице приведены области существования наиболее распространенных функций.

ln(x)	x > 0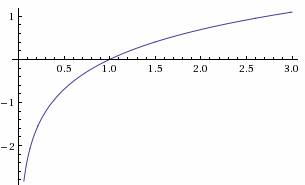
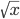	x ≥ 0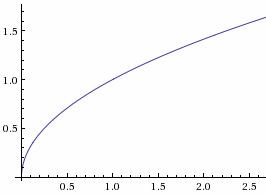
tgx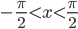
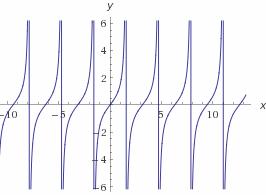ctgx	0 < x< π
arcsinx	-1 ≤ x ≤ 1
arccosx	-1 ≤ x ≤ 1

Пример. Требуется найти область определения функции, для этого нужно знать области определения элементарных функций.

Найдем область определения 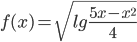. Функция определена при тех значениях x, для которых 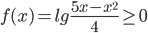. Это неравенство будет выполнено, если 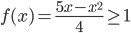, т.е. x²–5x+4≤0. Решая это неравенство методом интервалов, находим область определения – промежуток [1;4]. Зная f(x), можно найти и т.д.