Общие сведения
Функцией вида р = f(r) называется зависимость ее значения от переменной величины “r” или аргумента. Функциональные тождества бывают простыми и сложными. К первым относится класс выражений, состоящих из одной переменной простого типа. Во втором случае содержится несколько аргументов или аргумент является также функцией, т. е. подчиняется определенному закону.
Монотонной называется функция, постоянно убывающая или возрастающая на заданном промежутке. Если она постоянно убывает или возрастает, то считается строго монотонной. Пусть дана функция р = f(r). Она дифференцируема на некотором интервале (а;b), является возрастающей или убывающей, когда справедливы равенства f(r1) <= f(r2) или f(r1) >= f(r2) соответственно. Кроме того, нужно учитывать, что r1 < r2 или r1 <= r2. Необходимо отметить, что точки r1 и r2 должны принадлежать (а;b).
Когда f(r) является строгой (только убывающей или возрастающей — постоянство), тогда знак «<=» или «>=» следует заменить на строгий «<» или «>»: f(r1) < f(r2) или f(r1) > f(r2) соответственно. Вышеописанные понятия можно записать математическим способом, который считается более компактным:
- Возрастающая: ∀ r1, r2 ∈ (a;b): r1 < r2 ⇒ f(r1) <= f(r2). Расшифровывается запись таким образом: для любых (∀) точек r1 и r2, принадлежащих (∈) интервалу (a;b), при условии, что r1 < r2, следует (⇒) выполнение неравенства f(r1) <= f(r2).
- Строго возрастающая: ∀ r1, r2 ∈ (a;b): r1 < r2 ⇒ f(r1) < f(r2).
- Убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) >= f(r2).
- Строго убывающая: ∀ r1, r2 ∈ (a;b): r1 > r2 ⇒ f(r1) > f(r2).
Следует отметить, что промежутками монотонности функции называются интервалы, на которых она возрастает или убывает. После определений необходимо рассмотреть основные теоремы, позволяющие использовать соотношения для решения различных задач.
Теорема о пределе
Теорема о пределе монотонной функции применяется для решения задач по высшей математике с использованием пределов. Ее формулировка следующая: если функция вида р = f(r) является дифференцируемой и монотонной на интервале (а;b), то в точке r0, принадлежащей заданному интервалу, она имеет конечные пределы с левой и правой стороны, а в точках r0 = a и r0 = b у нее существуют правосторонние и левосторонние границы.
Чтобы доказать утверждение, следует задать некоторую функцию, которая является монотонной. Кроме того, она должна возрастать на некотором интервале [а;b]. После этого нужно выбрать любую точку r0 ∈ (a;b]. В результате этого для ∀ r ∈ [a;r0) ⇒ f(r) <= f(r0) ⇒ f(r) ограничена сверху на [a;r0) ⇒ при существующих (∃ – знак существования) верхних границах (sup) функции f(r) = M <= f(r0). По определению для ∀ r ∈ [a;r0) ⇒ f(r) <= M.
Следует предположить, что существует некоторая переменная “e”, которая больше нуля. Она также определена на текущем интервале. Следовательно, выполняется неравенство М – е < f(e). Пусть q = r0 – e и t – значение r0 c левой границей 0 – q. Если выполняется условие ∀ r ∈ (е;r0) = (t;r0), то f(e) <= f(r). В итоге получается, что ∀ е > 0 ∃ q > 0 для r ∈ (t;r0): М – е < f(e) < f(r) <= M < M + e. Следовательно, |f(r) – M| < e. Левый предел, в котором х стремится к точке r0: lim [f(r)] |(r -> r0 – 0) = M. Отсюда следует такое соотношение: f(r0 – 0) = sup f(r), a <= r < r0.
Таким же образом доказывается правосторонний предел в точке r0 ∈ [a;b). Получается такое соотношение: f(r0 + 0) = inf f(r), r0 < r <= b. Теорема доказана. Кроме того, существуют следствия, полученные при доказательстве утверждения о пределе:
- Возрастание: f(r0 – 0) = lim [f(r)] |(r -> r0 – 0) <= lim [f(r)] |(r -> r0 + 0) = f(r0 + 0).
- Убывание: f(r0 – 0) = lim [f(r)] |(r -> r0 – 0) >= lim [f(r)] |(r -> r0 + 0) = f(r0 + 0).
Чтобы понять математические обозначения sup и inf, необходимо представить множество значений функции. Первый термин обозначает максимальное значение сверху, а второй — минимальное снизу.
Критерии возрастания и убывания
Существуют определенные признаки, по которым можно определить монотонность функции p = f(r) на некотором интервале (а;b). Для этого в математике есть еще три теоремы:
- Для убывающей и возрастающей.
- Если является строго убывающей или строго возрастающей.
- Определение по точке, производной и интервалу.
Первая теорема имеет такую формулировку: дифференцируемая функция p = f(r) на интервале (а;b) является убывающей, когда выполняется неравенство f'(r) <= 0, а также возрастающей при f'(r) >= 0 соответственно (при r ∈ данному интервалу).
Формулировка следующего утверждения только для строго возрастающей монотонной функции. В первом случае должно выполняться не одно, а два условия: f'(r) > 0 и f'(r) тождественно не эквивалентна нулю на промежутке в любой точке, принадлежащей интервалу. Для строго убывающей условия немного отличаются от предыдущих: f'(r) < 0 и производная f'(r) также не равна нулевому значению на указанном промежутке. Третья теорема позволяет определить характер монотонности p = f(r) в заданной точке r0 ∈ (а;b). Существует два варианта соотношений: для убывающей f'(r0) < 0 и возрастающей: f'(r0) > 0.
Основные свойства
Для функций на интервале (а;b) существуют некоторые утверждения, позволяющие исследовать составные выражения, а также решать различные задачи. К свойствам монотонных функций относятся следующие:
- Сумма двух убывающих (возрастающих) k = f(t) и l = f(v) является возрастающим (убывающим) выражением.
- Если k = f(t) возрастает, то -k = f(t) (противоположная) будет убывать. При убывании первой вторая будет возрастать соответственно.
- Когда у k = f(t) есть обратная вида k2 = 1 / f(t), тогда при убывании первой вторая будет возрастать. Если первая возрастает, то вторая убывает.
- Результатом произведения двух убывающих (возрастающих) является убывающая функция. Также должны выполняться такие условия: k = f(t) >= 0 и l = f(v) >= 0.
- Если k = f(t) возрастает или убывает на (а;b), а l = f(t) возрастает или убывает на (c;d), и (а;b) входит в (c;d), то композиция функций к∘ l (k(l(t))) также возрастает или убывает.
После изучения теорем и основных свойств нужно определить минимум базовых знаний, которые необходимы для исследования на монотонность любого выражения. Кроме того, следует знать графики некоторых функций. Для их построения можно использовать специальные онлайн-калькуляторы и программы, позволяющие выделять результаты разными цветами.
Базовые знания
Для исследования функции на монотонность специалисты рекомендуют руководствоваться некоторыми правилами, которые объединяются в универсальный алгоритм. Он является достаточным для выполнения такого задания и имеет следующий вид:
- Найти производную первого порядка – f'(r).
- Приравнять выражение, полученное в первом пункте, к 0.
- Найти критические точки, решив уравнение во втором пункте.
- Определить знак f'(r) на промежутках, полученных в результате разбиения критическими точками. Найти промежутки убывания и возрастания.
Последний пункт следует реализовывать при помощи таблицы. Необходимо строго придерживаться алгоритма, поскольку неверные действия способны существенно повлиять на результат.
Нахождение производной
Для поиска производной необходимо выполнить такие шаги: вынести константу, упростить выражение и воспользоваться таблицей дифференциалов элементарных функций (рис. 1). Первые два элемента считаются подготовительными, поскольку позволяют оптимизировать процесс вычисления. Для упрощения следует применять формулы сокращенного умножения, свойства дробей, разложение на множители и т. д. После приведения выражения к упрощенному виду нужно воспользоваться таблицей производных элементарных функций.
Рисунок 1. Дифференциалы простых выражений.
Однако при решении задач не всегда попадаются простые выражения. Для составных существуют определенные правила:
- Сумма: [k(t) + l(t)]’ = k'(t) + l'(t).
- Разность: [k(t) – l(t)]’ = k'(t) – l'(t).
- Произведение: [k(t) * l(t)]’ = k'(t) * l(t) + l'(t) * k(t).
- Частное: [k(t) / l(t)]’ = [k'(t) * l(t) – l'(t) * k(t)] / (l(t))^2.
- Сложная: [k(l(t))]’ = l'(t) * k'(t).
Специалисты рекомендуют для проверки использовать программы, но это не значит, что задачи должны решаться только с помощью онлайн-сервисов и математических пакетов.
Корни уравнений и критические точки
Следующим этапом является решение равенства с неизвестным. Необходимо отметить, что уравнения делятся на следующие виды: линейные, квадратные, кубические, биквадратные, тригонометрические, логарифмические, степенные, показательные и иррациональные.
Первый тип решается по очень простому алгоритму: следует перенести неизвестные в одну часть, а известные — в другую. Для решения квадратного уравнения (aw^2 + bw + c = 0) нужно его упростить, разложить на множители или вычислить дискриминант. Последний вычисляется по следующей формуле: D = b^2 – 4ac. Количество корней зависит от значения D и определяется по таким формулам:
- Два решения при D > 0: w1 = (-b – [D]^(1/2)) / 2a и w2 = (-b + [D]^(1/2)) / 2a.
- D = 0 (одно): w = (-b) / 2a.
- Нет корней, когда D < 0.
Используя метод разложения на множители, можно решить без D. Например, в выражении x(x-1)(x-4) = 0 рассматривается три уравнения: x1 = 0, х2 -1 = 0 и х3 – 4 = 0. Решение кубических и биквадратных равенств с неизвестной осуществляется методом разложения на множители. При этом понижается степень до 2, а дальше находятся его корни.
Для нахождения корней других уравнений следует воспользоваться заменой, а затем свести к линейному или квадратному. Следует отметить, что решая трансцендентные (логарифмы и показатели), следует знать правила логарифмирования и свойства степени. Корни также находятся при помощи замены.
Критическими называются точки, в которых функция меняет свое поведение (четность, периодичность, экстремумы и т. д.). При исследовании они записываются в специальную таблицу поведения в виде промежутков.
Пример решения
Задачи бывают нескольких типов. В одних следует найти промежутки монотонности, а во-вторых — доказать на основании теорем, что она возрастает или убывает на заданном промежутке. Например, необходимо найти промежутки монотонности функции z(y) = (y^2 + 1) / y. Следует отметить, что она является дифференцируемой. Ее область определения D(z) = (-бесконечность;0) U (0;+бесконечность). Решать ее нужно по алгоритму:
- Производная: [(y^2 + 1) / y]’ = (y^2 – 1) / y.
- Приравнять к 0: (y^2 – 1) / y = 0.
- Найти корни – критические точки (y – 1)(y + 1) / y = 0: y1 не равен 0, y2 = 1 и у3 = – 1.
- Построить таблицу.
| y | (-infinity;-1) | (-1;0) | (0;1) | (1;+infinity) |
| z’ | – | + | – | + |
| z | У | В | У | В |
Таблица 1. Интервалы монотонности.
Если функция является четной, то эта особенность не влияет на результат, поскольку ее производная может быть с отрицательным знаком. Примером является обычный тригонометрический косинус.
Таким образом определение монотонности функции на заданном промежутке является одним из элементов исследования ее поведения. Для осуществления этой операции применяются специальный алгоритм, теоремы и свойства.
Е
сли
для всех точек отрезка
при
выполняется равенство
,
то функция
называется возрастающей
на
.
При
выполнении условий
,
функция
называется убывающей
на
.
Интервалы,
в которых функция
только
возрастает или только убывает, называются
интервалами
монотонности
функции.
П
ризнак
возрастания.
Дифференцируемая функция
возрастает на отрезке
тогда и только тогда, когда её производная
.
П
ризнак
убывания.
Дифференцируемая функция
убывает на отрезке
тогда и только тогда, когда её производная
.
В
точках, отделяющих интервалы монотонности
функции, производная функции обращается
в нуль или не существует. Эти точки
называются критическими.
Для
нахождения интервалов монотонности
функции
необходимо
найти все её критические точки и
установить знак производной в каждом
из интервалов, на которые критические
точки разбивают область существования
функции.
Пример
7.13.
Найдите интервалы монотонности функции
.
Ф
ункция
определена на всей числовой оси. Найдём
её производную.
.
Найдём
критические точки, приравняв производную
к нулю.
— критические.
Результаты исследования занесём в
таблицу:
|
|
|
|
|
|
|
|
|
+ |
|
+ |
||
|
|
|
|
|
|
Т
аким
образом, функция
возрастает а интервалах
и
,
а убывает на интервале
.
§ 6. Экстремум функции. Необходимый признак.
Т
очка
называется точкой
максимума
(maximum)
функции
,
если значение функции в этой точке
больше её значений во всех точках
некоторого интервала, содержащего точку
,
т.е.
для любого
(
—
мало
по величине).
Т
очка
называется точкой
минимума
(minimum)
функции
,
если значение функции в этой точке
меньше её значений во всех точках
некоторого интервала, содержащего точку
,
т.е.
.
Точки,
в которых функция достигает максимума
или минимума, называются точками
экстремума
функции, а значения функции в этих точках
называют экстремальными.
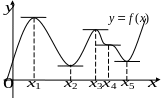
Ф
ункция,
заданная кривой на рисунке выше, в точках
и
достигает максимума, в точках
и
—
минимума, в точке
—
экстремума нет. Очевидно, что функция
имеет производную, равную нулю в
критических точках. Касательная к кривой
в этих точках параллельна оси
.
Необходимый
признак экстремума.
Если дифференцируемая функция достигает
в некоторой точке экстремума, то её
производная в этой точке равна нулю или
не существует.
§ 7. Достаточные признаки экстремума функции.
П
ервый
достаточный признак.
Пусть функция
непрерывна в некотором интервале,
содержащем критическую точку
и дифференцируема во всех точках этого
интервала (кроме, быть может самой точки
).
Тогда, если:
а)
при
,
при
,
то в точке
функция
достигает максимума;
б)
при
,
при
,
то в точке
функция
достигает
минимума.
В
торой
достаточный признак экстремума.
Пусть функция
имеет
в точке
производную
и
непрерывную вторую производную
.
Тогда, если
в точке
будет максимум, а если
в точке
будет минимум.
Пример
7.14. В
примере 7.13 точки
являются точками экстремума. В точке
функция достигает максимума, в точке
функция достигает минимума.
Пример
7.15.
Издержки предприятия выражаются формулой
,
где
—
объём производства. При каком объёме
производства средние издержки будут
минимальными?
С
редние
издержки выражаются формулой
.
Найдем минимум этой функции.
.
.
Найдем
вторую производную функции.
,
значит, по второму достаточному признаку
экстремума при
средние издержки достигают минимума.
Соседние файлы в предмете Высшая математика
- #
- #
Интервалы возрастания и убывания функции
С помощью данного сервиса можно найти интервалы возрастания и убывания функции в онлайн режиме с оформлением решения в Word.
- Решение онлайн
- Видеоинструкция
Исследование функции с помощью производной
Определение: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)>f(x).
Определение: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: f(x0)<f(x).
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная f′(x) обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции y=f(x) с помощью первой производной
- Найти производную функции f′(x).
- Найти критические точки по первой производной, т.е. точки, в которых производная обращается в нуль или терпит разрыв.
- Исследовать знак первой производной в промежутках, на которые найденные критические точки делят область определения функции f(x). Если на промежутке f′(x)<0, то на этом промежутке функция убывает; если на промежутке f′(x)>0, то на этом промежутке функция возрастает.
- Если в окрестности критической точки f′(x) меняет знак с «+» на «-», то эта точка является точкой максимума, если с «-» на «+», то точкой минимума.
- Вычислить значения функции в точках минимума и максимума.
С помощью приведенного алгоритма можно найти не только экстремумы функции, но и промежутки возрастания и убывания функции.
Пример №1: Найти промежутки монотонности и экстремумы функции: f(x)=x3–3x2.
Решение: Найдем первую производную функции f′(x)=3x2–6x.
Найдем критические точки по первой производной, решив уравнение 3x2–6x=0; 3x(x-2)=0 ;x = 0, x = 2
Исследуем поведение первой производной в критических точках и на промежутках между ними.
| x | (-∞, 0) | 0 | (0, 2) | 2 | (2, +∞) |
| f′(x) | + | 0 | – | 0 | + |
| f(x) | возрастает | max | убывает | min | возрастает |
f(0) = 03 – 3*02 = 0
f(2) = 23 – 3*22 = -4
Ответ: Функция возрастает при x∈(-∞ ; 0)∪(2; +∞); функция убывает при x∈(0;2);
точка минимума функции (2;-4); точка максимума функции (0;0).
Правило нахождения экстремумов функции y=f(x) с помощью второй производной
- Найти производную f′(x).
- Найти стационарные точки данной функции, т.е. точки, в которых f′(x)=0.
- Найти вторую производную f″(x).
- Исследовать знак второй производной в каждой из стационарных точек. Если при этом вторая производная окажется отрицательной, то функция в такой точке имеет максимум, а если положительной, то – минимум. Если же вторая производная равна нулю, то экстремум функции надо искать с помощью первой производной.
- Вычислить значения функции в точках экстремума.
Отсюда следует, что дважды дифференцируемая функция f(x) выпукла на отрезке [a, b], если вторая производная f”(x) ≥ 0 при всех х [a, b].
Все вычисления можно проделать в онлайн режиме.
Пример №2. Исследовать на экстремум с помощью второй производной функцию: f(x) = x2 – 2x – 3.
Решение: Находим производную: f′(x) = 2x – 2.
Решая уравнение f′(x) = 0, получим стационарную точку х=1. Найдем теперь вторую производную: f″(x) = 2.
Так как вторая производная в стационарной точке положительна, f″(1) = 2 > 0, то при x = 1 функция имеет минимум: fmin = f(1) = -4.
Ответ: Точка минимума имеет координаты (1; -4).
Алгебра и начала математического анализа, 11 класс
Урок №15. Возрастание и убывание функции.
Перечень вопросов, рассматриваемых в теме
1) Нахождение промежутков монотонности функции,
2) Определение алгоритма нахождения промежутков возрастания и убывания функции,
3) Решение задачи на нахождения промежутков возрастания и убывания функции
Глоссарий по теме
Алгоритм нахождения промежутков возрастания и убывания функции y = f(x)
- Найти D(f)
- Найти f‘(x).
- Определить, при каких значениях хf‘(x) ≥ 0 (на этих промежутках функция возрастает); при каких значениях х f‘(x) ≤ 0 (на этих промежутках функция убывает))
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
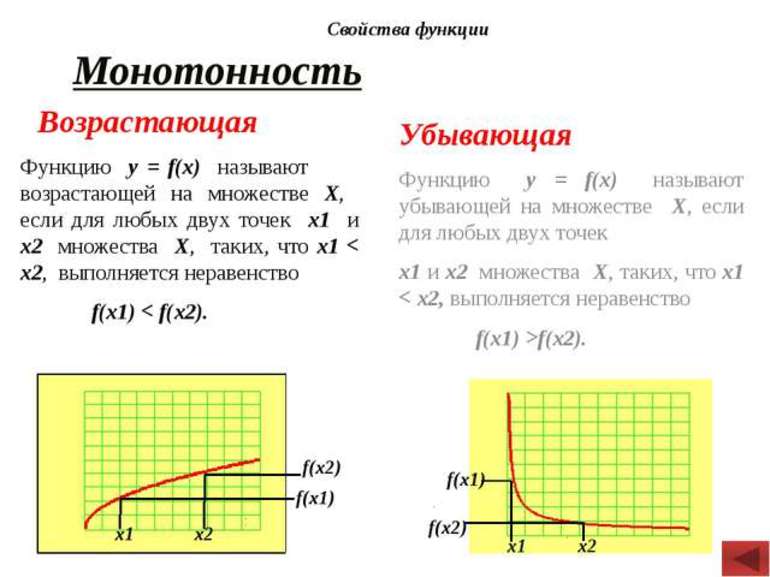
1. Функция y = f(x), определенная на промежутке Х, называется возрастающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) <f(x2)
2. Функция y = f(x), определенная на промежутке Х, называется убывающей на этом промежутке, если для любой пары чисел х1 и х2 из этого промежутка из неравенства х1< х2 следует неравенство f(x1) >f(x2)
Теоремы
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≥ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) возрастает на промежутке Х.
- Если во всех точках открытого промежутка Х выполняется неравенство f‘(x) ≤ 0 (причем равенство f‘(x) = 0 либо не выполняется, либо выполняется лишь в конечном множестве точек),то функция y = f(x) убывает на промежутке Х.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежутки монотонности функции
у = -3х3 + 4х2 + х – 10.
Решение
1.Найдем область определения функции.
D(y) =
2.Найдем производную функции.
y’ = (x – 1)(-9x – 1)
3.Определим, на каких промежутках производная положительна (на этих промежутках функция возрастает), на каких – отрицательна (на этих промежутках функция убывает).
Применим для этого метод интервалов. Для определения знака на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так как на интервале 
Так как на интервале 
Так как на интервале 
Так как в точках 
Следовательно, функция возрастает на 


Ответ: Функция возрастает на
Функция убывает на 

№2. Определите промежутки монотонности функции
у = х5–5х4 +5х3 – 4.
Решение:
y‘ =
- Функция возрастает на
; функция убывает на
.
Ответ: Функция возрастает на 
функция убывает на 





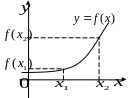
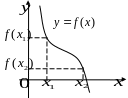










 ; функция убывает на
; функция убывает на  .
.