Как найти области сходимости степенных рядов

Выпишем общий член и следущий:

$$ u_n = frac{x^n}{n^2} $$

$$ u_{n+1} frac{x^{n+1}}{(n+1)^2} $$

Найдем отношения следующего и предыдущего члена ряда: $$ frac{u_{n+1}}{u_n} = frac{x^{n+1} n^2}{(n+1)^2 x^n} = frac{x n^2}{(n+1)^2} $$

Находим предел модуля полученного выражения:

$$ limlimits_{n to infty} bigg |frac{u_{n+1}}{u_n} bigg | = limlimits_{n to infty} bigg |frac{x n^2}{(n+1)^2} bigg | = $$

Так как $ n $ положительное, то палочки можно убрать. А $ x $ может принимать как положительные, так и отрицательные значения, поэтому его выносить за знак модуля не станем.

$$ = |x| limlimits_{n to infty} frac{n^2}{(n+1)^2} = frac{infty}{infty} = $$

Вынесем $ n^2 $ за скобки и выполним сокращение числителя и знаменателя:

$$ = |x| limlimits_{n to infty} frac{n^2}{n^2 (1+frac{1}{n})^2} = |x| limlimits_{n to infty} frac{1}{(1+frac{1}{n})^2} = $$

Вычисляем предел окончательно:

$$ =|x| cdot 1 = |x| $$

Итак, предел равен:

$$ limlimits_{n to infty} bigg |frac{x n^2}{(n+1)^2} bigg | = |x| $$

Составим строгое неравенство всегда меньшее единицы:

$$ |x|<1 $$

Раскроем модуль и получим, что интервал сходимости:

$$ -1 < x < 1 $$

Итак, интервал найден. Теперь необходимо найти область сходимости степенного ряда. А для этого исследуем поведение ряда на концах полученного интервала:

1) Возьмём левую границу $ x = -1 $

Подставляя $ x = -1 $ в исходный ряд, получаем ряд: $ sum_{n=1}^infty frac{(-1)^n}{n^2} $

Так как ряд знакочередующийся из-за  $ (-1)^n $, то исследуем сходимость по признаку Лейбница:

1) Ряд знакочередующийся

2) $ limlimits_{n to infty} bigg | frac{(-1)^n}{n^2} bigg | = limlimits_{n to infty} frac{1}{n^2} = 0 $

Выполнены оба условия, значит ряд сходится и точку $ x=-1 $ можно включить в область сходимости.

2) Возьмём правую границу $ x = 1 $

Подставим $ x = 1 $ в исходный ряд и получим: $ sum_{n=1}^infty frac{1}{n^2} $

Текущий ряд попадает под общий гармонический ряд, в котором $ p = 2 $. А так как $ p>1 $, то ряд сходится. Значит, можно точку $ x = 1 $ записать в область сходимости.

Итого, подведем итог: область сходимости степенного ряда $ sum_{n = 1}^infty frac{x^n}{n^2} $ записывается в виде: $ -1 leqslant x leqslant 1 $

Найдем радиус сходимости $ R = frac{b-a}{2} = frac{1+1}{2} = 1 $

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Лекция
4 1

4.1.
Функциональные ряды: основные понятия,
область сходимости 1

4.2.
Степенные ряды: основные понятия,
теорема Абеля 2

4.3.
Свойства степенных рядов 5

4.4.
Формула Тейлора 5

4.1. Функциональные ряды: основные понятия, область сходимости

Определение
1.
Ряд, члены которого являются функциями
одной
или нескольких независимых переменных,
определёнными
на некотором множестве,
будем называть функциональным
рядом.

Рассмотрим
функциональный ряд,
члены которого являются функциями одной
независимой переменной х.
Сумма первых n
членов ряда

является частичной суммой данного
функционального ряда. Общий член

есть функция от х,
определенная в некоторой области. Если
положить
,
получим числовой ряд
,
и если он сходится, т.е. существует предел
частичных сумм этого ряда,
где

− сумма числового ряда, тогда говорят,
что

− точка сходимости функционального
ряда
,
а если числовой ряд

расходится, то

называется точкой расходимости
функционального ряда.

Определение
2.
Областью
сходимости
функционального ряда

называется множество всех таких значений
х,
при которых функциональный ряд сходится.
Область сходимости, состоящая из всех
точек сходимости, обозначается
.
Отметим, что
.

Будем
говорить, что функциональный ряд сходится
в области
,
если для любого

он сходится как числовой, при этом его
сумма будет некоторой функцией

(это так называемая предельная
функция
последовательности
:
).

Как
находить область сходимости функционального
ряда
?
Можно использовать признак, аналогичный
признаку Даламбера. Для ряда

составляем

и рассматриваем предел при фиксированном
х:
.
Тогда

является решением неравенства

и решением уравнения

(берем только те решения уравнения, в
которых соответствующие числовые ряды
сходятся).

Пример
1.
Найти область сходимости ряда
.

Решение.
Обозначим
,
.
Составим и вычислим предел
,
тогда область сходимости определяется
неравенством

и уравнением
.
Исследуем дополнительно сходимость
исходного ряда в точках, являющимися
корнями уравнения: а) если
,
,
то получается расходящийся ряд
;
б) если
,
,
то ряд

сходится условно (по признаку Лейбница,
пример 1, лекция 3).
Таким образом,
область сходимости

ряда

имеет вид:
.

4.2. Степенные ряды: основные понятия, теорема Абеля

Рассмотрим
частный случай функционального ряда,
так называемый степенной
ряд:
,
где
.

Определение
3.
Степенным
рядом
называется функциональный ряд вида
,
где

−
постоянные числа, называемые
коэффициентами
ряда.

Степенной
ряд есть «бесконечный многочлен»,
расположенный по возрастающим степеням
.
(Любой числовой ряд

является частным случаем степенного
ряда при
.)

Рассмотрим
частный случай степенного ряда при
:
.
Выясним, какой вид имеет область
сходимости данного ряда
.

Теорема
1 (теорема Абеля).
1) Если степенной ряд
(*)
сходится в точке
,
то он абсолютно сходится при всяком х,
для которого справедливо неравенство
.
2)
Если же степенной ряд расходится при
,
то он расходится при всяком х,
для
которого
.

Доказательство.
1) По условию степенной ряд сходится в
точке
,
т е. сходится числовой ряд
(**),
а значит, по необходимому признаку
сходимости его общий член стремится к
0, т.е.
.
Следовательно, существует такое число
,
что все члены ряда ограничены этим
числом:
.

Рассмотрим
теперь любое х,
для которого
,
и составим ряд из абсолютных величин:
.
Запишем этот ряд в другом виде: т.к.
,
то
(***).

Из
неравенства

получаем
,
т.е. ряд
(****)
состоит из членов, которые больше
соответствующих членов ряда (***). Ряд

представляет собой сходящийся ряд
геометрической прогрессии с знаменателем
,
причем
,
т.к.
.
Следовательно, ряд (***) сходится при
.
Таким образом, степенной ряд

абсолютно сходится.

2)
Пусть теперь ряд

расходится при
,
иными словами, расходится числовой ряд
.
Докажем, что для любого х
()
ряд расходится. Доказательство ведется
от противного. Пусть при некотором
фиксированном

()
ряд сходится, тогда он сходится при всех

(см. первую часть данной теоремы), в
частности, при
,
что противоречит условию 2 теоремы.
Теорема доказана.

Следствие.
Теорема Абеля позволяет судить о
расположении точки сходимости степенного
ряда.
Если точка

является точкой сходимости степенного
ряда, то интервал

заполнен точками сходимости; если точкой
расходимости является точка
,
то бесконечные интервалы

заполнены точками расходимости (см.
рис. 1).

Рис.
1.

Можно
показать, что существует такое число
,
что при всех

степенной ряд

абсолютно сходится, а при

− расходится. Будем считать, что если
ряд сходится только в одной точке 0, то
,
а если ряд сходится при всех
,
то
.

Определение
4.
Интервалом
сходимости
степенного ряда

называется такой интервал
,
что при всех

этот ряд сходится и притом абсолютно,
а для всех х,
лежащих вне этого интервала, ряд
расходится. Число R
называется радиусом
сходимости
степенного ряда.

Замечание.
На концах интервала

вопрос о сходимости или расходимости
степенного ряда решается отдельно для
каждого конкретного ряда.

Покажем
один из способов определения интервала
и радиуса сходимости степенного ряда.

Рассмотрим
степенной ряд

и обозначим
.
Составим ряд из абсолютных величин его
членов:

и применим к нему признак
Даламбера.

Пусть
существует
,
где
.
По признаку Даламбера ряд сходится,
если
,
и расходится, если
.
Отсюда ряд сходится при
,
тогда интервал сходимости:
.
При

ряд расходится, т.к.
.
Используя обозначение
,
получим формулу для определения радиуса
сходимости степенного ряда:
,
где

− коэффициенты степенного ряда. Если
окажется, что предел
,
то полагаем
.

Для
определения интервала и радиуса
сходимости степенного ряда также можно
использовать радикальный признак Коши,
радиус сходимости ряда определяется
из соотношения
.

Определение
5.
Обобщенным
степенным рядом называется ряд вида
.
Его также называют рядом по степеням
.
Для такого ряда интервал сходимости
имеет вид:
,
где

− радиус сходимости.

Покажем,
как находится радиус сходимости для
обобщенного степенного ряда.

,
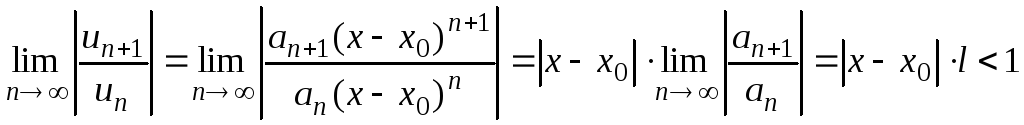т.е.
,
где
.

Если
,
то
,
;
если
,
то

и область сходимости
.

Пример
2.
Найти область сходимости ряда
.

Решение.
Обозначим
.
Составим предел
.
Решаем неравенство:
,

,
следовательно, интервал сходимости
имеет вид:
,
причем R
= 5. Дополнительно исследуем концы
интервала сходимости: а)
,
,
получаем ряд
,
который
расходится;
б)
,

,
получаем ряд
,
который сходится условно. Таким образом,
область сходимости:
,
.

Пример
3.
Ряд

расходится для всех
,
т.к.

при
,
радиус сходимости
.

Пример
4.
Ряд

сходится при всех
,
радиус сходимости
.

Пример 1:

Найти область сходимости ряда:

Решение от преподавателя:

Пример 2:

Найти область сходимости ряда:

Решение от преподавателя:

Пример 3:

Найти область сходимости ряда:

Решение от преподавателя:

Областью сходимости степенного ряда является интервал (-R;R), где: 

R – радиус сходимости. Вычислим его: 

x₁ = 2 – 1 = 1 
x₂ = 2 + 1 = 3 
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (1;3) 
Теперь проверим сходимость ряда на концах этого интервала. 
Пусть x = 1 
Получаем ряд: 

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. 
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется 

б) По второму признаку Лейбница предел ряда должен стремится к 0. 

Второе условие Лейбница выполняется. 
Ряд сходится, значит, x = 1 – точка сходимости. 
При x = 3 
получаем ряд: 

числовой знакоположительный ряд. 
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл: 

Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 3 – точка расходимости. 
Таким образом, данный степенной ряд является сходящимся при x [1;3) 

Пример 4:

Исследовать область сходимости функционального ряда:

Решение от преподавателя:

Пример 5:

Найти область сходимости степенного ряда:

Решение от преподавателя:

Пример 6:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом члены ряда не определены при х=-3/11, а если х≠-3/11, то

      

при любом х – ряд расходится всюду.

Пример 7:

Найти область сходимости ряда:

Решение от преподавателя:

Областью сходимости степенного ряда является интервал (-R;R), где: 

R – радиус сходимости. Вычислим его: 

x1 = -1 – 2 = -3 
x2 = -1 + 2 = 1 
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-3;1) 
Теперь проверим сходимость ряда на концах этого интервала. 
Пусть x = -3 
Получаем ряд: 

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. 
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие не выполняется 
1<2<3 
б) По второму признаку Лейбница предел ряда должен стремится к 0. 

Второе условие Лейбница не выполняется. 
Ряд расходится, значит, x = -3 – точка расходимости. 
При x = 1 
получаем ряд: 

числовой знакоположительный ряд. 
Исследуем его сходимость при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:

Так как несобственный интеграл расходится, то расходится и исследуемый ряд. Значит, x = 1 – точка расходимости. 
Таким образом, данный степенной ряд является сходящимся при x (-3;1) 

Пример 8:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом

       

Следовательно, ряд сходится, если

       

и расходится, если

       

Если x=4/9, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).

Если x=2/3, то ряд принимает вид – такой ряд расходится (по признаку сравнения, т.к. и ряд  расходится (гармонический ряд)).

Окончательно получаем область сходимости исходного ряда: [4/9;2/3).

Пример 9:

Найдите множество абсолютной (условной) сходимости ряда:

Решение от преподавателя:

Пример 10:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом

       

Следовательно, ряд сходится, если

       

и расходится, если

       

Если x=-3/7, то ряд принимает вид  – знакочередующийся ряд с монотонно убывающими по абсолютной величине, стремящимися к нулю членами. Такой ряд сходится (по теореме Лейбница).

Если x=-1/7, то ряд принимает вид  – такой ряд также сходится (обобщенный гармонический ряд с параметром p=11>1).

Окончательно получаем область сходимости исходного ряда: [-3/7;-1/7].

Пример 11:

Найдите множества абсолютной (условной) сходимости ряда

Решение от преподавателя:

Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница. 

 Проверяем выполнение признака Лейбница:

Если члены знакочередующегося ряда монотонно убывают по абсолютной величине и стремятся к нулю, то ряд сходится.

Ряд знакочередующийся. Составим ряд из абсолютных величин членов данного ряда

По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется

Второе условие Лейбница выполняется. 

Данный ряд сходится, так как удовлетворяет условиям признака Лейбница для знакочередующихся рядов.

Следовательно, ряд условно сходящийся.

Следовательно, сходится условно и исходный ряд.

Область сходимости ряда:(-∞; +∞)

Пример 12:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид – обобщенный гармонический ряд с параметром .

Такой ряд сходится, если

       

Однако и поэтому  при любом х – ряд всюду расходится.

Пример 13:

Найти область сходимости ряда:

Решение от преподавателя:

По признаку Лейбница ряд расходится

Т. о., область сходимости имеет вид (-1; 1)

Пример 14:

Найти область сходимости ряда:

Решение от преподавателя:

: общий член ряда имеет вид , при этом

     

Следовательно, ряд сходится, если

       

и расходится, если

       

Если x=1/6, то ряд принимает вид  – такой ряд расходится (не выполнено необходимое условие сходимости).

Если x=3/2, то ряд принимает вид  – такой ряд также расходится (также не выполнено необходимое условие сходимости).

Окончательно получаем область сходимости исходного ряда: .

Пример 15:

Найти область сходимости ряда:

Решение от преподавателя:

Содержание:

1. Радиус сходимости и круг сходимости степенного ряда

Степенным рядом называется ряд

где — коэффициенты степенного ряда.

 Областью сходимости степенного ряда называется совокупность тех значений х, при которых степенной ряд (14.1) сходится.

Число R — такое, что при ряд (14.1) сходится, а при — расходится, называется радиусом сходимости степенного ряда.

Интервал называется интервалом сходимости степенного ряда. При ряд может как сходиться, так и расходиться.

Радиус сходимости степенного ряда может быть найден по формуле:

Формула (14.2) применима, если, начиная с некоторого номера , все

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Для степенного ряда вида

радиус сходимости находится по формуле (14.2), а интервал сходимости из условия , т.е. имеет вид:

Пример с решением 1:

Найти области сходимости степенных рядов:

Решение:

а) Найдем радиус сходимости ряда по формуле (14.2): т.е. интервал сходимости ряда

Теперь выясним поведение ряда на концах интервала сходимости.

Возможно вам будут полезны данные страницы:

На левом конце при — данный степенной ряд принимает вид этот ряд сходится по признаку Лейбница (см. §13.3, п. 4). На правом конце при

нический ряд (§ 13.2, п. 3) при у которого все члены с четными номерами равны нулю. Так как , то этот ряд сходится.

Следует отметить, что сходимость ряда на левом конце интервала сходимости при — могла быть установлена с помощью достаточного признака сходимости знакопеременного ряда, так как ряд, составленный из абсолютных величин его членов, т.е. ряд сходится. Итак, область сходимости данного ряда

Обращаем внимание на то, что при исследовании сходимости степенного ряда на концах интервала сходимости в ситуации, когда получаемый ряд — с положительными членами, применять признак Даламбера не имеет смысла, так как при этом всегда будем получать с нерешенным вопросом о сходимости ряда: в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, интегральный, необходимый признаки и т.д.)

б) Найдем радиус сходимости по формуле (14.2):

т.е область сходимости ряда

в) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что при

т.е. необходимый признак сходимости не выполняется, и ряд расходится.

Итак, область сходимости ряда состоит из одной точки х = 0.

г) Найдем радиус сходимости по формуле (14.2)

Для нахождения предела заменим бесконечно малые величины

при им эквивалентными

получим В соответствии с п. 4 интервал сходимости находится из условия , или (1; 3).

Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при х = 1 данный ряд принимает вид

при любом натуральном ).

Так как при любом есть сходящийся обобщенный гармонический ряд при , то по признаку сравнения данный ряд сходится.

На правом конце при степенной ряд принимает вид , т.е. является знакочередующимся рядом и по достаточному признаку сходимости знакопеременного (а значит, и знакочередующегося) ряда сходится, так как сходится ряд, составленный из абсолютных величин его членов, т.е. ряд . Итак, область сходимости данного ряда [I; 3].

д) Выпишем несколько первых членов ряда:

Очевидно, что находить радиус сходимости по формуле (14.2) в данном случае не представляется возможным, так как коэффициенты ряда (14.1) и т.д. равны нулю. Поэтому применим непосредственно признак Даламбера. Данный ряд будет абсолютно сходиться, если и расходиться, если Поэтому найдем Следовательно, ряд сходится при или на интервале Исследуем сходимость на концах интервала сходимости.

При ряд принимает вид п~ -I (-1/ = 1 f (-1Г = _lf 1 _ 1+1

„=1 п 3″-’ п з1 2 3

Этот ряд сходится по признаку Лейбница (§ 13.3).

При ряд принимает вид расходящийся

гармонический ряд. Итак, область сходимости ряда [-1/3; 1/3).

е) Так как члены ряда, стоящие на нечетных местах, отсутствуют, т.е. коэффициенты ряда и т.д., то формулу (14.2) для нахождения радиуса сходимости использовать нельзя. Можно применить непосредственно признак Даламбера, как это делалось в примере в п. д). Но в данном случае удобнее сделать замену Тогда ряд примет вид Область сходимости этого ряда получена в п. а): Возвращаясь к переменной х, получим откуда т.е. область сходимости ряда

Радиус сходимости и круг сходимости степенного ряда

Определение 1. Функциональные ряды вида

где — заданные комплексные числа, — комплексное переменное, называются степенными рядами. Числа называются коэффициентами степенного ряда (33.1).

Предполагая, что коэффициенты ряда и число фиксированы, будем исследовать поведение ряда (33.1) при различных .

Если в ряде (33.1) выполнить замену переменного, положив , то получим ряд

Очевидно, что исследование сходимости ряда (33.1) эквивалентно исследованию сходимости ряда (33.2), поэтому в дальнейшем будем рассматривать ряды вида (33.2), используя, как правило, для обозначения переменной букву , а не

ТЕОРЕМА 1 (первая теорема Абеля). Если степенной ряд сходится при , то он сходится, и притом абсолютно, при любом , для которого

Доказательство. Пусть ряд

сходится. Тогда его n-й член стремится к нулю при

(см. п. 30.1), поэтому последовательность ограничена, т. е. существует такая постоянная , что

В силу этого, для n-го члена ряда (33.3) имеет место оценка Если (рис. 9), то ряд являясь суммой геометрической прогрессии со знаменателем сходится. Поэтому, согласно признаку сравнения (см. п. 30.5), сходится и ряд а это означает абсолютную сходимость ряда (33.3) при

СЛЕДСТВИЕ. Если степенной ряд (33.3) расходится при , то он расходится и при всяком , для которого

Действительно, если и ряд (33.4) расходится, то расходится и ряд (33.3), так как если бы он сходился, то, в силу доказанного, сходился бы и ряд (33.4).

Неравенство задает на комплексной плоскости С замкнутый круг радиуса R с центром в точке

Определение 2. Пусть задан ряд . Если R — неотрицателъное число или обладает тем свойством, что при всех z, для которых ряд (33.3) сходится, а при всех z, для которых , ряд (33.3) расходится, то R называется радиусом сходимости степенного ряда (33.3).

Множество точек , для которых , называется кругом сходимости ряда (33.3).

Если , то круг сходимости вырождается в точку, а если , то круг сходимости совпадает со всей комплексной плоскостью С.

ТЕОРЕМА 2. У всякого степенного ряда (33.3) существует радиус сходимости R. Внутри круга сходимости, т. е. при любом , для которого ряд (33.3) сходится абсолютно. На любом круге , где г фиксировано и , ряд (33.3) сходится равномерно.

Доказательство. Обозначим через А множество всех неотрицательных чисел х, в которых ряд сходится. При х = 0 этот ряд заведомо сходится, поэтому множество А не пусто и, следовательно, имеет конечную или бесконечную верхнюю грань. Пусть sup А = R. Покажем, что R — радиус сходимости ряда (33.3). Действительно, пусть и Согласно определению верхней грани, существует такое , что (см. определение 4′ в п. 3.4). В силу определения множества А, для указанного х ряд (33.5) сходится, поэтому, согласно первой теореме Абеля, в выбранной точке г сходится абсолютно ряд Если , то выберем такое действительное число х, что ; тогда снова, в силу определения множества А, ряд (33.5) в такой точке х расходится — она лежит на действительной оси правее всех точек, в которых ряд (33.5) сходится. Поэтому, согласно следствию из первой теоремы Абеля, для выбранного z расходится и ряд

Итак, действительно, R является радиусом сходимости ряда (33.3).

Если теперь , то, по доказанному, ряд (33.3) при z = г абсолютно сходится, т. е. сходится числовой ряд А так как для любой точки круга (рис. 10)

то, согласно признаку Вейерштрасса (см. п. 32.3), на этом круге ряд (33.3) сходится равномерно. □

Таким образом, областью сходимости всякого степенного ряда является всегда «круг», т. е. обычный круг, исключая, быть может, некоторое множество точек ограничивающей его окружности (будем для краткости называть ее границей круга сходимости), в которых он может расходиться.

Пример с решением 2:

Подчеркнем, что радиус сходимости степенного ряда (33.3) обладает следующим свойством: для каждого числа z такого, что , указанный ряд абсолютно сходится, а для каждого z такого, что , он просто, а следовательно, и подавно абсолютно расходится (расходится ряд, составленный из абсолютных величин членов данного ряда). Это следует, очевидно, из определения радиуса сходимости и теоремы 2.

Члены степенного ряда являются непрерывными функциями и, как было показано, на всяком круге, лежащем вместе со своей границей внутри круга сходимости, степенной ряд сходится равномерно, поэтому его сумма непрерывна на всяком указанном круге. Очевидно, что для любой точки z круга сходимости, |z| < R, можно подобрать круг, содержащий эту точку и лежащий вместе с границей в круге сходимости (достаточно взять его радиус г таким, что |z| < г < R), поэтому степенной ряд непрерывен в каждой точке г, лежащей внутри его круга сходимости: |z| < R. Рассмотрим теперь случай, когда степенной ряд сходится в точке , лежащей на границе его круга сходимости. Отметим, что случай может быть сведен к случаю z = R простой заменой переменного

ТЕОРЕМА 3 (вторая теорема Абеля). Если R — радиус сходимости ряда и этот ряд сходится при то он сходится равномерно на отрезке [0, R] действительной оси.

СЛЕДСТВИЕ. Если степенной ряд (33.3) сходится при z = R, то его сумма непрерывна на отрезке [0, /?] действительной оси.

Доказательство. Пусть Представим ряд Члены ряда

не зависят от х, поэтому его сходимость означает и его равномерную сходимость. Последовательность же ограничена

на отрезке , ее члены неотрицательны: и она убывает в каждой точке (при она не строго убывает, точнее, является стационарной). Поэтому, в силу признака Абеля равномерной сходимости рядов (см. теорему 7 в п. 32.3), ряд (33.3) равномерно сходится на отрезке .

Следствие вытекает из того, что сумма равномерно сходящегося ряда непрерывных функций является также непрерывной функцией.

Все сказанное с помощью преобразования типа , (— новая переменная, фиксировано) переносится и на общие степенные ряды вида (33.1). В частности, областью сходимости такого степенного ряда всегда является круг вида , конечно, как и выше, с точностью до точек ограничивающей его окружности. Этот круг называется кругом сходимости (ряда (33.1)), aR — его радиусом сходимости.

Пример с решением 3:

Радиус сходимости равен нулю, т. е. этот ряд сходится только при

Действительно, исследуя абсолютную сходимость этого ряда по признаку Даламбера, при любом получим

Таким образом, рассматриваемый ряд не сходится абсолютно при любом ; отсюда, в силу следствия из первой теоремы Абеля, он расходится при любом .

Пример с решением 4:

Радиус сходимости ряда равен , так как было показано (см. п. 32.1), что этот ряд сходится при любом .

Пример с решением 5:

Сумма бесконечной геометрической прогрессии

сходится при и расходится при . Поэтому ее радиус сходимости R = 1. Отметим, что во всех точках границы круга сходимости, т. е. во всех точках окружности , ряд (33.6) расходится, так как для общего члена ряда имеем следовательно, он не стремится к нулю при .

Пример с решением 6:

Ряд

сходится при , так как при выполнении этого условия

При ряд (33.7) расходится, поскольку в этом случае т. е. не выполняется необходимое условие сходимости ряда. Радиус сходимости ряда (33.7), как и ряда (33.6), равен единице, однако в каждой точке границы круга сходимости ряд (33.7), в отличие от ряда (33.6), сходится.

Пример с решением 7:

Ряд имеет радиус сходимости R = 1.

Действительно, применив признак Даламбера для определения z, при которых ряд абсолютно сходится (расходится), получим

и, следовательно, при данный ряд сходится, причем абсолютно, а при он расходится. При получается расходящийся гармонический ряд , а при z = -1 — сходящийся ряд (см. и. 30.3 и 30.9). Таким образом, в этом п = О П

примере на границе круга сходимости есть точки, в которых ряд сходится, и точки, в которых он расходится.

Таким образом, область сходимости степенного ряда не совпадает, вообще говоря, с его кругом сходимости, а состоит из внутренности этого круга, т. е. множества , и, быть может, еще из некоторого множества точек, лежащих на его границе.

Из рассмотренных примеров видно, что иногда радиус сходимости R степенного ряда находится с помощью признака Даламбера сходимости рядов с положительными членами .

Действительно, справедливо следующее утверждение: если существует предел

В самом деле, если число R определено этой формулой и то

поэтому ряд (33.3) для такого z сходится (и притом абсолютно).

Если же и, следовательно, ряд (33.3) абсолютно расходится. Таким образом, R действительно является радиусом сходимости ряда (33.3).

Аналогично можно найти величину радиуса сходимости R и с помощью признака Коши (см. теорему 9 в п. 30.6), если только существует предел (конечный или бесконечный) . В этом случае

Действительно, если число R задается этой формулой и если , то

и поэтому ряд (33.3) сходится. Если же , то и, следовательно, ряд (33.3) абсолютно не сходится.

Таким образом, R является радиусом сходимости ряда (33.3).

Затруднения при использовании таких методов определения радиуса сходимости степенного ряда могут возникнуть, например, уже в том случае, когда в рассматриваемом ряде имеются коэффициенты со сколь угодно большими номерами, равные нулю. Тогда можно попробовать применить один из этих методов, предварительно перенумеровав подряд все члены ряда с отличными от нуля коэффициентами (отчего его сходимость и сумма в случае, если он сходится, не изменяются).

Поясним сказанное на примере. Пусть требуется определить радиус сходимости ряда Признак Даламбера неприменим для определения сходимости этого ряда, так как отношение не имеет смысла

для четных номеров п. Не дает ответа здесь и признак Коши, поскольку нетрудно проверить, что здесь предел не существует.

Однако если положить , и записать данный ряд в виде

,

то, исследовав абсолютную сходимость этого ряда с помощью признака Даламбера, получим

Отсюда следует, что рассматриваемый ряд абсолютно сходится, когда , т. е. когда , и абсолютно расходится, когда . Таким образом, радиус сходимости этого степенного ряда равен 1.

Подчеркнем, что с помощью признака Даламбера и признака Коши можно найти радиус сходимости не для произвольного степенного ряда, а лишь для такого, у которого существуют указанные выше пределы (быть может, после новой нумерации членов).

Сходимость степенного ряда.
Радиус и область сходимости степенного ряда

Краткая теория

---

Функциональным рядом называется ряд вида:

где

 – функции,
определенные на некотором множестве

.

Множество

 всех
точек сходимости ряда (*) называется его областью
сходимости.

В области сходимости 

 определены функции:

( n-я частичная сумма ряда)

(сумма ряда)

(остаток ряда)

Ряд

называется абсолютно сходящимся, если
сходится ряд

Из всех функциональных рядов наиболее
часто применяют степенные ряды, которыми называют ряды вида

Действительные числа

 называют коэффициентами ряда.

Неотрицательное число

,
такое, что ряд (**) сходится в интервале

 и расходится вне этого интервала, называется
радиусом сходимости этого ряда, а интервал

 – интервалом сходимости ряда.

Радиус сходимости степенного ряда можно
найти по формулам:

или

Свойства степенных рядов

1. Сумма степенного ряда при всех
значениях

 из интервала сходимости есть непрерывная
функция.

---

2. Степенной ряд в его интервале
сходимости можно почленно дифференцировать, то есть:

---

3. Степенной ряд можно интегрировать по
любому отрезку, содержащемуся в интервале сходимости, причем:

Пример решения задачи

---

Задача

Найдите
область сходимости степенного ряда:

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Радиус
сходимости степенного ряда можно найти по формуле:

В
нашем случае:

Интервал
сходимости:

Исследуем сходимость ряда
на концах интервала:

При

Это
знакопеременный ряд.

 -абсолютные величины членов ряда монотонно
убывают

По
признаку Лейбница ряд сходится

При

Это
ряд Дирихле – сходится, так как показатель степени в знаменателе больше единицы

Область
сходимости:

Ответ:

.