Как найти оборот в минуту

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 декабря 2013 года; проверки требует 31 правка.

Оборо́т в мину́ту (обозначение об/мин, 1/мин или мин⁻¹, также часто используется английское обозначение rpm (revolutions per minute)^[1]) — единица частоты вращения, т. е. количества полных оборотов, совершённых вокруг фиксированной оси, по отношению к промежутку времени. Используется для выражения скорости вращения механических компонентов.

Частота вращения[править | править код]

Частота вращения — физическая величина, равная числу полных оборотов за единицу времени. В Международной системе единиц (СИ) единица частоты вращения — секунда в минус первой степени (с⁻¹, s⁻¹), оборот в секунду (об/с, 1/с или с⁻¹). Часто используются и такие единицы, как оборот в минуту, оборот в час и т. д.

Один оборот в минуту равен обороту в секунду, делённому на 60:

1 об/мин = 1/мин = 1/(60 с) = 1/60 об/с ≈ 0,01667 об/с.

Обратно: один оборот в секунду равен 60 оборотам в минуту.

Физическая величина, связанная с частотой вращения, — это угловая скорость: в Международной системе единиц (СИ) она выражается в радианах в секунду (рад·с⁻¹, или рад/с):

1 об/мин = 2π рад·мин⁻¹ = 2π/60 рад·с⁻¹ = 0,1047 рад·с⁻¹ ≈ 1/10 рад·с⁻¹.

Примеры[править | править код]

• На граммофонных пластинках частота вращения указывается в оборотах в минуту (об/мин). По стандарту применяются 16²⁄₃, 33¹⁄₃, 45 или 78 об/мин (⁵⁄₁₈, ⁵⁄₉, ³⁄₄, или 1,3 об/с соответственно).
• Современные стоматологические бормашины имеют частоту вращения до 800 000 об/мин (13 300 об/с).
• Секундная стрелка часов вращается с частотой 1 об/мин.
• Проигрыватели компакт-дисков производят чтение со скоростью 150 кБ/с — и скорость вращения диска при считывании ближе к центру равна примерно 500 об/мин (8 об/с), а на внешней границе — 200 об/мин (3,5 об/с). Приводы компакт-дисков имеют частоту вращения, кратную этим числам, даже если используется переменная скорость чтения.
• DVD-проигрыватели обычно читают диски с постоянной линейной скоростью. А частота вращения при этом изменяется от 1530 об/мин (25,5 об/с) при чтении у внутреннего края до 630 об/мин (10,5 об/с) на внешней стороне диска.^[2] Также DVD-приводы могут запускаться на скорости, кратной вышеназванным числам.
• Во время отжима частота вращения барабана стиральной машины может составлять от 500 до 2000 об/мин (8–33 об/с).
• Турбина генератора ТЭС вращается со скоростью 3000 об/мин (50 об/с) или 3600 об/мин (60 об/с), в зависимости от страны (см. стандарты частоты переменного тока). Вал генератора гидроэлектростанции может вращаться медленнее: до 2 об/с (при этом частота сети 50 Гц получается за счёт наличия большего количества полюсов катушек статора).
• Двигатель легкового автомобиля работает, как правило, на частоте вращения 2500 об/мин (41 об/с), на холостом ходу — около 1000 об/мин (16 об/с), а максимальные обороты — 6000—10 000 об/мин (100—166 об/с).
• Воздушный винт самолёта обычно вращается со скоростью между 2000 и 3000 об/мин (30—50 об/с).
• Компьютерный жёсткий диск с интерфейсами ATA или SATA вращается со скоростью 5400 или 7200 об/мин (90 или 120 об/с), а очень редко — 10 000 об/мин. Серверные жёсткие диски с интерфейсами SCSI и SAS используют скорость 10 000 или 15 000 об/мин (160 или 250 об/с).
• Двигатель болида «Формулы-1» может развить 18 000 об/мин (300 об/с) (по регламенту сезона 2009).
• Центрифуга по обогащению урана вращается со скоростью 90 000 об/мин (1500 об/с) или быстрее.^[3].
• Газотурбинный двигатель вращается со скоростью в десятки тысяч оборотов в минуту. Турбины для моделей самолётов могут разгоняться до 100 000 об/мин (1700 об/с), а самые быстрые — и до 165 000 об/мин (2750 об/с)^[4].
• Типичный 80-мм компьютерный вентилятор вращается со скоростью 800—3000 об/мин и питается от 12 В постоянного тока.
• Турбокомпрессор может достигнуть частоты вращения 290 000 об/мин (4800 об/с), а при спокойной езде используются 80 000—200 000 об/мин (1000—3000 об/с).
• Для имитации гравитации, комфортной для человека, которая была бы схожа с земным притяжением, скорость вращения космической станции (например, Стэнфордского тора) должна составлять 2 об/мин или менее, чтобы уменьшить эффект укачивания (это вызывается силой Кориолиса).

См. также[править | править код]

• Оборот (единица измерения)

Примечания[править | править код]

Была ли эта статья полезной?

Понятия и определения

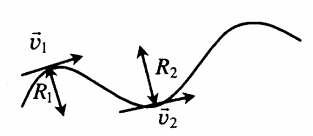
Криволинейное движение — движение, траекторией которого является кривая линия. Вектор скорости тела, движущегося по кривой линии, направлен по касательной к траектории. Любой участок криволинейного движения можно представить в виде движения по дуге окружности или по участку ломаной.

Движение по окружности с постоянной по модулю скоростью — частный и самый простой случай криволинейного движения. Это движение с переменным ускорением, которое называется центростремительным.

Особенности движения по окружности с постоянной по модулю скоростью:

1. Траектория движения тела есть окружность.
2. Вектор скорости всегда направлен по касательной к окружности.
3. Направление скорости постоянно меняется под действием центростремительного ускорения.
4. Центростремительное ускорение направлено к центру окружности и не вызывает изменения модуля скорости.

Период, частота и количество оборотов

Пусть тело двигается по окружности беспрерывно. Когда оно сделает один оборот, пройдет некоторое время. Когда тело сделает еще один оборот, пройдет еще столько же времени. Это время не будет меняться, потому что тело движется с постоянной по модулю скоростью. Такое время называют периодом.

Период — время одного полного оборота. Обозначается буквой T. Единица измерения — секунды (с).

t — время, в течение которого тело совершило N оборотов

За один и тот же промежуток времени тело может проходить лишь часть окружности или совершать несколько единиц, десятков, сотен или более оборотов. Все зависит от длины окружности и модуля скорости.

Частота — количество оборотов, совершенных в единицу времени. Обозначается буквой ν («ню»). Единица измерения — Гц.

N — количество оборотов, совершенных телом за время t.

Период и частота — это обратные величины, определяемые формулами:

Количество оборотов выражается следующей формулой:

Пример №1. Шарик на нити вращается по окружности. За 10 секунд он совершил 20 оборотов. Найти период и частоту вращения шарика.

Линейная и угловая скорости

Линейная скорость

Определение и формулы

Линейная скорость — это отношение пройденного пути ко времени, в течение которого этот путь был пройден. Обозначается буквой v. Единица измерения — м/с.

l — длина траектории, вдоль которой двигалось тело за время t

Линейную скорость можно выразить через период. За один период тело делает один оборот, то есть проходить путь, равный длине окружности. Поэтому его скорость равна:

R — радиус окружности, по которой движется тело

Если линейную скорость можно выразить через период, то ее можно выразить и через частоту — величину, обратную периоду. Тогда формула примет вид:

Выразив частоту через количество оборотов и время, в течение которого тело совершало эти обороты, получим:

Угловая скорость

Определение и формулы

Угловая скорость — это отношение угла поворота тела ко времени, в течение которого тело совершало этот поворот. Обозначается буквой ω. Единица измерения — радиан в секунду (рад./с).

ϕ — угол поворота тела. t — время, в течение которого тело повернулось на угол ϕ

Полезные факты

Радиан — угол, соответствующий дуге, длина которой равна ее радиусу. Полный угол равен 2π радиан.

За один полный оборот тело поворачивается на 2π радиан. Поэтому угловую скорость можно выразить через период:

Выражая угловую скорость через частоту, получим:

Выразив частоту через количество оборотов, формула угловой скорости примет вид:

Сравним две формулы:

Преобразуем формулу линейной скорости и получим:

Отсюда получаем взаимосвязь между линейной и угловой скоростями:

Полезные факты

• У вращающихся прижатых друг к другу цилиндров линейные скорости точек их поверхности равны: v₁ = v₂.
• У вращающихся шестерен линейные скорости точек их поверхности также равны: v₁ = v₂.
• Все точки вращающегося твердого тела имеют одинаковые периоды, частоты и угловые скорости, но разные линейные скорости. T₁ = T₂, ν₁ = ν₂, ω₁ = ω₂. Но v₁ ≠ v₂.

Пример №2. Период обращения Земли вокруг Солнца равен одному году. Радиус орбиты Земли равен 150 млн. км. Чему примерно равна скорость движения Земли по орбите? Ответ округлить до целых.

В году 365 суток, в одних сутках 24 часа, в 1 часе 60 минут, в одной минуте 60 секунд. Перемножив все эти числа между собой, получим период в секундах.

За каждую секунду Земля проходит расстояние, равное примерно 30 км.

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как a_ц.с.. Единица измерения — метры на секунду в квадрате (м/с²). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10³ секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10⁶. Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Алиса Никитина | Просмотров: 21.7k

Вращательное движение (Движение тела по окружности)

Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:

Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α

Вращательное движение, характеристики

Вращательное движение	Угловая скорость	Угловое ускорение
Равномерное	Постоянная	Равно нулю
Равномерно ускоренное	Изменяется равномерно	Постоянно
Неравномерно ускоренное	Изменяется неравномерно	Переменное

Угол поворота

Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).

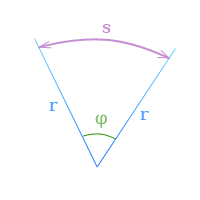
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана

[
φ = frac{s}{r}
]

Соотношение между единицами угла

[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]

$ 1 enspace рад = 57.3° $

$ 1° = 17.45 enspace мрад $

$ 1´ = 291 enspace мкрад $

Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.

Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).

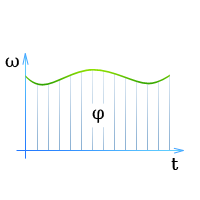
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).

Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).

Число оборотов

Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.

Единица СИ частоты (или числа оборотов)

[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]

В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.

Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.

Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то

Период

[
T = frac{1}{f} = frac{1}{n}
]

Угловое перемещение

Угловое перемещение равно произведению полного числа оборотов на 2π:

[
φ = 2 π N
]

Угловая скорость

Из формулы для одного оборота следует:

[
ω = 2 π f = frac{2π}{T}
]

Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.

Вращательное движение (движение тела по окружности)	стр. 422