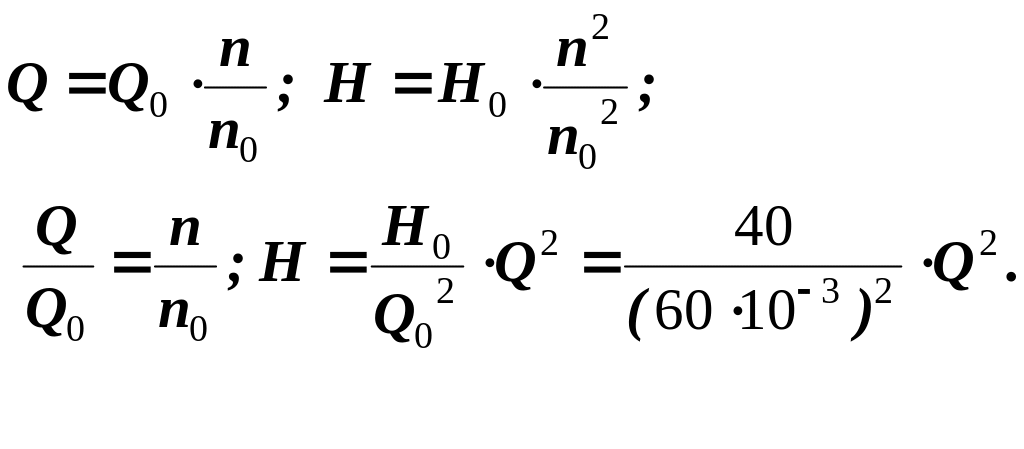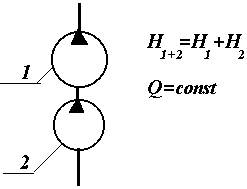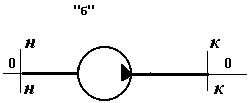| Главная / | Расчет гидронасоса online калькулятор / | Расчет необходимого числа оборотов вала насоса / |
Для расчета необходимого числа оборотов на валу насоса n (об/мин) необходимо ввести следующие данные: рабочий объем гидронасоса Vg (см.куб), расход/подача насоса Q (л/мин) и объемный КПД из интервала, приведенного ниже.
ВНИМАНИЕ! КПД вводить в виде дробного коэффициента от 0 до 1, то есть 100%=1; 90%=0.9; 50%=0.5 и т.д.
| Рабочий объем (Vg см.куб) | |
| Подача (Q л/мин) | |
| Объемный КПД (ƞ) | |
| Число оборотов (n об/мин) |
Объёмный КПД аксиально- поршневого насоса 0.9- 0.98
Объёмный КПД шестеренного насоса 0.85-0.95
Определение числа оборотов вала насоса, соответствующих новому значению подачи
Обратная
задача возникает при регулировании
подачи насоса в заданной гидравлической
сети (Рис.6 ).
Qk
Qk0
H,м
Q, л/с
1
2
3
K0
k
1 –
характеристика насоса Д-320 при n =
2950 об/мин; 2 – кривая подобных
режимов; 3 – кривая к.п.д. при n= 2950
об/мин.
Рис. 6. Иллюстрация
к определению числа оборотов вала
насоса,
соответствующих
новому значению подачи.
Пусть
линия 1 – характеристика насоса при числе
оборотов n1= 2950
об/мин. Необходимо определить обороты
n2, при которых
характеристика насоса пройдет через
точку K0 (Q0=6010-3
м3 /с, H0
=40м.) Найдем в координатах Q-H геометрическое
место точек режимов, подобных режиму,
который определяется точкой K0.
Для этого, подставив в уравнения (8) и
(9) координаты точки K0,
определим зависимость между напором и
подачей при различных значениях отношения
частот вращения n/n0:
|
|
(10) |
Уравнение (10) представляет собой параболу.
Эта парабола изображена на Рис.5 (линия
2). Она называется кривой подобных
режимов. Для всех точек, лежащих
на этой линии, отношение подач
пропорционально отношению частот
вращения.
Определяем
по графику подачу точки К – точки
пересечения параболы 2 и напорной
характеристики насоса 1 при n1
=2950 об/мин :
Qk
=7010-3 м3/с.
Составляем
пропорцию:
|
n2/2950 = |
откуда:
|
n2=295060/70 |
Отметим, что
для подобных режимов коэффициенты
полезного действия насоса ~ одинаковы,
следовательно :
k0
k
= 0,73.
Центробежные
насосы могут обеспечивать высокие
значения подачи при сравнительно
невысоких напорах.
Параллельное и последовательное соединение насосов
На насосных
станциях часто имеет место совместная
работа двух или нескольких насосов на
одну общую сеть, при этом насосы могут
включаться как параллельно, так и
последовательно.
|
а” – Параллельное соединение |
“б”- Последовательное соединение |
|
|
|
|
Q,л/с
H,м Q,л/с H,м |
|
Рис.7. Построение
суммарной характеристики двух насосов.
Параллельное
соединение применяется для увеличения
общей подачи насосной установки, а
последовательное – для увеличения общего
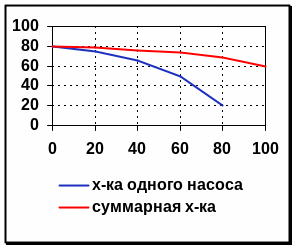
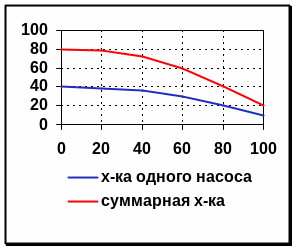
напора. Для анализа совместной
работы насосов строят их суммарную
характеристику.
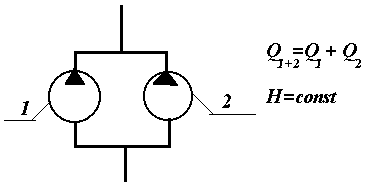
При параллельном соединении (Рис.7”а”)
проводят прямые, параллельные оси
расходов (прямые H=const) и складывают
расходы при постоянном напоре. При
последовательном соединении (Рис.7”б”)
проводят прямые, параллельные оси
напоров (Q=const) и складывают напоры
при постоянном расходе.
2.2. Гидравлическая сеть
Один и тот
же насос может работать с различными
гидравлическими сетями, как показано
на рис.8.
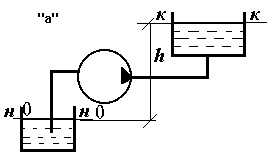
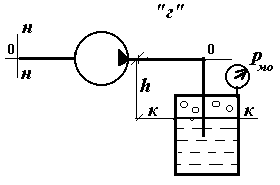
На схеме “а” насос поднимает
жидкость на высоту h; на схеме
“б” перемещает жидкость по
горизонтальному трубопроводу; на схеме
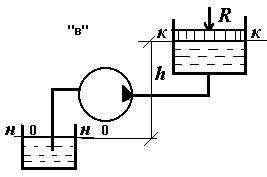
“в” поднимает жидкость в цилиндр,
на поршень которого действует сила R;
на схеме “г” перемещает жидкость
в закрытый резервуар, расположенный
ниже оси насоса с избыточным давлением
на свободной поверхности.
Очевидно,
что в разных схемах для перемещения
жидкости требуется различная энергия
(напор), в то же время зависимость напора
насоса от подачи определяется его
напорной характеристикой. Как же
“совместить” интересы насоса и
гидравлической сети? Для этого нужно
определить рабочую точку насоса.
Рабочая точка насоса –это
точка пересечения характеристики насоса
с характеристикой гидравлической сети.
Характеристика
гидравлической сети – зависимость
удельной энергии (напора), необходимой
для перемещения жидкости в данной
системе, от расхода жидкости в ней.
Уравнение гидравлической сети
выражает закон сохранения энергии для
начального и конечного сечений
гидравлической системы. Энергия,
которую необходимо передать жидкости,
записывается при этом в левую часть
уравнения в виде потребного напора
Hпотр.
Характеристику гидравлической сети
часто называют кривой потребного
напора.
|
|
|
|
|
|
Рис.8.
Иллюстрация включения насоса в различные
гидравлические сети
Для любой
насосной трубопроводной системы закон
сохранения энергии имеет вид:
|
eн |
(11) |
где
eн
– удельная (на единицу веса) энергия
жидкости в начальном сечении н-н
, eк
– удельная (на единицу веса)
энергия жидкости в конечном сечении
к-к , Hпотр–
потребный напор насоса, а hн-к
– потери удельной энергии на преодоление
гидравлических сопротивлений.
Чтобы получить
уравнение гидравлической сети, необходимо:
1). Выбрать
сечения для составления уравнения
сети и горизонтальную плоскость О
– О отсчета величин z,
которую удобно совместить с начальным
сечением;
2).Записать
закон сохранения энергии (11), раскрывая
содержание энергий eн
и eк
по уравнению Бернулли:
|
|
(12) |
3). Из уравнения
(12) определить потребный напор насоса
|
|
(13) |
4). Раскрыть
содержание слагаемых уравнения (13) для
данной гидравлической системы. Здесь:
zн,
pн,
н–
соответственно вертикальная отметка
относительно плоскости 0-0,
абсолютное давление и средняя скорость
в начальном сечении потока, а zк,
pк,
к
-то же в конечном сечении. Если сечение
расположено ниже плоскости 0-0,
отметка z
берется со знаком минус.
Потери энергии
hн-к
представляют собой сумму потерь энергии
на трение по длине и местных гидравлических
сопротивлений:
|
|
(14) |
где –
скорость движения жидкости в трубопроводе,
коэффициенты местных сопротивлений
i
определяются по справочным данным, а
коэффициент гидравлического трения
по следующим формулам:
|
=64/Re |
– ламинарный режим |
(15) |
|
=0,11(68/Re+э/d)0,25 |
– турбулентный режим |
(16) |
5). Выразить
скорости движения и число Re
через расход жидкости:
|
н=Q/н |
(17) |
где н
, к,
тр
– площади соответствующих сечений
потока, d–
диаметр трубопровода, а –
кинематический коэффициент вязкости
жидкости.
Результат
выполнения пунктов 4 и 5, например, для
схемы рис.8”а” имеет вид:
|
|
(18) |
6). Анализируем
уравнение (18). Поскольку площади начального
и конечного сечений много больше площади
сечения трубопровода, первыми двумя
слагаемыми в скобках уравнения (18) можно
пренебречь. Тогда:
|
|
(19) |
7). Изображаем
уравнение сети (19) на том же графике, что
и напорная характеристика насоса и
находим точку их пересечения.
Для построения
характеристики сети задаемся значениями
расхода Q
в диапазоне подач насоса, начиная от
нуля, подставляем эти значения в уравнение
(19) и определяем H.
При решении задачи в общем виде (без
численных значений), характеристику
сети проводим качественно, по виду
функции (19).
Hн
Q, л/с
H, м
Qн
н
Рис.9. Определение
рабочей точки насоса.
В нашем случае
при Q=0, H=h
(допустим 40м, рис.9). Далее, при увеличении
расхода Q
до Qкр
имеет место ламинарный режим движения
в трубе, коэффициент трения
обратно пропорционален расходу (
определяется по формуле (15)). При этом в
уравнении (19) первое слагаемое справа
(h)-
постоянно, второе слагаемое (потери по
длине) пропорционально Q
в первой степени, в третье слагаемое
(местные потери) пропорционально Q2.
В итоге характеристика сети имеет вид
параболы.
На пересечении
характеристик насоса и сети определяется
точка, в которой напор насоса равен
потребному. Это и есть рабочая точка
насоса в данной гидравлической сети.
Её координаты – Hн
и Qн.
При подаче
Qн на кривой
к.п.д. определяется коэффициент полезного
действия насоса, и далее, мощность на
валу насоса, по которой подбирается
приводной двигатель.
На рис.10
показаны характеристики гидравлических
сетей, изображенных на Рис.8. Уравнения
сетей имеют вид:
|
Сеть |
Уравнение |
Величина сi |
|
а |
|
h |
|
б |
|
0 |
|
в |
|
|
|
г |
|
|
сa
сг
в
б
а
г
св
Q, л/с
H,м
Qc
C
Рис.10.
Анализ показывает, что при ламинарном
режиме движения жидкости в трубопроводе
и при отсутствии местных гидравлических
сопротивлений (сеть”б”, рис.8),
характеристика сети представляет собой
прямую линию (линия “б”, Рис.10).
Точка
пересечения характеристики сети с осью
абсцисс (точка С, линия г)
определяет расход при движении жидкости
самотеком, то есть за счет разности
геометрических высот h (сеть
“г”, рис.8).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Зависимость подачи, напора и мощности от числа оборотов насоса
Одним из приемов расширения области применения центробежных насосов является изменение их числа оборотов.
Скорость вращения ротора центробежного насоса существенно влияет на его основные показатели: подачу Q, напор Н и мощность на валу насоса N.
При изменении скорости вращения ротора центробежного насоса с n1 до n2 оборотов в минуту подача, напор и мощность на валу изменяются в соответствии с уравнениями:
Эти соотношения называются законом пропорциональности.
Из приведенных уравнений закона пропорциональности следует:
По этим формулам производится пересчет характеристик насоса на новое число оборотов.
Для построения новой характеристики насоса при частоте вращения n2 следует на заданной характеристике насоса Н=f (Q) при частоте вращения n1 взять несколько произвольных точек при различных подачах Q и соответствующих им значений Н. Далее, используя законы пропорциональности, следует вычислить значения расхода Q2 и напора Н2. По новым значениям Q2 и Н2 построить новые точки и через них провести новую характеристику насоса Н=f (Q) при новом числе оборотов n2.
При построении кривой кпд (η-Q) пользуются тем, что кпд насоса при изменении числа оборотов в довольно широких пределах остается практически постоянным. Уменьшение числа оборотов до 50% практически не вызывает изменений кпд насоса.
Определение частоты вращения вала насоса, обеспечивающей подачу заранее обусловленного расхода воды.
Частоту вращения n2, соответствующую нужному расходу Q2 следует находить, используя законы пропорциональности, приведенные выше.
При этом следует знать, что если взять на заданной характеристике насоса Н при частоте вращения n1, то она будет характеризоваться определенными значениями расхода Q1 и напора Н1. Далее, при уменьшении частоты вращения до n2, используя законы пропорциональности, можно получить новые значения координат этой точки. Ее положение будет характеризоваться значениями Q2 и Н2. Если еще уменьшить частоту вращения до n3, то после перерасчета получим новые значения Q3 и Н3, характеризующие точку и т.д.
Если соединить все точки плавной кривой, то получим параболу, выходящую из начала координат. Следовательно, при изменении частоты вращения вала насоса значение напора и подачи насоса будут характеризоваться положением точек, лежащих на параболе, выходящей из начала координат и называемой параболой подобных режимов.
Для определения Q1 и Н1, входящих в соотношения
![clip_image002[1] clip_image002[1]](https://einsteins.ru/wp-content/uploads/2014/d16d100b8ee9_E786/clip_image0021_thumb.gif)
![clip_image004[1] clip_image004[1]](https://einsteins.ru/wp-content/uploads/2014/d16d100b8ee9_E786/clip_image0041_thumb.gif)
Так как парабола должна пройти через точку с координатами Q2 и Н2, постоянный коэффициент параболы k может быть найден по формуле:
Н2 берется с характеристики трубопровода при заданном расходе Q2 или вычисляется по формуле:
где Нг – геометрическая высота подъема; S – коэффициент сопротивления трубопровода.
Для построения параболы нужно задаться несколькими произвольными значениями Q. Точка пересечения параболы с характеристикой насоса Н при числе оборотов n1 определяет значения Q1 и H1, и частота вращения определяется, как

Потребная скорость вращения ротора насоса может быть определена аналитически:
для водопроводных центробежных насосов по формуле:
где n1 и nпотр – соответственно нормальное и потребное число оборотов в минуту;
Нг – геометрическая высота подъема;
Q потр – потребная подача;
n и m – соответственно число ниток водовода и число насосов;
а и b – параметры насоса;
S – сопротивление одной нитки водовода;
для фекальных центробежных насосов по формуле:
Расчет оборотов гидромотора
Для того чтобы вычислить количество оборотов гидромотора n (rpm), Вы должны знать следующие параметры
1) Подача насоса Q (л/мин), которая подается к гидромотору
2) коэффициент объемных потерь (КПД) , для гидромоторов он находится в диапазоне 0.85-0.95.
3) Объем гидромотора Vg, задается в пределах от 5cм3 до 250cм3
Если вы хотите купить расчет оборотов гидромотора , вы можете:
Ещё из раздела расчет гидропривода
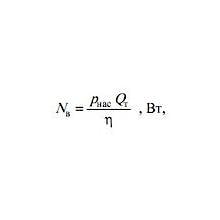
Этот калькулятор позволяет Вам вычислить три параметра, важные для проектирования гидравлической станции: – скорость потока Q (л/мин); – мощность N (кВт); – давление P (бар). Чтобы вычислить потребную мощность N (кВт) , Вы должны ввести следующие …

Для правильного расчета должно быть известно назначение трубопровода: всасывающая магистраль, напорная или сливная. Справочник по допустимой скорости жидкости в пределах этих типов магистралей приведен ниже. Расчетная скорость жидкости (м/с) должна …

Если известны геометрические размеры цилиндра, то можно вычислить площади поршня и объемы полостей цилиндра. Если известно давление гидравлической системы, то дополнительно можно вычислить усилие при выдвижении и втягивании штока. Мощность и …
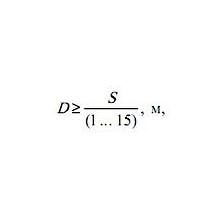
Здесь Вы можете вычислить геометрический размер цилиндра, зная необходимое усилие и рабочее давление гидроситемы. Общее усилие (Fst), Кг Количество цилиндров Давление ( P ), бар Диаметр поршня цилиндра ( fi ), мм Длина хода ( L ), мм Время …
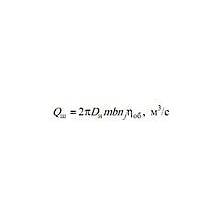
Этот калькулятор позволяет Вам вычислить или подачу Q (л/мин) или объем насоса Vg (cm3). Чтобы вычислить подачу насоса Q (l/min) , Вы должны ввести следующие данные: 1. Скорость вращения вала насоса n, для электродвигателей переменного тока это …
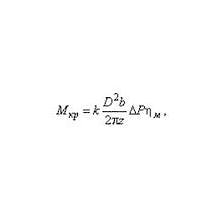
Крутящий момент на валу гидромотора М (кгм) может быть вычислен с использованием следующих параметров: 1. Давление P (бар). 2. Коэффициент объемных потерь, для гидромоторов он находится в диапазоне 0.85-0.95. 3. Объем гидромотора Vg, задается в …

Крутящий момент М (Нм), который требуется передать гидравлическому насосу от двигателя может быть вычислен с использованием следующих параметров: 1. Скорость вращения вала насоса n, для электродвигателей переменного тока это обычно – 960, 1370, 1450 …
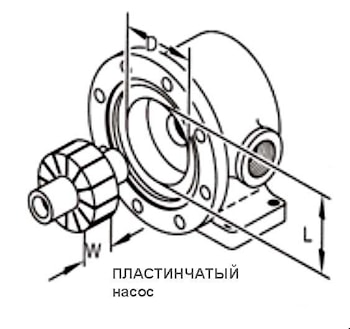
Этот калькулятор позволяет вычислить объемную подачу пластинчатого насоса за один оборот по геометрическим размерам. Тип Ширина ( W ), Диаметр ( D ), Длина ( L ) …
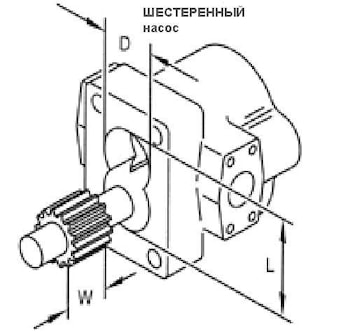
Данный калькулятор позволяет вычислить объемную подачу шестеренного насоса по его геометрическим размерам. Для этого необходимо замерить 3 размера в сантиметрах, в результате вычисления получается подача насоса с см3 за один оборот. Можно измерять в …