Прямая линия
- Обозначение прямой
- Свойства прямой
Прямая линия — это линия, не имеющая неровностей, скруглений и углов. Прямая линия бесконечна, она не имеет ни начала, ни конца. В геометрии прямая линия называется просто прямой.
Для изображения прямой на бумаге используется линейка. Чтобы начертить прямую, надо провести черту вдоль края линейки:
Так как прямая бесконечна, то какой бы длины не была проведена черта, она будет изображать только часть прямой.
Обозначение прямой
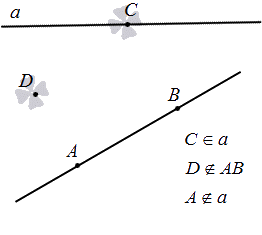
Прямая обозначается одной маленькой латинской буквой, например прямая a, или двумя большими латинскими буквами, поставленными при любых двух точках, лежащих на этой прямой, например прямая AB:
Обратите внимание, что точки на прямой можно обозначать короткими чёрточками.
Свойства прямой
1. Через любые две точки можно провести только одну прямую линию.
Это основное свойство прямой. Оно часто используется на практике, для прокладывания прямых линий с помощью двух каких-либо объектов.
2. Если две любые точки прямой лежат на плоскости, то все точки этой прямой лежат на той же плоскости.
3. Через одну точку можно провести бесконечно много прямых.
4. Есть точки лежащие на прямой и не лежащие на ней.
Точки N и M лежат на прямой a. Точка L не лежит на прямой a.
Для записи принадлежности точки к прямой используется символ принадлежности — ∈
. Например, запись M ∈ a обозначает, что точка M принадлежит прямой a. Для того, чтобы указать что точка не принадлежит прямой можно использовать символ ∉
. Например, запись L ∉ a обозначает, что точка L не принадлежит прямой a.
5. Из трёх разных точек, лежащих на одной прямой, только одна может лежать между двумя другими точками.
На рисунке изображена прямая с тремя точками A, B и C, лежащими на ней. Про эти точки можно сказать:
точка B лежит между точками A и C, точка B разделяет точки A и C
или
точки A и C лежат по разные стороны от точки B
.
Также можно сказать:
точки B и C лежат по одну сторону от точки A, они не разделяются точкой A
или
точки A и B лежат по одну сторону от точки C
.
6. Две прямые, лежащие на одной плоскости, или пересекаются друг с другом в одной точке, или являются параллельными.
Пряма́я — одно из фундаментальных понятий евклидовой геометрии. При систематическом изложении геометрии прямые линии обычно принимаются за одно из исходных (неопределяемых) понятий[1], их свойства и связь с другими понятиями (например, точки и плоскости) определяются аксиомами геометрии[2].
Прямая, наряду с окружностью, относится к числу древнейших геометрических фигур. Античные геометры считали эти две кривые «совершенными» и поэтому признавали только построения с помощью циркуля и линейки. Евклид описал линию как «длину без ширины», которая «равно лежит на всех своих точках»[3].
Аналоги прямых могут быть определены также в некоторых типах неевклидовых пространств. Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то отрезок прямой можно определить как самую короткую кривую, соединяющую эти точки. Например, в римановой геометрии роль прямых играют геодезические линии, которые являются кратчайшими; на сфере кратчайшими являются дуги больших кругов[4].
Свойства прямой в евклидовой геометрии[править | править код]
Участки прямой, ограниченные двумя её точками, называются отрезками.
- Через любую точку можно провести бесконечно много прямых.
- Через любые две несовпадающие точки можно провести единственную прямую.
- Две несовпадающие прямые на плоскости или пересекаются в единственной точке[5], или являются параллельными (следует из предыдущего).
- В трёхмерном пространстве существуют три варианта взаимного расположения двух несовпадающих прямых:
- прямые пересекаются;
- прямые параллельны;
- прямые скрещиваются.
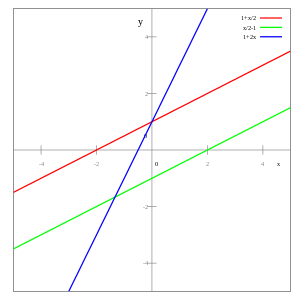
- Прямая линия — алгебраическая кривая первого порядка: в декартовой системе координат прямая линия задается на плоскости уравнением первой степени (линейное уравнение).
Уравнения прямой на плоскости[править | править код]
Способы задания прямой:
Общее уравнение прямой[править | править код]
Общее уравнение прямой линии на плоскости в декартовых координатах:
где 



При 



Вектор с координатами 
При 
Также уравнение можно переписать в виде
Уравнение прямой с угловым коэффициентом[править | править код]
Уравнение прямой линии, пересекающей ось 



Коэффициент 
В этом виде невозможно представить прямую, параллельную оси 
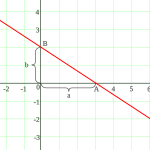
Получение уравнения прямой в отрезках
Уравнение прямой в отрезках[править | править код]
Уравнение прямой линии, пересекающей ось 



В этом виде невозможно представить прямую, проходящую через начало координат.
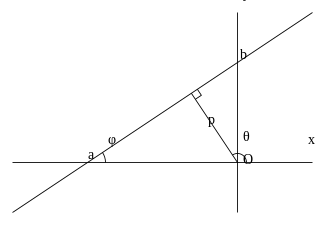
Нормальное уравнение прямой[править | править код]
где 




Если прямая задана общим уравнением 









Во избежание неопределённости знак перед радикалом выбирается так, чтобы соблюдалось условие 



Уравнение прямой, проходящей через две заданные несовпадающие точки[править | править код]
Если заданы две несовпадающие точки с координатами 

или
или в общем виде
Получение векторного параметрического уравнения прямой
Векторное параметрическое уравнение прямой[править | править код]
Векторное параметрическое уравнение прямой задается вектором 


Параметрические уравнения прямой[править | править код]
Параметрические уравнения прямой могут быть записаны в виде:
где 



Смысл параметра 
Каноническое уравнение прямой[править | править код]
Каноническое уравнение получается из параметрическиx уравнений делением одного уравнения на другое:
где 




Уравнение прямой в полярных координатах[править | править код]
Уравнение прямой в полярных координатах 

или
Тангенциальное уравнение прямой[править | править код]
Тангенциальное уравнение прямой на плоскости:
Числа 

Уравнения прямой в пространстве[править | править код]
Векторное параметрическое уравнение прямой в пространстве:
где 



Параметрические уравнения прямой в пространстве:
где 
некоторой фиксированной точки 

Каноническое уравнение прямой в пространстве:
где 
некоторой фиксированной точки 

Общее векторное уравнение прямой[уточнить] в пространстве:
- Поскольку прямая является пересечением двух различных плоскостей, заданных соответственно общими уравнениями:
и
то уравнение прямой можно задать системой этих уравнений:
Векторное уравнение прямой в пространстве[6]:196-199:
- Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой
на фиксированный направляющий вектор прямой
:
где фиксированный вектор 

Взаимное расположение точек и прямых на плоскости[править | править код]
Три точки 


Отклонение точки 

где знак перед радикалом противоположен знаку 
В пространстве расстояние от точки 
можно найти как минимальное расстояние от заданной точки до произвольной точки прямой. Коэффициент 
Взаимное расположение нескольких прямых на плоскости[править | править код]
Две прямые, заданные уравнениями
или
пересекаются в точке
Угол 
При этом под 





Эти прямые параллельны, если 



Любую прямую, параллельную прямой с уравнением 

Если же уравнение прямой задано как 

Если знак перед радикалом противоположен 

Для того, чтобы три прямые
пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если 



Некоторые специальные типы прямых[править | править код]
- Прямая Александрова
- Прямая Симсона
- Прямая Суслина[en]
- Прямая Эйлера
- Числовая прямая
Примечания[править | править код]
- ↑ Coxeter, 1969, p. 4
- ↑ Математическая энциклопедия, 1984, с. 721—722.
- ↑ Прокл Диадох. Комментарий к первой книге «Начал» Евклида / Университет Дмитрия Пожарского. — М., 2013. — С. 116. — 368 с.
- ↑ Норден А. П. Краткий курс дифференциальной геометрии. — М.: Физматгиз, 1958. — С. 214—215. — 244 с.
- ↑ Faber, Appendix B, p. 300.
- ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
Литература[править | править код]
- Маркушевич А. И. Замечательные кривые, Популярные лекции по математике. — Выпуск 4. — Гостехиздат, 1952 г. — 32 стр.
- Прямая // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
- Coxeter, H.S.M (1969), Introduction to Geometry (2nd ed.), New York: John Wiley & Sons, ISBN 0-471-18283-4
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, ISBN 0-8247-1748-1
- Pedoe, Dan (1988), Geometry: A Comprehensive Course, Mineola, NY: Dover, ISBN 0-486-65812-0
- Wylie, Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill, ISBN 0-07-072191-2
Ссылки[править | править код]
- Прямая на плоскости, справочник математических формул «Прикладная математика»
- Прямая в пространстве, справочник математических формул «Прикладная математика»
Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.
Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.
Запомните
Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.
Плоскость нельзя измерять, потому что она бесконечная.
Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.
Прямая линия
Запомните
Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.
Даже когда мы рисуем на листе бумаги небольшой кусок прямой линии, то мы предполагаем, что этот лист бумаги – это бесконечная плоскость, и мы можем мысленно раздвинуть видимые границы бумаги и продлить прямую бесконечно долго.
Обозначение прямой
В основном прямую, как и любую другую линию, обозначают при помощи строчной (маленькой) буквы латинского алфавита.
Иногда обозначение прямой линии происходит при помощи двух точек, которые принадлежат (часто говорят просто – лежат на) этой прямой. В этом случае ее обозначают названием этих двух точек.
Например, на рисунке 1 обозначены такие прямые:
- c
- KL
Рис. 1 Обозначение прямой линии
Если на одной прямой лежат три и более известных нам точек, то обозначить эту линию можно любой из комбинаций имен любых двух точек.
Рис. 2 Обозначение прямой с несколькими точками
На рисунке 2 видно, что на одной прямой b лежат четыре точки: D, G, H, O. Поэтому данную прямую мы можем назвать любым из этих семи имен: b, DG, DH, DO, GH, GO или HO.
Некоторые свойства прямой
Две точки, лежащие на одной прямой, создают отрезок этой прямой.
Через две любые точки на плоскости можно провести единственную прямую.
Рис. 3 Отрезок на прямой
Две разные прямые могут пересекаться или не пересекаться.
Две прямые пересекаются в том случае, если у них есть общая точка.
И наоборот, если у двух разных прямых нет общей точки, тогда эти прямые не пересекаются.
Рис. 5 Пересечение прямых
На рисунке 5 можно видеть, что прямые l и q пересекаются в точке O, а прямые q и g не пересекаются.
Обозначение пересечения письменно записывается при помощи символа ∩: l ∩ q — прямая l пересекается с прямой q.
Как вам уже известно из этого урока, на рисунках мы можем отображать только часть прямых (поскольку они бесконечные), и что их можно мысленно увеличивать, делать более протяженными. Поэтому, если мысленно продлить прямые l и g, то станет понятно, что они тоже пересекаются.
Взаимное расположение точек и прямой, а также их обозначение, точно такое же, как и у всех линий вообще.
Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.
Луч
Определение
Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.
Рис. 6 Деление прямой линии точкой
На рисунке 1 точка O делит прямую a на две части, то есть, на два луча. Один из них, как вы видите, длится бесконечно вправо, а другой – бесконечно влево. Оба они начинаются в одной и той же точке O, которую называют началом луча.
У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.
Обозначение луча
Луч, как и прямую, обозначают двумя способами.
Рис. 7 Обозначение луча
На рисунке 2 приведены примеры обозначения луча:
- a – строчной (маленькая) буква латинского алфавита;
- OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу.
Луч имеет второе название – полупрямая.
Два луча, которые лежат на одной прямой, начинаются в одной точке и направлены в разные стороны, называются дополнительными друг другу лучами, поскольку в соединенном виде они формируют одну прямую линию в точке их начала.
Если лучи лежат на одной прямой, начинаются в одной точке и направлены в одну сторону, их называют совпадающие, или говорят, что эти лучи совпадают.
Рис. 8 Дополнительные друг другу и совпадающие лучи
На рисунке 8 видно, что:
- CB и CH – дополнительные друг другу лучи,
- BC и BH – совпадающие лучи,
- HC и HB – совпадающие лучи.
Статья рассказывает о понятии прямой на плоскости. Рассмотрим основные термины и их обозначения. Поработаем со взаимным расположением прямой и точки и двух прямых на плоскости. Поговорим об аксиомах. В итоге обсудим методы и способы задания прямой на плоскости.
Прямая на плоскости – понятие
Для начала необходимо иметь четкое представление о том, что такое плоскость. Любую поверхность чего-либо можно отнести к плоскости, только от предметов она отличается своей безграничностью. Если представить, что плоскость – это стол, то в нашем случае он не будет иметь границ, а будет бесконечно огромен.
Если карандашом дотронуться до стола, останется отметина, которую можно называть «точкой». Таким образом, получим представление о точке на плоскости.
Рассмотрим понятие прямой линии на плоскости. Если провести прямую на листе, то она отобразится на нем с ограниченной длиной. Мы получили не всю прямую, а только ее часть, так как на самом деле она не имеет конца, как и плоскость. Поэтому изображение прямых и плоскостей в тетради формальное.
Взаимное расположение прямой и точки
Имеем аксиому:
На каждой прямой и в каждой плоскости могут быть отмечены точки.
Точки обозначают как большими, так и маленькими латинскими буквами. Например, А и D или a и d.
Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.
Чтобы обозначить, принадлежит точка плоскости или точка прямой, используют знак «∈». Если в условии дано, что точка A лежит на прямой a, тогда это имеет такую форму записи A∈a. В случае, когда точка А не принадлежит, тогда другая запись A∉a.
Справедливо суждение:
Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.
Данное высказывание считается акисомой, поэтому не требует доказательств. Если рассмотреть это самостоятельно, видно, что при существующих двух точках имеется только один вариант их соединения. Если имеем две заданные точки А и В, то прямую, проходящую через них можно назвать данными буквами, например, прямая АВ. Рассмотрим рисунок, приведенный ниже.
Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:
Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.
Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.
Если дано, что точки А и Р – концы отрезка, значит, его обозначение примет вид РА или АР. Так как обозначения отрезка и прямой совпадают, рекомендовано дописывать или договаривать слова «отрезок», «прямая».
Краткая запись принадлежности включает в себя использование знаков ∈ и ∉. Для того, чтобы зафиксировать расположение отрезка относительно заданной прямой, применяют ⊂. Если в условии дано, что отрезок АР принадлежит прямой b, значит, и запись будет выглядеть следующим образом: АР⊂b.
Случай принадлежности одновременно трех точек одной прямой имеет место быть. Это верно, когда одна точка лежит между двумя другими. Данное утверждение принято считать аксиомой. Если даны точки А, В, С, которые принадлежат одной прямой, а точка В лежит между А и С, следует, что все заданные точки лежат на одной прямой, так как лежат по обе стороны относительно точки B .
Точка делит прямую на две части, называемые лучами. Имеем аксиому:
Любая точка O, находящаяся на прямой, делит ее на два луча, причем две любые точки одного луча лежат по одну сторону луча относительно точки O, а другие – по другую сторону луча.
Взаимное расположение прямых на плоскости
Расположение прямых на плоскости может принимать вид двух состояний.
Две прямые на плоскости могут совпадать.
Такая возможность появляется, когда прямые имеют общие точки. Исходя из аксиомы, написанной выше, имеем, что через две точки проходит прямая и только одна. Значит, что при прохождении 2 прямых через заданные 2 точки, они совпадают.
Две прямые на плоскости могут пересекаться.
Данный случай показывает, что имеется одна общая точка, которую называют пересечением прямых. Вводится обозначение пересечение знаком ∩. Если имеется форма записи a∩b=M, то отсюда следует, что заданные прямые a и b пересекаются в точке M.
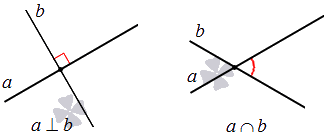
При пересечении прямых имеем дело образовавшимся углом. Отдельному рассмотрению подвергается раздел пересечения прямых на плоскости с образованием угла в 90 градусов, то есть прямого угла. Тогда прямые называют перпендикулярными. Форма записи двух перпендикулярных прямых такая: a⊥b, а это значит, что прямая a перпендикулярна прямой b.
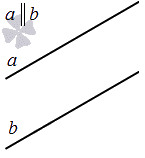
Две прямые на плоскости могут быть параллельны.
Только в том случае, если две заданные прямые не имеют общих пересечений, а, значит, и точек, они параллельны. Используется обозначение, которое можно записать при заданной параллельности прямых a и b: a∥b.
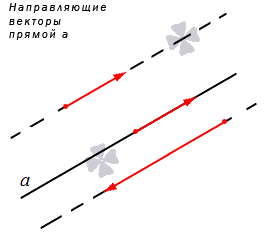
Прямая на плоскости рассматривается вместе с векторами. Особое значение придается нулевым векторам, которые лежат на данной прямой или на любой из параллельных прямых, имеют название направляющие векторы прямой. Рассмотрим рисунок, расположенный ниже.
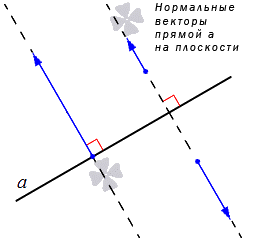
Ненулевые векторы, расположенные на прямых, перпендикулярных данной, иначе называют нормальными векторами прямой. Подробно имеется описание в статье нормальный вектор прямой на плоскости. Рассмотрим рисунок ниже.
Если на плоскости даны 3 линии, их расположение может быть самое разное. Есть несколько вариантов их расположения: пересечение всех, параллельность или наличие разных точек пересечения. На рисунке показано перпендикулярное пересечение двух прямых относительно одной.
Для этого приводим необходимы факторы, доказывающие их взаимное расположение:
- если две прямые параллельны третьей, тогда они все параллельны;
- если две прямые перпендикулярны третьей, тогда эти две прямые параллельны;
- если на плоскости прямая пересекла одну параллельную прямую, тогда пересечет и другую.
Рассмотрим это на рисунках.
Способы задания прямой на плоскости
Прямая на плоскости может быть задана несколькими способами. Все зависит от условия задачи и на чем будет основано ее решение. Эти знания способны помочь для практического расположения прямых.
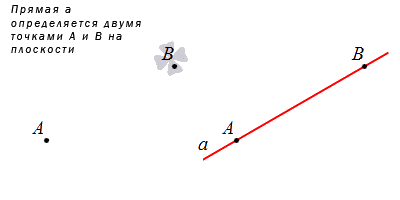
Прямая задается при помощи указанных двух точек, расположенных в плоскости.
Из рассмотренной аксиомы следует, что через две точки можно провести прямую и притом только одну единственную. Когда прямоугольная система координат указывает координаты двух несовпадающих точек, тогда можно зафиксировать уравнение прямой, проходящей через две заданные точки. Рассмотрим рисунок, где имеем прямую, проходящую через две точки.
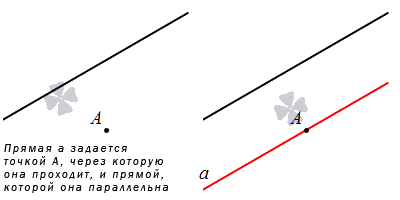
Прямая может быть задана через точку и прямую, которой она параллельна.
Данный способ имеет место на существование, так как через точку можно провести прямую, параллельную заданной, причем, только одну. Доказательство известно еще из школьного курса по геометрии.
Если прямая задана относительно декартовой системы координат, тогда возможно составление уравнения прямой, проходящей через заданную точку параллельно заданной прямой. Рассмотрим принцип задания прямой на плоскости.
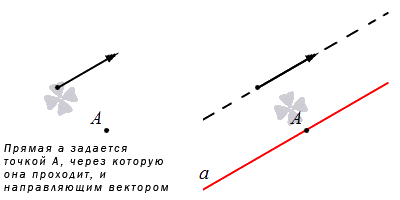
Прямая задается через указанную точку и направляющий вектор.
Когда прямая задается в прямоугольной системе координат, есть возможность составления канонического и параметрического уравнений на плоскости. Рассмотрим на рисунке расположение прямой при наличии направляющего вектора.
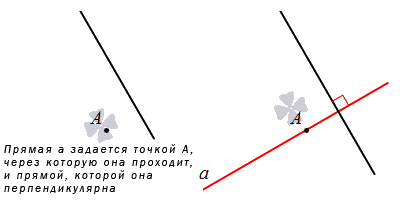
Четвертым пунктом задания прямой имеет смысл, когда указана точка, через которую ее следует начертить, и прямая, перпендикулярная ей. Из аксиомы имеем:
Через заданную точку, расположенную на плоскости, пройдет только одна прямая, перпендикулярная заданной.
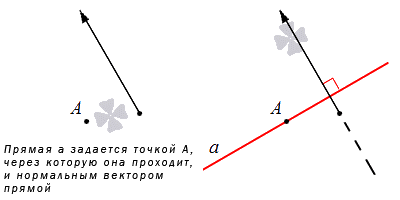
И последний пункт, относящийся к заданию прямой на плоскости, это при указанной точке, через которую проходит прямая, и при наличии нормального вектора прямой. При известных координатах точки, которая расположена на заданной прямой, и координатах нормального вектора есть возможность записывания общего уравнения прямой.
Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне
просто дать определения. Но на практике оказалось, что это не так.
Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так
и не пришли к единому определению.
Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом
их описывают.
Запомните!
Точка — элементарная фигура, не
имеющая частей.
Прямая состоит из множества
точек и простирается бесконечно
в обе стороны.
На рисунке изображена прямая a и точки D, F, G и
H. Точки F и G
лежат на прямой a.
Точки D и H
не
лежат на прямой a.
В тексте точку обозначают символом «(·)».
Принадлежность и непринадлежность точки
прямой обозначают символами «∈» и «∉». Знак принадлежности можно запомнить как
зеркальное отображение буквы «Э» или как знак евро «€» .
То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:
- (·)F ∈ a — точка F принадлежит прямой a (другими словами, точка F лежит на прямой a);
- (·)G ∈ a — точка G принадлежит прямой a;
- (·)D ∉ a — точка D не принадлежит прямой a (другими словами, точка D не лежит на прямой a);
- (·)H ∉ a — точка H не принадлежит прямой a.
Как обозначить прямую
Прямую обычно обозначают одной
маленькой латинской буквой.
Прямую, на которой отмечены
две точки, иногда обозначают
по названиям этих точек большими латинскими точками.
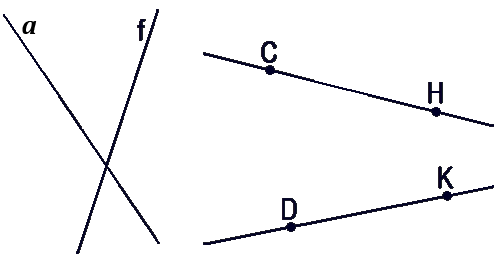
- На рисунке изображены:
- Прямая a
- Прямая f
- Прямая CH
- Прямая DK
Точки D, E и F — лежат на одной прямой, поэтому:
прямая DE,
прямая EF и
прямая DF —
это три разных имени одной и той же прямой.
Разбор примера
Проведите прямую, обозначьте её буквой a и
отметьте точки A и B, лежащие на этой прямой, и
точки P, Q и R, не лежащие на ней. Опишите
взаимное расположение точек A, B, P, Q, R и
прямой a, используя символы ∈ и ∉.
Решение задачи
Проведём прямую.
Обозначим её буквой a.
Отметим точки (·)A и (·)B, лежащие на прямой a.
Отметим точки (·)P, (·)Q и (·)R, не лежащие на прямой a.
Опишем взаимное расположение точек и прямой.
- (·)A ∈ a
- (·)B ∈ a
- (·)P ∉ a
- (·)Q ∉ a
- (·)R ∉ a
Задача решена.
Как обозначается пересечение прямых
На рисунке прямые a и b
не пересекаются.
Прямые b и
c пересекаются.
Хотя на чертеже не видно, но прямые a и
c тоже пересекаются (это становится ясно, если мысленно
продолжить вниз прямые a и с).
В тексте пересечение прямых обозначают
символом ∩. Информацию на рисунке выше можно записать следующим образом:
- b ∩ c — прямые b и с пересекаются;
- a ∩ c — прямые a и с пересекаются.
Прямые e и g имеют общую точку M.
Другими словами, прямые пересекаются в точке M. Геометрическими обозначениями
пересечение прямых в точке записывается так:
e ∩ g = (·)M
Прямые e и f не имеют общей точки — т.е. они не
пересекаются.
Взаимное расположение прямой и точек
Запомните!
Через любые две точки можно
провести прямую, и притом
только одну.
Через одну точку (·)A можно провести
сколько угодно прямых.
Через две точки
(·)A и (·)B можно провести
только одну прямую.
Сколько общих точек имеют две прямые
Запомните!
Две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.
Первый случай расположения прямых
На рисунке выше мы видим, что у прямых f и e
нет общих точек, т.к. эти
прямые не пересекаются.
Второй случай расположения прямых
Возможен вариант, что прямые f и e
пересекаются и, значит, имеют одну общую точку (·)M.
Третий случай расположения прямых
Предположим, что прямые
f и e имеют две или больше общих точек.
Например, точки (·)A и (·)B.
Но мы знаем, что через две
точки можно провести только одну прямую. Значит,
прямые f и e совпадают и наше предположение, что
у двух прямых может быть две или более общих точек неверно.
Вывод: две прямые либо имеют только
одну общую точку, либо не имеют
общих точек.
Разбор примера
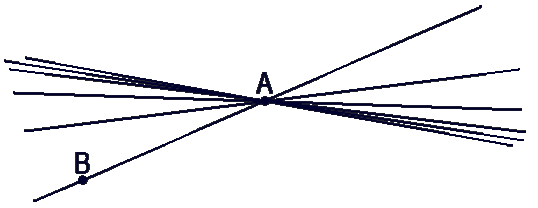
Проведите три прямые так, чтобы каждые две из
них пересекались. Обозначьте все точки
пересечения этих прямых. Сколько получилось
точек? Рассмотрите все возможные случаи.
Решение задачи
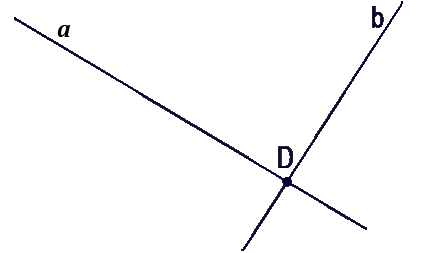
Проведём две прямые a и b так, чтобы эти две
прямые пересекались, и обозначим точку
пересечения.
Как мы видим, точка пересечения только одна. Мы
можем провести третью прямую так, чтобы она
тоже проходила через эту точку пересечения.
Теперь прямая a пересекается
с прямой b,
прямая b пересекается с прямой c и
прямая c пересекается с прямой a.
В этом случае
у нас только одна точка
пересечения всех прямых — точка (·)D.
Но возможен и другой вариант. Мы можем провести третью прямую c так,
чтобы она не проходила через точку (·)D. Тогда
получится
три точки пересечения — (·)D, (·)E и (·)F.
Прямая a пересекается
с прямой b
в точке (·)D,
прямая b пересекается с прямой c в точке (·)F и
прямая c пересекается с прямой a
в точке (·)E. Условие задачи выполнено.
Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.
Ответ: точек пересечения получается одна или
три.
Что такое отрезок
Запомните!
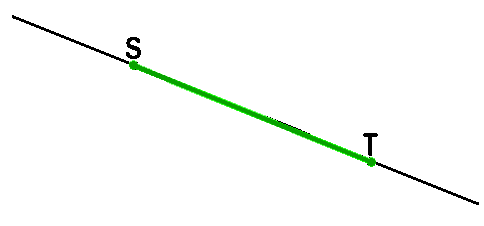
Отрезок —
часть прямой, ограниченная
двумя точками.
Две точки, ограничивающие отрезок, называются
концами отрезка. У отрезка на рисунке выше концы
называются S и
T.
Сам отрезок можно назвать ST
или TS. Когда изображают отрезок, оставшиеся от
прямой хвосты можно не рисовать.
В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 июля 2018 в 19:19
Тимофей Программист
Профиль
Благодарили: 0
Сообщений: 1
Тимофей Программист
Профиль
Благодарили: 0
Сообщений: 1
Диагональ AC параллелограмма ABCD является диаметром окружности, которая делит отрезки AD и CD в точках E и F соответственно. CF = 11. FD = 5. AE:ED = 1:4. Найти площадь данного параллелограмма.
0
Спасибо
Ответить
13 июля 2018 в 1:01
Ответ для Тимофей Программист
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
S = 80√15
0
Спасибо
Ответить
3 октября 2016 в 20:57
Ольга Смирнова
Профиль
Благодарили: 0
Сообщений: 1
Ольга Смирнова
Профиль
Благодарили: 0
Сообщений: 1
На плоскости проведены четыре прямые и отмечены точки, в которых эти прямые попарно пересекаются. Какое наибольшее число таких точек могло получиться?
0
Спасибо
Ответить
5 октября 2016 в 19:08
Ответ для Ольга Смирнова
Никита Фролов
Профиль
Благодарили: 0
Сообщений: 1
Никита Фролов
Профиль
Благодарили: 0
Сообщений: 1
наибольшее число точек пересечения-5
0
Спасибо
Ответить
7 октября 2016 в 19:14
Ответ для Ольга Смирнова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Максимум 6 точек.
Вообще, для N прямых наибольшее число точек пересечения равно .
Никита не прав.
0
Спасибо
Ответить
7 октября 2016 в 19:15
Ответ для Ольга Смирнова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Это не верно.
0
Спасибо
Ответить
6 июля 2016 в 18:28
Ирина Поджарова
Профиль
Благодарили: 0
Сообщений: 2
Ирина Поджарова
Профиль
Благодарили: 0
Сообщений: 2
В равнобедренном треугольнике высота равна 45 см, а основание относится к боковой стороне как 4:3. Найти радиус вписанного круга.
0
Спасибо
Ответить
7 июля 2016 в 8:45
Ответ для Ирина Поджарова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для решения задачи воспользуемся формулой радиуса окружности вписанной в равнобедренный треугольник:
r= · ?
0
Спасибо
Ответить
7 июля 2016 в 8:53
Ответ для Ирина Поджарова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
, где a — сторона треугольника, b-основание.
Необходимо найти a и b.
Высота в равнобедренном треугольнике вычисляется по формуле:
h=?(a2 — ). из условия видно, что b=
0
Спасибо
Ответить
7 июля 2016 в 8:55
Ответ для Ирина Поджарова
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
b=4a/3. Знаем, что h=45, можем вычислить длину основания. Зная длину основания можем вычислить длину стороны. Сзная длину стороны и основания можем вычислить радиус вписанной окружности. Дальше-дело техники. Удачи.
P.S. Прошу прощения, что много сообщений, какие то проблемы с браузером.
0
Спасибо
Ответить
9 июля 2016 в 7:28
Ответ для Ирина Поджарова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
(3x)2 = (2x)2 + 452
x2 = 405.
(45 ? r)2 = r2 + x2
r = 18.
0
Спасибо
Ответить
19 мая 2016 в 23:29
Иван Черновалов
Профиль
Благодарили: 0
Сообщений: 1
Иван Черновалов
Профиль
Благодарили: 0
Сообщений: 1
Провести касательные к элипсу
+
= 1 которые параллельны прямой 2x-y+17=0 (ответ 12x-13y+-169=0)
0
Спасибо
Ответить
7 июня 2016 в 2:23
Ответ для Иван Черновалов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Касательные имеют вид 2x — y + c = o.
Параметр с находим из условия, что уравнение
+ = 1 имеет 1 корень.
0
Спасибо
Ответить
26 января 2016 в 19:47
Ян Кифа
Профиль
Благодарили: 0
Сообщений: 1
Ян Кифа
Профиль
Благодарили: 0
Сообщений: 1
незнайка начертил 3 прямые линии на каждой из них поставил 3 точки всего он поставил 6 точек начерти как он это зделал
0
Спасибо
Ответить
31 января 2016 в 18:36
Ответ для Ян Кифа
Roma Bobrov
Профиль
Благодарили: 0
Сообщений: 1
Roma Bobrov
Профиль
Благодарили: 0
Сообщений: 1
.—–.
.—–.
.—–.
0
Спасибо
Ответить
19 сентября 2016 в 10:53
Ответ для Ян Кифа
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Две линии просто пересекаются. третья линия пересекает две линии вертикально. Точки стоят на пересечениях и по одной на каждой линии.
0
Спасибо
Ответить
19 ноября 2015 в 18:19
Анна Вопилова
Профиль
Благодарили: 0
Сообщений: 1
Анна Вопилова
Профиль
Благодарили: 0
Сообщений: 1
При каком значении высоты прямоугольная трапеция с острым углом 45 и периметром P = 4(1 + ? 2) имеет наибольшую площадь?
0
Спасибо
Ответить
8 июня 2016 в 21:52
Ответ для Анна Вопилова
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
2.
0
Спасибо
Ответить
22 августа 2015 в 15:21
Мария Кузнецова
Профиль
Благодарили: 0
Сообщений: 3
Мария Кузнецова
Профиль
Благодарили: 0
Сообщений: 3
Всем снова привет)
Еще не могу разобраться в такой задаче:
Длина одной стороны четырёхугольника составляет 3/11 его периметра, длина другой
— 4/11,
а сумма равна 28 см.
Найдите периметр четырёхугольника.
Это 1731 из виленкина 5 класс, если что!
0
Спасибо
Ответить
22 августа 2015 в 15:42
Ответ для Мария Кузнецова
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Здравствуй, Мария.
Прежде чем приступить к решению задачи ВНИМАТЕЛЬНО прочитаем условие задачи и
подчеркнём в условии все важные данные.
В этой задаче важно заметить, что в условии говорится не
о прямоугольнике, а о четырёхугольнике.
Поэтому мы не можем пользоваться
формулой нахождения периметра прямоугольника:
P = 2(a + b)
Запишем условие задачи в краткой записи, где a,b — стороны четырёхугольника, P — периметр.
№ 1731
|
Дано: a = 3/11 · P P = ? |
Решение: Прежде всего вспомним, что если в условии записано «составляет от» чего-то, значит это |
Также находим b:
Подставим эти значения в выражение:
У нас получилось уравнение с одним неизвестным. Обе дроби с одинаковыми знаменателями,
поэтому сложить их для нас не составит труда. (Если вы не помните как правильно складывать дроби,
освежить свои знания можно в уроке: “Сложение дробей”.)
Чтобы найти «P» вспомним правило: «Чтобы найти неизвестный множитель надо произведение разделить на известный множитель.»
Разделим дроби по правилам деления дробей.
Ответ: периметр равен 44 см
Кратко оформить задачу можно следующим образом.
№ 1731
|
Дано: a = 3/11 · P P = ? |
Решение:
|
Ответ: P = 44 см
0
Спасибо
Ответить
13 июля 2015 в 14:25
Денис Кежватов
Профиль
Благодарили: 0
Сообщений: 1
Денис Кежватов
Профиль
Благодарили: 0
Сообщений: 1
Сколько равносторонних треугольников
умещается внутри окружности, если стороны треугольников равны радиусу окружности?
0
Спасибо
Ответить
31 августа 2016 в 10:15
Ответ для Денис Кежватов
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Вспомним свойство равностороннего треугольника: углы при каждом из оснований равны между собой и равны 60°.
Окружность равна 360°. Значит 360°/60° = 6.
Ответ 6 равносторонних треугольников умещается внутри окружности, если стороны треугольников равны радиусу этой окружности.
Если нарисовать это на бумаге, становится гораздо понятнее и очевиднее.
0
Спасибо
Ответить

































![[{vec r},{vec a}]={vec M},](https://wikimedia.org/api/rest_v1/media/math/render/svg/940ec5302c287b63f2e45bbfb8501d3ec4133d15)


















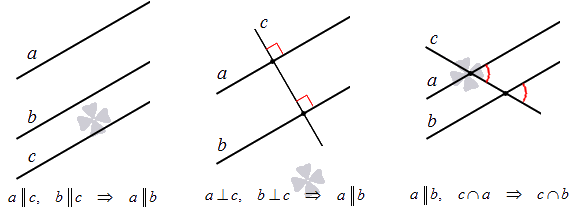







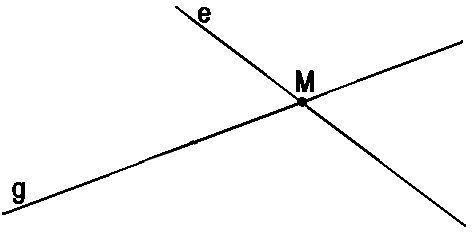
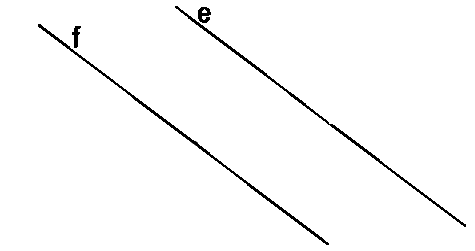
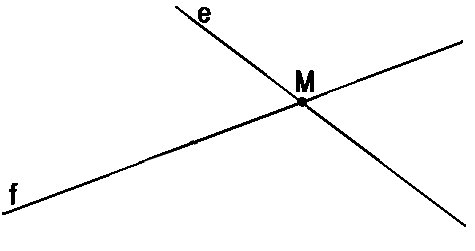

















.png)
.png)
.png)
.png)
.png)
.png)
.png)

