Углы – это геометрические фигуры, образованные двумя лучами, которые выходят из одной точки. Обозначения углов регламентированы ГОСТ 2.307-2011 «Нанесение размеров и предельных отклонений».
Как обозначается угол на чертеже
Угол на чертеже обозначается с помощью универсального и общепринятого символа, на котором показаны два луча, выходящие из одной точки. За символом указывается размер угла в градусах, минутах и секундах. Острый угол символа направлен в сторону уклона.
Обозначение углов на чертеже по ГОСТу
Согласно ГОСТ 2.307 размеры делятся на линейные и угловые. И если в линейных размерах не ставят единицы измерения, т. к. всегда подразумевается, что значения приведены в миллиметрах, то для угловых размеров обязательно указывается значок градуса, минуты и секунды, в зависимости от того, в каких величинах измеряется угол.
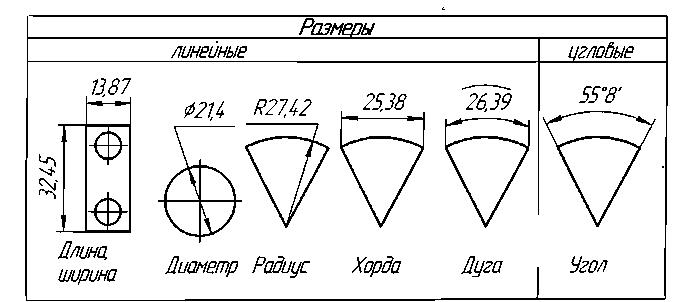
Рисунок 1. Линейные и угловые размеры
Как показать угол на чертеже
Чтобы показать размер используются сплошные тонкие линии, они могут быть выносные или размерные. Любой угол имеет вершину и две стороны. Градусами или минутами обычно обозначается внутренняя сторона угла. В качестве условного обозначения используется символ в виде острого угла, далее указывается числовое значение и единицы измерения. Следует помнить о том, что минута — это одна шестидесятая часть градуса, а секунда одна шестидесятая часть минуты. Градусы обозначаются с помощью маленького круга в верхнем правом углу возле значения, минуты обозначаются одной надстрочной запятой, а секунды двумя надстрочными запятыми.
Допуск угла
В ГОСТ 8908-81 приведены стандарты на допуски углов, применяемые в машиностроении, при меньшей стороне угла до 2,5 м. Значения уклона и угла уклона приведены в таблице (рис. 1). Стандартом установлено 17 степеней точности допусков, которые зависят от длин сторон и размера угла.
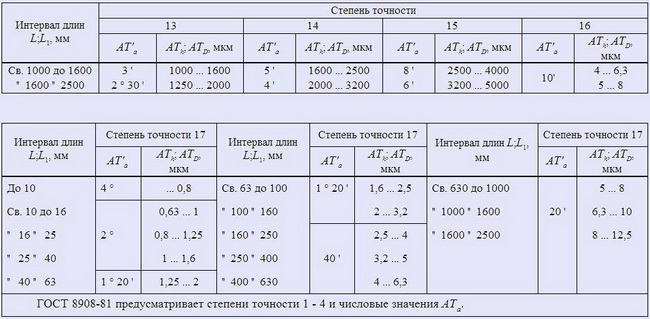
Рисунок 2. Степень точности допуска угла
Виды углов на чертеже
На чертежах могут быть обозначены следующие виды углов:
- острый – менее 90 градусов;
- прямой – равен 90 градусам;
- тупой – более 90 и менее 180 градусов;
- развернутый – равен 180 градусам.
Обозначение у прямого и развернутого угла ставится при необходимости.
Углы наклона
Угол уклона часто встречается как на машиностроительных, так и на строительных чертежах. Он показывает, под каким углом к базовой линии расположен наклонный элемент. Для обозначения наклона используется универсальный символ, который ставится перед размерным числом. К примеру, на строительном чертеже отмостка всегда имеет уклон, для обозначения этого уклона ставится символ и значение в 5 промилле.
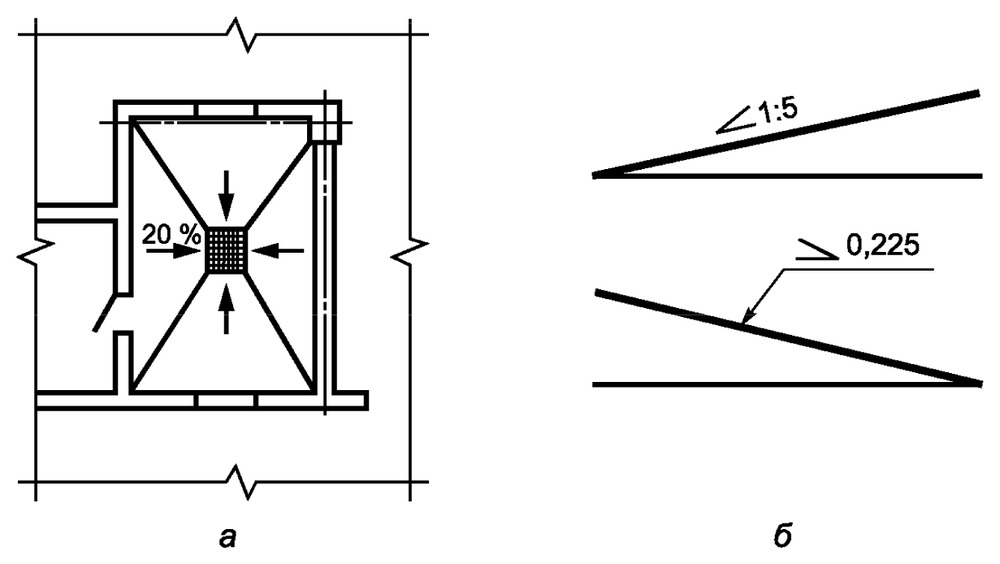
Рисунок 3. Обозначение уклона на плане кровли
Промилле — это одна тысячная или десятая часть процента, поэтому к знаку промилле добавлен еще один нолик. Через промилле в строительных чертежах указывается уклон пандусов и других наклонных поверхностей.
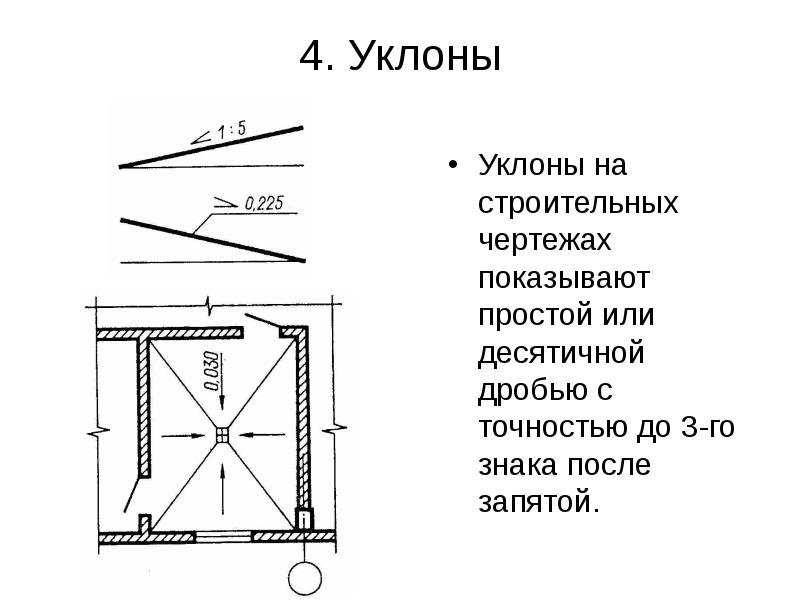
Рисунок 4. Уклон на чертеже
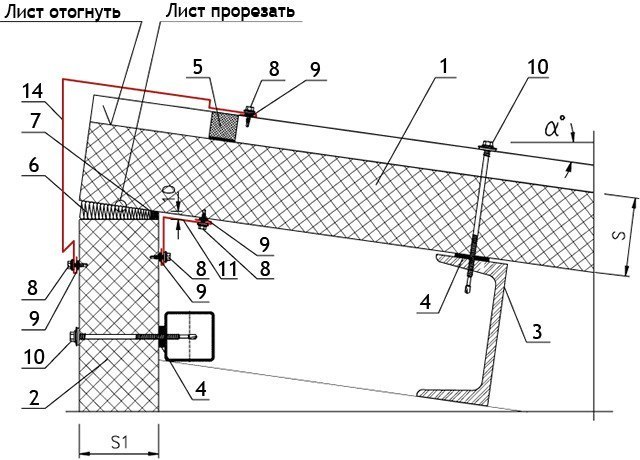
Рисунок 5. На узле сопряжения сендвич панелей указывается угол под которым конструкции крпятся друг к другу
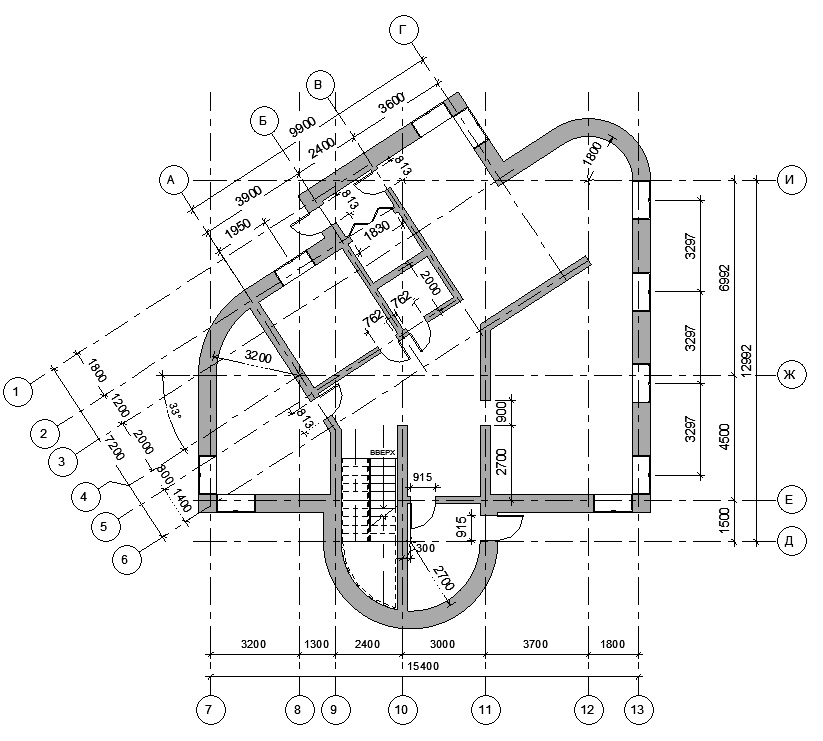
Рисунок 6. Углы. На строительном чертеже обозначен угол в 33 градуса
Угол преломления
Преломление возникает на границе двух сред, при этом угол падения равен углу отражения. Падающий и отраженный лучи показывают на чертеже, а значение угла наносят относительно вертикали, прямого угла.
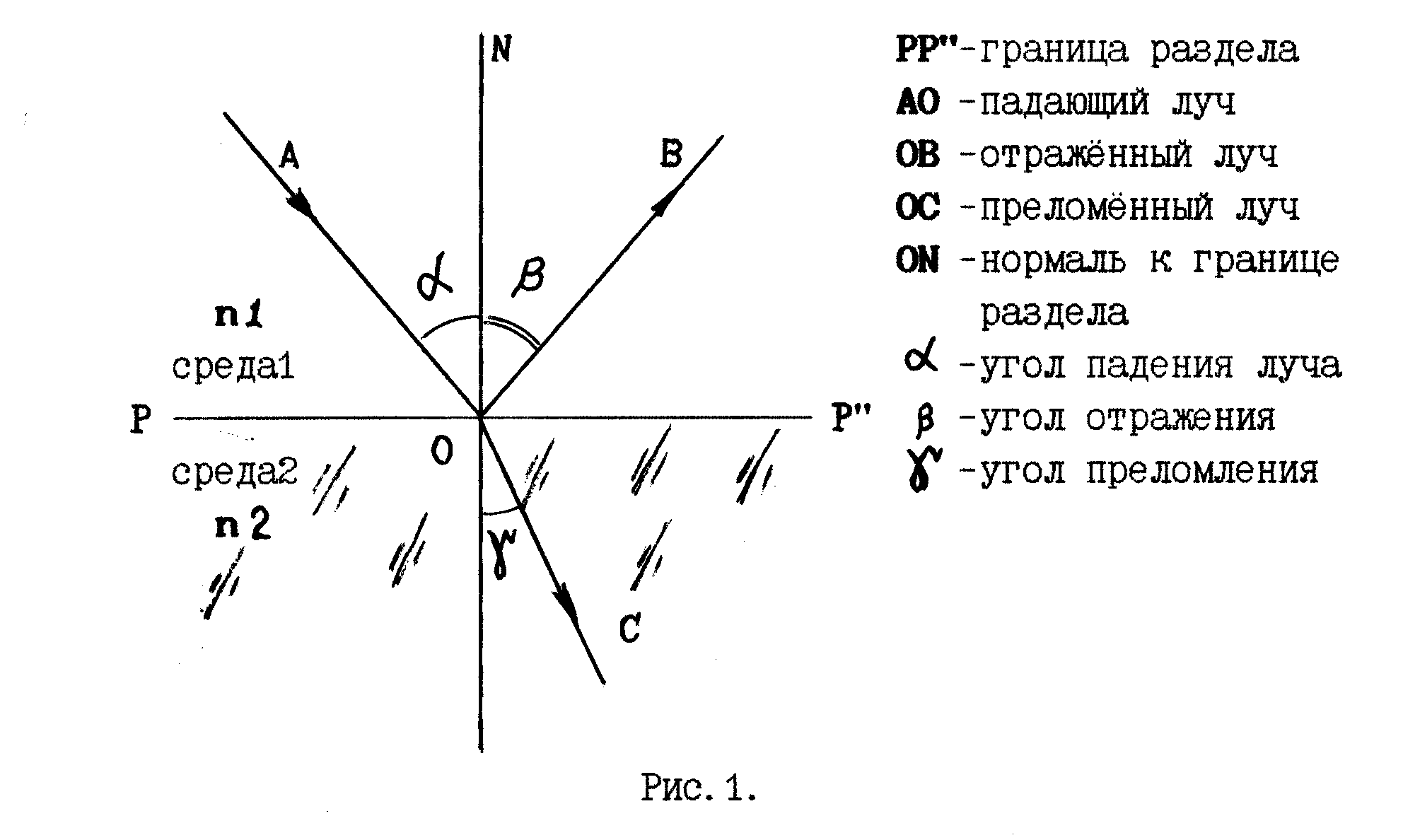
Рисунок 7. Угол преломления
Вертикальные углы
Согласно определению вертикальными называют два угла, в том случае, если стороны одного угла являются продолжением сторон другого. Такие углы будут попарно равны. Обычно на чертеже их обозначают с помощью полукруга или двойного полукруга.
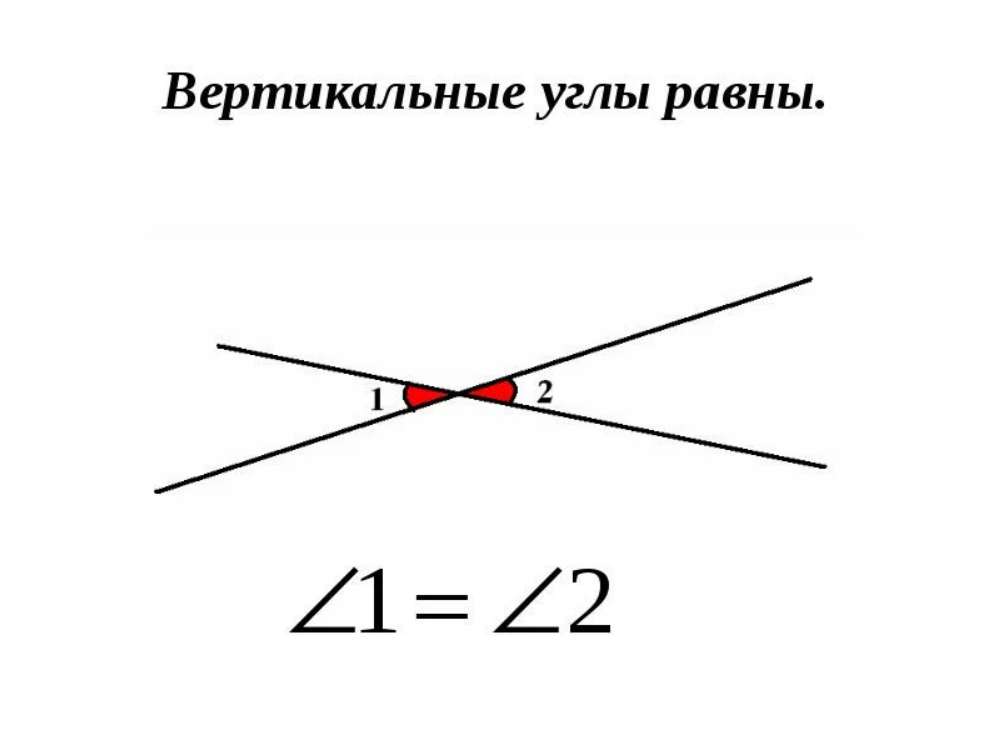
Рисунок 8. Вертикальные углы, пример обозначения
Многогранные углы
Понятие многогранного угла относится к трехмерному пространству, такой угол состоит из плоских углов, которые его образуют, имея общую точку. При этом они не должны лежать в одной плоскости.
У многогранного угла есть два свойства:
- сумма плоских углов многогранного угла превышает 360 градусов;
- существует плоскость, пересекающая все ребра многогранного угла.
По количеству граней многогранные углы делят на трехгранные, четырехгранные, пятигранные и так далее.
Самым показательным примером многогранного угла является вершина четырехугольной пирамида. Многогранный угол может быть невыпуклым и выпуклым.
Смежные углы
Смежными называются углы, которые имеют одну общую сторону, а две другие их стороны являются продолжением друг друга. Сумма смежных углов равна 180 градусам. Поэтому, если известно значение одного угла, то найти значение второго не составляет труда.
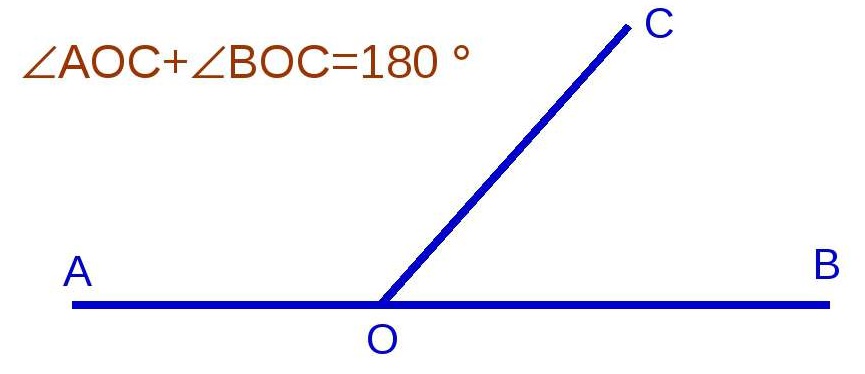
Рисунок 9. Пример смежных углов
Углы фаски
Деталь может иметь скос или скругление, которое называется фаской. Обозначение фаски установлено в ГОСТ 2.307-2011, обычно ее показывают размерными линиями. Запрещено использовать осевые и контурные линии для обозначения фаски. На чертеже обязательно указывают ширину, размер скоса и угол относительно главной оси элемента или механизма. Если на чертеже показана фаска, но не указан угол, то подразумевается ее стандартное значение 45 градусов. Обозначение выполняется с помощью выносной линии или с помощью линейных размеров.
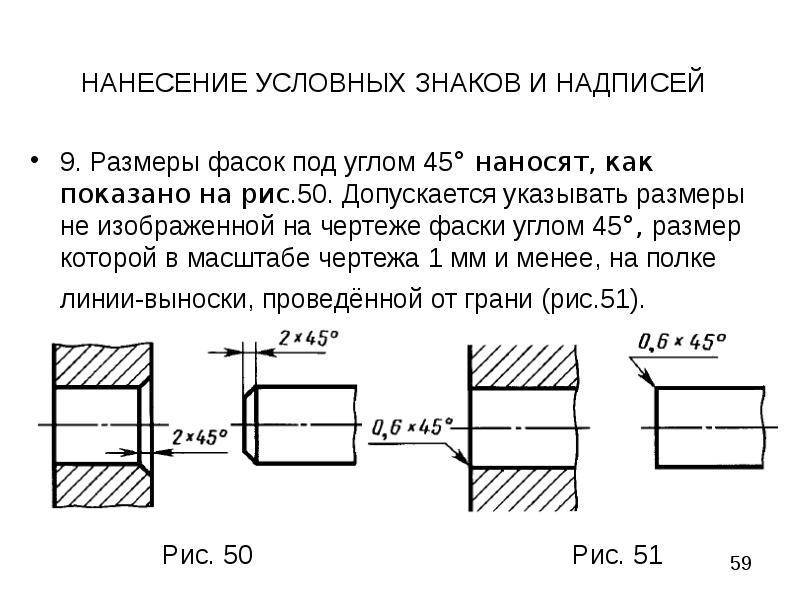
Рисунок 10. Обозначение фаски по ГОСТ
Внешние углы на чертеже
На чертежах может потребоваться указать внешний угол треугольника, это угол смежный с любым из внутренних углов. Следовательно, у каждой вершины можно построить два равных внешних угла. Также существует теорема, доказывающая что внешний угол равен сумме двух внутренних углов, которые не смежны с ним.
Центральные углы на чертеже
Центральным называется угол, который равен градусной мере дуги, на которую он опирается. Центральный угол отличается от вписанного тем, что вершин вписанного угла лежит на окружности, и он равен половине дуги, на которую опирается. Вписанные и центральные углы имеют зависимость, например, если нарисовать их на одной окружности, то вписанный угол будет равен половине центрального, если они опираются на одну дугу. Таким образом, зная один угол, можно определить другой.
Ответы на вопросы
Как обозначается радиус окружности на чертеже?
Для обозначения радиуса используется значок R, после которого указывается значение в миллиметрах и сплошная тонкая линия со стрелкой на конце. Радиус проводят от центра окружности к обозначаемому отрезку. Обычно указывают только радиус, диаметр при необходимости можно найти путем удвоения радиуса.
Как указать прямой угол?
При обозначении острого или тупого угла в основании между лучами проводят полукруг, если угол прямой в его основании рисуют квадрат.
Как отсчитывают угол на чертеже?
Угол образовывается двумя лучами, чтобы найти его значение используют транспортир.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Углы в геометрии
Поддержать сайт![]()
Запомните!
![]()
Угол — это геометрическая фигура, которая состоит из двух лучей и вершины.
Вершина угла — это точка, в которой два луча берут начало.
Стороны угла — это лучи, которые образуют угол.
Например:
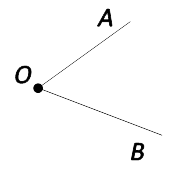
Вершина угла — точка «O».
Стороны угла — «OA» и «OB».
Для обозначения угла в тексте используется символ:
 AOB
AOB
Способы обозначения углов
-
Одной заглавной латинской буквой, указывающей его вершину.
Угол: O
O
-
Тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные
на сторонах угла.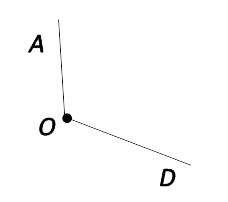
Угол: AOD
AODНазывать угол можно с любого края, но НЕ с вершины.
Угол с рисунка выше имеет два названия:
 AOD
AOD
и DOA.
DOA.
Запомните!
![]()
При таком обозначении вершина угла должна всегда находиться в середине названия.
Единица измерения углов — градусы. Углы измеряют с помощью специального прибора — транспортира.
Для обозначения градусов в тексте используется символ: °
50 градусов обозначаются так: «50°»
Виды углов
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Прямой | Равен 90° | 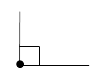 |
| Острый | Меньше 90° |
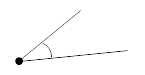 |
| Тупой | Больше 90° |
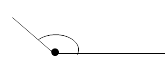 |
| Развернутый | Равен 180° |
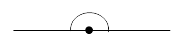 |
Запомните!
![]()
Два угла могут иметь одну общую сторону.
Обратите внимание на рисунок ниже. Попробуйте сосчитать и назвать все углы на изображении.
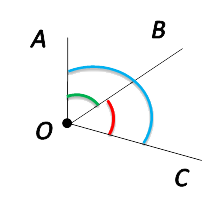
Если насчитали три угла, то вы правы. Давайте их назовём:
 AOB
AOB  BOC
BOC AOC
AOC
Углы  AOB и
AOB и
 BOC
BOC
имеют общую сторону OB.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
2 мая 2020 в 5:47
Люба Капитонова

Профиль
Благодарили: 0
Сообщений: 1

Люба Капитонова
Профиль
Благодарили: 0
Сообщений: 1
В треугольнике ABC угол А равен 120 градусам. Точка D находится внутри треугольника такт, что угол DBC = 2ABD и DCB = 2ACD. Опредлить меру угла BDC в градусах.
0
Спасибо
Ответить
6 мая 2020 в 16:09
Ответ для Люба Капитонова
Галина Федотова

Профиль
Благодарили: 0
Сообщений: 3

Галина Федотова
Профиль
Благодарили: 0
Сообщений: 3
ABD=x, DBC=2x, ACD=y, DCB=2y,
3x+3y+120=180, x+y=20
BDC+2x+2y=180
BDC=180-2(x+y)=180-40=140
0
Спасибо
Ответить
2 августа 2019 в 16:08
Артем Хохлов

Профиль
Благодарили: 0
Сообщений: 1

Артем Хохлов
Профиль
Благодарили: 0
Сообщений: 1
Добрый день! Есть 2 фигуры: круг и прямоугольник. Центр окружности всегда расположен в левом нижнем углу прямоугольника. Известны радиус окружности, ширина и высота прямоугольника. Окружность всегда пересекается с прямоугольником в 2х точках (А и Б): в верхней и нижней стороне прямоугольника. Нужна формула для расчета угла между точками А и Б.
0
Спасибо
Ответить
18 сентября 2019 в 8:55
Ответ для Артем Хохлов
Андрей Фогель

Профиль
Благодарили: 0
Сообщений: 1

Андрей Фогель
Профиль
Благодарили: 0
Сообщений: 1
a < R < b, где a — высота, b — длина прямоугольника.
Треугольник AOB будет равнобедренным. Думаю, что для вашей задачи пригодятся следующие формулы:

0
Спасибо
Ответить
21 января 2016 в 16:17
Сергей Фадеев

Профиль
Благодарили: 0
Сообщений: 6

Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
начертите угод в 270 градусов без ленейки![]()
0
Спасибо
Ответить
19 сентября 2016 в 10:42
Ответ для Сергей Фадеев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Угол 270 градусов, это три угла по 90. 180-это половина окружности, дорисовываем ещё 90 градусов и получаем-270. Можно нарисовать окружность, разделить её на 4 части и отметить три из них — это будет 270. Можно начертить угол в 90 градусов -всё что лежит за этим углом- и будет угол в 270.
0
Спасибо
Ответить
1 февраля 2017 в 12:01
Ответ для Сергей Фадеев
Олег Сергиевский

Профиль
Благодарили: 0
Сообщений: 3

Олег Сергиевский
Профиль
Благодарили: 0
Сообщений: 3
Не то, что — 270, любой угол чертится — сразу, без проблем, всего — за два движения!
0
Спасибо
Ответить
1 февраля 2017 в 12:02
Ответ для Сергей Фадеев
Олег Сергиевский

Профиль
Благодарили: 0
Сообщений: 3

Олег Сергиевский
Профиль
Благодарили: 0
Сообщений: 3
0
Спасибо
Ответить
1 февраля 2017 в 12:04
Ответ для Сергей Фадеев
Олег Сергиевский

Профиль
Благодарили: 0
Сообщений: 3

Олег Сергиевский
Профиль
Благодарили: 0
Сообщений: 3
0
Спасибо
Ответить
21 января 2016 в 16:14
Сергей Фадеев

Профиль
Благодарили: 0
Сообщений: 6

Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
начертите угод в 270 градусов без ленейки![]()
0
Спасибо
Ответить
19 сентября 2016 в 10:43
Ответ для Сергей Фадеев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
0
Спасибо
Ответить
16 сентября 2015 в 14:53
Никита Иванов

Профиль
Благодарили: 0
Сообщений: 2

Никита Иванов
Профиль
Благодарили: 0
Сообщений: 2
Один из смежных углов в 3 раза больше другого. Какова величина кождого из смежных углов?
0
Спасибо
Ответить
16 сентября 2015 в 19:53
Ответ для Никита Иванов
Никита Семеренко

Профиль
Благодарили: 0
Сообщений: 2

Никита Семеренко
Профиль
Благодарили: 0
Сообщений: 2
45 и 135
0
Спасибо
Ответить
5 сентября 2016 в 14:29
Ответ для Никита Иванов
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Общая величина углов равна 180.
х + 3х = 180
4х = 180
х = 45
3 · 45 = 135
Ответ: 45° и 135°
0
Спасибо
Ответить
У этого термина существуют и другие значения, см. Угол (значения).
| Угол | |
|---|---|
| ∠ | |
| Размерность | безразмерная |
| Единицы измерения | |
| СИ | радиан |
| Другие единицы | градус, минута, секунда, град, тысячная |
У́гол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла)[1].
Общие сведения[править | править код]

Два луча (BA и ВС), выходящие из общей вершины B, образуют на плоскости две области, являющиеся внутренними областями двух плоских углов
Плоскость, содержащая обе стороны угла, делится углом на две области. Каждая из этих областей, объединённая со сторонами угла, называется плоским углом (или просто углом, если это не вызывает разночтений). Один из плоских углов (обычно меньший из двух) иногда условно называют внутренним, а другой — внешним. Точки плоского угла, не принадлежащие его сторонам, образуют внутреннюю область плоского угла.
В другом, эквивалентном варианте определения плоским углом называется часть плоскости, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую лежащую в этой плоскости линию (которая называется линией, стягивающей данный плоский угол).
Часто для краткости углом называют также угловую меру, то есть число, определяющее величину угла.
Кроме наиболее часто встречающихся плоских углов, в качестве углов могут рассматриваться и более общие объекты — фигуры, образованные пересекающимися дугами, полуплоскостями и другими фигурами как в евклидовой, так и в других типах геометрии в метрических пространствах различной размерности.
Обозначение углов[править | править код]

«∠», обозначение угла в геометрии

Для обозначения угла имеется общепринятый символ: 
В математических выражениях углы часто обозначают строчными греческими буквами: α, β, γ, θ, φ и др. Как правило, данные обозначения также наносятся на чертёж для устранения неоднозначности в выборе внутренней области угла. Чтобы избежать путаницы с числом пи, символ π, как правило, для этой цели не используется. Для обозначения телесных углов (см. ниже) часто применяют буквы ω и Ω.
Также часто угол обозначают тремя символами точек, например 



См. вариации и обобщения.
Реже используются обозначения прямых, образующих стороны угла. Например, 


Так, для рисунка справа записи γ, 

Иногда для обозначения углов используются строчные латинские буквы (a, b, c, …) и цифры.
На чертежах углы отмечаются небольшими одинарными, двойными или тройными дужками, проходящими по внутренней области угла с центрами в вершине угла. Равенство углов может отмечаться одинаковой кратностью дужек или одинаковым количеством поперечных штрихов на дужке. Если необходимо указать направление отсчёта угла, оно отмечается стрелкой на дужке. Прямые углы отмечаются не дужками, а двумя соединёнными равными отрезками, расположенными таким образом, что вместе со сторонами они образуют небольшой квадрат, одна из вершин которого совпадает с вершиной угла.
Угловая мера[править | править код]
Угловая мера, позволяющая сравнивать плоские углы, может быть введена следующим образом. Два плоских угла называются равными (или конгруэнтными), если они могут быть совмещены так, что совпадут их вершины и обе стороны. От любого луча на плоскости в данную сторону можно отложить единственный угол, равный данному. Если один угол может быть размещён полностью внутри другого угла таким образом, что вершина и одна из сторон этих углов совпадают, то первый угол меньше второго. Назовём прилежащими два угла, расположенные так, что сторона одного совпадает со стороной другого (а значит, совпадают и вершины), но их внутренние области не пересекаются. Угол, составленный из несовпадающих сторон двух прилежащих углов, назовём сложенным из этих углов. Каждому углу можно поставить в соответствие число (угловую меру) таким образом, что:
- равным углам соответствует равная угловая мера;
- меньшему углу соответствует меньшая угловая мера;
- у угла, стороны которого совпадают (нулевого угла), угловая мера равна нулю (то же справедливо и для угла между параллельными прямыми);
- каждый ненулевой угол имеет определённую угловую меру, большую нуля;
- (аддитивность) угловая мера угла равна сумме угловых мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
В некоторых системах обозначений, если есть необходимость различать угол и его меру, для угла (геометрической фигуры) используют обозначение 


Мера угла
θ в радианах равна отношению длины стягивающей его дуги
s к её радиусу
r
Угол измеряют:
- в градусах, минутах, секундах;
- в радианах;
- в оборотах;
- в градах, минутах, секундах;
- в часах, минутах и секундах;
- в тысячных и делениях угломера;
- в румбах.
Наиболее распространённая градусная мера — градус, минута, секунда, в которой за 1° принимается 1/180 от развёрнутого угла (см. ниже), одна минута 


Радианная мера угла — отношение длины s стягивающей дуги к её радиусу r. Радианная мера используется в математическом анализе (например, как числовой аргумент тригонометрических функций и при определении числовых (табличных и графических) значений обратных аркфункций), в планиметрии и механике (при рассмотрении вращения около точки или оси и других процессов, описываемых с помощью тригонометрических функций, — колебаний, волн и так далее).
Углы можно измерять также в оборотах. Один оборот — это полный угол (то есть угол в 360 градусов). Про произвольный угол говорят, что он составляет x оборотов, если x — отношение длины s дуги, стягивающей угол, к длине L окружности, содержащей эту дугу.
Градовая мера измерения углов была предложена к применению исторически, в настоящее время почти нигде не используется, поскольку не вытеснила более распространённую шестидесятеричную градусную.
Измерение углов в градусной мере восходит к Древнему Вавилону, где использовалась шестидесятеричная система счисления, следы которой сохранились у нас в делении времени и углов. Один градус (1/360 полного угла) делится на 60 угловых минут (или минут дуги), в свою очередь минута делится на 60 угловых секунд (секунд дуги). Меньшие углы измеряются в дольных единицах секунды, образуемыми с помощью приставок СИ (угловая миллисекунда, угловая микросекунда и т.д.).
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ основной единицей измерения угла является радиан.

В морской терминологии углы измеряются в румбах. 1 румб равен 1⁄32 от полной окружности (360 градусов) компаса, то есть 11,25 градуса, или 11°15′.
В астрономии угол прямого восхождения и часовой угол в экваториальной системе координат измеряются в часах, минутах и секундах (составляющих соответственно 1⁄24, 1⁄1440 и 1⁄86 400 полной окружности); это связано с угловой скоростью осевого вращения Земли, составляющей приблизительно 1 оборот за 24 часа[2]. Таким образом, за один час (минуту, секунду) времени небесная сфера «поворачивается» примерно на 1 час (минуту, секунду) в угловой мере. Остальные угловые величины в астрономии выражаются обычно в градусах, минутах и секундах дуги. Одна секунда (минута) прямого восхождения равна 15 секундам (минутам) дуги.
В артиллерии и оружейном деле используются также тысячные и деления угломера.
В некоторых контекстах, таких как идентификация точки в полярных координатах или описание ориентации объекта в двух измерениях относительно его базовой ориентации, углы, отличающиеся на целое число полных оборотов, фактически являются эквивалентными. Например, в таких случаях можно считать эквивалентными углы 15° и 360015° (= 15° + 360°×1000). В других контекстах, таких как идентификация точки на спиральной кривой или описание совокупного вращения объекта в двух измерениях относительно его начальной ориентации, углы, отличающиеся на ненулевое целое число полных оборотов, не эквивалентны.
Некоторые плоские углы имеют специальные названия. Кроме вышеназванных единиц измерения (радиан, румб, градус и тому подобное), к ним относятся:
- квадрант (прямой угол, 1⁄4 окружности);
- секстант (1⁄6 окружности);
- октант (1⁄8 окружности; кроме того, в стереометрии октантом называется трёхгранный угол, образованный тремя взаимно перпендикулярными плоскостями),

Обозначение угла уклона дороги на дорожном знаке
Иногда углы (например, угол уклона поверхности) измеряют не собственно угловой мерой, а её тангенсом (или синусом), то есть отношением подъёма по наклонной плоскости к проекции на горизонталь пройденного по ней пути (или к самому этому пути). Для обычного случая малых углов уклона это отношение примерно равно углу, выраженному в радианах (tg α ≈ sin α ≈ α, при α < 0,1 разница между этими величинами менее 1 %). При этом отношение выражается обычно в процентах или промилле. Например, уклон дороги в 10 % означает, что на каждые 100 метров пути (в проекции на горизонталь) дорога поднимается на 10 м; угол к горизонту равен arctg(10/100) ≈ 5,71° ≈ 0,1 радиана.
Такой способ измерения углов не является, строго говоря, угловой мерой, так как не обладает свойством аддитивности (см. выше).
См. также приближения для малых углов[en].
Направление отсчёта углов[править | править код]

Стрелкой показано направление отсчёта углов
В математике и физике, обычно, положительным направлением отсчёта углов считается направление против часовой стрелки. Обычно, угол начинают измерять от луча, начало которого совпадает с центром системы координат (СК), а направление совпадает с положительным направлением оси абсцисс (в полярной СК, цилиндрической СК, сферической СК, СК на тригонометрической окружности и других).
В географии и геодезии за начало отсчёта углов по азимуту принято направление «на север»; угол отсчитывается по часовой стрелке.
Таким образом, направлению «на восток» соответствует азимутальный угол 90°, «на юг» — 180°, «на запад» — 270°. В артиллерии предпочитают направление полярной оси «на юг» и соответствующий полярный угол называют также азимутом (направление «на запад» соответствует азимутальному углу 90°).
Типы углов[править | править код]
-
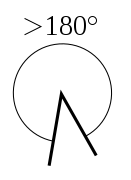
Выпуклый угол
-
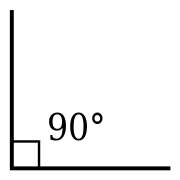
Прямой угол
-

Полный угол
-

Острый угол
-

Тупой угол
-
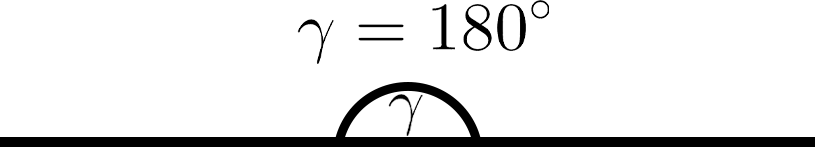
Развёрнутый угол
В зависимости от величины углы называются следующим образом.
- Нулевой угол (0°); стороны нулевого угла совпадают, его внутренняя область — пустое множество.
- Острый угол (от 0° до 90°, не включая граничные значения).
- Прямой угол (90°); стороны прямого угла перпендикулярны друг другу.
- Тупой угол (от 90° до 180°, не включая граничные значения).
- Косой угол (любой, не равный 0°, 90°, 180° или 270°).
- Развёрнутый угол (180°); сторонами развёрнутого угла являются две полупрямые одной прямой, то есть два луча, направленных в противоположные стороны.
- Невыпуклый угол (от 0° до 180° включительно).
- Выпуклый угол (от 180° до 360°, не включая граничные значения).
- Полный угол (360°) — см. оборот (единица измерения).
Биссектриса[править | править код]
Биссектрисой (от лат. bi- «двойное» и sectio «разрезание») угла называется луч, выходящий из вершины угла и проходящий через его внутреннюю область, который образует с его сторонами два равных угла. Расстояние любой точки биссектрисы от сторон угла одинаково (и, обратно, любая точка внутренней области угла, равноудалённая от сторон угла, лежит на его биссектрисе).
Плоские углы[править | править код]
Термин плоский угол употребляется как синоним термина угол, определённого в начале статьи, для отличия его от употребляемого в стереометрии понятия телесного угла (в том числе двугранного, трёхгранного или многогранного угла).
Под свойствами плоских углов нередко понимают соотношения величин углов (смежных, дополнительных, прилегающих, вертикальных — см. ниже) в случае, когда углы лежат в одной плоскости (для планиметрии это подразумевается само собой, однако для стереометрии уточнение необходимо, иначе перечисленные ниже соотношения не имеют места, а сами углы, если не лежат в одной плоскости, не называются смежными или прилегающими (вертикальные всегда лежат в одной плоскости автоматически).
Вертикальные и прилежащие углы[править | править код]
-

Вертикальные углы. Две пары углов (A и B, C и D) попарно равны
-
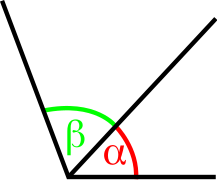
Прилежащие углы. Величина угла, образованного внешними (не общими) их сторонами, равна сумме величин их самих (α + β)
-

Дополнительные углы a и b (взаимно дополняют друг друга до прямого угла). Оба дополнительных угла являются острыми
-
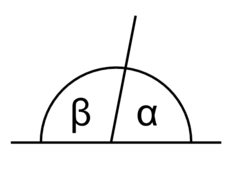
Смежные углы — на этом рисунке острый (α) и тупой (β) — образуют развёрнутый угол (α + β)
-
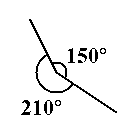
Сопряжённые углы — образуют полный угол (360°); на этом рисунке частный пример: 150° + 210° = 360°
- Вертикальные углы — два угла на плоскости, которые образуются при пересечении двух прямых и не имеющие общих сторон (стороны одного угла являются продолжением сторон другого). Их основное свойство: вертикальные углы равны.
- Прилежащие углы — два угла на плоскости, имеющие общими по одной вершине и по одной из двух сторон, но не пересекающиеся внутренними областями. Величина угла, образованного двумя внешними (не общими) сторонами прилежащих углов, равна сумме величин самих прилежащих углов (на рисунке α + β).
Частные случаи прилежащих углов.
- Если прилежащие углы равны, то их общая сторона — биссектриса.объединённого угла.
- Дополнительные углы — два угла с общей вершиной на плоскости, одна из сторон которых — общая, а оставшиеся стороны составляют прямой угол. Сумма дополнительных углов равна 90°. Синус, тангенс и секанс угла равны соответственно косинусу, котангенсу и косекансу дополнительного угла.
- Смежные углы — два угла с общей вершиной на плоскости, одна из двух сторон которых общая, а оставшиеся две стороны лежат на одной прямой (не совпадая). Сумма двух смежных углов равна 180°. То есть два смежных угла на плоскости — это два прилежащих угла, дающих в сумме 180°.
- Сопряжённые углы — два угла на плоскости, имеющие общими одну вершину и две стороны, по которым они примыкают (граничат) друг к другу, но различаются внутренними областями; объединение таких двух углов представляет собой всю плоскость, а, как прилежащие углы, они образуют в сумме полный угол; сумма их величин равна 360°.
Плоские углы с (анти)параллельными сторонами[править | править код]

Углы с параллельными сторонами.
Углы, стороны которых попарно параллельны и сонаправлены (или попарно параллельны и противоположно направлены), равны друг другу. Пара углов, у которых одна пара сторон параллельна и сонаправлена друг другу, а вторая пара сторон параллельна и противоположно направлена, составляют в сумме по величине развёрнутый угол, то 180° (см. рисунок) — поскольку их можно параллельным переносом превратить в смежные углы («склеив» сонаправленные стороны).
Углы со взаимно перпендикулярными сторонами[править | править код]
- Два угла со взаимно перпендикулярными сторонами равны, если оба они острые или оба тупые.
Внешний угол треугольника[править | править код]
- Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с внешним углом.
Углы многоугольника[править | править код]
Сумма внутренних углов αi произвольного n-угольника без самопересечений равна 
Так,
- сумма внутренних углов треугольника равна 180°,
- четырёхугольника — 360°,
- пятиугольника — 540° и так далее.
Следствие[править | править код]
Назовём внешним углом βi (внимание, это не обычное определение внешнего угла) угол, дополняющий внутренний угол αi до полного угла: βi = 360° − αi.
Сумма внешних углов произвольного n-угольника без самопересечений равна 
Центральный и вписанный угол[править | править код]
Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов.
-
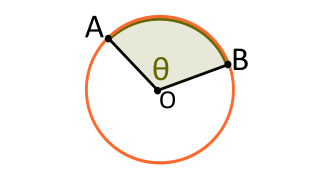
Центральный угол
-

Вписанный угол
- Центральный угол — угол с вершиной в центре окружности. Величина центрального угла равна градусной мере дуги, заключённой между сторонами этого угла.
- Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность. Величина вписанного угла равна половине градусной меры дуги, ограниченной его сторонами. Все вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол θ равен половине величины центрального угла 2θ, , опирающегося у основания на окружности на ту же самую дугу (розового цвета). То есть угол θ не меняет своей величины от вершины к вершине, взятой на окружности (зелёный и голубой углы). Внешний угол для вписанного с другой стороны угла окружности имеет ту же величину θ (коричневого цвета)
Величина вписанного угла равна половине величины центрального угла, опирающегося у основания на окружности на ту же самую дугу (см. рис.).
Вариации и обобщения[править | править код]
Величиной ориентированного угла между прямыми 








б) 


Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла, расширив его область определения на всю числовую прямую 
Понятие угла обобщается на рассматриваемый в стереометрии телесный угол.
Телесный угол[править | править код]
Обобщением плоского угла на стереометрию является телесный угол — часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая называется поверхностью, стягивающей данный телесный угол).
Телесные углы измеряются в стерадианах (одна из основных единиц СИ), а также во внесистемных единицах — в частях полной сферы (то есть полного телесного угла, составляющего 4π стерадиан), в квадратных градусах, квадратных минутах и квадратных секундах.
Телесными углами являются, в частности, следующие геометрические тела:
- двугранный угол — часть пространства, ограниченная двумя пересекающимися плоскостями;
- трёхгранный угол — часть пространства, ограниченная тремя пересекающимися плоскостями;
- многогранный угол — часть пространства, ограниченная несколькими плоскостями, пересекающимися в одной точке.
Двугранный угол может характеризоваться как линейным углом (углом между образующими его плоскостями), так и телесным углом (в качестве вершины может быть выбрана любая точка на его ребре — прямой пересечения его граней). Если линейный угол двугранного угла (в радианах) равен φ, то его телесный угол (в стерадианах) равен 2φ.
Угол между кривыми[править | править код]

Угол между двумя кривыми в точке Р определяется как угол между касательными А и В в P.
Как в планиметрии, так и в стереометрии, а также в ряде других геометрий можно определить угол между гладкими кривыми в точке пересечения: по определению, его величина равна величине угла между касательными к кривым в точке пересечения.
Угол и скалярное произведение[править | править код]
Понятие угла можно определить для линейных пространств произвольной природы (и произвольной, в том числе бесконечной размерности), на которых аксиоматически введено положительно определённое скалярное произведение 








В частности, можно ввести понятие угла между непрерывными на некотором интервале ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


В римановой геометрии можно аналогично определить угол между касательными векторами с помощью метрического тензора 






Угол в метрическом пространстве[править | править код]
Также существует ряд работ, в которых вводится понятие угла между элементами метрического пространства.
Пусть 

К. Менгер ввёл понятие угла между вершинами 



В 1932 году Вильсон рассмотрел в качестве угла следующее выражение:

Нетрудно видеть, что введённое выражение всегда имеет смысл и удовлетворяет трём аксиомам Менгера.
Кроме того, угол Вильсона обладает тем свойством, что в евклидовом пространстве он эквивалентен углу между элементами 

Измерение углов[править | править код]
Одним из самых распространённых инструментов для построения и измерения углов является транспортир (а также линейка — см. ниже); как правило, он используется для построения угла определённой величины. Для более или менее точного измерения углов разработано много инструментов:
- угломер;
- гониометр — прибор для лабораторного измерения углов;
- кипрегель — геодезический угломерный инструмент.
Угловым расстоянием (или просто углом) между двумя объектами для наблюдателя называется мера угла, в вершине которого находится наблюдатель, а объекты лежат на сторонах. Для грубой оценки углов между двумя удалёнными предметами можно использовать кисть руки. На расстоянии вытянутой руки угловому расстоянию в 1 градус (1°) соответствует ширина мизинца (см. также ниже; угловая ширина среднего пальца на расстоянии вытянутой руки составляет около 2°), углу в 10 градусов — ширина сжатого кулака, расположенного горизонтально (либо поперечник ладони), углу в 20 градусов (или около 15°÷17°÷20°) — расстояние между кончиками разведённых большого и указательного пальца (пядь), а угловое расстояние от конца мизинца до конца большого пальца равно примерно четверти прямого угла. Это усреднённые данные. Рекомендуется уточнить их для своей собственной руки.
Различные методы и устройства для измерения углов характеризуются угловым разрешением, то есть минимальным углом, который может быть измерен с помощью данного метода. Наилучшим угловым разрешением обладают различные интерферометрические методы, позволяющие измерить в некоторых случаях углы в несколько микросекунд дуги (~10−11 радиана).
Примеры практических тригонометрических измерений[править | править код]
- Решение задач простым способом
Как измерить угол (например, на карте) с помощью сторон треугольника (например, при отсутствии инженерного/тригонометрического калькулятора (и таблиц) и отсутствии ПК (MS Office Excel) для вычисления cos) и подручными средствами — линейки с миллиметровыми делениями?
По сторонам угла отложите отрезки по 60 мм и концы соедините прямой линией. Длина этой линии в миллиметрах покажет примерно величину угла в градусах. Таким способом можно с достаточной (приемлемой) точностью измерять острые углы до 60°. Если угол больше 60°, измеряют его дополнение до 90°, 180, 270° или 360°. Для измерения дополнения до 90° или 270° из вершины угла строится с помощью треугольника перпендикуляр к одной из сторон (в равнобедренном треугольнике — медиана-биссектриса, она же является высотой).
Как измерить угол линейкой (при визуальном ориентировании на местности …и сравнить угол по карте — см. пункт 1)?
Поместите линейку с миллиметровыми делениями перед собой на расстоянии 57 см (не более 60 см) от глаза. В этом случае деление, равное 1 см, будет соответствовать углу визирования в 1°. В справедливости данного способа вы легко убедитесь, если помните, что дуга центрального угла в 1° составляет примерно 1/57 часть радиуса. Точность измерения углов с помощью линейки (также как и с помощью пальцев; см. ниже) зависит от точности положения линейки (или пальцев) на необходимом расстоянии от глаза. В этом можно быстро натренироваться с помощью нитки, длина которой соответствует расстоянию от глаза до пальцев вытянутой руки.
Как можно измерять и откладывать на местности углы без применения угломерных приборов?
Наиболее просто это можно сделать сравнением измеряемого угла с прямым. Прямой угол вы можете отложить направлениями рук, одна из которых вытянута вдоль плеч, а вторая с поднятым большим пальцем направлена так, чтобы палец правой руки был перед правым глазом (соответственно палец левой руки — перед левым глазом). Прямой угол можно глазомерно поделить на две или три равные части, каждая из которых будет соответствовать 45° или 30°.
Меньшие значения углов можно отложить или измерить на местности следующим приёмом. Прежде всего измерьте линейкой ширину трёх сомкнутых пальцев своей руки: указательного, среднего и безымянного. Если она у вас будет равна 6 см, то при вытянутой на 60 см руке угол визирования на них составит примерно 6°. Соответственно угол визирования на каждый из этих трёх пальцев будет равен в среднем 2°. Если же ширина трёх пальцев получится у вас, например, 5 см, то, чтобы углы визирования были такими же, руку надо вытягивать на 50 см.
При вытянутой руке угол визирования на большой и указательный пальцы, раздвинутые под прямым углом, составляет примерно 15°. Как это проверить и уточнить?
Прежде всего заметьте на местности ориентир и от него отложите угол 90°. Это можно сделать приёмом, описанным в предыдущей задаче. Затем от ориентира отложите шесть углов по 15° визированием на большой и указательный пальцы, раздвинутые под прямым углом. Последнее отложение угла должно составить на местности прямой угол. Если этого точно не получилось, нужно повторить отложения, держа вытянутую руку немного ближе или дальше от глаза (порядка 60 см). Этим самым вы определите расстояние, на которое нужно вытягивать руку для отложения угла 15°[3].
Углы также можно вычислить (рассчитать) с помощью различных измерительных приборов и приспособлений — посредством тригонометрии на счётной линейке, инженерном калькуляторе (в том числе калькулятор (Windows)), с помощью функций таблицы MS Office Excel: (1) cos, (2) затем arccos, и (3) перевести, также функциями, значение радианов в градусы (°) (при наличии ПК; существуют и on-line-вычисление углов треугольника по заданным сторонам);
Существуют также специальные тригонометрические таблицы: sin, cos, а также arccos, arcsin, последние, кстати, могут быть (в том числе и чаще всего) с перерасчётом в градусы.
В аналитической геометрии угол между прямыми в координатной плоскости, например, задаётся уравнением:
(см. Линейная функция; см. также #Угол и скалярное произведение)
Примечания[править | править код]
- ↑ Сидоров Л. А. Угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. — Т. 5: Слу — Я. — Стб. 467—468. — 1248 стб. : ил. — 150 000 экз.
- ↑ В действительности истинный период обращения Земли относительно неподвижных звёзд примерно на 4 минуты короче, чем 24 часа, см. звёздное время.
- ↑ Куприн А. М. На местности и по карте. — М. Недра, 1982. — 112 с.
См. также[править | править код]
- Азимут (астрономия)
- Азимут (геодезия)
- Антипараллельные прямые
- Апертурный угол
- Астрономическая рефракция
- Двугранный угол
- Дирекционный угол
- Изогона
- Кастор (угол)
- Магнитный азимут
- Многоугольник
- Наклон, уклон
- Ортогональность
- Параллельные прямые
- Угол поворота
- Позиционный угол и Угловое расстояние (Полярные координаты)
- Полигонометрия
- Решение треугольников
- Румб
- Сингония
- Склонение (астрономия) и Часовой угол (Системы небесных координат)
- Телесный угол
- Трёхгранный угол
- Триангуляция
- Тригонометрический параллакс & Параллактический угол
- Тригонометрия
- Угловая скорость (& CAV)
- Угловая частота
- Угловое разрешение
- Угловое ускорение
- Угловой коэффициент (Линейная функция)
- Угловой размер
- Углы Эйлера
- Угол места
- Угол обзора
- Угол поля зрения объектива
- Угол скольжения
- Категория:Углы
Литература[править | править код]
- Барабанов О. О. Начала истории прямого угла // История науки и техники. — 2015. — № 1. — С. 16—27.‘
- Погорелов А. В. Геометрия: учебник для 7—11 классов средней школы. — М.: Просвещение, 1992. — 383 с. — ISBN 9785090038546.
- Сидоров Л. А. Угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. — Т. 5: Слу — Я. — Стб. 467‒468. — 1248 стб. : ил. — 150 000 экз.
- Двугранный угол // Математическая энциклопедия : [в 5 т.] / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1979. — Т. 2: Д — Коо. — Стб. 50. — 1104 стб. : ил. — 150 000 экз.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30‒31. — ISBN 5-94057-170-0.
- Угломерные приборы/Угол (плоский) // Большая Советская энциклопедия (в 30 т.) / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: «Советская Энциклопедия», 1977. — Т. XXVI. — С. 459‒460. — 624 с.
- Weisstein, Eric W. Line Bisector (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Angle (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Polygon (англ.) на сайте Wolfram MathWorld.
- K. Menger. New Fondations of Euclidean Geometry (англ.) // THE AMERICAN JOURNAL OF MATHEMATICS 53 : журнал. — 1931. — P. 721‒745.
- W. A. Wilson. On angles in certain metric spaces (англ.) // Bulletin of American Mathematical Society 39. — 1932. — P. 580‒588.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Угол. Обозначение углов
Угол – геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
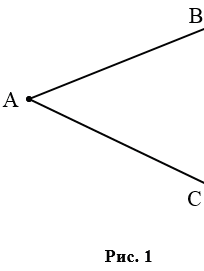
На рис. 1 лучи АВ и АС – стороны угла, точка А – вершина угла.
При записи угла в середине пишут букву, обозначающую его вершину. Сам угол на рис. 1 обозначают так:  ВАС или
ВАС или  САВ (этот угол нельзя обозначить так:
САВ (этот угол нельзя обозначить так:  АВС или
АВС или  СВА или
СВА или  ВСА или
ВСА или  АСВ, т.к. точки В и С не являются вершинами данного угла). Этот же угол можно обозначить и короче, по его вершине:
АСВ, т.к. точки В и С не являются вершинами данного угла). Этот же угол можно обозначить и короче, по его вершине:  А.
А.
Если углы имеют общую вершину, то их нельзя обозначить одной буквой. Так на рис. 2 углы имеют общую вершину Е, поэтому мы можем использовать для данных углов только следующие обозначения:  МЕК или
МЕК или  КЕМ,
КЕМ,  МЕР или
МЕР или  РЕМ,
РЕМ,  РЕК или
РЕК или  КЕР. Говорят, что луч ЕР в данном случае делит угол
КЕР. Говорят, что луч ЕР в данном случае делит угол  МЕК (или
МЕК (или  КЕМ) на два угла:
КЕМ) на два угла:  МЕР (или
МЕР (или  РЕМ) и
РЕМ) и  РЕК (или
РЕК (или  КЕР).
КЕР).
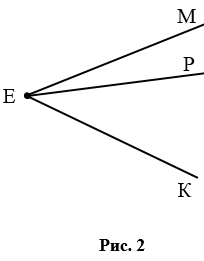
Также иногда углы обозначают цифрами, например, на рис.3 мы имеем  1.
1.
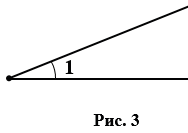
Углы, как и отрезки, можно сравнивать между собой. Чтобы сравнить два угла можно наложить один угол на другой. Если при наложении одного угла на другой они совпадут, то эти углы равны.
Биссектриса – луч, который делит угол на два равных угла. На рис. 4 углы НОМ и DОМ равны, значит, луч ОМ – биссектриса угла НОD.
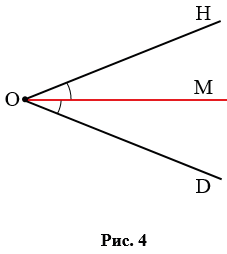
Прямой угол – угол, который можно построить с помощью угольника (рис. 5).

Если начертить два прямых угла с общей вершиной и одной общей стороной, то две другие стороны этих углов составят прямую (рис. 6). Считают, что лучи, составляющие прямую, также образуют угол, который называют развернутым.
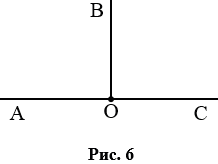
На рис. 6  АОВ и
АОВ и  ВОС – прямые,
ВОС – прямые,  АОС – развернутый.
АОС – развернутый.
Развернутый угол равен двум прямым углам, а прямой угол составляет половину развернутого.
Острый угол – угол, который меньше прямого угла. На рис. 7  МОN – острый.
МОN – острый.
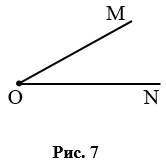
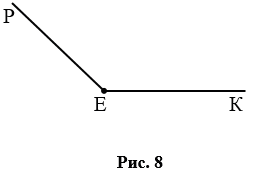
Тупой угол – угол, который больше прямого угла, но меньше развернутого. На рис. 8  РЕК – тупой.
РЕК – тупой.
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Прямоугольный параллелепипед. Пирамида.
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб. Объем куба
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 1657,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1686,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1703,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1775,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1812,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 287,
Мерзляк, Полонский, Якир, Учебник
Номер 290,
Мерзляк, Полонский, Якир, Учебник
Номер 1190,
Мерзляк, Полонский, Якир, Учебник
Номер 10,
Мерзляк, Полонский, Якир, Учебник
Номер 11,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 392,
Мерзляк, Полонский, Якир, Учебник
Номер 687,
Мерзляк, Полонский, Якир, Учебник
Номер 1220,
Мерзляк, Полонский, Якир, Учебник
Номер 1236,
Мерзляк, Полонский, Якир, Учебник
Номер 1237,
Мерзляк, Полонский, Якир, Учебник
Задание 173,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 247,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 611,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 773,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1546,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 759,
Мерзляк, Полонский, Якир, Учебник
Задание 81,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
8 класс
Номер 422,
Мерзляк, Полонский, Якир, Учебник
Определение
Геометрия — это раздел математики, который занимается изучением форм и их измерений. Он также фокусируется на относительной конфигурации форм и их пространственных свойствах.
Все геометрические фигуры состоят из точек, линий, лучей и плоской поверхности. Когда две линии или лучи сходятся в одной точке, измерение между двумя линиями называется углом. В этой статье мы собираемся обсудить, что такое угол, каковы различные типы углов и их значение с примерами.
Определение угла в математике
Определение
Что такое угол? Угол это — геометрическая фигура, образованная двумя лучами или линиями, имеющими общую конечную точку (вершину). Два луча называются сторонами угла, а точка, в которой пересекаются лучи, называется вершиной.
Угол, лежащий в плоскости, не обязательно должен лежать в евклидовом пространстве. В случае, если углы образованы пересечением двух плоскостей в евклидовом или другом пространстве, такие углы считаются двугранными.
Стороны угла – лучи, которые образуют угол (А, В).
Вершина угла – точка, из которой выходят лучи (О).
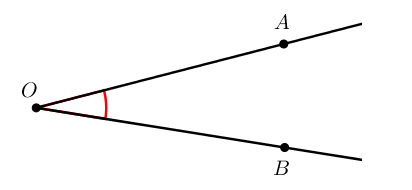
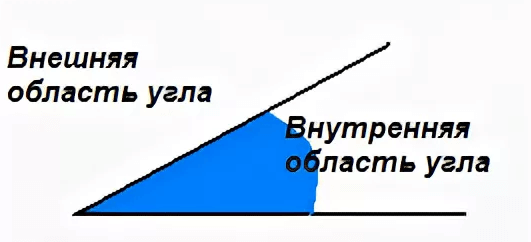
Угол делит плоскость на две части. Если угол не развернутый, то одна часть плоскости называется областью внутреннего угла, а другая часть называется областью внешнего угла. Ниже приведена картинка, поясняющая, какие части являются внешними, а какие внутренними.
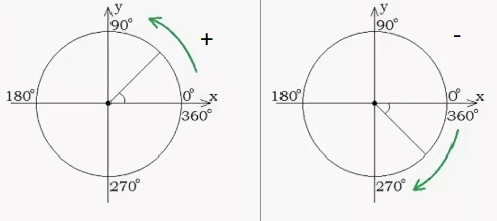
Если углы измеряются по линии, мы можем найти два разных типа углов, например, положительный угол и отрицательный угол.
- Положительный угол: если угол идет против часовой стрелки, то он называется положительным углом.
- Отрицательный угол: если угол направлен по часовой стрелке, то он называется отрицательным углом.
Интересно
Слово «угол» произошло от латинского слова Angulus, означающего «небольшой изгиб».
Понятие угла впервые использовал Евдем, который определил угол как отклонение от прямой линии.
Как обозначить углы?
Фигура угол отмечается символом «∠». Есть два разных способа обозначения углов:
- Способ 1:
Как правило, угол обозначается строчными буквами, такими как «а», «х» и т. д., или греческими буквами альфа (α), бета (β), тэта (θ) и т. д. - Способ 2:
Используя три буквы на фигурах. Средняя буква должна быть вершиной (фактический угол).
Например, ABC — треугольник. Чтобы представить угол A равным 60 градусам, мы можем определить его как ∠BAC = 60 °.
Типы углов
Существует шесть типов углов. Каждый тип угла имеет уникальную идентификацию на основе измерения угла.
Давайте прочитаем о каждом типе угла в отдельности вместе с их свойствами.
- Острый угол – это угол, градусная мера которого больше 0° и меньше 90°.
- Прямой угол — когда измерение угла равно 90 градусов, он известен как прямой угол.
Прямой угол можно легко наблюдать, так как он образует форму буквы L. - Тупой угол — когда измерение угла меньше 180 градусов, но больше 90 градусов,
это тупой угол. - Развернутый угол — угол, образованный прямой линией, называется прямым углом. Это
половина полного оборота круга. Размер прямого угла равен 180°. - Выпуклый угол – это угол, величина которого больше 180°, но меньше 360°.
- Полный угол — когда измерение угла равно 360 градусам, это полный угол.
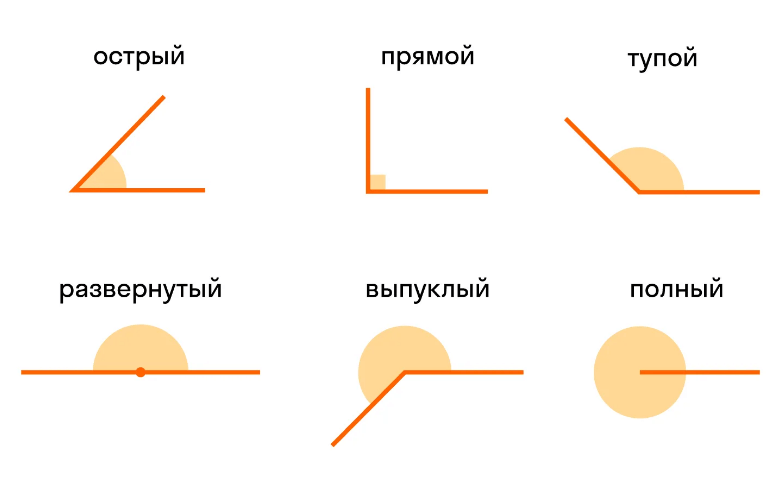
Ряд углов образуется при пересечении секущей двух или более прямых. Конкретные названия даны паре углов, что зависит от расположения угла по отношению к прямым. Линии могут быть как параллельными, так и непараллельными.
Углы образованные при пересечении двух прямых
При пересечении двух прямых образуются два вида углов:
- смежные;
- вертикальные.
Смежные углы
Определение
Два угла называются смежными, если они имеют общую вершину и одну общую сторону, а две другие стороны расположены на одной прямой и образуют развернутый угол. Смежные углы между собой дополняемые, так как являются продолжением один другого.
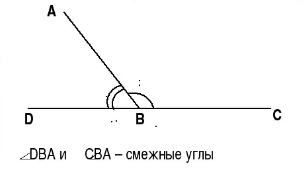
Свойства смежных углов
- Сумма смежных углов равна 180°
- Если оба смежных угла равны между собой, то они являются прямыми.
- В паре смежных углов всегда один острый, а другой тупой, или оба угла прямые.
- Синусы смежных углов равны.
- Косинусы, тангенсы и котангенсы смежных углов равны, но имеют противоположный знак.
Вертикальные углы
Определение
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
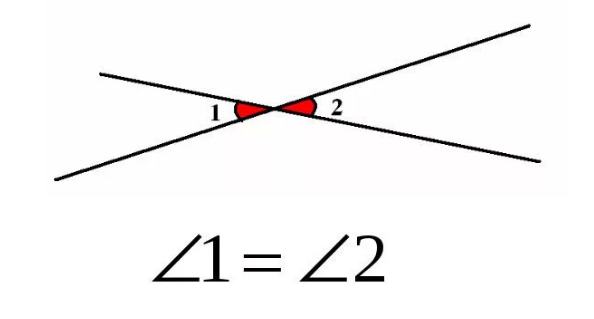
Пример:
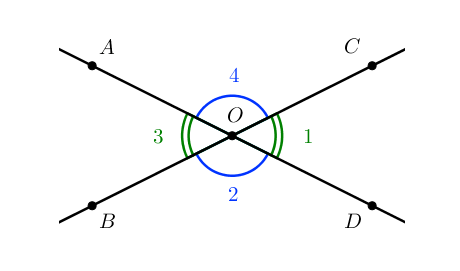
Пары углов 1 и 3; 2 и 4 – являются вертикальными
По свойству вертикальных углов:
[angle C O D=angle A O B]
[angle B O D=angle A O C]
Пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1 — являются смежными
По свойству смежных углов:
[angle C O D+angle D O B=180^{circ}]
[angle D O B+angle B O A=180^{circ}]
[angle B O A+angle A O C=180^{circ}]
[angle A O C+angle C O D=180^{circ}]
| Смежные углы | Вертикальные углы |
| Два угла с общей стороной и вершиной называются смежными. | Когда две прямые пересекаются друг с другом, то пары противоположных углов, образованных при вершине, называются вертикальными углами. |
| Имеют общую сторону и общую вершину. | Имеют общую вершину, но не имеют общую сторону |
| Смежные углы не всегда равны по величине | Вертикально противоположные углы равны по величине |
Сравнение углов
Для сравнения углов можно использовать простейший метод — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны данных углов совпадают, то углы равны. В противном случае угол, который находится внутри другого, будет меньше. Вот два наглядных примера с равными и неравными углами:
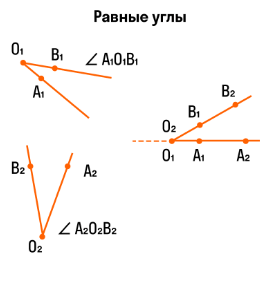
[angle A_{1} O_{1} B_{1}] и [angle A_{2} O_{2} B_{2}] полностью совмещаются при наложении следовательно: [angle A_{1} O_{1} B_{1}=angle A_{2} O_{2} B_{2}]
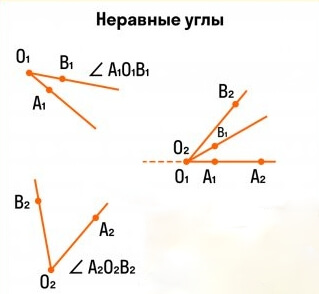
[angle A_{1} O_{1} B_{1}] и [ angle A_{2} O_{2} B_{2}] не совмещаются при наложении: [angle A_{1} O_{1} B_{1} neq angle A_{2} O_{2} B_{2}]
Причем: [angle A_{1} O_{1} B_{1}<angle A_{2} O_{2} B_{2}]
При этом развернутые углы всегда являются равными.
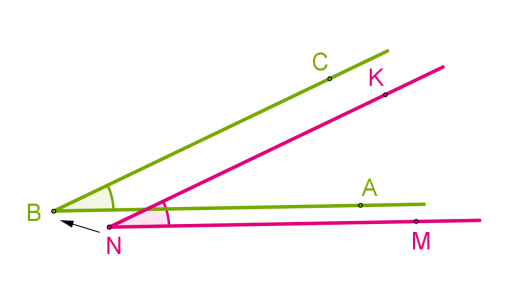
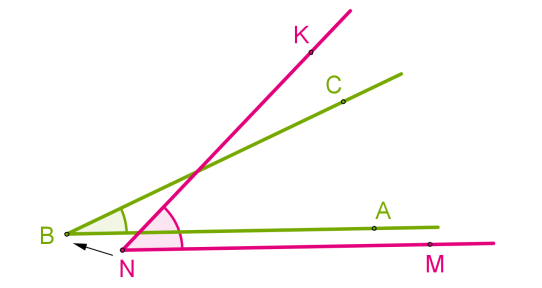
Совмещение углов [angle A B C] и [angle M N K] происходит следующим образом:
- Вершину B одного угла совмещаем с вершиной N другого угла.
- Сторону BA одного угла накладываем на сторону NM другого угла так, чтобы стороны BC и NK располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠ABC = ∠MNK.
Если нет, то один угол — меньше другого: ∠ABC<∠MNK.
Некоторые важные теоремы, основанные на прямых и углах:
- Если две параллельные прямые пересечены секущей, то смежные внутренние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то противоположные внешние углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то соответствующие углы имеют одинаковую величину.
- Если две параллельные прямые пересечены секущей, то внутренние углы по одну сторону от этой секущей смежные.
- Вертикальные углы равны, когда прямая пересекает прямые. Линии могут быть как параллельными, так и непараллельными.
Измерение углов
Существует несколько единиц измерения углов. Рассмотрим наиболее часто используемые единицы измерения:
Градусная мера
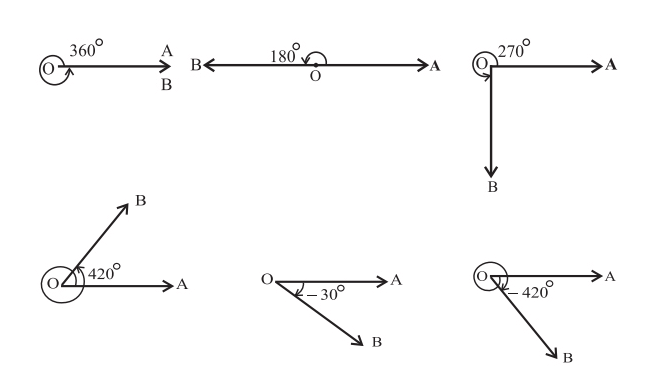
Полный оборот, т. е. когда начальная и конечная стороны находятся в одном и том же положении после вращения по часовой стрелке или против часовой стрелки, делится на 360 единиц, называемых градусами. Итак, если поворот от начальной стороны к конечной стороне составляет [left(frac{1}{360}right)] оборота, то говорят, что угол имеет меру в один градус. Обозначается как 1°.
Мы измеряем время в часах, минутах и секундах, где 1 час = 60 минут, а 1 минута = 60 секунд. Точно так же при измерении углов
- 1 градус = 60 минут, обозначаемый как 1° = 60′.
- 1 минута = 60 секунд, обозначаемая как 1 ′ = 60 ″.
Радианная мера
Радианная мера немного сложнее, чем градусная. Представьте круг с радиусом 1 единица. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
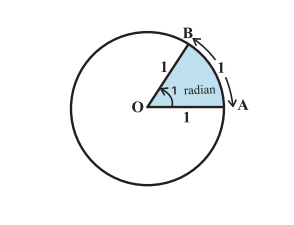
Вот еще несколько примеров углов: -1 радиан, радиан, [1 frac{1}{2}] радиан, [-1 frac{1}{2}] радиан.
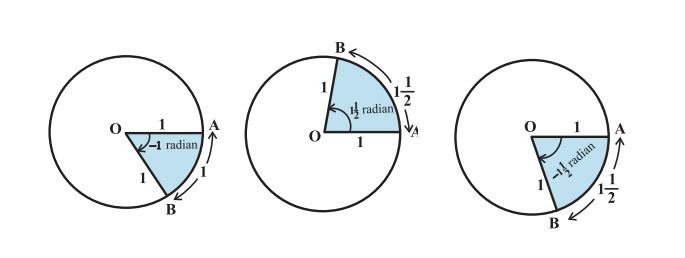
Длина окружности = [2 pi r ldots] где r — радиус окружности. Следовательно, для круга с радиусом 1 единица длины окружности равна [2 pi]. Следовательно, один полный оборот начальной стороны образует в центре угол [2 pi] радиан. Обобщая это, имеем:
В окружности радиуса r дуга длины r образует угол в 1 радиан в центре. Следовательно, в окружности радиуса r дуга длины l будет опираться на угол = [frac{l}{r}] радиан. Обобщая это, мы имеем в окружности радиуса r, если дуга длины l образует угол θ радиан в центре, то:
[theta=frac{l}{r}]
[l=r theta]
Связь между степенью и радианными мерами
По определениям степени и радиана мы знаем, что угол, образуемый окружностью в центре, равен:
- 360° – по градусной мере
- [2 pi] радиан — в радианах
Следовательно, [2 pi] радиан = 360° ⇒ [pi] радиан = 180°. Теперь подставим приблизительное значение [pi] как [frac{22}{7}] в уравнении выше и получить, 1 радиан [frac{180^{circ}}{pi}=57^{circ} 16^{prime}]. Кроме того, [1^{0}=frac{pi}{180^{circ}}] радиан = 0,01746 радиан примерно. Ниже таблица, изображающая соотношение между градусами и радианами некоторых распространенных углов:
| Градусы | [30^{circ}] | [45^{circ}] | [60^{circ}] | [90^{circ}] | [180^{circ}] | [270^{circ}] | [360^{circ}] |
| Радианы | [frac{pi}{6}] | [frac{pi}{4}] | [frac{pi}{3}] | [frac{pi}{2}] | [pi] | [frac{3pi}{2}] | [2pi] |
Пример
Преобразуйте 40° 20′ в радианы.
Решение: мы знаем, что 1° = 60′, следовательно, 20′ = [frac{1^{0}}{3}].
Следовательно,
[40^{circ} 20^{prime}=40 frac{1}{3}=frac{121}{3}];
Кроме того, мы знаем, что
радианная мера = [frac{pi}{180^{0}} x] градусную меру
Следовательно, радианная мера [40^{circ} 20^{prime}=frac{pi}{180} times frac{121}{3}=frac{121 pi}{540}] радиан.
Нет времени решать самому?
Наши эксперты помогут!
Как измерить угол
Для измерения углов используется транспортир:
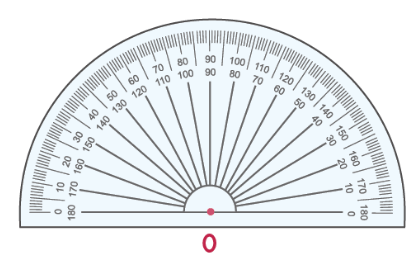
Попробуем измерить угол [angle A O B]
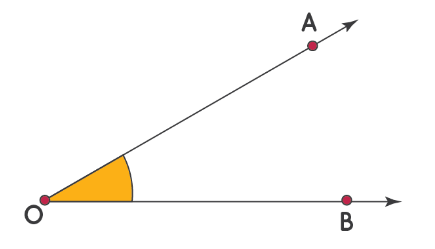
Шаги для измерения угла [angle mathrm{AOB}].
Шаг 1: совместите транспортир с лучом OB, как показано ниже. Начните чтение с отметки 0 ° в правом нижнем углу транспортира.
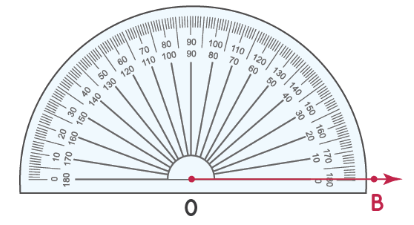
Шаг 2: Число на транспортире, совпадающее со вторым лучом, является мерой угла. Измерьте угол, используя число на «нижней дуге» транспортира. Таким образом, ∠ AOB = 37°
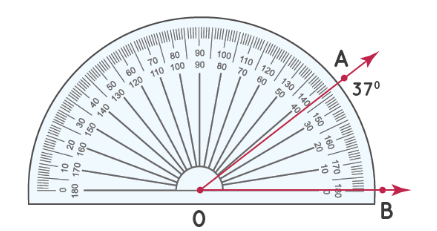
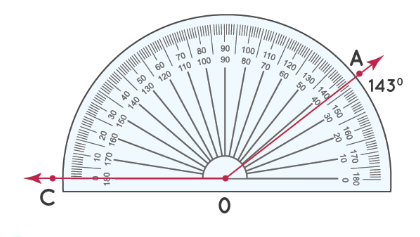
Далее попробуем измерить этот ∠AOC:
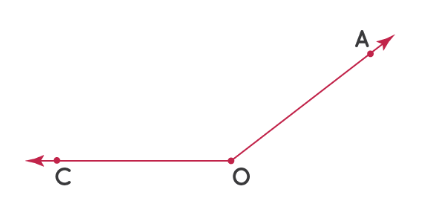
Шаг 1: Измерьте угол от отметки 0° в левом нижнем углу.
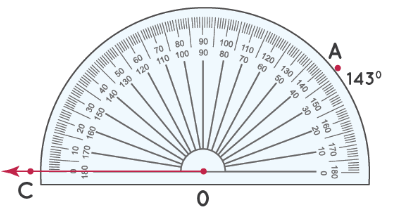
Шаг 2: Число на «верхней дуге» транспортира, совпадающее с OA, является мерой ∠ AOC. Таким образом, ∠ AOC = 143°
Как построить углы
Используем транспортир для построения углов. Нарисуем угол 50°.
Шаг 1: сначала нарисуйте луч OB и совместите транспортир с OB, как показано.
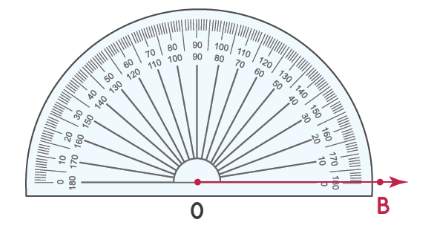
Шаг 2: поместите точку над отметкой на транспортире, которая соответствует 50°.
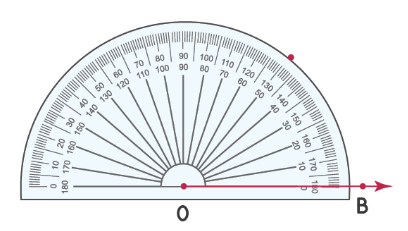
Шаг 3: Уберите транспортир и нарисуйте луч, начинающийся в точке О и проходящий через эту точку. Таким образом, ∠AOB – искомый угол, т.е. ∠AOB = 50°.

Примечание. Если луч идет в другом направлении, мы измеряем угол от отметки 0° в левом нижнем углу.
На изображении ниже показано, как нарисовать угол 50°, когда луч указывает в другом направлении.
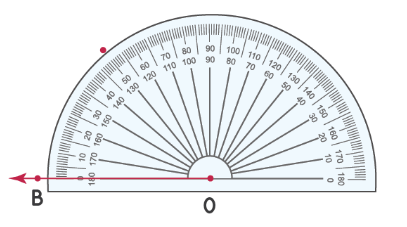
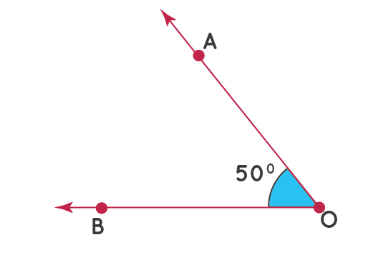
Обозначение углов на чертеже
Для комфортного отображения дуг, углов применяют чертежи. Не всегда возможно грамотно изобразить и обозначить тот или другой угол, дугу или наименование. Равные углы имеют определение в виде идентичного числа дуг, а неравноценные в виде различного.
На чертеже запечатлено корректное обозначение острых, равных и неравных углов.
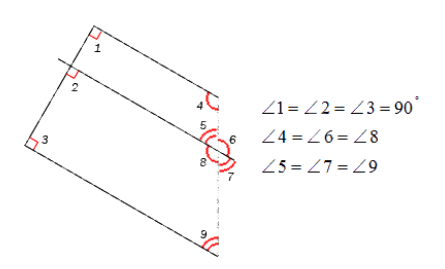
Если нужно обозначить более трех углов, то применяются специальные обозначения дуг, например, зубчатые или волнистые, но в принципе это не имеет особого значения.
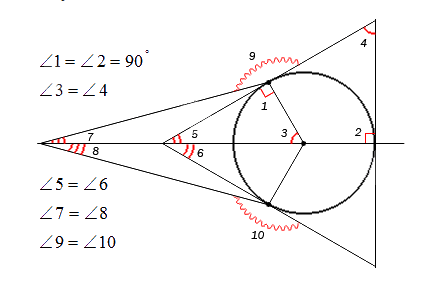
Обозначение углов должно быть простым, чтобы не препятствовать иным значениям. При решении задачи рекомендовано обозначать только нужные для решения углы, чтобы не перегружать весь чертеж. Это не помешает решению задачи, а также придаст эстетичный облик чертежу.


