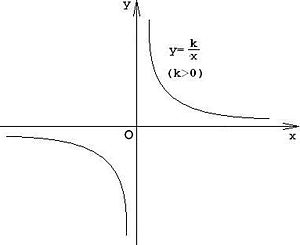
Обратная пропорциональность — коротко о главном
Определение:
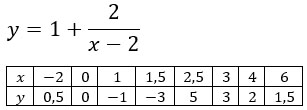
Функция, описывающая обратную пропорциональность, – это функция вида ( displaystyle y=frac{k}{x-a}+b ), где ( kne 0), ( xne 0) и ( xne а)
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или, что то же самое, ( Dleft( y right)=mathbb{R}backslash left{ 0 right})
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент ( displaystyle k)
( displaystyle k) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента ( displaystyle k) влияет на то, в каких четвертях расположен график:
если ( displaystyle k>0), то ветви гиперболы расположены в ( displaystyle I) и ( displaystyle III) четвертях;
если ( displaystyle k<0), то во ( displaystyle II) и ( displaystyle IV).
Коэффициент ( displaystyle a)
Если внимательно посмотреть на знаменатель, видим, что ( displaystyle a) – это такое число, которому не может равняться ( displaystyle x).
То есть ( x=a) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции
Коэффициент ( b)
Число ( b) отвечает за смещение графика функции вверх на величину ( b), если ( b>0), и смещение вниз, если ( b<0).
Следовательно, ( y=b) – это горизонтальная асимптота.
Алгоритм построения графика функции ( displaystyle y=frac{k}{x-a}+b)
- Определяем коэффициенты ( displaystyle k), ( displaystyle a) и ( displaystyle b).
- Строим график функции ( displaystyle y=frac{k}{x}) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на ( displaystyle a). Но проще двигать не график, а оси, так что ось ( displaystyle Oy) сдвигаем влево на ( displaystyle a).
- График должен быть сдвинут вверх на ( displaystyle b). Но проще двигать не график, а оси, так что ось ( displaystyle Ox) сдвигаем вниз на ( displaystyle b).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.
Что такое функция
Ты помнишь, что функция – это определенного рода зависимость?
Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.
Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.
Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.
Ну и на всякий случай немного повторим…
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).
Что значит «допустимому значению»?
Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Все дело в понятии «область определения»: для некоторых функций не все аргументы можно подставить в зависимость. Например, для функции ( y=sqrt{x}) отрицательные значения аргумента ( x) – недопустимы.
Функция, описывающая обратную зависимость
Это функция вида ( displaystyle y=frac{k}{x}), где ( kne 0).
По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.
Давай определим область определения. Чему может быть равен ( x)? Или, по-другому, чему он не может быть равен?
Единственное число, на которое нельзя делить – это ( 0), поэтому ( xne 0):
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right))
или, что то же самое,
( Dleft( y right)=mathbb{R}backslash left{ 0 right})
Такая запись означает, что ( x) может быть любым числом, кроме ( 0).
- Знак «( mathbb{R})» обозначает множество действительных чисел, то есть всех возможных чисел.
- Знаком «( backslash )» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»).
- Число ( 0) в фигурных скобках означает просто число ( 0).
Получается, что из всех возможных чисел мы исключаем ( 0)).
Множество значений функции, оказывается, точно такое же: ведь если ( kne 0), то на что бы мы его не делили, ( 0) не получится:
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
Также возможны некоторые вариации формулы ( y=frac{k}{x}). Например, ( y=frac{k}{x+a}) – это тоже функция, описывающая обратную зависимость.
Определи самостоятельно область определения и область значений этой функции. Должно получиться:
- ( Dleft( y right)=left( -infty ;-a right)cup left( -a;+infty right))
- ( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)).
Давай посмотрим на такую функцию: ( displaystyle y=frac{x-5}{{{x}^{2}}-25}).
Является ли она обратной зависимостью?
На первый взгляд сложно сказать: ведь при увеличении ( x) увеличивается и знаменатель дроби, и числитель, так что непонятно, будет ли функция уменьшаться, и если да, то будет ли она уменьшаться пропорционально?
Чтобы понять это, нам необходимо преобразовать выражение таким образом, чтобы в числителе не было переменной:
( displaystyle y=frac{x-5}{{{x}^{2}}-25}=frac{x-5}{left( x-5 right)left( x+5 right)}=frac{1}{x+5},text{ }xne 5).
Действительно, мы получили обратную зависимость, но с оговоркой: ( xne 5).
Почему так? А потому, что выражение ( left( x-5 right)) было в исходном выражении в знаменателе, поэтому если мы возьмём значение ( x=5) и подставим его в исходную функцию (а ведь именно её нам нужно исследовать), то что мы получим?
Ноль, делённый на ноль. Но ведь на ноль нельзя делить ничего, даже другой ноль. Поэтому ( x) никак не может быть равен ( 5).
Но почему тогда мы также не пишем ( xne -5)? Оно ведь тоже в знаменателе!
А всё потому, что оно как было в знаменателе, так там и осталось, следовательно мы и так видим, что такое значение икса невозможно.
А поэтому — зачем лишний раз писать? Да-да, математики — народ ленивый, без надобности напрягаться не станут:)
Решения
Пример 1
( displaystyle y=1-frac{3}{x+2})
Пример 2
Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).
Напомню, что для этого надо найти корни соответствующего квадратного уравнения: ( displaystyle {{x}^{2}}+4{x}-5=0).
Я найду их устно с помощью теоремы Виета: ( displaystyle {{x}_{1}}=-5), ( displaystyle {{x}_{2}}=1). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».
Итак, получаем: ( displaystyle {{x}^{2}}+4{x}-5=left( x+5 right)left( x-1 right)), следовательно:
( displaystyle y=frac{x+5}{left( x+5 right)left( x-1 right)}=frac{1}{x-1},text{ }xne -5)
Пример 3
Ты уже попробовал решить сам? В чем загвоздка?
Наверняка в том, что в числителе у нас ( displaystyle 2x), а в знаменателе – просто ( displaystyle x).
Это не беда. Нам нужно будет сократить на ( displaystyle left( x+2 right)), поэтому в числителе следует вынести ( displaystyle 2) за скобки (чтобы в скобках ( displaystyle x) получился уже без коэффициента):
( displaystyle y=frac{2{x}-3}{x+1}=frac{2left( x-frac{3}{2} right)}{x+1}=2cdot frac{x-1,5}{x+1}=2cdot frac{x+1-1-1,5}{x+1}=…) дальше сам.
Ответ: ( displaystyle y=2-frac{5}{x+1}).
График обратной пропорциональности
Как всегда, начнем с самого простого случая: ( displaystyle y=frac{1}{x}).
Составим таблицу.
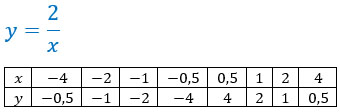
Таблица обратной пропорциональности (зависимости)
| ( displaystyle mathbf{x}) | ( displaystyle -3) | ( displaystyle -2) | ( displaystyle -1) | ( displaystyle -0,5) | ( displaystyle 0,5) | ( displaystyle 1) | ( displaystyle 2) | ( displaystyle 3) | ( displaystyle 4) |
| ( displaystyle mathbf{y}) | ( displaystyle -frac{1}{3}) | ( displaystyle -frac{1}{2}) | ( displaystyle -1) | ( displaystyle -2) | ( displaystyle 2) | ( displaystyle ;1) | ( displaystyle frac{1}{2}) | ( displaystyle frac{1}{3}) | ( displaystyle frac{1}{4}) |
Нарисуем точки на координатной плоскости:
Теперь их надо плавно соединить, но как?
Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.
Это график гиперболы и выглядит он так:
Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.
Каждая из них стремится своими концами приблизиться к осям ( displaystyle Ox) и ( displaystyle Oy), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:
Оно и понятно: так как ( displaystyle xne 0), график не может пересекать ось ( displaystyle Oy). Но и ( displaystyle yne 0), так что график никогда не коснется и оси ( displaystyle Ox).
Ну что же, теперь посмотрим на что влияют коэффициенты.
На что влияют коэффициенты
Рассмотрим такие функции:
( displaystyle y=frac{1}{x};text{ }y=frac{2}{x};text{ }y=frac{4}{x};text{ }y=-frac{1}{x};text{ }y=-frac{3}{x}):
Ух ты, какая красота!
Все графики построены разными цветами, чтобы легче было их друг от друга отличать.
Итак, на что обратим внимание в первую очередь?
Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси ( displaystyle Ox).
Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
А что, если функция выглядит сложнее, например, ( displaystyle y=frac{1}{x-1}+2)?
В этом случае гипербола будет точно такой же, как обычная ( displaystyle y=frac{1}{x}), только она немного сместится. Давай думать, куда?
Чему теперь не может быть равен ( x)? Правильно, ( xne 1). Значит, график никогда не достигнет прямой ( x=1).
А чему не может быть равен ( y)? Теперь ( yne 2). Значит, теперь график будет стремиться к прямой ( y=2), но никогда ее не пересечет.
Итак, теперь прямые ( x=1) и ( y=2) выполняют ту же роль, которую выполняют координатные оси для функции ( displaystyle y=frac{1}{x}).
Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):
Более подробно о том, как строятся такие графики, мы выучим чуть позже.
А теперь попробуй решить несколько примеров для закрепления.
Обратная пропорциональность в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.
И правда, вспомним формулу скорости: ( displaystyle v=frac{S}{t}), где ( v) – скорость, ( t) – время в пути, ( S) – расстояние (путь).
Отсюда можно выразить время: ( displaystyle t=frac{S}{v})
Пример:
Человек едет на работу со средней скоростью ( 40) км/ч, и доезжает за ( 1) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью ( 60) км/ч?
Решение:
Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:
( displaystyle 60) км/ч – ( 60) мин.
( displaystyle 60) км/ч – ( x) мин.
Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:
( displaystyle frac{40}{x}=frac{60}{60}text{ }Rightarrow text{ }x=40)(мин).
То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.
Функция (то есть зависимость) времени в минутах от скорости:
( displaystyle tleft( v right)=frac{S}{v}).
Известно, что ( tleft( 40 right)=60), тогда:
( frac{S}{40}=60text{ }Rightarrow text{ }S=40cdot 60=2400).
Нужно найти ( tleft( 60 right)):
( displaystyle tleft( 60 right)=frac{2400}{60}=40) (мин).
Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.
Придумал? Молодец, если да. Удачи!
Принципы построения графика обратной пропорциональности (гиперболы)
Теперь давай научимся строить простейшую гиперболу – ( displaystyle y=frac{k}{x}).
Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.
Например, построим гиперболу ( displaystyle y=frac{3}{x}).
Составим таблицу из ( 4) точек, которые принадлежат одной ветке (например, правой):
| ( x) | ( frac{1}{2}) | ( displaystyle 1) | ( displaystyle 3) | ( displaystyle 6) |
| ( y) | ( displaystyle 6) | ( displaystyle 3) | ( displaystyle 1) | ( frac{1}{2}) |
Отмечаем точки на рисунке:
Проводим через них плавную линию, которая краями приближается к осям:
Это одна ветвь гиперболы
Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:
Отлично, осталось вспомнить, что собой представляет вторая ветвь?
Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
Вот:
Еще один полезный факт.
Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны ( sqrt{k}) для правой ветви гиперболы, и ( -sqrt{k}) для левой.
Для функций, у которых ( k) – точный квадрат (например, ( 1), ( 4) или ( displaystyle frac{1}{4})), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.
В этом случае достаточно даже трех точек, чтобы построить график.
Например, построим график функции ( displaystyle y=frac{4}{x})
Как и в прошлый раз, начнем с правой ветви.
Точка симметрии: ( displaystyle x=y=2). Выберем еще одну точку, например, ( displaystyle x=1), ( displaystyle y=4). У третьей точки координаты будут наоборот: ( displaystyle x=4), ( displaystyle y=1).
Рисуем:
И теперь симметрично отображаем эту ветвь в третью координатную четверть:
Теперь выясним, что будет, если ( displaystyle k<0)?
Очень просто: если есть график функции с таким же по величине, но положительным ( displaystyle k), то нужно просто отразить его относительно оси ( displaystyle Ox)
То есть правая ветвь теперь будет ниже оси ( displaystyle Ox) (в ( displaystyle IV) четверти), а левая – выше (в ( displaystyle III) четверти).
Принцип построения же останется прежним:
Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:
Обратная пропорциональность и её график
Рассмотрим функцию, которая задается формулой
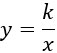
Такая функция называется обратной пропорциональностью, причем x ≠ 0 (т.к. на 0 делить нельзя). Число k также отлично от 0 (в противном случае функция перестанет являться обратной пропорциональностью). Её графиком является гипербола, состоящая из двух ветвей. Ты сможешь увидеть ее ниже.
Перед разбором тренировочных экзаменационных заданий очень хочется вспомнить, что конкретно влияет на расположение и вид графика.
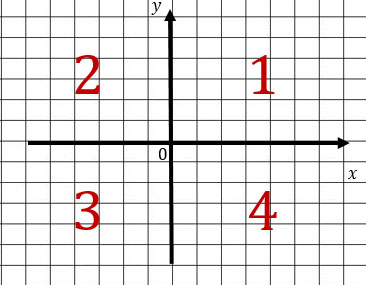
Напомню, что координатная плоскость делится на 4 координатных четверти. У каждой четверти есть свой порядковый номер (см. рисунок).
Так вот к чему я это?
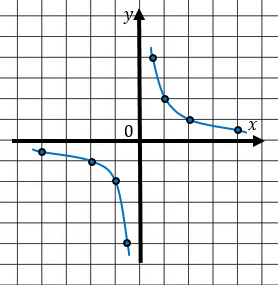
Если k > 0, то ветви гиперболы располагаются в 1 и 3 четвертях.
Если k < 0, то ветви гиперболы располагаются во 2 и 4 четвертях.
Убедимся в этом) Построим два графика.
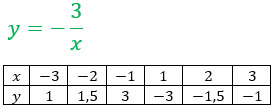
Чем больше точек ты запишешь, тем точнее получится график.
В обоих случаях ветви гиперболы никогда не пересекут оси Ох и Оу, т.к. ни х, ни у нулю равняться не могут. Это значит, что оси являются для графика асимптотами – ветви гиперболы бесконечно стремятся к ним, но никогда их не пересекают.
Но не всегда оси будут асимптотами.
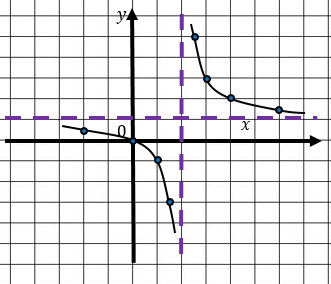
Например, в следующей функции асимптотами будут являться прямые х = 2 и у = 1.
Практикум по гиперболам.
Оказывается, что на сайте ФИПИ все задания чисто с гиперболами однотипные, поэтому разберу только два задания, похожих друг на друга (почему они оси не прорисовывают не пойму).
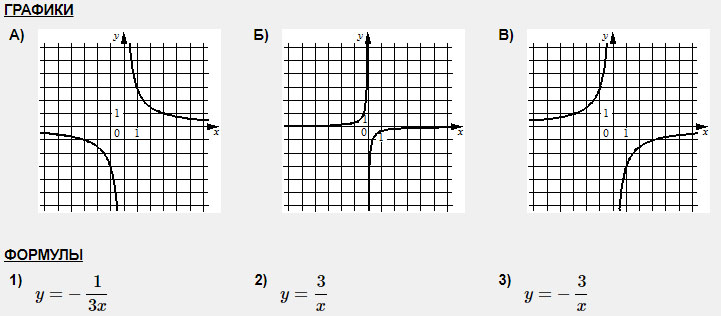
Задание 1. Установите соответствие между графиками и их функциями.
Из общей массы выделяется график Б, т.к. ветви этой гиперболы находятся очень близко к началу координат. А из формул выделяется формула 1, т.к. в ее знаменателе икс умножен на 3. Вывод: график Б и формула 1 созданы друг для друга!
Далее, ветви графика А расположены в 1 и 3 четвертях плоскости, значит коэффициент k положительный. К А подходит формула 2.
И остались график В и формула 3.
Всё)
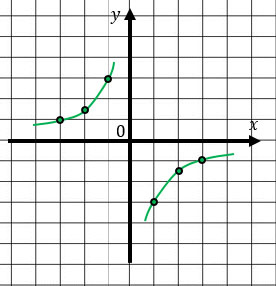
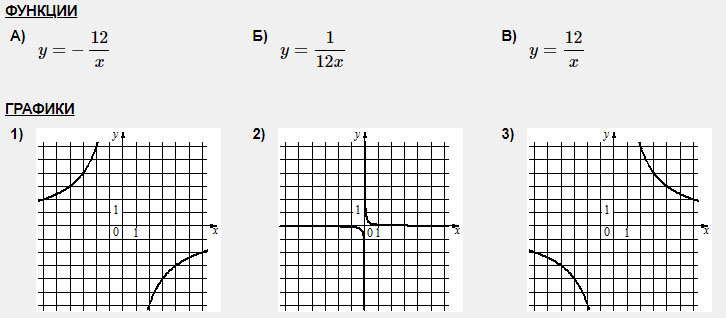
Задание 2. Установите соответствие между функциями и их графиками.
Аналогично предыдущему заданию.
Б-2
А-1
В-3
21
Май 2013
Категория: Справочные материалыФункции и графики
Обратная пропорциональность
2013-05-21
2019-08-13

, где
.
Число называется коэффициентом обратной пропорциональности.
Графиком функции является гипербола.
Гипербола состоит из двух одинаковых частей, кроме того, у неё есть асимптоты (оси ОХ и ОY) — прямые, к которым она стремится, уходя в бесконечность.
Пример 1.
Построим график функции
Построение:
Заполняем таблицу:
Мы вольны брать любые значения , кроме
. Но, конечно, мы подбираем те, подсчет значений
в которых удобен.
Отмечаем на координатной плоскости точки (-6;-1), (-3;-2) и т.д. Соединяем их плавной линией. Чем больше точек будет взято, тем точнее будет график функции.
И, уж конечно, он не «обрывается» в точках (-6;-1), (6,1). Ничто не мешает нам взять в качестве значение, например,
и получить
И так далее.
Пример 2.
Построить график функции
Построение:
Автор: egeMax |
Нет комментариев
| Метки: графики функций
Сегодня мы рассмотрим, какие величины называются обратно пропорциональными, как выглядит график обратной пропорциональности и как все это может вам пригодится не только на уроках математики, но и вне школьных стен.
Такие разные пропорциональности
Пропорциональностью называют две величины, которые взаимно зависимы друг от друга.
Зависимость может быть прямой и обратной. Следовательно, отношения между величинами описывают прямая и обратная пропорциональность.
Прямая пропорциональность – это такая зависимость двух величин, при которой увеличение либо уменьшение одной из них ведет к увеличению либо уменьшению другой. Т.е. их отношение не изменяется.
Например, чем больше усилий вы прилагаете для подготовки к экзаменам, тем выше ваши оценки. Или чем больше вещей вы берете с собой в поход, тем тяжелее нести ваш рюкзак. Т.е. количество затраченных на подготовку к экзаменам усилий прямо пропорционально полученным оценкам. И количество запакованных в рюкзак вещей прямо пропорционально его весу.
Обратная пропорциональность – это функциональная зависимость, при которой уменьшение либо увеличение в несколько раз независимой величины (ее называют аргументом) вызывает пропорциональное (т.е. во столько же раз) увеличение либо уменьшение зависимой величины (ее называют функцией).
Проиллюстрируем простым примером. Вы хотите купить на рынке яблок. Яблоки на прилавке и количество денег в вашем кошельке находятся в обратной пропорциональности. Т.е. чем больше вы купите яблок, тем меньше денег у вас останется.
Функция и ее график
Функцию обратной пропорциональности можно описать как y = k/x. В котором x ≠ 0 и k ≠ 0.
Эта функция обладает следующими свойствами:
- Областью ее определения является множество всех действительных чисел, кроме x = 0. D(y): (-∞; 0) U (0; +∞).
- Областью значений являются все действительные числа, кроме y = 0. Е(у): (-∞; 0) U (0; +∞).
- Не имеет наибольших и наименьших значений.
- Является нечетной и ее график симметричен относительно начала координат.
- Непериодическая.
- Ее график не пересекает оси координат.
- Не имеет нулей.
- Если k > 0 (т.е. аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
- При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные – (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).
График функции обратной пропорциональности называется гиперболой. Изображается следующим образом:
Задачи на обратную пропорциональность
Чтобы стало понятнее, давайте разберем несколько задач. Они не слишком сложные, а их решение поможет вам наглядно представить, что такое обратная пропорциональность и как эти знания могут пригодиться в вашей обычной жизни.
Задача №1. Автомобиль движется со скоростью 60 км/ч. Чтобы доехать до места назначения, ему потребовалось 6 часов. Сколько времени ему потребуется, чтобы преодолеть такое же расстояние, если он будет двигаться со скоростью в 2 раза выше?
Можем начать с того, что запишем формулу, которая описывает отношения времени, расстояния и скорости: t = S/V. Согласитесь, она очень напоминает нам функцию обратной пропорциональности. И свидетельствует о том, что время, которое автомобиль проводит в пути, и скорость, с которой он движется, находятся в обратной пропорциональности.
Чтобы убедиться в этом, давайте найдем V2, которая по условию выше в 2 раза: V2 = 60 * 2 = 120 км/ч. Затем рассчитаем расстояние по формуле S = V * t = 60 * 6 = 360 км. Теперь совсем несложно узнать время t2, которое требуется от нас по условию задачи: t2 = 360/120 = 3 ч.
Как видите время в пути и скорость движения действительно обратно пропорциональны: со скоростью в 2 раза выше изначальной автомобиль потратит в 2 раза меньше времени на дорогу.
Решение этой задачи можно записать и в виде пропорции. Для чего сначала составим такую схему:
↓ 60 км/ч – 6 ч ↑
↓120 км/ч – х ч ↑
Стрелки обозначают обратно пропорциональную зависимость. А также подсказывают, что при составлении пропорции правую часть записи надо перевернуть: 60/120 = х/6. Откуда получаем х = 60 * 6/120 = 3 ч.
Задача №2. В мастерской трудятся 6 рабочих, которые с заданным объемом работы справляются за 4 часа. Если количество рабочих сократить в 2 раза, сколько времени потребуется оставшимся, чтобы выполнить тот же объем работы?
Запишем условия задачи в виде наглядной схемы:
↓ 6 рабочих – 4 ч ↑
↓ 3 рабочих – х ч ↑
Запишем это в виде пропорции: 6/3 = х/4. И получим х = 6 * 4/3 = 8 ч. Если рабочих станет в 2 раза меньше, оставшиеся затратят на выполнение всей работы в 2 раза больше времени.
Задача №3. В бассейн ведут две трубы. Через одну трубу вода поступает со скоростью 2 л/с и наполняет бассейн за 45 минут. Через другую трубу бассейн наполнится за 75 минут. С какой скоростью вода поступает в бассейн через эту трубу?
Для начала приведем все данные нам по условию задачи величины к одинаковым единицам измерения. Для этого выразим скорость наполнения бассейна в литрах в минуту: 2 л/с = 2 * 60 = 120 л/мин.
Поскольку из условия следует, что через вторую трубу бассейн заполняется медленнее, значит, и скорость поступления воды ниже. На лицо обратная пропорциональность. Неизвестную нам скорость выразим через х и составим такую схему:
↓ 120 л/мин – 45 мин ↑
↓ х л/мин – 75 мин ↑
А затем составим пропорцию: 120/х = 75/45, откуда х = 120 * 45/75 = 72 л/мин.
В задаче скорость наполнения бассейна выражена в литрах в секунду, приведем полученный нами ответ к такому же виду: 72/60 = 1,2 л/с.
Задача №4. В небольшой частной типографии печатают визитки. Сотрудник типографии работает со скоростью 42 визитки в час и трудится полный рабочий день – 8 часов. Если бы он работал быстрее и печатал 48 визиток за час, насколько раньше он смог бы уйти домой?
Идем проверенным путем и составляем по условию задачи схему, обозначив искомую величину как х:
↓ 42 визитки/ч – 8 ч ↑
↓ 48 визитки/ч – х ч ↑
Перед нами обратно пропорциональная зависимость: во сколько раз больше визиток в час напечатает сотрудник типографии, во столько же раз меньше времени ему потребуется на выполнение одной и той же работы. Зная это, составим пропорцию:
42/48 = х/8, х = 42 * 8/48 = 7ч.
Таким образом, справившись с работой за 7 часов, сотрудник типографии смогу бы уйти домой на час раньше.
Заключение
Нам кажется, что эти задачи на обратную пропорциональность действительно несложные. Надеемся, что теперь вы тоже считаете их такими. А главное, что знание об обратно пропорциональной зависимости величин действительно может оказаться для вас полезным еще не раз.
Не только на уроках математики и экзаменах. Но и тогда, когда вы соберетесь отправиться в путешествие, пойдете за покупками, решите немного подработать в каникулы и т.п.
Расскажите нам в комментариях, какие примеры обратной и прямой пропорциональной зависимости вы замечаете вокруг себя. Пускай это будет такая игра. Вот увидите, как это увлекательно. Не забудьте «расшарить» эту статью в социальных сетях, чтобы ваши друзья и одноклассники тоже смогли поиграть.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Функция обратной пропорциональности
Содержание:
-
Какая функция называется обратной пропорциональностью
- Свойства обратно пропорциональной функции
-
Что представляет собой график обратно пропорциональной зависимости
- Особенности построения, пример
Какая функция называется обратной пропорциональностью
Определение
Обратная пропорциональность представляет собой зависимость функции, при которой изменение независимой величины (аргумента) влечет пропорциональное изменение зависимой величины (функции).
Исходя из данного описания, во сколько раз увеличивается аргумент, во столько же раз уменьшается функция, и, наоборот, во сколько раз уменьшается аргумент, во столько же раз увеличивается функция.
Пример
Вы намерены приобрести в магазине апельсины. Фрукты на прилавке и сумма, которой вы располагаете, находятся в обратной пропорциональности. Это означает, что чем больше количество купленных вами апельсинов, тем меньше остаток денежных средств в вашем кошельке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Функцию обратной пропорциональности можно записать на математическом языке так:
(y=frac kx)
В данной формуле переменные x и k — не равно нулю.
Свойства обратно пропорциональной функции
- Область определения — все действительные числа, кроме значения x, равного нулю, то есть промежуток D(x):(−∞; 0) U (0; +∞).
- Множество значений — все числа, исключая y=0, то есть: E(y):(−∞; 0) U (0; +∞).
- У функции отсутствуют максимальное и минимальное значения.
- Функция нечетная, ее график симметричен по отношению к точке (0; 0), то есть началу координат.
- Функция неповторяющаяся, следовательно, не является периодической.
- График не пересекает оси абсцисс и ординат.
- Функция не имеет 0.
- При k>0 у функции y=k/x на промежутках от −∞ до 0 и от 0 до +∞ наблюдается убывание. При k<0 у функции y=k/x на промежутках от −∞ до 0 и от 0 до +∞ наблюдается возрастание.
- y=k/x (k>0) на промежутке от −∞ до 0 отрицательна, а на участке от 0 до +∞ — положительна. y=k/x (k<0) на участке (0; +∞) — меньше нуля, а на промежутке (−∞; 0) — больше нуля.
Что представляет собой график обратно пропорциональной зависимости
График функции y=k/x при x≠0 и y≠0 имеет вид гиперболы.
Определение
Гипербола — в математике это понятие обозначает плоскую кривую второго порядка, состоящую из двух частей.
Ветви гиперболы лежат в разных четвертях системы координат симметрично по отношению к началу координат (0; 0). Если коэффициент k принимает значения, больше нуля, то компоненты диаграммы располагаются в первой и третьей четвертях, если k меньше нуля — во второй и четвертой.
Особенности построения, пример
Пусть, функция задана формулой:
(y=frac3x)
- Так как коэффициент 3 положительный, то гипербола расположится в 1 и 3 четвертях.
- Вычислим значения y, задав произвольные значения независимой переменной x. Так определим координаты точек, по которым произведем построение графика. Напомним, что x и y не должны ровняться нулю.
- Так как ветви гиперболы располагаются в двух четвертях, возьмем абсциссы больше 0 (x=1, x=2, x=3, x=6) и меньше 0 (x=−1, x=−2, x=−3, x=−6).
- Далее вычислим ординаты, подставив выбранные значения x в исходное уравнение: у=3/1=3; y=3/2= 1,5; у=3/3=1; у=3/6=0,5; у=3/−1=−3; y=3/−2=−1,5; у=3/−3=−1; y=3/−6=−0,5.
- В результате предыдущих математических операций получилось восемь точек с координатами: A(6; 0,5), B(3; 1), C(2; 1,5), D(1; 3), A1(−6; −1/2), B1(−3; −1), C1(−2; −1,5), D1(−1; −3). Плавно проведем через них кривые и получим график заданной функции: