Как найти обратное расстояние

Как найти обратное расстояние

Доступно с лицензией Geostatistical Analyst.

  • Степенная функция
  • Окрестность поиска
  • Когда используется IDW

Метод обратных взвешенных расстояний (IDW) однозначно предполагает, что объекты, которые находятся поблизости, более подобны друг другу, чем объекты, удаленные друг от друга. Чтобы проинтерполировать значение для неизмеренного положения, IDW использует измеренные значения вокруг интерполируемого местоположения. Наиболее близкие к проинтерполированному местоположению измеренные значения оказывают большее влияние на прогнозируемое значение, чем удаленные от него на значительное расстояние. IDW предполагает, что каждая измеренная точка оказывает локальное влияние, которое уменьшается с увеличением расстояния. Это придает больший вес точкам, расположенным ближе всего к интерполируемому местоположению. Вес точки уменьшается как функция от расстояния. Поэтому метод носит название обратных взвешенных расстояний. Веса, назначенные точкам данных, представлены в следующем примере:

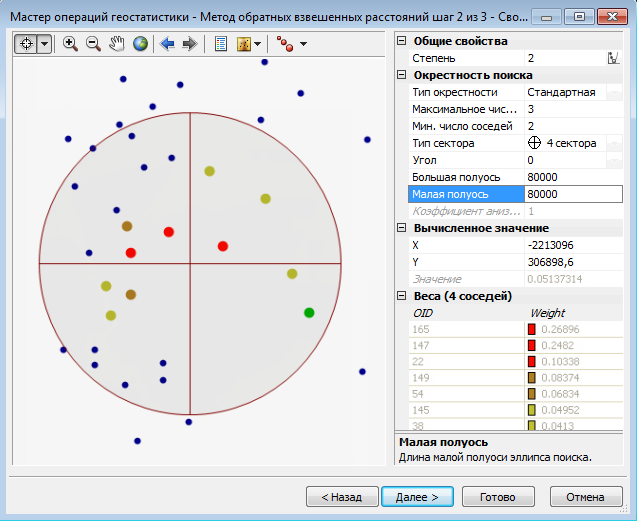
Иллюстрация окрестности поиска

Иллюстрация окрестности поиска

Окно Weights (Веса) содержит список весов, назначенных каждой точке данных, которая используется для интерполяции значения в местоположении, отмеченном перекрестием.

Более подробно о методах интерполяции в ArcGIS ArcGIS Geostatistical Analyst Extension

Степенная функция

Как было указано выше, веса пропорциональны обратным расстояниям (между точкой данных и интерполируемым местоположением), возведенными в степень p. В результате по мере увеличения расстояния вес будет стремительно уменьшаться. Степень уменьшения весов зависит от значения p. Если p = 0, уменьшения с увеличением расстояния не происходит, а поскольку все веса λi одинаковы, прогнозируемое значение будет являться средним для всех значений искомого фрагмента. По мере увеличения значения p веса отдаленных точек будут стремительно уменьшаться. Если значение p слишком высоко, то на интерполяцию окажут влияние только точки, расположенные в непосредственной близости.

Веса IDW

Иллюстрация уменьшения весов с изменением расстояния

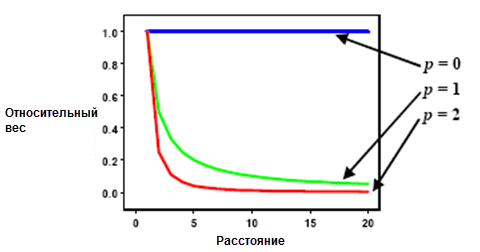
Geostatistical Analyst использует значения степеней, большие или равные 1. Если p = 2, метод называется интерполяцией обратных взвешенных квадратов расстояний. p = 2 используется как значение, установленное по умолчанию, хотя теоретическое обоснование для предпочтения этого значения отсутствует. Влияние изменения значения p должно исследоваться с помощью просмотра выходных данных и проверки перекрестных статистических данных.

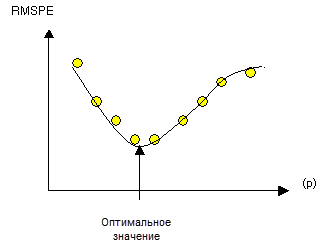
Оптимальное значение степени может быть определено минимизацией среднеквадратичной ошибки интерполяции (RMSPE). RMSPE — это статистическая величина, которая рассчитывается во время перекрестной проверки. RMSPE определяет ошибки интерполируемой поверхности. Модуль Geostatistical Analyst выполняет оценку нескольких значений степени для определения того значения, которое выдает наименьшую ошибку RMSPE. Рисунок внизу иллюстрирует вычисление оптимальной степени модулем Geostatistical Analyst. Ошибки RMSPE построены для нескольких различных значений степени, но с использованием одного набора данных. Кривая подобрана к точкам (квадратичная интерполяция по методу локальных полиномов), и исходя из данных кривой, степень, которая обеспечивает наименьшую ошибку RMSPE, считается оптимальной.

График степенной функции

Пример графика степенной функции

Окрестность поиска

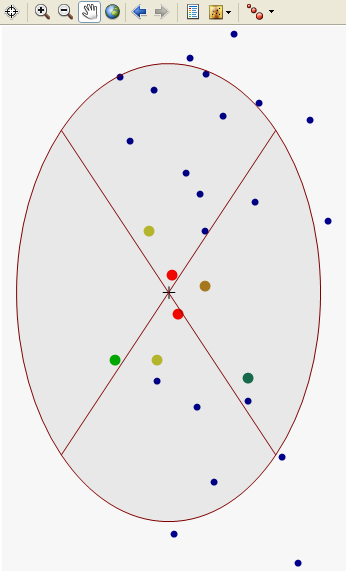
Поскольку объекты, находящиеся поблизости друг от друга, более сходны, чем объекты, находящиеся на большом расстоянии, то по мере удаления от местоположений измеренные значения будут находиться в несущественных отношениях со значением проинтерполированного местоположения. Для увеличения скорости вычислений можно исключить большинство удаленных точек, которые оказывают незначительное влияние на интерполяцию. В результате общей принятой практикой стало ограничение количества измеренных значений с помощью определения окрестности поиска. Форма окрестности накладывает ограничения на дальность и место поиска измеренных значений, используемых для интерполяции. Другие параметры окрестности ограничивают местоположения, которые будут использоваться в форме. На следующем рисунке представлено пять измеренных точек (соседи), которые используются для прогнозирования значения в точке, где измерения не проводились (показана желтым цветом).

Сосед

Пример окрестности поиска

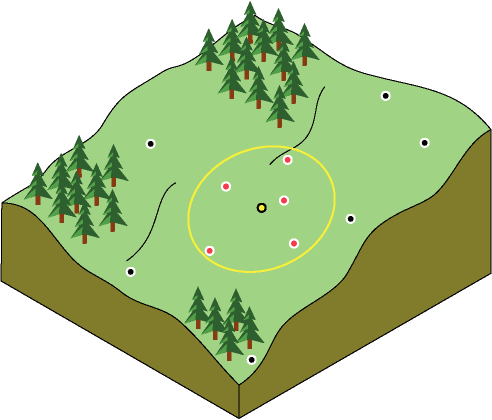
Форма окрестности оказывает влияние на входные данные и поверхность, которую необходимо создать. При отсутствии направленных воздействий на данные можно рассматривать точки одновременно во всех направлениях. Для этого определите окрестность поиска как окружность. Но если присутствует направленное воздействие на данные, например преобладающий ветер, можно изменить форму окрестности поиска на эллипс с большой осью, параллельной ветру. Настройка на такое направленное воздействие оправдана, поскольку известно, что положения с наветренной стороны от интерполируемого местоположения более сходны на отдаленных расстояниях, чем положения, которые перпендикулярны ветру, но расположены ближе к интерполируемой точке.

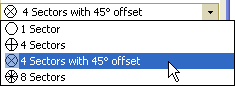
После определения формы окрестности можно наложить ограничение на использование местоположения точек данных в этой окрестности. Можно задать максимальное и минимальное количество положений для использования и разделить окрестность на сектора. При разделении окрестности на сектора к каждому сектору применяются максимальные и минимальные ограничения. Несколько различных секторов, которые могут использоваться, приведены ниже.

Сектора окрестности

Точки, выделенные в виде данных, демонстрируют положения и веса, которые используются для интерполяции местоположения в центре эллипса (положение перекрестия). Окрестности поиска ограничиваются внутренним пространством эллипса. В приведенном ниже примере двум красным точки будет присвоен вес больше 10 процентов. В восточном секторе вес точки (коричневой) составит 5–10 %. Веса остальных точек окрестности поиска будут ниже.

Вес сектора окрестности

Пример весов сектора окрестности

Когда используется IDW

Поверхность, рассчитанная с помощью IDW, зависит от выбора степени (p) и стратегии поиска окрестности. IDW – это жесткий интерполятор, в котором минимальные и максимальные значения (см. рисунок ниже) на интерполированной поверхности могут встречаться только в опорных точках.

Профиль обратных взвешенных расстояний

Пример профиля обратных взвешенных расстояний

Выходная поверхность чувствительна к кластеризации и наличию выпадающих значений. IDW предполагает, что смоделированные явления приводятся в действие локальными изменениями, которые могут быть получены (смоделированы) с помощью определения подходящей окрестности поиска. Так как IDW не предусматривает вычисление стандартных ошибок интерполяции, обоснование использования этой модели может быть проблематичным.

Источник

В инверсной геометрии, обратное расстояние равно aw ay измерения «расстояния » между двумя окружностями, независимо от того, пересекаются ли окружности друг с другом, касаются друг друга или не пересекаются друг с другом.

Содержание

  • 1 Свойства
  • 2 Формула расстояния
  • 3 Для других геометрий
  • 4 Применения
    • 4.1 Цепи Штейнера
    • 4.2 Круговые уплотнения
  • 5 Ссылки
  • 6 Внешние ссылки

Свойства

Обратное расстояние остается неизменным, если круги перевернуты или преобразованы с помощью преобразования Мёбиуса. Одна пара окружностей может быть преобразована в другую с помощью преобразования Мёбиуса тогда и только тогда, когда обе пары имеют одинаковое обратное расстояние.

Аналог теоремы Бекмана – Куорлза верен для инверсивное расстояние: если биекция набора кругов в инверсной плоскости сохраняет обратное расстояние между парами кругов на некотором выбранном фиксированном расстоянии δ { displaystyle delta} delta , то это должно быть преобразование Мебиуса, сохраняющее все обратные расстояния.

Формула расстояния

Для двух окружностей на евклидовой плоскости с радиусами r { displaystyle r}r и R { displaystyle R}R и расстояние d { displaystyle d}d между их центрами, обратное расстояние может определяется формулой

I = d 2 – r 2 – R 2 2 r R. { displaystyle I = { frac {d ^ {2} -r ^ {2} -R ^ {2}} {2rR}}.}{displaystyle I = { frac {d ^ {2} -r ^ {2} -R ^ {2}} {2rR}}.}

Эта формула дает:

  • значение больше 1 для двоих непересекающиеся окружности,
  • значение 1 для двух окружностей, которые касаются друг друга и обе находятся вне друг друга,
  • значение от -1 до 1 для двух пересекающихся окружностей,
    • значение 0 для двух окружностей, которые пересекаются друг с другом под прямыми углами,
  • значение -1 для двух окружностей, которые касаются друг друга, одна внутри другой,
  • и значение меньше -1, когда один кружок содержит другой.

(Некоторые авторы определяют абсолютное обратное расстояние как абсолютное значение обратного расстояния.)

Некоторые авторы модифицируют эту формулу, взяв обратный гиперболический косинус значения, указанного выше, а не самого значения. То есть, вместо использования числа I { displaystyle I}I в качестве обратного расстояния, расстояние определяется как число δ { displaystyle delta} delta согласно уравнению

δ = arcosh ⁡ (I). { displaystyle delta = operatorname {arcosh} (I).} delta = operatorname {arcosh} (I).

Хотя преобразование обратного расстояния таким образом усложняет формулу расстояния и предотвращает ее применение к пересекающимся парам окружностей, у него есть то преимущество, что ( как обычное расстояние для точек на линии) расстояние становится аддитивным для окружностей в пучке окружностей. То есть, если три круга принадлежат одному карандашу, то (используя δ { displaystyle delta} delta вместо I { displaystyle I}I как обратное расстояние) одно из трех попарных расстояний будет суммой двух других.

В других геометриях

Также возможно определить обратное расстояние для окружностей на сфере или для окружностей в гиперболической плоскости.

Приложения

Цепи Штейнера

A Цепь Штейнера для двух непересекающихся окружностей – это конечная циклическая последовательность дополнительных окружностей, каждая из который касается двух данных окружностей и двух своих соседей по цепочке. Поризм Штейнера утверждает, что если две окружности имеют цепочку Штейнера, у них бесконечно много таких цепей. Цепочке разрешено оборачиваться более одного раза вокруг двух кругов, и ее можно охарактеризовать рациональным числом p { displaystyle p}p , числитель которого равен количеству кругов в цепочке, а знаменатель это количество раз, когда он оборачивается. Все цепочки для одних и тех же двух кругов имеют одинаковое значение p { displaystyle p}p . Если обратное расстояние между двумя окружностями (после вычисления обратного гиперболического косинуса) равно δ { displaystyle delta} delta , тогда p { displaystyle p}p можно найти по формуле

p = π sin – 1 ⁡ tanh ⁡ (δ / 2). { displaystyle p = { frac { pi} { sin ^ {- 1} tanh ( delta / 2)}}.}p = { frac { pi} { sin ^ {{- 1}} tanh ( delta /2)}}.

И наоборот, каждые два непересекающихся круга, для которых эта формула дает рациональное число будет поддерживать цепочку Штейнера. В более общем смысле, произвольная пара непересекающихся окружностей может быть сколь угодно точно аппроксимирована парами окружностей, которые поддерживают цепочки Штейнера, значения p { displaystyle p}p являются рациональными приближениями к значение этой формулы для данных двух кругов.

Упаковка кругов

Инверсное расстояние было использовано для определения концепции обратного расстояния упаковки кругов : коллекция кругов так, что указанное подмножество пар кругов (соответствующих ребрам плоского графа ) имеет заданное обратное расстояние друг относительно друга. Эта концепция обобщает упаковки кругов, описываемые теоремой об упаковке кругов, в которой указанные пары кругов касаются друг друга. Хотя о существовании упаковок круговых обратных расстояний известно меньше, чем об упаковках касательных кругов, известно, что, когда они существуют, они могут быть однозначно заданы (с точностью до преобразований Мёбиуса) заданным максимальным плоским графом и набор евклидовых или гиперболических обратных расстояний. Это свойство жесткости можно обобщить в широком смысле на евклидовы или гиперболические метрики на триангулированных многообразиях с угловыми дефектами в их вершинах. Однако для коллекторов со сферической геометрией эти упаковки больше не уникальны. В свою очередь, упаковки окружностей с обратным расстоянием использовались для построения приближений к конформным отображениям.

Ссылки

Внешние ссылки

Источник

В инверсной геометрии, обратное расстояние равно aw ay измерения «расстояния » между двумя окружностями, независимо от того, пересекаются ли окружности друг с другом, касаются друг друга или не пересекаются друг с другом.

Содержание

  • 1 Свойства
  • 2 Формула расстояния
  • 3 Для других геометрий
  • 4 Применения
    • 4.1 Цепи Штейнера
    • 4.2 Круговые уплотнения
  • 5 Ссылки
  • 6 Внешние ссылки

Свойства

Обратное расстояние остается неизменным, если круги перевернуты или преобразованы с помощью преобразования Мёбиуса. Одна пара окружностей может быть преобразована в другую с помощью преобразования Мёбиуса тогда и только тогда, когда обе пары имеют одинаковое обратное расстояние.

Аналог теоремы Бекмана – Куорлза верен для инверсивное расстояние: если биекция набора кругов в инверсной плоскости сохраняет обратное расстояние между парами кругов на некотором выбранном фиксированном расстоянии δ { displaystyle delta} delta , то это должно быть преобразование Мебиуса, сохраняющее все обратные расстояния.

Формула расстояния

Для двух окружностей на евклидовой плоскости с радиусами r { displaystyle r}r и R { displaystyle R}R и расстояние d { displaystyle d}d между их центрами, обратное расстояние может определяется формулой

I = d 2 – r 2 – R 2 2 r R. { displaystyle I = { frac {d ^ {2} -r ^ {2} -R ^ {2}} {2rR}}.}{displaystyle I = { frac {d ^ {2} -r ^ {2} -R ^ {2}} {2rR}}.}

Эта формула дает:

  • значение больше 1 для двоих непересекающиеся окружности,
  • значение 1 для двух окружностей, которые касаются друг друга и обе находятся вне друг друга,
  • значение от -1 до 1 для двух пересекающихся окружностей,
    • значение 0 для двух окружностей, которые пересекаются друг с другом под прямыми углами,
  • значение -1 для двух окружностей, которые касаются друг друга, одна внутри другой,
  • и значение меньше -1, когда один кружок содержит другой.

(Некоторые авторы определяют абсолютное обратное расстояние как абсолютное значение обратного расстояния.)

Некоторые авторы модифицируют эту формулу, взяв обратный гиперболический косинус значения, указанного выше, а не самого значения. То есть, вместо использования числа I { displaystyle I}I в качестве обратного расстояния, расстояние определяется как число δ { displaystyle delta} delta согласно уравнению

δ = arcosh ⁡ (I). { displaystyle delta = operatorname {arcosh} (I).} delta = operatorname {arcosh} (I).

Хотя преобразование обратного расстояния таким образом усложняет формулу расстояния и предотвращает ее применение к пересекающимся парам окружностей, у него есть то преимущество, что ( как обычное расстояние для точек на линии) расстояние становится аддитивным для окружностей в пучке окружностей. То есть, если три круга принадлежат одному карандашу, то (используя δ { displaystyle delta} delta вместо I { displaystyle I}I как обратное расстояние) одно из трех попарных расстояний будет суммой двух других.

В других геометриях

Также возможно определить обратное расстояние для окружностей на сфере или для окружностей в гиперболической плоскости.

Приложения

Цепи Штейнера

A Цепь Штейнера для двух непересекающихся окружностей – это конечная циклическая последовательность дополнительных окружностей, каждая из который касается двух данных окружностей и двух своих соседей по цепочке. Поризм Штейнера утверждает, что если две окружности имеют цепочку Штейнера, у них бесконечно много таких цепей. Цепочке разрешено оборачиваться более одного раза вокруг двух кругов, и ее можно охарактеризовать рациональным числом p { displaystyle p}p , числитель которого равен количеству кругов в цепочке, а знаменатель это количество раз, когда он оборачивается. Все цепочки для одних и тех же двух кругов имеют одинаковое значение p { displaystyle p}p . Если обратное расстояние между двумя окружностями (после вычисления обратного гиперболического косинуса) равно δ { displaystyle delta} delta , тогда p { displaystyle p}p можно найти по формуле

p = π sin – 1 ⁡ tanh ⁡ (δ / 2). { displaystyle p = { frac { pi} { sin ^ {- 1} tanh ( delta / 2)}}.}p = { frac { pi} { sin ^ {{- 1}} tanh ( delta /2)}}.

И наоборот, каждые два непересекающихся круга, для которых эта формула дает рациональное число будет поддерживать цепочку Штейнера. В более общем смысле, произвольная пара непересекающихся окружностей может быть сколь угодно точно аппроксимирована парами окружностей, которые поддерживают цепочки Штейнера, значения p { displaystyle p}p являются рациональными приближениями к значение этой формулы для данных двух кругов.

Упаковка кругов

Инверсное расстояние было использовано для определения концепции обратного расстояния упаковки кругов : коллекция кругов так, что указанное подмножество пар кругов (соответствующих ребрам плоского графа ) имеет заданное обратное расстояние друг относительно друга. Эта концепция обобщает упаковки кругов, описываемые теоремой об упаковке кругов, в которой указанные пары кругов касаются друг друга. Хотя о существовании упаковок круговых обратных расстояний известно меньше, чем об упаковках касательных кругов, известно, что, когда они существуют, они могут быть однозначно заданы (с точностью до преобразований Мёбиуса) заданным максимальным плоским графом и набор евклидовых или гиперболических обратных расстояний. Это свойство жесткости можно обобщить в широком смысле на евклидовы или гиперболические метрики на триангулированных многообразиях с угловыми дефектами в их вершинах. Однако для коллекторов со сферической геометрией эти упаковки больше не уникальны. В свою очередь, упаковки окружностей с обратным расстоянием использовались для построения приближений к конформным отображениям.

Ссылки

Внешние ссылки

  • Вайсштейн, Эрик У. «Обратное расстояние». MathWorld.
Источник

From Wikipedia, the free encyclopedia

Inverse distance weighting (IDW) is a type of deterministic method for multivariate interpolation with a known scattered set of points. The assigned values to unknown points are calculated with a weighted average of the values available at the known points. This method can also be used to create spatial weights matrices in spatial autocorrelation analyses (e.g. Moran’s I).[1]

The name given to this type of method was motivated by the weighted average applied, since it resorts to the inverse of the distance to each known point (“amount of proximity”) when assigning weights.

Definition of the problem[edit]

The expected result is a discrete assignment of the unknown function u in a study region:

{displaystyle u(x):xto mathbb {R} ,quad xin mathbf {D} subset mathbb {R} ^{n},}

where mathbf{D} is the study region.

The set of N known data points can be described as a list of tuples:

{displaystyle [(x_{1},u_{1}),(x_{2},u_{2}),...,(x_{N},u_{N})].}

The function is to be “smooth” (continuous and once differentiable), to be exact ({displaystyle u(x_{i})=u_{i}}) and to meet the user’s intuitive expectations about the phenomenon under investigation. Furthermore, the function should be suitable for a computer application at a reasonable cost (nowadays, a basic implementation will probably make use of parallel resources).

Shepard’s method[edit]

Historical reference[edit]

At the Harvard Laboratory for Computer Graphics and Spatial Analysis, beginning in 1965, a varied collection of scientists converged to rethink, among other things, what are now called geographic information systems.[2]

The motive force behind the Laboratory, Howard Fisher, conceived an improved computer mapping program that he called SYMAP, which, from the start, Fisher wanted to improve on the interpolation. He showed Harvard College freshmen his work on SYMAP, and many of them participated in Laboratory events. One freshman, Donald Shepard, decided to overhaul the interpolation in SYMAP, resulting in his famous article from 1968.[3]

Shepard’s algorithm was also influenced by the theoretical approach of William Warntz and others at the Lab who worked with spatial analysis. He conducted a number of experiments with the exponent of distance, deciding on something closer to the gravity model (exponent of -2). Shepard implemented not just basic inverse distance weighting, but also allowed barriers (permeable and absolute) to interpolation.

Other research centers were working on interpolation at this time, particularly University of Kansas and their SURFACE II program. Still, the features of SYMAP were state-of-the-art, even though programmed by an undergraduate.

Basic form[edit]

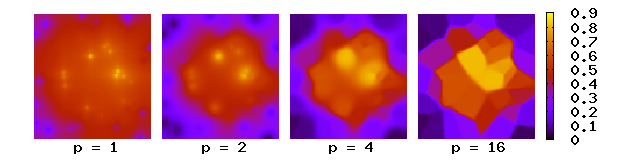
Shepard’s interpolation for different power parameters p, from scattered points on the surface z=exp(-x^{2}-y^{2})

Given a set of sample points {displaystyle {mathbf {x} _{i},u_{i}|{text{for }}mathbf {x} _{i}in mathbb {R} ^{n},u_{i}in mathbb {R} }_{i=1}^{N}}, the IDW interpolation function {displaystyle u(mathbf {x} ):mathbb {R} ^{n}to mathbb {R} } is defined as:

{displaystyle u(mathbf {x} )={begin{cases}{dfrac {sum _{i=1}^{N}{w_{i}(mathbf {x} )u_{i}}}{sum _{i=1}^{N}{w_{i}(mathbf {x} )}}},&{text{if }}d(mathbf {x} ,mathbf {x} _{i})neq 0{text{ for all }}i,\u_{i},&{text{if }}d(mathbf {x} ,mathbf {x} _{i})=0{text{ for some }}i,end{cases}}}

where

w_{i}({mathbf {x}})={frac {1}{d({mathbf {x}},{mathbf {x}}_{i})^{p}}}

is a simple IDW weighting function, as defined by Shepard,[3] x denotes an interpolated (arbitrary) point, xi is an interpolating (known) point, d is a given distance (metric operator) from the known point xi to the unknown point x, N is the total number of known points used in interpolation and p is a positive real number, called the power parameter.

Here weight decreases as distance increases from the interpolated points. Greater values of p assign greater influence to values closest to the interpolated point, with the result turning into a mosaic of tiles (a Voronoi diagram) with nearly constant interpolated value for large values of p. For two dimensions, power parameters pleq 2 cause the interpolated values to be dominated by points far away, since with a density rho of data points and neighboring points between distances r_{0} to R, the summed weight is approximately

{displaystyle sum _{j}w_{j}approx int _{r_{0}}^{R}{frac {2pi rrho ,dr}{r^{p}}}=2pi rho int _{r_{0}}^{R}r^{1-p},dr,}

which diverges for Rrightarrowinfty and pleq 2. For M dimensions, the same argument holds for {displaystyle pleq M}. For the choice of value for p, one can consider the degree of smoothing desired in the interpolation, the density and distribution of samples being interpolated, and the maximum distance over which an individual sample is allowed to influence the surrounding ones.

Shepard’s method is a consequence of minimization of a functional related to a measure of deviations between tuples of interpolating points {x, u} and i tuples of interpolated points {xi, ui}, defined as:

phi ({mathbf {x}},u)=left(sum _{{i=0}}^{{N}}{{frac {(u-u_{i})^{2}}{d({mathbf {x}},{mathbf {x}}_{i})^{p}}}}right)^{{{frac {1}{p}}}},

derived from the minimizing condition:

{displaystyle {frac {partial phi (mathbf {x} ,u)}{partial u}}=0.}

The method can easily be extended to other dimensional spaces and it is in fact a generalization of Lagrange
approximation into a multidimensional spaces. A modified version of the algorithm designed for trivariate interpolation was developed by Robert J. Renka and is available in Netlib as algorithm 661 in the toms library.

Example in 1 dimension[edit]

Shepard’s interpolation in 1 dimension, from 4 scattered points and using p = 2

Modified Shepard’s method[edit]

Another modification of Shepard’s method calculates interpolated value using only nearest neighbors within R-sphere (instead of full sample). Weights are slightly modified in this case:

{displaystyle w_{k}(mathbf {x} )=left({frac {max(0,R-d(mathbf {x} ,mathbf {x} _{k}))}{Rd(mathbf {x} ,mathbf {x} _{k})}}right)^{2}.}

When combined with fast spatial search structure (like kd-tree), it becomes efficient N log N interpolation method suitable for large-scale problems.

See also[edit]

  • Field (geography)
  • Gravity model
  • Kernel density estimation
  • Spatial analysis
  • Tobler’s first law of geography
  • Tobler’s second law of geography

References[edit]

  1. ^ “Spatial Autocorrelation (Global Moran’s I) (Spatial Statistics)”. ArcGIS Pro Documentation. ESRI. Retrieved 13 September 2022.
  2. ^ Chrisman, Nicholas. “History of the Harvard Laboratory for Computer Graphics: a Poster Exhibit” (PDF).
  3. ^ a b Shepard, Donald (1968). “A two-dimensional interpolation function for irregularly-spaced data”. Proceedings of the 1968 ACM National Conference. pp. 517–524. doi:10.1145/800186.810616.
Источник

Данный метод является точным, поскольку исходные точки данных используются для построения треугольников и, следовательно, принадлежат интерполяционной функции.

Метод триангуляции работает наилучшим образом в случае, когда множество экспериментальных данных содержит от 200 до 1000 точек, равномерно распределенных в рассматриваемой области. Использование этого метода для построения интерполяционной функции по небольшому числу хаотически распределенных точек приводит к появлению явных треугольных граней на графике поверхности и больших прямолинейных сегментов на карте изолиний. При больших множествах экспериментальных данных (>1000 точек) метод триангуляции работает очень медленно.

Метод триангуляции особенно эффективен, если требуется сохранить линии разрывов поверхности.

Если Вы выберете метод триангуляции (Triangulation with Linear Interpolation) в качестве метода построения сеточной функции (Gridding Method) и щелкнете по клавише Options (Опции), то на экране откроется панель диалога

Triangulation Options (Опции метода триангуляции).

*Групповое окно Anisotropy (Анизотропия) позволяет задать весовые множителей для разных осей анизотропии. Более подробную информацию об этой опции можно получить в разделе “Анизотропия (Anisotropy)” данной Справочной системы.

*Групповое окно Data Treatment (Обработка данных) определяет способ включения повторных наблюдений в операцию построения интерполяционной функции. Более подробную информацию об этой опции можно получить в разделе “Обработка данных (Data Treatment)” данной Справочной системы.

*При нажатии клавиши Reset (Сброс) все установки, выполненные Вами в панели диалога Triangulation Options (Опции метода триангуляции), сбрасываются и всем параметрам метода возвращаются их значения по умолчанию.

Метод построения сеточной функции Inverse Distance to a Power (Степень обратного расстояния) может быть как точным, так и сглаживающим интерполяционным методом.

Этот метод основан на вычислении весовых коэффициентов, с помощью которых взвешиваются значения экспериментальных Z-значений в точках наблюдений при построении интерполяционной функции.

Параметр Power (Степень) определяет, как быстро уменьшаются весовые множители с ростом расстояния до узла сети. При больших значениях параметра Power точкам наблюдений, более близким к рассматриваемому узлу сети, присваиваются большие доли общего веса; при меньших значениях параметра Power веса убывают более плавно с ростом расстояния до узла сети.

Вес, присвоенный отдельной точке данных при вычислении узла сети, пропорционален заданной степени (power) обратного расстояния от точки наблюдения до узла сети. При вычислении интерполяционной функции в каком-то узле сети сумма всех назначенных весов равна единице, а весовой коэффициент каждой экспериментальной точки является долей этого общего единичного веса. Если точка наблюдения совпадает с узлом сети, то весовой коэффициент этой точки полагается равным единице, а всем другим наблюденным точкам присваиваются нулевые веса. Другими словами, в этом случае узлу сети присваивается значение соответствующего наблюдения, и, следовательно, данный метод работает как точный интерполятор.

Недостатком метода обратных расстояний является генерация структур типа “бычий глаз” вокруг точек наблюдений с большими значениями функции. Для уменьшения влияния этих точек Вы можете задать параметр, который сглаживает интерполяционную функцию. Если значение сглаживающего параметра больше нуля, то ни одному наблюдению не присваивается весь вес при вычеслении функции в каком-то узле сети, даже если точка наблюдения совпадает с этим узлом.

Метод обратных расстояний является очень быстрым методом построения сеточной функции. Если число точек данных не превышает 500, то сеть строится очень быстро, даже если Вы выбираете опцию All Data (Все данные) при задании типа поиска (Search Type).

Если Вы выберете метод обратных расстояний (Inverse Distance to a Power) в качестве метода построения сеточной функции (Gridding Method) и щелкнете по клавише Options (Опции), то на экране откроется панель диалога

Inverse Distance Options (Опции метода обратных расстояний).

*Групповое окно Parameters (Параметры) позволяет задать степень (Power) обратного расстояния и параметр сглаживания (Smoothing), используемые для построения интерполяционной функции.

Параметр Power (Степень) определяет, как быстро уменьшаются весовые множители с ростом расстояния до узла сети. При стремлении параметра Power к нулю сгенерированная поверхность приближается к горизонтальной плоскости, проходящей через среднее значение всех наблюдений выборки. При стремлении параметра Power к бесконечности сгенерированная поверхность становится многогранной: каждой вершине этой многогранной поверхности присваивается значение наблюдения, ближайшего к соответствующему узлу сети.

Параметр Smoothing (Сглаживание) позволяет задать для Ваших данных так называемый фактор “неопределенности”. Чем больше параметр сглаживания, тем меньшее влияние имеет каждая отдельная экспериментальная точка при определении значения интерполяционной функции в узле сети.

*Групповое окно Anisotropy (Анизотропия) позволяет задать весовые множителей для разных осей анизотропии. Более подробную информацию об этой опции можно получить в разделе “Анизотропия (Anisotropy)” данной Справочной системы.

*Групповое окно Data Treatment (Обработка данных) определяет способ включения повторных наблюдений в операцию построения интерполяционной функции. Более подробную информацию об этой опции можно получить в разделе “Обработка данных (Data Treatment)” данной Справочной системы.

*При нажатии клавиши Reset (Сброс) все установки, выполненные Вами в панели диалога Inverse Distance Options (Опции метода обратных расстояний) сбрасываются и всем параметрам метода возвращаются их значения по умолчанию.

2.2.5. Метод минимальной кривизны (Minimum Curvature)

Метод Minimum Curvature (Минимальной кривизны) широко используется в науках о Земле. Поверхность, построенная с помощью этого метода, аналогична тонкой упругой пленке, проходящей через все экспериментальные точки данных с минимальным числом изгибов. Метод минимальной кривизны, однако, не является точным методом. Он генерирует наиболее гладкую поверхность, которая проходит настолько близко к экспериментальным точкам, насколько это возможно, но эти экспериментальные точки не обязательно принадлежат интерполяционной поверхности.

Если Вы выберете метод минимальной кривизны (Minimum Curvature) в качестве метода построения сеточной функции (Gridding Method) и щелкнете по клавише Options (Опции), то на экране откроется панель диалога Minimum

Curvature Options (Опции метода минимальной кривизны).

*Групповое окно Parameters (Параметры) позволяет Вам задать критерий сходимости для метода минимальной кривизны.

Параметр Max Residuals (Максимальная невязка) измеряется в тех же единицах, что и экспериментальные данные. Наиболее подходящее значение этого параметра равно, примерно, 10% от точности исходных данных. Если исходные экспериментальные данные измерены с точностью 1.0 единиц измерения, то значение Max Residuals рекомендуется положить равным 0.1. Итерации продолжаются до тех пор, пока максимальная невязка для всей итерации не станет меньше значения параметра Max Residuals.

Параметр Max Iterations (Максимальное число итераций) разумно выбрать в интервале от N до 2N, где N – число узлов генерируемой сети. Например, если метод минимальной кривизны используется для построения сети, размером 50×50, то значение параметра Max Iterations следует выбирать в интервале от 2500 до 5000.

*Групповое окно Anisotropy (Анизотропия) позволяет задать весовые множителей для разных осей анизотропии. Более подробную информацию об этой опции можно получить в разделе “Анизотропия (Anisotropy)” данной Справочной системы.

*Групповое окно Data Treatment (Обработка данных) определяет способ включения повторных наблюдений в операцию построения интерполяционной функции. Более подробную информацию об этой опции можно получить в разделе “Обработка данных (Data Treatment)” данной Справочной системы.

*При нажатии клавиши Reset (Сброс) все установки, выполненные Вами в панели диалога Minimum Curvature Options (Опции метода минимальной кривизны) сбрасываются и всем параметрам метода возвращаются их значения по умолчанию.

2.2.6. Метод полиномиальной регрессии (Polynomial Regression)

Метод Polynomial Regression (Полиномиальной регрессии) используется для выделения больших трендов и структур в Ваших данных. Это метод, строго говоря, не является интерполяционным методом, поскольку сгенерированная поверхность не проходит через экспериментальные точки.

Если Вы выберете метод полиномиальной регрессии (Polynomial Regression) в качестве метода построения сеточной функции (Gridding Method) и щелкнете по клавише Options (Опции), то на экране откроется панель диалога

Polynomial Regression Options (Опции метода полиномиальной регрессии).

*Групповое окно Surface Definition (Определение поверхности) позволяет Вам выбрать тип полиномиальной регрессии, который Вы хотите использовать для анализа экспериментальных данных.

Когда Вы выбираете какой-то тип регрессии, в левой части панели диалога отображается общая полиномиальная форма уравнения регрессии, а параметры в групповом окне Parameters принимают значения, соответствующие выбранному уравнению регрессии.

ВSURFERе реализованы следующие типы уравнений регрессии:

–Simple planar surface (Простая плоская поверхность);

–Bi-Linear saddle(Билинейная седлообразная поверхность);

–Quadratic surface (Квадратичная поверхность);

–Cubic surface (Кубическая поверхность).

Опция User defined polynomial (Определенный пользователем полином) позволяет Вам задать полиномиальное уравнение регрессии с помощью параметров группового окна Parameters.

*В групповом окне Parameters (Параметры) Вы можете задать максимальные степени по переменным X и Y в полиномиальном уравнении регрессии.

При изменении значений параметров в групповом окне Parameters соответствующим образом меняется вид уравнения регрессии в панели диалога.

Параметр Max X Order (Максимальная степень по X) задает максимальную степень по переменной X в уравнении полиномиальной регрессии.

Параметр Max Y Order (Максимальная степень по Y) задает максимальную степень по переменной Y в уравнении полиномиальной регрессии.

Параметр Max Total Order (Максимальная общая степень) задает максимальную сумму степеней по переменным X и Y (Max X Order и Max Y Order). В уравнение регрессии включаются все те комбинации X и Y компонент, сумма степеней которых не превосходит Max Total Order.

*Групповое окно Data Treatment (Обработка данных) определяет способ включения повторных наблюдений в операцию построения интерполяционной функции. Более подробную информацию об этой опции можно получить в разделе “Обработка данных (Data Treatment)” данной Справочной системы.

*Если включен переключатель Copy the regression coefficients to the clipboard (Скопировать коэффициенты регрессии в буфер обмена), то копия коэффициентов регрессии, вычисленных при построении регрессионной поверхности, пересылается в буфер обмена Windows.

*При нажатии клавиши Reset (Сброс) все установки, выполненные Вами в панели диалога Polynomial Regression Options (Опции метода полиномиальной регрессии) сбрасываются и всем параметрам метода возвращаются их значения по умолчанию.

2.2.7. Метод Шепарда (Shepard’s Method)

Метод Шепарда (Shepard’s Method) подобен методу обратных расстояний (Inverse Distance to a Power). Он также использует обратные расстояния при вычислении весовых коэффициентов, с помощью которых взвешиваются значения экспериментальных Z-значений в точках наблюдений. Отличие состоит в том, что при построении интерполяционной функции в локальных областях используется метод наименьших квадратов. Это уменьшает вероятность появления на сгенерированной поверхности структур типа “бычий глаз”.

Метод Шепарда может быть как точным, так и сглаживающим интерполяционным методом.

Если Вы выберете метод Шепарда (Shepard’s Method) в качестве метода построения сеточной функции (Gridding Method) и щелкнете по клавише Options (Опции), то на экране откроется панель диалога Shepard’s Method Options (Опции метода Шепарда).

*В групповом окне Parameters (Параметры) Вы можете задать сглаживающий параметр, используемый для построения сеточной функции.

При ненулевом параметре Smoothing (Сглаживание) метод Шепарда работает как сглаживающий интерполятор. Чем больше параметр сглаживания, тем меньшее влияние имеет каждая отдельная экспериментальная точка при определении значения интерполяционной функции в узле сети.

Наиболее разумными значения этого параметра являются значения из интервала от 0 до 1.

*Групповое окно Anisotropy (Анизотропия) позволяет задать весовые множителей для разных осей анизотропии. Более подробную информацию об этой опции можно получить в разделе “Анизотропия (Anisotropy)” данной Справочной системы.

*Групповое окно Data Treatment (Обработка данных) определяет способ включения повторных наблюдений в операцию построения интерполяционной функции. Более подробную информацию об этой опции можно получить в разделе “Обработка данных (Data Treatment)” данной Справочной системы.

*При нажатии клавиши Reset (Сброс) все установки, выполненные Вами в панели диалога Shepard’s Method Options (Опции метода Шепарда) сбрасываются и всем параметрам метода возвращаются их значения по умолчанию.

2.3.Рекомендации по выбору метода построения сети (Recomendations for Choosing a Gridding Method)

ВSURFERе реализовано несколько методов построения сеточных функций. Различные методы могут привести к разным результатам при интерполяции Ваших данных. Предлагаемые в данном разделе рекомендации можно рассматривать, как первый шаг при принятии решения о выборе наилучшего метода построения сети. Здесь

приводятся только самые общие соображения, и в конечном счете предпочтение следует отдать тому методу, который производит карту, наилучшим образом представляющую Ваши экспериментальные данные.

Для большинства множеств экспериментальных данных самым эффективным является метод Криге (Kriging) с линейной (Linear) вариаграммой. Этот метод задается по умолчанию, и мы будем наиболее часто рекомендовать его для использования. Второй по распространенности метод – это метод радиальных базисных функций (Radial Basis Functions) с мультиквадратичной (Multiquadratic) базисной функцией. Любой их этих методов пригоден для построения разумного представления Ваших данных.

Ниже приведен краткий обзор методов построения сетей с указанием их основных достоинств и недостатков.

*Метод обратных расстояний (Inverse Distance to a Power) является достаточно быстрым, но имеет тенденцию генерировать структуры типа “бычий глаз” вокруг точек наблюдений с высокими значениями функции.

*Метод Криге (Kriging) – один из наиболее гибких и часто используемых методов. Этот метод задается в SURFERе по умолчанию. Для большинства множеств экспериментальных данных метод Криге с линейной вариаграммой является наиболее эффективным. Однако, на множествах большого размера он работает достаточно медленно.

*Метод минимума кривизны (Minimum Curvature) генерирует гладкие поверхности и для большинства множеств экспериментальных данных работает достаточно быстро.

*Метод полиномиальной регрессии (Polynomial Regression) используется для выделения больших трендов и структур в Ваших данных. Это метод работает очень быстро для множеств любого размера, но, строго говоря, он не является интерполяционным методом, поскольку сгенерированная поверхность не проходит через экспериментальные точки.

*Метод радиальных базисных функций (Radial Basis Functions) так же, как и метод Криге, является очень гибким и генерирует гладкую поверхность, проходящую через экспериментальные точки. Результаты работы этого метода очень похожи на результаты метода Криге. Он эффективен для большинства множеств экспериментальных данных.

*Метод Шепарда (Shepard’s Method) подобен методу обратных расстояний (Inverse Distance to a Power), но он,

как правило, не генерирует структуры типа “бычий глаз”, особенно когда задан сглаживающий параметр.

*Метод триангуляции (Triangulation with Linear Interpolation) для множеств экспериментальных точек средних размеров (от 250 до 1000 наблюдений) работает достаточно быстро и строит хорошее представление данных. Этот метод генерирует явные треугольные грани на графике поверхности.

Одним из достоинств метода триангуляции является то, что при достаточном количестве экспериментальных точек он может сохранить линии разрывов, определенные исходным множеством данных. Если имеется достаточное число точек по обе стороны от линии разрыва, то сеточная функция, построенная методом триангуляции, отобразит этот разрыв.

2.4. Учет исходных данных при построении сеточной функции (Honoring Original Data During Gridding)

Учет исходных данных при построении сеточной функции означает, что исходные экспериментальные точки данных непосредственно включаются в сеточный файл. В общем случае методы построения сети не гарантируют, что точки данных будут учтены точно. Но есть несколько приемов, с помощью которых Вы можете улучшить соответствие между исходными данными и сеточным файлом.

Методы построения сеточных функций, реализованные в SURFERе, можно разбить на два класса: точные интерполяторы и сглаживающие интерполяторы. Некоторые точные интерполяторы могут включать сглаживающий параметр; ненулевое значение этого параметра превращает точный интерполятор в сглаживающий.

Точные интерполяторы учитывают исходную экспериментальную точку точно (то есть включают ее в сеточный файл) тогда, когда эта точка совпадает с узлом генерируемой сети. Если точка данных не совпадает с узлом сети, то она не включается в сеточный файл, даже если Вы используете точный интерполятор. Для того, чтобы повысить вероятность учета исходных точек, следует увеличить плотность сеточных линий в направлениях X и Y. Это увеличит шанс, что Ваши экспериментальные точки совпадут с узлами сети и, следовательно, войдут непосредственно в сеточный файл.

Перечисленные ниже методы являются точными интерполяторами:

*Inverse Distance to a Power (Степень обратного расстояния), если Вы не задаете сглаживающий параметр;

*Kriging (Метод Криге), если Вы не задаете параметр Nugget Effect (“эффект самородка”);

*Radial Basis Functions (Радиальные базисные функции), если Вы не задаете параметр RI;

*Shepard’s Method (Метод Шепарда), если Вы не задаете сглаживающий параметр;

*Triangulation with Linear Interpolation (Триангуляция с линейной интерполяцией).

Соседние файлы в папке Surfer

  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий