Как научится выводить вторичные формулы из первичных? (по физике)
Мастер
(1376),
закрыт
5 лет назад
Головолом Головоломович
Мыслитель
(8066)
7 лет назад
тема это: эквивалентные преобразования уравнений.
правило 1) к обеим частям исходного уравнения можно прибавить или отнять любое число
правило 2) обе части исходного уравнения можно умножить или разделить на любое ненулевое число.
в вашем случае:
I = E/(r+R), домножаем обе части уравнения на (r+R) имеем
I*(r+R) = E, теперь делим обе части на I
r+R = E/I, теперь вычитаем из обеих частей R (или r), имеем
r = (E/I) – R, (или R = (E/I) – r)
Наташенька
Ученик
(174)
5 лет назад
Тоже искала в интернете. Можешь, ещё попробовать в ютуб вбить свой вопрос и посмотреть разные объяснения. Ну или найти репетитора хорошего. Успехов!
muha karimov
Ученик
(151)
1 год назад
Такая же проблема. Я вот часто когда преобразую формулы я применяю метод крестика из пропорции. Тоесть я крайние пропорции умножаю между собой то же самое я делая с средними членами пропорции. Часто благодаря пропорции мне не сложно преобразовывать формулы, однако слишком сложные формулы мне не получается преобразовывать методом крестика.
Как выводить формулы по физике из формулы
Содержание
- Природные явления
- Вперед, в будущее!
- Понимание мира
- Инструкция
- Основные формулы по физике динамика, кинематика, статика
- Основные формулы молекулярной физики и термодинамики
- Основные формулы по физике: электричество

Да не переживай это проблема многих моих одноклассников хоть я и в 9 кл.Учителя показывают это чаще всего методом треугольника,но мне кажется это не удобно да и запутаться легко.Покажу наиболее простой способ,которым я пользуюсь.
Допустим дана формула:
Ну более простая. тебе из этой формулы нужно найти время.Ты берешь и в эту формулу подставляешь числа только разные,исходя из алгебры.допустим:
и тебе наверное хорошо видно,что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике:t=s/v
УДАЧИ:))попробуй сама:)будут вопросы пиши в личку)
Posted By admin on 06.12.2018
При решении задач часто требуется выведение расчётной формулы из различных законов физики, определений физических величин. Здесь очень важно не запутаться в математических правилах, иначе ответ получится неверным. Для самопроверки правильности рассуждений используются хитрые приёмчики. Например, правило треугольника или проверка по окончательной формуле размерности искомой физической величины, когда с наименованиями проделываются все те же действия, что и с самими, данными в условии, величинами. Если в итоге получается верное наименование искомой величины, значит, и формула выведена правильно. Например, так как v = S : t, то [v] = м : с = м/с.
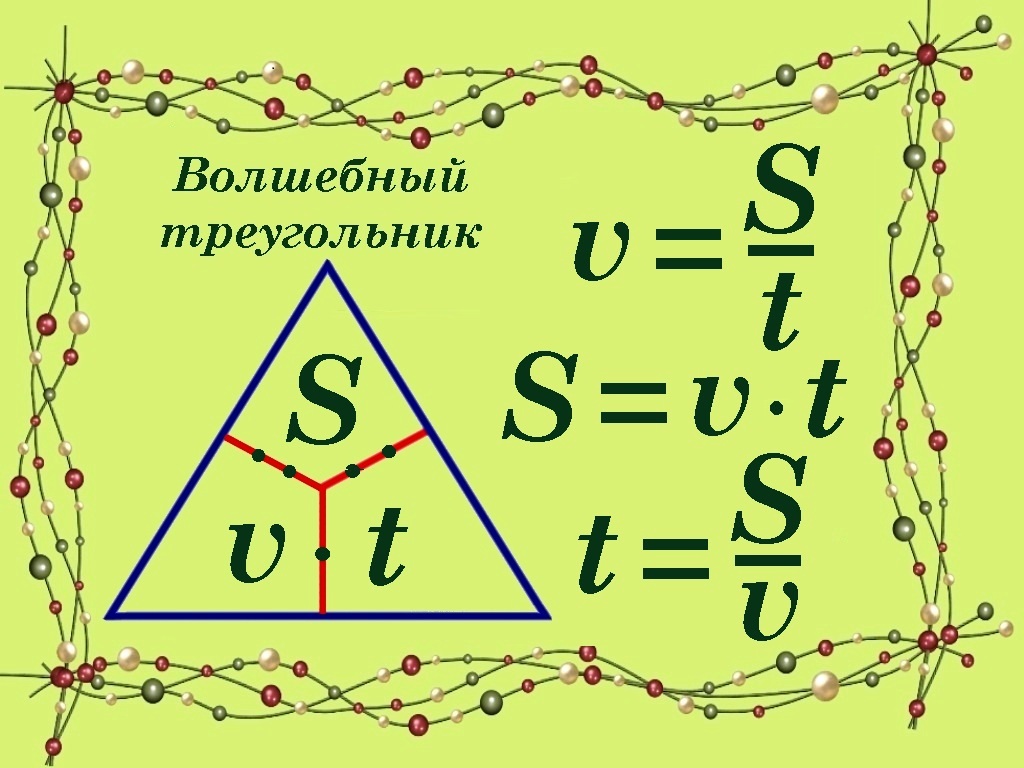
Если знать секрет волшебного треугольника, то нет необходимости для выведения расчётных формул различных физических величин из законов или определений припоминать правила нахождения неизвестного множителя, делителя или делимого. Достаточно правильно расположить элементы формулы в треугольнике. Например, по определению скорость v – это путь, пройденный телом за единицу времени и поэтому она равна отношению величины пройденного расстояния S к потраченному на него времени t, то есть v = S/t. Разместим в левой нижней части треугольника частное v, в верхней части треугольника делимое S, а в правой нижней части треугольника делитель t. Тогда из рисунка видно, что S = v · t, так как v и t находятся в треугольнике рядом на одной строке. Неизвестное время t = S/v, так как путь S расположен в верхней части треугольника, то есть как бы в числителе, а скорость v находится в нижней части треугольника, то есть как бы в знаменателе.
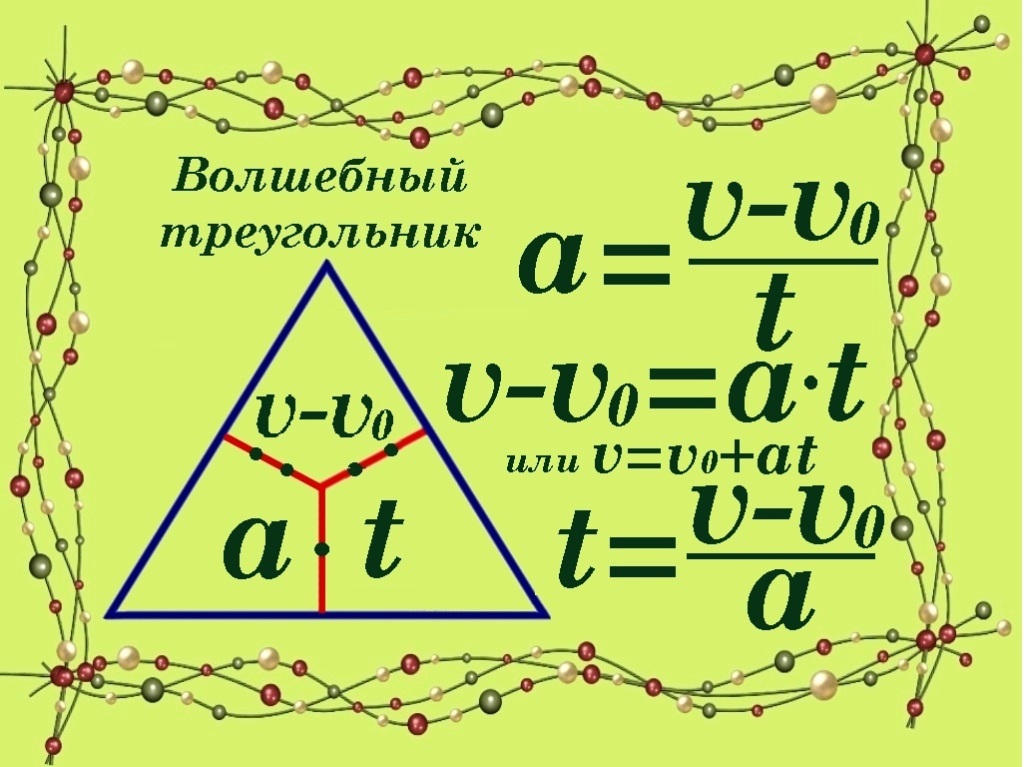
Используя определение ускорения для прямолинейного движения, легко получить формулы для расчёта пройденного пути при равноускоренном движении.

Проиллюстрируем правило треугольника на определении понятия плотности ρ, как массы вещества m, заключённой в единичном объёме V, то есть ρ = m/V. Очевидно, что m = ρ · V и V = m/ρ.
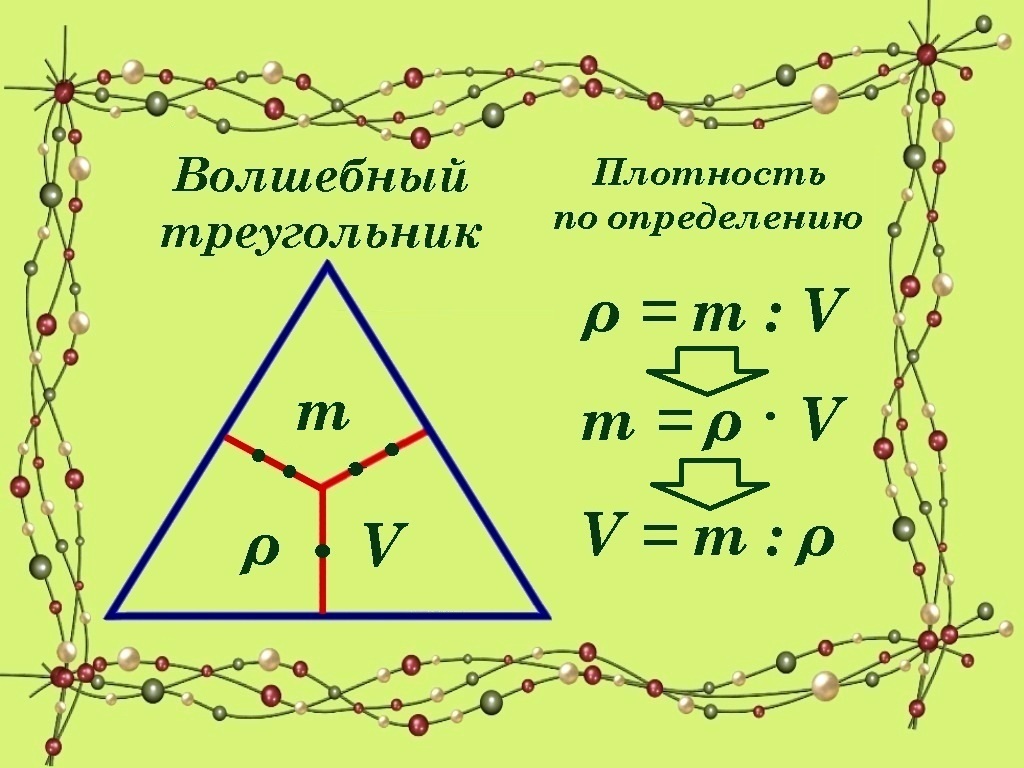
Для закона Ома на участке электрической цепи сила тока I прямо пропорциональна напряжению U на данном участке и обратно пропорциональна его сопротивлению R, то есть I = U/R. Из треугольника легко получаем, что U = I · R, а R = U/I.
Откуда берутся физические формулы ? Упрощенно схему получения формул можно представить так: вопрос, выдвигаются гипотезы, проводится серия экспериментов. Результаты обрабатываются, возникают конкретные формулы , и это дает начало новой физической теории либо продолжает и развивает уже имеющуюся.
Уясните физику рассматриваемого процесса. Какими параметрами он описывается, и как эти параметры меняются на протяжении времени? Зная основные определения и понимая физику процесса, легко получить формулы . Как правило, между величинами или квадратами величин устанавливаются прямо пропорциональные или обратно пропорциональные зависимости, вводится .
Путем математических преобразований можно из первичных формул вывести вторичные. Если вы научитесь делать это легко и быстро, последние можно будет не запоминать. Основной метод преобразований – метод подстановки: -либо величина выражается из одной формулы и подставляется в другую. Важно лишь, чтобы эти формулы соответствовали одному и тому же процессу или явлению.
Также уравнения можно складывать между собой, делить, перемножать. Функции по времени очень часто интегрируют или дифференцируют, получая новые зависимости. Логарифмирование подойдет для функций. При выводе формулы опирайтесь на результат, который вы хотите в итоге получить.
Вся человеческая жизнь окружена множеством разнообразных явлений. Ученые-физики занимаются изучением этих явлений; их инструментарием выступают математические формулы и достижения предшественников.
Природные явления
Вперед, в будущее!
Понимание мира
Бывает и наоборот — толкают математиков на создание гипотез и нового логического аппарата. Связь физики и математики — одной из важнейших научных дисциплин подкрепляет авторитет физики.
Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
Представим полный дифференциал внутренней энергии через частные производные по параметрам и :

После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость в любом термодинамическом процессе и для любой макроскопической системы, если известны калорическое и термическое уравнения состояния.
Рассмотрим процесс при постоянном давлении и получим общее соотношение между и .
Исходя из полученной формулы, можно легко найти связь между теплоемкостями и в идеальном газе. Этим мы и займемся. Впрочем, ответ уже известен, мы его активно использовали в 7.5.
Уравнение Роберта Майера
Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда

Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе
Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости .
Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости  уравнение процесса наглядно представляется в виде графика — кривой процесса. Кривая, изображающая политропический процесс, называется политропой. Уравнение политропического процесса для любого вещества может быть получено на основе первого начала термодинамики с использованием его термического и калорического уравнений состояния. Продемонстрируем, как это делается на примере вывода уравнения процесса для идеального газа.
уравнение процесса наглядно представляется в виде графика — кривой процесса. Кривая, изображающая политропический процесс, называется политропой. Уравнение политропического процесса для любого вещества может быть получено на основе первого начала термодинамики с использованием его термического и калорического уравнений состояния. Продемонстрируем, как это делается на примере вывода уравнения процесса для идеального газа.
Вывод уравнения политропического процесса в идеальном газе
Требование постоянства теплоёмкости в процессе позволяет записать первое начало термодинамики в виде
Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
Разделив () на , находим
Интегрированием (9.15), получаем

Это уравнение политропы в переменных
Исключая из уравнения () , с помощью равенства получаем уравнение политропы в переменных
Параметр называется показателем политропы, который может принимать согласно () самые разные значения, положительные и отрицательные, целые и дробные. За формулой () скрывается множество процессов. Известные вам изобарный, изохорный и изотермический процессы являются частными случаями политропического.
К этому классу процессов относится также адиабатный или адиабатический процесс . Адиабатным называется процесс, проходящий без теплообмена (). Реализовать такой процесс можно двумя способами. Первый способ предполагает наличие у системы теплоизолирующей оболочки, способной изменять свой объем. Второй – заключается в осуществлении столь быстрого процесса, при котором система не успевает обмениваться количеством теплоты с окружающей средой. Процесс распространения звука в газе можно считать адиабатным благодаря его большой скорости.
Физика – наука о природе. Она описывает процессы и явления окружающего мира на макроскопическом уровне – уровне небольших тел, сравнимых с размерами самого человека. Для описания процессов физика использует математический аппарат.
Инструкция
Откуда берутся физические формулы ? Упрощенно схему получения формул можно представить так: ставится вопрос, выдвигаются гипотезы, проводится серия экспериментов. Результаты обрабатываются, возникают конкретные формулы , и это дает начало новой физической теории либо продолжает и развивает уже имеющуюся.
Человеку, изучающему физику, не надо заново проходить весь этот сложный путь. Достаточно освоить центральные понятия и определения, ознакомиться со схемой эксперимента, научиться выводить основополагающие формулы . Естественно, без прочных математических знаний не обойтись.
Итак, выучите определения физических величин, относящихся к рассматриваемой теме. У каждой величины есть свой физический смысл, который вы должны понимать. Например, 1 кулон – это заряд, проходящий через поперечное сечение проводника за 1 секунду при силе тока в 1 ампер.
Уясните физику рассматриваемого процесса. Какими параметрами он описывается, и как эти параметры меняются на протяжении времени? Зная основные определения и понимая физику процесса, легко получить простейшие формулы . Как правило, между величинами или квадратами величин устанавливаются прямо пропорциональные или обратно пропорциональные зависимости, вводится коэффициент пропорциональности.
Путем математических преобразований можно из первичных формул вывести вторичные. Если вы научитесь делать это легко и быстро, последние можно будет не запоминать. Основной метод преобразований – метод подстановки: какая-либо величина выражается из одной формулы и подставляется в другую. Важно лишь, чтобы эти формулы соответствовали одному и тому же процессу или явлению.
Также уравнения можно складывать между собой, делить, перемножать. Функции по времени очень часто интегрируют или дифференцируют, получая новые зависимости. Логарифмирование подойдет для степенных функций. При выводе формулы опирайтесь на результат, который вы хотите в итоге получить.
Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.
Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!
Основные формулы по физике динамика, кинематика, статика
Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.
Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.

После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику

Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!

Основные формулы молекулярной физики и термодинамики
Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.

Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.
Кстати! Для всех наших читателей сейчас действует скидка 10% на .

Основные формулы по физике: электричество
Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.


И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.

На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».
Эта статья будет интересна тем, кто пытается понять работу сложных формул.
В Excel есть инструменты, которые позволяют отследить работу формулы по шагам. Первый из них называется Вычислить формулу и находится на вкладке Формулы — Зависимости формул в версиях Excel, начиная с Excel 2007, и в меню Сервис — Зависимости формул в более ранних версиях. Второй, менее известный, но от этого не менее удобный, — функциональная клавиша F9.
Разберём работу этих инструментов на нескольких примерах.
Пример 1. Дана таблица, содержащая сведения о персонале предприятия. Требуется по введённому табельному номеру определить фамилию сотрудника.
Для решения этой задачи в ячейку H3 ведём табельный номер, а в ячейку I3 формулу =ИНДЕКС($B$2:$B$25;ПОИСКПОЗ(H3;$E$2:$E$25;0))
Чтобы отследить работу формулы, поставим курсор в ячейку с формулой и нажмём кнопку Вычислить формулу . При этом откроется диалоговое окно Вычисление формулы

В этом окне мы видим саму формулу, а также кнопку Вычислить , с помощью которой мы будем отслеживать пошаговое выполнение формулы. При нажатии на кнопку Вычислить будет вычислен подчёркнутый фрагмент. На следующих изображениях мы видим результат работы формулы



Теперь посмотрим, как с этой же формулой поможет разобраться клавиша F9 .
Выделим в строке формул ссылку I3 , нажмём F9 , выделим фрагмент $E$2:$E$37 и снова нажмём F9 . Клавиша F9 вычисляет выделенные фрагменты формулы, и мы можем видеть не только результат функции, но и аргументы в виде массивов. Согласитесь, что при таком подходе формула становится “прозрачной”, и становится очевиден результат функции ПОИСКПОЗ()

Чтобы привести формулу в первоначальный вид, нажмём ESC .
Ещё немного потренируемся: выделим фрагмент $B$2:$B$37 , нажмём F9 , затем выделим функцию ПОИСКПОЗ(I3;$E$2:$E$37;0) и снова F9. Видим массив фамилий, среди которых будет выбрана третья по счёту

ВАЖНО. При выделении фрагмента формулы следует следить за его корректностью с точки зрения правил построения выражений: количеством открывающихся и закрывающихся скобок, целостностью функций и т.д.
После анализа формулы не забывайте нажимать ESC для возврата к исходному виду.
ВЫВОД. Оба инструмента выполняют одну задачу, но клавиша F9 , на мой взгляд, более гибкий инструмент, так как позволяет вычислить произвольный фрагмент формулы независимо от того, находится он в начале или в середине формулы, а так же разбить формулу на произвольные фрагменты в отличие от инструмента Вычислить формулу . Поэтому следующие примеры будут посвящены именно клавише F9
Пример 2. На основе таблицы из Примера 1 создать список табельных номеров и фамилий сотрудников одного из отделов, указанного в отдельной ячейке. Формула, решающая эту задачу, выглядит так: =ИНДЕКС($E$2:$E$25;НАИМЕНЬШИЙ(ЕСЛИ($A$2:$A$25=$H$7;СТРОКА($A$1:$A$24));СТРОКА(A1))) , причём это — формула массива, которую следует вводить сочетанием клавиш + +

Основой этой формулы является функция ИНДЕКС() , которая позволяет вывести элемент массива по указанному индексу (порядковому номеру). Первым аргументом этой функции указывается диапазон ячеек с табельными номерами. Выделив в формуле фрагмент $E$2:$E$25 и нажав F9 , мы увидим значения исходного массива

Порядковый номер для выбора элемента массива вычисляется с помощью функции НАИМЕНЬШИЙ(ЕСЛИ(.
Разобьём эту часть формулы на составляющие. Выделим фрагмент $A$2:$A$25=$H$7 и нажмём F9 . Это логическое выражение даёт значение ИСТИНА , если значение ячейки диапазона $A$2:$A$25 равно выбранному названию отдела $H$7 , и ЛОЖЬ , если не равно.
Выделим фрагмент СТРОКА($A$1:$A$24) и нажмём F9 , получим массив чисел, идущих по порядку от 1 до 24.

Теперь предсказуем результат функции ЕСЛИ() — это массив, в котором значения ИСТИНА заменятся на порядковые номера, а значения ЛОЖЬ останутся на месте. Увидеть это можно, выделив функцию ЕСЛИ целиком с закрывающей скобкой и нажав F9
Далее в действие вступает функция НАИМЕНЬШИЙ() , которая первым аргументом имеет вышеуказанный массив, а вторым — функцию СТРОКА(A1) . Обращаем внимание, что во всей формуле это единственная относительная ссылка, которая будет изменяться при копировании формулы по строкам, а именно в первом случае даст 1, на следующей строке 2 и т.д. по порядку. В итоге в ячейке I7 формула, “расшифрованная” с помощью клавиши F9 , будет иметь вид

А скопированная в ячейку I8

Если понадобится применить данную формулу для другого диапазона, изменится исходный диапазон в функции ИНДЕКС(), а также изменится верхняя граница диапазона функции СТРОКА(), в то время как нижняя граница остаётся всегда $A$1. Важно, чтобы количество строк исходного диапазона совпадало с количеством строк в функции СТРОКА().
Фамилии в столбец J можно вставить с помощью формулы, разобранной в Примере 1.
Физика
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ. Лучше не решать физическую задачу по шагам: найти из одной формулы значение физической величины, затем подставлять ее во вторую формулу. Почему? Во-первых, получается неточный результат в вычислениях после многократного округления. Во-вторых, многие задачи нет возможности решить таким путем, из-за того, что нет значения некоторой физической величины. Но тупик часто заключается в том, что если бы мы подставляли в буквенном виде одну формулу в другую, то та неизвестная физическая величина сократилась бы. Поэтому учимся на примерах выражать из формулы необходимую физическую величину. Главное правило: букву, которую необходимо выразить, представляем в уме за x, остальные буквы представляем известными значениями. В этом случае получим совершенно обычное математическое уравнение.
Выведение переменной из формулы
Данную статью я начну с общего алгоритма выражения переменной, а затем уже будем разбираться на конкретных примерах.
Пусть дана какая-то формула.
1) Если она содержит скобки, то раскрываем их и приводим подобные слагаемые;
2) Если есть знаменатель, то избавляемся от него, умножив обе части формулы на этот знаменатель (если знаменателей несколько, то умножаем обе части равенства на общий знаменатель);
3) Если есть корни, то обе части возводим в степень, равную показателю корня;
4) Переносим все члены с нужной нам переменной в одну сторону;
5) Если таких членов несколько, то выносим нужную нам переменную за скобку в качестве общего множителя. Если нет, то этот шаг пропускаем.
6) Делим обе части формулы на все сомножители нужной нам переменной.
7) Если нужная переменная возведена в n-ую степень, то нужно из обеих частей формулы извлечь корень n-ой степени.
На самом деле, всё не так ужасно) На ОГЭ так вообще простые задания.
Вот парочка примеров.
1) Центростремительное ускорение при движении по окружности вычисляется по формуле a=ω 2 R, где ω — угловая скорость, R — радиус окружности. Выразим из этой формулы R и ω.
Выразим радиус R, разделив обе части на его сомножитель ω 2 :

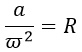
Но обычно пишут так, чтобы искомая переменная была слева:
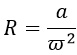
Теперь выразим угловую скорость. Разделим обе части равенства на сомножитель угловой скорости (на R, короче говоря):
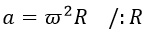
Получается вот такая запись:
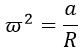
Нужная нам угловая скорость возведена в квадрат. Избавиться от степени нам поможет квадратный корень:
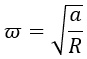
Теперь возьмем формулу с дробью.
2) Площадь четырехугольника можно вычислить по формуле
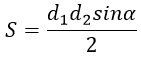
Выразим из нее d1.
Избавляемся от знаменателя, умножив обе части равенства на 2 (т.к. знаменатель равен двум).
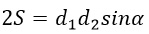
Чтобы выразить d1 разделим обе части на сомножители d2 и sinα.
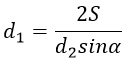
Точно также выражаются d2 и sinα. Можешь даже самостоятельно попробовать.
Еще один пример. Последний.
3) Дана формула
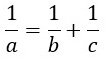
Выразим из нее переменную b.
Формула содержит дроби, поэтому надо избавится от знаменателей. Умножим обе части равенства на общий знаменатель abc.
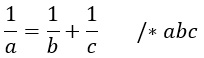
Получится такое выражение:
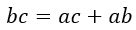
Перенесем все члены равенства, содержащие переменную b в левую часть.
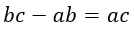
Вынесем b за скобки как общий множитель.
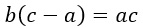
Разделим обе части равенства на (с — а).
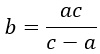
Что-то не выражается? Напиши мне свой пример. Используй функцию “Предложить новость”.
Правила вывода величины из формулы (7-11 класс)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Правила вывода величины из формулы
Формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Иногда для решения задач необходимо вывести неизвестную величину из формулы. Для этого существуют несколько правил.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная « b ». В последней колонке выражена величина « с »


Примеры вывода физической величины из формулы

Курс повышения квалификации
Педагогические основы деятельности учителя общеобразовательного учреждения в условиях ФГОС

Курс повышения квалификации
Анализ урока как инструмент развития профессиональных компетенций учителя в соответствии с требованиями ФГОС
- Сейчас обучается 26 человек из 16 регионов

Курс повышения квалификации
Теория и методика преподавания предмета «Астрономия» в условиях реализации ФГОС СОО
- Сейчас обучается 67 человек из 35 регионов

«Домашнее обучение. Лайфхаки для родителей»
- подготовка к ЕГЭ/ОГЭ и ВПР
- по всем предметам 1-11 классов
«Такие разные дети: преимущества тьюторской позиции учителя»
Свидетельство и скидка на обучение каждому участнику
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 909 890 материалов в базе
«Интеграция современного искусства в детское творчество»
Свидетельство и скидка на обучение
каждому участнику
Ищем педагогов в команду «Инфоурок»
- ЗП до 91 000 руб.
- Гибкий график
- Удаленная работа
Другие материалы
- Физика
- 7 класс
- Тесты
- Учебник: «Физика», Перышкин А.В.
- 02.05.2018
- 482
- 0
- Физика
- 7 класс
- Другие методич. материалы
- Учебник: «Физика», Перышкин А.В.
- 02.05.2018
- 8598
- 28
- Физика
- 10 класс
- Презентации
- Учебник: «Физика. Базовый и профильный уровни», Тихомирова С.А., Яворский Б.М.
- Тема: Глава 1. Кинематика
- 02.05.2018
- 3214
- 47
- Физика
- 7 класс
- Тесты
- Учебник: «Физика», Перышкин А.В.
- Тема: Глава 3. Давление твёрдых тел, жидкостей и газов
- 02.05.2018
- 13283
- 149
- Физика
- 9 класс
- Другие методич. материалы
- Учебник: «Физика», Перышкин А.В., Гутник Е.М.
- Тема: § 13 Свободное падение тел
- 02.05.2018
- 340
- 0
- Физика
- 7 класс
- Презентации
- Учебник: «Физика», Перышкин А.В.
- Тема: §55 Механическая работа. Единицы работы
- 02.05.2018
- 258
- 1
- Физика
- 10 класс
- Презентации
- Учебник: «Физика. Базовый и профильный уровни», Тихомирова С.А., Яворский Б.М.
- Тема: § 19. Сила трения
- 02.05.2018
- 2054
- 25
- Физика
- 8 класс
- Конспекты
- Учебник: «Физика», Перышкин А.В.
- Тема: Приложение к Главе 1
- 02.05.2018
- 443
- 0
«Практический подход в работе с утратой смысла жизни: логотерапия»
Свидетельство и скидка на обучение каждому участнику
Вам будут интересны эти курсы:
- Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
- Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»
- Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
- Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
- Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
- Курс повышения квалификации «Организация маркетинга в туризме»
- Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
- Курс повышения квалификации «Психодинамический подход в консультировании»
- Курс профессиональной переподготовки «Организация технической поддержки клиентов при установке и эксплуатации информационно-коммуникационных систем»
- Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
- Курс профессиональной переподготовки «Эксплуатация и обслуживание общего имущества многоквартирного дома»
- Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
- Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
- 02.05.2018 2588
- DOCX 186.2 кбайт
- Оцените материал:
Настоящий материал опубликован пользователем Абдуллаева Гульбахор Уришовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 5 лет и 8 месяцев
- Подписчики: 9
- Всего просмотров: 1158579
- Всего материалов: 1214
40%
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
 60 минут
60 минут
«Политическая карта как объект изучения в школьном курсе географии. Объекты и субъекты, уникальные характеристики, динамизм и изменчивость политической карты»
 25 минут
25 минут
«Мозаичный декор из цветного стекла»
 64 минуты
64 минуты
«Развитие коммуникативных способностей школьников на уроках и во внеурочной деятельности»
Подарочные сертификаты
- Курсы «Инфоурок»
- Онлайн-занятия с репетиторами на IU.RU
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 110 человек из 46 регионов


- Сейчас обучается 486 человек из 70 регионов


- Сейчас обучается 140 человек из 54 регионов


Описание презентации по отдельным слайдам:
-

1 слайд
Выразить переменную из формулы
Дудников Ю. А.МБОУ Качалинская СОШ
2017 -

2 слайд
1. В той части формулы, где содержится переменная, которую нужно выразить, расставьте порядок действий. В одночленах и многочленах, не содержащих искомую величину, порядок действий не расставляем.
2. Найдите в выражении последнее действие, и перенести одночлен или многочлен, исполняющий это действие через знак равенства первым, но уже с противоположным действием. Таким образом, перенесите из одной части равенства в другую все известные величины. В заключение перепишите формулу так, чтобы неизвестная переменная стояла слева.
Порядок выражения переменной
-

3 слайд
2
S
a
t
2
=
1
2
2
S
a
t
2
=
1
2
S
a
t
=
2
3
S
a
t
2
=
1
2
2
S
a
t
= -

4 слайд
a
=
1
1
2
1
0
–
t
υ
υ
0
t
a
=
+
υ
υ
t
a
=
+
0
υ
υ
t
a
–
=
0
υ
υ -

5 слайд
1
2
1
2
+
S
=
a
h
3
1
1
2
h
=
+
2
)
(
a
b
b
2
S
+
=
(
)
h
b
a
2
S
+
=
h
a
b
2
S
–
=
h
b
a
h
2
S
–
=
a
b -

6 слайд
1
2
1
1
a
=
υ
υ
0
–
t
t
=
υ
υ
0
–
a
Заново расставляем порядок действий, так как нужная переменная оказалась в другой части формулы.
–
t
=
υ
0
a
υ -

7 слайд
1
2
1
2
+
S
=
υ
0
t
3
1
1
2
t
=
+
2
0
)
(
υ
υ
υ
2
S
+
=
(
)
t
0
υ
υ
2
S
+
=
t
0
υ
υ
2
S
–
=
t
0
υ
υ
t
2
S
–
=
0
υ
υ -

8 слайд
m
Q
–
=
(
)
c
0
t
t
к
m
Q
–
=
c
0
t
t
к
m
Q
+
=
c
0
t
t
к
Q
m
+
=
c
0
t
t
к
1
2
1 -

9 слайд
3
1
2
1
2
1
υυ
2
S
2
=
0
2
–
a
υ
–
2
S
a
2
=
υ
2
0
2
S
a
2
=
+
2
0
υ
υ
1
2
S
a
=
2
+
0
υ
υ
2
2
S
a
=
+
0
υ
υ -

10 слайд
1
g
ℓ
=
T
2
π
g
ℓ
=
T
2
π
2
2
g
ℓ
=
T
4
π
2
2
g
ℓ
T
4
π
=
2
2
ℓ
=
T
4
π
g
3
2
2
3
3 -

11 слайд
ν
h
=
+
ν
кр
h
m
2
2
υ
3
ν
h
–
=
ν
кр
h
m
2
2
υ
2
1
1
4
3
2
ν
h
–
=
ν
кр
h
m
2
υ
(
)
2
ν
h
–
=
ν
кр
h
m
2
υ
(
)
ν
h
–
=
ν
кр
h
m
2
υ
(
)
ν
h
–
=
ν
кр
h
m
2
υ
(
)
2
1
1
2 -

12 слайд
=
T
T
х
–
Т
η
н
н
=
T
T
х
–
Т
η
н
н
–
T
T
х
=
Т
η
н
н
–
–
T
х
=
Т
η
н
–
(
1
)
–
1
=
T
T
х
–
н
η
1
=
T
T
х
–
н
η
1 -

13 слайд
k
d
=
–
C
2
d
–
–
k
d
=
C
2
d
(
)
–
–
k
d
=
C
2
d
–
C
+
k
d
=
C
2
d
+
C
(
)
+
k
1
=
C
2
d
+
C
+
k
1
=
C
2
d
+
C -

14 слайд
1
1
1
2
1
2
2
+
S
=
υ
0
t
3
t
=
+
2
0
)
(
υ
υ
υ
2
S
+
=
(
)
t
0
υ
υ
2
S
+
=
t
0
υ
υ
2
S
–
=
t
0
υ
υ
t
2
S
–
=
0
υ
υ -

15 слайд
x
a
+
t
k
+
b
=
1
2
2
3
5
1
4
x
a
–
t
k
+
b
=
1
2
2
3
1
4
(
x
a
–
t
k
+
b
=
1
2
2
3
1
)
2
(
x
a
–
t
k
+
b
=
1
2
2
)
2
)
(
1
x
a
–
t
k
+
b
=
1
2
)
2
)
(
1
(
x
a
–
t
k
+
b
=
1
)
2
)
(
( -

16 слайд
1
S
=
+
K
2
=
E
m
a
x
–
b
)
+
K
2
E
m
a
x
–
b
(
+
K
E
m
)
2
a
x
–
b
(
=
S
+
K
E
m
2
a
x
–
b
=
S
2
a
x
+
K
E
m
+
b
=
S
m
+
K
E
+
b
=
S
S
2
a
x
+
K
E
+
b
=
S
S
m
x
a
+
K
E
+
b
=
S
S
m
2
1
4
3
1
3
2
2
4
1
3
2
1
1 -

17 слайд
h
+
g
R
G
=
)
2
M
(
h
+
g
R
G
=
)
2
M
(
h
+
g
R
G
=
)
2
M
(
h
+
g
R
G
=
M
h
–
g
R
G
=
M -

18 слайд
1
1
F
1
1
=
+
f
1
d
F
1
1
=
–
f
1
d
F
d
1
=
–
f
F
d
F
d
1
=
–
f
F
d
F
d
=
–
f
F
d
2
Приведем к общему знаменателю левую часть формулы
Если дроби равны, то обратные им дроби тоже равны. Перевернем дроби, для того чтобы неизвестная переменная оказалась в числителе. -

19 слайд
1
1
k
1
2
=
+
f
3
d
k
1
2
=
–
f
3
d
k
d
=
–
f
k
d
2
3
2
1
–
k
d
2
=
f
k
d
3
1
Приведем к общему знаменателю левую часть формулы
Переворачиваем дробь.
k
d
2
=
–
f
k
d
3
1 -

20 слайд
X
A
+
=
(
)
ω
φ
t
s
i
n
X
A
+
=
(
)
ω
φ
t
s
i
n
X
A
+
=
a
ω
φ
t
s
i
n
r
c
X
A
–
=
a
ω
φ
t
s
i
n
r
c
φ
X
A
–
=
a
ω
t
s
i
n
r
c
ω
1 -

21 слайд
U
U
X
β
=
2
l
o
g
0
δ
U
U
X
β
=
2
l
o
g
0
δ
U
U
X
β
=
0
δ
2
U
U
X
β
=
0
δ
2 -

22 слайд
f
0
f
1
=
–
c
υ
(
f
0
f
1
=
–
c
υ
)
f
0
f
1
=
–
c
υ
f
0
f
1
=
–
c
υ
f
0
f
1
=
–
c
υ
(
)
Краткое описание документа:
В каждой задаче по физике требуется из формулы выразить неизвестную, следующим шагом подставить численные значения и получить ответ, в некоторых случаях необходимо только выразить неизвестную величину. Способов выведения неизвестной из формулы много. Если посмотреть страницы Интернета, то мы увидим множество рекомендаций по этому поводу. Это говорит о том, что единого подхода к решению этой проблемы научное сообщество еще не выработало, а те способы, которые используются, как показывает опыт работы в школе – все они малоэффективны. До 90% учащихся выпускных классов не умеют правильно выразить неизвестное. Те же, кто умеют это делать – выполняют громоздкие преобразования. Очень странно, но физики, математики, химики имеют разные подходы, объясняя методы переноса параметров через знак равенства (предлагают правила треугольника, креста или пропорций др.) Можно сказать, что имеют разную культуру работы с формулами. Можно представить, что происходит с большинством учеников, которые встречается с разными трактовками решения данной проблемы, последовательно посещая уроки этих предметов. Эту ситуацию описывает типичный диалог в сети:
Научите выражать из формул величины. 10 класс, мне стыдно не знать, как из одной формулы делать другую.
Да не переживай – это проблема многих моих одноклассников, хоть я и в 9 кл. Учителя показывают это чаще всего методом треугольника, но мне кажется, что это неудобно, да и запутаться легко. Покажу наиболее простой способ, которым я пользуюсь…
Допустим, дана формула:
S=vt
Ну более простая….тебе из этой формулы нужно найти время. Ты берешь и в эту формулу подставляешь числа только разные, исходя из алгебры. Допустим:
S=vt
45=9*5
и тебе наверное хорошо видно, что чтобы найти время в алгебраическом выражении 5 нужно 45/9 т.е переходим к физике: t=s/v
У большинства учащихся формируется психологический блок. Часто учащиеся отмечают, что при чтении учебника трудности в первую очередь вызывают те фрагменты текста, в которых много формул, что «длинные выводы все равно не понять», но при этом возникает чувство неполноценности, неверия в свои силы.
Я, предлагаю следующее решение данной проблемы – большинство учащихся все – таки могут решать примеры и, следовательно, расставлять порядок действий. Используем это их умение.
1. В той части формулы, где содержится переменная, которую нужно выразить, надо расставь порядок действий, причем в одночленах, не содержащих искомую величину этого делать не будем.
2. Затем в обратной последовательности вычислений перенесите элементы формулы в другую часть формулы ( через знак равенства) с противоположным действием ( « минус» – «плюс», «разделить» – « умножить», « возведение в квадрат» – «извлечение корня квадратного»).
То есть найдем в выражении последнее действие и перенесем одночлен или многочлен, исполняющий это действие, через знак равенства первым, но уже с противоположным действием. Таким образом, последовательно, находя последнее действие в выражении, перенесите из одной части равенства в другую все известные величины. В заключение перепишем формулу так, чтобы неизвестная переменная стояла слева.
Получаем четкий алгоритм работы, точно знаем, сколько преобразований необходимо выполнить. Можем для тренировки использовать уже известные формулы, можем выдумывать свои. Для начала работы над усвоением данного алгоритма была создана презентация.
Опыт работы с учащимися показывает, что данный способ хорошо воспринимается ими. Реакция учителей на мое выступление на фестивале «Учитель профильной школы» также говорит о положительном зерне, заложенном в этой работе.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 991 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 02.01.2018
- 1341
- 26
- 30.12.2017
- 428
- 1
- 30.12.2017
- 593
- 2
Рейтинг:
5 из 5
- 29.12.2017
- 2526
- 1
- 27.12.2017
- 925
- 10
- 26.12.2017
- 4468
- 6
- 26.12.2017
- 900
- 0
- 25.12.2017
- 639
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Основы туризма и гостеприимства»
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс профессиональной переподготовки «Экскурсоведение: основы организации экскурсионной деятельности»
-
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «История и философия науки в условиях реализации ФГОС ВО»
-
Курс повышения квалификации «Основы построения коммуникаций в организации»
-
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
-
Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»
-
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
Правила вывода величины из формулы
Формула – это правило вычисления одной величины через другие, записанное при помощи их буквенных обозначений.
Иногда для решения задач необходимо вывести неизвестную величину из формулы. Для этого существуют несколько правил.
Формулы можно преобразовывать по правилам математики. Рассмотрим примеры. В левой колонке таблицы вы видите исходные формулы. В средней колонке каждая из формул преобразована так, что «выражена» величина, обозначенная «b». В последней колонке выражена величина «с»
Примеры вывода физической величины из формулы



