Как найти обратную функцию для данной

Как найти обратную функцию для данной


Загрузить PDF


Загрузить PDF

Одной из важнейших составляющих алгебры является понятие обратной функции. Обратная функции обозначается как f^-1(х) и графически представляется как отражение графика исходной функции относительно прямой у=х. В этой статье мы расскажем вам, как найти обратную функцию.

Шаги

  1. Изображение с названием Find the Inverse of a Function Step 1

    1

    Убедитесь, что данная функция биективна. Только биективные функции имеют обратные функции.

    • Функция биективна, если она проходит тест вертикальной и горизонтальной прямыми. Проведите вертикальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Потом проведите горизонтальную прямую через график функции и подсчитайте количество раз, которое прямая пересекает график функции. Если каждая прямая пересекает график функции только один раз, то функция биективна.
      • Если график не проходит тест вертикальной прямой, то он не задан функцией.
    • Для алгебраического определения биективности функции подставьте f(а) и f(b) в данную функцию и определите, выполняется ли равенство a=b. В качестве примера рассмотрим функцию f(x) = 3x+5.
      • f(a) = 3a + 5; f(b) = 3b + 5
      • 3a + 5 = 3b + 5
      • 3a = 3b
      • a = b
    • Таким образом, данная функция биективна.

  2. Изображение с названием Find the Inverse of a Function Step 2

    2

    В данной функции поменяйте местами «х» и «у». Помните, что f(х) — другое написание «у».

    • “f(x)” или “y” представляет собой функцию, а “х” — переменную. Чтобы найти обратную функцию, нужно поменять местами функцию и переменную.
    • Пример: рассмотрим функцию f(x) = (4x+3)/(2x+5), которая является биективной. Поменяв местами «х» и «у», получите x = (4y + 3)/(2y + 5).

  3. Изображение с названием Find the Inverse of a Function Step 3

    3

    Найдите «у». Решите новое уравнение и найдите «у».

    • Возможно, чтобы найти значение выражения и упростить его, вам понадобятся алгебраические приемы вроде умножения дробей или разложения на множители.
    • Решение нашего примера:
      • х = (4y + 3)/(2y + 5)
      • х(2y + 5) = 4y + 3 — избавьтесь от дроби. Для этого умножьте обе части уравнения на знаменатель дроби (2у + 5).
      • 2xy + 5x = 4y + 3 — раскройте скобки.
      • 2xy – 4y = 3 – 5x — перенесите все члены с переменной (в данном случае это «у») на одну сторону уравнения.
      • у (2x – 4) = 3 – 5x — вынесите «у» за скобку.
      • у = (3 – 5x)/(2x – 4) — разделите обе части уравнения на (2х-4), чтобы получить окончательный ответ.

  4. Изображение с названием Find the Inverse of a Function Step 3

    4

    Замените «у» на f^-1(х). Это есть обратная функция для исходной функции.

    • Окончательный ответ: f^-1(x) = (3 – 5x)/(2x – 4). Это обратная функция для f(х) = (4x + 3)/(2x + 5) .

    Реклама

Об этой статье

Эту страницу просматривали 212 791 раз.

Была ли эта статья полезной?

Источник

Понятие обратной функции и ее определение в алгебре

Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет называться непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.

Две этих функции, f и g, будут взаимно обратными.

Обратная функция – это что такое? Дадим определение взаимно обратимой функции (что такое обратимая функция – определение). 

Для чего вообще нам нужно понятие обратных функций?

Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений. Также понятие особенностей обратных функций помогают в решении операций по извлечению n-ой степени (она обратна возведению в степень).

На самом деле это не является чем-то сложным. Онлайн, как и в нашем материале, вы можете найти много примеров обратной функции, которые помогут в этом убедиться. 

Важно знать, что любая функция y = y (x) – это определенное правило, которое определяет соответствие между двумя значениями: x и y. К примеру, функция y = x² ставит соответственно каждому действительному числу его в квадрат. Можно сделать определенную таблицу, в которой будут располагаться значения этой функции для целых аргументов.

x -2 -1 0 1 2
y = x² 4 1 0 1 4

Как найти функцию обратную данной

Как найти обратную функцию?

Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z 

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным. Вот несколько примеров обратной функции. 

Пример 1

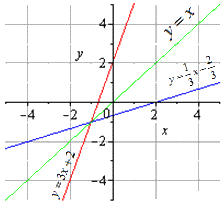
Условие: какая функция будет обратной для y=3x+2?

Решение

Область определений и область значений линейной функции, данной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x, то есть выразив  x через y.

Мы получим x=13y-23. Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x – функцией. Переставим их, чтобы получить более привычную форму записи:

y=13x-23 

Ответ: функция y=13x-23 будет обратной для y=3x+2.

Обе взаимообратные функции можно отобразить на графике следующим образом:

Как найти функцию обратную данной

На графике мы находим симметричность обоих графиков относительно y=x (они отображаются симметрично). Эта прямая является биссектрисой первого и третьего квадрантов. Что это позволило нам доказать? Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.

Возьмем онлайн-пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Пример 2

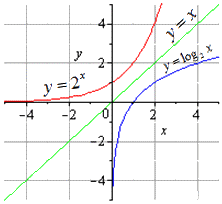
Условие: определите, какая функция будет обратной для y=2x.

Решение

Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0; +∞. Теперь нам нужно выразить x через y, то есть решить указанное уравнение через x. Мы получаем x=log2y. Переставим переменные и получим y=log2x.

В итоге этого примера у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.

Ответ: y=log2x.

Графически обе функции будут выглядеть или иметь следующее отображение:

Как найти функцию обратную данной

Также взаимно обратные функции можно рассматривать на примере теорем.

Предположим, мы имеем определенную, с возрастающей или убывающей монотонностью, а также непрерывную в определенном промежутке x функцию y = f(x). Значит, в промежутке значений y этой функции существует и обратная функция. Она также монотонно убывает или возрастает. Также ее можно определить как непрерывную (в промежутке y).

Основные свойства взаимно обратных функций

В этом пункте мы перечислим основные свойства обратимых функций y=f(x) и x=g(y). Какими же свойствами обладают взаимообратные функции?

Определение 1
  1. Первое (исходное) свойство мы уже вывели ранее: y=f(g(y)) и x=g(f(x)).
  2. Второе свойство вытекает из первоначального (первого) и означает, что область определения y=f(x) будет совпадать с областью значений обратной функции x=g(y), и наоборот.
  3. Графики обратных функций будут симметричными (находиться в симметрии) относительно y=x.
  4. Если y=f(x) является возрастающей, то и x=g(y) будет возрастать, а если y=f(x) убывает, то убывает и x=g(y).

Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать, так как это не одно и тоже даже исходя из названий. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифмов не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте характеристику, что это верно только при положительном y.

А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.

Не забывайте про этот момент, особенно если приходится работать с  тригонометрическими и обратными тригонометрическими функциями.  Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись

arcsinsin7π3=arcsinsin2π+π3==по формуле привидения=arcsinsinπ3=π3

А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!

Графики взаимно обратных функций

  • Основные взаимно обратные функции: степенные

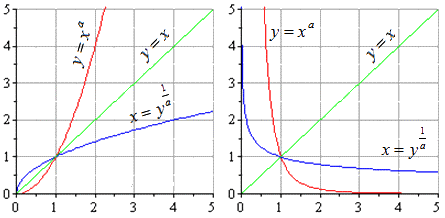
Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Замена букв будет давать соответственно y=xa и x=y1a.

Сделаем график. На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

Графики взаимно обратных функций

  • Основные взаимно обратные функции: показательные и логарифмические

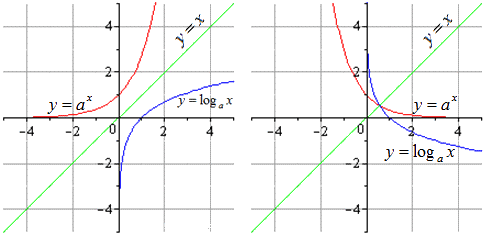
Возьмем a, которое будет положительным числом, не равным 1.

Узнаем, какими будут графики для функций с a>1 и a<1. Они будут выглядеть так:

Графики взаимно обратных функций

  • Основные взаимно обратные функции: тригонометрические и обратные тригонометрические

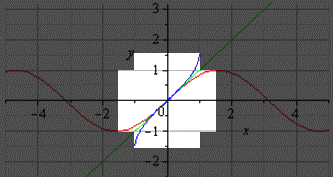
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

Графики взаимно обратных функций

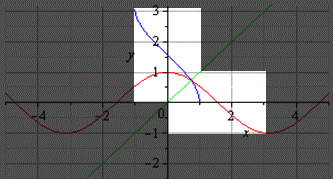
Если построить график главной ветви косинуса и арккосинуса, то он будет выглядеть так:

Графики взаимно обратных функций

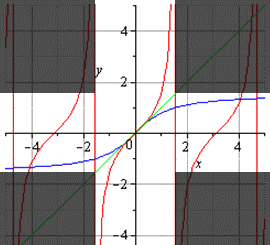
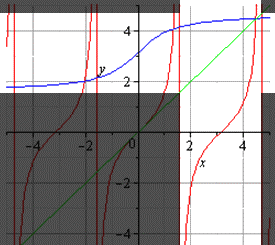
Если строить график главной ветви арктангенса и тангенса, то он будет таким:

Графики взаимно обратных функций

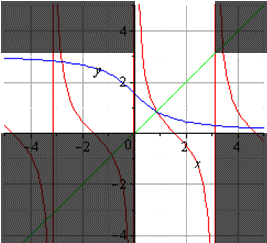
График главной ветви арккотангенса и котангенса будет таким:

Графики взаимно обратных функций

В случае построения обратных ветвей, отличные от главных, то обратную тригонометрическую функцию мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.

Графики взаимно обратных функций

Это все свойства обратных функций, о которых мы хотели бы вам рассказать.

Источник

Нахождение формулы для функции, обратной данной

Пользуясь формулой (y = f(x)), следует выразить (x) через (y), а в полученной формуле (x = g(y)) заменить (x) на (y), а (y) на (x).

Пример:

найти функцию, обратную для функции 

y=x2,x∈0;+∞)

.

Функция

y=x2

 возрастает на промежутке

0;+∞)

. Делаем вывод, что обратная функция существует. Если значения (x) принадлежат промежутку

0;+∞)

, то 

x=y

. Заменим (x) на (y), а (y) на (x), получим обратную функцию

y=x,x∈0;+∞)

. Обратная функция определена на промежутке

0;+∞)

 и её график симметричен графику функции

y=x2,x∈0;+∞)

 относительно прямой (y=x).

obratnaja.png

Источник
  1. Функция, обратная данной
  2. Алгоритм вывода формулы функции, обратной данной
  3. Свойства взаимно обратных функций
  4. Примеры

Функция, обратная данной

По определению (см. §34 справочника для 7 класса)

Функция – это соответствие, при котором каждому значению независимой переменной соответствует единственное значение зависимой переменной.

Пусть некоторое соответствие задано таблицей:

x

-4

-3

-2

-1

0

1

2

3

4

y

-2

-1,5

-1

-0,5

0

0,5

1

1,5

2

Множество значений X = {-4;-3;…;4} отображается в множество значений Y = {-2;-1,5;…;2}: $X xrightarrow{f} Y$. При этом каждому значению x соответствует единственное значение y, т.е., данное соответствие f является функцией.

С другой стороны, мы можем рассмотреть обратное отображение $Y xrightarrow{g} X$, заданное той же таблицей. При этом каждому значению y соответствует единственное значение x, т.е., обратное соответствие $g = f^{-1}$ также является функцией.

Функцию $f: X xrightarrow{f} Y$ с областью определения X и областью значений Y называют обратимой, если обратное ей соответствие $g: Y xrightarrow{g} g X$ также является фунцией.

Если функция f обратима, то обратное ей соответствие $g = f^{-1}$ называют обратной функцией к f.

Например: аналитическое выражение для функции $X xrightarrow{f} Y$, заданной таблицей $y = f(x) = frac{x}{2}$. Обратное соответствие $Y xrightarrow{g} X$ также является функцией x = g(y) = 2y.

Функция g – обратная функция к f.

В общем случае формулы функций записывают в виде y(x). При такой записи, функции $y = frac{x}{2}$ и y=2x являются взаимно обратными.

Алгоритм вывода формулы функции, обратной данной

На входе: множества X и Y, для которых оба соответствия $X xrightarrow{f} Y$ и $Y xrightarrow{g} X$ являются функциями.

Шаг 1. В формуле для исходной функции заменить обозначения аргумента и значения: $x rightarrow y$, $y rightarrow x$.

Шаг 2. Из полученной формулы выразить y(x). Искомое выражение для обратной функции найдено.

Шаг 3. Учесть ограничения для области определения и области значений исходной и/или обратной функций.

Например:

1) Пусть исходная функция $y = frac{x}{2}$

Шаг 1. Меняем аргумент и значение: $x = frac{y}{2}$

Шаг 2. Находим y из полученной формулы: y = 2x – искомая обратная функция

Шаг 3. Ограничений на x и y нет

2) Пусть исходная функция y = -2x+3

Шаг 1. Меняем аргумент и значение: x = -2y+3

Шаг 2. Находим y из полученной формулы: $y = frac{-x+3}{2}$ – искомая обратная функция

Шаг 3. Ограничений на x и y нет

3) Пусть исходная функция $y = sqrt{x+1}$

Шаг 1. Меняем аргумент и значение: $x = sqrt{y+1}$

Шаг 2. Находим y из полученной формулы: $y = x^2-1$ – искомая обратная функция

Шаг 3. На исходную функцию накладываются ограничения

на $x:x+1 ge 0 Rightarrow x ge -1$, на $y:y ge 0$

Тогда исходная функция определяется на множествах $y ge -1$, $x ge 0$

4) Пусть исходная функция $y = 2x^2+1$

Шаг 1. Меняем аргумент и значение: $x = 2y^2+1$

Шаг 2. Находим y из полученной формулы: $y = sqrt{frac{x-1}{2}}$ – искомая обратная функция

Шаг 3. На обратную функцию накладываются ограничения

на $x:x-1 ge 0 Rightarrow x ge 1$, на $y:y ge 0$

Тогда исходная функция определяется на множествах $y ge 1$, $x ge 0$

Исходная функция — парабола получает ограничения из-за обратной функции; только в этом случаи функции будут взаимно обратными.

Свойства взаимно обратных функций

Пусть f и g – взаимно обратные функции. Тогда:

1. Область определения функции f является областью значений функции g, а область значений функции f является областью определения функции g.

2. Функции f и g либо одновременно возрастающие, либо одновременно убывающие.

3. Если f – нечётная, то и g – нечётная.

4. Графики f и g симметричны относительно биссектрисы 1-й четверти y = x.

5. Справедливы тождества f(g(x) ) = x и g(f(x) ) = x.

Например:

Графики пар взаимно обратных функций, найденных выше:

Примеры

Пример 1. Задайте формулой функцию, обратную данной.

а) y = 5x-4

Меняем аргумент и значение: x = 5y-4

Получаем: $y = frac{x+4}{5}$ – искомая обратная функция

б) y = -3x+2

Меняем аргумент и значение: x = -3y+2

Получаем: $y = frac{-x+2}{3}$ – искомая обратная функция

в) y = 4x+1, где $-1 le x le 5$

Меняем аргумент и значение: x = 4y+1

Получаем: $y = frac{x-1}{4}$

Требуем, чтобы: $-1 le y le 5 Rightarrow -1 le frac{x-1}{4} le 5 Rightarrow -4 le x-1 le 20 Rightarrow -3 le x le 21$

Итак, искомая обратная функция: $y = frac{x-1}{4}$, где -3 $le x le 21$

г) $y=- frac{1}{2} x+7$, где $2 le x le 9$

Меняем аргумент и значение: $x=-frac{1}{2} y+7$

Получаем: y = 2(-x+7) = -2x+14

Требуем, чтобы: $2 le y le 9 Rightarrow 2 le -2x+14 le 9 Rightarrow -12 le -2x le -5 Rightarrow$

$6 ge x ge 2,5 Rightarrow 2,5 le x le 6$

$y = -2x+14,где 2,5 le x le 6$ – искомая обратная функция

Пример 2. Найдите функцию, обратную данной.

Постройте график исходной и обратной функции в одной системе координат.

а) $y=x^2,x le 0$

Обратная функция

$x = y^2 Rightarrow y = pm sqrt{x}$

При этом $y le 0$

Поэтому выбираем

$y = – sqrt{x}$ – искомая обратная функция

 Пример 2. а)

б) y = x-3, $-1 le x le 4$

Обратная функция

$x = y-3 Rightarrow y = x+3$

При этом $-1 le y le 4 Rightarrow -1 le x+3 le 4$

$Rightarrow -4 le x le 1$

y = x+3, $-4 le x le 1$ – искомая обратная

функция

 Пример 2. б)

в) $y = frac{1}{x+1} $

Обратная функция

$x = frac{1}{y+1} Rightarrow y = frac{1}{x} -1$

 Пример 2. в)

г) $y = 1+ sqrt{x-3}$

Область определения: $x ge 3$

Область значений: $y ge 1$

Обратная функция:

$x = 1+ sqrt{y-3} Rightarrow y = (x-1)^2+3$

Область определения: $x ge 1$

Область значений: $y ge 3$

 Пример 2. г)
Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 июля 2022 года; проверки требуют 13 правок.

Функция f и обратная ей функция f^{-1}. Если f(a)=3, то f^{-1}(3)=a

Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. Например, если функция от x даёт y, то обратная ей функция от y даёт x. Обратная функция функции f обычно обозначается f^{-1}, иногда также используется обозначение f^{mathrm{inv}}.

Функция, имеющая обратную, называется обратимой.

Определение[править | править код]

Функция g:Yto X называется обратной к функции f:Xto Y, если выполнены следующие тождества:

Связанные определения[править | править код]

Существование[править | править код]

Чтобы найти обратную функцию, нужно решить уравнение y = f(x) относительно x. Если оно имеет более чем один корень, то функции, обратной к f не существует. Таким образом, функция f(x) обратима на интервале (a;b) тогда и только тогда, когда на этом интервале она взаимно-однозначна.

Для непрерывной функции F(y) выразить y из уравнения x - F(y) = 0 возможно в том и только том случае, когда функция F(y) строго монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её строгой монотонности. Например, sqrt{x} является обратной функцией к x^{2} на [0, +infty), хотя на промежутке (-infty, 0] обратная функция другая: -sqrt{x}.

Для существования обратной функции не являются необходимыми ни непрерывность, ни монотонность исходной функции. Пример: функция {displaystyle y=x+D(x),} где D(x) — функция Дирихле, разрывна и не монотонна, однако обратная для неё существует[2]: {displaystyle x=y-D(y).}

Примеры[править | править код]

Свойства[править | править код]

Графики функции и обратной ей

Графики функции и обратной ей

y = F(x) Leftrightarrow x = F^{-1}(y)

или

Fleft(F^{-1}(y)right) = y,; forall y in Y,
F^{-1}(F(x)) = x,; forall x in X,

или короче

F circ F^{-1} = mathrm{id}_Y,
F^{-1} circ F = mathrm{id}_X,

где circ означает композицию функций, а mathrm{id}_X, mathrm{id}_Y — тождественные отображения на X и Y соответственно.

left(F^{-1}right)^{-1} = F.

Теорема. Композиция любых двух обратимых функций является обратимой функцией, то есть {displaystyle {left(fcirc gright)}^{-1}=g^{-1}circ f^{-1}}.

Доказательство
Поскольку {displaystyle alpha circ {alpha }^{-1}={alpha }^{-1}circ alpha =e} и {displaystyle alpha circ e=ecirc alpha =alpha } для любой обратимой функции alpha , где e — тождественное преобразование, то можно записать следующие равенства.

Имеем: {displaystyle e=eLongleftrightarrow e=fcirc f^{-1}Longleftrightarrow e=fcirc gcirc g^{-1}circ f^{-1}Longleftrightarrow e=left(fcirc gright)circ left(g^{-1}circ f^{-1}right).}

Подействуем слева функцией {displaystyle {left(fcirc gright)}^{-1}} и получим: {displaystyle {left(fcirc gright)}^{-1}circ mid e=left(fcirc gright)circ left(g^{-1}circ f^{-1}right)Longleftrightarrow {left(fcirc gright)}^{-1}circ e={left(fcirc gright)}^{-1}circ left(fcirc gright)circ left(g^{-1}circ f^{-1}right)Longleftrightarrow {left(fcirc gright)}^{-1}=ecirc left(g^{-1}circ f^{-1}right)Longleftrightarrow {left(fcirc gright)}^{-1}=g^{-1}circ f^{-1}.}
Теорема доказана.

Это утверждение легко запомнить так: «Пиджак надевают после рубашки, а снимают раньше».

Разложение в степенной ряд[править | править код]

Обратная функция аналитической в некоторой окрестности точки x_{0} функции может быть представлена в виде степенного ряда:

{displaystyle f^{-1}(y)=sum _{k=0}^{infty }A_{k}(x_{0}){frac {(y-f(x_{0}))^{k}}{k!}},}

где функции A_k задаются рекурсивной формулой:

{displaystyle A_{n}(x)={begin{cases}x;,;n=0\{frac {A_{n-1}'(x)}{f'(x)}};,;n>0end{cases}}}

См. также[править | править код]

  • Теорема Лагранжа об обращении рядов
  • Обратные тригонометрические функции
  • Обратимая функция

Примечания[править | править код]

  1. ↑ Куликов Л.Я. “Алгебра и теория чисел: Учебное пособие для педагогических институтов”
  2. ↑ Шибинский В. М. Примеры и контрпримеры в курсе математического анализа. Учебное пособие. — М.: Высшая школа, 2007. — С. 29—30. — 543 с. — ISBN 978-5-06-005774-4.
Источник

Добавить комментарий