Как найти обратную функцию для функции онлайн

---

Как пользоваться калькулятором обратной функции

bold{mathrm{Basic}}	bold{alphabetagamma}	bold{mathrm{ABGamma}}	bold{sincos}	bold{gedivrightarrow}	bold{overline{x}spacemathbb{C}forall}	bold{sumspaceintspaceproduct}	bold{begin{pmatrix}square&square\square&squareend{pmatrix}}	bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx} ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square} left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec alpha beta gamma delta zeta eta theta iota kappa lambda mu nu xi pi rho sigma tau upsilon phi chi psi omega A B Gamma Delta E Z H Theta K Lambda M N Xi Pi P Sigma T Upsilon Phi X Psi Omega sin cos tan cot sec csc sinh cosh tanh coth sech arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge (square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset vee wedge neg oplus cap cup square^{c} subset subsete superset supersete int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x} (2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5) (1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1) mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить} arcsin sin sqrt{square} 7 8 9 div arccos cos ln 4 5 6 times arctan tan log 1 2 3 – pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

• обратная:y=frac{x^2+x+1}{x}
  

• обратная:f(x)=x^3
  

• обратная:f(x)=ln (x-5)
  

• обратная:f(x)=frac{1}{x^2}
  

• обратная:y=frac{x}{x^2-6x+8}
  

• обратная:f(x)=sqrt{x+3}
  

• обратная:f(x)=cos(2x+5)
  

• обратная:f(x)=sin(3x)
  
• Показать больше

Описание

Шаг за шагом найти обратную функцию

function-inverse-calculator

inverse f(x…

ru

Блог-сообщения, имеющие отношение к Symbolab

Functions

A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…

Read More

Введите Задачу

Сохранить в блокнот!

Войти

Главная страница | Навигация | Помогите нам | Предложитe лучший вариант перевода

Калькулятор Обратных Функций

Введите функцию для вычисления её обратной функции:

Переменные:

 

Примеры вычисления обратных функций

Математическиe настройки Калькулятор производных Вычисление интегралов Определённые интегралы Калькулятор пределов Калькулятор рядов Решение уравнений Упрощениe выражений Разложение на множители Калькулятор выражений Обратная функция Ряд Тейлорa Калькулятор матриц Матричная арифметика Построение графиков Решение 2D-фигyp Решение 3D-фигур Простые числа Факторизатор чисел Числа Фибоначчи Числа Бернулли Числа Эйлера Комплексные числа Вычисление факториалов Гамма-функция Комбинаторный калькулятор Калькулятор дробей Статистический калькулятор Редактор уравнений LaTeX

Свойства чисел 0 / 12 Примеры: 3628800, 9876543211, 12586269025

Химические инструменты

Математические настройки для вашего сайта Выберите язык:
Deutsch
English
Español
Français
Italiano
Nederlands
Polski
Português
Русский
中文
日本語
한국어 Империя чисел – мощные математические инструменты для каждого | Связь с веб-мастером
Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.

© 2023
numberempire.com
Все права защищены
   

Step 1:

Enter the function below for which you want to find the inverse.

The inverse function calculator finds the inverse of the given function.

If f(x) is a given function, then the inverse of the function is calculated by interchanging the variables and expressing x as a function of y i.e. x=f(y).

Step 2:

Click the blue arrow to submit. Choose “Find the Inverse” from the topic selector and click to see the result in our Precalculus Calculator!

Examples

Find the Inverse
Find the Inverse
Find the Inverse
Find the Inverse

Popular Problems

Find the Inverse y=x+5
Find the Inverse y=ex+2
Find the Inverse y=x2-1
Find the Inverse y=2×2-5
Find the Inverse y=3x+2

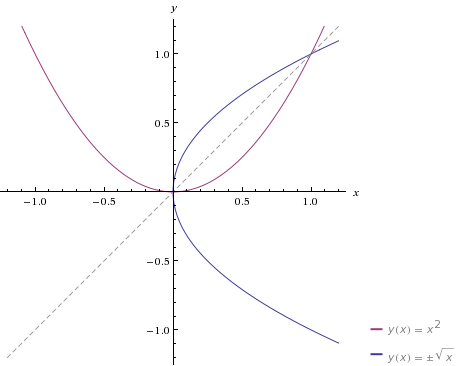
Для начала немного теории. Если есть функция (y=f(x)), то (y) зависит от аргумента (x). Но, получается что и наоборот, (x) зависит от (y), если из уравнения функции выразить (x) через (y). Если в этой зависимости переобозначить (x) и (y), то и получится обратная функция к данной. При этом графики обратных функций будут относительно биссектрисы первой и третьей четверти. На рисунке слева (кликнуть для увеличения), вы можете видеть графики двух взаимно обратных функций (y=x^2) и (y=pmsqrt{x}). Алгоритм нахождения обратной функции прост. Шаг первый: из данной функции выразить (x) через (y). Шаг второй: в полученном выражении поменять (x) на (y) и (y) на (x). Но, не всегда просто сделать эти преобразования. Поэтому, специально для наших посетителей предлагаем онлайн-решебник, который легко справится с задачей нахождения обратной функции и построит графики данной и обратной функции. Для этого Вам понадобится воспользоваться командой inverse и набрать в строке решателя Вашу функцию. Приведем несколько примеров команд для нахождения обратных функций.

inverse y=x^2

Или вот пример посложнее:

inverse y = x^3+x^2+3x+5

Например, для тригонометрических фукнций:

inverse y = sin(2x)+cos(2x)

Чтобы попробовать как это работает – скопируйте код примера и вставьте в наш решатель, а затем нажмите кнопку решить. Если обратная функция существует, то решатель ее найдет. Если такой функции нет – выдаст сообщение. Помните, не все функции имеют обратные. Пишите решенные вами примеры в комментариях.

---

Похожие публикации

2015-11-21 • Просмотров [ 69992 ]

---