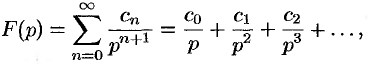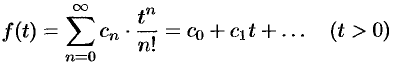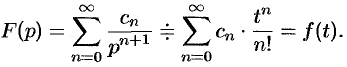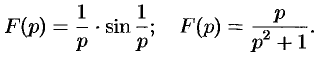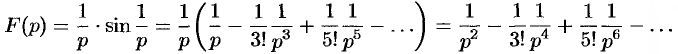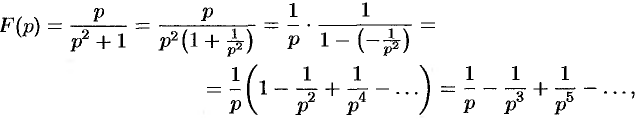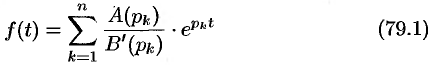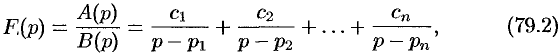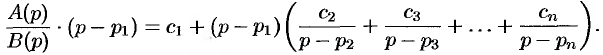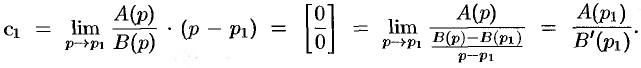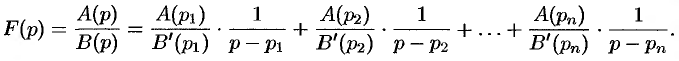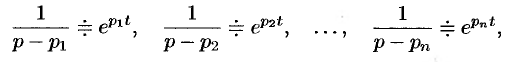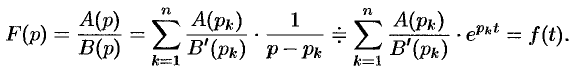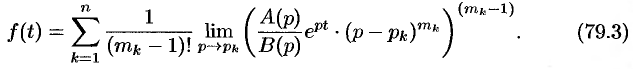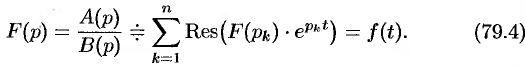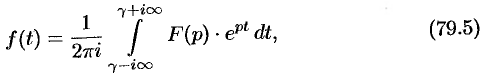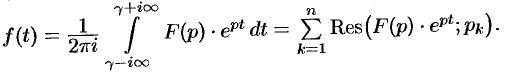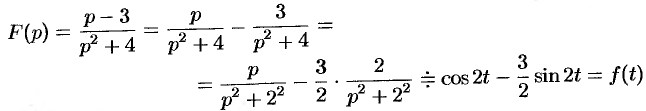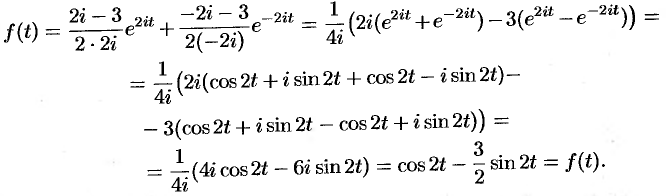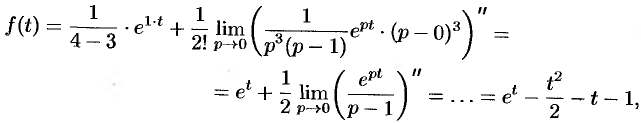Как найти обратную функцию лапласа

Символы со сходным начертанием: L · Ⅼ · Լ · լ · ւ

Преобразова́ние Лапла́са (ℒ) — интегральное преобразование, связывающее функцию F(s) комплексного переменного (изображение) с функцией f(x) вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.

Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Определение[править | править код]

Прямое преобразование Лапласа[править | править код]

Преобразованием Лапласа функции вещественной переменной f(t) называется функция F(s) комплексной переменной ^[1], такая что:

$F(s)={mathcal {L}}left{f(t)right}=int limits _{0}^{infty }e^{{-st}}f(t),dt.$

Правая часть этого выражения называется интегралом Лапласа.

Функцию f(t) называют оригиналом в преобразовании Лапласа, а функцию F(s) называют изображением функции f(t) .

В литературе связь между оригиналом и изображением часто обозначают так: и , причём изображение принято записывать с заглавной буквы.

Обратное преобразование Лапласа[править | править код]

Обратным преобразованием Лапласа функции комплексного переменного F(s) называется функция f(t) вещественной переменной, такая что:

${displaystyle f(t)={mathcal {L}}^{-1}{F(s)}={frac {1}{2pi i}}lim _{omega rightarrow infty }int limits _{sigma _{1}-iomega }^{sigma _{1}+iomega }e^{st}F(s),ds,}$

где $sigma _{1}$ — некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича^[2].

Двустороннее преобразование Лапласа[править | править код]

Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции f(x) участвуют значения x<0 .

Двустороннее преобразование Лапласа определяется следующим образом:

$F(s)={mathcal {L}}{f(x)}=int limits _{{-infty }}^{{+infty }}e^{{-sx}}f(x),dx.$

Дискретное преобразование Лапласа[править | править код]

Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.

Различают -преобразование и -преобразование.

-преобразование

Пусть $x_{d}(t)=sum limits _{{n=0}}^{infty }x(nT)cdot delta (t-nT)$ — решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени , где — целое число, а — период дискретизации.

Тогда, применяя преобразование Лапласа, получим:

${mathcal {D}}{x_{d}(t)}=sum limits _{{n=0}}^{infty }x(nT)cdot e^{{-snT}}.$

-преобразование

Если применить следующую замену переменных:

$z=e^{{sT}},$

получим -преобразование:

${mathcal {Z}}{x_{d}(t)}=sum limits _{{n=0}}^{infty }x(nT)cdot z^{{-n}}.$

Свойства и теоремы[править | править код]

Абсолютная сходимость

Если интеграл Лапласа абсолютно сходится при $sigma =sigma _{0}$ , то есть существует предел

$lim _{{bto infty }}int limits _{0}^{b}|f(x)|e^{{-sigma _{0}x}},dx=int limits _{0}^{infty }|f(x)|e^{{-sigma _{0}x}},dx,$

то он сходится абсолютно и равномерно для $sigma geqslant sigma _{0}$ и F(s) — аналитическая функция при $sigma geqslant sigma _{0}$ ( — вещественная часть комплексной переменной ). Точная нижняя грань $sigma _{a}$ множества чисел sigma , при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции f(x) .

Условия существования прямого преобразования Лапласа

Преобразование Лапласа существует в смысле абсолютной сходимости в следующих случаях:

: преобразование Лапласа существует, если существует интеграл $int limits _{0}^{infty }|f(x)|,dx$ ;
$sigma >sigma _{a}$ : преобразование Лапласа существует, если интеграл $int limits _{0}^{{x_{1}}}|f(x)|,dx$ существует для каждого конечного $x_{1}>0$ и $|f(x)|leqslant Ke^{{sigma _{a}x}}$ для $x>x_{2}geqslant 0$ ;
или $sigma >sigma _{a}$ (какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции (производная от ) для $sigma >sigma _{a}$ .

Примечание: это достаточные условия существования.

Условия существования обратного преобразования Лапласа

Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:

Если изображение — аналитическая функция для $sigma geqslant sigma _{a}$ и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём ${mathcal {L}}^{{-1}}{F(s)}=0$ для .
Пусть $F(s)=varphi [F_{1}(s),;F_{2}(s),;ldots ,;F_{n}(s)]$ , так что $varphi (z_{1},;z_{2},;ldots ,;z_{n})$ аналитична относительно каждого $z_{k}$ и равна нулю для $z_{1}=z_{2}=ldots =z_{n}=0$ , и $F_{k}(s)={mathcal {L}}{f_{k}(x)};;(sigma >sigma _{{ak}}colon k=1,;2,;ldots ,;n)$ , тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.

Примечание: это достаточные условия существования.

Теорема о свёртке

Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов:

{mathcal {L}}{f(x)*g(x)}={mathcal {L}}{f(x)}cdot {mathcal {L}}{g(x)}.

Доказательство

Для свёртки

${displaystyle (f*g)(x)=int _{0}^{infty }dy,f(x-y)g(y)}$

Преобразование Лапласа:

${displaystyle {mathcal {L}}left{(f*g)(x)right}=int _{0}^{infty }dx,e^{-sx}int _{0}^{infty }dy,f(x-y)g(y)}$

Для новой переменной

${displaystyle {mathcal {L}}left{(f*g)(x)right}=int _{0}^{infty }dt,e^{-s(t+y)}int _{0}^{infty }dy,f(t)g(y)=int _{0}^{infty }dt,e^{-st}f(t)int _{0}^{infty }dy,e^{-sy}g(y)={mathcal {L}}left{f(x)right}cdot {mathcal {L}}left{g(x)right}}$

■

Умножение изображений

$f(x)g(0)+int limits _{0}^{x}f(x-tau )g'(tau ),dtau =sF(s)G(s).$

Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.

Дифференцирование и интегрирование оригинала

Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа:

${mathcal {L}}{f'(x)}=scdot F(s)-f(0^{+}).$

В более общем случае (производная -го порядка):

${displaystyle {mathcal {L}}{f^{(n)}(x)}=s^{n}cdot F(s)-s^{n-1}f(0^{+})-s^{n-2}f^{(1)}(0^{+})-ldots -sf^{(n-2)}(0^{+})-f^{(n-1)}(0^{+}).}$

Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала, делённое на свой аргумент:

${mathcal {L}}left{int limits _{0}^{x}f(t),dtright}={frac {F(s)}{s}}.$

Дифференцирование и интегрирование изображения

Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком:

${mathcal {L}}^{{-1}}{F'(s)}=-xf(x).$

Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, делённый на свой аргумент:

${mathcal {L}}^{{-1}}left{int limits _{s}^{{+infty }}F(s),dsright}={frac {f(x)}{x}}.$

Запаздывание оригиналов и изображений. Предельные теоремы

Запаздывание изображения:

${mathcal {L}}{e^{{ax}}f(x)}=F(s-a);$

${mathcal {L}}^{{-1}}{F(s-a)}=e^{{ax}}f(x).$

Запаздывание оригинала:

${mathcal {L}}{f(t-a)H(t-a)}=e^{{-as}}F(s);$

${mathcal {L}}^{{-1}}{e^{{-as}}F(s)}=f(x-a)H(x-a).$

где H(x) — функция Хевисайда.

Теоремы о начальном и конечном значении (предельные теоремы):

$f(infty )=lim _{{sto 0}}sF(s)$

, если все полюсы функции

находятся в левой полуплоскости.

Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, например, используется для анализа устойчивости траектории динамической системы.

Другие свойства

Линейность:

Умножение на число:

${mathcal {L}}{f(ax)}={frac {1}{a}}Fleft({frac {s}{a}}right).$

Прямое и обратное преобразование Лапласа некоторых функций[править | править код]

Ниже представлена таблица преобразования Лапласа для некоторых функций.

№	Функция	Временная область $x(t)={mathcal {L}}^{{-1}}{X(s)}$	Частотная область
1	дельта-функция
1a	запаздывающая дельта-функция		$e^{{-tau s}}$
2	запаздывание -го порядка с частотным сдвигом	${frac {(t-tau )^{n}}{n!}}e^{{-alpha (t-tau )}}cdot H(t-tau )$	${frac {e^{{-tau s}}}{(s+alpha )^{{n+1}}}}$
2a	степенная -го порядка	${frac {t^{n}}{n!}}cdot H(t)$	${frac {1}{s^{{n+1}}}}$
2a.1	степенная -го порядка	${frac {t^{q}}{Gamma (q+1)}}cdot H(t)$	${frac {1}{s^{{q+1}}}}$
2a.2	функция Хевисайда		${frac {1}{s}}$
2b	функция Хевисайда с запаздыванием		${frac {e^{{-tau s}}}{s}}$
2c	«ступенька скорости»		${frac {1}{s^{2}}}$
2d	-го порядка с частотным сдвигом	${frac {t^{n}}{n!}}e^{{-alpha t}}cdot H(t)$	${frac {1}{(s+alpha )^{{n+1}}}}$
2d.1	экспоненциальное затухание	$e^{{-alpha t}}cdot H(t)$	${frac {1}{s+alpha }}$
3	экспоненциальное приближение	$(1-e^{{-alpha t}})cdot H(t)$	${frac {alpha }{s(s+alpha )}}$
4	синус		${frac {omega }{s^{2}+omega ^{2}}}$
5	косинус		${frac {s}{s^{2}+omega ^{2}}}$
6	гиперболический синус		${frac {alpha }{s^{2}-alpha ^{2}}}$
7	гиперболический косинус		${frac {s}{s^{2}-alpha ^{2}}}$
8	экспоненциально затухающий синус	$e^{{-alpha t}}sin(omega t)cdot H(t)$	${frac {omega }{(s+alpha )^{2}+omega ^{2}}}$
9	экспоненциально затухающий косинус	$e^{{-alpha t}}cos(omega t)cdot H(t)$	${frac {s+alpha }{(s+alpha )^{2}+omega ^{2}}}$
10	корень -го порядка		$s^{{-(n+1)/n}}cdot Gamma left(1+{frac {1}{n}}right)$
11	натуральный логарифм	$ln left({frac {t}{t_{0}}}right)cdot H(t)$	$-{frac {t_{0}}{s}}[ln(t_{0}s)+gamma ]$
12	функция Бесселя первого рода порядка	$J_{n}(omega t)cdot H(t)$	${frac {omega ^{n}left(s+{sqrt {s^{2}+omega ^{2}}}right)^{{-n}}}{{sqrt {s^{2}+omega ^{2}}}}}$
13	модифицированная функция Бесселя первого рода порядка	$I_{n}(omega t)cdot H(t)$	${frac {omega ^{n}left(s+{sqrt {s^{2}-omega ^{2}}}right)^{{-n}}}{{sqrt {s^{2}-omega ^{2}}}}}$
14	функция Бесселя второго рода нулевого порядка	$Y_{0}(alpha t)cdot H(t)$	$-{frac {2{mathrm {arsh}}(s/alpha )}{pi {sqrt {s^{2}+alpha ^{2}}}}}$
15	модифицированная функция Бесселя второго рода нулевого порядка	$K_{0}(alpha t)cdot H(t)$
16	функция ошибок		${frac {e^{{s^{2}/4}}{mathrm {erfc}}(s/2)}{s}}$
Примечания к таблице: — функция Хевисайда; — дельта-функция; — гамма-функция; — постоянная Эйлера — Маскерони; — вещественная переменная; — комплексная переменная; , , и — вещественные числа; — целое число. Причинная система — система, в которой импульсная передаточная функция равна нулю для любого момента времени .

Применения преобразования Лапласа[править | править код]

Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники:

Решение систем дифференциальных и интегральных уравнений — с помощью преобразования Лапласа легко переходить от сложных понятий математического анализа к простым алгебраическим соотношениям.^[3]
Расчёт передаточных функций динамических систем, таких, к примеру, как аналоговые фильтры.
Расчёт выходных сигналов динамических систем в теории управления и обработке сигналов — так как выходной сигнал линейной стационарной системы равен свёртке её импульсной характеристики с входным сигналом, преобразование Лапласа позволяет заменить эту операцию на простое умножение.
Расчёт электрических схем. Производится путём решения дифференциальных уравнений, описывающих схему операторным методом.
Решение нестационарных задач математической физики.

Процедура решения дифференциального уравнения с использованием преобразования Лапласа состоит в следующем:

По заданному входному воздействию с помощью таблиц соответствий находят изображение.
По д.у. составляют передаточную функцию.
Находят изображение величины пунктов 1 и 2.
Определяют оригинал.^[4]

Связь с другими преобразованиями[править | править код]

Фундаментальные связи[править | править код]

Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.

Преобразование Лапласа — Карсона[править | править код]

Преобразование Лапласа — Карсона (иногда называют просто преобразование Карсона, иногда, не совсем корректно, используют преобразование Карсона, называя его преобразованием Лапласа) получается из преобразования Лапласа путём домножения изображения на комплексную переменную:

${mathcal {L}}_{K}{f(x)}=sF(s).$

Преобразование Карсона широко используется в теории электрических цепей, так как при таком преобразовании размерности изображения и оригинала совпадают, поэтому коэффициенты передаточных функций имеют физический смысл.

Двустороннее преобразование Лапласа[править | править код]

Двустороннее преобразование Лапласа ${mathcal {L}}_{B}$ связано с односторонним с помощью следующей формулы:

${mathcal {L}}_{B}{f(x);;s}={mathcal {L}}{f(x);;s}+{mathcal {L}}{f(-x);;-s}.$

Преобразование Фурье[править | править код]

Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом :

$F(omega )={mathcal {F}}{f(x)}={mathcal {L}}{f(x)}{Big |}_{{s=iomega }}=F(s){Big |}_{{s=iomega }}=int limits _{{-infty }}^{{+infty }}e^{{-iomega x}}f(x),dx.$

Примечание: в этих выражениях опущен масштабирующий множитель ${frac {1}{{sqrt {2pi }}}}$ , который часто включается в определения преобразования Фурье.

Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.

Преобразование Меллина[править | править код]

Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина

$G(s)={mathcal {M}}left{g(theta )right}=int limits _{0}^{infty }theta ^{s}{frac {g(theta )}{theta }},dtheta$

положим $theta =e^{{-x}}$ , то получим двустороннее преобразование Лапласа.

Z-преобразование[править | править код]

-преобразование — это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных:

$zequiv e^{{sT}},$

где $T=1/f_{s}$ — период дискретизации, а $f_{s}$ — частота дискретизации сигнала.

Связь выражается с помощью следующего соотношения:

$X_{q}(s)=X(z){Big |}_{{z=e^{{sT}}}}.$

Преобразование Бореля[править | править код]

Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.

См. также[править | править код]

Первая теорема разложения
Вторая теорема разложения
Преобразование Фурье
D с чертой-преобразование
Дифференциальные уравнения

Примечания[править | править код]

↑ В отечественной литературе обозначается также через . См., например,
Диткин В. А., Кузнецов П. И. Справочник по операционному исчислению: Основы теории и таблицы формул. — М.: Государственное издательство технико-теоретической литературы, 1951. — 256 с.
↑ Жевержеев В. Ф., Кальницкий Л. А., Сапогов Н. А. Специальный курс высшей математики для втузов. — М., Высшая школа, 1970. — с. 231
↑ Ващенко-Захарченко М. Е. Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений. — Киев, 1862.
↑ Архитектура системы автоматического управления группой малых беспилотных летательных аппаратов // Информационные технологии и вычислительные системы. — 2018-03-20. — ISSN 2071-8632. — doi:10.14357/20718632180109.

Литература[править | править код]

Ван дер Поль Б., Бремер Х. . Операционное исчисление на основе двустороннего преобразования Лапласа. — М.: Издательство иностранной литературы, 1952. — 507 с.
Диткин В. А., Прудников А. П. . Интегральные преобразования и операционное исчисление. — М.: Главная редакция физико-математической литературы издательства «Наука», 1974. — 544 с.
Диткин В. А., Кузнецов П. И. . Справочник по операционному исчислению: Основы теории и таблицы формул. — М.: Государственное издательство технико-теоретической литературы, 1951. — 256 с.
Карслоу Х., Егер Д. . Операционные методы в прикладной математике. — М.: Издательство иностранной литературы, 1948. — 294 с.
Кожевников Н. И., Краснощёкова Т. И., Шишкин Н. Е. . Ряды и интегралы Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа. — М.: Наука, 1964. — 184 с.
Краснов М. Л., Макаренко Г. И. . Операционное исчисление. Устойчивость движения. — М.: Наука, 1964. — 103 с.
Микусинский Я. . Операторное исчисление. — М.: Издательство иностранной литературы, 1956. — 367 с.
Романовский П. И. . Ряды Фурье. Теория поля. Аналитические и специальные функции. Преобразования Лапласа. — М.: Наука, 1980. — 336 с.

Ссылки[править | править код]

Преобразование Лапласа и его некоторые свойства (dsplib.org) Архивная копия от 12 августа 2018 на Wayback Machine
Преобразование Лапласа на сайте exponenta.ru

Источник

Обратное преобразование Лапласа функции

вычисляется по формуле Меллина:

Причем

и
.

Данная операция является обратной по отношению к прямому
преобразованию Лапласа,
где функцию изображение

находят по заданной функции оригинала
.

Обратное преобразование Лапласа
записывается следующим образом:
.

Стоит отметить, что функцию

можно также найти исходя из первой теоремы разложения. Если функция

раскладывается в ряд Лорана в окрестности бесконечно удаленной точки, т.е.

тогда

В тоже время на практике, для нахождения функции оригинала

по заданной функции изображения
,
пользуются различными приёмами вроде
разложения дроби в сумму дробей
и применением правил операционного исчисления.

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha вычисляет способе найти обратное преобразование Лапласа практически для любой заданной функции.

Источник

From Wikipedia, the free encyclopedia

In mathematics, the inverse Laplace transform of a function F(s) is the piecewise-continuous and exponentially-restricted^{[clarification needed]} real function f(t) which has the property:

{mathcal {L}}{f}(s)={mathcal {L}}{f(t)}(s)=F(s),

where denotes the Laplace transform.

It can be proven that, if a function F(s) has the inverse Laplace transform f(t), then f(t) is uniquely determined (considering functions which differ from each other only on a point set having Lebesgue measure zero as the same). This result was first proven by Mathias Lerch in 1903 and is known as Lerch’s theorem.^[1]^[2]

The Laplace transform and the inverse Laplace transform together have a number of properties that make them useful for analysing linear dynamical systems.

Mellin’s inverse formula[edit]

An integral formula for the inverse Laplace transform, called the Mellin’s inverse formula, the Bromwich integral, or the Fourier–Mellin integral, is given by the line integral:

${displaystyle f(t)={mathcal {L}}^{-1}{F(s)}(t)={frac {1}{2pi i}}lim _{Tto infty }int _{gamma -iT}^{gamma +iT}e^{st}F(s),ds}$

where the integration is done along the vertical line Re(s) = γ in the complex plane such that γ is greater than the real part of all singularities of F(s) and F(s) is bounded on the line, for example if the contour path is in the region of convergence. If all singularities are in the left half-plane, or F(s) is an entire function , then γ can be set to zero and the above inverse integral formula becomes identical to the inverse Fourier transform.

In practice, computing the complex integral can be done by using the Cauchy residue theorem.

Post’s inversion formula[edit]

Post’s inversion formula for Laplace transforms, named after Emil Post,^[3] is a simple-looking but usually impractical formula for evaluating an inverse Laplace transform.

The statement of the formula is as follows: Let f(t) be a continuous function on the interval [0, ∞) of exponential order, i.e.

$sup_{t>0} frac{f(t)}{e^{bt}} < infty$

for some real number b. Then for all s > b, the Laplace transform for f(t) exists and is infinitely differentiable with respect to s. Furthermore, if F(s) is the Laplace transform of f(t), then the inverse Laplace transform of F(s) is given by

${displaystyle f(t)={mathcal {L}}^{-1}{F}(t)=lim _{kto infty }{frac {(-1)^{k}}{k!}}left({frac {k}{t}}right)^{k+1}F^{(k)}left({frac {k}{t}}right)}$

for t > 0, where F^(k) is the k-th derivative of F with respect to s.

As can be seen from the formula, the need to evaluate derivatives of arbitrarily high orders renders this formula impractical for most purposes.

With the advent of powerful personal computers, the main efforts to use this formula have come from dealing with approximations or asymptotic analysis of the Inverse Laplace transform, using the Grunwald–Letnikov differintegral to evaluate the derivatives.

Post’s inversion has attracted interest due to the improvement in computational science and the fact that it is not necessary to know where the poles of F(s) lie, which make it possible to calculate the asymptotic behaviour for big x using inverse Mellin transforms for several arithmetical functions related to the Riemann hypothesis.

Software tools[edit]

InverseLaplaceTransform performs symbolic inverse transforms in Mathematica
Numerical Inversion of Laplace Transform with Multiple Precision Using the Complex Domain in Mathematica gives numerical solutions^[4]
ilaplace performs symbolic inverse transforms in MATLAB
Numerical Inversion of Laplace Transforms in Matlab
Numerical Inversion of Laplace Transforms based on concentrated matrix-exponential functions in Matlab

References[edit]

^ Cohen, A. M. (2007). “Inversion Formulae and Practical Results”. Numerical Methods for Laplace Transform Inversion. Numerical Methods and Algorithms. Vol. 5. pp. 23–44. doi:10.1007/978-0-387-68855-8_2. ISBN 978-0-387-28261-9.
^ Lerch, M. (1903). “Sur un point de la théorie des fonctions génératrices d’Abel”. Acta Mathematica. 27: 339–351. doi:10.1007/BF02421315.
^ Post, Emil L. (1930). “Generalized differentiation”. Transactions of the American Mathematical Society. 32 (4): 723–781. doi:10.1090/S0002-9947-1930-1501560-X. ISSN 0002-9947.
^ Abate, J.; Valkó, P. P. (2004). “Multi-precision Laplace transform inversion”. International Journal for Numerical Methods in Engineering. 60 (5): 979. Bibcode:2004IJNME..60..979A. doi:10.1002/nme.995. S2CID 119889438.

External links[edit]

Tables of Integral Transforms at EqWorld: The World of Mathematical Equations.

This article incorporates material from Mellin’s inverse formula on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Источник

Обратное преобразование Лапласа

Теоремы разложения

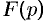
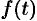
Рассмотрим две теоремы, называемые теоремами разложения, позволяющие по заданному изображению находить соответствующий ему оригинал .

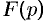
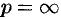
Теорема 79.1. Если функция в окрестности точки может быть представлена в виде ряда Лорана

то функция

является оригиналом, имеющим изображение 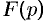, т. е.

Примем эту теорему без доказательства.

Пример №79.1.

Найти оригинал 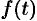, если

Решение:

Имеем

Следовательно, на основании теоремы 79.1 .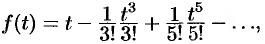

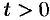
Запишем лорановское разложение функции 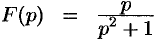в окрестности точки :

где , т. е. . Следовательно, , т. е. .

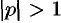
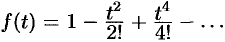
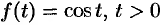
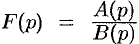
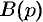
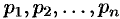
Теорема 79.2. Если правильная рациональная дробь, знаменатель которой имеет лишь простые корни (нули) , то функция

является оригиналом, имеющим изображение .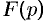

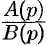
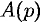
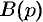
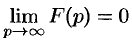
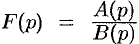
Отметим, что дробь должна быть правильной (степень многочлена ниже степени многочлена ); в противном случае не выполняется необходимый признак существования изображения (п. 78.1), т. е. не может быть изображением.

Разложим правильную рациональную дробь 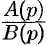на простейшие:

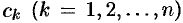
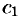
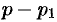
где — неопределенные коэффициенты. Для определения коэффициента этого разложения умножим обе части этого равенства почленно на :

Переходя в этом равенстве к пределу при 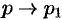, получаем

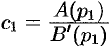
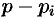
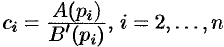
Итак, . Аналогичным путем (умножая обе части равенства (79.2) на ) найдем .

Подставляя найденные значения 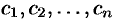в равенство (79.2), получим

Так как по формуле (78.3)

то на основании свойства линейности имеем

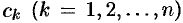
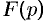
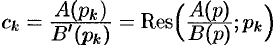
Замечание. Легко заметить., что коэффициенты определяются как вычеты комплексной функции в простых полюсах (формула (77.4)): .

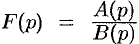
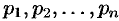
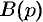
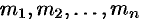
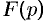
Можно показать, что если — правильная дробь, но корни (нули) знаменателя имеют кратности соответственно, то в этом случае оригинал изображения определяется формулой

Теорему 79.2 можно сформулировать следующим образом:

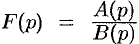
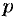
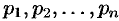
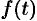
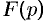
Теорема 79.3. Если изображение является дробно-рациональной функцией от и — простые или кратные полюсы этой функции, то оригинал , соответствующий изображению , определяется формулой

Формула Римана-Меллина

Общий способ определения оригинала по изображению дает обратное преобразование Лапласа (формула обращения Римана-Меллина), имеющее вид

где интеграл берется вдоль любой прямой .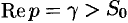

При определенных условиях интеграл (79.5) вычисляется по формуле

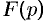
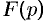
Замечание. На практике отыскание функции-оригинала обычно проводят по следующему плану: прежде всего следует по таблице оригиналов и изображений попытаться отыскать для заданного изображения соответствующий ему оригинал; второй путь состоит в том, что функцию стараются представить в виде суммы простейших рациональных дробей, а затем, пользуясь свойством линейности, найти оригинал; наконец, использовать теоремы разложения, свойство умножения изображений, формулу обращения и т.д.

Пример №79.2.

Найти оригинал по его изображению .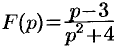

Решение:

Проще всего поступить так:

(использовали свойство линейности и формулы (78.5) и (78.6)).

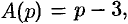
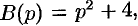
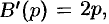
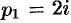
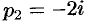
Если же использовать теорему 79.2 разложения, то будем иметь: корни знаменателя и и, согласно формуле (79.1),

Пример №79.3.

Найти функцию-оригинал, если ее изображение задано как .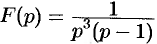

Решение:

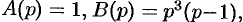
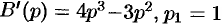
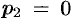
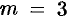
Здесь — простой корень знаменателя, — 3-кратный корень (). Используя формулы (79.1) и (79.3), имеем:

т. е. .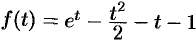

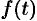
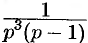
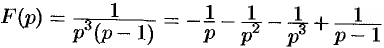
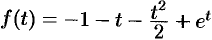
Приведем другой способ нахождения . Разобьем дробь на сумму простейших дробей: . Следовательно, .

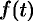
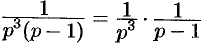
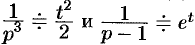
Приведем третий способ нахождения . Представим как произведение , и так как , то, пользуясь свойством умножения изображений, имеем:

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Решение задач по высшей математике

Другие темы по высшей математике возможно вам они будут полезны:

Источник

Обратное преобразование Лапласа

При практическом применении преобразования Лапласа всегда приходится решать обратную задачу – построение оригинала по его изображению. Общий метод построения оригинала f(t) по заданному изображению F(p) базируется на теореме обращения ( формуле Меллина ):

(3.22)

где интегрирование проводится по любой бесконечной прямой 7 0Re p = 7g 0, лежащей в полуплоскости абсолютной сходимости интеграла Лапласа [7,8]. Непосредственно формулой (3.22) для нахождения оригинала по известному изображению пользуютя редко. При нахождении оригинала по его изображению обычно применяют таблицы соответствия между оригиналами и их изображениями [5] и свойства преобразования Лапласа.

В самом распространенном случае, когда изображение F(p) является дробно – рациональной функцией вида

где A(p) и B(p) – многочлены, причем степень многочлена B(p) больше степени многочлена A(p), оригинал может быть найден разложением дроби A(p) /B(p) на простейшие.

Пример. Дано изображение