Как найти обратную функцию на интервале

Понятие обратной функции и ее определение в алгебре

Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет называться непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.

Две этих функции, f и g, будут взаимно обратными.

Обратная функция – это что такое? Дадим определение взаимно обратимой функции (что такое обратимая функция – определение). 

Для чего вообще нам нужно понятие обратных функций?

Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений. Также понятие особенностей обратных функций помогают в решении операций по извлечению n-ой степени (она обратна возведению в степень).

На самом деле это не является чем-то сложным. Онлайн, как и в нашем материале, вы можете найти много примеров обратной функции, которые помогут в этом убедиться. 

Важно знать, что любая функция y = y (x) – это определенное правило, которое определяет соответствие между двумя значениями: x и y. К примеру, функция y = x² ставит соответственно каждому действительному числу его в квадрат. Можно сделать определенную таблицу, в которой будут располагаться значения этой функции для целых аргументов.

Как найти функцию обратную данной

Как найти обратную функцию?

Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z 

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным. Вот несколько примеров обратной функции. 

Обе взаимообратные функции можно отобразить на графике следующим образом:

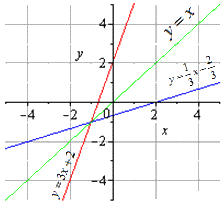
На графике мы находим симметричность обоих графиков относительно y=x (они отображаются симметрично). Эта прямая является биссектрисой первого и третьего квадрантов. Что это позволило нам доказать? Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.

Возьмем онлайн-пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Графически обе функции будут выглядеть или иметь следующее отображение:

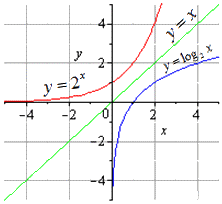
Также взаимно обратные функции можно рассматривать на примере теорем.

Предположим, мы имеем определенную, с возрастающей или убывающей монотонностью, а также непрерывную в определенном промежутке x функцию y = f(x). Значит, в промежутке значений y этой функции существует и обратная функция. Она также монотонно убывает или возрастает. Также ее можно определить как непрерывную (в промежутке y).

Основные свойства взаимно обратных функций

В этом пункте мы перечислим основные свойства обратимых функций y=f(x) и x=g(y). Какими же свойствами обладают взаимообратные функции?

Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать, так как это не одно и тоже даже исходя из названий. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифмов не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте характеристику, что это верно только при положительном y.

А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.

Не забывайте про этот момент, особенно если приходится работать с  тригонометрическими и обратными тригонометрическими функциями.  Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись

arcsinsin7π3=arcsinsin2π+π3==по формуле привидения=arcsinsinπ3=π3

А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!

Графики взаимно обратных функций

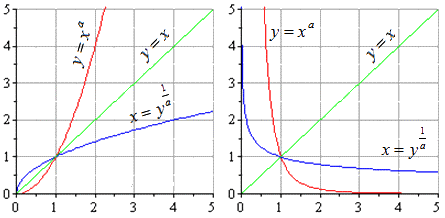
• Основные взаимно обратные функции: степенные

Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Замена букв будет давать соответственно y=xa и x=y1a.

Сделаем график. На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

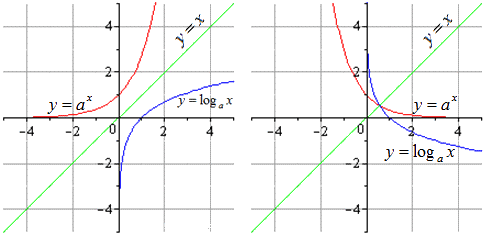
• Основные взаимно обратные функции: показательные и логарифмические

Возьмем a, которое будет положительным числом, не равным 1.

Узнаем, какими будут графики для функций с a>1 и a<1. Они будут выглядеть так:

• Основные взаимно обратные функции: тригонометрические и обратные тригонометрические

Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

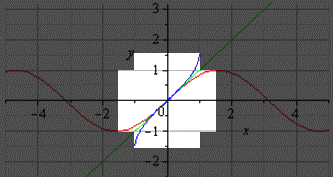
Если построить график главной ветви косинуса и арккосинуса, то он будет выглядеть так:

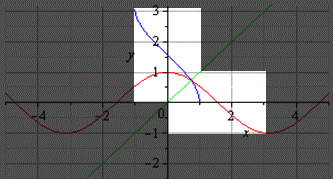
Если строить график главной ветви арктангенса и тангенса, то он будет таким:

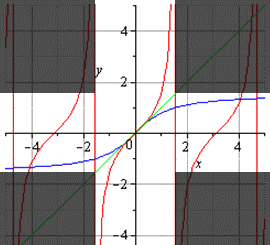
График главной ветви арккотангенса и котангенса будет таким:

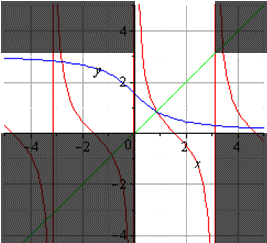
В случае построения обратных ветвей, отличные от главных, то обратную тригонометрическую функцию мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.

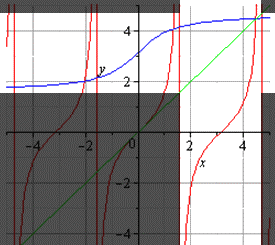
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.

Была ли эта статья полезной?

Теорема об обратной функции

8 января 2022

Одна из важнейших теорем, с помощью которой можно определить: имеет функция обратную или нет? Точнее, под словом «нет» следует подразумевать «требуется дополнительное исследование».

Урок будет состоять из двух частей:

1. Собственно, теорема об обратной функции — формулировка и доказательство.
2. Примеры нахождения обратных функций.

Сразу скажу: теорема простая, доказательство тоже несложное, а сама идея с геометрической точки зрения предельно логична и понятна. Начнём?

1. Теорема об обратной функции

Теорема 1. (об обратной функции) Пусть функция $y=fleft( x right)$ строго возрастает и непрерывна на отрезке $left[ a;b right]$.

Тогда существует обратная функция $x=gleft( y right)$ такая, что:

1. $gleft( y right)$ строго возрастает.
2. $gleft( y right)$ определена на отрезке $left[ fleft( a right);fleft( b right) right]$ и непрерывна на нём.
3. $gleft( y right)={{f}^{-1}}left( y right)$, т.е. $gleft( fleft( x right) right)=x$.

Прежде чем доказывать эту теорему, отметим важный факт: чтобы функция $y=fleft( x right)$ была обратима, она должна быть биекцией, т.е. каждому значению $y$ должно соответствовать ровно одно значение $x$ такое, что $y=fleft( x right)$.

Из урока про инъективные и сюръективные отображения мы знаем, что функцию $fleft( x right)$ можно считать биекцией, если выполнены два условия:

1. $fleft( x right)$ является инъекцией (или вложением): из условия ${{x}_{1}}ne {{x}_{2}}$ следует неравенство$fleft( {{x}_{1}} right)ne fleft( {{x}_{2}} right)$.
2. $f:Ato E$ является сюръекцией (или накрытием): для всякого элемента $min E$ найдётся элемент $ain A$ такой, что $fleft( a right)=m$.

Вот на проверке этих двух условий и будет строиться доказательство существования обратной функции. А уж затем мы докажем её свойства.

1.1. Доказательство теоремы

Итак, чтобы $fleft( x right):Mto N$ была обратима, она должна быть биекцией, т.е. инъекцией и сюръекцией одновременно.

1. Докажем, что $fleft( x right)$ — инъекция, т.е. разным значениям переменной соответствует разное значение функции.

Действительно, функция $fleft( x right)$ отображает отрезок $left[ a;b right]$ в отрезок $left[ fleft( a right);fleft( b right) right]$. Обозначим для краткости $fleft( a right)=M$, $fleft( b right)=N$.

Концы исходного отрезка отображаются в концы образа, а для всякого $xin left( a;b right)$ в силу строгой монотонности функции имеем:

[a lt x lt bRightarrow M lt fleft( x right) lt N]

Следовательно, при любом $xin left[ a;b right]$ величина $fleft( x right)$ обязательно будет лежать на отрезке $left[ M;N right]$.

Кроме того, в силу строгого возрастания функции $fleft( x right)$ для любых ${{x}_{1}}in left[ a;b right]$ и ${{x}_{2}}in left[ a;b right]$ таких, что ${{x}_{1}}ne {{x}_{2}}$ имеем:

[begin{align} & {{x}_{1}} gt {{x}_{2}}Rightarrow fleft( {{x}_{1}} right) gt fleft( {{x}_{2}} right) \ & {{x}_{1}} lt {{x}_{2}}Rightarrow fleft( {{x}_{1}} right) lt fleft( {{x}_{2}} right) \ end{align}]

Другими словами, если ${{x}_{1}}ne {{x}_{2}}$, то $fleft( {{x}_{1}} right)ne fleft( {{x}_{2}} right)$. А это и означает, что $fleft( x right)$ — инъекция (или вложение).

2. Теперь докажем, что $fleft( x right)$ — сюръекция.

Имеем: некая функция $fleft( x right)$ отображает отрезок $left[ a;b right]$ на множество $left[ M;N right]$ и при этом является строго возрастающей, т.е. монотонной на этом отрезке $left[ a;b right]$.

Следовательно, для $fleft( x right)$ выполняется критерий непрерывности монотонной функции: для всякого $Sin left[ M;N right]$ найдётся число ${{x}_{0}}in left[ a;b right]$ такое, что $fleft( {{x}_{0}} right)=S$.

Другими словами, у всякой точки $S$ на отрезке $left[ M;N right]$ найдётся прообраз ${{x}_{0}}$ на отрезке $left[ a;b right]$. А это и означает, что $fleft( x right)$ — сюръекция (или накрытие).

3. Итак, мы доказали, что $fleft( x right)$ — инъекция и сюръекция. Следовательно, $fleft( x right)$ — биекция, и существует обратная функция $gleft( y right)={{f}^{-1}}left( y right)$ такая, что

[begin{align} & gleft( fleft( x right) right)={{f}^{-1}}left( fleft( x right) right)=x \ & fleft( gleft( y right) right)=fleft( {{f}^{-1}}left( y right) right)=y \ end{align}]

Поскольку функция $fleft( x right)$ определена на отрезке $left[ a;b right]$ и отображает его на $left[ M;N right]$, то с обратной функцией $gleft( y right)$ всё наоборот: она определена на отрезке $left[ M;N right]$ и отображает его на $left[ a;b right]$. Осталось доказать, что $gleft( y right)$ строго возрастает и непрерывна на $left[ M;N right]$.

4. Покажем строгое возрастание $gleft( y right)$. Мы уже знаем, что $fleft( x right)$ строго возрастает и $fleft( gleft( y right) right)=y$. Возьмём любые ${{y}_{1}}in left[ M;N right]$ и ${{y}_{2}}in left[ M;N right]$ такие, что ${{y}_{1}} lt {{y}_{2}}$, и посчитаем ${{x}_{1}}=gleft( {{y}_{1}} right)$ и ${{x}_{2}}=gleft( {{y}_{2}} right)$.

Возможны три варианта:

1. ${{x}_{1}}={{x}_{2}}$. В этом случае $fleft( {{x}_{1}} right)=fleft( {{x}_{2}} right)$. Но $fleft( {{x}_{1}} right)={{y}_{1}}$ и $fleft( {{x}_{2}} right)={{y}_{2}}$, и тогда получается ${{y}_{1}}={{y}_{2}}$, что противоречит условию ${{y}_{1}} lt {{y}_{2}}$.
2. ${{x}_{1}} gt {{x}_{2}}$. Тогда в силу строгого возрастания имеем $fleft( {{x}_{1}} right) gt fleft( {{x}_{2}} right)$, т.е. ${{y}_{1}} gt {{y}_{2}}$, что вновь противоречит условию ${{y}_{1}} lt {{y}_{2}}$.
3. ${{x}_{1}} lt {{x}_{2}}$. Тогда $fleft( {{x}_{1}} right) lt fleft( {{x}_{2}} right)$, т.е. ${{y}_{1}} lt {{y}_{2}}$ что совпадает с условием. Следовательно, это единственно возможный вариант.

Итак, простым перебором всех возможных вариантов мы показали, что если ${{y}_{1}} lt {{y}_{2}}$, то $gleft( {{y}_{1}} right) lt gleft( {{y}_{2}} right)$. А это и означает, что функция $x=gleft( y right)$ монотонно возрастает.

5. Теперь докажем непрерывность $gleft( y right)$.

Мы уже знаем, что

1. $gleft( y right)$ определена на отрезке, поскольку образ $fleft( x right)$ — отрезок $left[ M;N right]$ (см. п. 3).
2. $gleft( y right)$ монотонна на $left[ M;N right]$ — доказали только что (см. п. 4).

Кроме того, мы знаем, что $gleft( fleft( x right) right)=x$. При этом для всякого ${{x}_{0}}in left[ a;b right]$ мы можем предъявить число

[{{y}_{0}}=fleft( {{x}_{0}} right)in left[ M;N right]]

такое что

[gleft( {{y}_{0}} right)=gleft( fleft( {{x}_{0}} right) right)={{x}_{0}}]

Следовательно, для функции $gleft( y right)$ выполняются все требования критерия непрерывности (монотонность на отрезке и существование прообраза). Поэтому и сама функция $gleft( y right)$ непрерывна на $left[ M;N right]$, что и требовалось доказать.

2. Простейшие приложения

Отметим, что функция $y=fleft( x right)$ становится биекцией именно благодаря строгой монотонности. Без монотонности нельзя гарантировать биекцию и, следовательно, обратимость.

Рассмотрим несколько примеров.

Пример 1. Функция $y=sin x$ строго монотонна и непрерывна при $xin left[ -{pi }/{2};;{pi }/{2}; right]$. Найдите обратную.

Рассмотрим часть синусоиды для $xin left[ -{pi }/{2};;{pi }/{2}; right]$:

Действительно, на этом отрезке синус монотонно растёт и непрерывен. При этом отрезок $left[ -{pi }/{2};;{pi }/{2}; right]$ отображается $left[ -1;1 right]$.

Следовательно, существует обратная функция, определённая на отрезке $left[ -1;1 right]$ и отображающая его в $left[ -{pi }/{2};;{pi }/{2}; right]$:

Обратная функция — это $y=arcsin x$, которая действительно определена на отрезке $left[ -1;1 right]$, строго возрастает и принимает значения в диапазоне $left[ -{pi }/{2};;{pi }/{2}; right]$.

Пример 2. Функция $y={{text{e}}^{x}}$ строго монотонна и непрерывна на $xin mathbb{R}$. Найдите обратную.

Вообще-то этот пример не подходит под условия сегодняшней теоремы. Потому что $xin mathbb{R}$ — это не отрезок.

Тем не менее, функция обратима. Поскольку исходная функция $y={{text{e}}^{x}}$ определена на $mathbb{R}$ и отображает его в $left( 0;+infty right)$, то обратная будет определена на множестве $left( 0;+infty right)$ и отображает его в $mathbb{R}$.

Как нетрудно догадаться, речь идёт о натуральном логарифме: $gleft( x right)=ln x$. Изобразим обе функции на одной координатной плоскости:

Красным нарисован график функции $y={{text{e}}^{x}}$, синим — график обратной функции $y=ln x$. Нетрудно видеть, что эти графики симметричны относительно прямой $y=x$, которая нарисована зелёным пунктиром. Впрочем, это уже совсем другая история.

Пример 3. Функция $y={{x}^{2}}$ строго монотонна и непрерывна на множестве $xin left[ 0;+infty right)$. Найдите обратную.

Очевидно, речь идёт об обычной квадратичной функции. Точнее, мы рассматриваем «правую» ветвь этой параболы. Здесь функция $y={{x}^{2}}$ строго возрастает и непрерывна, поэтому у неё есть обратная:

Функция, обратная к квадратичной — это обычный арифметический квадратный корень. И вновь графики $y={{x}^{2}}$ при $xge 0$ и $y=sqrt{x}$ симметричны относительно прямой $y=x$.

Такой же трюк можно провернуть с $y=operatorname{tg}x$, $y=cos x$ (в этом случае $xin left[ 0;pi right]$) и множеством других функций. Но думаю, идея понятна.:)

Смотрите также:

1. Теорема Кантора о равномерной непрерывности
2. Критерий непрерывности монотонной функции
3. Тест к уроку «Что такое логарифм» (средний)
4. Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
5. Задачи про температуру и энергию звезд
6. Задача B4 про три дороги — стандартная задача на движение

Пусть множества $X$ и $Y$ включены в множество действительных чисел. Введем понятие обратимой функции.

Теперь мы можем ввести понятие обратной функции.

Сформулируем теорему:

Введем теперь, непосредственно, понятие взаимно обратных функций.

Свойства взаимно обратных функций

Пусть функции $y=f(x)$ и $x=g(y)$ взаимно обратные, тогда

1. $y=f(gleft(yright))$ и $x=g(f(x))$

2. Область определения функции $y=f(x)$ равна области значения функции$ x=g(y)$. А область определения функции $x=g(y)$ равна области значения функции$ y=f(x)$.

3. Графики функций $y=f(x)$ и $x=g(y)$ симметричны относительно прямой $y=x$.

4. Если одна из функций возрастает (убывает), то и другая функция возрастает (убывает).

«Взаимно обратные функции» 👇

Нахождение обратной функции

1. Решается уравнение $y=f(x)$ относительно переменной $x$.

2. Из полученных корней находят те, которые принадлежат промежутку $X$.

3. Найденные $x$ ставят в соответствия числу $y$.

Задачи на нахождение обратных функций

В этой части рассмотрим обратные функции для некоторых элементарных функций. Задачи будем решать по схеме, данной выше.