Как найти обратную функцию по графику

Была ли эта статья полезной?

План урока:

Взаимно обратные функции

Кубический корень

Корни n-ой степени

Арифметические корни n-ой степени

Свойства корня n-ой степени

Сравнение корней

Взаимно обратные функции

Напомним, что любая функция у = у(х) представляет собой некоторое правило, которое устанавливает соответствие между значениями х и значениями у. В частности, функция у = х² ставит в соответствие каждому действительному числу его квадрат. Приведем таблицу, содержащую значения этой функции для целых аргументов от – 2 до 2:

Но если есть соответствие между х и у, то должно существовать и обратное соответствие между у и х. Действительно, строки таблички можно «перевернуть» и она примет следующий вид:

Мы получили два взаимно обратных соответствия. Однако второе из них функцией не является, ведь функция должна ставить в соответствие своему аргументу только одно значение функции. Однако, судя по второй таблице, числу у = 1 соответствует сразу два х: х = – 1 и х = 1. В таком случае математики говорят, что исходная функция у = х² является необратимой.

Теперь изучим зависимость у = х³. Построим табличку и для неё:

Теперь «перевернем таблицу» и получим следующее:

Мы видим, что как каждому значению х соответствует единственное значение у, так и наоборот, каждому у соответствует единственное значение х. В математике для подобных соответствий используют понятие взаимно-однозначное соответствие.

Для лучшего понимания этого определения отвлечемся от чисел. Пусть в футбольном чемпионате играет несколько команд. Они образуют множество Х команд-участниц соревнования. За множество У примем отдельных футболистов, выступающих на турнире. Каждому игроку соответствует единственная команда, за которую он выступает, но обратное неверно – каждой команде соответствует несколько игроков. Значит, это пример соответствия, не являющегося взаимно-однозначным.

Пусть тренеры команд образуют множество Z. Каждый тренер тренирует лишь одну команду, и наоборот, каждую команду тренирует единственный тренер. Значит, между множествами X и Z есть взаимно-однозначное соответствие.

Вернемся к функциям. Если соответствие, которое задает функция у = у(х), является взаимно-однозначным, то каждому значению у будет соответствовать единственное значение х. Значит, существует некоторая функция х = х(у). Пары функций у = у(х) и х = х(у) называются взаимно обратными функциями.

Ещё раз скажем, что не для любой функции существует обратная функция, ведь не все они определяют взаимно-однозначное соответствие. Если всё же для у = у(х) есть обратная функция х = х(у), то у = у(х) называют обратимой функцией.

Покажем, какие функции являются обратными, на примере пары у = 4х + 12 и у = 0,25х – 3. Возьмем, например, значение х = 5 и подставим его в у = 4х + 12:

у = 4х + 12 = 4•5 + 12 = 32

Получили 32. Подставим это число в обратную функцию:

у = 0,25х – 3 = 0,25•32 – 3 = 8 – 3 = 5

Получили именно то число, которое первоначально подставили в первую функцию! Возьмем другое произвольное число, например, 10, и подставим его в у = 4х + 12:

у = 4•10 + 12 = 40 + 12 = 52

Полученный результат подставляем в у = 0,25х – 3:

у = 0,25•52 – 3 = 13 – 3 = 10

Снова получили исходное число! Выберете сами ещё несколько произвольных чисел и убедитесь, что и с ними будет происходить то же самое.

Посмотрим, как получить обратную функцию. Пусть дана зависимость

у = 5х + 20

Это, по сути, выражение для вычисления у. Выразим из него х:

у = 5х + 20

у – 20 = 5х

(у – 20)/5 = х

х = у/5 – 20/5

х = 0,2у – 4

Получили зависимость х от у. Чтобы мы получили из нее обратную функцию, необходимо просто поменять местами буквы х и у:

у = 0,2х – 4

Убедитесь самостоятельно на нескольких примерах, что полученная функция обратна функции у = 5х + 20.

Пример. Найдите функцию, обратную зависимости у = 1/(х + 7).

Решение. Умножим обе части равенства у = 1/(х + 7) на (х + 7):

у(х + 7) = 1

Далее поделим обе части нау:

х + 7 = 1/у

Перенесем семерку вправо и получим формулу для вычисления х:

х = 1/у – 7

Для получения обратной функции просто меняем х и у местами:

у = 1/х – 7

Ответ: у = 1/х – 7.

Предположим, у нас есть у= у(х), чей график нам известен, и необходимо построить график взаимно обратной функции. Как это сделать? Если одна точка на координатной прямой имеет координаты (a; b) и принадлежит функции у = у(х), то, обратной функции должна принадлежать точка (b; a):

Эти точки симметричны относительно прямой у = х:

Поэтому для построения графика обратной функции достаточно симметрично отобразить его относительно прямой у = х.

С помощью этого правила построим график функции, обратной у = х³:

Практика показывает, что не все школьники (да и взрослые тоже) понимают, что означает симметричность относительно прямой у = х, ведь эта прямая наклонена. Здесь требуется довольно высокий уровень пространственного мышления. Куда проще понять симметрию относительно вертикальной или горизонтальной линии. Поэтому мы покажем ещё один способ построения обратных функций, который состоит из двух этапов.

Он заключается в том, что сначала график отображают симметрично относительно вертикальной оси Оу:

На втором этапе полученное отображение поворачивают по часовой стрелке относительно начала координат:

Заметим важное правило. При построении обратной функции области определения и области значений меняются местами. Действительно, если какое-то число входит в область значения функции, то это значит, что его можно подставить в обратную функцию. Но это в свою очередь означает, что она входит в область определения обратной функции. Проиллюстрируем это правило картинкой:

До сих пор мы рассматривали способы построения обратных функций, но ведь в самом начале урока говорилось о том, что обратная функция существует не всегда. Действительно, попытаемся построить обратную функцию для у = х²:

Получилась та же парабола, но «лежащая на боку». Является ли она графиком функции? Нет. На рисунке проведена вертикальная линия, которая пересевает график в двух точках. Это значит, что одному значению х (в данном случае х = 5) соответствует сразу два значения у. Но подобное соответствие не является функцией. Это значит, что у = х² – необратимая функция.

Есть ли какой-то признак, позволяющий быстро сказать, является ли функция обратимой? Оказывается, есть. Если функция строго монотонна (то есть либо только возрастает, либо только убывает), то это гарантирует, что она ещё и обратима. Покажем это с помощью рисунков. Известно, что каждому значению строго монотонной функции соответствует лишь один аргумент. С точки зрения геометрии это означает, что любая горизонтальная линия пересекает монотонную функцию не более чем в одной точке:

К слову, это свойство мы использовали для решения некоторых уравнений. Теперь отобразим график симметрично прямой у = х, причем также отобразим и горизонтальные линии:

Горизонтальные линии превратились в вертикальные, при этом они всё также пересекают график не более чем в одной точке. Но это как раз и означает, что график задает функцию, а не какое-то другое соответствие. Отсюда делаем вывод – любая строго монотонная функция обратима.

Снова вернемся к функции у = х². Мы уже показали, что она необратима. Но теперь наложим на нее дополнительное ограничение: х⩾0. Тогда от графика параболы останется только одна ветвь. Для нее уже можно построить обратную функцию:

Можно сделать вывод – обратимость функции зависит не только от самого вида функции, но и от того, на какой области определения ее рассматривают.

Кубический корень

Ранее мы изучили понятие квадратного корня. Напомним, что извлечение квадратного корня – это операция, обратная возведению в квадрат. Другими словами, функция

является обратной для у = х².

Встает вопрос – а можно ли придумать функцию, обратную возведению в куб? Конечно же да, ведь мы убедились в том, что функция у = х³ обратима. Называют же функцию, обратную у = х³, кубическим корнем.

Можно дать и другое определение, не использующее понятие функции:

Например, мы знаем, что число 5 в кубе равно 125:

5³ = 125

Это значит, что кубический корень из 125 равен 5.

Для обозначения кубического корня используют тот же знак радикала, что и для квадратного корня. Чтобы их отличать друг от друга, в случае с кубическим корнем перед знаком радикала ставят тройку:

Заметим важное отличие кубического и квадратного корня. Мы привыкли, что под знаком радикала не должно стоять отрицательное число. Но кубический корень из отрицательного числа извлечь можно. Например, мы знаем, что (– 6)³ = – 216. Отсюда следует, что

График кубического корня можно получить, просто построив функцию, обратную у = х³:

Корни n-ой степени

Аналогично кубическому корню можно ввести понятие и корня произвольной n-ой степени.

Для обозначения корня n-ой степени используется знак радикала, перед которым стоит число n. Приведем пример. Мы знаем, что 2⁵ = 32. Это значит, что корень 5-ой степени из 32 равен 2:

Мы помним, что все степенные функции вида у = хⁿ схожи друг с другом и при этом могут быть разбиты на два класса, в зависимости от четности или нечетности показателя степени n. Если n– четное число (2, 4, 6…), то график будет похож на параболу у = х², просто он будет чуть сильнее «прижат» к оси Ох вблизи точки О (0;0), но вместе с тем он будет и быстрее возрастать:

Если же показателем n является нечетное число, то график у = хⁿ будет схож с графиком у = х³:

Мы видим, что при нечетном показателе получается строго монотонная (возрастающая) функция. Следовательно, она обратима. Функция, обратная функции у = хⁿ, и будет корнем степени n.

Если n нечетно, то корень можно извлечь и из отрицательного числа. Так, известно, что (– 3)⁷ = – 2187. Это значит, что корень седьмой степени из (– 2187) равен (– 3):

Очевидно, что корень получится отрицательным, если под ним стоит отрицательное число. Если же подкоренное выражение положительно, то и сам корень положителен. Более того, можно заметить, что корень из отрицательного числа равен корню из противоположенного ему положительного числа, взятого со знаком минус:

В общем случае графики всех корней нечетных степеней будут похожи на график кубического корня:

Несколько сложнее дело обстоит в том случае, если показатель n является четным. Мы уже выяснили, что у = х² – это необратимая функция. Аналогично и любая другая степенная функция у = хⁿ необратима. Однако у = х² обратима, если наложить дополнительное ограничение: х ≥ 0. Аналогично, при использовании такого же ограничения, обратимой будет и любая функция у = хⁿ, где n – четное число. График такой функции будет похож на квадратный корень:

При четном значении n корень n-ой степени нельзя извлечь из отрицательного числа. Действительно, попробуем возвести в четную степень положительное число:

5⁴ = 5•5•5•5 = 625

Получили другое положительное число. Теперь попробуем возвести в четную степень отрицательное число:

(– 5)⁴ = (– 5)•(– 5)•(– 5)•(– 5) = 625

Результат снова положительный! Минусы у отрицательных чисел «сократились» друг с другом, и получилось положительное произведение. Но раз при возведении в четную степень всегда получается неотрицательное число, значит, и под четным корнем должно также стоять неотрицательное число. Поэтому подкоренное выражение не может быть отрицательным.

Арифметические корни n-ой степени

Мы видим, что складывается не очень удобная для математиков ситуация: корни n-ой степени из отрицательного числа можно извлечь, если n – нечетное число, но при четном n такая операция уже недопустима. Это порождает много проблем при работе с корнями. Для устранения этих проблем вводится понятие арифметического корня степени n. Его особенность в том, что он всегда извлекается из неотрицательного числа и сам принимает значения, не меньшие нуля.

Заметим, что корень нечетной степени из отрицательного числа всегда можно выразить с помощью арифметического корня, просто вынеся знак минус из-под корня:

Поэтому арифметических корней вполне хватает для работы в любых ситуациях.

Определение корня можно записать в более формализованном виде:

Это значит, что

Проиллюстрируем использование этой формулы:

Свойства корня n-ой степени

Далее рассмотрим некоторые свойства корней степени n, помогающие вычислять их значения. Сразу скажем, что они во многом идентичны свойствам квадратного корня.

Для доказательства этого свойства правую часть в n-ую степень:

Приведем примеры использования этого свойства:

Отсюда следует, что множители можно вносить и выносить из-под знака корня:

Следующее свойство помогает извлекать корни из дробей.

Доказывается это свойство так же, как и первое. Возведем в n-ую степень правую часть формулы:

Продемонстрируем применение доказанного тождества:

Заметим, что если под корнем находится степень какого-то числа, то ее вынести из-под радикала:

Доказать это можно, разложив число a^m в произведение:

a^m =a•a•a…•a

Всего справа стоит m множителей. Теперь извлечем корень степени n:

Справа всё те же m множителей, а потому

Таким образом, получаем, что

Покажем несколько примеров использования этого правила:

Далее посмотрим, как извлекать корень из другого корня.

Для доказательства возведем корень в левой части формулы в степень mn:

По определению корня получаем, что

Проиллюстрируем использование данного правила:

Последнее свойство, которое нам осталось изучить, называют основным свойством корня.

Доказательство записывается всего в одну строчку:

Степени в корне и под ним можно «сокращать»:

Сравнение корней

Естественно, что большинство корней – это не целые, а иррациональные числа, которые довольно сложно вычислять. Тем не менее есть несколько правил, которые помогают оценивать их значение. Из графиков корней видно, что все они являются возрастающими функциями. Поэтому, если необходимо сравнить два корня одной степени, достаточно сравнить их подкоренные выражения. Тот корень, у которого под корнем стоит большее число, и будет больше

В частности, справедливы неравенства:

В случае, если у корней различаются степени, следует постараться преобразовать их так, чтобы степени всё же совпали.

Пример. Сравните числа

Решение. Преобразуем первое число, чтобы у нас получился корень шестой степени:

Так как 121 > 119, то и

Пример. Сравните числа

Решение. Сначала избавимся от вложенных корней:

Получили два кубических корня. Меньше тот из них, у которого под радикалом меньшее число:

Пример. Сравните корни

Решение. Имеем корни 7-ой и 4-ой степени. К какой одинаковой степени можно привести оба корня? Это число 28, ведь оно представляет собой произведение 7•4:

Так как 16384 > 14641, то и

Понятие обратной функции и ее определение в алгебре

Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет называться непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.

Две этих функции, f и g, будут взаимно обратными.

Обратная функция – это что такое? Дадим определение взаимно обратимой функции (что такое обратимая функция – определение). 

Для чего вообще нам нужно понятие обратных функций?

Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений. Также понятие особенностей обратных функций помогают в решении операций по извлечению n-ой степени (она обратна возведению в степень).

На самом деле это не является чем-то сложным. Онлайн, как и в нашем материале, вы можете найти много примеров обратной функции, которые помогут в этом убедиться. 

Важно знать, что любая функция y = y (x) – это определенное правило, которое определяет соответствие между двумя значениями: x и y. К примеру, функция y = x² ставит соответственно каждому действительному числу его в квадрат. Можно сделать определенную таблицу, в которой будут располагаться значения этой функции для целых аргументов.

Как найти функцию обратную данной

Как найти обратную функцию?

Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z 

Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.

Разберем несколько задач на нахождение функций, обратных заданным. Вот несколько примеров обратной функции. 

Обе взаимообратные функции можно отобразить на графике следующим образом:

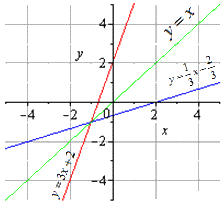
На графике мы находим симметричность обоих графиков относительно y=x (они отображаются симметрично). Эта прямая является биссектрисой первого и третьего квадрантов. Что это позволило нам доказать? Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.

Возьмем онлайн-пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.

Графически обе функции будут выглядеть или иметь следующее отображение:

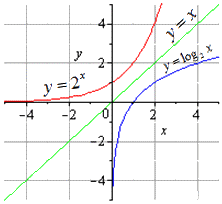
Также взаимно обратные функции можно рассматривать на примере теорем.

Предположим, мы имеем определенную, с возрастающей или убывающей монотонностью, а также непрерывную в определенном промежутке x функцию y = f(x). Значит, в промежутке значений y этой функции существует и обратная функция. Она также монотонно убывает или возрастает. Также ее можно определить как непрерывную (в промежутке y).

Основные свойства взаимно обратных функций

В этом пункте мы перечислим основные свойства обратимых функций y=f(x) и x=g(y). Какими же свойствами обладают взаимообратные функции?

Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать, так как это не одно и тоже даже исходя из названий. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифмов не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте характеристику, что это верно только при положительном y.

А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.

Не забывайте про этот момент, особенно если приходится работать с  тригонометрическими и обратными тригонометрическими функциями.  Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись

arcsinsin7π3=arcsinsin2π+π3==по формуле привидения=arcsinsinπ3=π3

А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!

Графики взаимно обратных функций

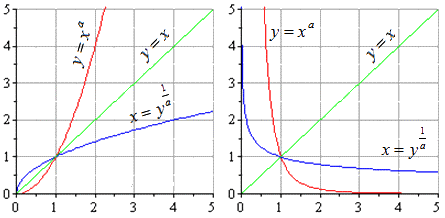
• Основные взаимно обратные функции: степенные

Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Замена букв будет давать соответственно y=xa и x=y1a.

Сделаем график. На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):

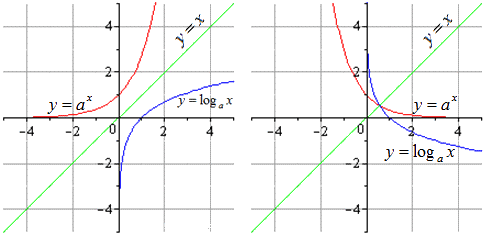
• Основные взаимно обратные функции: показательные и логарифмические

Возьмем a, которое будет положительным числом, не равным 1.

Узнаем, какими будут графики для функций с a>1 и a<1. Они будут выглядеть так:

• Основные взаимно обратные функции: тригонометрические и обратные тригонометрические

Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):

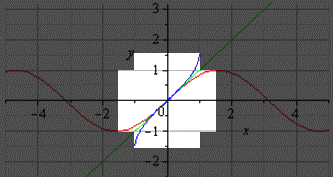
Если построить график главной ветви косинуса и арккосинуса, то он будет выглядеть так:

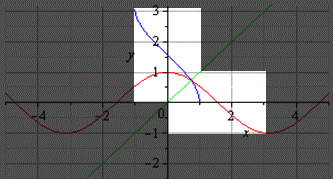
Если строить график главной ветви арктангенса и тангенса, то он будет таким:

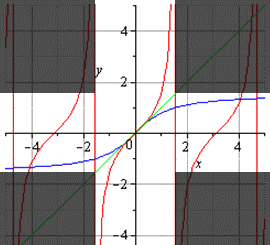
График главной ветви арккотангенса и котангенса будет таким:

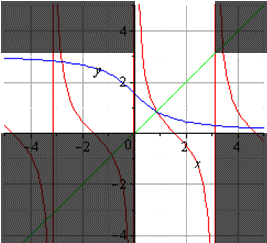
В случае построения обратных ветвей, отличные от главных, то обратную тригонометрическую функцию мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.

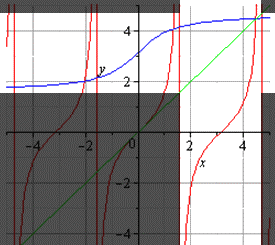
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.

Если в результате композиции двух функций

и

получается тождественная функция

, то говорят, что эти две функции являются инверсиями друг друга.

Если применение функции

к входу дает

выход

, то применение другой функции

к

должно вернуть значение

. Следовательно, обратная функция обращает функцию. Область данной функции становится областью обратной функции, а область данной функции становится областью обратной функции.

В общем, обратная функция — это отражение функции начала координат относительно прямой

. Ее можно получить, заменив

на

.

Если даны графики двух функций, можно определить, являются ли они обратными друг другу. Если графики обеих функций симметричны относительно прямой y = x, то мы говорим, что эти две функции являются обратными друг другу. Это объясняется тем, что если

лежит на функции, то

лежит на ее обратной функции:

Обратная функция — это любая функция, которая никогда не принимает одно и то же значение дважды. Другими словами, для каждого значения

существует только одно значение

. Это означает, что каждый элемент кодомена является образом не более чем одного элемента его области.

Кроме того, обратная функция проходит тесты на вертикальную линию и горизонтальную линию: