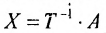Как найти обратную матрицу диагональной матрицы - Сайт, где вы сможете решить свои вопросы

A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an “m by n” matrix when it has “m” rows and “n” columns and is written as an “m × n” matrix. For example, the order of the matrix that has five rows and four columns is “5 × 4.” We have different types of matrices, such as rectangular, square, triangular, symmetric, singular, etc. The image given below is an “m × n” matrix that has “m” rows and “n” columns.

What is a Diagonal Matrix?

A diagonal matrix is a square matrix in which all of the elements except the principal diagonal elements are zeroes. It is both upper and lower triangular, as all the elements except the main diagonal elements are zeros. A square matrix “A = [a_ij]” is said to be a diagonal matrix if a_ij = 0 when i ≠ j. The matrix given below represents a diagonal matrix of order “5 × 5.”

Examples of a Diagonal Matrix

Some common examples of diagonal matrices of different orders are given below:

Diagonal Matrix of order (3 × 3)

Diagonal Matrix of order (4 × 4)

Properties of a Diagonal Matrix

The following are the properties of the Singular Matrix:

Every diagonal matrix is a square matrix, i.e., a matrix that has an equal number of rows and columns.
Scalar matrices, identity matrices, and null matrices are examples of diagonal matrices, as their non-principal diagonal elements are zeros.
The resultant matrix of the sum of two diagonal matrices is also a diagonal matrix.
The resultant matrix of the product of diagonal matrices is also a diagonal matrix, where the main diagonal elements of the resultant matrix are products of the corresponding elements of the original matrices.

If $A = left[begin{array}{cc} -3 & 0\ 0 & -3 end{array}right]$ and $B = left[begin{array}{cc} 8 & 0\ 0 & 5 end{array}right]$ , then $AB = left[begin{array}{cc} -24 & 0\ 0 & -15 end{array}right]$ .

A diagonal matrix is a symmetric matrix, as the transpose of a diagonal matrix is the same matrix itself.

If $D = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right]$ is a diagonal matrix, then $D^{T} = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right]$ , i.e., D = D^T.

A diagonal matrix is a symmetric matrix, as the transpose of a diagonal matrix is the same matrix itself.

If $A = left[begin{array}{cc} -5 & 0\ 0 & 11 end{array}right]$ and $B = left[begin{array}{cc} 7 & 0\ 0 & -13 end{array}right]$ are two diagonal matrices, then

$A + B = B + A = left[begin{array}{cc} 2 & 0\ 0 & -2 end{array}right]$

$AB = BA = left[begin{array}{cc} -35 & 0\ 0 & -143 end{array}right]$

Block Diagonal Matrix

The term “block matrix” refers to a matrix that is divided into blocks. In such matrices, the non-diagonal blocks are zero matrices, whereas the main diagonal blocks are square matrices. A matrix “A = [a_ij]” is called a block diagonal matrix when a_ij = 0, for i ≠ j, i.e., when the non-diagonal blocks are zero.

$A = left[begin{array}{cccccc} a_{11} & 0 & 0 & . & . & 0\ 0 & a_{22} & 0 & . & . & 0\ 0 & 0 & a_{33} & . & . & 0\ . & . & . & . & . & .\ . & . & . & . & . & .\ 0 & 0 & 0 & . & . & a_{nn} end{array}right]_{ntimes n}$

Determinant of a Diagonal Matrix

The determinant of a diagonal matrix is equal to the product of its principal diagonal elements.

If,

$D = left[begin{array}{ccc} a_{11} & 0 & 0\ 0 & a_{22} & 0\ 0 & 0 & a_{33} end{array}right]$

|D| = a₁₁× a₂₂× a₃₃.

Inverse of a Diagonal Matrix

The inverse of a diagonal matrix is also a diagonal matrix with the principal diagonal’s elements being the reciprocals of the corresponding elements of the original matrix.

If $D = left[begin{array}{ccc} a_{11} & 0 & 0\ 0 & a_{22} & 0\ 0 & 0 & a_{33} end{array}right]$ , then $D^{-1} = left[begin{array}{ccc} frac{1}{a_{11}} & 0 & 0\ 0 & frac{1}{a_{22}} & 0\ 0 & 0 & frac{1}{a_{33}} end{array}right]$ .

Anti-Diagonal Matrix

An anti-diagonal matrix, or non-diagonal matrix, is said to be the mirror image of a diagonal matrix concerning the placement of the elements. In an anti-diagonal matrix, all elements are zero except the diagonal (not the principal diagonal) elements from the upper right edge to the lower left edge. The matrix given below is an anti-diagonal matrix of order “3 × 3.”

$A = left[begin{array}{ccc} 0 & 0 & a_{11}\ 0 & a_{22} & 0\ a_{33} & 0 & 0 end{array}right]$

Also, Check

Minors and Cofactors of Determinants
Adjoint of a Matrix
Determinant of a Matrix

Solved Examples on Diagonal Matrix

Example 1: If $A = left[begin{array}{ccc} -4 & 0 & 0\ 0 & 11 & 0\ 0 & 0 & 7 end{array}right]$ , then prove that A = A^T.

Solution:

Given matrix, A = $left[begin{array}{ccc} -4 & 0 & 0\ 0 & 11 & 0\ 0 & 0 & 7 end{array}right]$

$A^{T} = left[begin{array}{ccc} -4 & 0 & 0\ 0 & 11 & 0\ 0 & 0 & 7 end{array}right]$ = A

So, A = A^T

Hence proved.

Example 2: Find the determinant of the matrix given below.

$D = left[begin{array}{ccc} -5 & 0 & 0\ 0 & 0 & 0\ 0 & 0 & 14 end{array}right]$

Solution:

Given matrix, D = $left[begin{array}{ccc} -5 & 0 & 0\ 0 & 0 & 0\ 0 & 0 & 14 end{array}right]$

We can notice that the given matrix is a diagonal matrix. We know that the determinant of a diagonal matrix is equal to the product of its principal diagonal elements.

So, |D| = -5 × 0 × 14 = 0

Hence, the determinant of the given matrix is 0.

Example 3: Find the inverse of the matrix given below.

$B = left[begin{array}{cc} 11 & 0\ 0 & 17 end{array}right]$

Solution:

We can notice that the given matrix is a diagonal matrix. We know that the inverse of a diagonal matrix is obtained by replacing the principal diagonal’s elements with the reciprocals of the corresponding elements of the original matrix, while the rest of the elements remain the same.

So, $B^{-1} = left[begin{array}{cc} frac{1}{11} & 0\ 0 & frac{1}{17} end{array}right]$ .

Example 4: Prove that A + B = B + A, if $A = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right]$ and $B = left[begin{array}{cc} -10 & 0\ 0 & 13 end{array}right]$ .

Solution:

Given matrices,

$A = left[begin{array}{cc} 6 & 0\ 0 & 7 end{array}right] and B = left[begin{array}{cc} -10 & 0\ 0 & 13 end{array}right]$

$A + B = left[begin{array}{cc} -4 & 0\ 0 & 20 end{array}right]$

$B + A = left[begin{array}{cc} -4 & 0\ 0 & 20 end{array}right]$

So, A + B = B + A

Hence, proved.

FAQs on Diagonal Matrix

Question 1: Define a diagonal matrix.

Answer:

A diagonal matrix is a square matrix in which all of the elements except the principal diagonal elements are zeroes.

Question 2: Is an identity matrix a diagonal matrix?

Answer:

An identity matrix is a square matrix whose principal diagonal elements are ones and the rest of the elements are zeros. So, an identity matrix or unit matrix is a diagonal matrix.

Question 3: What is the determinant of a diagonal matrix?

Answer:

The determinant of a diagonal matrix is equal to the product of its principal diagonal elements.

If $D = left[begin{array}{ccc} a_{11} & 0 & 0\ 0 & a_{22} & 0\ 0 & 0 & a_{33} end{array}right]$ , then |D| = a₁₁ × a₂₂× a₃₃.

Question 4: Is a zero matrix a diagonal matrix?

Answer:

A diagonal matrix is a square matrix whose non-diagonal elements are zeroes. We know that in a zero matrix all its elements are zeroes. So, we can conclude that a zero matrix is a diagonal matrix.

Last Updated :
09 Jan, 2023

Like Article

Save Article

Источник

Макеты страниц

Рассмотрим матрицу а, преобразующую вектор и в вектор

Иначе говоря, речь идет о таблице коэффициентов, входящих в линейных соотношений

Рассмотрим матрицу , определяющую обратное преобразование от нового вектора к прежнему вектору и

иначе говоря, таблицу коэффициентов, входящих в следующие линейные соотношения:

Матрица [3 называется обратной по отношению к матрице а и обозначается через

Коэффициенты системы соотношений (2) можно получить из системы (1), решив ее относительно Они могут быть вычислены по известной формуле Крамера:

Здесь — определитель матрицы – алгебраическое дополнение соответствующего элемента т. е. определитель, который получают, вычеркивая в строку и столбец, пересекающиеся на элементе снабженный

множителем Следует обратить внимание на то, что элемент находящийся на пересечении строки и столбца в соответствует а минору относящемуся к элементу который находится на пересечении строки I и столбца На практике вычисление матрицы, обратной а, осуществляется так:

1. Выписывают матрицу а, транспонированную по отношению к а.

2. Заменяют каждый элемент матрицы а определителем, полученным в результате вычеркивания строки и столбца, на которых расположен данный элемент.

3. Этот определитель сопровождают знаком плюс, если сумма индексов элемента четная, и знаком минус — в противном случае.

4. Делят полученную матрицу на определитель матрицы а. Пример. Требуется вычислить матрицу, обратную

Матрица а будет

Заменим каждый элемент определителем, полученным при вычеркивании соответствующей строки и столбца:

Переменим знаки у элементов с нечетной суммой индексов. Тогда

Разделим на Таким образом, получаем

Матрица, обратная матрице произведения двух матриц, равна произведению обратных матриц, взятых в обратном порядке, т. е.

Действительно, рассмотрим произведение . В силу ассоциативности операции умножения Обозначая и учитывая, что находим

Это правило непосредственно распространяется и на произведение любого числа матриц:

Замечания. 1. При вычислении обратной матрицы предполагается, что определитель матрицы отличен от нуля, иначе говоря, что матрица невырождена: В противном случае определить обратную матрицу невозможно.

Сказанное относится и ко всем не квадратным матрицам. Их можно всегда сделать квадратными, прибавив необходимое число нулей, но тогда определитель матрицы будет равен нулю.

2. В случае диагональной матрицы обратная матрица также диагональна. Элементы ее, не равные нулю, представляют собой обратные величины диагональных элементов заданной матрицы:

3. Мы видели, что правило умножения двух матриц то же, что и умножения двух определителей. Однако аналогия между матричным исчислением и операциями с определителями на этом и заканчивается. В частности, правило умножения на число и правило сложения очень различны. Действительно,

Точно так же

Мы не останавливаемся, конечно, на глубоком различии сущности обоих понятий. Предыдущее замечание было сделано только для того, чтобы внешняя аналогия не привела к ошибкам из-за смешения правил вычисления.

Источник

Содержание:

Теоремы существования и единственности обратной матрицы:

Рассмотрим квадратную матрицу:

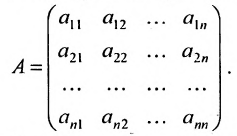
Определение 4.1.1. Матрица, которая в результате умножения на матрицу А, равна единичной матрице Е, называется обратной А и обозначается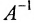

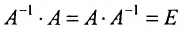Отметим, что если А и В квадратные матрицы одного порядка, то определитель 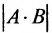произведения матриц равен произведению

определителей множителей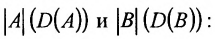

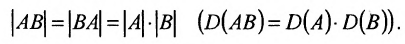
Теорема 4.1.1. (теорема существования). Для существования обратной матрицы необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы .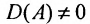

Доказательство. Необходимость. Пусть обратная матрица 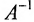существует. Докажем, что .

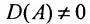Так как обратная матрица существует, то 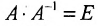и 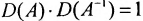.Поскольку правая часть не равна нулю, то ни один из множителей левой части не может быть равен нулю. Следовательно 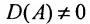, что означает, что матрица A невырожденная.

Достаточность. Пусть 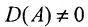, докажем, что обратная матрица существует.

Вычислим алгебраические дополнения 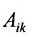каждого элемента 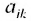в определителе D(A). Из полученных алгебраических дополнений построим матрицу:

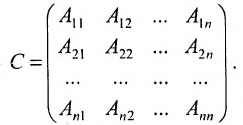
Матрица С называется союзной, или присоединенной, по отношению к матрице А, причем в i-й строке союзной матрицы С стоят алгебраические дополнения элементов i-го столбца матрицы А. Составим произведение матриц С и А, тогда элемент произведения, стоящий в i-й строке и k-м столбце, равен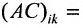

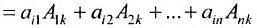. На основании теоремы разложения сумма произведений элементов определителя на их алгебраические дополнения равна величине определителя. А сумма парных произведений какого-нибудь ряда определителя на алгебраические дополнения параллельного ряда равна нулю (см. теорему аннулирования). Значит, все недиагональные элементы матрицы АС равны нулю, а диагональные равны D(A), следовательно:

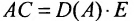(4.1.1)

Так как 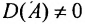, то равенство (4.1.1) можно умножить на скаляр 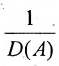. Получим:

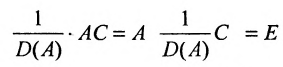
Тогда матрица 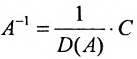будет обратной для матрицы А. Теорема доказана.

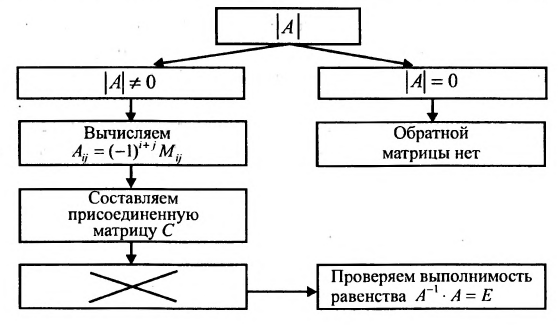
Сформулируем алгоритм нахождения обратной матрицы:.

Вычислите определитель 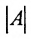исходной квадратной матрицы
Если определитель равен нулю, то исходная матрица не имеет обратной; если определитель не равен нулю, то переходите ко второму шагу.
Вычислите алгебраические дополнения элементов определителя исходной матрицы.
Составьте присоединенную матрицу С, записав алгебраические дополнения элементов строк в столбцы.
Умножьте элементы присоединенной матрицы на обратную величину определителя 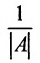исходной матрицы, тем самым постройте обратную матрицу .
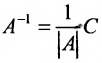Выполните проверку, т. е. рассмотрите произведение 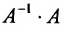или 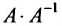. Должны получить единичную матрицу.

Этот алгоритм можно представить в виде следующей схемы:

Теорема 4.1.2. (теорема единственности). Для каждой неособенной матрицы А существует единственная обратная матрица.

Доказательство. Допустим, что наряду с обратной матрицей 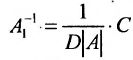существует другая обратная матрица 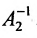. Тогда по определению 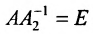. Умножая обе части этого равенства слева на 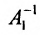, получим .

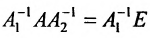Поскольку 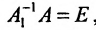, то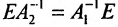, а это значит, что 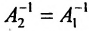. Теорема доказана.

Вычислив определители левой и правой частей равенства 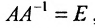, получим 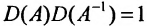, следовательно 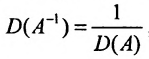то есть определители матриц 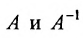взаимно обратные.

Замечание. Формула 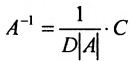позволяет найти явные выражения для элементов обратной матрицы через элементы матрицы А (см. алгоритм 1). Однако построение союзной матрицы очень трудоемкая операция при больших размерностях матриц. Поэтому доказанная формула, в большей мере, важна в теоретическом отношении.

Свойства обратной матрицы. Подобная матрица

Укажем некоторые свойства обратной матрицы:

Обратная матрица является невырожденной, т.е. .
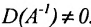Обратной матрице 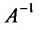будет матрица .
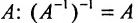Обратная к транспонированной матрице равна транспонированной обратной матрице: .
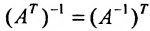Если матрица А симметрическая, то такой же будет обратная матрица: .
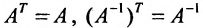Матрица, обратная к произведению матриц, равна произведению обратных матриц, взятых в обратном порядке при условии, что обратные матрицы существуют: .
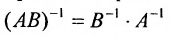Если А такова, что обратная к ней матрица равна транспонированной матрице А, то говорят, что А – ортогональная матрица и .
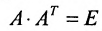Обратная для блочной квазидиагональной матрицы равна квазидиагональной матрице, состоящей из обратных матриц диагональных клеток:

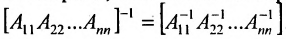
Понятие обратной матрицы позволяет ввести следующее определение:

Определение 4.2.1. Квадратная матрица А называется подобной матрице В, если существует невырожденная матрица Т, для

которой выполняется равенство .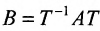

Говорят, что матрица А трансформируется в матрицу В при помощи матрицы Т.

Отношение подобия обладает тремя основными свойствами:

а) рефлексивности: А подобна А;
б) симметричности: если А подобна В, то и В подобна А;
в) транзитивности: если А подобна В и В подобна С, то и А подобна С.

Приложения обратной матрицы в экономических исследованиях

Применение обратных матриц в экономических исследованиях столь многочисленно и разнообразно, что мы приведём отдельные примеры использования обратной матрицы в экономических исследованиях.

Пример:

Предположим, что затраты времени оборудования при выпуске изделий пропорциональны количеству готовых изделий и пусть известна квадратная матрица Т норм затрат времени оборудования на различные изделия на различных типах оборудования. Если задана матрица-столбец А затрат времени на различных типах оборудования, необходимое для выполнения производственной профаммы, то определение возможного выпуска готовых изделий X осуществляется с использованием обратной матрицы :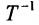

Валовой выпуск продукции X также можно определить, зная матрицу Z норм затрат рабочего времени рабочих различных категорий и фонд рабочего времени F по категориям рабочих, вычислив произведение обратной матрицы 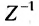на F, т.е. .

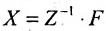Пример:

Рассмотрим четырёхсскторнос описание экономики, в котором выделены две отрасли: сельское хозяйство и промышленность, один первичный фактор производства – труд и государственный сектор, который потребляет продукцию обеих отраслей и использует труд. Государственный сектор ничего не производит для экономики и его потребление представляет собой конечный спрос на товары, производимые в этих секторах. В процессе производства каждая отрасль потребляет некоторое количество продукции другой, отрасли, а также труд; рабочая сила нуждается в продукции обеих отраслей и, наряду с этим, в затратах труда для своего воспроизводства. Трудовые ресурсы могут быть свободно импортированы и экспортированы, таким образом, никогда не может быть безработицы или излишнего спроса на труд. Основной капитал и запасы продукции поддерживаются на одном и том же уровне в течение всего периода. Наблюдая за потоками продукции между четырьмя секторами экономики составим таблицу «затраты-выпуск», табл.4.3.1.

Таблица 4.3.1

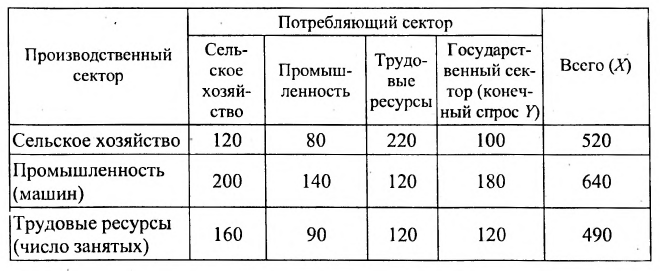
Сумма показателей в строках даёт общий выпуск каждой отрасли и суммарное число занятых. Суммы показателей по столбцам показывают затраты данного сектора, необходимые для производства всего объёма продукции. Следовательно, каждый столбец описывает производственную функцию данного сектора. Так, например, первый столбец характеризует основной производственный процесс, который в текущем периоде применяется в сельском хозяйстве. Для производства 520 т продукции сельского хозяйства требуется 120 т сельскохозяйственной продукции, 200 машин и 160 работников. Определим валовой выпуск продукции для конечного спроса, определяемого матрицей-столбцом: .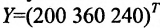

Решение:

Пусть 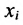– валовой выпуск продукции i,i=1,2,3; а 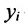-конечный спрос на продукцию /. Валовой выпуск каждого вида продукции должен быть равен сумме продукции, использованной при производстве всех видов продукции, плюс конечный спрос на эту же продукцию:

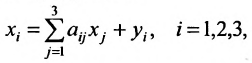
где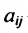– количество продукции i, используемое при производстве единицы продукции j. В матричном обозначении получим:

X = AX + Y, (4.3.1)

где X, Y- матрицы столбцы, а А- матрица коэффициентов прямых затрат. Все её элементы неотрицательны.

Воспользовавшись алгебраическими операциями над матрицами, перепишем уравнение (4.3.1) в виде: EX – АХ = Y, (E-A)X = Y. Умножив последнее матричное уравнение слева на обратную матрицу 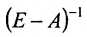получаем матричное уравнение для определения матрицы-столбца валового выпуска продукции:

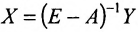. (4.3.2)

Следовательно, для определения валового выпуска продукции X в новом периоде нам нужно последовательно определить элементы матрицы А, Е-А и обратной матрицы 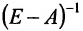. Элементы матрицы А определим воспользовавшись предположением о пропорциональной зависимости между затратами и объёмами производства, т.е. линейными однородными функциями производственных затрат: 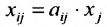. Тогда элементы матрицы А определим из разноств: 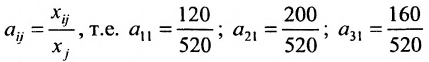Выполнив вычисления (разделив элементы первого столбца таблицы 4.3.1 на 520, второго – на 640, третьего – на 490), получаем матрицу А:

Далее вычисляем элементы матрицы Е-А:

вычисляем определитель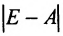

и алгебраические дополнения элементов матрицы (Е-А):

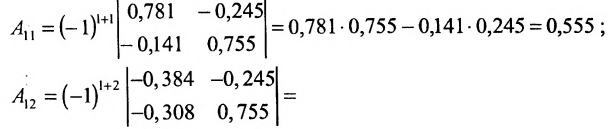
Составляем из алгебраических дополнений присоединённую матрицу С:

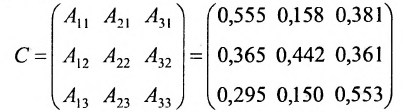
и вычисляем элементы обратной матрицы :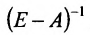

Тогда в силу (4.3) находим валовой выпуск продукции: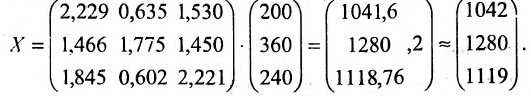

Таким образом, для удовлетворения новых показателей спроса необходимо будет произвести приблизительно 1042 т продукции сельского хозяйства, 1280 машин и нанять 1119 работников.

Особенности матриц в ценностном и натуральном выражении

Матрица коэффициентов прямых материальных затрат А, рассмотренная нами в примере предыдущего пункта, относится к классу неотрицательных матриц, так как матрица-столбец 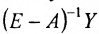должна быть неотрицательна.

Определение 4.4.1. Если решение системы (4.3.1) сществует для любой неотрицательной матрицы Y конечного спроса, то матрица А называется продуктивной.

Поэтому элементы матрицы А не могут принимать произвольные положительные значения. Все диагональные элементы матрицы А должны быть меньше единицы. В противном случае производство лишается всякого смысла (если 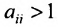, то 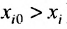). Произведение коэффициентов, симметричных относительно главной диагонали, должно быть также меньше единицы: 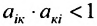. Указанные ограничения на значения элементов матрицы А не зависят от единиц измерения. Однако в общем случае выбор единиц измерения существенно влияет на анализ свойств матриц межотраслевого баланса. Для матриц межотраслевого баланса в ценностном выражении обычно выполняются условия 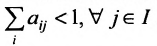• Если же для некоторой k-и отрасли 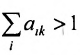, то экономически это означает, что данная отрасль настолько убыточна, что её убытки перекрывают расходы на амортизацию и оплату труда.

Так как норму матрицы А можно определить по формуле

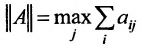, то при условии что 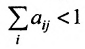норма матрицы А меньше единицы, т.е. .

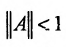Если норма матрицы А меньше единицы, то

1) ;
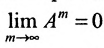2) ;
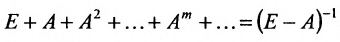3) ;
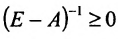4) все собственные 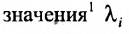матрицы А по модулю меньше единицы, а наибольшее собственное значение положительно (теорема Фрабеииуса-Перропа);
5) все главные 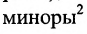матрицы (Е – А) положительны и меньше единицы.

Отметим, что в матрицах межотраслевого баланса в натуральном выражении условия 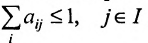, практически никогда не выполняются. Более того, многие элементы этих матриц больше единицы. Однако можно подобрать такие новые измерители (матрицу T), что для подобной матрицы 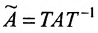будет выполняться 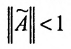и следствия из него.

Подобные матрицы имеют равные по величине собственные значения и главные миноры;

Для продуктивности матрицы А необходимо и достаточно, чтобы выполнялось одно из приведенных ниже условий:

Все главные миноры матрицы (Е – А) положительны и меньше единицы.
Все собственные значения матрицы А по модулю меньше единицы.
Матрица 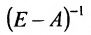полуположительна.

Условие 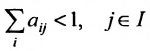является достаточным для продуктивностн матрицы А.

Матрица 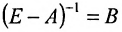называется матрицей коэффициентов полных затрат, а её элементы- коэффициентами полных затрат. Они 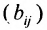показывают, какой должен быть валовой выпуск i-Й отрасли для того, чтобы обеспечить выпуск единицы конечного продукта j-й отрасли.

Коэффициенты полных затрат 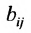не меньше коэффициентов прямых затрат: 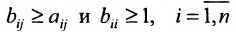так как они характеризуют совокупность прямых и косвенных затрат.

Вернёмся к примеру 1.12 и проанализируем матрицы коэффициентов прямых затрат А и полных затрат :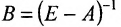

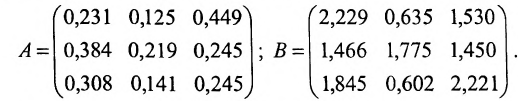
Элементы матрицы А удовлетворяют условиям:

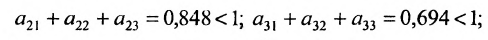
4) норма матрицы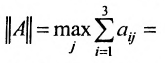

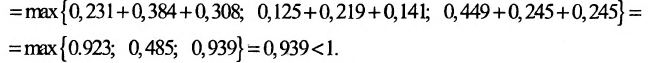
Значит матрица А является продуктивной и для неё существует обратная матрица 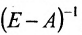, называемая матрицей полных затрат.

Из вида матрицы В следует, что все коэффициенты полных затрат 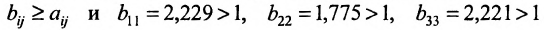. Например, элементы первого столбца матрицы В показывают, что для того чтобы произвести единицу конечной продукции сельского хозяйства нужно произвести 2,222 единиц сельского хозяйства, 1,766 единиц промышленности и занять 1,845 работников.

Определение обратной матрицы

Рассмотрим квадратную матрицу

Обозначим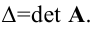

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если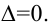

Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение 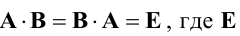– единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через 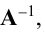так что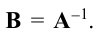

Обратная матрица вычисляется по формул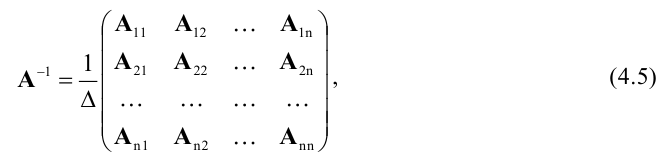е где 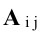– алгебраические дополнения элементов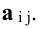

Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

Заказать решение задач по высшей математике

Пример:

Для матрицы 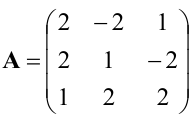найти обратную.

Решение:

Находим сначала детерминант матрицы А:

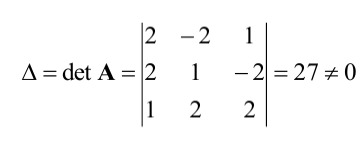
значит, обратная матрица существует и мы ее можем найти по формуле: 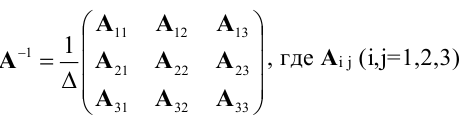– алгебраические дополнения элементов 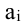исходной матрицы. 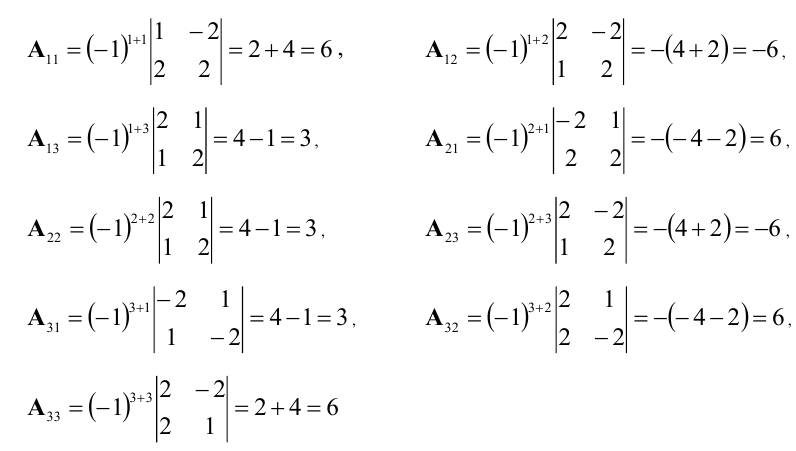откуда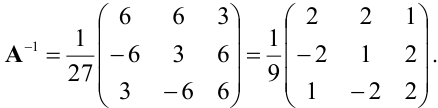

Пример:

Методом элементарных преобразований найти обратную матрицу для матрицы: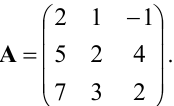

Решение:

Приписываем к исходной матрице справа единичную матрицу того же порядка: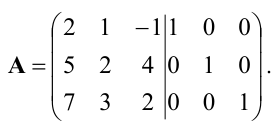

С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие преобразования над правой матрицей. Для этого поменяем местами первый и второй столбцы: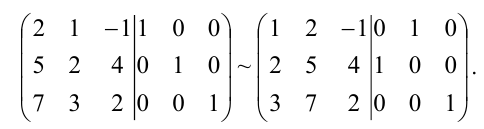

К третьему столбцу прибавим первый, а ко второму – первый, умноженный на -2:

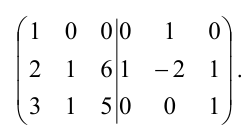
Из первого столбца вычтем удвоенный второй, а из третьего – умноженный на 6 второй;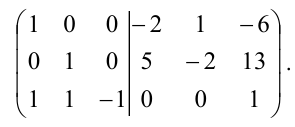

Прибавим третий столбец к первому и второму: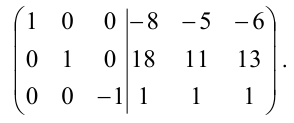

Умножим последний столбец на -1: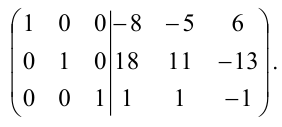

Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,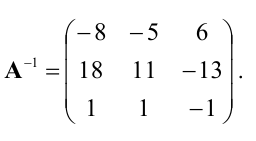

Что такое обратная матрица и как её решать

Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной.

Диагональная матрица, элементы 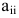которой равны единице, называется единичной матрицей. Обозначение: Е.

Пусть А – квадратная матрица порядка n. Матрица 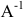называется обратной к А, если выполнены равенства

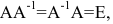
где Е – единичная матрица порядка n.

Внимание! Обратная матрица существует только для невырожденной квадратной матрицы.

Квадратная матрица, определитель которой отличен от нуля, называется невырожденной. В противном случае матрица называется вырожденной.

Теорема:

Для невырожденной матрицы 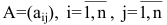существует единственная обратная матрица

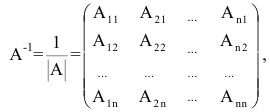
где 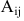– алгебраические дополнения элементов 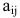матрицы А.

Пример:

Найти матрицу X из матричного уравнения АХ=В, где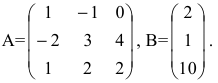

Решение:

Умножим уравнение АХ=В на 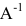слева:

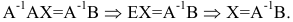
Найдем 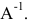Обратная матрица к А существует, т.к. матрица А невырожденная:

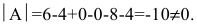
Вычислим алгебраические дополнения элементов матрицы А:

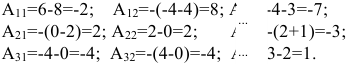
Следовательно,

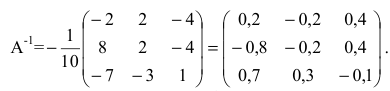
Произведение матриц 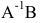существует, т.к. количество столбцов матрицы А равно количеству строк матрицы В и равно 3. Найдем его: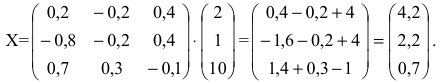

Ранг матрицы – определение и вычисление
Определители второго и третьего порядков и их свойства
Метод Гаусса – определение и вычисление
Прямая линия на плоскости и в пространстве
Определённый интеграл
Кратный интеграл
Ряды в математике
Дифференциальные уравнения с примерами

Источник

Условие
обратимости. Матрица

называется обратной к матрице ,
если ,
где
– единичная матрица. Матрица ,
для которой существует обратная матрица,
называется обратимой.

Так как равенство

возможно лишь для квадратных матриц

одинакового размера, то обратимой может
быть лишь квадратная матрица. Однако,
не каждая квадратная матрица обратима.

Квадратная матрица

называется вырожденной, если ,
и невырожденной, если .

Теорема 5.1.
(Критерий обратимости) Матрица

обратима тогда и только тогда, когда
она не вырождена.

Доказательство.
Пусть
обратимая. Тогда существует матрица

такая, что .
Из этого равенства и теоремы 4.3 следует,
что .
Следовательно ,
т.е. матрица
не вырождена.

Пусть теперь
матрица
не вырождена. Рассмотрим вспомогательную
матрицу

где –
алгебраическое дополнение элемента

матрицы .
Матрица
называется присоединённой или взаимной
к матрице .
Покажем, что матрица
является обратной к матрице .
Тем самым будет доказана обратимость
матрицы .

Рассмотрим матрицу
.
В позиции
матрицы
стоит элемент ,

.
Из теоремы 4.4. и определения определителя
n-го
порядка следую, что
при
и
при .
Следовательно

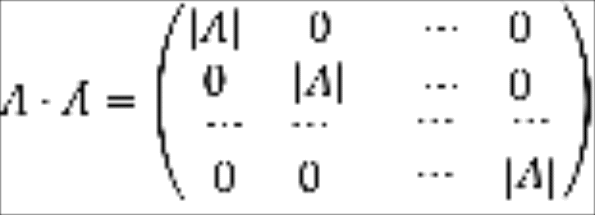
Из последнего
равенства следует, что .

Совершенно
аналогично доказывается, что

,
т.е. .

Теорема 5.1 доказана.

Теорема 5.2. (О
единственности обратной матрицы) Если

– квадратная невырожденная матрица, то
существует единственная обратная к ней
матрица.

Доказательство.
Т.к. матрица

невырождена, то в силу теоремы 5.1, она
обратима, при этом матрица
является обратной к матрице .

Пусть
– произвольная матрица, удовлетворяющая
равенствам .
Единственность обратной матрицы будет
доказана, если .

Умножая равенство

слева на матрицу ,
получим

(1)

С другой стороны

=.
(2)

Сравнивая равенства
(1) и (2) приходим к выводу .

Теорема 5.2 доказана.

В качестве примера
найдём обратную к матрице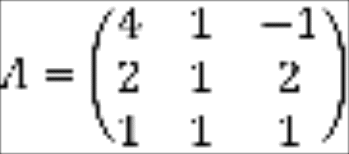

Как уже известно,
обратную матрицу
можно найти по формуле

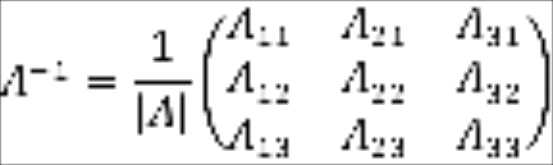
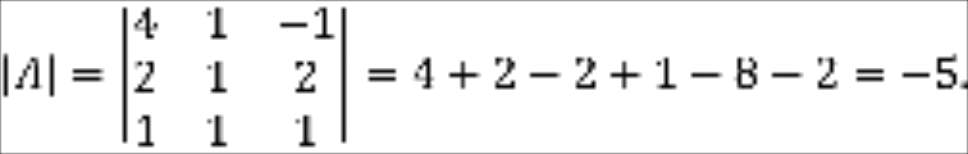
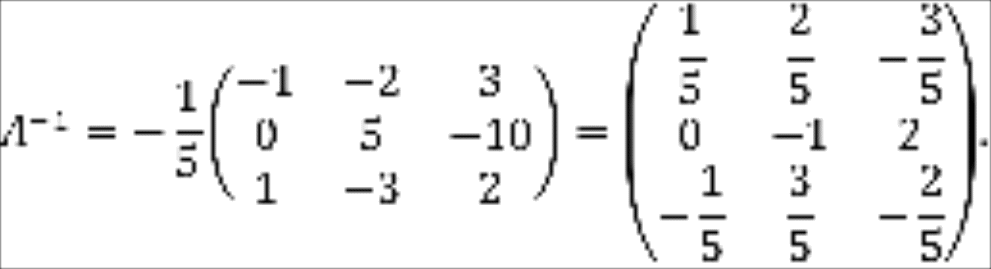
Проверить
самостоятельно, что .

Теорема 5.3.
(обратимость призведения двух невырожденных
матриц)
Пусть
квадратные невырожденные матрицы
порядка .
Тогда матрица
обратима и при этом

Доказательство.
В силу
теоремы 4.3 .
Т.е. матрица
– невырождена. Следовательно, в силу
теоремы 5.1 обратима.

Рассмотрим матрицу

Рассмотрим теперь
матрицу

Из равенств (3), (4)
и определения обратной матрицы следует,
что .

Обратная к
невырожденной диагональной матрице.
Пусть
– невырожденная диагональная матрица
порядка .

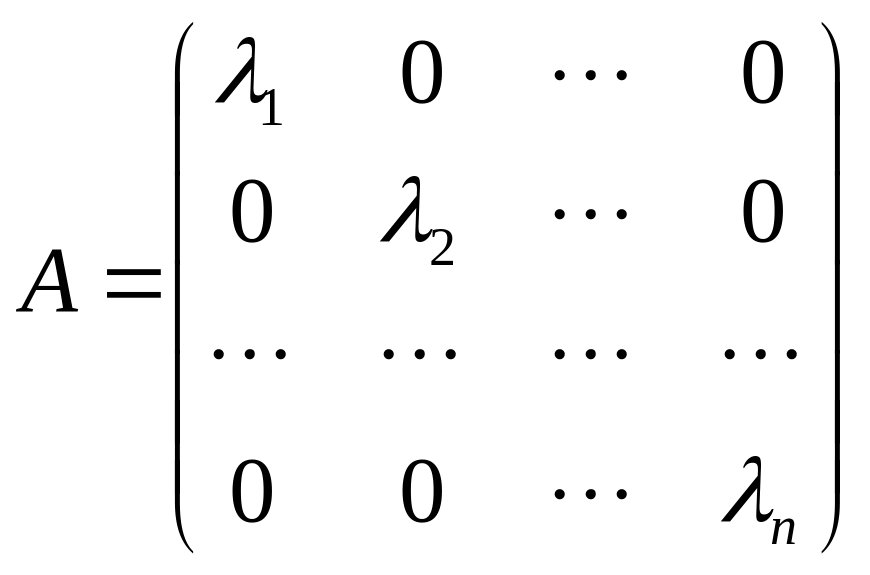
Тогда .
Из условия невырожденности матрицы
следует, что

Легко проверить,
что обратной к матрице
будет матрица

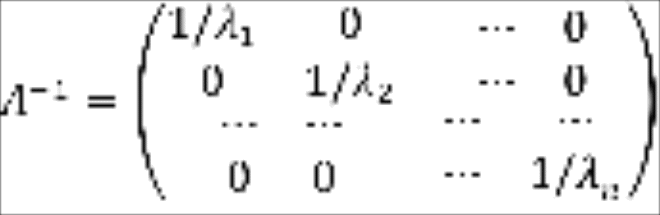
(Проверить
самостоятельно).

Замечание. Из
теоремы 4.3 непосредственно вытекает
справедливость равенства

(проверить самостоятельно).

§6. Ранг матрицы.

Понятие ранга
матрицы. Пусть

– произвольная матрица размера ,

– произвольное натуральное число,
удовлетворяющее неравенству .
Выберем в матрице
произвольные
строк и
столбцов с номерами
и
соответственно. Элементы матрицы,
стоящие на пересечении выбранных строк
и столбцов, образуют квадратную матрицу
k-го
порядка. Определитель этой матрицы
называется минором k-го
порядка, расположенным в строках с
номерами
и столбцах с номерами .

Для обозначения
минора будем пользоваться символом
или .

Рангом ненулевой
матрицы называется максимальный порядок
ненулевых миноров этой матрицы. Ранг
нулевой матрицы по определению считается
равным нулю.

Ранг матрицы будем
обозначать символами

Из определения
ранга матрицы вытекают следующие факты:

1.Ранг матрицы не
превосходит её размеров: есл,
то

2.Равенство
равносильно выполнению двух условий:
а) в матрице A
существует ненулевой минор порядка r;
б) любой минор более высокого порядка
(если такой существует) равен нулю.

Пусть .
Любой ненулевой минор порядка
называется базисным минором. Строки и
столбцы матрицы ,
в которых расположен базисный минор
называются базисными строками и
столбцами.

Теорема 6.1.
При транспонировании матрицы её ранг
не изменяется.

Доказательство.
Справедливость приведенной теоремы
вытекает из следующих двух фактов: 1.
Определители транспонированных матриц
равны; 2. При транспонировании базисные
строки матрицы
становятся базисными столбцами матрицы
,
а базисные столбцы – базисными строками.

Теорема
6.2. Элементарные
преобразования матрицы не изменяют её
ранга.

Справедливость
теоремы непосредственно вытекает из
определения ранга, так как, при элементарных
преобразованиях матрицы, любой её
ненулевой минор преобразуется в ненулевой
минор.

Теорема
6.3. Ранг
трапециевидной матрицы равен числу её
ненулевых строк.

Доказательство.
Пусть матрица
имеет вид

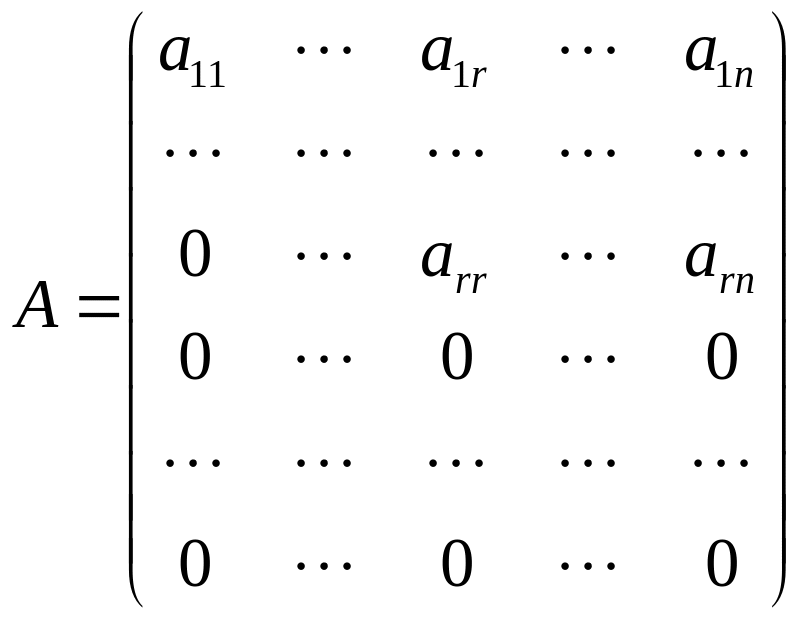
Рассмотрим
минор

порядка

,
расположенный в левом верхнем углу
матрицы

.

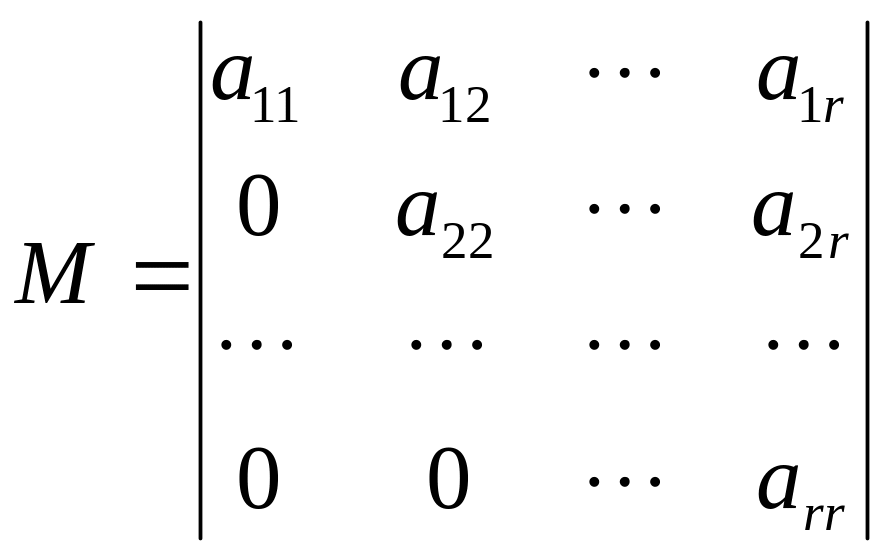
В силу теоремы 4.2

.

Пусть

–
любой минор, порядок которого больше

.
Так как, в матрице

всего

ненулевых строк, то минор

содержит строку, целиком состоящую из
нулей т.е.

.
Следовательно .

Доказательство теоремы 6.3, для
верхних травециевидных матриц остальных
трех типов проводится аналогично.

Метод Гаусса вычисления ранга.
Теоретическую основу этого метода
составляют, доказанные выше, теоремы
6.2 и 6.3. Суть метода Гаусса вычисления
ранга матрицы состоит в приведении этой
матрицы элементарными преобразованиями
к верхней трапециевидной форме и подсчете
ненулевых строк полученной трапециевидной
матрицы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
14.11.201995.23 Кб01.doc
#
03.08.2019142.65 Mб191.doc
#
26.09.201950.69 Кб01.doc
#
09.02.201529.7 Кб81.doc
#
24.09.2019146.43 Кб01.doc
#
27.09.2019321.02 Кб21.doc
#
13.09.2019314.37 Кб01.doc

Источник

Диагональная матрица — квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю:

${displaystyle D={begin{bmatrix}d_{11}&0&cdots &0\0&d_{22}&cdots &0\cdots &cdots &cdots &cdots \0&0&cdots &d_{nn}end{bmatrix}}}$

Диагональная матрица с элементами $(d_{{1}},d_{{2}},dots ,d_{{n}})$ , стоящими на главной диагонали, обозначается ${displaystyle mathrm {diag} ,{d_{1},d_{2},dots ,d_{n}}}$ .

Является одновременно и верхнетреугольной и нижнетреугольной. Диагональная матрица симметрична: ${displaystyle D^{intercal }=D}$ . Ранг диагональной матрицы равен количеству ненулевых элементов, находящихся на главной диагонали.

Диагональные матрицы можно складывать и перемножать почленно:

${displaystyle mathrm {diag} ,{a_{1},a_{2},dots ,a_{n}}+mathrm {diag} ,{b_{1},b_{2},dots ,b_{n}}=mathrm {diag} ,{a_{1}+b_{1},a_{2}+b_{2},dots ,a_{n}+b_{n}}}$ ,

${displaystyle mathrm {diag} ,{a_{1},a_{2},dots ,a_{n}}mathrm {diag} ,{b_{1},b_{2},dots ,b_{n}}=mathrm {diag} ,{a_{1}b_{1},a_{2}b_{2},dots ,a_{n}b_{n}}}$ .

Определитель диагональной матрицы равен произведению диагональных элементов: ${mathrm {det}},D=d_{{11}}d_{{22}}dots d_{{nn}}$ .

Алгебраическое дополнение недиагонального элемента диагональной матрицы равно нулю, то есть:

${displaystyle D_{ij}={begin{cases}0,&ineq j\prod limits _{i=1}^{n-1}d_{ii},&i=jend{cases}}}$

Обратная матрица для диагональной матрицы равна:

${displaystyle D^{-1}={begin{bmatrix}d_{11}^{-1}&0&cdots &0\0&d_{22}^{-1}&cdots &0\cdots &cdots &cdots &cdots \0&0&cdots &d_{nn}^{-1}end{bmatrix}}=mathrm {diag} ,{d_{11}^{-1},d_{22}^{-1},dots ,d_{nn}^{-1}}}$

Диагональными являются нулевая матрица, единичная матрица, скалярная матрица (все элементы главной диагонали равны).

В некоторых случаях недиагональная матрица может быть приведена к диагональному виду путём замены базиса; достаточным условием является различность всех собственных значений матрицы (в общем случае матрица приводима лишь к жордановой форме).

Источник

What is a Diagonal Matrix?

Examples of a Diagonal Matrix

Properties of a Diagonal Matrix

Block Diagonal Matrix

Determinant of a Diagonal Matrix

Inverse of a Diagonal Matrix

Anti-Diagonal Matrix

Solved Examples on Diagonal Matrix

FAQs on Diagonal Matrix

Question 1: Define a diagonal matrix.

Question 2: Is an identity matrix a diagonal matrix?

Question 3: What is the determinant of a diagonal matrix?

Question 4: Is a zero matrix a diagonal matrix?

Свойства обратной матрицы. Подобная матрица

Особенности матриц в ценностном и натуральном выражении

Определение обратной матрицы

Что такое обратная матрица и как её решать

§6. Ранг матрицы.

Вам также может понравиться

Как найти гостиницу в челябинске

Как найти основание трапеции по формуле площади

Как найти призрака на улице

Добавить комментарий Отменить ответ