Syntax
Description
example
Y = inv( computesX)
the inverse of
square matrix X.
-
X^(-1)is equivalent toinv(X). -
x = Abis computed differently
thanx = inv(A)*band is recommended for solving
systems of linear equations.
Examples
collapse all
Inverse Matrix
Compute the inverse of a 3-by-3 matrix.
X = [1 0 2; -1 5 0; 0 3 -9]
X = 3×3
1 0 2
-1 5 0
0 3 -9
Y = 3×3
0.8824 -0.1176 0.1961
0.1765 0.1765 0.0392
0.0588 0.0588 -0.0980
Check the results. Ideally, Y*X produces the identity matrix. Since inv performs the matrix inversion using floating-point computations, in practice Y*X is close to, but not exactly equal to, the identity matrix eye(size(X)).
ans = 3×3
1.0000 0.0000 -0.0000
0 1.0000 -0.0000
0 -0.0000 1.0000
Solve Linear System
Examine why solving a linear system by inverting the matrix using inv(A)*b is inferior to solving it directly using the backslash operator, x = Ab.
Create a random matrix A of order 500 that is constructed so that its condition number, cond(A), is 1e10, and its norm, norm(A), is 1. The exact solution x is a random vector of length 500, and the right side is b = A*x. Thus the system of linear equations is badly conditioned, but consistent.
n = 500; Q = orth(randn(n,n)); d = logspace(0,-10,n); A = Q*diag(d)*Q'; x = randn(n,1); b = A*x;
Solve the linear system A*x = b by inverting the coefficient matrix A. Use tic and toc to get timing information.
tic y = inv(A)*b; t = toc
Find the absolute and residual error of the calculation.
Now, solve the same linear system using the backslash operator .
The backslash calculation is quicker and has less residual error by several orders of magnitude. The fact that err_inv and err_bs are both on the order of 1e-6 simply reflects the condition number of the matrix.
The behavior of this example is typical. Using Ab instead of inv(A)*b is two to three times faster, and produces residuals on the order of machine accuracy relative to the magnitude of the data.
Input Arguments
collapse all
X — Input matrix
square matrix
Input matrix, specified as a square matrix. If X is
badly scaled or nearly singular, then the inv calculation
loses numerical accuracy. Use rcond or cond to check the condition number of
the matrix.
Data Types: single | double
Complex Number Support: Yes
More About
collapse all
Matrix Inverse
A matrix X is invertible
if there exists a matrix Y of the same size such
that XY=YX=In,
where In is
the n-by-n identity matrix.
The matrix Y is called the inverse of X.
A matrix that has no inverse is singular. A square matrix is
singular only when its determinant is exactly zero.
Tips
-
It is seldom necessary to form the explicit inverse
of a matrix. A frequent misuse ofinvarises when
solving the system of linear equations Ax = b.
One way to solve the equation is withx = inv(A)*b.
A better way, from the standpoint of both execution time and numerical
accuracy, is to use the matrix backslash operatorx = Ab.
This produces the solution using Gaussian elimination, without explicitly
forming the inverse. Seemldividefor
further information.
Algorithms
inv performs an LU decomposition of the
input matrix (or an LDL decomposition if the input matrix is Hermitian).
It then uses the results to form a linear system whose solution is
the matrix inverse inv(X). For sparse inputs, inv(X) creates
a sparse identity matrix and uses backslash, Xspeye(size(X)).
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
-
Singular matrix inputs can produce nonfinite values
that differ from MATLAB® results.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
-
Xmust be nonsparse. -
The MATLAB
invfunction prints a warning ifX
is badly scaled or nearly singular. ThegpuArray
invis unable to check for this condition. Take action
to avoid this condition.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2022a: Improved performance when inverting large triangular matrices
The inv function shows improved performance when operating on
large triangular matrices.
For example, inverting a 5,000-by-5,000 upper triangular matrix is about 3.7x
faster than in the previous release.
function timingInv rng default A = randn(5e3); [~,R] = lu(A); tic Y = inv(R); toc end
The approximate execution times are:
R2021b: 1.1 s
R2022a: 0.3 s
The code was timed on a Windows® 10, Intel®
Xeon® CPU W-2133 @ 3.60 GHz test system by calling the
timingInv function.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Inverse function in MATLAB is used to find the inverse of a matrix. Suppose A is a matrix and B is the inverse of a then A*B will be an identity matrix. This function computes the inverse of a square matrix. This is used while solving linear equations. We can compute the inverse of a matrix by passing it to inv().
Syntax:
inv(A)
Parameters:
It takes a matrix as parameter.
Returns:
It returns a matrix which is inverse of input matrix.
Below are some examples which depict how to compute the inverse of a matrix in MATLAB.
Example 1: This example takes a 3×3 matrix as input and computes its inverse using inv() function.
Matlab
A = [1 2 0; 3 1 4; 5 6 7]
inv(A)
Output:
Example 2: Here is another example that takes a 2×2 matrix as input and computes its inverse.
Matlab
Output:
Example 3: This example uses a singular matrix and tries to find its inverse. It will show a warning that the matrix is a singular matrix. Different versions of MATLAB gave a different value of inverse for singular matrix. This is due to the different versions of Math Kernel Library used in different versions of MATLAB.
Matlab
A = [2 4 6;2 0 2;6 8 14]
inv(A)
Output:
warning: matrix singular to machine precision, rcond = 1.34572e-17
Last Updated :
28 Apr, 2021
Like Article
Save Article
Синтаксис
Описание
пример
Y = inv( вычисляет инверсию квадратной матрицы X)X.
-
X^(-1)эквивалентноinv(X). -
x = Abвычисляется по-другому, чемx = inv(A)*bи рекомендуется для решения систем линейных уравнений.
Примеры
свернуть все
Обратная матрица
Вычислить обращение матрицы 3х3.
X = [1 0 2; -1 5 0; 0 3 -9]
X = 3×3
1 0 2
-1 5 0
0 3 -9
Y = 3×3
0.8824 -0.1176 0.1961
0.1765 0.1765 0.0392
0.0588 0.0588 -0.0980
Проверяйте результаты. Идеально, Y*X производит единичную матрицу. Начиная с inv выполняет матричную инверсию с помощью расчетов с плавающей точкой, в практике Y*X близко к, но не точно равен, единичная матрица eye(size(X)).
ans = 3×3
1.0000 0.0000 -0.0000
0 1.0000 -0.0000
0 -0.0000 1.0000
Решение линейной системы
Исследуйте почему, решив линейную систему путем инвертирования матрицы с помощью inv(A)*b является нижним к решению его непосредственно использование оператора обратной косой черты, x = Ab.
Создайте случайный матричный A из порядка 500, который создается так, чтобы его число обусловленности, cond(A), 1e10, и его норма, norm(A), 1. Точное решение x случайный вектор из длины 500, и правой стороной является b = A*x. Таким образом система линейных уравнений плохо обусловливается, но сопоставимая.
n = 500; Q = orth(randn(n,n)); d = logspace(0,-10,n); A = Q*diag(d)*Q'; x = randn(n,1); b = A*x;
Решите линейную систему A*x = b путем инвертирования матрицы коэффициентов A. Используйте tic и toc получить время выполнения.
tic y = inv(A)*b; t = toc
Найдите абсолютную погрешность и остаточную ошибку вычисления.
Теперь решите ту же линейную систему с помощью оператора обратной косой черты .
Вычисление обратной косой чертой быстрее и имеет на несколько порядков меньшую ошибку. Факт, что err_inv и err_bs находятся оба порядка 1e-6 просто отражает число обусловленности матрицы.
Поведение этого примера типично. Используя Ab вместо inv(A)*b в два – три раза быстрее, и производит остаточные значения порядка машинной точности относительно величины данных.
Входные параметры
свернуть все
X — Введите матрицу
квадратная матрица
Введите матрицу в виде квадратной матрицы. Если X плохо масштабируется или почти сингулярный, затем inv вычисление теряет числовую точность. Использование rcond или cond проверять число обусловленности матрицы.
Типы данных: single | double
Поддержка комплексного числа: Да
Больше о
свернуть все
Обращение матриц
Матрица A X является обратимым, если там существует матричный Y одного размера таким образом, что XY=YX=In, где In n– n единичная матрица. Матричный Y называется инверсией X.
Матрица, которая не имеет обратной, сингулярна. Квадратная матрица сингулярна только, когда ее определитель в точности равен нулю.
Советы
-
Редко необходимо сформировать явную инверсию матрицы. Частое неправильное употребление
invвозникает при решении системы линейных уравнений Ax = b. Один способ решить уравнение сx = inv(A)*b. Лучший путь, с точки зрения и времени выполнения и числовой точности, состоит в том, чтобы использовать матричный оператор обратной косой чертыx = Ab. Это производит решение с помощью Исключения Гаусса, явным образом не формируя инверсию. Смотритеmldivideдля получения дополнительной информации.
Алгоритмы
inv выполняет LU-разложение входной матрицы (или разложение LDL, если входная матрица является Эрмитовой). Это затем использует результаты сформировать линейную систему, решение которой является обратной матрицей inv(X). Для разреженных входных параметров, inv(X) создает разреженную единичную матрицу и использует обратную косую черту, Xspeye(size(X)).
Расширенные возможности
Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.
Указания и ограничения по применению:
-
Сингулярные матричные входные параметры могут произвести неличные значения, которые отличаются от MATLAB® результаты.
Основанная на потоке среда
Запустите код в фоновом режиме с помощью MATLAB® backgroundPool или ускорьте код с Parallel Computing Toolbox™ ThreadPool.
Эта функция полностью поддерживает основанные на потоке среды. Для получения дополнительной информации смотрите функции MATLAB Запуска в Основанной на потоке Среде.
Массивы графического процессора
Ускорьте код путем работы графического процессора (GPU) с помощью Parallel Computing Toolbox™.
-
XmustBeNonsparse. -
MATLAB
invфункционируйте распечатывает предупреждение еслиXплохо масштабируется или почти сингулярный.gpuArray
invне может проверять на это условие. Примите меры, чтобы избежать этого условия.
Для получения дополнительной информации смотрите функции MATLAB Запуска на графическом процессоре (Parallel Computing Toolbox).
Распределенные массивы
Большие массивы раздела через объединенную память о вашем кластере с помощью Parallel Computing Toolbox™.
Указания и ограничения по применению:
-
XmustBeNonsparse.
Для получения дополнительной информации смотрите функции MATLAB Запуска с Распределенными Массивами (Parallel Computing Toolbox).
Представлено до R2006a
Syntax
Description
example
Y = inv( computesX)
the inverse of
square matrix X.
-
X^(-1)is equivalent toinv(X). -
x = Abis computed differently
thanx = inv(A)*band is recommended for solving
systems of linear equations.
Examples
collapse all
Inverse Matrix
Compute the inverse of a 3-by-3 matrix.
X = [1 0 2; -1 5 0; 0 3 -9]
X = 3×3
1 0 2
-1 5 0
0 3 -9
Y = 3×3
0.8824 -0.1176 0.1961
0.1765 0.1765 0.0392
0.0588 0.0588 -0.0980
Check the results. Ideally, Y*X produces the identity matrix. Since inv performs the matrix inversion using floating-point computations, in practice Y*X is close to, but not exactly equal to, the identity matrix eye(size(X)).
ans = 3×3
1.0000 0.0000 -0.0000
0 1.0000 -0.0000
0 -0.0000 1.0000
Solve Linear System
Examine why solving a linear system by inverting the matrix using inv(A)*b is inferior to solving it directly using the backslash operator, x = Ab.
Create a random matrix A of order 500 that is constructed so that its condition number, cond(A), is 1e10, and its norm, norm(A), is 1. The exact solution x is a random vector of length 500, and the right side is b = A*x. Thus the system of linear equations is badly conditioned, but consistent.
n = 500; Q = orth(randn(n,n)); d = logspace(0,-10,n); A = Q*diag(d)*Q'; x = randn(n,1); b = A*x;
Solve the linear system A*x = b by inverting the coefficient matrix A. Use tic and toc to get timing information.
tic y = inv(A)*b; t = toc
Find the absolute and residual error of the calculation.
Now, solve the same linear system using the backslash operator .
The backslash calculation is quicker and has less residual error by several orders of magnitude. The fact that err_inv and err_bs are both on the order of 1e-6 simply reflects the condition number of the matrix.
The behavior of this example is typical. Using Ab instead of inv(A)*b is two to three times faster, and produces residuals on the order of machine accuracy relative to the magnitude of the data.
Input Arguments
collapse all
X — Input matrix
square matrix
Input matrix, specified as a square matrix. If X is
badly scaled or nearly singular, then the inv calculation
loses numerical accuracy. Use rcond or cond to check the condition number of
the matrix.
Data Types: single | double
Complex Number Support: Yes
More About
collapse all
Matrix Inverse
A matrix X is invertible
if there exists a matrix Y of the same size such
that XY=YX=In,
where In is
the n-by-n identity matrix.
The matrix Y is called the inverse of X.
A matrix that has no inverse is singular. A square matrix is
singular only when its determinant is exactly zero.
Tips
-
It is seldom necessary to form the explicit inverse
of a matrix. A frequent misuse ofinvarises when
solving the system of linear equations Ax = b.
One way to solve the equation is withx = inv(A)*b.
A better way, from the standpoint of both execution time and numerical
accuracy, is to use the matrix backslash operatorx = Ab.
This produces the solution using Gaussian elimination, without explicitly
forming the inverse. Seemldividefor
further information.
Algorithms
inv performs an LU decomposition of the
input matrix (or an LDL decomposition if the input matrix is Hermitian).
It then uses the results to form a linear system whose solution is
the matrix inverse inv(X). For sparse inputs, inv(X) creates
a sparse identity matrix and uses backslash, Xspeye(size(X)).
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
-
Singular matrix inputs can produce nonfinite values
that differ from MATLAB® results.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For
more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
-
Xmust be nonsparse. -
The MATLAB
invfunction prints a warning ifX
is badly scaled or nearly singular. ThegpuArray
invis unable to check for this condition. Take action
to avoid this condition.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more
information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
expand all
R2022a: Improved performance when inverting large triangular matrices
The inv function shows improved performance when operating on
large triangular matrices.
For example, inverting a 5,000-by-5,000 upper triangular matrix is about 3.7x
faster than in the previous release.
function timingInv rng default A = randn(5e3); [~,R] = lu(A); tic Y = inv(R); toc end
The approximate execution times are:
R2021b: 1.1 s
R2022a: 0.3 s
The code was timed on a Windows® 10, Intel®
Xeon® CPU W-2133 @ 3.60 GHz test system by calling the
timingInv function.
Introduction to Matlab Inverse Function
In Matlab, the Inverse function is obtained by applying the ‘ finverse ’ command. This command returns the value of the given function variable. In finverse f stands for function and after finverse, there will be parameters or argument list inside the brackets depending upon the requirement. if function depends only on one variable then inside bracket there will be one argument which if function (f) and if function depends on two arguments then there will be two parameters inside the brackets.
Syntax:
There are two syntaxes, it varies depending upon variable dependency.
Y = finverse (f)
This command is used if there are multiple variables in the function.
Y = finverse (f, var)
this command is used if there is only one dependent variable in function.
Examples of Matlab Inverse Function
The examples of Matlab Inverse functions are given below:
1. The inverse of cos x
sym x ;
Y ( x ) =
Cos ( x )
z = finverse ( y )
Z ( x ) =
a cos ( x )
| Input program | Command window | Comments |
| >> sym x ; | Input x | |
| >> y ( x ) = cos ( x ) | y(x) = cos ( x ) |
Inverse of ‘ y ’ with respect to independent variable ‘ x’ |
| >> z = finverse ( y ) | Z ( x ) = a cos( x ) |
The output of inverse of ‘ y ’ |
2. Inverse of 1/tan(x)
sym x ;
y ( x ) = 1 / tan ( x )
Y ( x ) =
1 / tan ( x )
z = finverse ( y )
Z ( x ) =
a tan ( 1 / x )</code
| Input program | Command window | Comments |
| >> sym x ; | Input ‘ x ’ | |
| >> y ( x ) = 1 / tan ( x ) | Y ( x ) = 1 / tan ( x ) |
The inverse of ‘ y ’ with respect to independent variable ‘ x ’ |
| >> z = finverse ( y ) | Z ( x ) = a tan ( 1 / x ) |
The output of inverse of ‘ y ’ |
3. The inverse of exponential ( x – 5 y )
syms x y
finverse ( exp ( x - 5 * y) , x )
ans =
5 * y + log ( x )
| Input code | Command window | Comments |
| Syms x y | Input parameters ‘ x ‘and ‘ y ’ | |
| Finverse ( exp ( x – 5 * y ) , x ) | ans =
5*y+log(x) |
The output of a function with respect to two variables |
4. The inverse of log (x-y)
syms x y
finverse ( log ( x – y ), y )
ans =
x – exp ( y )
| Input code | Command window | Comments |
| Syms x y | Input parameters ‘ x ’ and ‘ y ’ | |
| finverse ( log ( x – y ), y ) | ans = x – exp ( y ) |
The output of a function with respect to two variables |
The Inverse of Matrix
To find the inverse of any matrix ‘inv’ command is used. Consider two variables u and v independently. Where v is output var and u is input variable. Then command to find inverse will be v = inv ( u ). Here u^-1 is almost equal to inv(u).
1. Matlab code to find the inverse of the above matrix;
Consider matrix u ;
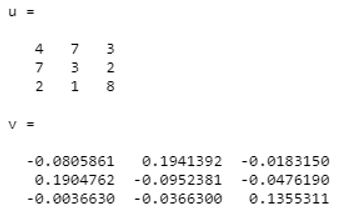
| U = | 4 | 7 | 3 |
| 7 | 3 | 2 | |
| 2 | 1 | 8 |
u=[ 4 7 3; 7 3 2;2 1 8]
v=inv(u)
To obtain the inverse of the matrix there is one condition, the input matrix must be ‘square matrix’. otherwise, it will give the error. let see one example of the odd matrix (rectangular matrix).
2. Matlab code to obtain the inverse
Consider matrix U,
| U = | 6 | 6 | 8 |
| 4 | 4 | 6 | |
| 2 | 3 | 4 | |
| 9 | 1 | 2 |
u=[ 6 4 2 9; 6 4 3 1;8 6 4 2]
v=inv(u)
3. Matlab code to obtain inverse ;
Now consider,
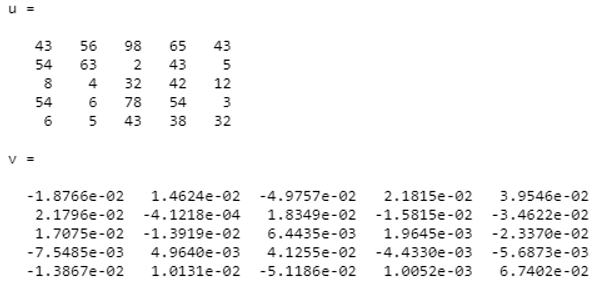
| U = | 43 | 54 | 8 | 54 | 6 |
| 56 | 63 | 4 | 6 | 5 | |
| 98 | 2 | 32 | 78 | 43 | |
| 65 | 43 | 42 | 54 | 38 | |
| 43 | 5 | 12 | 3 | 32 |
u=[43 56 98 65 43;54 63 2 43 5;8 4 32 42 12;54 6 78 54 3;6 5 43 38 32]
v=inv(u)
Conclusion
Function inverse is one of the complex theories in mathematics but by using Matlab we can easily find out Inverse of any function by giving an argument list. One simple syntax is used to find out inverse which is ‘finverse’ followed by the variable specification.
Recommended Articles
This is a guide to Matlab Inverse Function. Here we discuss the inverse of the matrix along with the examples of Matlab Inverse Function. You can also go through our other suggested articles to learn more–
- Matrix in Matlab
- Matlab Commands
- Math Functions in Java
- How to Install MATLAB